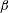1 Introduction
Inertial instability is a robust phenomenon that has been routinely discussed by meteorologists for almost eight decades. It has gradually attracted the attention of oceanographers. It is essentially centrifugal instability formulated in a rotating frame of reference. In the paper by Rayleigh (1916), the condition for centrifugal instability of columnar circular flows (a vortex) was formulated for the first time. It requires
for some range of
![]() $R$
within the flow. In (1.1),
$R$
within the flow. In (1.1),
![]() $L=RU(R)$
is the angular momentum,
$L=RU(R)$
is the angular momentum,
![]() $U(R)$
is the swirl velocity and
$U(R)$
is the swirl velocity and
![]() $R$
is the radial distance from the axis of the flow (see figure 1
a). The instability is manifested as overturning motions in the meridional plane. In a homogeneous fluid, they are, for example, the toroidal vortices observed in Taylor–Couette flow (Drazin & Reid Reference Drazin and Reid1981). The vortices alternate in sign and are stacked upon each other along the axis of the flow (figure 1
b). Rayleigh derived (1.1) with an ‘exchange argument’. He imagined two fluid rings, at different radial distances
$R$
is the radial distance from the axis of the flow (see figure 1
a). The instability is manifested as overturning motions in the meridional plane. In a homogeneous fluid, they are, for example, the toroidal vortices observed in Taylor–Couette flow (Drazin & Reid Reference Drazin and Reid1981). The vortices alternate in sign and are stacked upon each other along the axis of the flow (figure 1
b). Rayleigh derived (1.1) with an ‘exchange argument’. He imagined two fluid rings, at different radial distances
![]() $R$
, exchanging locations. This leads to changes in the swirl velocity of each ring because angular momentum is assumed to be conserved. If the sum total of kinetic energy of the two fluid rings decreases, total energy conservation implies that energy becomes available for secondary motions in the meridional plane if the exchange is within the region where
$R$
, exchanging locations. This leads to changes in the swirl velocity of each ring because angular momentum is assumed to be conserved. If the sum total of kinetic energy of the two fluid rings decreases, total energy conservation implies that energy becomes available for secondary motions in the meridional plane if the exchange is within the region where
![]() $\unicode[STIX]{x1D6F7}<0$
. The amount of energy released by the exchange depends on the distance between the rings in the radial direction. Exchanges of rings purely in the axial direction are energy neutral.
$\unicode[STIX]{x1D6F7}<0$
. The amount of energy released by the exchange depends on the distance between the rings in the radial direction. Exchanges of rings purely in the axial direction are energy neutral.

Figure 1. (a) Overturning motions in an unstable circular vortex with some swirl velocity
![]() $U(R)$
are initially confined to the unstable region where the Rayleigh discriminant
$U(R)$
are initially confined to the unstable region where the Rayleigh discriminant
![]() $\unicode[STIX]{x1D6F7}<0$
. (b) Side view of the vertically stacked streamwise vortices associated with inertial stability in a barotropic vortex. The signs of circulation or streamwise vorticity are alternating, as indicated by ‘
$\unicode[STIX]{x1D6F7}<0$
. (b) Side view of the vertically stacked streamwise vortices associated with inertial stability in a barotropic vortex. The signs of circulation or streamwise vorticity are alternating, as indicated by ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $-$
’. In the absence of any boundaries, at sufficiently high Reynolds number
$-$
’. In the absence of any boundaries, at sufficiently high Reynolds number
![]() $Re$
, these secondary vortices or ‘rolls’ grow in strength and develop nonlinear interactions with their neighbours above and below. This leads to inward and outward motions carrying along angular momentum.
$Re$
, these secondary vortices or ‘rolls’ grow in strength and develop nonlinear interactions with their neighbours above and below. This leads to inward and outward motions carrying along angular momentum.
The ellipticity of the vortices shown in figure 1 increases with increasing Reynolds number
![]() $Re$
. The major axes are along the radial direction, the direction of maximal energy release in the energy argument. If allowed to freely evolve, the stacked vortices act by advection to redistribute angular momentum (see Kloosterziel, Carnevale & Orlandi Reference Kloosterziel, Carnevale and Orlandi2007a
).
$Re$
. The major axes are along the radial direction, the direction of maximal energy release in the energy argument. If allowed to freely evolve, the stacked vortices act by advection to redistribute angular momentum (see Kloosterziel, Carnevale & Orlandi Reference Kloosterziel, Carnevale and Orlandi2007a
).
If the problem is formulated in a frame of reference rotating with constant angular velocity
![]() $\unicode[STIX]{x1D6FA}$
, with the axis of the flow aligned with the rotation vector (see figure 1
a), the angular momentum is
$\unicode[STIX]{x1D6FA}$
, with the axis of the flow aligned with the rotation vector (see figure 1
a), the angular momentum is
![]() $L=R(U+\unicode[STIX]{x1D6FA}R)$
. The criterion is then
$L=R(U+\unicode[STIX]{x1D6FA}R)$
. The criterion is then
![]() $(2U/R+f)Q<0$
, where
$(2U/R+f)Q<0$
, where
![]() $f=2\unicode[STIX]{x1D6FA}$
is the ‘Coriolis’ parameter and
$f=2\unicode[STIX]{x1D6FA}$
is the ‘Coriolis’ parameter and
![]() $Q=R^{-1}\,\text{d}L/\text{d}R=f+\text{d}U/\text{d}R+U/R$
is the absolute vorticity. For large
$Q=R^{-1}\,\text{d}L/\text{d}R=f+\text{d}U/\text{d}R+U/R$
is the absolute vorticity. For large
![]() $R$
, so that
$R$
, so that
![]() $2U/R\ll f$
, the condition for instability of (almost) parallel shear flows is obtained:
$2U/R\ll f$
, the condition for instability of (almost) parallel shear flows is obtained:
![]() $fQ<0$
(see, e.g., Charney Reference Charney and Morel1973).
$fQ<0$
(see, e.g., Charney Reference Charney and Morel1973).
In the exchange argument, conservation of
![]() $L$
is crucial. This presupposes that circular symmetry is maintained (‘symmetric instability’ is often used in the literature instead of inertial instability). However, mathematical analysis indicates that this constraint can be relaxed. For example, Sipp & Jacquin (Reference Sipp and Jacquin2000) generalized the study of Bayly (Reference Bayly1988) to include background rotation and concluded that the instability criterion becomes
$L$
is crucial. This presupposes that circular symmetry is maintained (‘symmetric instability’ is often used in the literature instead of inertial instability). However, mathematical analysis indicates that this constraint can be relaxed. For example, Sipp & Jacquin (Reference Sipp and Jacquin2000) generalized the study of Bayly (Reference Bayly1988) to include background rotation and concluded that the instability criterion becomes
![]() $(U/{\mathcal{R}}+f)Q<0$
for flows with convex non-circular streamlines and local curvature
$(U/{\mathcal{R}}+f)Q<0$
for flows with convex non-circular streamlines and local curvature
![]() ${\mathcal{R}}$
.
${\mathcal{R}}$
.
It is not difficult to include stratification in the exchange argument, but then potential energy changes have to be taken into account, while
![]() $U$
can also vary along the axis of rotation (baroclinic flows). It is then found that the absolute vorticity
$U$
can also vary along the axis of rotation (baroclinic flows). It is then found that the absolute vorticity
![]() $Q$
just needs to be replaced by the Ertel potential vorticity
$Q$
just needs to be replaced by the Ertel potential vorticity
![]() $Q_{E}$
. This was noted by Fjørtoft (Reference Fjørtoft1950), but the studies of Ertel (Reference Ertel1942a
,Reference Ertel
b
) were not widely known then. Hoskins (Reference Hoskins1974) rediscovered the instability criterion
$Q_{E}$
. This was noted by Fjørtoft (Reference Fjørtoft1950), but the studies of Ertel (Reference Ertel1942a
,Reference Ertel
b
) were not widely known then. Hoskins (Reference Hoskins1974) rediscovered the instability criterion
![]() $fQ_{E}<0$
via normal-mode analysis. Potential vorticity such that
$fQ_{E}<0$
via normal-mode analysis. Potential vorticity such that
![]() $fQ_{E}<0$
in some region is often referred to as ‘anomalous’ vorticity in the literature and is considered to be an indicator that inertial instability may be triggered. Flows with
$fQ_{E}<0$
in some region is often referred to as ‘anomalous’ vorticity in the literature and is considered to be an indicator that inertial instability may be triggered. Flows with
![]() $Q_{E}\approx 0$
are said to be ‘near neutral stability’, which is oftentimes seen as a sign that inertial instability has occurred.
$Q_{E}\approx 0$
are said to be ‘near neutral stability’, which is oftentimes seen as a sign that inertial instability has occurred.
The motivation for this paper is the following. One can imagine that winds near the equator impart westward momentum to the upper ocean. After some time, strong vertical shear would have built up, with maximal retrograde velocity at the surface and with
![]() $\text{d}L/\text{d}R<0$
over some depth range below the surface. The condition for instability (1.1) is met at the equator when the westward velocity drops a mere
$\text{d}L/\text{d}R<0$
over some depth range below the surface. The condition for instability (1.1) is met at the equator when the westward velocity drops a mere
![]() $1.5~\text{cm}~\text{s}^{-1}$
over 100 m depth when
$1.5~\text{cm}~\text{s}^{-1}$
over 100 m depth when
![]() $\unicode[STIX]{x1D6FA}$
is the Earth’s angular velocity (
$\unicode[STIX]{x1D6FA}$
is the Earth’s angular velocity (
![]() $\unicode[STIX]{x1D6FA}=7.26\times 10^{-5}~\text{rad}~\text{s}^{-1}$
) and it is assumed that the upper layer is not stratified. This estimate follows from setting
$\unicode[STIX]{x1D6FA}=7.26\times 10^{-5}~\text{rad}~\text{s}^{-1}$
) and it is assumed that the upper layer is not stratified. This estimate follows from setting
![]() $\text{d}U/\text{d}R\lesssim -2\unicode[STIX]{x1D6FA}$
so that
$\text{d}U/\text{d}R\lesssim -2\unicode[STIX]{x1D6FA}$
so that
![]() $Q<0$
for large
$Q<0$
for large
![]() $R$
. Without stratification, inertial instability implies motions as sketched in figure 2. Given the scarcity of detailed studies of near-equatorial inertial instability incorporating the full Coriolis force, in this exploratory study we survey just the homogeneous case without the complicating influence of stratification.
$R$
. Without stratification, inertial instability implies motions as sketched in figure 2. Given the scarcity of detailed studies of near-equatorial inertial instability incorporating the full Coriolis force, in this exploratory study we survey just the homogeneous case without the complicating influence of stratification.

Figure 2. Schematic showing a possible scenario for the initial growth of the instability of a sufficiently swift westward flowing surface-confined jet in the dynamics with the full Coriolis force. (a) Alternating vortices with their major axis aligned with the unstable direction perpendicular to the lines of constant distance
![]() $R$
from the axis of rotation. Here,
$R$
from the axis of rotation. Here,
![]() $R_{0}$
is the planetary radius,
$R_{0}$
is the planetary radius,
![]() $\unicode[STIX]{x1D719}$
is the latitude, and
$\unicode[STIX]{x1D719}$
is the latitude, and
![]() $\unicode[STIX]{x1D6FA}_{\bot }=\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D6FA}_{\bot }=\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D6FA}_{\Vert }=\unicode[STIX]{x1D6FA}\cos \unicode[STIX]{x1D719}$
are the components of
$\unicode[STIX]{x1D6FA}_{\Vert }=\unicode[STIX]{x1D6FA}\cos \unicode[STIX]{x1D719}$
are the components of
![]() $\unicode[STIX]{x1D734}$
normal and tangent to the surface of the sphere. (b) The same as seen in (a) but in the local Cartesian
$\unicode[STIX]{x1D734}$
normal and tangent to the surface of the sphere. (b) The same as seen in (a) but in the local Cartesian
![]() $\{x,y,z\}$
coordinate system with corresponding unit vectors
$\{x,y,z\}$
coordinate system with corresponding unit vectors
![]() $\{\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\}$
. Lines of constant distance
$\{\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\}$
. Lines of constant distance
![]() $R$
from the rotation axis appear as parabolas,
$R$
from the rotation axis appear as parabolas,
![]() $R\approx R_{0}+z-y^{2}/2R_{0}$
, according to (2.6). The equator is at
$R\approx R_{0}+z-y^{2}/2R_{0}$
, according to (2.6). The equator is at
![]() $y=0$
and the surface is at
$y=0$
and the surface is at
![]() $z=0$
. A westward flow is indicated with
$z=0$
. A westward flow is indicated with
![]() $U\boldsymbol{i}$
. Eastward is the direction of increasing
$U\boldsymbol{i}$
. Eastward is the direction of increasing
![]() $x$
.
$x$
.
The equations of motion governing the evolution in spherical coordinates are briefly discussed in § 2. The equations are simplified by assuming that all motions are confined to an outer thin fluid layer (thin compared with the planet radius
![]() $R_{0}$
) and vanish outside a narrow latitudinal region about the equator. The rotation vector
$R_{0}$
) and vanish outside a narrow latitudinal region about the equator. The rotation vector
![]() $\unicode[STIX]{x1D734}$
is approximated near the equator by the ‘traditional’
$\unicode[STIX]{x1D734}$
is approximated near the equator by the ‘traditional’
![]() $\unicode[STIX]{x1D6FD}$
-plane component
$\unicode[STIX]{x1D6FD}$
-plane component
![]() $\unicode[STIX]{x1D6FA}_{\bot }=\unicode[STIX]{x1D6FD}y$
normal to the sphere (with
$\unicode[STIX]{x1D6FA}_{\bot }=\unicode[STIX]{x1D6FD}y$
normal to the sphere (with
![]() $y$
the distance from the equator) and the ‘non-traditional’ component
$y$
the distance from the equator) and the ‘non-traditional’ component
![]() $\unicode[STIX]{x1D6FA}_{\Vert }=\unicode[STIX]{x1D6FA}$
tangent to the sphere (see figure 2). With both components, the full Coriolis dynamics is expected to be well approximated in the vicinity of the equator.
$\unicode[STIX]{x1D6FA}_{\Vert }=\unicode[STIX]{x1D6FA}$
tangent to the sphere (see figure 2). With both components, the full Coriolis dynamics is expected to be well approximated in the vicinity of the equator.
In § 2.1, we present a simple but instructive Lagrangian derivation of the (linear) stability criterion for ideal fluids which follows with the simplified set of equations and indicates the relation with Rayleigh’s energy argument. Assuming no stratification, in § 2.2 this yields a near-equatorial approximation of the criterion (1.1). In § 2.3, we introduce the flow we investigate: at the surface it has the Gaussian velocity profile
![]() $U=U_{0}\exp (-y^{2}/2L^{2})$
, with
$U=U_{0}\exp (-y^{2}/2L^{2})$
, with
![]() $U_{0}$
the peak velocity amplitude at the equator (
$U_{0}$
the peak velocity amplitude at the equator (
![]() $y=0$
) and
$y=0$
) and
![]() $L$
a length scale defining the latitudinal width of the flow. With the full Coriolis force, this flow has to decay with depth
$L$
a length scale defining the latitudinal width of the flow. With the full Coriolis force, this flow has to decay with depth
![]() $z$
in order to be steady in an unstratified environment. With the traditional
$z$
in order to be steady in an unstratified environment. With the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane approximation, a steady flow has to be depth-independent.
$\unicode[STIX]{x1D6FD}$
-plane approximation, a steady flow has to be depth-independent.
In § 2.4, we briefly outline the theory that exists regarding the so-called ‘scale-selection’ problem, and in § 2.5, we sketch how to predict the outcome of the instability in the high-Reynolds-number limit, after the complicated turbulent nonlinear phase of the instability has disappeared.
In § 3, the numerical code is described. Results from linearized simulations are presented in § 4, with precise new results concerning the fastest growing normal modes in both the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane and full Coriolis force dynamics. We determine their spatial structure and the variation of rates of growth and vertical/horizontal length scales with Reynolds number
$\unicode[STIX]{x1D6FD}$
-plane and full Coriolis force dynamics. We determine their spatial structure and the variation of rates of growth and vertical/horizontal length scales with Reynolds number
![]() $Re$
. In § 5, we present high-resolution simulations of the turbulent nonlinear evolutions that result in the full Coriolis force dynamics when the instability unfolds at high Reynolds numbers
$Re$
. In § 5, we present high-resolution simulations of the turbulent nonlinear evolutions that result in the full Coriolis force dynamics when the instability unfolds at high Reynolds numbers
![]() $Re$
and compare the outcome with the prediction from § 2.5.
$Re$
and compare the outcome with the prediction from § 2.5.
In § 6, we summarize the main results and indicate why the full Coriolis force dynamics instead of the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane dynamics could be important when considering near-equatorial inertial instability in the presence of realistic stably stratified environments.
$\unicode[STIX]{x1D6FD}$
-plane dynamics could be important when considering near-equatorial inertial instability in the presence of realistic stably stratified environments.
2 Equations of motion, approximations, theory and model flows
For an incompressible fluid, in a frame rotating with constant angular velocity, the Euler equations of motion in the Boussinesq approximation are
Here,
![]() $\text{D}/\text{D}_{t}$
is the material time derivative,
$\text{D}/\text{D}_{t}$
is the material time derivative,
![]() $\boldsymbol{u}$
is the three-dimensional velocity vector,
$\boldsymbol{u}$
is the three-dimensional velocity vector,
![]() $\unicode[STIX]{x1D6F7}$
is the geopotential (the sum of the gravitational potential and the centrifugal potential),
$\unicode[STIX]{x1D6F7}$
is the geopotential (the sum of the gravitational potential and the centrifugal potential),
![]() $p$
is the pressure and
$p$
is the pressure and
![]() $\unicode[STIX]{x1D70C}$
is the density, with
$\unicode[STIX]{x1D70C}$
is the density, with
![]() $\unicode[STIX]{x1D70C}_{0}$
a constant reference density and
$\unicode[STIX]{x1D70C}_{0}$
a constant reference density and
![]() $\unicode[STIX]{x1D734}$
the angular velocity vector. The second term in (2.1a
) is the Coriolis force brought to the left-hand side. Considering the motions of a fluid on a spherical planet, the equations of motion are
$\unicode[STIX]{x1D734}$
the angular velocity vector. The second term in (2.1a
) is the Coriolis force brought to the left-hand side. Considering the motions of a fluid on a spherical planet, the equations of motion are
(Veronis Reference Veronis1963; Gill Reference Gill1982). Here,
![]() $\unicode[STIX]{x1D703}$
is the longitude (increasing eastward),
$\unicode[STIX]{x1D703}$
is the longitude (increasing eastward),
![]() $\unicode[STIX]{x1D719}$
is the latitude (increasing northward with
$\unicode[STIX]{x1D719}$
is the latitude (increasing northward with
![]() $\unicode[STIX]{x1D719}=0$
at the equator),
$\unicode[STIX]{x1D719}=0$
at the equator),
![]() $r$
is the radial distance from the centre,
$r$
is the radial distance from the centre,
![]() $u$
is the eastward velocity,
$u$
is the eastward velocity,
![]() $v$
is the northward velocity and
$v$
is the northward velocity and
![]() $w$
is the velocity along increasing
$w$
is the velocity along increasing
![]() $r$
, and as usual
$r$
, and as usual
![]() $\unicode[STIX]{x1D734}$
is parallel to the axis of the planet, running from the South Pole to the North Pole (see figure 2
a). For consistency, geopotential surfaces must also be spherical, i.e.
$\unicode[STIX]{x1D734}$
is parallel to the axis of the planet, running from the South Pole to the North Pole (see figure 2
a). For consistency, geopotential surfaces must also be spherical, i.e.
![]() $\unicode[STIX]{x1D6F7}=gr$
, where
$\unicode[STIX]{x1D6F7}=gr$
, where
![]() $g$
in (2.2c
) is the gravitational constant (see Gerkema et al. (Reference Gerkema, Zimmerman, Maas and van Haren2008) and references therein).
$g$
in (2.2c
) is the gravitational constant (see Gerkema et al. (Reference Gerkema, Zimmerman, Maas and van Haren2008) and references therein).
The Coriolis force terms contain
![]() $\unicode[STIX]{x1D6FA}_{\bot }=\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D6FA}_{\bot }=\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D6FA}_{\Vert }=\unicode[STIX]{x1D6FA}\cos \unicode[STIX]{x1D719}$
, which are the components of
$\unicode[STIX]{x1D6FA}_{\Vert }=\unicode[STIX]{x1D6FA}\cos \unicode[STIX]{x1D719}$
, which are the components of
![]() $\unicode[STIX]{x1D734}$
normal to the sphere and tangent to the sphere respectively (see figure 2
a). The component
$\unicode[STIX]{x1D734}$
normal to the sphere and tangent to the sphere respectively (see figure 2
a). The component
![]() $\unicode[STIX]{x1D6FA}_{\Vert }$
of the rotation vector is often neglected, and its contribution in (2.2a
) and (2.2c
) is indicated by ‘NT’ (‘non-traditional’). In near-equatorial regions where
$\unicode[STIX]{x1D6FA}_{\Vert }$
of the rotation vector is often neglected, and its contribution in (2.2a
) and (2.2c
) is indicated by ‘NT’ (‘non-traditional’). In near-equatorial regions where
![]() $\unicode[STIX]{x1D6FA}_{\bot }$
is small compared with
$\unicode[STIX]{x1D6FA}_{\bot }$
is small compared with
![]() $\unicode[STIX]{x1D6FA}_{\Vert }$
, it is not a priori obvious that discarding
$\unicode[STIX]{x1D6FA}_{\Vert }$
, it is not a priori obvious that discarding
![]() $\unicode[STIX]{x1D6FA}_{\Vert }$
is warranted unless further physical arguments are provided.
$\unicode[STIX]{x1D6FA}_{\Vert }$
is warranted unless further physical arguments are provided.
In view of the cumbersome nature of (2.2a
)–(2.2c
), it is desirable to simplify them. How to do this properly has been widely discussed since the 1960s (see Gerkema et al. (Reference Gerkema, Zimmerman, Maas and van Haren2008), Dellar (Reference Dellar2011) and references therein). First, if one assumes that the fluid motions on a planet with radius
![]() $R_{0}$
are contained in an outer ‘thin shell’ with thickness
$R_{0}$
are contained in an outer ‘thin shell’ with thickness
![]() $H$
(see figure 2) and
$H$
(see figure 2) and
![]() $H/R_{0}\ll 1$
, away from the polar regions, the curvature terms
$H/R_{0}\ll 1$
, away from the polar regions, the curvature terms
![]() $(\cdots )/r$
on the left-hand sides of (2.2a
)–(2.2c
) are
$(\cdots )/r$
on the left-hand sides of (2.2a
)–(2.2c
) are
![]() $O({\mathcal{U}}/2\unicode[STIX]{x1D6FA}R_{0})\times$
Coriolis forces, with
$O({\mathcal{U}}/2\unicode[STIX]{x1D6FA}R_{0})\times$
Coriolis forces, with
![]() ${\mathcal{U}}$
any reasonable velocity scale. If
${\mathcal{U}}$
any reasonable velocity scale. If
![]() ${\mathcal{U}}\ll \unicode[STIX]{x1D6FA}R_{0}$
, the curvature terms can be discarded (on the Earth,
${\mathcal{U}}\ll \unicode[STIX]{x1D6FA}R_{0}$
, the curvature terms can be discarded (on the Earth,
![]() $\unicode[STIX]{x1D6FA}R_{0}\approx 500~\text{m}~\text{s}^{-1}$
). Second, if it is assumed that the phenomena of interest occur within a narrow latitudinal band about a reference latitude
$\unicode[STIX]{x1D6FA}R_{0}\approx 500~\text{m}~\text{s}^{-1}$
). Second, if it is assumed that the phenomena of interest occur within a narrow latitudinal band about a reference latitude
![]() $\unicode[STIX]{x1D719}_{0}$
, further simplifications follow by introducing local Cartesian coordinates
$\unicode[STIX]{x1D719}_{0}$
, further simplifications follow by introducing local Cartesian coordinates
![]() $\{x,y,z\}$
with corresponding unit vectors
$\{x,y,z\}$
with corresponding unit vectors
![]() $\{\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\}$
(see figure 2
b). With latitude
$\{\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\}$
(see figure 2
b). With latitude
![]() $y=R_{0}(\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{0})$
(positive northward),
$y=R_{0}(\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{0})$
(positive northward),
![]() $\unicode[STIX]{x1D6FA}_{\bot }$
and
$\unicode[STIX]{x1D6FA}_{\bot }$
and
![]() $\unicode[STIX]{x1D6FA}_{\Vert }$
are approximated by truncated Taylor series of
$\unicode[STIX]{x1D6FA}_{\Vert }$
are approximated by truncated Taylor series of
![]() $\sin (\unicode[STIX]{x1D719}_{0}+y/R_{0})$
and
$\sin (\unicode[STIX]{x1D719}_{0}+y/R_{0})$
and
![]() $\cos (\unicode[STIX]{x1D719}_{0}+y/R_{0})$
in the small quantity
$\cos (\unicode[STIX]{x1D719}_{0}+y/R_{0})$
in the small quantity
![]() $y/R_{0}$
. The remaining two coordinates are
$y/R_{0}$
. The remaining two coordinates are
![]() $x=(R_{0}\cos \unicode[STIX]{x1D719}_{0})\unicode[STIX]{x1D703}$
(positive eastward) and
$x=(R_{0}\cos \unicode[STIX]{x1D719}_{0})\unicode[STIX]{x1D703}$
(positive eastward) and
![]() $z=r-R_{0}$
(negative with increasing depth). To lowest order in small quantities, (2.1) is recovered with the velocity vector
$z=r-R_{0}$
(negative with increasing depth). To lowest order in small quantities, (2.1) is recovered with the velocity vector
![]() $\boldsymbol{u}=u\boldsymbol{i}+v\boldsymbol{j}+w\boldsymbol{k}$
,
$\boldsymbol{u}=u\boldsymbol{i}+v\boldsymbol{j}+w\boldsymbol{k}$
,
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}=g\boldsymbol{k}$
and the material derivative
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}=g\boldsymbol{k}$
and the material derivative
![]() $\text{D}_{t}=\unicode[STIX]{x2202}_{t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
, with
$\text{D}_{t}=\unicode[STIX]{x2202}_{t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
, with
![]() $\unicode[STIX]{x1D735}=\boldsymbol{i}\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x+\boldsymbol{j}\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y+\boldsymbol{k}\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z$
, but with the important difference that
$\unicode[STIX]{x1D735}=\boldsymbol{i}\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x+\boldsymbol{j}\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y+\boldsymbol{k}\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z$
, but with the important difference that
![]() $2\unicode[STIX]{x1D734}=\tilde{f}\boldsymbol{j}+f\boldsymbol{k}$
, with
$2\unicode[STIX]{x1D734}=\tilde{f}\boldsymbol{j}+f\boldsymbol{k}$
, with
(see, e.g., LeBlond & Mysak Reference LeBlond and Mysak1978). The seemingly ad hoc neglect of the variation of
![]() $\unicode[STIX]{x1D6FA}_{\Vert }$
with latitude
$\unicode[STIX]{x1D6FA}_{\Vert }$
with latitude
![]() $y$
is rooted in the fact that, at this level of approximation,
$y$
is rooted in the fact that, at this level of approximation,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D734}=0$
. This is desirable because the equations then inherit angular momentum and potential vorticity conservation laws from (2.2a
)–(2.2c
) (see Grimshaw Reference Grimshaw1975). Further refinements with
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D734}=0$
. This is desirable because the equations then inherit angular momentum and potential vorticity conservation laws from (2.2a
)–(2.2c
) (see Grimshaw Reference Grimshaw1975). Further refinements with
![]() $\unicode[STIX]{x1D6FA}_{\bot }$
and
$\unicode[STIX]{x1D6FA}_{\bot }$
and
![]() $\unicode[STIX]{x1D6FA}_{\Vert }$
varying with latitude
$\unicode[STIX]{x1D6FA}_{\Vert }$
varying with latitude
![]() $y$
and depth
$y$
and depth
![]() $z$
are discussed by Dellar (Reference Dellar2011) and Tort et al. (Reference Tort, Dubos, Bouchut and Zeitlin2014). If
$z$
are discussed by Dellar (Reference Dellar2011) and Tort et al. (Reference Tort, Dubos, Bouchut and Zeitlin2014). If
![]() $\unicode[STIX]{x1D6FA}_{\Vert }$
is ignored (
$\unicode[STIX]{x1D6FA}_{\Vert }$
is ignored (
![]() $\tilde{f}=0$
), the traditional
$\tilde{f}=0$
), the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane approximation follows; if the latitudinal variation of
$\unicode[STIX]{x1D6FD}$
-plane approximation follows; if the latitudinal variation of
![]() $f$
with
$f$
with
![]() $\unicode[STIX]{x1D6FD}y$
is neglected, the midlatitude
$\unicode[STIX]{x1D6FD}y$
is neglected, the midlatitude
![]() $f$
-plane approximation follows.
$f$
-plane approximation follows.
The non-traditional near-equatorial
![]() $\unicode[STIX]{x1D6FD}$
-plane approximation (NTA) follows by setting
$\unicode[STIX]{x1D6FD}$
-plane approximation (NTA) follows by setting
![]() $\unicode[STIX]{x1D719}_{0}=0$
, so that according to (2.4),
$\unicode[STIX]{x1D719}_{0}=0$
, so that according to (2.4),
![]() $f=\unicode[STIX]{x1D6FD}y$
,
$f=\unicode[STIX]{x1D6FD}y$
,
![]() $\tilde{f}=2\unicode[STIX]{x1D6FA}$
and
$\tilde{f}=2\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D6FD}=2\unicode[STIX]{x1D6FA}/R_{0}$
. The equations approximating the full Coriolis force dynamics near the equator are then
$\unicode[STIX]{x1D6FD}=2\unicode[STIX]{x1D6FA}/R_{0}$
. The equations approximating the full Coriolis force dynamics near the equator are then
plus (2.1b
) and (2.1c
). The traditional approximation (from here on indicated by ‘TA’) is obtained by dropping the Coriolis terms indicated by NTA in (2.5a
), (2.5c
), which are the approximations of the NT terms in (2.2a
), (2.2c
). With the TA, the properties of the usual
![]() $f$
-plane dynamics follow: only horizontal motions are affected by rotation, with the Coriolis force
$f$
-plane dynamics follow: only horizontal motions are affected by rotation, with the Coriolis force
![]() $\unicode[STIX]{x1D6FD}y\boldsymbol{k}\times \boldsymbol{u}$
being to the right with respect to the velocity direction in the Northern Hemisphere and to the left in the Southern Hemisphere (
$\unicode[STIX]{x1D6FD}y\boldsymbol{k}\times \boldsymbol{u}$
being to the right with respect to the velocity direction in the Northern Hemisphere and to the left in the Southern Hemisphere (
![]() $y>0$
and
$y>0$
and
![]() $y<0$
respectively). If the NTA terms are retained, in addition to the forces in the TA, vertical velocities induce a zonal force and zonal velocities a vertical force via
$y<0$
respectively). If the NTA terms are retained, in addition to the forces in the TA, vertical velocities induce a zonal force and zonal velocities a vertical force via
![]() $2\unicode[STIX]{x1D6FA}\boldsymbol{j}\times \boldsymbol{u}$
.
$2\unicode[STIX]{x1D6FA}\boldsymbol{j}\times \boldsymbol{u}$
.
The radial distance
![]() $R$
(figure 2
a) from the axis of rotation plays an important role below and will appear in the Cartesian coordinates as a parabola because
$R$
(figure 2
a) from the axis of rotation plays an important role below and will appear in the Cartesian coordinates as a parabola because
What was a straight line (
![]() $R=\text{const.}$
) in figure 2(a) appears curved in the local Cartesian coordinate system in figure 2(b).
$R=\text{const.}$
) in figure 2(a) appears curved in the local Cartesian coordinate system in figure 2(b).
If it is assumed that at all times in the along flow direction
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x=0$
, then (2.5a
) implies conservation of geostrophic or absolute momentum
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x=0$
, then (2.5a
) implies conservation of geostrophic or absolute momentum
![]() $m$
,
$m$
,
and
![]() $R$
approximated by (2.6). This conservation law is equivalent to the conservation of angular moment
$R$
approximated by (2.6). This conservation law is equivalent to the conservation of angular moment
![]() $l$
that follows from (2.2a
) when
$l$
that follows from (2.2a
) when
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
(see, e.g., Phillips Reference Phillips1966),
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
(see, e.g., Phillips Reference Phillips1966),
However,
if
![]() $|R-R_{0}|\ll R_{0}$
, or
$|R-R_{0}|\ll R_{0}$
, or
![]() $|z|/R_{0}\ll 1$
,
$|z|/R_{0}\ll 1$
,
![]() $(|y|/R_{0})^{2}\ll 1$
in (2.6) and, apart from a constant, the absolute momentum
$(|y|/R_{0})^{2}\ll 1$
in (2.6) and, apart from a constant, the absolute momentum
![]() $m\approx l/R_{0}$
.
$m\approx l/R_{0}$
.
Numerous studies exist where the symmetry condition
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x=0$
or
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x=0$
or
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
is relaxed, mainly in the context of traditional
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
is relaxed, mainly in the context of traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane or midlatitude
$\unicode[STIX]{x1D6FD}$
-plane or midlatitude
![]() $f$
-plane dynamics. Often, depth-independent (barotropic) flows are considered in fluids with constant buoyancy frequency
$f$
-plane dynamics. Often, depth-independent (barotropic) flows are considered in fluids with constant buoyancy frequency
![]() $N$
. The choice of constant
$N$
. The choice of constant
![]() $N$
is convenient because then the linear stability can be investigated with normal-mode analysis of perturbations proportional to
$N$
is convenient because then the linear stability can be investigated with normal-mode analysis of perturbations proportional to
![]() $\exp (\text{i}(k_{x}x+k_{z}z))$
. Early studies examining the competition between symmetric (inertial) instability and ‘asymmetric’ instability (
$\exp (\text{i}(k_{x}x+k_{z}z))$
. Early studies examining the competition between symmetric (inertial) instability and ‘asymmetric’ instability (
![]() $k_{x}\neq 0$
) are, for example, those of Boyd & Christidis (Reference Boyd and Christidis1982) and Dunkerton (Reference Dunkerton1983), who considered uniform shear flows
$k_{x}\neq 0$
) are, for example, those of Boyd & Christidis (Reference Boyd and Christidis1982) and Dunkerton (Reference Dunkerton1983), who considered uniform shear flows
![]() $U(y)=U_{0}+\unicode[STIX]{x1D6EC}y$
on the traditional equatorial
$U(y)=U_{0}+\unicode[STIX]{x1D6EC}y$
on the traditional equatorial
![]() $\unicode[STIX]{x1D6FD}$
-plane. Analysis of arbitrary parallel shear flows
$\unicode[STIX]{x1D6FD}$
-plane. Analysis of arbitrary parallel shear flows
![]() $U(y)$
was carried by Griffiths (Reference Griffiths2008a
). For circular flows, see Billant & Gallaire (Reference Billant and Gallaire2005). If scale-dependent damping via viscosity is taken into account, an intricate interplay between the scales of the perturbations, the Reynolds number
$U(y)$
was carried by Griffiths (Reference Griffiths2008a
). For circular flows, see Billant & Gallaire (Reference Billant and Gallaire2005). If scale-dependent damping via viscosity is taken into account, an intricate interplay between the scales of the perturbations, the Reynolds number
![]() $Re$
and the stratification result. The ensuing ‘scale-selection’ problem is briefly touched upon in § 2.4 below. However, it appears that generally in the inviscid limit, for very large vertical wavenumbers
$Re$
and the stratification result. The ensuing ‘scale-selection’ problem is briefly touched upon in § 2.4 below. However, it appears that generally in the inviscid limit, for very large vertical wavenumbers
![]() $k_{z}$
, pure inertial instability (
$k_{z}$
, pure inertial instability (
![]() $k_{x}=0$
) amplifies more rapidly than asymmetric inertial instability due to zonally slowly varying perturbations (small
$k_{x}=0$
) amplifies more rapidly than asymmetric inertial instability due to zonally slowly varying perturbations (small
![]() $k_{x}$
). Nonlinear numerical experiments show that if the growth rates of the symmetric and asymmetric modes are comparable, at high
$k_{x}$
). Nonlinear numerical experiments show that if the growth rates of the symmetric and asymmetric modes are comparable, at high
![]() $Re$
, extremely entangled flows develop (see Carnevale et al.
Reference Carnevale, Kloosterziel, Orlandi and van Sommeren2011; Carnevale, Kloosterziel & Orlandi Reference Carnevale, Kloosterziel and Orlandi2013; Ribstein, Plougonven & Zeitlin Reference Ribstein, Plougonven and Zeitlin2014).
$Re$
, extremely entangled flows develop (see Carnevale et al.
Reference Carnevale, Kloosterziel, Orlandi and van Sommeren2011; Carnevale, Kloosterziel & Orlandi Reference Carnevale, Kloosterziel and Orlandi2013; Ribstein, Plougonven & Zeitlin Reference Ribstein, Plougonven and Zeitlin2014).
A small body of work also exists that considers the stability of non-parallel flows
![]() $U(x,y)$
(Dunkerton Reference Dunkerton1993; Clark & Haynes Reference Clark and Haynes1996) and time-dependent flows
$U(x,y)$
(Dunkerton Reference Dunkerton1993; Clark & Haynes Reference Clark and Haynes1996) and time-dependent flows
![]() $U(y,t)$
(D’Orgeville & Hua Reference D’Orgeville and Hua2005; Natarov & Richards Reference Natarov and Richards2009). Space limitations prohibit going into any further details, but the recent study by Tort, Ribstein & Zeitlin (Reference Tort, Ribstein and Zeitlin2016) warrants a mention. In a first of its kind, they performed a linear stability analysis of a jet in a continuously stratified environment on the ‘non-traditional’ midlatitude
$U(y,t)$
(D’Orgeville & Hua Reference D’Orgeville and Hua2005; Natarov & Richards Reference Natarov and Richards2009). Space limitations prohibit going into any further details, but the recent study by Tort, Ribstein & Zeitlin (Reference Tort, Ribstein and Zeitlin2016) warrants a mention. In a first of its kind, they performed a linear stability analysis of a jet in a continuously stratified environment on the ‘non-traditional’ midlatitude
![]() $f$
-plane. They considered the dynamics retaining the non-traditional component of the rotation vector with constant
$f$
-plane. They considered the dynamics retaining the non-traditional component of the rotation vector with constant
![]() $\tilde{f}$
as in (2.4) as well as the traditional constant Coriolis parameter
$\tilde{f}$
as in (2.4) as well as the traditional constant Coriolis parameter
![]() $f$
. They reported on the effect of stratification (none/weak/strong), contrasted the TA results with NTA results, hydrostatic with non-hydrostatic results and rates of growth of instabilities for both zonally symmetric perturbations (
$f$
. They reported on the effect of stratification (none/weak/strong), contrasted the TA results with NTA results, hydrostatic with non-hydrostatic results and rates of growth of instabilities for both zonally symmetric perturbations (
![]() $k_{x}=0$
) and zonally varying perturbations. They concluded that with both the TA and NTA, for sufficiently large vertical wavenumber
$k_{x}=0$
) and zonally varying perturbations. They concluded that with both the TA and NTA, for sufficiently large vertical wavenumber
![]() $k_{z}$
, the symmetric instability has the fastest rate of growth. In addition, Tort et al. (Reference Tort, Ribstein and Zeitlin2016) report that symmetric and asymmetric instabilities can have significantly higher rates of growth in the NTA dynamics than with the TA.
$k_{z}$
, the symmetric instability has the fastest rate of growth. In addition, Tort et al. (Reference Tort, Ribstein and Zeitlin2016) report that symmetric and asymmetric instabilities can have significantly higher rates of growth in the NTA dynamics than with the TA.
2.1 General linear theory à la Solberg
In this exploratory study of near-equatorial inertial instability, we shall only consider the symmetric inertial instability. As noted above, this implies conservation of momentum. Much insight is obtained with the heuristic argument of Solberg (Reference Solberg1936), which is easily adapted to our system (the ‘parcel method’ of Solberg in meteorology is further discussed in Holton (Reference Holton1992)). It is convenient to write the equations (2.5b,c
) for the meridional motions
![]() $\boldsymbol{v}=v\boldsymbol{j}+w\boldsymbol{k}$
as
$\boldsymbol{v}=v\boldsymbol{j}+w\boldsymbol{k}$
as
(a constant term has been absorbed by the pressure). For a steady zonal flow
![]() $\boldsymbol{u}=U\boldsymbol{i}$
, we will indicate the associated momentum with
$\boldsymbol{u}=U\boldsymbol{i}$
, we will indicate the associated momentum with
The balance is described by
(with
![]() $P$
the pressure field and
$P$
the pressure field and
![]() $\bar{\unicode[STIX]{x1D70C}}$
the density field), and the thermal wind balance is
$\bar{\unicode[STIX]{x1D70C}}$
the density field), and the thermal wind balance is
Solberg’s argument is a Lagrangian argument with the velocity
![]() $\boldsymbol{v}$
seen as the time derivative of a meridional displacement vector
$\boldsymbol{v}$
seen as the time derivative of a meridional displacement vector
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{x}(t)$
, which we write as
$\unicode[STIX]{x1D6FF}\boldsymbol{x}(t)$
, which we write as
![]() $\boldsymbol{v}=\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FF}\boldsymbol{x}$
. Under small displacements, to lowest order, conservation of momentum and density are
$\boldsymbol{v}=\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FF}\boldsymbol{x}$
. Under small displacements, to lowest order, conservation of momentum and density are
with
![]() $\unicode[STIX]{x1D6FF}m$
and
$\unicode[STIX]{x1D6FF}m$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}$
the local perturbations. If we denote the pressure perturbation with respect to the balance pressure
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}$
the local perturbations. If we denote the pressure perturbation with respect to the balance pressure
![]() $P$
with
$P$
with
![]() $p^{\prime }$
, the equations of motion (2.10) are
$p^{\prime }$
, the equations of motion (2.10) are
Subtracting the balanced part (2.12) and substituting from (2.14), one finds the linearized equations
or in vector–matrix notation
with
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\displaystyle -\unicode[STIX]{x1D6FD}y\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}y} & \displaystyle -\unicode[STIX]{x1D6FD}y\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}z}\\ \displaystyle -\frac{g}{\unicode[STIX]{x1D70C}_{0}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}y}+2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}y} & \displaystyle N^{2}+2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}z}\end{array}\right)\quad \text{and}\quad \displaystyle N^{2}=-\frac{g}{\unicode[STIX]{x1D70C}_{0}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}z}.\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\displaystyle -\unicode[STIX]{x1D6FD}y\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}y} & \displaystyle -\unicode[STIX]{x1D6FD}y\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}z}\\ \displaystyle -\frac{g}{\unicode[STIX]{x1D70C}_{0}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}y}+2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}y} & \displaystyle N^{2}+2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}z}\end{array}\right)\quad \text{and}\quad \displaystyle N^{2}=-\frac{g}{\unicode[STIX]{x1D70C}_{0}}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}z}.\end{eqnarray}$$
Here,
![]() $N^{2}$
is the usual square of the buoyancy frequency. In view of the thermal wind balance (2.13),
$N^{2}$
is the usual square of the buoyancy frequency. In view of the thermal wind balance (2.13),
![]() $\unicode[STIX]{x1D648}=\left(\!\begin{smallmatrix}A & -B\\ -B & C\end{smallmatrix}\!\right)$
is a symmetric
$\unicode[STIX]{x1D648}=\left(\!\begin{smallmatrix}A & -B\\ -B & C\end{smallmatrix}\!\right)$
is a symmetric
![]() $2\times 2$
matrix. Thus, the eigenvalues
$2\times 2$
matrix. Thus, the eigenvalues
![]() $\{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\}$
are real and the corresponding eigenvectors
$\{\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\}$
are real and the corresponding eigenvectors
![]() $\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$
are orthogonal.
$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$
are orthogonal.
Solberg (Reference Solberg1936) argued that the flow is unstable if the displaced element accelerates away from its original position; if ‘pushed back’, it is stable. In this sense, there is stability if both eigenvalues of
![]() $\unicode[STIX]{x1D648}$
are positive because then (2.17) with
$\unicode[STIX]{x1D648}$
are positive because then (2.17) with
![]() $p^{\prime }=0$
is a 2D harmonic oscillator equation. Instability follows if an eigenvalue
$p^{\prime }=0$
is a 2D harmonic oscillator equation. Instability follows if an eigenvalue
![]() $\unicode[STIX]{x1D706}_{i}<0$
because then a displacement
$\unicode[STIX]{x1D706}_{i}<0$
because then a displacement
![]() $\unicode[STIX]{x1D6FF}x_{i}$
in the
$\unicode[STIX]{x1D6FF}x_{i}$
in the
![]() $\boldsymbol{e}_{i}$
-direction would amplify in time with the exponential rate
$\boldsymbol{e}_{i}$
-direction would amplify in time with the exponential rate
![]() $\exp (\sqrt{-\unicode[STIX]{x1D706}_{i}}t)$
. Excluding convective instability due to unstable stratification (
$\exp (\sqrt{-\unicode[STIX]{x1D706}_{i}}t)$
. Excluding convective instability due to unstable stratification (
![]() $N^{2}<0$
), inertial instability is then associated with just one negative eigenvalue, say
$N^{2}<0$
), inertial instability is then associated with just one negative eigenvalue, say
![]() $\unicode[STIX]{x1D706}_{1}<0$
, and the preferred direction of the instability is along
$\unicode[STIX]{x1D706}_{1}<0$
, and the preferred direction of the instability is along
![]() $\boldsymbol{e}_{1}$
, i.e. displacements in this direction exhibit maximal growth.
$\boldsymbol{e}_{1}$
, i.e. displacements in this direction exhibit maximal growth.
Refinements of this simple argument were developed by Ooyama (Reference Ooyama1966), who took into account the pressure perturbations. He proved stability/instability with an energy norm, as follows with the signs of
![]() $\unicode[STIX]{x1D706}_{1}(\boldsymbol{x})$
and
$\unicode[STIX]{x1D706}_{1}(\boldsymbol{x})$
and
![]() $\unicode[STIX]{x1D706}_{2}(\boldsymbol{x})$
. Earlier, Fjørtoft (Reference Fjørtoft1950) arrived at the stability conditions with normal-mode analysis, but Ooyama pointed out that often normal modes cannot exist in bounded domains, as was first noted by Høiland (Reference Høiland1962). Related approaches, i.e. stability proofs through the use of invariant quadratic functionals, are found in Kloosterziel & Carnevale (Reference Kloosterziel and Carnevale2007) and in Fruman & Shepherd (Reference Fruman and Shepherd2008) for compressible flows.
$\unicode[STIX]{x1D706}_{2}(\boldsymbol{x})$
. Earlier, Fjørtoft (Reference Fjørtoft1950) arrived at the stability conditions with normal-mode analysis, but Ooyama pointed out that often normal modes cannot exist in bounded domains, as was first noted by Høiland (Reference Høiland1962). Related approaches, i.e. stability proofs through the use of invariant quadratic functionals, are found in Kloosterziel & Carnevale (Reference Kloosterziel and Carnevale2007) and in Fruman & Shepherd (Reference Fruman and Shepherd2008) for compressible flows.
Since much depends on the (spatial) properties of the eigenvalues of
![]() $\unicode[STIX]{x1D648}$
, it should be noted that
$\unicode[STIX]{x1D648}$
, it should be noted that
where
![]() $\boldsymbol{Q}$
is the absolute vorticity vector and
$\boldsymbol{Q}$
is the absolute vorticity vector and
![]() $Q_{E}$
is the Ertel potential vorticity, i.e.
$Q_{E}$
is the Ertel potential vorticity, i.e.
With the traditional approximation (TA) in the lower row of
![]() $\unicode[STIX]{x1D648}$
, the terms multiplied by
$\unicode[STIX]{x1D648}$
, the terms multiplied by
![]() $2\unicode[STIX]{x1D6FA}$
need to be discarded and
$2\unicode[STIX]{x1D6FA}$
need to be discarded and
![]() $M=M_{TA}=U-(1/2)\unicode[STIX]{x1D6FD}y^{2}$
.
$M=M_{TA}=U-(1/2)\unicode[STIX]{x1D6FD}y^{2}$
.
If Rayleigh’s argument mentioned in the introduction is extended to include stratification, i.e. if potential energy changes are included, the coefficients of
![]() $\unicode[STIX]{x1D648}$
appear as follows. If fluid elements located at
$\unicode[STIX]{x1D648}$
appear as follows. If fluid elements located at
![]() $\boldsymbol{x}-(\unicode[STIX]{x1D6FF}\boldsymbol{x})/2$
,
$\boldsymbol{x}-(\unicode[STIX]{x1D6FF}\boldsymbol{x})/2$
,
![]() $\boldsymbol{x}+(\unicode[STIX]{x1D6FF}\boldsymbol{x})/2$
exchange positions, the energy change is
$\boldsymbol{x}+(\unicode[STIX]{x1D6FF}\boldsymbol{x})/2$
exchange positions, the energy change is
![]() $\unicode[STIX]{x0394}E=\unicode[STIX]{x1D6FF}\boldsymbol{x}\boldsymbol{\cdot }\unicode[STIX]{x1D648}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{x}$
. Diagonalized, this is
$\unicode[STIX]{x0394}E=\unicode[STIX]{x1D6FF}\boldsymbol{x}\boldsymbol{\cdot }\unicode[STIX]{x1D648}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{x}$
. Diagonalized, this is
![]() $\unicode[STIX]{x0394}E=\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D6FF}x_{1}^{2}+\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D6FF}x_{2}^{2}$
. For infinitesimal
$\unicode[STIX]{x0394}E=\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D6FF}x_{1}^{2}+\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D6FF}x_{2}^{2}$
. For infinitesimal
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{x}$
,
$\unicode[STIX]{x1D6FF}\boldsymbol{x}$
,
![]() $\unicode[STIX]{x0394}E<0$
when, for example,
$\unicode[STIX]{x0394}E<0$
when, for example,
![]() $\unicode[STIX]{x1D706}_{1}<0$
and
$\unicode[STIX]{x1D706}_{1}<0$
and
![]() $\unicode[STIX]{x1D6FF}x_{1}\neq 0$
. If, additionally,
$\unicode[STIX]{x1D6FF}x_{1}\neq 0$
. If, additionally,
![]() $\unicode[STIX]{x1D706}_{2}\geqslant 0$
, maximal energy release is found for an exchange along the direction defined by
$\unicode[STIX]{x1D706}_{2}\geqslant 0$
, maximal energy release is found for an exchange along the direction defined by
![]() $\unicode[STIX]{x1D706}_{1}$
, i.e. along
$\unicode[STIX]{x1D706}_{1}$
, i.e. along
![]() $\boldsymbol{e}_{1}$
. The orientation of the secondary motions sketched in figure 1(a) in circular flows without stratification is explained with the far more sophisticated approach of Ooyama (Reference Ooyama1966). He showed that if, in some region,
$\boldsymbol{e}_{1}$
. The orientation of the secondary motions sketched in figure 1(a) in circular flows without stratification is explained with the far more sophisticated approach of Ooyama (Reference Ooyama1966). He showed that if, in some region,
![]() $\unicode[STIX]{x1D706}_{1}(\boldsymbol{x})<0$
, an initial field of displacements
$\unicode[STIX]{x1D706}_{1}(\boldsymbol{x})<0$
, an initial field of displacements
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{x}(\boldsymbol{x})$
can be chosen that leads to unbounded growth. For this, the displacements have to be concentrated within sufficiently elongated elliptically shaped subdomains, with the major axis of the ellipses along the ‘instability’ direction locally defined by
$\unicode[STIX]{x1D6FF}\boldsymbol{x}(\boldsymbol{x})$
can be chosen that leads to unbounded growth. For this, the displacements have to be concentrated within sufficiently elongated elliptically shaped subdomains, with the major axis of the ellipses along the ‘instability’ direction locally defined by
![]() $\boldsymbol{e}_{1}$
wherever
$\boldsymbol{e}_{1}$
wherever
![]() $\unicode[STIX]{x1D706}_{1}(\boldsymbol{x})<0$
. Early numerical experiments by Yanai & Tokiaka (Reference Yanai and Tokiaka1969) proved the validity of Ooyama’s prediction.
$\unicode[STIX]{x1D706}_{1}(\boldsymbol{x})<0$
. Early numerical experiments by Yanai & Tokiaka (Reference Yanai and Tokiaka1969) proved the validity of Ooyama’s prediction.

Figure 3. Side view of a slice of the spherical planet rotating with angular velocity
![]() $\unicode[STIX]{x1D6FA}$
. The distance from the rotation axis is
$\unicode[STIX]{x1D6FA}$
. The distance from the rotation axis is
![]() $R$
. The local Cartesian coordinates
$R$
. The local Cartesian coordinates
![]() $y,z$
are indicated. With the complete Coriolis force (NTA), Taylor columns
$y,z$
are indicated. With the complete Coriolis force (NTA), Taylor columns
![]() $U=U(R)$
are invariant along lines of constant distance
$U=U(R)$
are invariant along lines of constant distance
![]() $R\approx R_{0}+z-y^{2}/2R_{0}$
.
$R\approx R_{0}+z-y^{2}/2R_{0}$
.
2.2 Homogeneous fluid
In a homogeneous fluid (constant density
![]() $\bar{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{0}$
), steady zonal flows
$\bar{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{0}$
), steady zonal flows
![]() $\boldsymbol{u}=U\boldsymbol{i}$
have to be Taylor columns according to the Taylor–Proudman theorem; that is, flows that do not vary parallel to the axis of rotation:
$\boldsymbol{u}=U\boldsymbol{i}$
have to be Taylor columns according to the Taylor–Proudman theorem; that is, flows that do not vary parallel to the axis of rotation:
![]() $(\unicode[STIX]{x1D734}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}=0$
(Pedlosky Reference Pedlosky1987). This means with (2.6) that only
$(\unicode[STIX]{x1D734}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}=0$
(Pedlosky Reference Pedlosky1987). This means with (2.6) that only
![]() $U=U(R)=U(z-y^{2}/2R_{0})$
can be steady. This is sketched in figure 3. The stability tensor
$U=U(R)=U(z-y^{2}/2R_{0})$
can be steady. This is sketched in figure 3. The stability tensor
![]() $\unicode[STIX]{x1D648}$
reduces to
$\unicode[STIX]{x1D648}$
reduces to
 $$\begin{eqnarray}\unicode[STIX]{x1D648}=\left(\begin{array}{@{}cc@{}}\displaystyle -\unicode[STIX]{x1D6FD}y\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}y} & \displaystyle -\unicode[STIX]{x1D6FD}y\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}z}\\ \displaystyle 2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}y} & \displaystyle 2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}z}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D648}=\left(\begin{array}{@{}cc@{}}\displaystyle -\unicode[STIX]{x1D6FD}y\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}y} & \displaystyle -\unicode[STIX]{x1D6FD}y\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}z}\\ \displaystyle 2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}y} & \displaystyle 2\unicode[STIX]{x1D6FA}\frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}z}\end{array}\right),\end{eqnarray}$$
with eigenvalues and eigenvectors
having left out a common normalizing factor in
![]() $\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$
. Specifically,
$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$
. Specifically,
with
![]() $R$
approximated by the parabolas (2.6). The direction
$R$
approximated by the parabolas (2.6). The direction
![]() $\boldsymbol{e}_{2}$
associated with
$\boldsymbol{e}_{2}$
associated with
![]() $\unicode[STIX]{x1D706}_{2}=0$
is everywhere tangent to
$\unicode[STIX]{x1D706}_{2}=0$
is everywhere tangent to
![]() $R=\text{const.}$
, i.e. along the direction of
$R=\text{const.}$
, i.e. along the direction of
![]() $\unicode[STIX]{x1D734}$
. This ‘neutrally stable’ direction is parallel to the orientation of the Taylor column sketched in figure 3 and is the direction in which in Rayleigh’s argument an exchange does not liberate energy. The direction
$\unicode[STIX]{x1D734}$
. This ‘neutrally stable’ direction is parallel to the orientation of the Taylor column sketched in figure 3 and is the direction in which in Rayleigh’s argument an exchange does not liberate energy. The direction
![]() $\boldsymbol{e}_{1}$
is perpendicular to the lines of constant
$\boldsymbol{e}_{1}$
is perpendicular to the lines of constant
![]() $R$
. The criterion for instability (
$R$
. The criterion for instability (
![]() $\unicode[STIX]{x1D706}_{1}<0$
) is nothing but Rayleigh’s criterion (1.1) with the approximations we have made: as noted above after (2.9),
$\unicode[STIX]{x1D706}_{1}<0$
) is nothing but Rayleigh’s criterion (1.1) with the approximations we have made: as noted above after (2.9),
![]() $L\approx R_{0}M$
and in (1.1)
$L\approx R_{0}M$
and in (1.1)
because
![]() $2L/R^{2}\approx 2\unicode[STIX]{x1D6FA}$
if
$2L/R^{2}\approx 2\unicode[STIX]{x1D6FA}$
if
![]() $|U|\ll \unicode[STIX]{x1D6FA}R_{0}$
(on the Earth,
$|U|\ll \unicode[STIX]{x1D6FA}R_{0}$
(on the Earth,
![]() $\unicode[STIX]{x1D6FA}R_{0}\approx 500~\text{m}~\text{s}^{-1}$
).
$\unicode[STIX]{x1D6FA}R_{0}\approx 500~\text{m}~\text{s}^{-1}$
).
When
![]() $\unicode[STIX]{x1D706}_{1}(\boldsymbol{x})<0$
in some region, the flow is unstable and the preferred direction of the instability is along
$\unicode[STIX]{x1D706}_{1}(\boldsymbol{x})<0$
in some region, the flow is unstable and the preferred direction of the instability is along
![]() $\boldsymbol{e}_{1}$
, which near the equator is almost perpendicular to the surface, i.e. upward/downward, parallel to lines of increasing depth
$\boldsymbol{e}_{1}$
, which near the equator is almost perpendicular to the surface, i.e. upward/downward, parallel to lines of increasing depth
![]() $z$
(as sketched in figure 2
b). We believe that this has rarely been investigated in any detail.
$z$
(as sketched in figure 2
b). We believe that this has rarely been investigated in any detail.
2.3 Model flow
Within a homogeneous fluid, with the NTA, only flows
![]() $U(z-y^{2}/2R_{0})$
are steady (see § 2.2). These are flows
$U(z-y^{2}/2R_{0})$
are steady (see § 2.2). These are flows
![]() $U(R)$
with
$U(R)$
with
![]() $R$
approximated by (2.6). We shall use the simple example
$R$
approximated by (2.6). We shall use the simple example
From here on,
![]() $L$
defines the latitudinal width of the jet – not the angular momentum – and
$L$
defines the latitudinal width of the jet – not the angular momentum – and
![]() $U_{0}$
is the peak surface velocity at the equator. At the surface (
$U_{0}$
is the peak surface velocity at the equator. At the surface (
![]() $z=0$
), this flow matches the Gaussian jet we recently studied in the context of the TA approximation (see Kloosterziel, Orlandi & Carnevale Reference Kloosterziel, Orlandi and Carnevale2015). However, then a balanced flow has to be a Taylor column
$z=0$
), this flow matches the Gaussian jet we recently studied in the context of the TA approximation (see Kloosterziel, Orlandi & Carnevale Reference Kloosterziel, Orlandi and Carnevale2015). However, then a balanced flow has to be a Taylor column
![]() $U(y)$
and there is no
$U(y)$
and there is no
![]() $z$
-dependence. With the NTA, the amplitude has to decay with depth below the surface,
$z$
-dependence. With the NTA, the amplitude has to decay with depth below the surface,
![]() $z<0$
, with a vertical scale
$z<0$
, with a vertical scale
![]() $L^{2}/R_{0}$
. If
$L^{2}/R_{0}$
. If
![]() $R_{0}\approx 6380$
km (Earth’s radius), for
$R_{0}\approx 6380$
km (Earth’s radius), for
![]() $L=25$
km, the decay scale is a mere 100 m, for
$L=25$
km, the decay scale is a mere 100 m, for
![]() $L=50$
km, approximately 400 m, etc.
$L=50$
km, approximately 400 m, etc.
Only the westward flowing current can be unstable (
![]() $U_{0}<0$
). With non-dimensional
$U_{0}<0$
). With non-dimensional
![]() $\tilde{z}=zR_{0}/L^{2}$
,
$\tilde{z}=zR_{0}/L^{2}$
,
![]() ${\tilde{y}}=y/L$
, it follows with (2.23) that
${\tilde{y}}=y/L$
, it follows with (2.23) that
For instability (
![]() $\unicode[STIX]{x1D706}_{1}<0$
), it is required that
$\unicode[STIX]{x1D706}_{1}<0$
), it is required that
![]() $A>1$
(
$A>1$
(
![]() $A$
is an equatorial Rossby number). With
$A$
is an equatorial Rossby number). With
![]() $\unicode[STIX]{x1D6FA}=7.26\times 10^{-5}~\text{rad}~\text{s}^{-1}$
(Earth’s radius angular velocity), this requires a westward peak velocity
$\unicode[STIX]{x1D6FA}=7.26\times 10^{-5}~\text{rad}~\text{s}^{-1}$
(Earth’s radius angular velocity), this requires a westward peak velocity
![]() $|U_{0}|\gtrsim 1.5~\text{cm}~\text{s}^{-1}$
if
$|U_{0}|\gtrsim 1.5~\text{cm}~\text{s}^{-1}$
if
![]() $L=25$
km, if
$L=25$
km, if
![]() $L=50$
km,
$L=50$
km,
![]() $|U_{0}|\gtrsim 6~\text{cm}~\text{s}^{-1}$
, and so on.
$|U_{0}|\gtrsim 6~\text{cm}~\text{s}^{-1}$
, and so on.

Figure 4. Schematic illustrating the prediction of absolute momentum mixing. In (a), a Taylor-column flow as sketched in figure 3 is assumed, which is unstable for
![]() $R>R_{ins}$
where absolute momentum decreases:
$R>R_{ins}$
where absolute momentum decreases:
![]() $\text{d}M/\text{d}R<0$
(dark grey area). For smaller
$\text{d}M/\text{d}R<0$
(dark grey area). For smaller
![]() $R$
, the flow is stable (uncoloured area). In the unstable (dark grey) area, the overturning motions as sketched in figure 2 are expected to emerge. At high Reynolds numbers, through nonlinear interactions, these secondary motions are expected to propagate towards the rotation axis (indicated by fat horizontal black arrows). By doing so, they advect and mix momentum. In (b), we show the expected final state. A new Taylor columnar flow is established with constant absolute momentum
$R$
, the flow is stable (uncoloured area). In the unstable (dark grey) area, the overturning motions as sketched in figure 2 are expected to emerge. At high Reynolds numbers, through nonlinear interactions, these secondary motions are expected to propagate towards the rotation axis (indicated by fat horizontal black arrows). By doing so, they advect and mix momentum. In (b), we show the expected final state. A new Taylor columnar flow is established with constant absolute momentum
![]() $m=M_{c}$
between the axial radius
$m=M_{c}$
between the axial radius
![]() $R=R_{l}$
and the surface (light grey area), while the momentum is unchanged for
$R=R_{l}$
and the surface (light grey area), while the momentum is unchanged for
![]() $R<R_{l}$
(uncoloured area). The flow is stable because everywhere
$R<R_{l}$
(uncoloured area). The flow is stable because everywhere
![]() $\text{d}M/\text{d}R\geqslant 0$
. Continuity at
$\text{d}M/\text{d}R\geqslant 0$
. Continuity at
![]() $R=R_{l}$
is established by setting
$R=R_{l}$
is established by setting
![]() $M_{c}=M(R_{l})$
, and
$M_{c}=M(R_{l})$
, and
![]() $M_{c}$
, and then also
$M_{c}$
, and then also
![]() $R_{l}$
, is determined by conservation of total (area integrated) momentum according to (2.32).
$R_{l}$
, is determined by conservation of total (area integrated) momentum according to (2.32).
If exponential growth of small perturbations is assumed, i.e.
![]() $\exp (\unicode[STIX]{x1D6FE}t)$
, the initial growth rate
$\exp (\unicode[STIX]{x1D6FE}t)$
, the initial growth rate
![]() $\unicode[STIX]{x1D6FE}$
of a displacement
$\unicode[STIX]{x1D6FE}$
of a displacement
![]() $\unicode[STIX]{x1D6FF}x_{1}$
is via Solberg’s approach locally
$\unicode[STIX]{x1D6FF}x_{1}$
is via Solberg’s approach locally
![]() $\unicode[STIX]{x1D6FE}=\sqrt{-\unicode[STIX]{x1D706}_{1}}$
, where
$\unicode[STIX]{x1D6FE}=\sqrt{-\unicode[STIX]{x1D706}_{1}}$
, where
![]() $\unicode[STIX]{x1D706}_{1}<0$
. The instability region is contained in between the parabola
$\unicode[STIX]{x1D706}_{1}<0$
. The instability region is contained in between the parabola
![]() $\tilde{z}-{\tilde{y}}^{2}/2=-\text{ln}\,A$
and the surface
$\tilde{z}-{\tilde{y}}^{2}/2=-\text{ln}\,A$
and the surface
![]() $\tilde{z}=0$
. The lowest point on the instability boundary parabola is at depth
$\tilde{z}=0$
. The lowest point on the instability boundary parabola is at depth
![]() $\tilde{z}_{ins}=-\text{ln}\,A$
and it meets the surface at
$\tilde{z}_{ins}=-\text{ln}\,A$
and it meets the surface at
![]() ${\tilde{y}}_{\pm }=\pm \sqrt{2\ln A}$
. With the approximation (2.6), the boundary is the line of constant distance
${\tilde{y}}_{\pm }=\pm \sqrt{2\ln A}$
. With the approximation (2.6), the boundary is the line of constant distance
![]() $R=R_{0}-(L^{2}/R_{0})\ln A$
from the rotation axis. For smaller
$R=R_{0}-(L^{2}/R_{0})\ln A$
from the rotation axis. For smaller
![]() $R$
, one has
$R$
, one has
![]() $\text{d}M/\text{d}R>0$
, and for larger
$\text{d}M/\text{d}R>0$
, and for larger
![]() $R$
, the instability region is where
$R$
, the instability region is where
![]() $\text{d}M/\text{d}R<0$
(see (2.23) again and figure 4
a). The fastest rate of growth,
$\text{d}M/\text{d}R<0$
(see (2.23) again and figure 4
a). The fastest rate of growth,
![]() $\unicode[STIX]{x1D6FE}_{\infty }$
, is at the equator at the surface, i.e. at
$\unicode[STIX]{x1D6FE}_{\infty }$
, is at the equator at the surface, i.e. at
![]() $\{{\tilde{y}},\tilde{z}\}=\{0,0\}$
. Everywhere, the instability direction is along
$\{{\tilde{y}},\tilde{z}\}=\{0,0\}$
. Everywhere, the instability direction is along
![]() $\boldsymbol{e}_{1}$
, i.e. radial or normal to lines of constant
$\boldsymbol{e}_{1}$
, i.e. radial or normal to lines of constant
![]() $R$
(see the end of § 2.1). If time is scaled with
$R$
(see the end of § 2.1). If time is scaled with
![]() $T=1/2\unicode[STIX]{x1D6FA}$
, non-dimensionally,
$T=1/2\unicode[STIX]{x1D6FA}$
, non-dimensionally,
With the TA, the flow that has the same surface signature as (2.25) is
which is also only unstable when flowing westward with
![]() $A>1$
. The eigenvalues and eigenvectors of
$A>1$
. The eigenvalues and eigenvectors of
![]() $\unicode[STIX]{x1D648}$
are
$\unicode[STIX]{x1D648}$
are
with
![]() $M_{TA}=U-(1/2)\unicode[STIX]{x1D6FD}y^{2}$
. Analogous to the NTA example, the neutral stability direction
$M_{TA}=U-(1/2)\unicode[STIX]{x1D6FD}y^{2}$
. Analogous to the NTA example, the neutral stability direction
![]() $\boldsymbol{e}_{2}$
is parallel to the axis of the column, but this is now aligned with the traditional rotation component
$\boldsymbol{e}_{2}$
is parallel to the axis of the column, but this is now aligned with the traditional rotation component
![]() $\unicode[STIX]{x1D734}_{\bot }=(\unicode[STIX]{x1D6FD}y/2)\boldsymbol{k}$
, i.e. upwards/downwards. If
$\unicode[STIX]{x1D734}_{\bot }=(\unicode[STIX]{x1D6FD}y/2)\boldsymbol{k}$
, i.e. upwards/downwards. If
![]() $\unicode[STIX]{x1D706}_{1}<0$
for some latitudinal range, the instability direction is horizontally/laterally. If
$\unicode[STIX]{x1D706}_{1}<0$
for some latitudinal range, the instability direction is horizontally/laterally. If
![]() $A>1$
, two instability regions appear on either side of the equator where
$A>1$
, two instability regions appear on either side of the equator where
![]() $\unicode[STIX]{x1D706}_{1}<0$
(see Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015) and figure 5 below). The outer edges of the instability region are again at
$\unicode[STIX]{x1D706}_{1}<0$
(see Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015) and figure 5 below). The outer edges of the instability region are again at
![]() ${\tilde{y}}={\tilde{y}}_{\pm }=\pm \sqrt{2\ln A}$
. Maximal growth is at
${\tilde{y}}={\tilde{y}}_{\pm }=\pm \sqrt{2\ln A}$
. Maximal growth is at
![]() ${\tilde{y}}=\pm {\tilde{y}}_{m}$
inside the two regions:
${\tilde{y}}=\pm {\tilde{y}}_{m}$
inside the two regions:
with
![]() $W_{0}$
the Lambert
$W_{0}$
the Lambert
![]() $W$
-function. For example,
$W$
-function. For example,
![]() ${\tilde{y}}_{m}\approx 1.12$
when
${\tilde{y}}_{m}\approx 1.12$
when
![]() $A=5$
. The fastest non-dimensional rate of growth is
$A=5$
. The fastest non-dimensional rate of growth is
These simple considerations suggest that narrow flows (small
![]() $L/R_{0}$
) will exhibit a far slower development of the instability when the traditional approximation (TA) is adopted than with the full Coriolis dynamics (NTA).
$L/R_{0}$
) will exhibit a far slower development of the instability when the traditional approximation (TA) is adopted than with the full Coriolis dynamics (NTA).

Figure 5. Contour plots of zonal vorticity
![]() $\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x2202}_{y}w-\unicode[STIX]{x2202}_{z}v$
from linearized simulations of the barotropic Gaussian jet in the TA with
$\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x2202}_{y}w-\unicode[STIX]{x2202}_{z}v$
from linearized simulations of the barotropic Gaussian jet in the TA with
![]() $A=5$
,
$A=5$
,
![]() $L/R_{0}=0.25$
and (a)
$L/R_{0}=0.25$
and (a)
![]() $Re=10^{5}$
, (b)
$Re=10^{5}$
, (b)
![]() $Re=10^{6}$
. The initial condition is a random pointwise perturbation. The view is from positive to negative
$Re=10^{6}$
. The initial condition is a random pointwise perturbation. The view is from positive to negative
![]() $x$
. The grey/black contours correspond to positive/negative
$x$
. The grey/black contours correspond to positive/negative
![]() $\unicode[STIX]{x1D714}_{x}$
. The boundaries of the linear instability region are
$\unicode[STIX]{x1D714}_{x}$
. The boundaries of the linear instability region are
![]() ${\tilde{y}}_{\pm }=\sqrt{2\ln A}\approx \pm 1.79$
. The latitudes of maximum instability are
${\tilde{y}}_{\pm }=\sqrt{2\ln A}\approx \pm 1.79$
. The latitudes of maximum instability are
![]() $\pm {\tilde{y}}_{m}\approx \pm 1.12$
. The equator (
$\pm {\tilde{y}}_{m}\approx \pm 1.12$
. The equator (
![]() ${\tilde{y}}=0$
) is marked by the dotted vertical line. Only a portion of the computational domain is shown.
${\tilde{y}}=0$
) is marked by the dotted vertical line. Only a portion of the computational domain is shown.
2.4 Viscous modifications of linear theory: scale selection
In the above simple theory, applied to the Gaussian jets in both the TA and NTA cases, no viscosity is taken into account. The subscript ‘
![]() $\infty$
’ in (2.27) and (2.31) indicates that this is the expected maximal rate of growth in the limit of vanishing viscosity (
$\infty$
’ in (2.27) and (2.31) indicates that this is the expected maximal rate of growth in the limit of vanishing viscosity (
![]() $\unicode[STIX]{x1D708}=0$
) or Reynolds number
$\unicode[STIX]{x1D708}=0$
) or Reynolds number
![]() $Re\rightarrow \infty$
. In the case of the traditional approximation dynamics (TA) with
$Re\rightarrow \infty$
. In the case of the traditional approximation dynamics (TA) with
![]() $U=U(y)$
, and assuming
$U=U(y)$
, and assuming
![]() $N(z)=N$
, a constant, a simple normal-mode analysis is possible with perturbations proportional to
$N(z)=N$
, a constant, a simple normal-mode analysis is possible with perturbations proportional to
![]() $\exp (\text{i}k_{z}z)$
. For inviscid flow, it is found that the overturning motions associated with inertial instability are amplified more rapidly the higher the value of
$\exp (\text{i}k_{z}z)$
. For inviscid flow, it is found that the overturning motions associated with inertial instability are amplified more rapidly the higher the value of
![]() $k_{z}$
; that is, the smaller their vertical scale (e.g. Dunkerton Reference Dunkerton1981; Smyth & McWilliams Reference Smyth and McWilliams1998; Griffiths Reference Griffiths2003a
; Kloosterziel & Carnevale Reference Kloosterziel and Carnevale2008). This can be understood with the energy analysis of Ooyama (Reference Ooyama1966). Maximal energy is extracted from the background flow by motions predominantly in the unstable direction predicted by Solberg’s argument (see the end of § 2.1). Constant stratification
$k_{z}$
; that is, the smaller their vertical scale (e.g. Dunkerton Reference Dunkerton1981; Smyth & McWilliams Reference Smyth and McWilliams1998; Griffiths Reference Griffiths2003a
; Kloosterziel & Carnevale Reference Kloosterziel and Carnevale2008). This can be understood with the energy analysis of Ooyama (Reference Ooyama1966). Maximal energy is extracted from the background flow by motions predominantly in the unstable direction predicted by Solberg’s argument (see the end of § 2.1). Constant stratification
![]() $N$
introduces a lower-wavenumber cutoff for instability: only perturbations with
$N$
introduces a lower-wavenumber cutoff for instability: only perturbations with
![]() $k_{z}>k_{c}^{N}$
can exhibit inertial instability. Increasing
$k_{z}>k_{c}^{N}$
can exhibit inertial instability. Increasing
![]() $N$
has the effect of increasing
$N$
has the effect of increasing
![]() $k_{c}^{N}$
, thus requiring smaller vertical scales for the instability to proceed. This was demonstrated with numerical simulations by Kloosterziel et al. (Reference Kloosterziel, Carnevale and Orlandi2007a
).
$k_{c}^{N}$
, thus requiring smaller vertical scales for the instability to proceed. This was demonstrated with numerical simulations by Kloosterziel et al. (Reference Kloosterziel, Carnevale and Orlandi2007a
).
The addition of viscosity, which preferentially damps small-scale motions, introduces a viscous upper wavenumber cutoff
![]() $k_{c}^{\unicode[STIX]{x1D708}}$
, which is such that
$k_{c}^{\unicode[STIX]{x1D708}}$
, which is such that
![]() $k_{c}^{\unicode[STIX]{x1D708}}\rightarrow \infty$
for
$k_{c}^{\unicode[STIX]{x1D708}}\rightarrow \infty$
for
![]() $Re\rightarrow \infty$
. Thus, the instability can only grow if
$Re\rightarrow \infty$
. Thus, the instability can only grow if
![]() $k_{c}^{N}<k_{z}<k_{c}^{\unicode[STIX]{x1D708}}$
. That is, for finite but large enough Reynolds numbers, only perturbations with vertical scales within a finite range will be amplified. Within this range, a maximum growth rate is found at a specific vertical scale. Hence, if a flow is subjected to small perturbations and the ‘fastest’ mode is excited, one expects meridional motions with the vertical scale of the fastest growing mode to emerge. For the TA, the characteristic behaviour is that as
$k_{c}^{N}<k_{z}<k_{c}^{\unicode[STIX]{x1D708}}$
. That is, for finite but large enough Reynolds numbers, only perturbations with vertical scales within a finite range will be amplified. Within this range, a maximum growth rate is found at a specific vertical scale. Hence, if a flow is subjected to small perturbations and the ‘fastest’ mode is excited, one expects meridional motions with the vertical scale of the fastest growing mode to emerge. For the TA, the characteristic behaviour is that as
![]() $Re$
increases, the vertical scale of the fastest growing mode diminishes, and interestingly its horizontal scale also diminishes, with the mode becoming ever more concentrated in
$Re$
increases, the vertical scale of the fastest growing mode diminishes, and interestingly its horizontal scale also diminishes, with the mode becoming ever more concentrated in
![]() $y$
at the locations predicted by (2.30).
$y$
at the locations predicted by (2.30).
This scale selection in inertial instability for near-equatorial flows with the full Coriolis dynamics has to the best of our knowledge never before been investigated in any detail. For the NTA, we shall show in § 4 that, for the surface-confined jet (2.25) and
![]() $N=0$
, the upper limit
$N=0$
, the upper limit
![]() $\unicode[STIX]{x1D6FE}_{\infty }$
(2.27) is approached via surface-confined modes that with increasing
$\unicode[STIX]{x1D6FE}_{\infty }$
(2.27) is approached via surface-confined modes that with increasing
![]() $Re$
have ever smaller scales and contract towards the equator (see figure 6 below). Asymptotic analysis detailed in appendix A explains much of the measured behaviour that we present in § 4.
$Re$
have ever smaller scales and contract towards the equator (see figure 6 below). Asymptotic analysis detailed in appendix A explains much of the measured behaviour that we present in § 4.

Figure 6. Contour plots of
![]() $\unicode[STIX]{x1D714}_{x}$
from linearized simulations of the Gaussian jet in the NTA with
$\unicode[STIX]{x1D714}_{x}$
from linearized simulations of the Gaussian jet in the NTA with
![]() $A=5$
,
$A=5$
,
![]() $L/R_{0}=0.25$
and (a)
$L/R_{0}=0.25$
and (a)
![]() $Re=10^{5}$
, (b)
$Re=10^{5}$
, (b)
![]() $Re=10^{6}$
. The coordinate system of lines parallel and perpendicular to the planet rotation axis are drawn as thin dashed lines in the background. The aspect ratio of the plots is such that the units of length in the unscaled physical variables
$Re=10^{6}$
. The coordinate system of lines parallel and perpendicular to the planet rotation axis are drawn as thin dashed lines in the background. The aspect ratio of the plots is such that the units of length in the unscaled physical variables
![]() $y$
and
$y$
and
![]() $z$
are the same in each direction, ensuring that the aspect ratios of the rolls as shown are the physical aspect ratios. Only a portion of the computational domain is shown.
$z$
are the same in each direction, ensuring that the aspect ratios of the rolls as shown are the physical aspect ratios. Only a portion of the computational domain is shown.
2.5 Nonlinear equilibration
In our first detailed study of the unfolding of inertial instability of barotropic vortices on the midlatitude
![]() $f$
-plane (Kloosterziel et al.
Reference Kloosterziel, Carnevale and Orlandi2007a
), we discovered that for large
$f$
-plane (Kloosterziel et al.
Reference Kloosterziel, Carnevale and Orlandi2007a
), we discovered that for large
![]() $Re$
, the outcome of the fully nonlinear turbulent evolution can be predicted. This was extended to parallel shear flows on the
$Re$
, the outcome of the fully nonlinear turbulent evolution can be predicted. This was extended to parallel shear flows on the
![]() $f$
-plane (Kloosterziel, Orlandi & Carnevale Reference Kloosterziel, Orlandi and Carnevale2007b
) and recently to barotropic flows like the Gaussian jet on the traditional equatorial
$f$
-plane (Kloosterziel, Orlandi & Carnevale Reference Kloosterziel, Orlandi and Carnevale2007b
) and recently to barotropic flows like the Gaussian jet on the traditional equatorial
![]() $\unicode[STIX]{x1D6FD}$
-plane (Kloosterziel et al.
Reference Kloosterziel, Orlandi and Carnevale2015). The prediction is that the instability mixes angular momentum or absolute momentum to such an extent that a new barotropic (depth-independent) inertially stable flow emerges. Stability is accomplished by mixing momentum to a homogeneous state with no gradients. Over some spatial range, this means that the flow has become neutrally stable (both eigenvalues of
$\unicode[STIX]{x1D6FD}$
-plane (Kloosterziel et al.
Reference Kloosterziel, Orlandi and Carnevale2015). The prediction is that the instability mixes angular momentum or absolute momentum to such an extent that a new barotropic (depth-independent) inertially stable flow emerges. Stability is accomplished by mixing momentum to a homogeneous state with no gradients. Over some spatial range, this means that the flow has become neutrally stable (both eigenvalues of
![]() $\unicode[STIX]{x1D648}$
become zero). The range over which the mixing alters the original flow is determined by the constraint that total momentum is conserved.
$\unicode[STIX]{x1D648}$
become zero). The range over which the mixing alters the original flow is determined by the constraint that total momentum is conserved.
For the full Coriolis dynamics, we predict that the instability will mix the absolute momentum from the surface downwards. The basic idea is sketched in figure 4. A thoroughly mixed region is expected to form between distance
![]() $R=R_{l}$
from the rotation axis and the surface. In our Cartesian formulation, this will be some parabola
$R=R_{l}$
from the rotation axis and the surface. In our Cartesian formulation, this will be some parabola
![]() $\tilde{z}-{\tilde{y}}^{2}/2=\text{const}$
. Between this parabola and the surface, the new flow will have some constant momentum
$\tilde{z}-{\tilde{y}}^{2}/2=\text{const}$
. Between this parabola and the surface, the new flow will have some constant momentum
![]() $m=M_{c}$
. The value of
$m=M_{c}$
. The value of
![]() $M_{c}$
is determined by the ‘boundary condition’ that at the hypothesized location
$M_{c}$
is determined by the ‘boundary condition’ that at the hypothesized location
![]() $R=R_{l}$
, the new momentum distribution is continuous, i.e.
$R=R_{l}$
, the new momentum distribution is continuous, i.e.
![]() $M_{c}=M(R_{l})$
, and that the new flow is stable, which means that the mixed region (light grey area in figure 4
b) encompasses the original instability region that started at
$M_{c}=M(R_{l})$
, and that the new flow is stable, which means that the mixed region (light grey area in figure 4
b) encompasses the original instability region that started at
![]() $R=R_{ins}$
, as sketched in figure 4(a) (dark grey area). With this information, we can determine both
$R=R_{ins}$
, as sketched in figure 4(a) (dark grey area). With this information, we can determine both
![]() $R_{l}$
and
$R_{l}$
and
![]() $M_{c}$
by the constraint that the domain integrated momentum is conserved (it should be noted that, even at finite
$M_{c}$
by the constraint that the domain integrated momentum is conserved (it should be noted that, even at finite
![]() $Re$
, free-slip boundaries mean that the bulk momentum cannot change). Thus, one needs to solve
$Re$
, free-slip boundaries mean that the bulk momentum cannot change). Thus, one needs to solve
At the equator, the parabola describing
![]() $R_{l}$
is at non-dimensional depth
$R_{l}$
is at non-dimensional depth
![]() $\tilde{z}_{l}$
. For the Gaussian jet with
$\tilde{z}_{l}$
. For the Gaussian jet with
![]() $A>1$
, we find with (2.32) how
$A>1$
, we find with (2.32) how
![]() $\tilde{z}_{l}$
varies with
$\tilde{z}_{l}$
varies with
![]() $A$
by solving a transcendental relation between
$A$
by solving a transcendental relation between
![]() $\tilde{z}$
and
$\tilde{z}$
and
![]() $A$
(see appendix B, where details are provided). We verify these predictions in § 5.
$A$
(see appendix B, where details are provided). We verify these predictions in § 5.
3 Method of numerical simulation
For the present study, we restrict ourselves to zonally invariant (
![]() $x$
-independent) flow. This will capture the pure inertial instability unaffected by other instabilities, such as barotropic instability, that rely on variation in the zonal direction
$x$
-independent) flow. This will capture the pure inertial instability unaffected by other instabilities, such as barotropic instability, that rely on variation in the zonal direction
![]() $x$
. This decomposition is particularly interesting when the inertial instability proves to be faster than other possible instabilities, as illustrated in Carnevale et al. (Reference Carnevale, Kloosterziel and Orlandi2013), where we compared inertial instability in zonally invariant flow with that in fully three-dimensional flow in an
$x$
. This decomposition is particularly interesting when the inertial instability proves to be faster than other possible instabilities, as illustrated in Carnevale et al. (Reference Carnevale, Kloosterziel and Orlandi2013), where we compared inertial instability in zonally invariant flow with that in fully three-dimensional flow in an
![]() $f$
-plane context. Our simulations here are based on a staggered-mesh channel model described in detail in Orlandi (Reference Orlandi2000). This numerical scheme conserves energy when run inviscidly. Energy dissipation results only from explicit viscosity. We add this in order to investigate the scale-selection issue briefly described in § 2.4. For this study, we find it convenient to write the Navier–Stokes equations in such a way that the flow is explicitly decomposed into the background flow
$f$
-plane context. Our simulations here are based on a staggered-mesh channel model described in detail in Orlandi (Reference Orlandi2000). This numerical scheme conserves energy when run inviscidly. Energy dissipation results only from explicit viscosity. We add this in order to investigate the scale-selection issue briefly described in § 2.4. For this study, we find it convenient to write the Navier–Stokes equations in such a way that the flow is explicitly decomposed into the background flow
![]() $U$
and the perturbation to that flow, henceforth written as
$U$
and the perturbation to that flow, henceforth written as
![]() $(u,v,w)$
. Thus, we have instead of (2.5a–c
), after setting
$(u,v,w)$
. Thus, we have instead of (2.5a–c
), after setting
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}$
and modifying the pressure with the hydrostatic term
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}$
and modifying the pressure with the hydrostatic term
![]() $\unicode[STIX]{x1D70C}_{0}gz$
,
$\unicode[STIX]{x1D70C}_{0}gz$
,
and
Here,
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
![]() $\unicode[STIX]{x1D6FB}^{2}=(\unicode[STIX]{x2202}_{y}^{2}+\unicode[STIX]{x2202}_{z}^{2})$
is the two-dimensional Laplace operator. Although there are three velocity components, they only depend on time and the two spatial coordinates
$\unicode[STIX]{x1D6FB}^{2}=(\unicode[STIX]{x2202}_{y}^{2}+\unicode[STIX]{x2202}_{z}^{2})$
is the two-dimensional Laplace operator. Although there are three velocity components, they only depend on time and the two spatial coordinates
![]() $y$
and
$y$
and
![]() $z$
in this study. It should be noted that we can ‘switch’ the dynamics between traditional (TA) and non-traditional (NTA) dynamics by neglecting or retaining the non-traditional terms ‘NTA’ in (3.1) and (3.3).
$z$
in this study. It should be noted that we can ‘switch’ the dynamics between traditional (TA) and non-traditional (NTA) dynamics by neglecting or retaining the non-traditional terms ‘NTA’ in (3.1) and (3.3).
The term
![]() $F$
represents an external force applied to the flow. If we take
$F$
represents an external force applied to the flow. If we take
![]() $F=0$
, then (3.1)–(3.4) are the fully nonlinear Navier–Stokes equations describing the free decay of the jet. On the other hand, in studying the linear instability, the purely viscous decay of the jet is not of interest, and we will then, besides neglecting all terms nonlinear in the fields
$F=0$
, then (3.1)–(3.4) are the fully nonlinear Navier–Stokes equations describing the free decay of the jet. On the other hand, in studying the linear instability, the purely viscous decay of the jet is not of interest, and we will then, besides neglecting all terms nonlinear in the fields
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
, set
$w$
, set
![]() $F=-\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}U$
, thus cancelling the purely viscous decay of the background flow
$F=-\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}U$
, thus cancelling the purely viscous decay of the background flow
![]() $U$
.
$U$
.
The surface boundary condition applied to the inviscid equations of motion would be the typical condition of no flow through the boundary. This is not sufficient for the Navier–Stokes equations. With the introduction of finite viscosity, the equations of evolution become second order in spatial derivatives, and thus require additional constraints to ensure a unique solution. The typical boundary conditions for the Navier–Stokes equations for an idealized flat surface would be either no slip (
![]() $U+u=v=w=0$
) for a solid surface or free slip
$U+u=v=w=0$
) for a solid surface or free slip
![]() $\unicode[STIX]{x2202}(U+u)/\unicode[STIX]{x2202}z=0$
for a free surface. More complicated conditions at the surface could also be introduced to mimic some important natural air–sea interaction, but such complications are beyond the scope of this paper. Even the simple no-slip or free-slip conditions applied to the surface introduce a problem for studying the stability of our inviscid solution
$\unicode[STIX]{x2202}(U+u)/\unicode[STIX]{x2202}z=0$
for a free surface. More complicated conditions at the surface could also be introduced to mimic some important natural air–sea interaction, but such complications are beyond the scope of this paper. Even the simple no-slip or free-slip conditions applied to the surface introduce a problem for studying the stability of our inviscid solution
![]() $U(y,z)$
in (2.25) since it is non-zero at the surface and has a non-zero vertical gradient there. We can mitigate this problem, from a numerical point of view, by separating the basic flow
$U(y,z)$
in (2.25) since it is non-zero at the surface and has a non-zero vertical gradient there. We can mitigate this problem, from a numerical point of view, by separating the basic flow
![]() $U$
and the perturbation
$U$
and the perturbation
![]() $(u,v,w)$
, as we have done in (3.1)–(3.4). With this decomposition, we can resolve the problem to a certain extent by applying the no-slip or free-slip conditions to the perturbation alone. This leaves the decision as to which set of conditions is best to use for our purpose. The disadvantage of the no-slip condition is that vorticity is generated at the boundary if there is any surface lateral flow. This creates boundary layer vortices that then move off into the interior of the flow. Although such boundary layer effects are interesting, they are not the focus of this work. The advantage of free-slip (i.e. stress-free) conditions is that such boundary vorticity creation is eliminated, allowing us to focus on the vorticity generated only due to the interplay of rotation and advection. In addition to the surface, we will apply free slip on the bottom and on artificial but necessary latitudinal boundaries as well, for the same reason.
$(u,v,w)$
, as we have done in (3.1)–(3.4). With this decomposition, we can resolve the problem to a certain extent by applying the no-slip or free-slip conditions to the perturbation alone. This leaves the decision as to which set of conditions is best to use for our purpose. The disadvantage of the no-slip condition is that vorticity is generated at the boundary if there is any surface lateral flow. This creates boundary layer vortices that then move off into the interior of the flow. Although such boundary layer effects are interesting, they are not the focus of this work. The advantage of free-slip (i.e. stress-free) conditions is that such boundary vorticity creation is eliminated, allowing us to focus on the vorticity generated only due to the interplay of rotation and advection. In addition to the surface, we will apply free slip on the bottom and on artificial but necessary latitudinal boundaries as well, for the same reason.
In each simulation, the initial velocity field was constructed from the basic steady inviscid velocity field
![]() $U$
plus small randomly generated perturbations in the
$U$
plus small randomly generated perturbations in the
![]() $v$
and
$v$
and
![]() $w$
fields at every point on the grid. The resolution required to resolve the spatial structure of flow will depend on the Reynolds number of the flow and on whether we are simulating linearized or fully nonlinear flow.
$w$
fields at every point on the grid. The resolution required to resolve the spatial structure of flow will depend on the Reynolds number of the flow and on whether we are simulating linearized or fully nonlinear flow.
Given the computational resources available to us, we explored as wide a range of Reynolds numbers as possible. For the linear problem, higher Reynolds numbers can be achieved than for the nonlinear problem. In the linear case, the resolution only needs to be sufficient to resolve the structure of the inertially unstable modes. For the nonlinear studies, however, these unstable modes become turbulent and generate structures of smaller scale which must also be resolved, making the computational burden much greater. However, by adjusting the resolution as needed, going up to a maximum of
![]() $2049\times 2049$
grid points, we were able to obtain well-resolved results that indicate the asymptotic high-
$2049\times 2049$
grid points, we were able to obtain well-resolved results that indicate the asymptotic high-
![]() $Re$
trends. Moreover, for the nonlinear problem, the viscous decay of the background current becomes a serious issue for low Reynolds numbers. At sufficiently low
$Re$
trends. Moreover, for the nonlinear problem, the viscous decay of the background current becomes a serious issue for low Reynolds numbers. At sufficiently low
![]() $Re$
, that decay results in the generation of strong large-scale vortices and a strong surface boundary layer which completely dominate and obscure the effects of inertial instability. These issues restricted the range of
$Re$
, that decay results in the generation of strong large-scale vortices and a strong surface boundary layer which completely dominate and obscure the effects of inertial instability. These issues restricted the range of
![]() $Re$
explored. In all simulations, we report the Reynolds number defined by
$Re$
explored. In all simulations, we report the Reynolds number defined by
![]() $Re=|U_{0}|L/\unicode[STIX]{x1D708}$
based on the parameters
$Re=|U_{0}|L/\unicode[STIX]{x1D708}$
based on the parameters
![]() $L$
and
$L$
and
![]() $U_{0}$
from the background flow (the westward flowing Gaussian jet).
$U_{0}$
from the background flow (the westward flowing Gaussian jet).
Although the focus in this study is on the NTA dynamics, in § 4, the ‘NTA’ terms are switched off to extract detailed information about the early (linear) stages of the development of the instability in the westward flowing jet
![]() $U(y)$
(2.28) in the TA dynamics. The purpose is twofold: it complements Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015), where we focused primarily on the fully nonlinear evolution, and it offers a sharp contrast to the NTA dynamics.
$U(y)$
(2.28) in the TA dynamics. The purpose is twofold: it complements Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015), where we focused primarily on the fully nonlinear evolution, and it offers a sharp contrast to the NTA dynamics.
4 Linear viscous results
We next consider the linearized problem for jets over a wide range of
![]() $L/R_{0}$
, and will present in detail two examples representing relatively wide and narrow jets. For the wide-jet example, we will take
$L/R_{0}$
, and will present in detail two examples representing relatively wide and narrow jets. For the wide-jet example, we will take
![]() $L/R_{0}=0.25$
, which corresponds to approximately
$L/R_{0}=0.25$
, which corresponds to approximately
![]() $14^{\circ }$
of latitude, and for the narrow jet, we will take
$14^{\circ }$
of latitude, and for the narrow jet, we will take
![]() $L/R_{0}=0.05$
, corresponding to approximately
$L/R_{0}=0.05$
, corresponding to approximately
![]() $3^{\circ }$
of latitude.
$3^{\circ }$
of latitude.
As mentioned earlier (§ 2.3),
![]() $A=|U_{0}|/\unicode[STIX]{x1D6FD}L^{2}$
will be taken as the Rossby number for the flow. We will consider only the case of inertially unstable westward flowing jets (
$A=|U_{0}|/\unicode[STIX]{x1D6FD}L^{2}$
will be taken as the Rossby number for the flow. We will consider only the case of inertially unstable westward flowing jets (
![]() $U_{0}<0$
). For inviscid flow in the NTA, the steady Gaussian current
$U_{0}<0$
). For inviscid flow in the NTA, the steady Gaussian current
![]() $U$
will be unstable for any
$U$
will be unstable for any
![]() $A>1$
; however, low
$A>1$
; however, low
![]() $Re$
may stabilize the inviscidly unstable flow. For the range of
$Re$
may stabilize the inviscidly unstable flow. For the range of
![]() $Re$
that we will examine, we found that the choice
$Re$
that we will examine, we found that the choice
![]() $A=5$
always results in a vigorous instability, and we have fixed
$A=5$
always results in a vigorous instability, and we have fixed
![]() $A$
at this value for the work presented in this paper.
$A$
at this value for the work presented in this paper.
To determine the growth rates and spatial scales of the fastest growing modes, we ran simulations in the linear mode, as discussed above. The runs are started with the background state perturbed by very-small-amplitude random noise. The flow is allowed to evolve until the growth of the perturbation energy is essentially purely exponential and little if any change in the spatial structure of the growing perturbation is observed.
4.1 Spatial structure of the fastest growing modes
For the TA, both the linear and nonlinear evolutions have been discussed in great detail in Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015). Here, we will present only one representative example of linearized evolution in the TA case for comparison with the NTA results. Figure 5 shows the fastest growing mode in the TA from the linearized numerical simulations. They are visualized by plotting the zonal vorticity
![]() $\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x2202}_{y}w-\unicode[STIX]{x2202}_{z}v$
. It should be noted that, throughout this paper, the aspect ratio of the contour plots is chosen so that the units of length in the physical, i.e. unscaled, coordinates
$\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x2202}_{y}w-\unicode[STIX]{x2202}_{z}v$
. It should be noted that, throughout this paper, the aspect ratio of the contour plots is chosen so that the units of length in the physical, i.e. unscaled, coordinates
![]() $y$
and
$y$
and
![]() $z$
are equal on each axis. Thus, the aspect ratios of the rolls as seen in the plots are the physical aspect ratios. Therefore, we see in figure 5 that in the TA, the rolls have their major axes is aligned parallel to the surface. These vortices line up in two vertical stacks, one on either side of the equator. The stacks are centred at the locations predicted by (2.30), i.e. for
$z$
are equal on each axis. Thus, the aspect ratios of the rolls as seen in the plots are the physical aspect ratios. Therefore, we see in figure 5 that in the TA, the rolls have their major axes is aligned parallel to the surface. These vortices line up in two vertical stacks, one on either side of the equator. The stacks are centred at the locations predicted by (2.30), i.e. for
![]() $A=5$
at
$A=5$
at
![]() $\pm {\tilde{y}}_{m}\approx \pm 1.12$
. The bounds on the unstable region are at
$\pm {\tilde{y}}_{m}\approx \pm 1.12$
. The bounds on the unstable region are at
![]() ${\tilde{y}}_{\pm }=\pm \sqrt{2\ln A}\approx \pm 1.79$
. By comparing the rolls in the two panels, we see that as
${\tilde{y}}_{\pm }=\pm \sqrt{2\ln A}\approx \pm 1.79$
. By comparing the rolls in the two panels, we see that as
![]() $Re$
increases, both the width and the height of the rolls decrease. This shrinking of the rolls in both directions as
$Re$
increases, both the width and the height of the rolls decrease. This shrinking of the rolls in both directions as
![]() $Re$
increases is not just for the equatorial problem, but is generally the case in inertial instability.
$Re$
increases is not just for the equatorial problem, but is generally the case in inertial instability.
The major axes of the rolls are parallel to the horizontal instability direction
![]() $\boldsymbol{e}_{1}$
(2.29) associated with maximal growth of displacements in Solberg’s argument or the direction of maximal energy release in Rayleigh’s exchange argument (see the end of § 2.1). Moreover, they emerge spontaneously in the instability region with the shape envisioned by Ooyama (Reference Ooyama1966) for growth of meridional kinetic energy: highly elongated along the
$\boldsymbol{e}_{1}$
(2.29) associated with maximal growth of displacements in Solberg’s argument or the direction of maximal energy release in Rayleigh’s exchange argument (see the end of § 2.1). Moreover, they emerge spontaneously in the instability region with the shape envisioned by Ooyama (Reference Ooyama1966) for growth of meridional kinetic energy: highly elongated along the
![]() $\boldsymbol{e}_{1}$
direction.
$\boldsymbol{e}_{1}$
direction.
The evolution in the NTA case is different in several important respects. First of all, it should be noted that the fastest growing mode shown for the wide-jet case (
![]() $L/R_{0}=0.25$
) in figure 6 for NTA simulations nicely verifies the pattern predicted in figure 2(b). Each roll in the mode is oriented with its long axis perpendicular to the parabolas of constant distance from the planet rotation axis.
$L/R_{0}=0.25$
) in figure 6 for NTA simulations nicely verifies the pattern predicted in figure 2(b). Each roll in the mode is oriented with its long axis perpendicular to the parabolas of constant distance from the planet rotation axis.
Again, this is the
![]() $\boldsymbol{e}_{1}$
instability direction (2.22) via Solberg’s/Rayleigh’s argument or Ooyama’s proof of instability but with the full Coriolis force taken into account (see § 2.2). The resulting ‘stack’ of rolls is aligned with the Earth’s rotation axis, as predicted in figure 2. Another important difference from the TA case is that the fastest growing mode in the NTA is confined near the surface (see figure 6). This is due to the flow itself being surface-confined. This mode contracts towards a point located at the surface at the equator, i.e. towards
$\boldsymbol{e}_{1}$
instability direction (2.22) via Solberg’s/Rayleigh’s argument or Ooyama’s proof of instability but with the full Coriolis force taken into account (see § 2.2). The resulting ‘stack’ of rolls is aligned with the Earth’s rotation axis, as predicted in figure 2. Another important difference from the TA case is that the fastest growing mode in the NTA is confined near the surface (see figure 6). This is due to the flow itself being surface-confined. This mode contracts towards a point located at the surface at the equator, i.e. towards
![]() $\{y,z\}=\{0,0\}$
as
$\{y,z\}=\{0,0\}$
as
![]() $Re$
increases. This is the predicted position of maximal growth according to the simple theory in § 2.2.
$Re$
increases. This is the predicted position of maximal growth according to the simple theory in § 2.2.

Figure 7. (a) Amplitude of the
![]() $\unicode[STIX]{x1D714}_{x}$
rolls seen in figure 5, as a function of latitude (solid lines). The latitudinal profile is Gaussian:
$\unicode[STIX]{x1D714}_{x}$
rolls seen in figure 5, as a function of latitude (solid lines). The latitudinal profile is Gaussian:
![]() $\exp (-({\tilde{y}}-{\tilde{y}}_{m})^{2}/2h^{2})$
, with
$\exp (-({\tilde{y}}-{\tilde{y}}_{m})^{2}/2h^{2})$
, with
![]() ${\tilde{y}}=y_{m}\approx 1.12$
(dashed lines). The best fit for the scale
${\tilde{y}}=y_{m}\approx 1.12$
(dashed lines). The best fit for the scale
![]() $h$
diminishes with increasing
$h$
diminishes with increasing
![]() $Re$
:
$Re$
:
![]() $h=0.255$
, 0.164 and 0.125 respectively. (b) Amplitude of the most intense rolls near the equator like those shown in figure 6, as a function of depth (solid lines). The measured profiles are fitted with
$h=0.255$
, 0.164 and 0.125 respectively. (b) Amplitude of the most intense rolls near the equator like those shown in figure 6, as a function of depth (solid lines). The measured profiles are fitted with
![]() $\text{Ai}(-\unicode[STIX]{x1D706}_{0}-\tilde{z}/\unicode[STIX]{x1D701})$
(dashed lines, see text), where Ai is the Airy function,
$\text{Ai}(-\unicode[STIX]{x1D706}_{0}-\tilde{z}/\unicode[STIX]{x1D701})$
(dashed lines, see text), where Ai is the Airy function,
![]() $\unicode[STIX]{x1D706}_{0}\approx 2.338$
and the vertical scale
$\unicode[STIX]{x1D706}_{0}\approx 2.338$
and the vertical scale
![]() $\unicode[STIX]{x1D701}$
diminishes with increasing
$\unicode[STIX]{x1D701}$
diminishes with increasing
![]() $Re$
:
$Re$
:
![]() $\unicode[STIX]{x1D701}=0.326$
,
$\unicode[STIX]{x1D701}=0.326$
,
![]() $\unicode[STIX]{x1D701}=0.180$
and
$\unicode[STIX]{x1D701}=0.180$
and
![]() $\unicode[STIX]{x1D701}=0.100$
respectively.
$\unicode[STIX]{x1D701}=0.100$
respectively.
In figure 5 for the TA, in each stack of rolls, the behaviour with depth
![]() $z$
is indistinguishable from purely sinusoidal, with scales decreasing with increasing
$z$
is indistinguishable from purely sinusoidal, with scales decreasing with increasing
![]() $Re$
. The structure of the rolls with latitude (horizontally) is extremely close to Gaussians of the form
$Re$
. The structure of the rolls with latitude (horizontally) is extremely close to Gaussians of the form
![]() $\exp (-({\tilde{y}}-{\tilde{y}}_{m})^{2}/2h^{2})$
, with
$\exp (-({\tilde{y}}-{\tilde{y}}_{m})^{2}/2h^{2})$
, with
![]() ${\tilde{y}}_{m}$
the theoretical location of maximal growth and
${\tilde{y}}_{m}$
the theoretical location of maximal growth and
![]() $h$
a horizontal scale that decreases with increasing
$h$
a horizontal scale that decreases with increasing
![]() $Re$
. This is illustrated with figure 7(a). In appendix A, we show that indeed each of the unstable modes in the TA is expected to have a horizontal structure proportional to the product of a Gaussian and a Hermite polynomial of some integral order
$Re$
. This is illustrated with figure 7(a). In appendix A, we show that indeed each of the unstable modes in the TA is expected to have a horizontal structure proportional to the product of a Gaussian and a Hermite polynomial of some integral order
![]() $n$
, i.e.
$n$
, i.e.
![]() $H_{n}({\tilde{y}})\exp (-({\tilde{y}}-{\tilde{y}}_{m})^{2}/2h^{2})$
. The fastest growing mode corresponds to
$H_{n}({\tilde{y}})\exp (-({\tilde{y}}-{\tilde{y}}_{m})^{2}/2h^{2})$
. The fastest growing mode corresponds to
![]() $n=0$
.
$n=0$
.
The cross-stream Gaussian structure of the modes centred about the line of maximal growth shown in figure 7(a) is canonical. Generally, for large
![]() $Re$
, in normal-mode analysis, an eigenvalue problem in the form of the quantum harmonic oscillator equation appears (see Dunkerton Reference Dunkerton1981; Bayly Reference Bayly1988; Sipp & Jacquin Reference Sipp and Jacquin2000; Griffiths Reference Griffiths2008a
,Reference Griffiths
b
and § A.1 in appendix A). It is always predicted for flows
$Re$
, in normal-mode analysis, an eigenvalue problem in the form of the quantum harmonic oscillator equation appears (see Dunkerton Reference Dunkerton1981; Bayly Reference Bayly1988; Sipp & Jacquin Reference Sipp and Jacquin2000; Griffiths Reference Griffiths2008a
,Reference Griffiths
b
and § A.1 in appendix A). It is always predicted for flows
![]() $U(y)$
for which
$U(y)$
for which
![]() $\unicode[STIX]{x1D706}_{1}=fQ$
has isolated negative minima away from any horizontally confining boundaries. However, we believe that here, for the first time, such theoretical predictions have been confirmed through precise numerical simulations.
$\unicode[STIX]{x1D706}_{1}=fQ$
has isolated negative minima away from any horizontally confining boundaries. However, we believe that here, for the first time, such theoretical predictions have been confirmed through precise numerical simulations.
In the NTA, the rolls stack along the surface, as seen in figure 6. We find that with depth
![]() $z$
, the structure of the modes near the equator in the NTA is well matched by Airy function behaviour (see figure 7
b). They take the form
$z$
, the structure of the modes near the equator in the NTA is well matched by Airy function behaviour (see figure 7
b). They take the form
![]() $\text{Ai}(-\unicode[STIX]{x1D706}_{0}-\tilde{z}/\unicode[STIX]{x1D701})$
, with
$\text{Ai}(-\unicode[STIX]{x1D706}_{0}-\tilde{z}/\unicode[STIX]{x1D701})$
, with
![]() $\unicode[STIX]{x1D701}$
a vertical scale that diminishes with increasing
$\unicode[STIX]{x1D701}$
a vertical scale that diminishes with increasing
![]() $Re$
. The constant
$Re$
. The constant
![]() $\unicode[STIX]{x1D706}_{0}\approx 2.338$
is the lowest eigenvalue that sets
$\unicode[STIX]{x1D706}_{0}\approx 2.338$
is the lowest eigenvalue that sets
![]() $\text{Ai}(-\unicode[STIX]{x1D706}_{0})=0$
. This is the analogue of the fact that the fastest growing mode in the TA corresponds to the lowest eigenvalue (
$\text{Ai}(-\unicode[STIX]{x1D706}_{0})=0$
. This is the analogue of the fact that the fastest growing mode in the TA corresponds to the lowest eigenvalue (
![]() $n=0$
) of the Hermite functions. This behaviour too follows from the analysis in appendix A when assuming that all variations with latitude
$n=0$
) of the Hermite functions. This behaviour too follows from the analysis in appendix A when assuming that all variations with latitude
![]() $y$
can be ignored. We believe that this is a truly novel result.
$y$
can be ignored. We believe that this is a truly novel result.
The measured amplitudes of the surface-confined patterns in figure 6 also have ever smaller latitudinal scales with increasing
![]() $Re$
. Quite remarkable is the observation that below the surface (
$Re$
. Quite remarkable is the observation that below the surface (
![]() $z<0$
) they cannot be distinguished from
$z<0$
) they cannot be distinguished from
![]() $\unicode[STIX]{x1D714}_{x}\propto \cos (l{\tilde{y}})\exp (-{\tilde{y}}^{2}/2\unicode[STIX]{x1D702}^{2})$
behaviour, with
$\unicode[STIX]{x1D714}_{x}\propto \cos (l{\tilde{y}})\exp (-{\tilde{y}}^{2}/2\unicode[STIX]{x1D702}^{2})$
behaviour, with
![]() $\unicode[STIX]{x1D702}$
a number that decreases with increasing
$\unicode[STIX]{x1D702}$
a number that decreases with increasing
![]() $Re$
, and
$Re$
, and
![]() $l$
a wavenumber that increases with
$l$
a wavenumber that increases with
![]() $Re$
. Thus, there is oscillatory behaviour within a Gaussian envelope whose width, measured by
$Re$
. Thus, there is oscillatory behaviour within a Gaussian envelope whose width, measured by
![]() $\unicode[STIX]{x1D702}$
, is not determined by the scale of the background jet which varies as
$\unicode[STIX]{x1D702}$
, is not determined by the scale of the background jet which varies as
![]() $\exp (-y^{2}/2L^{2})=\exp (-{\tilde{y}}^{2}/2)$
.
$\exp (-y^{2}/2L^{2})=\exp (-{\tilde{y}}^{2}/2)$
.
For example, for
![]() $Re=10^{6}$
, we find
$Re=10^{6}$
, we find
![]() $\unicode[STIX]{x1D702}=0.0374$
, so then the scale of the envelope is only approximately 4 % of that of the background flow. However, if we ignore this latitudinal variation of the envelope of the surface-confined modes for the NTA case, we can predict how rates of growth scale with the Reynolds number
$\unicode[STIX]{x1D702}=0.0374$
, so then the scale of the envelope is only approximately 4 % of that of the background flow. However, if we ignore this latitudinal variation of the envelope of the surface-confined modes for the NTA case, we can predict how rates of growth scale with the Reynolds number
![]() $Re$
and the horizontal/vertical scales. All details are given in appendix A, §§ A.3 and A.4.
$Re$
and the horizontal/vertical scales. All details are given in appendix A, §§ A.3 and A.4.
4.2 Growth rates and horizontal/vertical scales as functions of
 $Re$
and
$Re$
and
 $L$
$L$
In Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015), we studied the nonlinear development of the instability on the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane. Among other flows, the Gaussian barotropic jet was also considered. However, the effect of the variation of
$\unicode[STIX]{x1D6FD}$
-plane. Among other flows, the Gaussian barotropic jet was also considered. However, the effect of the variation of
![]() $Re$
on the width/height and the growth rate of the rolls has not been considered in any detail by us or anyone else, to the best of our knowledge. This is clearly of interest, and we shall now compare the results with the previously entirely unexplored NTA dynamics.
$Re$
on the width/height and the growth rate of the rolls has not been considered in any detail by us or anyone else, to the best of our knowledge. This is clearly of interest, and we shall now compare the results with the previously entirely unexplored NTA dynamics.
A series of linearized simulations of the type used to produce figure 5 (TA) and figure 6 (NTA) was performed over a wide range of values of
![]() $Re$
. The value of the growth rate of the fastest growing mode was calculated as half of the growth rate of the perturbation energy after all transients had died down and the growth appeared to be due to a single exponentially growing mode, with amplitude growing as
$Re$
. The value of the growth rate of the fastest growing mode was calculated as half of the growth rate of the perturbation energy after all transients had died down and the growth appeared to be due to a single exponentially growing mode, with amplitude growing as
![]() $\exp (\unicode[STIX]{x1D6FE}t)$
. The resulting graph of
$\exp (\unicode[STIX]{x1D6FE}t)$
. The resulting graph of
![]() $\unicode[STIX]{x1D6FE}$
versus
$\unicode[STIX]{x1D6FE}$
versus
![]() $Re$
for fixed
$Re$
for fixed
![]() $A=5$
and
$A=5$
and
![]() $L/R_{0}=0.25$
is shown in figure 8(a). The TA data have been fitted with
$L/R_{0}=0.25$
is shown in figure 8(a). The TA data have been fitted with
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\infty }-bRe^{-1/3}$
, with
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\infty }-bRe^{-1/3}$
, with
![]() $\unicode[STIX]{x1D6FE}_{\infty }$
given by (2.31), which for
$\unicode[STIX]{x1D6FE}_{\infty }$
given by (2.31), which for
![]() $A=5$
and
$A=5$
and
![]() $L/R_{0}=0.25$
is
$L/R_{0}=0.25$
is
![]() $\unicode[STIX]{x1D6FE}_{\infty }=0.362$
. With the NTA,
$\unicode[STIX]{x1D6FE}_{\infty }=0.362$
. With the NTA,
![]() $\unicode[STIX]{x1D6FE}_{\infty }$
is determined by (2.27), which for
$\unicode[STIX]{x1D6FE}_{\infty }$
is determined by (2.27), which for
![]() $A=5$
means
$A=5$
means
![]() $\unicode[STIX]{x1D6FE}_{\infty }=\sqrt{5-1}=2$
. This is well fitted with
$\unicode[STIX]{x1D6FE}_{\infty }=\sqrt{5-1}=2$
. This is well fitted with
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\infty }-bRe^{-1/4}$
in figure 8(a). Thus, in both the TA and the NTA, the growth rates asymptotically approach the appropriate inviscid upper bound as
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\infty }-bRe^{-1/4}$
in figure 8(a). Thus, in both the TA and the NTA, the growth rates asymptotically approach the appropriate inviscid upper bound as
![]() $Re\rightarrow \infty$
, but in the TA with
$Re\rightarrow \infty$
, but in the TA with
![]() $Re^{-1/3}$
while in the NTA with
$Re^{-1/3}$
while in the NTA with
![]() $Re^{-1/4}$
. This behaviour is predicted by the asymptotic analyses presented in appendix A.
$Re^{-1/4}$
. This behaviour is predicted by the asymptotic analyses presented in appendix A.

Figure 8. Statistics for the fastest growing normal mode with
![]() $A=5$
. (a) Effects of variation of
$A=5$
. (a) Effects of variation of
![]() $Re$
on the growth rate in both the TA and the NTA. In both cases,
$Re$
on the growth rate in both the TA and the NTA. In both cases,
![]() $\unicode[STIX]{x1D6FE}_{\infty }$
is the theoretical inviscid upper limit (see text): in the TA,
$\unicode[STIX]{x1D6FE}_{\infty }$
is the theoretical inviscid upper limit (see text): in the TA,
![]() $\unicode[STIX]{x1D6FE}_{\infty }=0.362$
, and in the NTA,
$\unicode[STIX]{x1D6FE}_{\infty }=0.362$
, and in the NTA,
![]() $\unicode[STIX]{x1D6FE}_{\infty }=\sqrt{1-A}=2$
. The parameter
$\unicode[STIX]{x1D6FE}_{\infty }=\sqrt{1-A}=2$
. The parameter
![]() $b$
was estimated as the best least-squares fit to the data over the range
$b$
was estimated as the best least-squares fit to the data over the range
![]() $Re\in [10^{5}:10^{6}]$
: 1.04 (TA); 8.94 (NTA). These results are from simulations with
$Re\in [10^{5}:10^{6}]$
: 1.04 (TA); 8.94 (NTA). These results are from simulations with
![]() $L/R_{0}=0.25$
. (b) Effects of variation of
$L/R_{0}=0.25$
. (b) Effects of variation of
![]() $Re$
on the spatial horizontal and vertical scales of the rolls in the TA. Here,
$Re$
on the spatial horizontal and vertical scales of the rolls in the TA. Here,
![]() $L_{v}$
and
$L_{v}$
and
![]() $L_{h}$
are given in units of
$L_{h}$
are given in units of
![]() $L^{2}/R_{0}$
and
$L^{2}/R_{0}$
and
![]() $L$
respectively, and a power-law fit to the
$L$
respectively, and a power-law fit to the
![]() $L_{v}$
and
$L_{v}$
and
![]() $L_{h}$
data is made with least-squares best-fit proportionality coefficients of
$L_{h}$
data is made with least-squares best-fit proportionality coefficients of
![]() $a=31.3$
and
$a=31.3$
and
![]() $a=1.45$
respectively. These results are from simulations with
$a=1.45$
respectively. These results are from simulations with
![]() $L/R_{0}=0.25$
. (c) Effects of variation of
$L/R_{0}=0.25$
. (c) Effects of variation of
![]() $Re$
on the spatial horizontal and vertical scales of the rolls in the NTA. A power-law fit to the simulation data for
$Re$
on the spatial horizontal and vertical scales of the rolls in the NTA. A power-law fit to the simulation data for
![]() $L_{v}$
and
$L_{v}$
and
![]() $L_{h}$
is made with least-squares best-fit proportionality coefficients of
$L_{h}$
is made with least-squares best-fit proportionality coefficients of
![]() $a=4.74$
and
$a=4.74$
and
![]() $a=0.404$
respectively. These results are from simulations with
$a=0.404$
respectively. These results are from simulations with
![]() $L/R_{0}=0.05$
. (d) Effects of variation in the NTA of
$L/R_{0}=0.05$
. (d) Effects of variation in the NTA of
![]() $L/R_{0}$
on the number of rolls
$L/R_{0}$
on the number of rolls
![]() $n=2L/L_{h}$
within the range
$n=2L/L_{h}$
within the range
![]() ${\tilde{y}}=[-1,+1]$
of the current. A least-squares fit over the range
${\tilde{y}}=[-1,+1]$
of the current. A least-squares fit over the range
![]() $L/R_{0}\in [0.01,0.25]$
to
$L/R_{0}\in [0.01,0.25]$
to
![]() $n=a(L/R_{0})^{-b}$
yields
$n=a(L/R_{0})^{-b}$
yields
![]() $a=20.3$
and
$a=20.3$
and
![]() $b=0.584$
. The Reynolds number is
$b=0.584$
. The Reynolds number is
![]() $10^{5}$
.
$10^{5}$
.
In figure 8(b), we show how the height and width of the rolls vary with
![]() $Re$
for the TA dynamics. The measured vertical length scales
$Re$
for the TA dynamics. The measured vertical length scales
![]() $L_{v}$
of the typical rolls seen in figure 5 were determined via vertical Fourier transform of
$L_{v}$
of the typical rolls seen in figure 5 were determined via vertical Fourier transform of
![]() $\unicode[STIX]{x1D714}_{x}$
along the vertical centreline at
$\unicode[STIX]{x1D714}_{x}$
along the vertical centreline at
![]() ${\tilde{y}}_{m}$
. From the resulting power spectrum, the mean wavelength was determined and the width
${\tilde{y}}_{m}$
. From the resulting power spectrum, the mean wavelength was determined and the width
![]() $L_{v}$
was computed as half of that wavelength. The measured horizontal scale
$L_{v}$
was computed as half of that wavelength. The measured horizontal scale
![]() $L_{h}$
of the rolls (with the Gaussian behaviour plotted in figure 7
a) was obtained as the horizontal half-width (distance between points where
$L_{h}$
of the rolls (with the Gaussian behaviour plotted in figure 7
a) was obtained as the horizontal half-width (distance between points where
![]() $\unicode[STIX]{x1D714}_{x}$
has its maximum value and half of that value) of the cell with the highest peak
$\unicode[STIX]{x1D714}_{x}$
has its maximum value and half of that value) of the cell with the highest peak
![]() $|\unicode[STIX]{x1D714}_{x}|$
in the domain. The data in figure 8(b) have been fitted with
$|\unicode[STIX]{x1D714}_{x}|$
in the domain. The data in figure 8(b) have been fitted with
![]() $L_{v}=aRe^{-1/3}$
and
$L_{v}=aRe^{-1/3}$
and
![]() $L_{h}=aRe^{-1/6}$
. These scaling laws were previously uncovered by Kloosterziel et al. (Reference Kloosterziel, Carnevale and Orlandi2007a
) for unstable circular vortices on the
$L_{h}=aRe^{-1/6}$
. These scaling laws were previously uncovered by Kloosterziel et al. (Reference Kloosterziel, Carnevale and Orlandi2007a
) for unstable circular vortices on the
![]() $f$
-plane. These exponents in the TA dynamics are expected from the general asymptotic analysis presented in appendix A, with the relevant material in § A.1, § A.2 adapted from Griffiths (Reference Griffiths2008b
) in Kloosterziel & Carnevale (Reference Kloosterziel and Carnevale2008).
$f$
-plane. These exponents in the TA dynamics are expected from the general asymptotic analysis presented in appendix A, with the relevant material in § A.1, § A.2 adapted from Griffiths (Reference Griffiths2008b
) in Kloosterziel & Carnevale (Reference Kloosterziel and Carnevale2008).
For the NTA dynamics, the vertical scale
![]() $L_{v}$
was measured as the vertical half-width (with respect to
$L_{v}$
was measured as the vertical half-width (with respect to
![]() $\unicode[STIX]{x1D714}_{x}$
), measured vertically downward from the point of maximum
$\unicode[STIX]{x1D714}_{x}$
), measured vertically downward from the point of maximum
![]() $|\unicode[STIX]{x1D714}_{x}|$
in the domain. These scales determine the Airy function behaviour with depth plotted in figure 7(b). The result along with a power-law fit is shown in figure 8(c). To measure the horizontal scales
$|\unicode[STIX]{x1D714}_{x}|$
in the domain. These scales determine the Airy function behaviour with depth plotted in figure 7(b). The result along with a power-law fit is shown in figure 8(c). To measure the horizontal scales
![]() $L_{h}$
in the NTA, we used a strategy similar to that used in the TA case, but here adapted to the fact that the rolls are primarily oriented vertically. The depth
$L_{h}$
in the NTA, we used a strategy similar to that used in the TA case, but here adapted to the fact that the rolls are primarily oriented vertically. The depth
![]() $z_{max}$
of the point at which the magnitude of the perturbation in
$z_{max}$
of the point at which the magnitude of the perturbation in
![]() $\unicode[STIX]{x1D714}_{x}$
was greatest was determined. The Fourier transform was taken on the horizontal line passing through this point, i.e. the transform of
$\unicode[STIX]{x1D714}_{x}$
was greatest was determined. The Fourier transform was taken on the horizontal line passing through this point, i.e. the transform of
![]() $\unicode[STIX]{x1D714}_{x}(y,z_{max})$
was performed in
$\unicode[STIX]{x1D714}_{x}(y,z_{max})$
was performed in
![]() $y$
. From the resulting power spectrum, the mean wavelength was determined and the width
$y$
. From the resulting power spectrum, the mean wavelength was determined and the width
![]() $L_{h}$
was computed as half of that wavelength. The resulting data are shown as solid circles in figure 8(c) and have been fitted with
$L_{h}$
was computed as half of that wavelength. The resulting data are shown as solid circles in figure 8(c) and have been fitted with
![]() $L_{v}=aRe^{-1/4}$
and
$L_{v}=aRe^{-1/4}$
and
![]() $L_{h}=aRe^{-3/8}$
. It should be noted that these powers are different from what we showed in figure 8(b) for the traditional dynamics. These different exponents are again expected from the asymptotic analysis of appendix A in §§ A.3 and A.4, which, however, ignores all variation with latitude
$L_{h}=aRe^{-3/8}$
. It should be noted that these powers are different from what we showed in figure 8(b) for the traditional dynamics. These different exponents are again expected from the asymptotic analysis of appendix A in §§ A.3 and A.4, which, however, ignores all variation with latitude
![]() $y$
.
$y$
.
Finally, we examine how the width of the rolls
![]() $L_{h}$
varies with the width of the current
$L_{h}$
varies with the width of the current
![]() $L$
in the NTA. This is in preparation for the next section where we study the nonlinear evolution of the jet with the full Coriolis force. In order to emphasize the difficulty that we will encounter in resolving the fully nonlinear flow as
$L$
in the NTA. This is in preparation for the next section where we study the nonlinear evolution of the jet with the full Coriolis force. In order to emphasize the difficulty that we will encounter in resolving the fully nonlinear flow as
![]() $L/R_{0}$
decreases, in figure 8(d) we plot the number of rolls
$L/R_{0}$
decreases, in figure 8(d) we plot the number of rolls
![]() $n=2L/L_{h}$
that would fit within a distance
$n=2L/L_{h}$
that would fit within a distance
![]() $L$
from the equator (i.e. within
$L$
from the equator (i.e. within
![]() ${\tilde{y}}=[-1,+1]$
). A fit of the measured data to
${\tilde{y}}=[-1,+1]$
). A fit of the measured data to
![]() $n=a(L/R_{0})^{-b}$
gives roughly
$n=a(L/R_{0})^{-b}$
gives roughly
![]() $a=20.3$
and
$a=20.3$
and
![]() $b=0.58$
. This suggest that
$b=0.58$
. This suggest that
![]() $n$
tends to infinity as
$n$
tends to infinity as
![]() $L$
tends to zero. The increase in the number of rolls
$L$
tends to zero. The increase in the number of rolls
![]() $n$
as
$n$
as
![]() $L/R_{0}$
decreases, or, in other words, the decrease of the latitudinal width of the rolls, makes it increasingly difficult to resolve the full current and still well resolve the inertial instability as
$L/R_{0}$
decreases, or, in other words, the decrease of the latitudinal width of the rolls, makes it increasingly difficult to resolve the full current and still well resolve the inertial instability as
![]() $L/R_{0}$
decreases. This increase of the ‘density of rolls’ with decreasing curvature
$L/R_{0}$
decreases. This increase of the ‘density of rolls’ with decreasing curvature
![]() $L/R_{0}$
is as of yet unexplained.
$L/R_{0}$
is as of yet unexplained.
5 Nonlinear evolution, mixing and equilibration
In Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015), we showed the fully nonlinear evolution of the instability in the TA dynamics. We found that in the initial phase of linear growth, the two stacks of alternating rolls seen in figure 6 appear. Then, with sufficiently high
![]() $Re$
, a nonlinear phase begins in which pairing of vorticity from each roll with the opposite signed vorticity from the roll just above and the roll below it produces two dipoles propagating horizontally in opposite directions, both towards and away from the equator. The interaction of these dipoles with all of the other similarly produced ones begins a turbulent phase which mixes momentum within and beyond the initially unstable region.
$Re$
, a nonlinear phase begins in which pairing of vorticity from each roll with the opposite signed vorticity from the roll just above and the roll below it produces two dipoles propagating horizontally in opposite directions, both towards and away from the equator. The interaction of these dipoles with all of the other similarly produced ones begins a turbulent phase which mixes momentum within and beyond the initially unstable region.
After the turbulent phase has died away, a new inertially stable barotropic flow emerges (a depth-independent Taylor column) with constant absolute momentum
![]() $M_{c}$
in the range
$M_{c}$
in the range
![]() $[-y_{mix},+y_{mix}]$
straddling the equator. There,
$[-y_{mix},+y_{mix}]$
straddling the equator. There,
![]() $\unicode[STIX]{x1D706}_{1}=-\unicode[STIX]{x1D6FD}y\,\text{d}M/\text{d}y=0$
. Outside that range, the flow is unchanged, with
$\unicode[STIX]{x1D706}_{1}=-\unicode[STIX]{x1D6FD}y\,\text{d}M/\text{d}y=0$
. Outside that range, the flow is unchanged, with
![]() $\unicode[STIX]{x1D706}_{1}>0$
. Thus, after equilibration, the growth rate of the instability vanishes everywhere (i.e.
$\unicode[STIX]{x1D706}_{1}>0$
. Thus, after equilibration, the growth rate of the instability vanishes everywhere (i.e.
![]() $\unicode[STIX]{x1D706}_{1}\geqslant 0$
everywhere). Homogenization of vertical vorticity
$\unicode[STIX]{x1D706}_{1}\geqslant 0$
everywhere). Homogenization of vertical vorticity
![]() $Q_{z}=\text{d}M/\text{d}y\approx 0$
that occurs during equilibration had been observed before by Griffiths (Reference Griffiths2003a
,Reference Griffiths
b
) for traditional
$Q_{z}=\text{d}M/\text{d}y\approx 0$
that occurs during equilibration had been observed before by Griffiths (Reference Griffiths2003a
,Reference Griffiths
b
) for traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane flows in a hydrostatic stratified environment. However, with the recipe outlined in § 2.5, we were able to precisely predict, for the first time, the mixing range (i.e.
$\unicode[STIX]{x1D6FD}$
-plane flows in a hydrostatic stratified environment. However, with the recipe outlined in § 2.5, we were able to precisely predict, for the first time, the mixing range (i.e.
![]() $y_{mix}$
) and the value of the mixed momentum
$y_{mix}$
) and the value of the mixed momentum
![]() $M_{c}$
. Since this material was presented in detail in Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015), we will not repeat it here.
$M_{c}$
. Since this material was presented in detail in Kloosterziel et al. (Reference Kloosterziel, Orlandi and Carnevale2015), we will not repeat it here.
We shall now investigate whether such a prediction is also possible for inertial instability with the full Coriolis force (NTA) via the Gaussian jet example. The time
![]() $t$
reported below is the non-dimensional time
$t$
reported below is the non-dimensional time
![]() $\tilde{t}=2\unicode[STIX]{x1D6FA}t$
, but the tilde has been omitted. To get the dimensional time
$\tilde{t}=2\unicode[STIX]{x1D6FA}t$
, but the tilde has been omitted. To get the dimensional time
![]() $t$
from the numbers in the figures, it should be noted that a day equals
$t$
from the numbers in the figures, it should be noted that a day equals
![]() $2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FA}$
, which means that to get the number of days corresponding the reported non-dimensional time
$2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FA}$
, which means that to get the number of days corresponding the reported non-dimensional time
![]() $t$
, one has to calculate
$t$
, one has to calculate
![]() $t/4\unicode[STIX]{x03C0}$
. Therefore, for example,
$t/4\unicode[STIX]{x03C0}$
. Therefore, for example,
![]() $t=90$
corresponds to
$t=90$
corresponds to
![]() $90/4\unicode[STIX]{x03C0}\approx 7$
days while
$90/4\unicode[STIX]{x03C0}\approx 7$
days while
![]() $t=5$
means 9.5 h.
$t=5$
means 9.5 h.
5.1 Non-traditional approximation: vortex dynamics
In what follows, the code is run in the fully nonlinear mode. The initial condition is again as in the linear simulations: random initial perturbation to the basic state with
![]() $A=5$
. For the wide jet with
$A=5$
. For the wide jet with
![]() $L/R_{0}=0.25$
, we showed the typical rolls near the surface in figure 6 for
$L/R_{0}=0.25$
, we showed the typical rolls near the surface in figure 6 for
![]() $Re=10^{5}$
and
$Re=10^{5}$
and
![]() $Re=10^{6}$
that emerge in the linearized dynamics. In the fully nonlinear dynamics, early in the evolution, the rolls form and grow just as in the linear simulations.
$Re=10^{6}$
that emerge in the linearized dynamics. In the fully nonlinear dynamics, early in the evolution, the rolls form and grow just as in the linear simulations.
As the rolls continue to amplify, nonlinear effects become evident. The primary change that occurs is that the vortices (the rolls seen in figure 6) start to ‘feel’ the shear created by their neighbours and begin to roll up in a manner already familiar from evolution on the
![]() $f$
-plane and the traditional
$f$
-plane and the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane (see Kloosterziel et al.
Reference Kloosterziel, Carnevale and Orlandi2007a
,Reference Kloosterziel, Orlandi and Carnevale
b
; Plougonven & Zeitlin Reference Plougonven and Zeitlin2009; Carnevale et al.
Reference Carnevale, Kloosterziel, Orlandi and van Sommeren2011, Reference Carnevale, Kloosterziel and Orlandi2013; Ribstein et al.
Reference Ribstein, Plougonven and Zeitlin2014; Kloosterziel et al.
Reference Kloosterziel, Orlandi and Carnevale2015). This action involves pairs of rolls of opposite signed vorticity. The tips of the pair roll up into a dipole. For each roll, one dipole tends to form at its tip near the surface and one at its tip deeper in the fluid. Dipoles are self-advecting structures. The dipoles that form near the surface are oriented so as to propagate towards the surface, which blocks their progress. The dipoles that form on the lower tips of the rolls are oriented so that they propagate downward towards greater depth. Through the agency of these propagating dipoles, the instability, which begins near the surface, fills out the region of linear instability and then goes beyond it.
$\unicode[STIX]{x1D6FD}$
-plane (see Kloosterziel et al.
Reference Kloosterziel, Carnevale and Orlandi2007a
,Reference Kloosterziel, Orlandi and Carnevale
b
; Plougonven & Zeitlin Reference Plougonven and Zeitlin2009; Carnevale et al.
Reference Carnevale, Kloosterziel, Orlandi and van Sommeren2011, Reference Carnevale, Kloosterziel and Orlandi2013; Ribstein et al.
Reference Ribstein, Plougonven and Zeitlin2014; Kloosterziel et al.
Reference Kloosterziel, Orlandi and Carnevale2015). This action involves pairs of rolls of opposite signed vorticity. The tips of the pair roll up into a dipole. For each roll, one dipole tends to form at its tip near the surface and one at its tip deeper in the fluid. Dipoles are self-advecting structures. The dipoles that form near the surface are oriented so as to propagate towards the surface, which blocks their progress. The dipoles that form on the lower tips of the rolls are oriented so that they propagate downward towards greater depth. Through the agency of these propagating dipoles, the instability, which begins near the surface, fills out the region of linear instability and then goes beyond it.
This action can be seen in figure 9 for a case with
![]() $L/R_{0}=0.25$
and
$L/R_{0}=0.25$
and
![]() $Re=10^{5}$
. The red/blue contours correspond to positive/negative values of
$Re=10^{5}$
. The red/blue contours correspond to positive/negative values of
![]() $\unicode[STIX]{x1D714}_{x}$
. The thick dashed parabola marks the limit of the linear instability region as determined by
$\unicode[STIX]{x1D714}_{x}$
. The thick dashed parabola marks the limit of the linear instability region as determined by
![]() $\unicode[STIX]{x1D706}_{1}=0$
, which for the NTA via (2.26) gives the parabola
$\unicode[STIX]{x1D706}_{1}=0$
, which for the NTA via (2.26) gives the parabola
![]() $\tilde{z}-{\tilde{y}}^{2}/2=-\ln A$
(with
$\tilde{z}-{\tilde{y}}^{2}/2=-\ln A$
(with
![]() ${\tilde{y}}=y/L$
,
${\tilde{y}}=y/L$
,
![]() $\tilde{z}=zR_{0}/L^{2}$
). The thick solid parabola marks the limit of the mixing range in the inviscid theory as determined by (B 8) in appendix B.
$\tilde{z}=zR_{0}/L^{2}$
). The thick solid parabola marks the limit of the mixing range in the inviscid theory as determined by (B 8) in appendix B.

Figure 9. Contour plots of zonal vorticity
![]() $\unicode[STIX]{x1D714}_{x}$
from a fully nonlinear unforced simulation of the wide jet (
$\unicode[STIX]{x1D714}_{x}$
from a fully nonlinear unforced simulation of the wide jet (
![]() $L/R_{0}=0.25$
) with
$L/R_{0}=0.25$
) with
![]() $A=5$
and
$A=5$
and
![]() $Re=10^{5}$
in the NTA. The
$Re=10^{5}$
in the NTA. The
![]() $|\unicode[STIX]{x1D714}_{x}|$
maximum in each plot is (a) 19, (b) 19, (c) 8.8, (d) 5.7. The corresponding contour increments
$|\unicode[STIX]{x1D714}_{x}|$
maximum in each plot is (a) 19, (b) 19, (c) 8.8, (d) 5.7. The corresponding contour increments
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{x}$
are (a) 4, (b) 2, (c) 1.5, (d) 0.5, and red/blue
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{x}$
are (a) 4, (b) 2, (c) 1.5, (d) 0.5, and red/blue
![]() $=$
positive/negative. The thick black dashed parabola is the limit of the linear instability region:
$=$
positive/negative. The thick black dashed parabola is the limit of the linear instability region:
![]() $\tilde{z}-{\tilde{y}}^{2}/2=-\ln A=-1.61$
for
$\tilde{z}-{\tilde{y}}^{2}/2=-\ln A=-1.61$
for
![]() $A=5$
. The thick grey parabola is the limit of the predicted equilibrium mixing region (at
$A=5$
. The thick grey parabola is the limit of the predicted equilibrium mixing region (at
![]() ${\tilde{y}}=0$
at depth
${\tilde{y}}=0$
at depth
![]() $\tilde{z}=\tilde{z}_{l}=-2.47$
, see text). The aspect ratio of the plots is such that the units of length in the unscaled physical variables
$\tilde{z}=\tilde{z}_{l}=-2.47$
, see text). The aspect ratio of the plots is such that the units of length in the unscaled physical variables
![]() $y$
and
$y$
and
![]() $z$
are the same in each direction, ensuring that the shape of the vortices as shown is the same as in the physical
$z$
are the same in each direction, ensuring that the shape of the vortices as shown is the same as in the physical
![]() $y{-}z$
coordinates. Only a portion of the computational domain is shown. In hours/days (see text), the time sequence is (a) 9.5 h (
$y{-}z$
coordinates. Only a portion of the computational domain is shown. In hours/days (see text), the time sequence is (a) 9.5 h (
![]() $t=5$
), (b) 19 h (
$t=5$
), (b) 19 h (
![]() $t=10$
), (c) 2 days (
$t=10$
), (c) 2 days (
![]() $t=25$
) and (d) 7 days (
$t=25$
) and (d) 7 days (
![]() $t=90$
).
$t=90$
).
In figure 9(a), we see that by non-dimensional time
![]() $t=5$
, which corresponds to
$t=5$
, which corresponds to
![]() $5/4\unicode[STIX]{x03C0}\approx 0.4$
days (9.5 h), the linear instability has grown sufficiently for the nonlinear effect of dipolar formation to have begun. In figure 9(b), we see that as the dipoles reach the limit of the theoretical mixing range, they begin to be diverted and some are distorted and destroyed. In figure 9(c), we see that some dipoles propagate somewhat beyond the limit of the mixing range before being stopped or turned around. The size of the dipoles decreases with increasing
$5/4\unicode[STIX]{x03C0}\approx 0.4$
days (9.5 h), the linear instability has grown sufficiently for the nonlinear effect of dipolar formation to have begun. In figure 9(b), we see that as the dipoles reach the limit of the theoretical mixing range, they begin to be diverted and some are distorted and destroyed. In figure 9(c), we see that some dipoles propagate somewhat beyond the limit of the mixing range before being stopped or turned around. The size of the dipoles decreases with increasing
![]() $Re$
, and so, as the results from our previous studies confirm, the higher the value of
$Re$
, and so, as the results from our previous studies confirm, the higher the value of
![]() $Re$
is, the less these dipoles penetrate beyond the theoretical boundary of the mixing range (Kloosterziel et al.
Reference Kloosterziel, Carnevale and Orlandi2007a
,Reference Kloosterziel, Orlandi and Carnevale
b
; Carnevale et al.
Reference Carnevale, Kloosterziel, Orlandi and van Sommeren2011, Reference Carnevale, Kloosterziel and Orlandi2013; Kloosterziel et al.
Reference Kloosterziel, Orlandi and Carnevale2015). Being smaller, the dipoles at higher
$Re$
is, the less these dipoles penetrate beyond the theoretical boundary of the mixing range (Kloosterziel et al.
Reference Kloosterziel, Carnevale and Orlandi2007a
,Reference Kloosterziel, Orlandi and Carnevale
b
; Carnevale et al.
Reference Carnevale, Kloosterziel, Orlandi and van Sommeren2011, Reference Carnevale, Kloosterziel and Orlandi2013; Kloosterziel et al.
Reference Kloosterziel, Orlandi and Carnevale2015). Being smaller, the dipoles at higher
![]() $Re$
can detect the mixing boundary more precisely, and they can have a smaller turning radius so that their motions can more effectively ‘describe’ where that boundary lies.
$Re$
can detect the mixing boundary more precisely, and they can have a smaller turning radius so that their motions can more effectively ‘describe’ where that boundary lies.
As the evolution proceeds, the absolute momentum in the mixing region becomes increasingly uniform (see below), the instability saturates and the perturbations begin to die away. By
![]() $t=90$
, the amplitudes of the vortices are down by a factor of approximately 4 from their peak values. We can note at this point the amazing ability of the small-scale structures, formed near the surface and around the equator, to effect the thorough mixing of momentum throughout the mixing region. Both the instability region and the mixing region are defined inviscidly. They do not change as
$t=90$
, the amplitudes of the vortices are down by a factor of approximately 4 from their peak values. We can note at this point the amazing ability of the small-scale structures, formed near the surface and around the equator, to effect the thorough mixing of momentum throughout the mixing region. Both the instability region and the mixing region are defined inviscidly. They do not change as
![]() $Re$
increases. On the other hand, the spatial scales of the most unstable mode shrink and the amplitude of the rolls becomes increasingly concentrated near
$Re$
increases. On the other hand, the spatial scales of the most unstable mode shrink and the amplitude of the rolls becomes increasingly concentrated near
![]() $(y,z)=(0,0)$
as
$(y,z)=(0,0)$
as
![]() $Re$
increases. However, with increasing
$Re$
increases. However, with increasing
![]() $Re$
, the dipoles, although of ever smaller scale, can persist longer and travel farther in the ever less viscous environment. Furthermore, their nonlinear interactions can create increasingly many more generations of vortices the higher the value of
$Re$
, the dipoles, although of ever smaller scale, can persist longer and travel farther in the ever less viscous environment. Furthermore, their nonlinear interactions can create increasingly many more generations of vortices the higher the value of
![]() $Re$
is. Thus, even with the shrinking of the region of generation, and the shrinking of the scale of the initially generated dipoles, the entire mixing region can still be engulfed with vortices, come to be thoroughly mixed, and, as it turns out, mixed more uniformly and precisely, as
$Re$
is. Thus, even with the shrinking of the region of generation, and the shrinking of the scale of the initially generated dipoles, the entire mixing region can still be engulfed with vortices, come to be thoroughly mixed, and, as it turns out, mixed more uniformly and precisely, as
![]() $Re$
increases.
$Re$
increases.
Another interesting feature in this simulation is that waves, with their crests roughly parallel to the parabolas drawn representing constant distance from the Earth’s rotation axis, are evident in the region outside the mixing region (see figure 9
d). These waves are created by disturbances in the mixing region and then propagate towards the bottom of the domain. They already exist at least by
![]() $t=10$
, but early on their amplitude is small compared with the maximum of
$t=10$
, but early on their amplitude is small compared with the maximum of
![]() $\unicode[STIX]{x1D714}_{x}$
in the vortices, so they are not evident in the early contour plots. However, as the peak amplitude of the vortices diminishes, the waves become evident in the contour plot if we decrease the contour level increment sufficiently, as we have done in figure 9(d). In an infinite domain, the waves could propagate away and completely escape, but in these simulations, in a finite box with free-slip conditions, they simply reflect from the bottom and from the walls and are only slowly dissipated by viscosity. Such waves have also been seen in studies of inertial instability on the traditional
$\unicode[STIX]{x1D714}_{x}$
in the vortices, so they are not evident in the early contour plots. However, as the peak amplitude of the vortices diminishes, the waves become evident in the contour plot if we decrease the contour level increment sufficiently, as we have done in figure 9(d). In an infinite domain, the waves could propagate away and completely escape, but in these simulations, in a finite box with free-slip conditions, they simply reflect from the bottom and from the walls and are only slowly dissipated by viscosity. Such waves have also been seen in studies of inertial instability on the traditional
![]() $f$
-plane (Kloosterziel et al.
Reference Kloosterziel, Carnevale and Orlandi2007a
; Plougonven & Zeitlin Reference Plougonven and Zeitlin2009; Ribstein et al.
Reference Ribstein, Plougonven and Zeitlin2014).
$f$
-plane (Kloosterziel et al.
Reference Kloosterziel, Carnevale and Orlandi2007a
; Plougonven & Zeitlin Reference Plougonven and Zeitlin2009; Ribstein et al.
Reference Ribstein, Plougonven and Zeitlin2014).
In most of the simulations that we have run, the waves are much less evident. This example was chosen to point out their presence. That these waves are simply inertial waves is implied by the facts that they propagate in the range where the main flow is very weak, their amplitude is small, suggesting linearity, there is no stratification and their frequencies of oscillation are in the expected range for internal gyroscopic waves. Since their nature is transitory with regard to our current examination of mixing of momentum
![]() $m$
, we have not examined them further.
$m$
, we have not examined them further.
5.2 Absolute momentum mixing
Our theory for the nonlinear saturation of inertial instability is based on mixing of the absolute momentum, as discussed in § 2.5. In terms of the decomposition of the velocity that we are using here, the full absolute momentum is written as
![]() $m=(U+u)-(1/2)\unicode[STIX]{x1D6FD}y^{2}+2\unicode[STIX]{x1D6FA}z$
. Mixing is driven by the vortex dynamics illustrated in figure 9. By time
$m=(U+u)-(1/2)\unicode[STIX]{x1D6FD}y^{2}+2\unicode[STIX]{x1D6FA}z$
. Mixing is driven by the vortex dynamics illustrated in figure 9. By time
![]() $t=200$
in this case with
$t=200$
in this case with
![]() $L/R_{0}=0.25$
, most residual vortex and wave activity is at a very low amplitude and the effect on
$L/R_{0}=0.25$
, most residual vortex and wave activity is at a very low amplitude and the effect on
![]() $m$
can be clearly seen in figure 10. Figure 10(a) shows the initial distribution
$m$
can be clearly seen in figure 10. Figure 10(a) shows the initial distribution
![]() $m=M=U-(1/2)\unicode[STIX]{x1D6FD}y^{2}+2\unicode[STIX]{x1D6FA}z$
. It should be noted that the thick black dashed contour marks the line of maximal
$m=M=U-(1/2)\unicode[STIX]{x1D6FD}y^{2}+2\unicode[STIX]{x1D6FA}z$
. It should be noted that the thick black dashed contour marks the line of maximal
![]() $M$
, that is where
$M$
, that is where
![]() $\unicode[STIX]{x2202}M/\unicode[STIX]{x2202}z=0$
. This dashed line forms the boundary of the instability region. It should be noted that
$\unicode[STIX]{x2202}M/\unicode[STIX]{x2202}z=0$
. This dashed line forms the boundary of the instability region. It should be noted that
![]() $\unicode[STIX]{x2202}M/\unicode[STIX]{x2202}z<0$
in the whole region extending from this dashed curve to the surface and that this negative gradient becomes very steep near the surface. In (b), we see that this gradient has been replaced by a nearly constant field. To be accurate, the region from the mixing boundary, the thick grey contour, up to the surface now exhibits only a weak positive vertical gradient of
$\unicode[STIX]{x2202}M/\unicode[STIX]{x2202}z<0$
in the whole region extending from this dashed curve to the surface and that this negative gradient becomes very steep near the surface. In (b), we see that this gradient has been replaced by a nearly constant field. To be accurate, the region from the mixing boundary, the thick grey contour, up to the surface now exhibits only a weak positive vertical gradient of
![]() $m$
. The contours outside the mixing region are essentially unchanged.
$m$
. The contours outside the mixing region are essentially unchanged.

Figure 10. Contour plots of initial and late-time absolute momentum
![]() $\tilde{m}=m/\unicode[STIX]{x1D6FD}L^{2}$
from a simulation with
$\tilde{m}=m/\unicode[STIX]{x1D6FD}L^{2}$
from a simulation with
![]() $Re=10^{5}$
,
$Re=10^{5}$
,
![]() $A=5$
and
$A=5$
and
![]() $L/R_{0}=0.25$
. All contours represent negative values. The contour increment is 0.16. The thick grey parabola is the predicted boundary of the uniformly mixed region expected in the inviscid limit, which at
$L/R_{0}=0.25$
. All contours represent negative values. The contour increment is 0.16. The thick grey parabola is the predicted boundary of the uniformly mixed region expected in the inviscid limit, which at
![]() ${\tilde{y}}=0$
is at the depth
${\tilde{y}}=0$
is at the depth
![]() $\tilde{z}=\tilde{z}_{l}=-2.47$
. The dashed black parabola is the line of maximum
$\tilde{z}=\tilde{z}_{l}=-2.47$
. The dashed black parabola is the line of maximum
![]() $M$
, which forms the boundary of the instability region. At its lowest point (at
$M$
, which forms the boundary of the instability region. At its lowest point (at
![]() ${\tilde{y}}=0$
), this is at
${\tilde{y}}=0$
), this is at
![]() $\tilde{z}=\tilde{z}_{ins}=-1.61$
. The time
$\tilde{z}=\tilde{z}_{ins}=-1.61$
. The time
![]() $t=200$
corresponds to approximately 16 days.
$t=200$
corresponds to approximately 16 days.

Figure 11. Plots of the vertical profiles of (a)
![]() $\tilde{m}=m/\unicode[STIX]{x1D6FD}L^{2}$
and (b)
$\tilde{m}=m/\unicode[STIX]{x1D6FD}L^{2}$
and (b)
![]() $\tilde{u} =u/\unicode[STIX]{x1D6FD}L^{2}$
at the equator at
$\tilde{u} =u/\unicode[STIX]{x1D6FD}L^{2}$
at the equator at
![]() $t=200$
for
$t=200$
for
![]() $A=5$
,
$A=5$
,
![]() $L/R_{0}=0.25$
and three values of
$L/R_{0}=0.25$
and three values of
![]() $Re$
,
$Re$
,
![]() $10^{4}$
,
$10^{4}$
,
![]() $3\times 10^{4}$
and
$3\times 10^{4}$
and
![]() $10^{5}$
. Also shown are the initial conditions (thin solid black curve) and the predicted inviscid equilibrium (thick solid grey) for which
$10^{5}$
. Also shown are the initial conditions (thin solid black curve) and the predicted inviscid equilibrium (thick solid grey) for which
![]() $\tilde{z}_{l}\approx -2.47$
,
$\tilde{z}_{l}\approx -2.47$
,
![]() $\tilde{M}_{c}\approx -2.89$
(see text). The results for
$\tilde{M}_{c}\approx -2.89$
(see text). The results for
![]() $Re=10^{4}$
,
$Re=10^{4}$
,
![]() $3\times 10^{4}$
and
$3\times 10^{4}$
and
![]() $10^{5}$
were averaged over 10, 100 and 200 realizations respectively. The time
$10^{5}$
were averaged over 10, 100 and 200 realizations respectively. The time
![]() $t=200$
corresponds to 16 days.
$t=200$
corresponds to 16 days.
Our inviscid prediction has two regions, that below the mixing boundary satisfying
![]() $m=M$
, the initial background distribution, and that above satisfying
$m=M$
, the initial background distribution, and that above satisfying
![]() $m=M_{c}$
, a constant. However, for any finite
$m=M_{c}$
, a constant. However, for any finite
![]() $Re$
, the smoothing effect of viscosity tends to erode the separation between these two regions and to create a positive gradient throughout the mixing region. To get a better idea of this viscous effect, it is useful to examine the vertical profiles of
$Re$
, the smoothing effect of viscosity tends to erode the separation between these two regions and to create a positive gradient throughout the mixing region. To get a better idea of this viscous effect, it is useful to examine the vertical profiles of
![]() $m$
at the equator for increasing
$m$
at the equator for increasing
![]() $Re$
. In figure 11(a), we see that as
$Re$
. In figure 11(a), we see that as
![]() $Re$
increases, the profile of
$Re$
increases, the profile of
![]() $m$
at
$m$
at
![]() $t=200$
systematically approaches that of the prediction shown as the thick grey curve. The flat part of the curve is at the predicted level
$t=200$
systematically approaches that of the prediction shown as the thick grey curve. The flat part of the curve is at the predicted level
![]() $\tilde{M}_{c}=M_{c}/\unicode[STIX]{x1D6FD}L^{2}\approx -2.89$
(see § 2.5 and appendix B). In order to eliminate effects of residual vortices or waves from the profiles, we have averaged the profiles over a number of realizations with different initial random seeds, as indicated in the figure caption.
$\tilde{M}_{c}=M_{c}/\unicode[STIX]{x1D6FD}L^{2}\approx -2.89$
(see § 2.5 and appendix B). In order to eliminate effects of residual vortices or waves from the profiles, we have averaged the profiles over a number of realizations with different initial random seeds, as indicated in the figure caption.
Figure 11(b) shows the ensemble averaged
![]() $u$
profiles, indicating how absolute momentum mixing changes the mean flow. It should be noted that the inviscid theory predicts that mixing will cause a drop in speed in the centre of the jet (at
$u$
profiles, indicating how absolute momentum mixing changes the mean flow. It should be noted that the inviscid theory predicts that mixing will cause a drop in speed in the centre of the jet (at
![]() $y=0$
,
$y=0$
,
![]() $z=0$
) from the initial
$z=0$
) from the initial
![]() $\tilde{U} _{0}\equiv |U_{0}|/\unicode[STIX]{x1D6FD}L^{2}=-A=-5$
to
$\tilde{U} _{0}\equiv |U_{0}|/\unicode[STIX]{x1D6FD}L^{2}=-A=-5$
to
![]() $\tilde{u} =\tilde{M}_{c}\approx -2.89$
, i.e. a drop of approximately 40 % in magnitude.
$\tilde{u} =\tilde{M}_{c}\approx -2.89$
, i.e. a drop of approximately 40 % in magnitude.
We wish now to illustrate how the inertial instability proceeds for a much narrower jet with
![]() $L/R_{0}=0.05$
. Choosing this value for our background current, we find that we cannot simulate the full width of the jet and fully resolve the turbulent flow that results at
$L/R_{0}=0.05$
. Choosing this value for our background current, we find that we cannot simulate the full width of the jet and fully resolve the turbulent flow that results at
![]() $Re=10^{5}$
as we did in the case of
$Re=10^{5}$
as we did in the case of
![]() $L/R_{0}=0.25$
treated above. The difficulty stems from the rapid increase in the number of rolls stacked in the latitudinal direction in the fastest growing mode as
$L/R_{0}=0.25$
treated above. The difficulty stems from the rapid increase in the number of rolls stacked in the latitudinal direction in the fastest growing mode as
![]() $L/R_{0}$
decreases, as illustrated in figure 8(d). To get around this, we use the following strategy: we keep the Reynolds number at the same value
$L/R_{0}$
decreases, as illustrated in figure 8(d). To get around this, we use the following strategy: we keep the Reynolds number at the same value
![]() $Re=10^{5}$
and set
$Re=10^{5}$
and set
![]() $L/R_{0}$
to the desired value 0.05. However, we truncate the latitudinal span of the domain that we will simulate. We do this by placing free-slip vertical walls within the background current at
$L/R_{0}$
to the desired value 0.05. However, we truncate the latitudinal span of the domain that we will simulate. We do this by placing free-slip vertical walls within the background current at
![]() ${\tilde{y}}=y/L=\pm 0.4$
. We resolve the latitudinal span with 2049 grid points. The vertical span of the computational domain is from the surface
${\tilde{y}}=y/L=\pm 0.4$
. We resolve the latitudinal span with 2049 grid points. The vertical span of the computational domain is from the surface
![]() $\tilde{z}=0$
down to
$\tilde{z}=0$
down to
![]() $\tilde{z}=zR_{0}/L^{2}=-8$
, which is covered by 1024 grid points.
$\tilde{z}=zR_{0}/L^{2}=-8$
, which is covered by 1024 grid points.

Figure 12. Contour plots of
![]() $\unicode[STIX]{x1D714}_{x}$
from a fully nonlinear unforced simulation with a narrow jet
$\unicode[STIX]{x1D714}_{x}$
from a fully nonlinear unforced simulation with a narrow jet
![]() $A=5$
,
$A=5$
,
![]() $L/R_{0}=0.05$
and
$L/R_{0}=0.05$
and
![]() $Re=10^{5}$
. The thick black dashed line is the limit of the linear instability region, as in the caption of figure 9. The thick grey solid line is the limit of the predicted equilibrium mixing region, which at
$Re=10^{5}$
. The thick black dashed line is the limit of the linear instability region, as in the caption of figure 9. The thick grey solid line is the limit of the predicted equilibrium mixing region, which at
![]() ${\tilde{y}}=0$
is at the depth
${\tilde{y}}=0$
is at the depth
![]() $\tilde{z}=\tilde{z}_{l}=-2.76$
(see the text). That prediction assumes that the unperturbed
$\tilde{z}=\tilde{z}_{l}=-2.76$
(see the text). That prediction assumes that the unperturbed
![]() $M$
varies little in the narrow latitudinal band afforded to the flow by the confining free-slip walls at latitudes
$M$
varies little in the narrow latitudinal band afforded to the flow by the confining free-slip walls at latitudes
![]() ${\tilde{y}}=\pm 0.4$
. The contour increment
${\tilde{y}}=\pm 0.4$
. The contour increment
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{x}=2$
for all panels (red/blue
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{x}=2$
for all panels (red/blue
![]() $=$
positive/negative). Only a portion of the computational domain is shown. The times correspond to (a) 9.5 h (
$=$
positive/negative). Only a portion of the computational domain is shown. The times correspond to (a) 9.5 h (
![]() $t=5$
), (b) 13 h (
$t=5$
), (b) 13 h (
![]() $t=7$
), (c) 19 h (
$t=7$
), (c) 19 h (
![]() $t=10$
) and (d) 34 h (
$t=10$
) and (d) 34 h (
![]() $t=18$
).
$t=18$
).

Figure 13. Plots of vertical profiles of (a)
![]() $\tilde{m}$
and (b)
$\tilde{m}$
and (b)
![]() $\tilde{u}$
at the equator at
$\tilde{u}$
at the equator at
![]() $t=25$
for three values of
$t=25$
for three values of
![]() $Re$
,
$Re$
,
![]() $3\times 10^{4}$
,
$3\times 10^{4}$
,
![]() $5\times 10^{4}$
and
$5\times 10^{4}$
and
![]() $10^{5}$
. Also shown are the initial conditions (thin solid black curve) and the predicted inviscid equilibrium (thick solid grey). The prediction is made assuming that the unperturbed
$10^{5}$
. Also shown are the initial conditions (thin solid black curve) and the predicted inviscid equilibrium (thick solid grey). The prediction is made assuming that the unperturbed
![]() $M$
varies little in the narrow latitudinal band afforded to the flow by the confining free-slip walls at latitudes
$M$
varies little in the narrow latitudinal band afforded to the flow by the confining free-slip walls at latitudes
![]() ${\tilde{y}}=\pm 0.4$
. The predicted values are
${\tilde{y}}=\pm 0.4$
. The predicted values are
![]() $\tilde{z}_{l}\approx -2.76$
,
$\tilde{z}_{l}\approx -2.76$
,
![]() $\tilde{M}_{c}\approx -3.08$
(see text). The results for
$\tilde{M}_{c}\approx -3.08$
(see text). The results for
![]() $3\times 10^{4}$
and
$3\times 10^{4}$
and
![]() $5\times 10^{4}$
are from ensembles of 20 realizations. The
$5\times 10^{4}$
are from ensembles of 20 realizations. The
![]() $Re=10^{5}$
result is averaged over 100 realizations (
$Re=10^{5}$
result is averaged over 100 realizations (
![]() $A=5$
,
$A=5$
,
![]() $L/R_{0}=0.05$
). The time
$L/R_{0}=0.05$
). The time
![]() $t=25$
corresponds to 48 h.
$t=25$
corresponds to 48 h.
The evolution of the vorticity field from a simulation with these parameters is shown in figure 12. The stages are very similar to those already seen in the
![]() $L/R_{0}=0.25$
case. There are no major differences save perhaps for the absence of evidence for waves in the latest stage of the flow, but even in the
$L/R_{0}=0.25$
case. There are no major differences save perhaps for the absence of evidence for waves in the latest stage of the flow, but even in the
![]() $L/R_{0}=0.25$
case, the strength of those waves varied greatly depending on the particular choice of seed for the initial random perturbation, the time of the contour plot and the contour level chosen.
$L/R_{0}=0.25$
case, the strength of those waves varied greatly depending on the particular choice of seed for the initial random perturbation, the time of the contour plot and the contour level chosen.
In the late stages of the evolution,
![]() $m$
and
$m$
and
![]() $u$
approach the inviscid predictions as
$u$
approach the inviscid predictions as
![]() $Re$
increases in the equilibration of the narrow jet (
$Re$
increases in the equilibration of the narrow jet (
![]() $L/R_{0}=0.05$
). However, with the free-slip walls restricting the flow to a narrow latitudinal strip around the equator, the mixing prediction has to be altered. With no such latitudinal boundaries, the turbulent phase of the flow is free to mix momentum horizontally over a wide latitudinal range, as well as vertically. In the restricted flow, mixing must be almost entirely vertical. In this strip, the parabolas are nearly flat and there is almost no latitudinal variation in the initial absolute momentum
$L/R_{0}=0.05$
). However, with the free-slip walls restricting the flow to a narrow latitudinal strip around the equator, the mixing prediction has to be altered. With no such latitudinal boundaries, the turbulent phase of the flow is free to mix momentum horizontally over a wide latitudinal range, as well as vertically. In the restricted flow, mixing must be almost entirely vertical. In this strip, the parabolas are nearly flat and there is almost no latitudinal variation in the initial absolute momentum
![]() $M(y,z)$
. Approximating
$M(y,z)$
. Approximating
![]() $M(y,z)$
as
$M(y,z)$
as
![]() $M(0,z)$
in this strip leads to a simplified relation predicting the new mixing depth and the new mixing value
$M(0,z)$
in this strip leads to a simplified relation predicting the new mixing depth and the new mixing value
![]() $M_{c}$
(see (B 9) in appendix B). For
$M_{c}$
(see (B 9) in appendix B). For
![]() $A=5$
, this gives
$A=5$
, this gives
![]() $\tilde{z}_{l}=-2.76$
. This is little deeper than for the unrestricted mixing which predicts
$\tilde{z}_{l}=-2.76$
. This is little deeper than for the unrestricted mixing which predicts
![]() $\tilde{z}_{l}=-2.47$
. The adjusted relation implies
$\tilde{z}_{l}=-2.47$
. The adjusted relation implies
![]() $\tilde{M}_{c}\approx -3.08$
, which is somewhat more negative than that for the unrestricted mixing where
$\tilde{M}_{c}\approx -3.08$
, which is somewhat more negative than that for the unrestricted mixing where
![]() $\tilde{M}_{c}\approx -2.89$
.
$\tilde{M}_{c}\approx -2.89$
.
The variation of
![]() $\tilde{m}$
with
$\tilde{m}$
with
![]() $Re$
is shown in figure 13(a) for
$Re$
is shown in figure 13(a) for
![]() $t=25$
. As in figure 11, these are averages over a number of realizations, as indicated in the figure caption. One can note how the profiles approach the inviscid prediction (thick grey curve) as
$t=25$
. As in figure 11, these are averages over a number of realizations, as indicated in the figure caption. One can note how the profiles approach the inviscid prediction (thick grey curve) as
![]() $Re$
increases. For later times, the effect of viscosity in smoothing the velocity field will result in a positive gradient of
$Re$
increases. For later times, the effect of viscosity in smoothing the velocity field will result in a positive gradient of
![]() $\tilde{m}$
in the mixing region for any finite
$\tilde{m}$
in the mixing region for any finite
![]() $Re$
. Figure 13(b) is the corresponding figure for the dependence of
$Re$
. Figure 13(b) is the corresponding figure for the dependence of
![]() $\tilde{u}$
on
$\tilde{u}$
on
![]() $Re$
in ‘equilibrium’. It should be noted that the inviscid theory predicts that
$Re$
in ‘equilibrium’. It should be noted that the inviscid theory predicts that
![]() $\tilde{u}$
will change from the initial value at the centre of the jet
$\tilde{u}$
will change from the initial value at the centre of the jet
![]() $\tilde{u} =-5$
to
$\tilde{u} =-5$
to
![]() ${\approx}-3$
, a drop of 40 % of its initial magnitude, just as in the
${\approx}-3$
, a drop of 40 % of its initial magnitude, just as in the
![]() $L/R_{0}=0.25$
case.
$L/R_{0}=0.25$
case.
Comparing the new equilibrium of the narrow jet shown in figure 13 at
![]() $t=25$
(after 2 days) to that of the wide jet in figure 11 at
$t=25$
(after 2 days) to that of the wide jet in figure 11 at
![]() $t=200$
(after 16 days), it is seen that in the former, the ensemble averaged profiles at high
$t=200$
(after 16 days), it is seen that in the former, the ensemble averaged profiles at high
![]() $Re$
are closer to the prediction than in the latter. This must not be taken as proof that generally narrow jets reach the equilibrium more quickly than wide jets. In the simulations, small initial perturbations may project to a lesser extent on fast growing modes than on slower ones. This may determine how long it takes to reach the new equilibrium after nonlinear effects have taken over. There is also some arbitrariness in deciding when the flow has equilibrated (there were always some small-amplitude residual vortical and wave motions). Either way, the evolution may be considered to be quite rapid.
$Re$
are closer to the prediction than in the latter. This must not be taken as proof that generally narrow jets reach the equilibrium more quickly than wide jets. In the simulations, small initial perturbations may project to a lesser extent on fast growing modes than on slower ones. This may determine how long it takes to reach the new equilibrium after nonlinear effects have taken over. There is also some arbitrariness in deciding when the flow has equilibrated (there were always some small-amplitude residual vortical and wave motions). Either way, the evolution may be considered to be quite rapid.
The narrow-jet example (
![]() $L/R_{0}=0.05$
) reveals that at high
$L/R_{0}=0.05$
) reveals that at high
![]() $Re$
, horizontal scales associated with the instability become quite small. In figure 12(a), we observe of the order of 50 rolls near the surface (this is subjective). The horizontal range corresponds to
$Re$
, horizontal scales associated with the instability become quite small. In figure 12(a), we observe of the order of 50 rolls near the surface (this is subjective). The horizontal range corresponds to
![]() $0.8\times L$
, and in terms of ‘density of rolls’
$0.8\times L$
, and in terms of ‘density of rolls’
![]() $n$
contained within a span
$n$
contained within a span
![]() $2L$
(see the end of § 4.2), this is approximately
$2L$
(see the end of § 4.2), this is approximately
![]() $n\approx 2.5\times 50=125$
. In the linearized dynamics, we measured
$n\approx 2.5\times 50=125$
. In the linearized dynamics, we measured
![]() $n=a/(L/R_{0})^{b}$
, with
$n=a/(L/R_{0})^{b}$
, with
![]() $a=20.3$
and
$a=20.3$
and
![]() $b=0.584$
for
$b=0.584$
for
![]() $Re=10^{5}$
(§ 4.2; see figure 8
d). With
$Re=10^{5}$
(§ 4.2; see figure 8
d). With
![]() $L/R_{0}=0.05$
, this empirical formula gives
$L/R_{0}=0.05$
, this empirical formula gives
![]() $n\approx 117$
. The ratio
$n\approx 117$
. The ratio
![]() $L/R_{0}=0.05$
corresponds to approximately
$L/R_{0}=0.05$
corresponds to approximately
![]() $3^{\circ }$
.
$3^{\circ }$
.
However, at
![]() $y=\pm L$
, the Gaussian jet still has approximately 60 % of its peak amplitude at
$y=\pm L$
, the Gaussian jet still has approximately 60 % of its peak amplitude at
![]() $y=0$
. Only at
$y=0$
. Only at
![]() $y=\pm 2L$
does it drop to 13 %. Defining the width of the jet as
$y=\pm 2L$
does it drop to 13 %. Defining the width of the jet as
![]() $W=4L$
, with
$W=4L$
, with
![]() $L/R_{0}=0.05$
,
$L/R_{0}=0.05$
,
![]() $W\approx 12^{\circ }$
. This is fairly wide, and one may consider narrower jets, with widths of say
$W\approx 12^{\circ }$
. This is fairly wide, and one may consider narrower jets, with widths of say
![]() $W=2^{\circ }$
, which is closer to the lateral extent of some of the subsurface equatorial jets in the Pacific Ocean (see Luyten & Swallow Reference Luyten and Swallow1976; Firing Reference Firing1987; Hua, Moore & Le Gentil Reference Hua, Moore and Le Gentil1997). This width corresponds to
$W=2^{\circ }$
, which is closer to the lateral extent of some of the subsurface equatorial jets in the Pacific Ocean (see Luyten & Swallow Reference Luyten and Swallow1976; Firing Reference Firing1987; Hua, Moore & Le Gentil Reference Hua, Moore and Le Gentil1997). This width corresponds to
![]() $L/R_{0}\approx 0.009$
. With this value, the density of rolls is expected to be of the order of
$L/R_{0}\approx 0.009$
. With this value, the density of rolls is expected to be of the order of
![]() $n\approx 320$
. In other words, the horizontal scale of the instability rolls in such a narrow jet is near the surface of the order of
$n\approx 320$
. In other words, the horizontal scale of the instability rolls in such a narrow jet is near the surface of the order of
![]() $(1/300)^{\circ }$
. On the Earth, with
$(1/300)^{\circ }$
. On the Earth, with
![]() $R_{0}=6380$
km, this means horizontal scales of 300–400 m if
$R_{0}=6380$
km, this means horizontal scales of 300–400 m if
![]() $Re=10^{5}$
. These scales get even smaller with larger
$Re=10^{5}$
. These scales get even smaller with larger
![]() $Re$
.
$Re$
.
In as much as the Reynolds number is not known or hard to define for oceanic flows, this may appear meaningless. However, it shows that if, in an ocean numerical model,
![]() $Re$
, based on
$Re$
, based on
![]() $U_{0}$
,
$U_{0}$
,
![]() $L$
and
$L$
and
![]() $\unicode[STIX]{x1D708}$
, is of order
$\unicode[STIX]{x1D708}$
, is of order
![]() $10^{5}$
or larger, the instability in jets with widths of just a few degrees will most likely not be resolved unless the computational domain is constrained to a very narrow latitudinal strip and very high horizontal resolutions are used. Apart from the speculative nature concerning the Reynolds number, there is another caveat: what is the influence of stratification on the instability? We shall briefly discuss this in our final section below.
$10^{5}$
or larger, the instability in jets with widths of just a few degrees will most likely not be resolved unless the computational domain is constrained to a very narrow latitudinal strip and very high horizontal resolutions are used. Apart from the speculative nature concerning the Reynolds number, there is another caveat: what is the influence of stratification on the instability? We shall briefly discuss this in our final section below.
6 Summary and discussion
In this study, we have extended our previous studies of inertial instability to flow in the near-equatorial regions. The origin of inertial instability is the centrifugal instability of swirling flows with an adverse distribution of angular momentum
![]() $L$
, as first explained by Rayleigh (1916) with the condition (1.1). The near-equatorial approximation (2.5a–c
) of the full set of equations of motion in spherical coordinates has been used since it is advantageous to work with simple Cartesian coordinates (theoretically and numerically). This introduces the traditional
$L$
, as first explained by Rayleigh (1916) with the condition (1.1). The near-equatorial approximation (2.5a–c
) of the full set of equations of motion in spherical coordinates has been used since it is advantageous to work with simple Cartesian coordinates (theoretically and numerically). This introduces the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane Coriolis parameter
$\unicode[STIX]{x1D6FD}$
-plane Coriolis parameter
![]() $f=\unicode[STIX]{x1D6FD}y$
but also the non-traditional component
$f=\unicode[STIX]{x1D6FD}y$
but also the non-traditional component
![]() $\tilde{f}=2\unicode[STIX]{x1D6FA}$
associated with the component
$\tilde{f}=2\unicode[STIX]{x1D6FA}$
associated with the component
![]() $\unicode[STIX]{x1D6FA}_{\Vert }$
of the rotation vector tangent to the surface. Keeping both parameters in the dynamics approximates the near-equatorial full Coriolis force.
$\unicode[STIX]{x1D6FA}_{\Vert }$
of the rotation vector tangent to the surface. Keeping both parameters in the dynamics approximates the near-equatorial full Coriolis force.
Only homogeneous flows have been considered and, first, in § 4, we have discussed in some detail the initial growth of the instability with the TA in the specific case of the barotropic (depth-independent) westward Gaussian jet
![]() $U(y)$
(2.28). The results complement our recent work where we only focused on the nonlinear development of the instability and its equilibration (Kloosterziel et al.
Reference Kloosterziel, Orlandi and Carnevale2015). We have extracted the fastest growing normal modes over a wide range of Reynolds number
$U(y)$
(2.28). The results complement our recent work where we only focused on the nonlinear development of the instability and its equilibration (Kloosterziel et al.
Reference Kloosterziel, Orlandi and Carnevale2015). We have extracted the fastest growing normal modes over a wide range of Reynolds number
![]() $Re$
. The measured variation of the maximal rate of exponential growth with
$Re$
. The measured variation of the maximal rate of exponential growth with
![]() $Re$
and the variation of horizontal and vertical scales with
$Re$
and the variation of horizontal and vertical scales with
![]() $Re$
(figure 8
b) agree well with the theoretical predictions. The same scaling laws were found by Kloosterziel et al. (Reference Kloosterziel, Carnevale and Orlandi2007a
) for inertially unstable barotropic vortices on the
$Re$
(figure 8
b) agree well with the theoretical predictions. The same scaling laws were found by Kloosterziel et al. (Reference Kloosterziel, Carnevale and Orlandi2007a
) for inertially unstable barotropic vortices on the
![]() $f$
-plane, both with and without stratification.
$f$
-plane, both with and without stratification.
Truly new results have been found for the NTA in § 4. Figure 6 reveals that the fastest growing modes are surface-confined. This is not surprising since the theory of § 2.1 applied to the jet in § 2.3 predicts maximal growth at the surface, but until now it was not clear what form the fastest growing modes in the scale-selection problem would take. Specifically, figure 7(b) shows that near the equator, the modes vary with depth as
![]() $\text{Ai}(-\unicode[STIX]{x1D706}_{0}-\tilde{z}/\unicode[STIX]{x1D701})$
, with
$\text{Ai}(-\unicode[STIX]{x1D706}_{0}-\tilde{z}/\unicode[STIX]{x1D701})$
, with
![]() $\unicode[STIX]{x1D706}_{0}\approx 2.338$
. The vertical scale
$\unicode[STIX]{x1D706}_{0}\approx 2.338$
. The vertical scale
![]() $\unicode[STIX]{x1D701}$
diminishes with increasing
$\unicode[STIX]{x1D701}$
diminishes with increasing
![]() $Re$
. Moreover, with decreasing
$Re$
. Moreover, with decreasing
![]() $L/R_{0}$
(narrower flows) at fixed depth
$L/R_{0}$
(narrower flows) at fixed depth
![]() $z$
, the latitudinal variation is almost indistinguishable from
$z$
, the latitudinal variation is almost indistinguishable from
![]() $\cos (l{\tilde{y}})\exp (-{\tilde{y}}^{2}/2\unicode[STIX]{x1D702}^{2})$
behaviour. The latitudinal wavenumber
$\cos (l{\tilde{y}})\exp (-{\tilde{y}}^{2}/2\unicode[STIX]{x1D702}^{2})$
behaviour. The latitudinal wavenumber
![]() $l$
within the Gaussian envelope increases with
$l$
within the Gaussian envelope increases with
![]() $Re$
(smaller horizontal scales). The scale of the envelope, determined by
$Re$
(smaller horizontal scales). The scale of the envelope, determined by
![]() $\unicode[STIX]{x1D702}$
, also decreases with increasing
$\unicode[STIX]{x1D702}$
, also decreases with increasing
![]() $Re$
to the point that at high
$Re$
to the point that at high
![]() $Re$
the modes as seen in figure 7(b) are confined to a very narrow latitudinal region about the equator. However, what is the origin for the ‘shrinking’ Gaussian envelope? In the analysis in appendix A, all variation with latitude
$Re$
the modes as seen in figure 7(b) are confined to a very narrow latitudinal region about the equator. However, what is the origin for the ‘shrinking’ Gaussian envelope? In the analysis in appendix A, all variation with latitude
![]() $y$
was ignored, i.e. the traditional near-equatorial component of the rotation vector
$y$
was ignored, i.e. the traditional near-equatorial component of the rotation vector
![]() $f=\unicode[STIX]{x1D6FD}y$
was discarded and
$f=\unicode[STIX]{x1D6FD}y$
was discarded and
![]() $U(y,z)$
was approximated by
$U(y,z)$
was approximated by
![]() $U(y=0,z)$
. This made simple normal-mode analysis possible, which predicts the measured behaviour surprisingly well (figure 8
a,c). A thorough mathematical analysis of the Eliassen–Sawyer equation (A 1) in appendix A, retaining the variability with
$U(y=0,z)$
. This made simple normal-mode analysis possible, which predicts the measured behaviour surprisingly well (figure 8
a,c). A thorough mathematical analysis of the Eliassen–Sawyer equation (A 1) in appendix A, retaining the variability with
![]() $y$
, will be required to explain the properties of the NTA modes to a more satisfactory degree. This should also explain the intriguing observation that the horizontal length scales of the rolls within the envelope decrease for fixed
$y$
, will be required to explain the properties of the NTA modes to a more satisfactory degree. This should also explain the intriguing observation that the horizontal length scales of the rolls within the envelope decrease for fixed
![]() $Re$
faster than with decreasing width
$Re$
faster than with decreasing width
![]() $L$
of the current (figure 8
d).
$L$
of the current (figure 8
d).
In § 5, we presented results for the nonlinear evolution of the instability under the full Coriolis force (NTA). The sequences of the nonlinear turbulent evolution in figure 9 (wide jet) and figure 12 (narrow jet) illustrate the dynamics. The dipoles that form at the surface by nonlinear ‘pairing’ of the cells or rolls similarly to the modes in the linear dynamics (figure 6) advect momentum upwards and downwards below the surface. This leads to advection and mixing of momentum
![]() $m$
. After a turbulent phase, the new flow that emerges has virtually constant momentum
$m$
. After a turbulent phase, the new flow that emerges has virtually constant momentum
![]() $m=M_{c}$
, as predicted in § 2.5. The higher the Reynolds number is, the closer the final flow approaches the prediction (figures 11
a and 13
a). The flows that emerge are again Taylor columns parallel to the axis of rotation. They are inertially stable since all negative radial gradients of momentum have disappeared (
$m=M_{c}$
, as predicted in § 2.5. The higher the Reynolds number is, the closer the final flow approaches the prediction (figures 11
a and 13
a). The flows that emerge are again Taylor columns parallel to the axis of rotation. They are inertially stable since all negative radial gradients of momentum have disappeared (
![]() $\text{d}m/\text{d}R\geqslant 0$
everywhere). In both examples, the westward velocity at the surface drops by approximately 40 % in amplitude (figures 11
b and 13
b), and although the bulk momentum is conserved, the prediction allows for an a priori estimate of the kinetic energy dissipation resulting from the instability in the limit
$\text{d}m/\text{d}R\geqslant 0$
everywhere). In both examples, the westward velocity at the surface drops by approximately 40 % in amplitude (figures 11
b and 13
b), and although the bulk momentum is conserved, the prediction allows for an a priori estimate of the kinetic energy dissipation resulting from the instability in the limit
![]() $Re\rightarrow \infty$
.
$Re\rightarrow \infty$
.
Our results suggest that the assumption of a homogeneous fluid is not as restrictive as it may appear to be. For flows with relatively small horizontal scales near the equator, a thin upper mixed layer may support the growth due to strong vertical shear, irrespective of the strength of stratification at greater depths. For example, in the central Pacific Ocean near the equator, the density mixed (unstratified) layer on average extends to at least 50 m depth and in the western Pacific sometimes to depths of even more than 100 m (Lukas & Lindstrom Reference Lukas and Lindstrom1991; Chiswell Reference Chiswell2016). At very high
![]() $Re$
, even such shallow layers may be able to support the incipient growth of modes shown in figure 6 and the early nonlinear development shown in figure 12, before the primarily downward mixing motions enter a stratified environment. For example, the narrow jet of width
$Re$
, even such shallow layers may be able to support the incipient growth of modes shown in figure 6 and the early nonlinear development shown in figure 12, before the primarily downward mixing motions enter a stratified environment. For example, the narrow jet of width
![]() $W=4L=2^{\circ }$
mentioned at the end of § 5.2 would have a vertical scale of amplitude decay of
$W=4L=2^{\circ }$
mentioned at the end of § 5.2 would have a vertical scale of amplitude decay of
![]() $L^{2}/R_{0}\approx 400$
m according to (2.25). However, as seen in figure 7(b), for very high
$L^{2}/R_{0}\approx 400$
m according to (2.25). However, as seen in figure 7(b), for very high
![]() $Re$
, the fastest growing modes tend to decay over a fraction of this scale. A jet of width
$Re$
, the fastest growing modes tend to decay over a fraction of this scale. A jet of width
![]() $W=1^{\circ }$
implies
$W=1^{\circ }$
implies
![]() $L^{2}/R_{0}=100$
m, which is even more accommodating. The estimates mentioned at the end of § 5.2 indicate that for such laterally confined flows, the horizontal scales associated with the instability will initially be very small. Moreover, the exact character of the background flow becomes unimportant.
$L^{2}/R_{0}=100$
m, which is even more accommodating. The estimates mentioned at the end of § 5.2 indicate that for such laterally confined flows, the horizontal scales associated with the instability will initially be very small. Moreover, the exact character of the background flow becomes unimportant.
In view of this, we expect that the restriction to idealized Taylor-column flows used in this study can be relaxed. The vertical confinement of the initial growth patterns is primarily due to sufficiently strong near-surface vertical shear, which in Rayleigh’s criterion (1.1) means adverse angular momentum with
![]() $\text{d}L/\text{d}R<0$
. This is very much a ‘local’ criterion, as Ooyama (Reference Ooyama1966) showed (see the end of § 2.1), and does not hinge on a particular relation between latitudinal and depth variations of the background flow like the Taylor-column requirement that
$\text{d}L/\text{d}R<0$
. This is very much a ‘local’ criterion, as Ooyama (Reference Ooyama1966) showed (see the end of § 2.1), and does not hinge on a particular relation between latitudinal and depth variations of the background flow like the Taylor-column requirement that
![]() $U=U(z-y^{2}/2R_{0})$
. In other words, (1.1) is a good indicator of instability of vertically sheared near-equatorial flows, while details of the variation with latitude are most likely unimportant. However, further studies are required to verify this.
$U=U(z-y^{2}/2R_{0})$
. In other words, (1.1) is a good indicator of instability of vertically sheared near-equatorial flows, while details of the variation with latitude are most likely unimportant. However, further studies are required to verify this.
If the above scenario with a thin upper mixed layer is studied in the future, the question is what the influence of the lower-layer stratification will be in the evolution of the flow. It is energetically difficult to cross isopycnals, and buoyancy may deflect the motions ‘sideways’ or, if the instability is vigorous enough, the stratification may be eroded by density mixing and deepen the mixed layer. This scenario is also of interest to consider with detailed numerical simulations.
If stratification extends to the surface, one might think that it will suppress the downward motions enough to halt the instability altogether. However, a simple example indicates that this is not necessarily true. If the same jet (2.25) is embedded in an arbitrary stably stratified environment with density
![]() $\bar{\unicode[STIX]{x1D70C}}(z)$
and
$\bar{\unicode[STIX]{x1D70C}}(z)$
and
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}/\unicode[STIX]{x2202}z<0$
, isopycnals are undisturbed (
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}/\unicode[STIX]{x2202}z<0$
, isopycnals are undisturbed (
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}/\unicode[STIX]{x2202}y=0$
). The determinant formula (2.19) reveals that then
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}/\unicode[STIX]{x2202}y=0$
). The determinant formula (2.19) reveals that then
![]() $\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}=N^{2}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
(
$\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}=N^{2}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
(
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}=-\unicode[STIX]{x1D6FD}y\unicode[STIX]{x2202}M/\unicode[STIX]{x2202}y$
). Thus, for any
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}=-\unicode[STIX]{x1D6FD}y\unicode[STIX]{x2202}M/\unicode[STIX]{x2202}y$
). Thus, for any
![]() $N^{2}(z)>0$
, the condition
$N^{2}(z)>0$
, the condition
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}<0$
implies instability (one negative eigenvalue), which is the same condition that the westward Gaussian jet (2.25) has Rossby number
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}<0$
implies instability (one negative eigenvalue), which is the same condition that the westward Gaussian jet (2.25) has Rossby number
![]() $A>1$
. In other words, no matter how strong the stratification is, the instability cannot be suppressed. The same condition appears in the TA dynamics when a depth-independent flow
$A>1$
. In other words, no matter how strong the stratification is, the instability cannot be suppressed. The same condition appears in the TA dynamics when a depth-independent flow
![]() $U(y)$
like (2.28) is considered. Then, the instability is ascribed to horizontal shear, which renders
$U(y)$
like (2.28) is considered. Then, the instability is ascribed to horizontal shear, which renders
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}y(\unicode[STIX]{x1D6FD}y-\text{d}U/\text{d}y)<0$
. In the NTA dynamics, we can interpret the instability as due to sufficiently strong vertical shear because, according to the thermal wind balance equation (2.13),
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}y(\unicode[STIX]{x1D6FD}y-\text{d}U/\text{d}y)<0$
. In the NTA dynamics, we can interpret the instability as due to sufficiently strong vertical shear because, according to the thermal wind balance equation (2.13),
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}=(\unicode[STIX]{x1D6FD}y)^{2}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}z+2\unicode[STIX]{x1D6FA})/2\unicode[STIX]{x1D6FA}$
. This brings us back to the root cause of inertial instability: Rayleigh’s criterion (1.1) is satisfied when near the equator
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}=(\unicode[STIX]{x1D6FD}y)^{2}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}z+2\unicode[STIX]{x1D6FA})/2\unicode[STIX]{x1D6FA}$
. This brings us back to the root cause of inertial instability: Rayleigh’s criterion (1.1) is satisfied when near the equator
![]() $\text{d}L/\text{d}R\approx R_{0}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}z+2\unicode[STIX]{x1D6FA})<0$
. Of course, with the support of an appropriately chosen stratification, via (2.13), arbitrary flows
$\text{d}L/\text{d}R\approx R_{0}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}z+2\unicode[STIX]{x1D6FA})<0$
. Of course, with the support of an appropriately chosen stratification, via (2.13), arbitrary flows
![]() $U(y,z)$
, not just Taylor columns
$U(y,z)$
, not just Taylor columns
![]() $U(R)\approx U(z-y^{2}/2R_{0})$
, can be chosen as steady initial conditions, but the above discussion indicates that further research on stratified flows incorporating the non-traditional component of the rotation vector is warranted.
$U(R)\approx U(z-y^{2}/2R_{0})$
, can be chosen as steady initial conditions, but the above discussion indicates that further research on stratified flows incorporating the non-traditional component of the rotation vector is warranted.
At this moment, it is unclear how things will then develop, i.e. what will the growth rates, scales, nonlinear development at high
![]() $Re$
, momentum mixing or mixing of Ertel potential vorticity
$Re$
, momentum mixing or mixing of Ertel potential vorticity
![]() $Q_{E}$
, and so on, be? Will a new steady flow emerge that can be predicted with simple recipes similar to that in § 2.5 for inertially unstable flows in an unstratified environment? Could it be that the TA is after all a good approximation if strong stratification is present everywhere? Clearly, numerous scenarios present themselves. We hope to address questions such as those posed above in the near future.
$Q_{E}$
, and so on, be? Will a new steady flow emerge that can be predicted with simple recipes similar to that in § 2.5 for inertially unstable flows in an unstratified environment? Could it be that the TA is after all a good approximation if strong stratification is present everywhere? Clearly, numerous scenarios present themselves. We hope to address questions such as those posed above in the near future.
Acknowledgements
G.F.C. acknowledges support from National Science Foundation grant OCE 11-29059. R.C.K. acknowledges support from National Science Foundation grants OCE 10-32256 and OCE 15-38559.
Appendix A. Weakly diffusive scale selection and normal-mode structures
The numerous results presented in § 4 can largely be explained through quite general asymptotic analysis. The traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane analysis below in §§ A.1 and A.2 is along the lines of the analysis of Griffiths (Reference Griffiths2008b
) in the appendix of Kloosterziel & Carnevale (Reference Kloosterziel and Carnevale2008), while for the full Coriolis dynamics (NTA) in §§ A.3 and A.4, a new approach is required, although in essence the idea is the same. For the analysis, we need to consider the viscous version of the Eliassen–Sawyer equation (after Sawyer Reference Sawyer1949 and Eliassen Reference Eliassen1951). This is derived from the Eulerian equations of motion in the following fashion. Cross-differentiation of the linearized
$\unicode[STIX]{x1D6FD}$
-plane analysis below in §§ A.1 and A.2 is along the lines of the analysis of Griffiths (Reference Griffiths2008b
) in the appendix of Kloosterziel & Carnevale (Reference Kloosterziel and Carnevale2008), while for the full Coriolis dynamics (NTA) in §§ A.3 and A.4, a new approach is required, although in essence the idea is the same. For the analysis, we need to consider the viscous version of the Eliassen–Sawyer equation (after Sawyer Reference Sawyer1949 and Eliassen Reference Eliassen1951). This is derived from the Eulerian equations of motion in the following fashion. Cross-differentiation of the linearized
![]() $v,w$
equations (3.2), (3.3) yields the perturbation equation for the zonal vorticity
$v,w$
equations (3.2), (3.3) yields the perturbation equation for the zonal vorticity
![]() $\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x2202}_{y}w-\unicode[STIX]{x2202}_{z}v$
. With the introduction of the streamfunction
$\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x2202}_{y}w-\unicode[STIX]{x2202}_{z}v$
. With the introduction of the streamfunction
![]() $\unicode[STIX]{x1D713}$
, i.e.
$\unicode[STIX]{x1D713}$
, i.e.
![]() $v=-\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D713}$
,
$v=-\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D713}$
,
![]() $w=\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}$
, the zonal vorticity component
$w=\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}$
, the zonal vorticity component
![]() $\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x2202}_{y}w-\unicode[STIX]{x2202}_{z}v=\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}$
. Time differentiation of the vorticity equation and substitution of
$\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x2202}_{y}w-\unicode[STIX]{x2202}_{z}v=\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}$
. Time differentiation of the vorticity equation and substitution of
![]() $\unicode[STIX]{x2202}_{t}u$
from the perturbation zonal velocity equation (3.1) yields
$\unicode[STIX]{x2202}_{t}u$
from the perturbation zonal velocity equation (3.1) yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}t^{2}}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\left(A\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}+B\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}y}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(B\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}+C\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}y}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D708}(2\unicode[STIX]{x1D6FA}\unicode[STIX]{x2202}_{y}+\unicode[STIX]{x1D6FD}y\unicode[STIX]{x2202}_{z})\unicode[STIX]{x1D6FB}^{2}u+\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}t^{2}}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\left(A\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}+B\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}y}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(B\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}+C\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}y}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D708}(2\unicode[STIX]{x1D6FA}\unicode[STIX]{x2202}_{y}+\unicode[STIX]{x1D6FD}y\unicode[STIX]{x2202}_{z})\unicode[STIX]{x1D6FB}^{2}u+\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713},\end{eqnarray}$$
with
It should be noted that these coefficients are just those of
![]() $\unicode[STIX]{x1D648}$
in (2.18) with
$\unicode[STIX]{x1D648}$
in (2.18) with
![]() $\bar{\unicode[STIX]{x1D70C}}=\text{const.}$
(homogeneous fluid). We have introduced some shorthand; in particular,
$\bar{\unicode[STIX]{x1D70C}}=\text{const.}$
(homogeneous fluid). We have introduced some shorthand; in particular,
![]() $A=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
is the Rayleigh discriminant for parallel shear flow on the traditional
$A=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
is the Rayleigh discriminant for parallel shear flow on the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane and
$\unicode[STIX]{x1D6FD}$
-plane and
![]() $C=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}$
is the ‘rotated’ Rayleigh discriminant for flows subject to rotation about the
$C=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}$
is the ‘rotated’ Rayleigh discriminant for flows subject to rotation about the
![]() $y$
axis (with rotation vector
$y$
axis (with rotation vector
![]() $\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}\boldsymbol{j}$
).
$\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}\boldsymbol{j}$
).
A.1 Traditional approximation: the non-diffusive system
In the limit of vanishing viscosity (
![]() $\unicode[STIX]{x1D708}\rightarrow 0$
or Reynolds number
$\unicode[STIX]{x1D708}\rightarrow 0$
or Reynolds number
![]() $Re\rightarrow \infty$
), the overturning motions associated with inertial instability are amplified most rapidly in the TA if their vertical scales (i.e. in the
$Re\rightarrow \infty$
), the overturning motions associated with inertial instability are amplified most rapidly in the TA if their vertical scales (i.e. in the
![]() $z$
-direction) are vanishingly small. This is clearly seen in figure 5.
$z$
-direction) are vanishingly small. This is clearly seen in figure 5.
In the TA,
![]() $2\unicode[STIX]{x1D6FA}=0$
and
$2\unicode[STIX]{x1D6FA}=0$
and
![]() $B=C=0$
in (A 1) and we must analyse
$B=C=0$
in (A 1) and we must analyse
Let us first set
![]() $\unicode[STIX]{x1D708}=0$
on the right-hand side. It should be noted that for the TA,
$\unicode[STIX]{x1D708}=0$
on the right-hand side. It should be noted that for the TA,
![]() $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
and we proceed with the assumption that
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
and we proceed with the assumption that
![]() $\unicode[STIX]{x1D706}_{1}<0$
or
$\unicode[STIX]{x1D706}_{1}<0$
or
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}<0$
for some range of
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}<0$
for some range of
![]() $y$
-values.
$y$
-values.
Generally, solutions (normal modes) are sought of the form
![]() $\unicode[STIX]{x1D713}=\exp (\unicode[STIX]{x1D6FE}t)\unicode[STIX]{x1D6F9}(y,z)$
. However, as is typical in these types of problems with no variation in the vertical, vertically periodic solutions are assumed, i.e. we set
$\unicode[STIX]{x1D713}=\exp (\unicode[STIX]{x1D6FE}t)\unicode[STIX]{x1D6F9}(y,z)$
. However, as is typical in these types of problems with no variation in the vertical, vertically periodic solutions are assumed, i.e. we set
![]() $\unicode[STIX]{x1D6F9}=\tilde{\unicode[STIX]{x1D713}}(y)\exp (\text{i}mz)$
, with
$\unicode[STIX]{x1D6F9}=\tilde{\unicode[STIX]{x1D713}}(y)\exp (\text{i}mz)$
, with
![]() $m$
a vertical wavenumber. This is of course a posteriori supported by the observations displayed in figure 6. Then, (A 3) with
$m$
a vertical wavenumber. This is of course a posteriori supported by the observations displayed in figure 6. Then, (A 3) with
![]() $\unicode[STIX]{x1D708}=0$
becomes
$\unicode[STIX]{x1D708}=0$
becomes
Assuming that
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
attains a negative minimum
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
attains a negative minimum
![]() $\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}<0$
at some
$\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}<0$
at some
![]() $y=\overline{y}$
, expressions for the eigenmodes and growth rates for large
$y=\overline{y}$
, expressions for the eigenmodes and growth rates for large
![]() $|m|$
can be obtained as follows. First, substitute in (A 4) a Taylor series
$|m|$
can be obtained as follows. First, substitute in (A 4) a Taylor series
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}=\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}+(1/2)\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}(y-\overline{y})^{2}+\cdots$
, where
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}=\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}+(1/2)\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}(y-\overline{y})^{2}+\cdots$
, where
![]() $\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}=\text{d}^{2}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}/\text{d}y^{2}$
evaluated at
$\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}=\text{d}^{2}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}/\text{d}y^{2}$
evaluated at
![]() $y=\overline{y}$
is assumed to be non-zero. Since
$y=\overline{y}$
is assumed to be non-zero. Since
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
has a minimum at
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
has a minimum at
![]() $\overline{y}$
, one then has
$\overline{y}$
, one then has
![]() $\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}>0$
. Further,
$\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}>0$
. Further,
![]() $\unicode[STIX]{x1D6FE}^{2}=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|$
, plus corrections in inverse (fractional) powers of
$\unicode[STIX]{x1D6FE}^{2}=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|$
, plus corrections in inverse (fractional) powers of
![]() $|m|$
are substituted and
$|m|$
are substituted and
![]() $(y-\overline{y})=LY$
is set, with
$(y-\overline{y})=LY$
is set, with
![]() $L$
a length scale and
$L$
a length scale and
![]() $Y$
the scaled
$Y$
the scaled
![]() $y$
-coordinate measured from
$y$
-coordinate measured from
![]() $y=\overline{y}$
. One then finds that for a consistent (balanced) set of expansions, one has to have
$y=\overline{y}$
. One then finds that for a consistent (balanced) set of expansions, one has to have
![]() $L\sim |m|^{-1/2}$
(this is seen from balancing
$L\sim |m|^{-1/2}$
(this is seen from balancing
![]() $|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}|/(m^{2}L^{2})\sim (1/2)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }L^{2}$
), and the optimal choice is
$|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}|/(m^{2}L^{2})\sim (1/2)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }L^{2}$
), and the optimal choice is
while
Substituting in (A 4), and writing
![]() $\text{d}^{2}/\text{d}y^{2}=a|m|\,\text{d}^{2}/\text{d}Y^{2}$
, the
$\text{d}^{2}/\text{d}y^{2}=a|m|\,\text{d}^{2}/\text{d}Y^{2}$
, the
![]() $O(1)$
terms cancel, and at
$O(1)$
terms cancel, and at
![]() $O(|m|^{-1})$
,
$O(|m|^{-1})$
,
This is the well-known quantum harmonic oscillator equation, which describes localized solutions provided that
with corresponding eigenfunctions
![]() $\tilde{\unicode[STIX]{x1D713}}=H_{n}(Y)\exp (-Y^{2}/2)$
, where
$\tilde{\unicode[STIX]{x1D713}}=H_{n}(Y)\exp (-Y^{2}/2)$
, where
![]() $H_{n}$
is the
$H_{n}$
is the
![]() $n$
th-order Hermite polynomial. The fastest growing mode has
$n$
th-order Hermite polynomial. The fastest growing mode has
![]() $n=0$
with
$n=0$
with
![]() $\tilde{\unicode[STIX]{x1D713}}=\exp (-Y^{2}/2)$
, and thus the spatial structure of normal modes is expected to approach
$\tilde{\unicode[STIX]{x1D713}}=\exp (-Y^{2}/2)$
, and thus the spatial structure of normal modes is expected to approach
with the growth rate
Thus, from this analysis, one expects that for increasing vertical wavenumber
![]() $|m|$
, the growth rate of standing normal modes uniformly increases towards its asymptotic value
$|m|$
, the growth rate of standing normal modes uniformly increases towards its asymptotic value
![]() $\unicode[STIX]{x1D6FE}_{\infty }=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|^{1/2}$
(which is
$\unicode[STIX]{x1D6FE}_{\infty }=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|^{1/2}$
(which is
![]() $\max \sqrt{-\unicode[STIX]{x1D706}_{1}}$
). It should be noted that in the case of the Gaussian jet,
$\max \sqrt{-\unicode[STIX]{x1D706}_{1}}$
). It should be noted that in the case of the Gaussian jet,
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
has two separate minima but, as the analysis shows, the modes become highly localized for large
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}$
has two separate minima but, as the analysis shows, the modes become highly localized for large
![]() $m$
and each region can be treated separately. This behaviour is also seen in figure 5, and in particular the Gaussian structure corresponds to the predicted
$m$
and each region can be treated separately. This behaviour is also seen in figure 5, and in particular the Gaussian structure corresponds to the predicted
![]() $n=0$
mode.
$n=0$
mode.
A.2 Traditional approximation: the diffusive system
We now evaluate the effect of diffusion on the inertial instability. If
![]() $\unicode[STIX]{x1D708}$
is small, the inertial instability remains strong, with the large-vertical-wavenumber limit remaining appropriate. We anticipate that (A 10) will be appropriate for moderately large
$\unicode[STIX]{x1D708}$
is small, the inertial instability remains strong, with the large-vertical-wavenumber limit remaining appropriate. We anticipate that (A 10) will be appropriate for moderately large
![]() $|m|$
, describing an almost inviscid growth rate increase, while as
$|m|$
, describing an almost inviscid growth rate increase, while as
![]() $|m|\rightarrow \infty$
, a relationship describing an almost completely diffusive decay would be more appropriate. We need to assess for what scaling of
$|m|\rightarrow \infty$
, a relationship describing an almost completely diffusive decay would be more appropriate. We need to assess for what scaling of
![]() $|m|$
, in terms of
$|m|$
, in terms of
![]() $\unicode[STIX]{x1D708}$
, the inviscid growth and diffusive decay terms balance, which will yield the most unstable modes. The inviscid scaling (A 5) is used again as well as the expansion (A 6) for the growth rate. This yields with (A 3) the viscously modified version of (A 7):
$\unicode[STIX]{x1D708}$
, the inviscid growth and diffusive decay terms balance, which will yield the most unstable modes. The inviscid scaling (A 5) is used again as well as the expansion (A 6) for the growth rate. This yields with (A 3) the viscously modified version of (A 7):
with
![]() $\unicode[STIX]{x1D6FB}^{2}=\text{d}^{2}/\text{d}y^{2}-|m|^{2}$
. On the right-hand side, as for
$\unicode[STIX]{x1D6FB}^{2}=\text{d}^{2}/\text{d}y^{2}-|m|^{2}$
. On the right-hand side, as for
![]() $\unicode[STIX]{x1D713}$
, the normal-mode ansatz
$\unicode[STIX]{x1D713}$
, the normal-mode ansatz
![]() $u=\exp (\unicode[STIX]{x1D70E}t)\tilde{u} (y)\exp (\text{i}mz)$
has also been used. It should be noted that in the Laplacian,
$u=\exp (\unicode[STIX]{x1D70E}t)\tilde{u} (y)\exp (\text{i}mz)$
has also been used. It should be noted that in the Laplacian,
and thus the vertical diffusion (represented by
![]() $-|m|^{2}=\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}z^{2}$
in
$-|m|^{2}=\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}z^{2}$
in
![]() $\unicode[STIX]{x1D6FB}^{2}$
) dominates for large
$\unicode[STIX]{x1D6FB}^{2}$
) dominates for large
![]() $|m|$
. The largest term on the right-hand side of (A 11) is then
$|m|$
. The largest term on the right-hand side of (A 11) is then
This is the dominant damping term for large
![]() $|m|$
, which competes with the inviscid tendency of ever faster growth rate with increasing
$|m|$
, which competes with the inviscid tendency of ever faster growth rate with increasing
![]() $|m|$
.
$|m|$
.
The linearized
![]() $u$
-equation (3.1) with
$u$
-equation (3.1) with
![]() $\unicode[STIX]{x2202}_{z}M=0$
(because in the TA,
$\unicode[STIX]{x2202}_{z}M=0$
(because in the TA,
![]() $M=M(y)$
) yields to lowest order
$M=M(y)$
) yields to lowest order
which is substituted in (A 13). This means that
However, the horizontally contracting scale for increasing
![]() $|m|$
implies that for large
$|m|$
implies that for large
![]() $m$
, we can use the local negative minimum
$m$
, we can use the local negative minimum
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}(y)\approx -|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|$
as an approximation, so that
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}(y)\approx -|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|$
as an approximation, so that
with
![]() $\unicode[STIX]{x1D6FE}\approx |\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|^{1/2}$
. Then, the eigenvalue problem (A 7) changes to
$\unicode[STIX]{x1D6FE}\approx |\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|^{1/2}$
. Then, the eigenvalue problem (A 7) changes to
and horizontally localized modes occur if, instead of (A 8),
This shows the competition between the inviscid growth tendency (second term) and the viscous damping with increasing
![]() $|m|$
(last term).
$|m|$
(last term).
To find the maximal rate of growth, we simply solve
![]() $\text{d}\unicode[STIX]{x1D6FE}^{2}/\text{d}|m|=0$
, which yields
$\text{d}\unicode[STIX]{x1D6FE}^{2}/\text{d}|m|=0$
, which yields
 $$\begin{eqnarray}|m_{\star }|=\left(\frac{(2n+1)}{4\unicode[STIX]{x1D708}}\left(\frac{|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}|}{2}\right)^{1/2}\right)^{1/3}.\end{eqnarray}$$
$$\begin{eqnarray}|m_{\star }|=\left(\frac{(2n+1)}{4\unicode[STIX]{x1D708}}\left(\frac{|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}|}{2}\right)^{1/2}\right)^{1/3}.\end{eqnarray}$$
The subscript ‘
![]() $\star$
’ indicates the vertical wavenumber for the fastest growing mode.
$\star$
’ indicates the vertical wavenumber for the fastest growing mode.
Substituting
![]() $m_{\star }$
back into
$m_{\star }$
back into
![]() $\unicode[STIX]{x1D6FE}^{2}$
, one finds the rate of growth of the fastest growing mode (for
$\unicode[STIX]{x1D6FE}^{2}$
, one finds the rate of growth of the fastest growing mode (for
![]() $n=0$
),
$n=0$
),
with
![]() $\unicode[STIX]{x1D6FE}_{\infty }=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|^{1/2}$
. Therefore, whichever definition one uses for
$\unicode[STIX]{x1D6FE}_{\infty }=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}}|^{1/2}$
. Therefore, whichever definition one uses for
![]() $Re$
(for example,
$Re$
(for example,
![]() $Re=U_{0}L/\unicode[STIX]{x1D708}$
), this means that for small
$Re=U_{0}L/\unicode[STIX]{x1D708}$
), this means that for small
![]() $\unicode[STIX]{x1D708}$
(large
$\unicode[STIX]{x1D708}$
(large
![]() $Re$
), the maximal growth rate approaches the inviscid maximum
$Re$
), the maximal growth rate approaches the inviscid maximum
![]() $\unicode[STIX]{x1D6FE}_{\infty }$
via
$\unicode[STIX]{x1D6FE}_{\infty }$
via
![]() $Re^{-1/3}$
, thus explaining figure 8(a). The expected spatial structure is
$Re^{-1/3}$
, thus explaining figure 8(a). The expected spatial structure is
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(y,z)\sim \exp (\text{i}m_{\star }z)\exp (-a|m_{\star }|(y-\overline{y})^{2}/2),\quad |m_{\star }|=\left(\frac{1}{4\unicode[STIX]{x1D708}}\left(\frac{|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}|}{2}\right)^{1/2}\right)^{1/3}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(y,z)\sim \exp (\text{i}m_{\star }z)\exp (-a|m_{\star }|(y-\overline{y})^{2}/2),\quad |m_{\star }|=\left(\frac{1}{4\unicode[STIX]{x1D708}}\left(\frac{|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\prime \prime }}|}{2}\right)^{1/2}\right)^{1/3}.\end{eqnarray}$$
The vertical wavenumber
![]() $m_{\star }$
increases with
$m_{\star }$
increases with
![]() $Re^{1/3}$
, so that the vertical length scale decreases as
$Re^{1/3}$
, so that the vertical length scale decreases as
![]() $L_{v}\propto Re^{-1/3}$
, as observed in figure 8(b), but the horizontal length scale
$L_{v}\propto Re^{-1/3}$
, as observed in figure 8(b), but the horizontal length scale
![]() $L_{h}\propto 1/\sqrt{|m_{\star }|}\propto Re^{-1/6}$
, which was also observed (figure 8
b).
$L_{h}\propto 1/\sqrt{|m_{\star }|}\propto Re^{-1/6}$
, which was also observed (figure 8
b).
A.3 Non-traditional approximation: the non-diffusive system and assumptions
In figure 7(b), we showed an excellent match between the observed vertical structures of the near-equatorial modes and Airy functions. The latter are derived below under the assumption that all variation with
![]() $y$
(latitude) can be ignored. This allows for the introduction of a streamfunction that is periodic in latitude (horizontally), which is equivalent to the periodicity in the vertical for the traditional
$y$
(latitude) can be ignored. This allows for the introduction of a streamfunction that is periodic in latitude (horizontally), which is equivalent to the periodicity in the vertical for the traditional
![]() $\unicode[STIX]{x1D6FD}$
-plane problem.
$\unicode[STIX]{x1D6FD}$
-plane problem.
Therefore, our working premise is that all variation of the background flow with
![]() $y$
can be ignored and that the dynamics is dominated by the non-traditional rotation component. In other words, we neglect
$y$
can be ignored and that the dynamics is dominated by the non-traditional rotation component. In other words, we neglect
![]() $\unicode[STIX]{x1D6FD}y$
and assume that the problem can be described through (A 1) with
$\unicode[STIX]{x1D6FD}y$
and assume that the problem can be described through (A 1) with
![]() $A=B=0$
. Moreover, the coefficient
$A=B=0$
. Moreover, the coefficient
![]() $C=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}(y,z)$
is replaced with its value at
$C=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}(y,z)$
is replaced with its value at
![]() $y=0$
and we set
$y=0$
and we set
![]() $\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}=0$
. In addition, on the right-hand side, the term
$\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}=0$
. In addition, on the right-hand side, the term
![]() $\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FD}y\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FB}^{2}u$
is also ignored, so that (A 1) reduces to
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FD}y\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FB}^{2}u$
is also ignored, so that (A 1) reduces to
Modes are assumed to be periodic in
![]() $y$
, i.e. of the form
$y$
, i.e. of the form
![]() $\exp (\unicode[STIX]{x1D6FE}t)\exp (\text{i}ly)\tilde{\unicode[STIX]{x1D713}}(z)$
, which reduces the problem to the analogue of (A 4) if
$\exp (\unicode[STIX]{x1D6FE}t)\exp (\text{i}ly)\tilde{\unicode[STIX]{x1D713}}(z)$
, which reduces the problem to the analogue of (A 4) if
![]() $\unicode[STIX]{x1D708}=0$
on the right-hand side:
$\unicode[STIX]{x1D708}=0$
on the right-hand side:
The prototypical problem we now analyse is that there is not, as in the traditional approximation, an interior minimum for some
![]() $z<0$
but instead we assume that
$z<0$
but instead we assume that
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}$
attains its negative minimum at the boundary
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}$
attains its negative minimum at the boundary
![]() $z=0$
, as is the case for the unstable Gaussian flow. All we know further is that
$z=0$
, as is the case for the unstable Gaussian flow. All we know further is that
![]() $\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}(z=0)={\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }(z=0)<0$
. In keeping with the previous notation, we indicate the negative minimum at
$\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}(z=0)={\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }(z=0)<0$
. In keeping with the previous notation, we indicate the negative minimum at
![]() $z=0$
with
$z=0$
with
![]() $\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}$
and its first (negative) derivative there with
$\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}$
and its first (negative) derivative there with
![]() $\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}$
.
$\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}$
.
Again, expressions for the eigenmodes and growth rates for large
![]() $|l|$
can be obtained by first substituting into (A 23) a Taylor series
$|l|$
can be obtained by first substituting into (A 23) a Taylor series
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}=\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}+\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}z+\cdots$
with
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}=\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}+\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}z+\cdots$
with
![]() $\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}<0$
. Next, we set
$\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}<0$
. Next, we set
![]() $z=LZ$
, with
$z=LZ$
, with
![]() $Z$
a scaled coordinate. The scale
$Z$
a scaled coordinate. The scale
![]() $L$
is determined by the dominant balance by
$L$
is determined by the dominant balance by
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}/(l^{2}L^{2})\sim {\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }L$
. This shows that
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}/(l^{2}L^{2})\sim {\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }L$
. This shows that
![]() $L\sim |l|^{-2/3}$
and, in particular,
$L\sim |l|^{-2/3}$
and, in particular,
 $$\begin{eqnarray}L=\left|\frac{\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}}{\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}}\right|^{1/3}\frac{1}{|l|^{2/3}}\quad \text{or}\quad Z=a|l|^{2/3}z,\quad \text{with}~a=\left|\frac{\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}}{\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}}\right|^{1/3},\end{eqnarray}$$
$$\begin{eqnarray}L=\left|\frac{\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}}{\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}}\right|^{1/3}\frac{1}{|l|^{2/3}}\quad \text{or}\quad Z=a|l|^{2/3}z,\quad \text{with}~a=\left|\frac{\overline{{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}^{\prime }}}{\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}}\right|^{1/3},\end{eqnarray}$$
is an optimal choice. This has to be matched with a balanced expansion of the square of the growth rate in inverse fractional powers of
![]() $|l|$
, which is
$|l|$
, which is
Then, at
![]() $O(1)$
, terms cancel in (A 23), and at
$O(1)$
, terms cancel in (A 23), and at
![]() $O(|l|^{-2/3})$
, we find
$O(|l|^{-2/3})$
, we find
Setting
we need to determine the eigenvalues
![]() $\unicode[STIX]{x1D706}_{n}$
of the equation
$\unicode[STIX]{x1D706}_{n}$
of the equation
The boundary conditions are that at the surface, the streamfunction
![]() $\tilde{\unicode[STIX]{x1D713}}(Z=0)=0$
, and that for
$\tilde{\unicode[STIX]{x1D713}}(Z=0)=0$
, and that for
![]() $Z\rightarrow -\infty$
, also
$Z\rightarrow -\infty$
, also
![]() $\tilde{\unicode[STIX]{x1D713}}(Z)\rightarrow 0$
. By setting
$\tilde{\unicode[STIX]{x1D713}}(Z)\rightarrow 0$
. By setting
![]() $Z^{\prime }=\unicode[STIX]{x1D706}_{n}+Z$
, the eigenvalue problem becomes
$Z^{\prime }=\unicode[STIX]{x1D706}_{n}+Z$
, the eigenvalue problem becomes
Equation (A 29) is the definition of the Airy function
![]() $\text{Ai}(-Z^{\prime })=\text{Ai}(-\unicode[STIX]{x1D706}_{n}-Z)$
, which oscillates for
$\text{Ai}(-Z^{\prime })=\text{Ai}(-\unicode[STIX]{x1D706}_{n}-Z)$
, which oscillates for
![]() $Z^{\prime }>0$
and decays when
$Z^{\prime }>0$
and decays when
![]() $Z^{\prime }<0$
. Therefore, the boundary condition at
$Z^{\prime }<0$
. Therefore, the boundary condition at
![]() $Z=z=0$
is the requirement that
$Z=z=0$
is the requirement that
![]() $\text{Ai}(-\unicode[STIX]{x1D706}_{n})=0$
. It is also correct in that it vanishes for
$\text{Ai}(-\unicode[STIX]{x1D706}_{n})=0$
. It is also correct in that it vanishes for
![]() $Z\rightarrow -\infty$
. This has an increasing sequence just like (A 8),
$Z\rightarrow -\infty$
. This has an increasing sequence just like (A 8),
and the gravest modes (fastest growing with
![]() $\unicode[STIX]{x1D706}_{0}$
) for large horizontal wavenumber
$\unicode[STIX]{x1D706}_{0}$
) for large horizontal wavenumber
![]() $|l|$
are
$|l|$
are
with the growth rate
This is the equivalent of (A 10) and shows that for increasing horizontal wavenumber
![]() $|l|$
, the growth rate increases towards its asymptotic value
$|l|$
, the growth rate increases towards its asymptotic value
![]() $\unicode[STIX]{x1D6FE}_{\infty }=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}|^{1/2}$
.
$\unicode[STIX]{x1D6FE}_{\infty }=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}|^{1/2}$
.
A.4 Non-traditional approximation: the diffusive system
The viscously modified system becomes, instead of (A 26),
after using the normal-mode ansatz
![]() $u=\exp (\unicode[STIX]{x1D6FE}t)\tilde{u} (y)\exp (\text{i}ly)\tilde{u} (z)$
. In the Laplacian(s) on the right-hand side, the horizontal diffusion (represented by
$u=\exp (\unicode[STIX]{x1D6FE}t)\tilde{u} (y)\exp (\text{i}ly)\tilde{u} (z)$
. In the Laplacian(s) on the right-hand side, the horizontal diffusion (represented by
![]() $-|l|^{2}=\unicode[STIX]{x2202}_{y}^{2}$
) dominates since
$-|l|^{2}=\unicode[STIX]{x2202}_{y}^{2}$
) dominates since
and therefore we have right-hand side
![]() ${\approx}-\unicode[STIX]{x1D708}[\text{i}2\unicode[STIX]{x1D6FA}l\tilde{u} -\unicode[STIX]{x1D6FE}l^{2}\tilde{\unicode[STIX]{x1D713}}]$
. The perturbation
${\approx}-\unicode[STIX]{x1D708}[\text{i}2\unicode[STIX]{x1D6FA}l\tilde{u} -\unicode[STIX]{x1D6FE}l^{2}\tilde{\unicode[STIX]{x1D713}}]$
. The perturbation
![]() $u$
-velocity equation is needed now:
$u$
-velocity equation is needed now:
but in keeping with ignoring all variation with
![]() $y$
, we set
$y$
, we set
![]() $Q_{z}=0$
(which is true exactly at the equator) and at lowest order
$Q_{z}=0$
(which is true exactly at the equator) and at lowest order
where, because of the concentration of modes about
![]() $z=0$
,
$z=0$
,
![]() $2\unicode[STIX]{x1D6FA}Q_{y}(z)=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}(z)$
was replaced with the negative minimum
$2\unicode[STIX]{x1D6FA}Q_{y}(z)=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}(z)$
was replaced with the negative minimum
![]() $-|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}|$
at
$-|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}|$
at
![]() $z=0$
and the rate of growth with its inviscid maximum
$z=0$
and the rate of growth with its inviscid maximum
![]() $\unicode[STIX]{x1D6FE}\approx |\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}|^{1/2}$
. Then, the eigenvalue problem becomes
$\unicode[STIX]{x1D6FE}\approx |\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}|^{1/2}$
. Then, the eigenvalue problem becomes
which implies that in order to satisfy the boundary conditions,
which is the equivalent of (A 18).
As before, there is the competition between the inviscid tendency of ever faster growth with increasing horizontal wavenumber
![]() $|l|$
(second term) and viscous damping (third term). Maximal growth occurs for
$|l|$
(second term) and viscous damping (third term). Maximal growth occurs for
![]() $n=0$
and
$n=0$
and
When put back in
![]() $\unicode[STIX]{x1D6FE}^{2}$
in (A 38), one finds (with
$\unicode[STIX]{x1D6FE}^{2}$
in (A 38), one finds (with
![]() $\unicode[STIX]{x1D6FE}_{\infty }=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}|^{1/2}$
)
$\unicode[STIX]{x1D6FE}_{\infty }=|\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FA}}}|^{1/2}$
)
which approaches the inviscid maximum
![]() $\unicode[STIX]{x1D6FE}_{\infty }$
via
$\unicode[STIX]{x1D6FE}_{\infty }$
via
![]() $Re^{-1/4}$
, thus explaining figure 8(a). The spatial structure of the fastest growing modes is
$Re^{-1/4}$
, thus explaining figure 8(a). The spatial structure of the fastest growing modes is
Therefore, the vertical scale
![]() $L_{v}\propto (Re^{3/8})^{-2/3}=Re^{-1/4}$
and, since
$L_{v}\propto (Re^{3/8})^{-2/3}=Re^{-1/4}$
and, since
![]() $l_{\star }\propto Re^{3/8}$
, horizontal scales vary as
$l_{\star }\propto Re^{3/8}$
, horizontal scales vary as
![]() $L_{h}\propto Re^{-3/8}$
. This was indeed seen in figure 8(c).
$L_{h}\propto Re^{-3/8}$
. This was indeed seen in figure 8(c).
Appendix B. Mixing prediction details
The prediction presumes that after the turbulent phase, momentum is mixed to constant
![]() $m=M_{c}$
(see the sketch in figure 4). Since the flow is expected to be Taylor-column-like again, the inner edge is expected on the inside to be along some radial distance
$m=M_{c}$
(see the sketch in figure 4). Since the flow is expected to be Taylor-column-like again, the inner edge is expected on the inside to be along some radial distance
![]() $R=\text{const.}$
, i.e. in the local Cartesian coordinates along a parabola, and on the outside by the surface
$R=\text{const.}$
, i.e. in the local Cartesian coordinates along a parabola, and on the outside by the surface
![]() $z=0$
. The only difficulty is geometric: the integration limits are between a curved and a straight boundary. With
$z=0$
. The only difficulty is geometric: the integration limits are between a curved and a straight boundary. With
![]() ${\tilde{y}}=y/L$
,
${\tilde{y}}=y/L$
,
![]() $\tilde{z}=zR/L^{2}$
, the parabola describing the mixed region is
$\tilde{z}=zR/L^{2}$
, the parabola describing the mixed region is
![]() $\tilde{z}-{\tilde{y}}^{2}/2=\tilde{z}_{l}<0$
. Conservation of momentum requires
$\tilde{z}-{\tilde{y}}^{2}/2=\tilde{z}_{l}<0$
. Conservation of momentum requires
Continuity of
![]() $M$
at the edge of the mixed regions means that
$M$
at the edge of the mixed regions means that
![]() $M_{c}=M(y=0,\tilde{z}_{l})$
. This is enough information to determine the mixing depth
$M_{c}=M(y=0,\tilde{z}_{l})$
. This is enough information to determine the mixing depth
![]() $\tilde{z}_{l}$
at the equator and hence the entire mixed region bounded by the parabola
$\tilde{z}_{l}$
at the equator and hence the entire mixed region bounded by the parabola
![]() $\tilde{z}-{\tilde{y}}^{2}/2=\tilde{z}_{l}$
and the surface
$\tilde{z}-{\tilde{y}}^{2}/2=\tilde{z}_{l}$
and the surface
![]() $\tilde{z}=0$
.
$\tilde{z}=0$
.
For convenience, we non-dimensionalize the moment:
Continuity at
![]() $\tilde{z}_{l}$
means
$\tilde{z}_{l}$
means
The integral involving the constant
![]() $\tilde{M}_{c}$
in (B 1) is
$\tilde{M}_{c}$
in (B 1) is
The area integral over the background momentum in
![]() $\tilde{M}$
on the left-hand side of (B 1) is
$\tilde{M}$
on the left-hand side of (B 1) is
On the left-hand side of (B 1), the remaining term associated with the relative momentum is
where we used the definition of the error function
Conservation (B 1) is then guaranteed by equating (B 6c
)
![]() $+$
(B 5c
)
$+$
(B 5c
)
![]() $=$
(B 4c
), which yields after substituting
$=$
(B 4c
), which yields after substituting
![]() $\tilde{M}_{c}$
from (B 3)
$\tilde{M}_{c}$
from (B 3)
For
![]() $A=5$
, solving (B 8) yields the values
$A=5$
, solving (B 8) yields the values
![]() $\tilde{z}_{l}=-2.47$
and
$\tilde{z}_{l}=-2.47$
and
![]() $\tilde{M}_{c}=M_{c}/\unicode[STIX]{x1D6FD}L^{2}\approx -2.89$
.
$\tilde{M}_{c}=M_{c}/\unicode[STIX]{x1D6FD}L^{2}\approx -2.89$
.
If all variation with
![]() $y$
is ignored and only mixing exactly at the equator is considered, one must set
$y$
is ignored and only mixing exactly at the equator is considered, one must set
![]() $y=0$
in the integrand in (B 6b
)
$y=0$
in the integrand in (B 6b
)
![]() $+$
(B 5b
)
$+$
(B 5b
)
![]() $=$
(B 4b
) and ignore the
$=$
(B 4b
) and ignore the
![]() $y$
-integral. This yields
$y$
-integral. This yields
Solving (B 9) for
![]() $A=5$
yields
$A=5$
yields
![]() $\tilde{z}_{l}\approx -2.76\tilde{M}_{c}\approx -3.08$
.
$\tilde{z}_{l}\approx -2.76\tilde{M}_{c}\approx -3.08$
.