No CrossRef data available.
Published online by Cambridge University Press: 07 October 2005
Design couples synthesis and analysis in iterative cycles, alternatively generating solutions, and evaluating their validity. The accuracy and depth of evaluation has increased markedly because of the availability of powerful simulation tools and the development of domain-specific knowledge bases. Efforts to extend the state of the art in evaluation have unfortunately been carried out in stovepipe fashion, depending on domain-specific views both of function and of what constitutes “good” design. Although synthesis as practiced by humans is an intentional process that centers on the notion of function, computational synthesis often eschews such intention for sheer permutation. Rather than combining synthesis and analysis to form an integrated design environment, current methods focus on comprehensive search for solutions within highly circumscribed subdomains of design. This paper presents an overview of the progress made in representing design function across abstraction levels proven useful to human designers. Through an example application in the domain of mechatronics, these representations are integrated across domains and throughout the design process.
Leifer (1994) casts design as a human, social activity. Design is customer driven because designers take input from nonexperts (customers) and translate it into engineering requirements that represent the desires of the customer without unduly constraining the design space. These requirements typically fall into those associated with function (what a design must do) and performance (measures of its effectiveness in doing it). Translation processes take place recursively throughout the design process, from initial customer objectives to design specs, function-based design to configuration design, and configuration design to detailed design. Design processes at higher levels of abstraction lead to specifications that further drive processes performed at lower levels of abstraction. The results of lower level design activities are used iteratively to redefine design goals at higher levels of abstraction. Because initial goals occur at many levels of abstraction, the quality of abstract design concepts cannot be fully evaluated until their implications at lower design levels are explored. This deeper investigation informs higher level design processes, helping to refine design goals.
Both the process of design and the product of this process are developed concurrently, as duals. When we talk about design as a knowledge-intensive process, we are talking not only about knowledge of how to generate design alternatives and select among them but also about knowledge of when to narrow or expand the design space and how to manage evaluation models with varying cost and accuracy.
Design is thus a transformation (by recursive, iterative translations) of an initial knowledge state to a final knowledge state. Because the initial and final states are representations of the artifact being designed expressed at different levels of abstraction, the state descriptions must be complete and unambiguous at their respective levels of abstraction. The start of the design process requires a sufficiently clear description of the intended end point of the process and the constraints within which the designed device must operate. Dym (1994a) defines a complete design as a set of fabrication specifications that allow the artifact to be built exactly as intended by the designer. Others suggest that the final specification include detailed representation of designer-intended function/behavior to improve downstream processes like manufacturing and troubleshooting (Umeda et al., 1994) capturing this information within the design process is a prime motivation for formalizing function-based design. Only the most routine designs are understood well enough initially to provide specifications complete enough to entail a design solution; in the general case, the initial specification must be refined through repeated testing throughout the design process. In Yoshikawa's Ideal Design (1981), complete knowledge of all possible specifications and designs affords a direct mapping from customer need to design attribute; Real Design introduces physics as an intermediary in the mapping, creating an evolutionary process where requirements are refined as solution classes and then specific solutions are proposed and evaluated.
Rather than a single layer of abstraction interposed between design requirements and solutions, Dym and Levitt (1991) and Ullman (1992b) propose the following six knowledge-state layers for design:
The detailing of the knowledge-state layers is not discussed here, beyond noting that the knowledge-level layers require various representation languages for proper expression, five of which are identified here (Dym, 1994b; Dym & Brey, 2000):
The knowledge-state layers and their representations are not independent: the more abstract the layer is, the more likely its rather vague knowledge will be expressed in text. At the other end of this spectrum, artifact types and artifact instances are increasingly specific descriptors typically expressed in graphical or physical terms.
At its core, function is an abstraction of behavior (Qian & Gero, 1996). Although physics can often be used to model the behavior of a design, functionality is a human interpretation of this behavior: Does this behavior accomplish the desired effect? Does this effect address the needs of the customer? For this reason, when we talk about function we must always relate function to a customer; when we talk about functional synthesis, we must expand the boundaries of synthesis beyond physics-mediated behavior into human-mediated function. Functional abstraction implies more than simply a subset relationship on behavior; it implies intent on the part of the designer situated in the context of the customer (Chandrasekaran & Josephson, 2000).
In the modern, life-cycle view of design, the role of “customer” is extended from the end user to all of those involved in the production, distribution, service, and retirement of a design. Although end-user notions of function predominate at the “function” layer, function pervades the six knowledge-state layers for life-cycle customers. For example, function relating to forming parts resides at the artifact type and instance levels; assembly functions occur at the embodiment and artifact type levels. Functional requirements at these lower levels come from two basic sources: the specific design (defining the parts that must be shaped and assembled) and the more generic processes used to produce it (assembly, automated assembly, primary forming process, secondary process, fixturing, etc.). In an examination of small mechatronic products, Verma and Wood (2001) find that 70% of the geometric features of a design relate to functions other than those attributable to the end user. In addition, these functions vary based on the manufacturing processes used, the production volume required, the method of distribution, and so forth. Design for X thus means establishing functional requirements for each X within the context of a design that also addresses end-user functional requirements.
Computational synthesis focuses on formal methods of generating candidate designs. The process is fundamentally one of composition: a set of building blocks is defined along with rules for combining them. These building blocks can be a collection of parts or a set of primitives (functional or geometric). We will divide computational synthesis into two loose classes based on the degree to which goal and domain knowledge is explicitly used for generating designs.
Where goals can be defined in the language of generation, computational synthesis takes on the character of a classification or derivation design task. Typical of this type of computational synthesis are efforts in the abstract functional design knowledge-state layer (Chakrabarti & Bligh, 1994; Qian & Gero, 1996; Sharpe & Bracewell, 1996; Kota & Chiou, 1997). Because goals essentially establish the boundary conditions of the design, search is focused on reducing differences between input and output by interposing functional units. From a strategy standpoint, this type of computational synthesis might be directed to define a single design solution or to enumerate all possible design solutions. We will label this tight coupling of goals and synthesis “strong” computational synthesis. Such methods typically focus on a single function/behavior goal for synthesis; additional goals like size, cost, or other aspects of technical performance might be used to select among the generated designs. Kota and Choiu (1997) perform strong synthesis for mechanism type design; desired input/output relationships are produced by stringing together catalog components whose individual behavior is expressed in input/output relationships.
Where design goals cannot be encoded in the representation most appropriate to generation, computational synthesis relies on iterative generate-test loops. In such a scheme, design goals are encoded as fitness functions defined over the design generation space. Because generation cannot be constrained directly by the representation, these methods tend toward random explorations, iteratively focused on areas most likely to accomplish the desired goal. The resulting large number of design candidate evaluations places a premium on both the efficiency of goal assessment and the effectiveness of candidate generation. This “weak” computational synthesis tends to work well in situations where design goals are difficult to encode directly in the representation least biased for the generation step. For example, 2-dimensional (2-D) truss structures can be generated in a graphical/pixel domain by adding and deleting “material.” The resulting design is evaluated through more abstract mathematical models of strength, deflection, mass, or cost (Reddy & Cagan, 1995). Alternatively, topology generation could employ a grammar to place new members into a design (Shea & Cagan, 1997), but the effectiveness of the new design must still be gauged in a separate evaluation step. In both cases, the resulting evaluation steps help to focus further synthesis (e.g., removing material from low stress areas, adding members to high stress areas). Evaluations of a more binary nature (e.g., is this item a “chair”?) produce still weaker synthesis methods.
Because it takes place at many different stages of the design process and in several different knowledge-state layers, it is difficult to categorize functional synthesis rigidly. At various stages of design, functional goals might be defined textually, numerically, or graphically; the native format goes a long way toward shaping the nature of synthesis; less formal (i.e., less computable) representations yield less formal definitions of building blocks and less sound composition rules.
The directionality conventions of business integration also frame a discussion of design integration. Vertical integration spans all abstraction levels within a single domain. For mechanical engineering this would mean proposing mechanical solutions to customer needs at the functional level, identifying mechanical means of accomplishing individual functions, developing a configuration and embodiment linking these functional units together, and generating detail design plans for parts and assemblies. The main issue in vertical integration is in the transition from one abstraction level to the next, first from higher to lower levels through goal specification. The combination of weak computational synthesis at high levels of abstraction with the imprecise evaluation metrics that can be applied to such abstract representations may lead to backtracking when strong synthesis at lower levels of abstraction finds contradictory goals or when more accurate design evaluations at even lower levels of abstraction find a design concept unacceptable.
Horizontal integration generates and evaluates solutions from all domains within a single abstraction layer. Integration at the functional level might mean the ability to consider both mechanical and electrical solutions to the same problem (e.g., designing hard vs. soft automation for a production line) or could broaden the scope of domains to political or social solutions to problems: should the excess nutrient problem in the Chesapeake Bay be addressed by controlling runoff with a civil dam structure, an environmental buffer, a mechanical filter, a computer-controlled fertilizer dispenser, development of different types of fertilizers, encouragement of organic farming methods, or legislation of farming practice? At lower levels, horizontal integration might be more straightforward, perhaps developing solutions in parallel for various materials and manufacturing processes. Circumscription, used by many “strong” computational synthesis methods to promote soundness (Takeda et al., 1990), limits the domain [e.g., energetic systems (Sharpe & Bracewell, 1996), mechanisms (Chakrabarti & Bligh, 1994; Kota & Chiou, 1997)] that any one method might search; horizontal integration requires exploring the functional boundary between synthesis methods or integrating functional representations and synthesis methods across domains.
A completely integrated design environment would feature both vertical and horizontal integration. However, until the issues surrounding integration along each of the above axes are understood, it is premature to talk about complete integration. Where does functional synthesis fit into these integration frameworks?
To address this question, we must look at the core components of functional synthesis: building blocks, composition rules, and evaluation functions. An additional organizational distinction also helps frame the discussion: top-down vertical integration would imply progression through increasingly less abstract representations, the results of search at each step passed down to lower levels of abstraction as functional goals. Bottom-up integration performs search at low levels of abstraction and controls this search through the evaluation of models of higher level functionality that build upon low-level behavior.
Top-down vertical integration requires translation between abstraction levels. For strong computational synthesis within each level, designs from higher levels of abstraction must be translated into goals at lower levels. Top-down weak computational synthesis might simply identify a set of “seed” building blocks for initiating the construction of lower level candidate designs. In either case, evaluation spans several levels of abstraction, from high-level functionality, to idealized behavior, to part count and cost.
The need to access low levels of design abstraction for accurate performance evaluation suggests a bottom-up approach to vertical integration in which synthesis is done at the lowest level of abstraction. Search control is extremely important in this mode because such low-level representations are naturally unbiased, a pixel representation can be readily searched for 2-D trusses, but a voxel representation for 3-D trusses is impractical compared to grammars that bias the design generation toward topologies of straight members. Success of the bottom-up approach lies in the ability to propagate structural descriptions to behavior-based evaluation and function. Thus, the bottom-up approach is most suitable to search where completeness is highly valued and evaluation is either inexpensive across all abstractions or inaccurate at all but the lowest levels of abstraction. Genetic/evolutionary methods predominate here, requiring both inexpensive evaluation metrics to identify promising candidates and simple composition mechanisms that use pools of such candidates to “design” new candidates with the hope of combining good features in a synergistic way.
Whereas vertical integration introduces the need to translate either functional goals or evaluation models between representations within a single domain, horizontal integration requires merging representations across domains. The ability to represent a larger range of solutions brings with it a cost in decreased representational bias, which in turn, means that more of the domain knowledge must be expressed using the representation rather than embedded in it. This includes strategic knowledge that may have been encoded in composition rules. Problem-solving methods and mechanisms that pertain to only a subset of designs in the broader representation must be preceded by appropriate screening logic. Likewise, effects that can be ignored in a subdomain may become significant in an expanded context. For example, a mechanical model of an electric motor might not include the RF noise that a motor's brushes emit; this noise could be critical in a mixed electromechanical domain.
The closer a design moves to the final artifact, the more difficult it is to horizontally integrate the design process. Concurrent engineering performed through collocation is a successful strategy of integrating manufacturing considerations into the earliest functional and embodiment phases of design. Its effectiveness lies in the exchange of informal information at high levels of abstraction where there is the largest freedom to explore design alternatives. Concurrent engineering applied at the later geometry-oriented stages of design has proven less successful. As prescribed by Pahl and Beitz (1988), function-based design is essentially horizontally integrated at the highest levels of abstraction. The emphasis early in the design process is on development of function–structures that are explicitly solution neutral. The selection of physical phenomena at the final stages of functional design goes a long way toward defining the relevant solution domain(s). Instead of trying to integrate synthesis across domains, horizontal integration could act at higher levels of abstraction to produce a range of possible goal sets for each solution subdomain. In mechatronics, horizontal integration might mean exploring in parallel several apportionments of functionality between the mechanical and computational domains; should a mouse generate separate x and y signals mechanically or should these signals be extracted computationally from a simpler mechanical system?
Functional synthesis is search. Vertical integration affords development of depth in this search. Strong computational synthesis further introduces a heuristic element for managing the search process; weak computational synthesis responds to poor design performance by backtracking within and across abstraction levels. Horizontal integration affords an increase in the breadth of search within each abstraction level. However, in doing so its reduced circumscription “weakens” domain-specific synthesis. Both horizontal and vertical integration are directed at improving the scope of the design search process, the issue is how to manage both the breadth of the search and the declared and implied knowledge required to conduct it under resource constraints.
A generate-test paradigm must maintain a balance on the efficiency of the two main activities. Generation efficiency can be measured along two metrics: completeness and soundness. Complete design generation is capable of producing all possible designs; sound generation produces only designs that are feasible. These two measures compete because improving completeness often means generating a greater proportion of infeasible designs; improving soundness might remove small pockets of interesting feasible design solutions from consideration.
On the evaluation side, a similar trade-off is found in cost versus accuracy. Evaluation at high levels of abstraction may be inexpensive (essentially free if it is encoded in the representation or composition rules), but inaccurate. Where uncertainty in the evaluation is explicit, it can be used to aid search control (Wood & Agogino, 2005). At high levels of abstraction, behavior prediction need only be accurate enough to eliminate infeasible (either from the standpoint of function/behavior or performance) designs. As abstraction is reduced, both function/behavior and performance evaluations gain accuracy: general operation, approximate cost, and approximate size at the functional level; idealized behavior, approximate size/shape, and more refined cost at the embodiment stage; actual behavior, cost, size, shape, and so forth, at the artifact instance level. Synthesis must proceed to the lowest level of abstraction to generate a design; if synthesis is essentially free, then it makes sense to generate all possibilities to the most detailed level of abstraction and simply choose the best design. However, under limited resources synthesis of a design must terminate once it is proven inferior.
Because design is driven by customer needs, most analytical evaluation models are at best approximations of the situations into which the design will be inserted. Estimating the value of a design from the perspective of the customer takes time and money. Even if we could afford to capture completely the future value of a design for a single customer, most designs are produced for a market of multiple heterogeneous customers, each with separate value functions. In such a market, the value attached to a design will be uncertain even if design behavior simulation is exact. Casting design as the transformation of the initial knowledge state into a solution cannot assume that this initial state is well enough defined to select a single best solution. Design is a process of learning, about both the design space and the design evaluation. Search in integrated design means coupled synthesis, evaluation, and refinement of evaluation metrics. Integrating functional synthesis challenges our ability to represent and reason about function at many levels of abstraction and across domains. To illustrate some of the challenges and trade-offs to be managed, we now describe an attempt in the domain of mechatronics at both vertical and horizontal integration applying, combining and extending existing representations and methods for reasoning about function.
Mechatronics is an emerging discipline at the interface between mechanical and electrical engineering. It is distinguished by the isolation of sensation from actuation, usually accomplished through digital control. The increasing presence of computers and data networks in everyday life positions mechatronics as a critical technology for the future: the demand for interfaces between the digital and physical world will only continue to increase.
In addition to its economic and technical importance, mechatronics provides an interesting setting for discussing design integration; it not only presents the challenge of horizontal integration across mechanical, electrical, and information domains, but through this integration it also presents a much larger space of design possibilities. Distinguishing among candidates from this increased design space affords (or, for optimal design, requires) consideration of many more aspects of design performance: packaging, manufacturability, cost, technical performance, and so forth. At the same time, because it is centered on a limited set of sensors and actuators, mechatronics provides a tractable set of building blocks in the phenomenon/embodiment knowledge layers.
We now present the functional synthesis of mechatronic devices throughout knowledge-state layers from client objectives to artifact type. At each layer, the salient functional representation is introduced along with how building blocks and composition rules are represented in it. This is followed by the treatment of goals/evaluations (strong vs. weak synthesis), followed by an illustrative example and the issues its functional synthesis raises.
At this highest level of design abstraction, client objectives are separated into two classes: what the design must do, and how to measure how well it does it. It is useful for this discussion to separate them into functional and performance goals, respectively. Typical methods for eliciting and objectifying the latter include quality function deployment (QFD) and the House of Quality (Hauser & Clausing, 1988), resulting in both evaluations of performance and approximate targets for success. Although these metrics will be used for evaluation, the main issue for functional synthesis at this most abstract layer of design is the development of functional goals.
Functional goals at this stage are at their most abstract. The systematic methods of Pahl and Beitz (1988) provide a good starting point for capturing them: the black-box function–structure. Here, a “box” is drawn around the system to be designed and the required input and output flows of energy, material, and information defined for this box. The box is then filled with transformations that should occur within the system: the system functions. Although Pahl and Beitz (1988) make no restriction on the language used to describe either function or flow, others have created lists of typical functions drawn from experience (e.g., Ullman, 1992a). Stone and Wood (2000) propose a restricted vocabulary for both function and flow that is intended as a basis representation from which any function can be composed. We will use this “functional basis” as the foundation for our representation of high-level function. Because many material and energy flows are spatially constrained in some way, the text-based flow representation is augmented with position-direction information.
At this design-initiating knowledge-state layer, the main activity is the generation of goals and evaluations that will be used throughout the rest of the design process. The building blocks used in this process consist of the desired input and output flow specifications and the description of the overall transformations that must take place. The functional basis provides a restricted set of flows and functions that can be used in this description, but the actual description must be derived from an analysis of the context of the customer need: a thoroughly human activity.
No formal composition takes place at this level, although considerable effort is involved in translating a human/physical context into the function–structure framework. The Pahl and Beitz (1988) methodology stresses abstraction of the problem at this stage, essentially expanding the borders of the system so that all possible solutions can be considered: a single design context might spawn several different system definitions even at this initial design stage.
Through the rest of the discussion we will trace the design of a force-feedback mouse. Figure 1a shows both a rough physical interpretation of the functional requirements, placing energy and material flows spatially while also defining basic size goals; Figure 1b captures the desired functionality as a black-box function–structure using the functional basis vocabulary: typically verb–object pairs. Together, these representations encode the need for a device of a certain basic size that supports the hand, receives human force input from it, generates a force reacted against a reference surface, and measures its own displacement with respect to the reference surface. Performance goals (not shown) include targets for cost, force generated, noise generated, position accuracy, and so forth.

(a) Spatial and (b) functional requirements for the force-feedback mouse example.
Even though functionality at this stage is abstract, getting here has already required many decisions. From the client standpoint, initial functional requirements are for a pointing/indicating device that generates feedback in response to position/velocity/indication; selecting the hand as the input interface to the user and the desktop as a reference surface drives the solution process toward mouse-style devices. Other interface definitions would generate different types of designs. The process of transforming client objectives situated in the rich context of the “real” world into the function–structure abstraction challenges computation: capturing context is extremely difficult; encoding it in computable form is even harder. For this reason, functional synthesis within the client layer is largely a human process. Separating performance goals from functional goals helps to partition the problem, making it easier to focus the human effort on establishing a black-box function–structure. Alternatively, McAdams et al. (1999) explore using case-based reasoning to identify critical functional units using an index based on preliminary performance goals elicited in the QFD process. Although this technique appears to hold promise, its inability to capture the totality of context for a design means it is best used as a heuristic to focus attention rather than as the basis for formal design composition.
Functional design encompasses a range of abstractions, starting with the black-box function–structure generated at the client objectives layer and decomposing it into progressively more concrete networks of functions. Functional design terminates with a topology of solution principles: functions distilled into distinct components or subsystems.
The function–structure is the primary representation; but where the black-box function–structure idealizes the system as a single functional unit, functional design decomposes this system-level view of the design into a network of simpler functions that, in aggregate, accomplish this ideal. Although the representation remains constant, its form changes to one in which each functional unit accomplishes only a single function and operates on only the flows necessary for that function. Figure 2 shows a “design” level decomposition of the black-box function–structure of Figure 1b.

“Design” level decomposition of a force feedback mouse (dotted boxes surround functions repeated for the y axis).
The basic building blocks are defined by the function–structure framework instantiated with functions and flows defined in the controlled vocabulary of the functional basis. The expressiveness afforded by function–structures exacts a price: there is no well-defined set of valid function/flow relationships from which to choose. The set of meaningful functions is a tiny subset of function–structures expressible using the functional basis. As in natural language, a dictionary (i.e., the functional basis) and a grammar (i.e., function–structures) are much more effective for interpreting human ideas than for generating them.
At the high level of abstraction at which functional design receives its goals (e.g., the function–structure of Fig. 1b), there is no well-defined catalog of functional units. As in any application without a strong logical basis, case experience can be applied (Maher & Pu, 1997). Generating building blocks from prior design instances for recombination into new designs can bias the synthesis of new functionality toward valid subfunction units. However, because function is an observer-centered human abstraction, it is not necessarily straightforward for to induce function from existing artifacts. Kurfman et al. (2003) find that the functional basis helps to regularize the representation of function in a reverse engineering context. Verma and Wood (2004) formalize the reverse engineering process, requiring functional descriptions for each individual part in a system. Such formalization produces consistent functional descriptions across the human reverse engineers, but results in a rather low level of abstraction in the resulting representation. Further complicating the issue, Gietka et al. (2002) find that high-level black-box and “design” function–structures of a product have little correspondence with the low-level function–structures derived from actual products, even when all functionality is represented using the functional basis. Thus, although building blocks can be induced from existing products, the shift in functional viewpoint between design and reverse engineering presents a significant challenge to the direct reuse of reverse engineering cases.
Function–structures are hierarchical; at high levels of abstraction, relatively few functions and flows are defined. As strange as it sounds, decomposition is the main compositional process in functional design. From the black-box level, flows and functions are segregated into distinct flow paths. Navinchandra (1988) demonstrate the effectiveness of this type of composition in the CADET system where means–ends analysis is applied between overall input and output flow definitions; each functional unit is represented as a set of qualitative input/output relationships over a canonical set of flow variables. In addition to using qualitative functional relationships to compose functional units along flow paths, CADET also stores “chunks” of functional units as cases for future reuse; compiling useful compositions can improve reasoning efficiency as the system gains functional “experience.”
One basic lesson from CADET is the need (or more appropriately the lack thereof) of expressing functionality: CADET's representation focuses exclusively on flow information from a function–structure. Functions are defined only by qualitative relationships between input and output flows. Although it seems counterintuitive to eliminate consideration of function from functional synthesis, remember that function at this stage is still subjective and changes with abstraction level. In contrast, flows are largely objective: although an electrical energy flow may be abstract in terms of frequency or voltage, its existence is objective. Verma and Wood (2003) identify several strategies for bridging the gap from reverse engineering case to design- and black-box level function–structures, the most successful of which focuses on aggregating functional units around the creation and destruction of flows “internal” to the design (i.e., any flow that is both created and consumed within the system). The combination of using reverse engineering to populate a case base of low-level design functions and of applying straightforward aggregation rules to compose these units into higher level functional “chunks” is similar in spirit to the case compilation used by CADET. In our framework, composition is less sound than in CADET due to the lack of even basic qualitative relationships for the functions. However, soundness is traded for completeness: virtually any functional arrangement can be constructed. This, coupled to relatively abstract encodings of flow information produces computational synthesis on the weak end of the spectrum. As a result, a large number of unsound results flow to lower levels of abstraction where more sound reasoning methods can identify and filter out poor high-level designs.
Although CADET uses qualitative physics to model functional behavior, these models bias the system toward monotonic elements. Removing this bias, important in a domain where digital signals are pervasive, also removes much of the ability to evaluate behavior at the functional level. Careful mapping of flow types will generate classes of designs that will do something; it is up to the synthesis processes at lower levels of abstraction to flesh out each design class in response to more detailed behavior/performance goals. In the end, whereas CADET focused on a single level of abstraction for both generation and evaluation, it could neither accurately predict the behavior of the resulting designs nor respond to nonmonotonic functional goals.
The black-box function–structure of Figure 1b is handed down to the functional level, essentially as a query of input/output flows and internal functions to the reverse engineering case base, which contains functions structures of design instances stored at multiple levels of abstraction (generated from low-level structures through the application of internal flow-based aggregation rules). For example, a common component in mass-produced computer mice is an encoder wheel, shown in Figure 3b. The light introduced internally to the device provides a path toward aggregating function, generating the function–structure shown in Figure 3a (function is labeled at this level of abstraction for clarity, aggregation rules for generating such functional descriptions are still under development).

Function–structures for the “sense” function in Figure 2: (a) an abstract function and (b) the actual functional unit in the ball mouse, reverse engineered at the “parts” level.
The result of the query identifies several possibilities for constructing the function of a force feedback mouse: functional units from different types of computer mice (mechanical “ball” mice and electronic-optical mice) lead the retrieval list, along with hand-held devices that generate force/displacement, like a power screwdriver. Essentially, the whole of the mouse functionality is retrieved (Fig. 4a,b), although only the main force/reaction flow from the screwdriver is retrieved (Fig. 4c). Composing the screwdriver and the two different mouse types can be done in different ways: for the mechanical mouse, there are already mechanical displacement energy flows in the system, so the mechanical force flow need merely be coupled into one of them; for the optical mouse, a parallel mechanical force/displacement flow must be introduced into the system.

Function–structures for two mice and a power screwdriver (dotted boxes surround functions repeated for the y axis).
Although the case-based methodology can create subsystems of arbitrary abstraction, in new designs these subsystems must still be integrated with each other. Function–structure flows provide a ready means of integrating subsystems by tapping off of existing flows or interposing functional units along a flow path. However, function–structures have an inherent weakness in this area; due to their reliance on “flow,” they are more readily adaptable to what is typically labeled a “through” variable (e.g., current, displacement, fluid flow, etc.) in bond-graph notation. For these through variables, it is appropriate to perform composition in function–structures by inserting functions into a flow. However, for across variables (e.g., voltage, force, pressure, etc.), it can be difficult to tell where in a functional–structure chain one might interpose a new unit. In the force feedback mouse example, we need to insert a functional unit that generates a force between the reference surface and the user's hand. A long string of functional units is defined in the through variable of displacement: how should composition inject a force into this flow? Should it just be done in parallel? Of course, bond graphs “know” that through and across variables are related; function–structures confound the two, allowing them to be used interchangeably. Removing modeling rigor complicates the composition process. The main issue is the interpretation of function: in formal models, function is often implied by mathematical models of input/output transformations; relaxing this bias to include function as a semantic concept greatly reduces the soundness of design generation. Replacing formal models with names creates ambiguity. In the end, flow definitions and interactions may be a much stronger form of design information.
Other issues arise at the terminal end of the functional design spectrum. It is at the solution principle level where one of the primary product design decisions is made: make versus buy. Because they are single parts, off the shelf components are generally encoded at a higher level of functional abstraction than customized assemblies: Figure 3a shows the function–structure for a rotational encoder; Figure 3b shows the same basic device implemented as a set of components in a mass-produced product. This example points out not only the need to allow different levels of abstraction at the solution principle level, it also illustrates the need to pass multiple design candidates to lower levels of abstraction where more detailed evaluations (like cost in the make/buy decision) can be made accurately. If enforced at this abstract stage, heuristics for manufacturability (like reducing part count) would likely favor the single-component solution over the one using multiple parts. Only at the detail design level does one find that the custom implementation leads to fewer total parts and a lower cost. Such uncertainty in performance predictions further reinforces the need to generate a large set of candidate designs and continue to flesh them out at lower levels of abstraction.
The function–structures defined at the functional stage are examined at the phenomenon level for functions in which the primary flow changes class (e.g., pressure to translation, electrical energy to rotation) or domain (e.g., energy to information). Such transduction is usually accomplished by exploiting physical phenomena. Functions that create flows not present at black-box level of abstraction represent critical decisions in the design process; the functional level of abstraction is identifies sets of physical phenomena around which the new design can be constructed. In our force-feedback example, one candidate set of physical phenomena is electric motors and optical encoders; a second is electric motors and optical displacement sensors. It is at the physical phenomena level that these components are instantiated as physical objects whose behavior can be modeled and whose basic performance trade-offs can be assessed.
Physical phenomena are well-defined components, such as sensors and actuators that transform flows from one domain to another. The building blocks that make up this set of components can be drawn from catalogs. Unfortunately, most catalogs provide access to components only at the instance level (i.e., a single part number). For example, a catalog might contain AC motors, DC motors, DC Brushless motors, or stepper motors. From the standpoint of the function–structure, each of these does the same thing: convert electrical energy into mechanical energy. As with function-level design, building blocks must span abstraction levels. Wood and Agogino (2005) provide a design space modeling methodology based on the induction of probability density functions from design instances. The use of probabilistic modeling allows for the representation of heterogeneous phenomena at high level of abstraction. Abstraction is spanned by extending the representation to capture more functional detail as selection reduces heterogeneity.
Composition is absent at the phenomenon level because the focus of this stage is more selection than synthesis. The function level is charged with passing precomposed units as function–structures whose phenomena are to be instantiated. Multiple abstractions of the same basic design (e.g., Fig. 2) are treated as different designs requiring different phenomena instantiations.
The physical phenomenon level is the first stage at which objective evaluation of candidate designs can be made. The broad spectrum of performance metrics elicited from the customer at the client objectives knowledge-state layer filter down to the physical phenomenon layer as system requirements. These include not only aspects of functional/behavioral performance (e.g., power, efficiency, accuracy, etc.), but also evaluations based on size, shape, cost, lead time, and so forth. The same design space modeling methodology that is useful for spanning abstraction is equally useful for inducing models of performance for which there is little analytical basis. By using probability densities to encode these models, notions of input and output can be discarded. Instead, performance goals can be applied as constraints whose impact is felt by design variables.
Figure 5 shows a set of probabilistic models derived from a catalog query on motors with power appropriate to the force feedback mouse. Functional parameters like torque and speed of a motor as well as physical parameters like length and diameter are related to a system-level requirement like mass. Because initial performance requirements are often uncertain, Wood and Agogino (2005) apply a decision–theoretic methodology that balances design selection against design requirement refinement. Here, torque specification can be used to induce properties like size and shape of a motor. Alternatively, size and shape can be used to induce likely torque ranges that could then be passed down to the embodiment knowledge-state layer for synthesis of a torque multiplication/reduction system.

Probability density contours for motor behavior in the desired range (design instances drawn from a motor catalog).
The main technical issues at this stage of functional synthesis relate to selection of components in isolation from the system in which they are to be inserted. This selection process is driven by system-level performance requirements that must be related to component-level performance. In both cases, the design must be further fleshed out before final component selection can take place. For this reason, the emphasis is on eliminating infeasible designs. For example, one of the performance requirements for our force-feedback mouse might include the amount of force required from the system and the velocities at which the force will act. Together, these generate a power requirement that can be related to other requirements like size or cost. Together, these requirements might lead to selection of a small, high-speed motor (or at least the elimination of larger, higher torque motors) for generating the power necessary for the design while still fitting within the physical envelope of a computer mouse. This then presents a starting point for synthesis at the next knowledge-state layer or, if system-level requirements cannot be met (e.g., in this case, there is no motor that can generate the necessary power within the provided envelope), reconsideration of either the current function-level design or the current system-level requirements.
Embodiment design addresses functions with less extreme transformations on flows (e.g., changing magnitude, direction, or position of a flow). Functionality at this embodiment knowledge-state layer builds on the topologies generated at the functional level of abstraction, introducing spatial aspects of function. Functional design provides a set of possible component topologies; these “components” are still abstract transformations from one flow type to another. Embodiment design must synthesize final topologies of real components and orient them spatially.
Function at this stage is much less subjective than before, more closely tied to physical behavior. Representation then focuses partly on behavior and partly on spatial relationships. For electrical energy and information flow domains, spatial relationships are generally unimportant, but for material and mechanical energy flows, spatial and impedance transformations are interrelated. Material flows are often defined by the size, shape, and mechanical behavior of the material under question. Due to their strong dependence on the context of the problem, these are best dealt with at higher levels of abstraction. Verma and Wood (2003) augment the functional basis language of material flows to help improve functional retrieval performance (retrieval being the keyword, little synthesis can take place without detailed description of the material in question).
For mechanical energy flows, the representation used at this stage is a hybrid of two different representations from the literature. Kota et al. (1997, 1999) use a matrix-oriented approach to capture the behavior of a set of standard mechanical components in terms of input and output rotations and translations. In addition to basic behavior, second-order effects are included like reversibility and linearity. The second representation comes from Chakrabarti and Bligh (1994, 1996a, 1996b); like Kota et al. (1997, 1999), first-order transformations of rotation and translations are captured. Second-order considerations in this case involve spatial information about the flows: do flow axes intersect or are they offset? Although both of these representations are built around a standard set of components, adding in a case-based component can help to overcome their basic inherent limitations: evaluation. Each representation can generally produce a large set of possible solutions; selecting among them becomes a problem (Chakrabarti & Bligh, 2001). Kota et al. (1997, 1999) turn to a heuristic to focus effort: favor the transformation of all translation flows into rotation. Dong and Wood (2004) use cases to generate estimates of size, number of parts, and power from actual implementations of the catalog components.
The physical phenomena laid out at the preceding stage establish the basic transformations that will take place within the system, these transformations must be oriented spatially and their “impedances” (i.e., force/velocity, torque/rotational velocity) matched with the rest of the system. Because flow domains remain constant throughout each transformation, building blocks are much more restricted in embodiment. For example, for designing mechanical systems a catalog of machine elements defines a set of building blocks. Table 1 shows a selection from such a catalog for components that transform rotation into displacement, along with representations from both the Kota et al. (1997, 1999) and Chakrabarti and Bligh (2001) perspectives.
Configuration design building blocks

Function–structures and physical phenomena provide a skeleton of flow transformations that must take place within the system; matching the impedances among these transformations often requires interposing intermediate components like gear reductions. In addition, transformations within a flow domain are often required; for example, transforming rotational torque into linear force. Finally, spatial constraints on input and output flow positions as well as overall system size and shape must be satisfied. Composition must satisfy all three of these main types of constraints while providing for the overall input/output goals handed down in the phenomenon-enhanced function–structures. Abstraction again is present in this process: class-level transformation (e.g., xx rotation → y translation) is generally accomplished through the application of simple rules. Potential solutions can then be screened for satisfaction of second level functional constraints (e.g., spatial- or impedance-based constraints).
From the standpoint of functionality, the design is “complete” at this stage of the process. Idealized behavioral models for each component can be composed into overall system-level behavior. System behavior can then be evaluated with respect to the functional goals established at the client objectives layer. This can help to establish some of the parameters of the embodiment building blocks: gear ratios, link lengths, and so forth. Because functional goals are only part of the design equation, these parameters are linked to issues like size, cost, power, and so forth, previously used for component selection at the physical phenomenon layer. Design screening is much finer at this stage because fairly accurate models of function, performance, size, and cost are all available.
For our force feedback mouse, designs for several different combinations of physical phenomena must be considered. Focusing on the use of rotational motors and the need to generate translational forces that span 2-D space, the building blocks of Table 1 create several possibilities. Figure 6 shows four such possibilities: two that apply crank-slider linkages to the problem, and two that apply cam-follower mechanisms. Each combination is broken down into two subcases: those for which the mechanisms are applied serially (e.g., the “y” crank-slider is mounted on the “x” slider) and those that act in parallel (e.g., “x” and “y” sliders are conjoined into a single element). The former combination rule produces sound machines that are guaranteed to produce the desired result; the latter is an example of an unsound composition rule that might create designs that do not function or whose functionality is not quite what is desired (the parallel crank-slider has 3 degrees of freedom, x and y translation, along with zz rotation).

Serial and parallel combinations of x and y crank-sliders and cam-followers.
Composition rules at this stage must be oriented toward the design “best practice” of function sharing. A function–structure might treat sensing position and generating force as separate flow streams; displacement and force are separated. In actuality, these bond graph conjugates can be combined into a single flow stream that contains both sets of functionality: force and displacement can be combined. Designs based on direct optical sensing of position cannot combine displacement sensing and force generation in the same way.
Multiple input/multiple output system designs must be generated with both serial and parallel composition rules; the combinatorics of this greatly increases the size of the design space, placing pressure on the system modeling/evaluation methods. In addition to the largely holonomic components used by Kota et al. (1997, 1999), completeness issues dictate the availability of nonholonomic components like friction drives. The standard mechanical “ball” mouse is a simple parallel combination of two orthogonal friction drives, accomplished by merging the frictional elements: two “wheels” become a single “ball.” The same combination is not feasible for the holonomic rack and pinion design. Such parallel combination can be encoded in composition rules (e.g., nonholonomic components can be combined off axes; an unsound but potentially useful composition), or at higher levels of abstraction where multiple input/multiple output “components” derived from design cases.
Adding to the combinatorial complexity is the introduction of spatial issues into the design evaluation. In general, function directions (e.g., the fixed x–y orientation of the mouse) constrain the orientation of mechanical components. In addition, sensors are often placed on or near circuit boards to eliminate manufacturing issues related to electrical cables, so the layout of mechanical devices must respond to the ability to place sensors on or around them as well. Merging spatial issues of function and packaging across two domains provides a significant challenge for both synthesis and evaluation.
The final issue is a windfall from the computation at the core of most mechatronic systems: the removal of strict spatial constraints (e.g., direction, orthogonality) through software transformations. In our example, many of the mechanisms useful for generating the 2-D forces produce poor packaging, placing at least one motor to the side of the mouse, causing access problems. Figure 7 shows a design in which both motors are packaged at the top of the mouse and their position information transformed in software. Formalizing this shift of constraint across domains from the mechanical to the information side of the problem is potentially tricky: simply inserting a “wild card” function into the mechanical function side of the representation seems simple enough, but guaranteeing that the information side of the representation is well informed enough to actually accomplish the necessary transformations is difficult.

Software-transformed axis, parallel crank-slider.
With its mechanical formality, the embodiment level of design has received the most research attention. However, even here the role of abstraction within a single knowledge-state layer is significant. In addition, the need to consider multiple-input/multiple output systems as whole rather than as isolated flow streams means that prior formal methods must afford the introduction of less sound, more informal types of components and compositions. Finally, the prevalence of systems in mechatronics that mix information and mechanical flows increases the significance of decisions like where and how to place the domain boundaries and which functionality is accomplished on each side. Although the final decision might best be delayed to the artifact type layer, the embodiment stage is at least charged with the need to produce a rich range of design topologies and layouts.
From an end-user perspective, little functionality is added at the artifact type knowledge-state layer. Given proposed configurations, two major aspects of the design remain undone: connections among components to enable the desired “flows” to actually flow and the provision of a reference from which functional units can act. This latter aspect may seem insignificant but plays a large role in the manufacturability of the final design: Verma and Wood's (2001) study of the functional role of geometric features in small products reveals two findings: the functional reference (referred to as the “ground”) can account for well over 50% of the geometric complexity of modern products; and most of this geometric complexity is related to improving the manufacturability of the product, either forming the parts themselves or easing the assembly process. Thus, functionality at the artifact type knowledge-state layer is primarily directed toward manufacturing. Fortunately, these “functions” tend to be rather generic across assembly processes and within part forming process classes.
The main goals at this stage of the design are to establish connections among parts that provide the desired client-oriented functionality while minimizing the manufacturing costs of the system. Manufacturing costs are generally either associated with the cost of forming parts or the cost of assembling them into systems. In design for manufacture, Boothroyd et al. (2001) typically stress reducing part count, possibly through part combination. However, part combination must be done in a way that is sensitive to the part forming processes and production volume: Fagade and Kazmer (1999) find that increasing the geometric complexity of low-volume parts can result in additional unjustified tooling costs.
Manufacturing function is rather straightforward: a system is merely an assembly of parts, each of which must be formed out of raw material and assembled along with other parts into the final product. The representation follows this basic layout: parts are the main entity, their basic manufacturing process is captured (e.g., machining, molding, deformation, etc.) along with primary (e.g., fixture plane, parting plane, etc.) and secondary (e.g., mold slide axes) manufacturing process axes. Assembly models connect parts to each other; the interfaces between parts are captured as connections. These connections have a dual role; in addition to modeling the process of joining two parts, connection models must also capture the degree of freedom of the connected system. For the former, primary and secondary assembly axes (relative to a functional axis) are captured for each connection. Functional aspects of connections are modeled using the contact type and contact matrices of Roth (1987). Table 2 illustrates these representations for a number of flexible joints available as building blocks at the artifact type layer.
Detail design building blocks

Although the representation is relatively straightforward, the geometric nature of parts and connections makes representing a complete set of building blocks prohibitively expensive. To deal with this problem we again turn to reverse engineering: “part” level decomposition produces building blocks containing connections between functional units and connections from functional units to the local reference. Note again that abstraction plays a major role. As Table 2 demonstrates, a functional connection can be composed of a single part or assembled from multiple parts. Building blocks must thus respond both to the functional demands of the configuration design (generally degree of freedom issues in connections among components) and to the relevant manufacturing functions in terms of part forming and assembly processes.
Composition processes follow this dual path: one goal of design at the artifact type layer is to connect together functional units defined at the embodiment layer, a second goal is to minimize the number of parts, the number of process axes, and the number of assembly axes. For the former goal, connection details that provide the required connection type are drawn from the reverse engineering database. If the manufacturing process and process axes are known for the components to be connected, composition can further select specific design details that support the manufacturing functionality of the components to be connected. Finally, composition further narrows the choice of connection to align assembly directions for the system as a whole. Of course, these selection processes must also be resolved with other functional and economic goals for the system, so they serve as heuristics for focusing attention rather than as strict composition rules. This trade-off is especially acute for the reference component (i.e., ground), which must satisfy these constraints over multiple connections; composition here must explore multiple ground components in multiple manufacturing process classes.
As the lowest level of abstraction in our investigation, the artifact type layer provides the final word on evaluation. In terms of client-oriented function, the ideal models of the embodiment layer give way to more accurate models that include friction or stiffness in the connections (modeled in the connection matrices of Table 2). In addition, good estimates of size and shape are available as well as reasonable estimates of part and assembly costs for the system. Although significant screening has taken place as a design passes through increasingly less abstract representations, final evaluation often depends on this lowest level of abstraction. This evaluation can then be fed back up the search tree, shaping exploration at successively higher levels of abstraction.
In taking the embodiment of Figure 6 as the set of connections to be instantiated, we see three single degree of freedom rotational joints along with two connections between motor and ground. Focusing on the former, Table 2 provides a set of building blocks for composition of the joints. The reverse engineering database ranges from single part flexure joints to fully bushed pin joints requiring five parts. Valid designs can be composed for any combination of these connections; the contact matrices for each provides a basic model for the behavior of the joint; the flexure joint acts as a torsional spring element, the other joints as sources of Coulomb friction. The behavior of the system to input displacements and output forces can thus be ascertained: the spring elements, while reducing part count and greatly easing the assembly process, produce a self-centering effect in the system that conflicts with the basic requirements. Other joint instantiations are subject to relationships between force capacity, friction, and play, all of which can be captured as probabilistic design models composed from design experience.
Estimating manufacturing cost can be a costly exercise. In examining the available metrics, it appears unnecessary to define component geometries fully. Swift and Booker (1997) provide a method in which shape complexity is estimated within a basic shape class (i.e., revolute, prism, thin wall, etc.), increasing as additional off-axis features are added. Shape complexity factors are then established for a suite of manufacturing process classes (and through them, indirectly, to materials). Thus, the artifact type layer need not produce a detailed geometric design, it need only produce a “skeleton” design containing parts, part orientations, connections among parts, connections between parts and the ground(s), and a spatial layout of ground part details. Shape class and complexity is then captured in connection details instantiated from the connection case base. For parts composed of multiple connections, the shape class can be estimated from the basic shape class of each connection and the sum of the manufacturing process axes throughout the part. In a parallel effort, Fagade and Kazmer (1999) regress even simpler measures of design complexity on tooling costs for injection molding, finding that the dominating factor in tooling expense is the number of toleranced features in the design. These are also simple to capture for each connection and perhaps even easier to process as connections are composed into parts: tolerances associated with each connection can simply be summed for the overall part.
Perhaps the most critical issue in design at the artifact type knowledge-state layer is the development of the functional ground. Maybe even more significant is that the ground itself is completely absent from all functional representations above the artifact type layer: it is simply taken for granted that components can be selected and organized with the proper spatial relationships. If manufacturing functionality is not considered, a large part of the design process is left unresolved, leaving design search at higher levels of abstraction unresolved with it and design evaluation incomplete.
An alternative to the proposed, abstract representation of manufacturing function is to capture more specific aspects of function tied directly to geometry. Raghavan and Stahovich (1998) have attempted to induce function from geometry by examining behavior with and without a geometric feature. In reverse engineering studies, most geometry has nonunique functionality; a shape can often be attributed both to end-user function and to assembly or manufacturing function. This ambiguity makes it difficult to capture detailed manufacturing function with consistency across reverse engineers; essentially, this is the same function interpretation problem experienced at high levels of abstraction. In addition, even if manufacturing function could be captured consistently, manufacturing-oriented functions are generally absent from the functional goal set, leaving no product-specific goals. For this reason, a generic approach has been chosen for composition. However, informal visual information in the case base can play a significant role in presenting the designer with multiple alternative design details from which to draw.
The utility of mirroring human abstraction mechanisms within computational design is readily demonstrated; representing function at multiple levels of abstraction helps not only to control the search process within each level but also to generate goals for lower level processes. In a generate-test design paradigm, search is controlled on the generate side through the application of formal representations and composition logics in “strong” functional synthesis or through “weak” synthesis that draws heavily on case compilation and abstraction. Search is also controlled on the “test” side of the paradigm as design candidate performance is estimated, these estimates improving as abstraction is reduced. Thus, the separation of overall design goals into functional and performance goals at the client objective stage provides a representational distinction that shapes synthesis throughout the design process.
Abstraction is also important within each knowledge-state layer, whether embodied in the fluid decompositions typical at the functional layer or the more distinct gross/fine behavioral models at the embodiment layer. Functional synthesis has often been treated at multiple abstraction levels in the past: Schmidt et al. (2000) using multilevel grammars primarily at the embodiment level, Sharpe and Bracewell (1996) extending bond graph-generated topologies with behavioral models for the generated designs. In general, this type of abstraction has been geared toward dealing with functional versus performance goals. Our example application extends these ideas of intralevel abstraction to all knowledge-state layers: client objectives separated into function and performance, functional decomposition supported through multiabstraction aggregation of reverse engineering cases, embodiment separated into gross and fine transformation, and artifact type connections into general contact-type specific contact mode. Physical phenomena capture transformation type in addition to multiabstraction behavioral models that can be applied for estimating performance at all levels of abstraction.
Abstraction is also a key component to the horizontal integration of functional synthesis. Operating at high levels of abstraction that generalize across domain boundaries opens the door to domain-independent solutions to problems. At the same time, once domains are mapped out at the physical phenomenon level, their functional boundaries can still shift to support specific heuristics like the “soft” axis transformation that generated the final mouse embodiment. There is still much work to be done in terms of merging representations across mechanical, electrical, and information domains. Our initial step of simply integrating a “software” mechanical transformation element must be extended carefully to cover additional situations while not obviating mechanical solutions altogether.
Even as abstraction makes much of the horizontal and intralayer vertical integration possible, the need to translate results from high abstraction levels into goals at lower levels is a significant issue for overall vertical integration. The representations chosen for the mechatronics application dovetail nicely: function–structures pervade the top two knowledge-state layers, these give way readily to physical phenomena, which in turn, present straightforward mechanical embodiment goals. The resulting design configurations map directly to the part/connection goals at the artifact type layer. In our case, off the shelf representations could be cobbled together to form a fairly cohesive whole; where direct translation cannot be forged, abstraction levels might be bridged by case-based, multiabstraction building blocks and weak computational synthesis. Still, the translation task remains difficult to formalize, especially at the extremes of the design process: the derivation of functional requirements from user needs and the development of final design details from skeleton designs.
As mentioned in the discussion of abstraction, search can be managed both in the generation of designs and through the elimination of poorly performing alternatives. This is not typically an either/or proposition but a matter of trading one versus the other within and between abstraction levels. A key trade-off is between the soundness and completeness of design space generation. Where formal representations allow building blocks and composition rules that can generate the whole of the design space without generating infeasible designs, search can be controlled primarily during function generation. This is typical for the type generation steps at the embodiment and artifact type layers. Where such formality of representation places too much bias on the generation step, completeness can only be assured through a sacrifice of soundness. The function–structure based representations used at high levels of abstraction demonstrate this: to maintain solution neutrality we must allow the generation of unsound designs. However, this relaxation of bias is not total; case-based reasoning biases design generation, drawing on functional units from existing designs rather than from the entire space of functions possible within the function–structure/functional basis representation. Similar biases are introduced at the artifact type layer for the generation of skeleton designs according to connections drawn from cases. In both instances, the quality of reasoning is determined largely by the size of the case base from which design fragments can be drawn and by the quality of information embodied in each case.
In the mechatronics application, soundness is sacrificed at both the highest and lowest levels of abstraction. Even at the embodiment stage, where soundness and completeness are both high, the topological designs that are generated are not guaranteed to produce feasible spatial configurations. This is true of all of the transitions, whether they lie within or between the abstraction layers in the example: functional designs are not guaranteed to have valid configurations; configuration designs are not guaranteed to have good detail designs; and the skeleton detail designs are not guaranteed to be manufacturable. To some degree, search control takes place automatically: as candidate designs from higher abstraction levels are propagated downward, those for which no feasible lower level design can be synthesized are pruned from the search. On the surface, this appears to be a simple solution to the problem of search control, but the weak synthesis modes at the initial stages of the design process mean that many infeasible function-level designs are passed down to levels where perfectly feasible designs result. Detailed behavioral models may be required to identify the high-level infeasibility.
An additional search control mechanism uses performance evaluation in the “test” phase of design synthesis. In integrated functional synthesis not only must performance models span multiple levels of abstraction, they must evaluate heterogeneous design candidate sets. Throughout the above discussion, reference is made to a decision-based design technique developed by Wood and Agogino (2005). By capturing design requirements as probabilistic targets and by generating design performance models based on design experience, this methodology meshes well with the needs of integrated design. Performance models based on function can be induced directly from the reverse engineering database to establish probabilities on many aspects of performance: size, cost, number of parts, power, and so forth. In addition, because each of these aspects is part of a large joint probability density function, the relationships among them are also modeled. “Test” might use performance evaluations with high uncertainty to focus on promising designs at the highest levels of abstraction. As design abstraction is reduced, the increased design detail conditions the joint probability with higher accuracy; based on designs with higher similarity to the described concept, the joint itself is a much more accurate representation of the local design space. In the end, through, design concept pruning is a decision process that responds not only to performance estimates but also to performance goals. In most design processes, refining these evaluation goals is as much a part of the design as generating the designs themselves (Yoshikawa, 1981; Takeda et al., 1990). In the end, controlling synthesis in an integrated design environment is a challenging mix of representational bias, abstraction, and evaluation.
Building blocks and composition rules embody the “background knowledge” typical of any artificial intelligence application. Both abstraction and search depend on the ability to generate design building blocks and manipulate them toward satisfying design goals. By integrating functional synthesis across abstractions, we are faced with several choices: Should building blocks at different levels of abstraction be designed to optimize design generation and evaluation within that level or to optimize translation between levels? Are building blocks at each level independent or are they tied together across abstraction levels? Should building blocks be based on theory or experience?
The reverse engineering methodology employed in the example application creates building blocks from experience. By examining cases from multiple levels of abstraction, we can generate building blocks that span abstraction levels. Translation is largely automatic: many to one mappings of design–configuration–function from the case base provide one to many mappings as the design process is executed and candidates are generated at each level of abstraction. Perhaps the most important advantage of integrating synthesis is the ability it affords of controlling at which abstraction level which type of knowledge should be applied. It is rather pointless to use function–structures to synthesize mechanical elements when this can be done with greater soundness and completeness at the embodiment level of abstraction. In fact, other than capturing information valuable for estimating performance, all mechanism information drawn from the case base at the function–structure stage is discarded. Synthesis at the functional stage draws from patterns of flow transformation useful in the past to create very abstract designs. Phenomena are then selected based on evaluation and instantiated within the basic flow structure, which is passed as an input/output specification to the embodiment layer. Here, synthesis follows first principles and building blocks draw from a small, well-defined set. This reliance on first principles is short-lived, extending briefly into artifact type synthesis where reasoning reverts to weaker, case-based methods for the final skeleton design. In the end, the ability to tailor the representation and reasoning modes to the background knowledge available within each layer is a significant argument for maintaining abstraction for functional synthesis.
Finally, because the set of building blocks used for most of the synthesis process is drawn from reverse engineering, the knowledge that is embodied is highly dependent on the case bases. Design search can only be as complete as the underlying case base. In addition, because knowledge is implied by the cases rather than explicitly stated, soundness of design generation is not guaranteed. Simply because design representations are drawn from cases does not eliminate the need to design a good knowledge representation. By drawing from a range of representations for function rather than attempting to create a monolithic model for function, the mechatronics application demonstrates the power of tailoring representation to subtask and placing subtasks within the overall design context.
Computational synthesis holds the promise of expanding the search space in design. Function is the foundation of design; developing computational methods for generating function is a key toward supporting present and future designers. However, because the very notion of function is so context dependent, care must be taken in the selection of the representation in which functional synthesis is done. Because no synthesis method can circumvent the constraint of resource limitations that plague all search processes, a balance must be struck between completeness and soundness in synthesis. Where a lack of soundness produces weak functional synthesis, evaluation plays an important role in limiting search.
As the success of computational synthesis in circumscribed domains is generalized, the need to support search at several levels of abstraction arises. Translation of goals across knowledge representations is a significant step toward supporting cross-abstraction synthesis. Selecting which design activities to perform within each level of abstraction is also critical: balancing overall soundness and completeness of synthesis requires careful selection of both the abstraction levels needed for design and the representations and knowledge used within them. Focusing functional synthesis only on abstraction levels where strong methods pertain serves only to generate many solution candidates that satisfy only a subset of possible functional requirements and can be evaluated with limited accuracy. Extending functional synthesis both upward toward less computable but more expressive function–structures and downward toward more geometric detail increases both the range of designs considered and the accuracy of selection among the candidates generated. Part of the bargain for potentially better designs is a sacrifice in soundness that requires additional effort on the part of the designer to ensure feasibility.

(a) Spatial and (b) functional requirements for the force-feedback mouse example.

“Design” level decomposition of a force feedback mouse (dotted boxes surround functions repeated for the y axis).

Function–structures for the “sense” function in Figure 2: (a) an abstract function and (b) the actual functional unit in the ball mouse, reverse engineered at the “parts” level.

Function–structures for two mice and a power screwdriver (dotted boxes surround functions repeated for the y axis).

Probability density contours for motor behavior in the desired range (design instances drawn from a motor catalog).

Configuration design building blocks

Serial and parallel combinations of x and y crank-sliders and cam-followers.
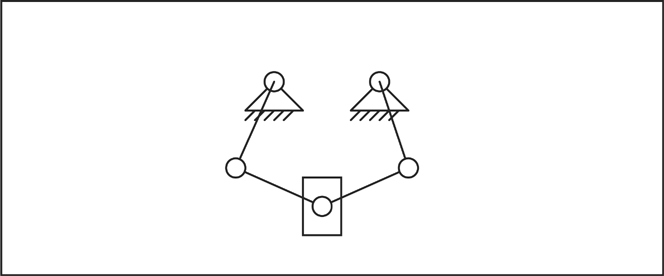
Software-transformed axis, parallel crank-slider.

Detail design building blocks