INTRODUCTION
The role of convexity of technology has proved to be crucial in the analysis of optimal one-sector growth models. The convergence of per-capita output toward a steady state follows directly from the assumption of diminishing returns to per-capita capital in the production of per-capita output [as in Ramsey (1928) and Cass (1965) growth models]. Departing from this usual assumption of diminishing returns, Romer (1986) shows that per-capita output can grow without bound and the levels of per-capita output need not converge across countries. In Romer (1986), knowledge accumulated by the agents is the basic form of capital. The additional knowledge for a single firm is the product of a research technology that requires an investment in terms of aggregate good as an input. The economywide knowledge has a positive external effect on the production of the aggregate good. In other words, knowledge in the economy is assumed to be an input with an increasing marginal product from a social-planner point of view.
In this paper, we use the general framework of the discrete-time version of Romer's (1986) model [see Le Van et al. (2002)]. Given the fact that a decreasing-returns-to-scale assumption is not an adequate description of economic reality when the economy is in a low state of development [see Skiba (1978) and Azariadis (1996)], we distinguish the individual production function of a developing country from that of a developed one. We incorporate an individual production technology that exhibits increasing returns to scale for small values of the capital stock, as in the case of a developing country, and diminishing returns for higher values of capital stock, as in the case of a developed country.
We prove the existence of solutions to the social-planner problem and characterize the properties of optimal paths. We show that there exists a critical stock such that for all initial stocks above this level, the economy can take off, whereas for initial stocks below this level, the economy can face a poverty trap, where the optimal stocks remain constant through time. In this respect, our analysis is in the same line as works by Clark (1971), Majumdar and Mitra (1982), and Dechert and Nishimura (1983). They show that a convex-concave production function faced by a social planner can lead to a poverty trap such that optimal stocks converge to zero over time. However, in contrast to these authors, we consider knowledge technology that induces a positive externality on production and encounter a social production function that exhibits globally increasing returns to scale. We address the following questions: Can a developing country take off by means of knowledge technology? How does quality of knowledge technology affect growth? What is the effect of fixed costs associated with production on the economy that uses a new technology? Does it always take off?
We prove that for a given initial stock, the economy can take off if the quality of knowledge technology increases and/or if the influence of fixed costs associated with production decreases. We show that even when the production function at the firm level exhibits decreasing returns to scale (for instance, in the case of a developed country), the economy can face a poverty trap if it is endowed with a low quality of knowledge technology. Considering two countries with the same production function and the same level of initial capital stock, we show that when one faces a poverty trap, the other can take off if it is endowed with a higher quality of knowledge technology. We provide the differences in the quality of knowledge technology and/or the fixed costs associated with production as an explanation for the nonconvergence of the economies.
We organize the rest of the paper as follows. In Section 2, we present the model and its assumptions. In Section 3, we study the existence of solutions to the social-planner problem. We analyze the properties and the convergence of optimal paths. We present the comparative statics results. Finally, in Section 4, we conclude.
MODEL
We consider a closed economy in which the preferences of the S identical consumers are globally represented by a strictly concave function of consumption. Assume the following:
Assumption 1. The function u is twice continuously differentiable, u′(c)>0, u″ (c)<0, ∀c>0 and u(0)=0, u′(0)=+∞.
We consider N individual firms that have technologies depending on a path (Kt)t[ges ]0 for aggregate knowledge. Thus, the instantaneous production of output for a firm is represented by a function F(kt, Kt, xt) of the firm specific knowledge kt, the aggregate knowledge Kt, and the level of all other factors xt, such as physical capital, labor, and so forth. Assumption 2 follows.
Assumption 2. F exhibits global increasing returns to scale of knowledge from a social point of view so that F(k, Nk, x) production per firm available to a social planner that can set economywide values for k is piecewise convex in k, for any fixed x.
Following Romer (1986) and Le Van et al. (2002), we assume that only the stock of knowledge can be augmented and the additional factors are available in fixed supply of
. Then, the optimal solution for x is assumed to be
. This allows us to have a problem that is essentially one-dimensional. Furthermore, to simplify and to have per-firm and per-capita values coincide, we restrict our attention to an equilibrium in which the number of firms and the number of consumers are equal, S=N.
We formalize how the instantaneous production of output for a firm depends on the firm-specific knowledge and the aggregate knowledge as follows:
where
is the production function that would be faced by a social planner that exhibits globally increasing returns. The individual functions f and h capture the effect of the private knowledge and the knowledge externality on the social production function, respectively. We distinguish the individual production function of a developing country from that of a developed country. Although decreasing returns is known to be a good approximation when the economy is in a high state of economic development, it seems to be irrelevant for less developed or developing countries. As noted by Skiba (1978), Azariadis (1996), and Askenazy and Le Van (1999), the returns to scale are increasing at early stages of development for small values of capital stock and increasing for higher capital stocks. Accordingly, we will consider two cases:
- a developed country where the individual production function is concave,
- a developing country where the individual production function is a linear function in an initial phase and concave afterward,
where , 0<δ<1, and μ+ρ>1. Note that A<0 as , .
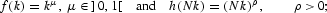
Remark 1. The influence of the fixed costs on the output can be measured through two indicators, which are
and δ. The fixed costs are more important if
increases or/and if δ decreases.
We require the following result, the proof of which is left to the readers.
LEMMA 1.
and
are increasing functions in
. The function
has, at
, left derivative
and right derivative
, which satisfy
. In other words,
is a convex function.
Note that the social production function
used here is not the type used in the models of Majumdar and Mitra (1982) and Dechert and Nishimura (1983). These models incorporate a social production function that exhibits increasing returns to scale for small values of capital stock and decreasing returns for large values. On the contrary, the social production function in our model exhibits globally increasing returns to scale. Under the parameter values of ρ=1, μ=1/3, δ=0.1, N=1, and
, the social production function for a developing economy is depicted in Figure 1.
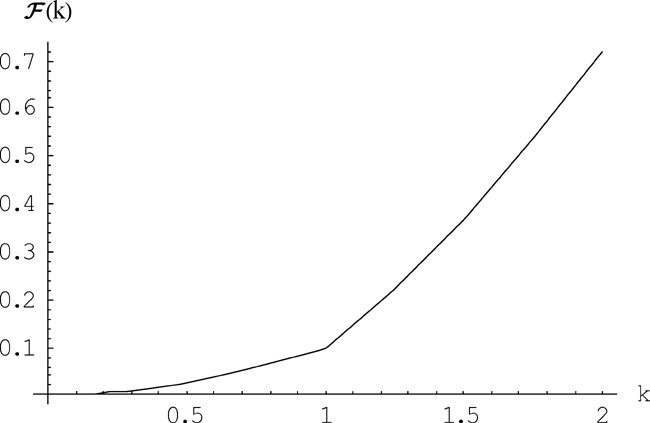
The economy's output is divided between current consumption and investment:
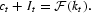
Additional knowledge can be produced by forgoing current consumption, but in contrast with Majumdar and Mitra (1982) and Dechert and Nishimura (1983), we do not assume it to be one-for-one. By investing an amount It of forgoing consumption, a firm with a current stock of private knowledge kt induces a rate of growth
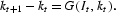
We have the following assumptions on knowledge technology:
Assumption 3. G is concave and homogenous of degree one. Then,
Assumption 4.
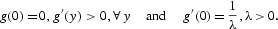
Assumption 5.
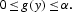
Remark 2. Note that, at zero, an increase of 1 percent in the amount of investment induces an increase of 1/λ percent in the stock of private knowledge, which enables us to interpret that 1/λ represents the quality of the knowledge technology.
Remark 3. The Romer (1986) model that is formalized in discrete time by Le Van et al. (2002) is the limit case of our model by letting λ→0.
SOCIAL OPTIMIZATION PROBLEM
In this economy, the social planner maximizes the intertemporal utility of the representative consumer subject to the feasibility constraints
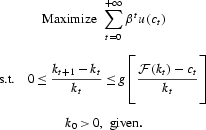
This is equivalent to
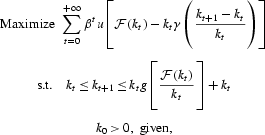
where γ [colone ] g−1.
Assuming that the stock of knowledge cannot be depreciated and considering Assumption 5, we obtain: kt[les ]kt+1[les ]kt(1+α), ∀t. Then, we have kt[les ]k0(1+α)t, which leads to
. In what follows, we make the following Assumption.
Assumption 6.
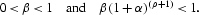
Let
. We also assume that
Assumption 7.
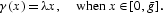
DEFINITION 1. A sequence
is called feasible from k0 if it satisfies the constraints of the social optimization problem,
Existence of a Solution
Existence of a solution follows from the fact that every feasible sequence from k0 belongs to a compact set for the product topology, and the objective function is continuous for this topology.
Compactness
Let
be a feasible path from k0. By Assumption 5, we have
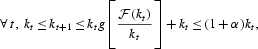
and so, ∀t, kt[les ](1+α)tk0. Then,
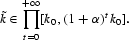
Thus,
belongs to a compact set for the topology. Since g and
are continuous, the feasible set from k0 is compact for the product topology.
Continuity of the objective function
The objective function is
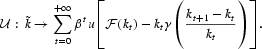
By means of the proof available in Le Van et al. (2002), we know that
is continuous for the product topology.
Value Function, Bellman Equation
Let V(k0) denote the value function of the social optimization problem. It is clear that the value function verifies the Bellman equation:
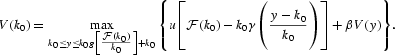
V is the unique continuous solution to the Bellman equation. Let
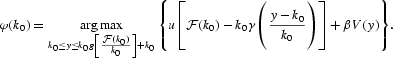
By the maximum theorem, φ is upper semicontinuous.
Properties of Optimal Paths
In this section, we prove that the optimal sequence of capital stocks is monotonic. The following lemma is useful for the proof. Later, we show that the sequence of optimal consumption
and capital stock
satisfy ∀t, ct>0, kt>0.
LEMMA 2. Let
. Then, the function [∂W(k, y)]/∂y is increasing in k.
Proof.
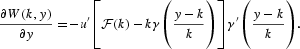
The function k→−γ′[(y−k)/k] is increasing and negative since γ is convex and increasing. Let
We have
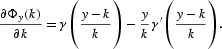
From the convexity of γ, we get
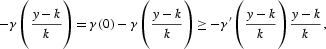
and, since γ′>0,
Thus,
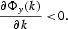
It is then easy to show that the function
is positive and decreasing. It is immediate that
is increasing in k.
LEMMA 3. Let
. The optimal growth model can be written as
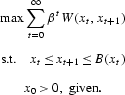
The value function verifies Bellman's equation,
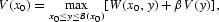
where B is an increasing function. Let {xt} and
be optimal paths starting from x0 and
, respectively. If
, then
.
Proof. The result comes from the fact that
is increasing in k. See Benhabib and Nishimura (1985).
PROPOSITION 1. If {kt, ct} is an optimal path from k0>0, then ∀t[ges ]0, kt>0, ct>0. Similarly, if k1∈φ(k0), then
.
Proof. The proof is based on the Inada condition of the utility function. See Le Van et al. (2002).
Convergence of Optimal Paths
The main purpose of this section is to prove the existence of a critical stock kc, such that for all initial stocks below kc, the capital stock remains constant through time, whereas above, it grows without bound. Note that we cannot apply the methods of Dechert and Nishimura (1983) in analyzing the socially optimal paths in our model since we encounter a piecewise convex production function faced by the social planer. However, the underlying idea in their proof can be used for our purpose. We first prove that there exists a value k*>0 such that, for any initial capital stock less than k*, any optimal capital path starting from this initial stock will remain constant. Second, it is proved that there exists k**>0 such that, for any initial capital stock larger than k**, any optimal capital path will converge to infinity. The supremum of such k* and the infimum of such k** will be shown to be equal and they define the critical value.
PROPOSITION 2. Let λ>0 be given. There exists k*>0 such that ∀k0<k*, k0>0,
optimal from k0 then kt=k0, ∀t.
Proof. See Appendix.
PROPOSITION 3. Let λ>0 be given. There exists k**>0 such that ∀k0>k**,
optimal from k0, then, kt<kt+1, ∀t and kt→+∞.
Proof. See Appendix.
PROPOSITION 4. Let k** be defined by
. Let k0>0. No optimal path from k0≠k** converges to k**.
Proof. See Appendix.
Remark 4. The value k** corresponds the low steady state in Dechert and Nishimura (1983).
THEOREM 1. Let λ>0 be given. Then there exists kc such that ∀k0<kc, any optimal path
from k0 will satisfy kt=k0, ∀t and ∀k0>kc, any optimal path
from k0 will satisfy kt<kt+1, ∀t, and kt→+∞.
Proof. Let kM be the supremum of the k∗ such that if k0<k∗, then any optimal path
from k0 will satisfy kt=k0, ∀t. Let km be the infimum of the k∗∗ such that if k0>k∗∗ then any optimal path
from k0 will converge to +∞. Our claim is that kM=km. It is obvious that kM[les ]km. Suppose kM<km. Take k0 and
such that
. From the very definition of kM and km, there exists an optimal path {kt} from k0, which is strictly increasing, and an optimal path
from
, which is stationary, that is,
, ∀t. The optimal policy being increasing, we have
, ∀t. Hence
. It is easy to check that
and this contradicts Proposition 4. Therefore, kM=km. Posing kc=kM=km ends the proof.
Comparative Statics
In the following propositions, we analyze how quality of knowledge technology and the fixed costs associated with production influence growth. We analyze whether the economy would be more inclined to take off or more prone to a poverty trap when a change in these factors occurs.
PROPOSITION 5. Given k0, if the quality of knowledge technology increases (i.e., λ decreases), the tendency of the economy to take off will increase.
Proof. It follows directly from Proposition 3. Consider k** such that
. We know that if k0>k**, then any path optimal from k0 is strictly increasing and grows without bound. By Lemma 1,
is an increasing function. Thus, (dk**)/(dλ)>0.
PROPOSITION 6. Given k0 and λ, if the influence of fixed costs diminishes (i.e., δ increases and/or
decreases), the tendency of the economy to take off will increase.
Proof. Consider the equality
and assume that
. We have
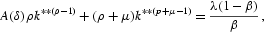
where
. By differentiating with respect to δ, we obtain
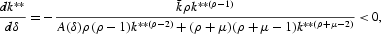
as the denominator is positive due to
. Then, given k0, a decrease in the influence of the fixed costs (i.e., δ increases), will favor economy to take off. Furthermore, by differentiating the given equality
with respect to
, under the assumption of
, we obtain that
. Accordingly, given k0, if the amount of fixed costs diminishes (i.e.,
decreases), the economy will have more tendency to take off.
CONCLUSION
In this paper, considering a convex-concave individual production function for a developing country, we have analyzed the properties of the optimal paths in a discrete-time version of Romer (1986) model. We have proved the existence of a critical stock such that for initial stocks below this level, the capital stock remains constant through time while above it grows without bound. We have analyzed the effects of three factors on this critical value: initial stock of knowledge, quality of knowledge technology, and the level of fixed costs associated with production. We have provided that quality-of-knowledge technology is the key factor. Indeed, by Proposition 2, it is shown that even when the production function has no fixed costs (i.e., for a developed country), the economy can face a poverty trap if the quality of the technology is low.
We give below three possible future developments of our work.
- A natural extension of this model would include two sectors. Sector 1 produces consumption goods through a production function F1 using a capital stock k1. In sector 2, investments in capital stock and in knowledge technology come from the production of a good using capital stock k2 and stock of knowledge k3 as inputs. Formally, we have for every period t,
where F2 is the individual production function and H is the externality function. This model may give an optimal choice between investments on capital stock and on knowledge technology. One can imagine that the quality of the knowledge technology will play an important role for such a problem.
- The model can be extended to allow for a discontinuity in the individual production function, leading to a structural break in the production technology, in order to analyze the theories of “big-push” on stages of economic growth. Such an analysis would imply a value function that is both noncontinuous and nonconcave [e.g., Ni and Wang (1996)] and requires the application of lattice programming technique proposed by Topkis (1978).
- Finally, it would be interesting to use continuous time in our model. One of the main difficulties will be the proof of existence of optimal solutions. Indeed, one can easily prove, as for the usual Ramsey model, that any sequence of feasible capital stocks and feasible consumption goods will belong to a closed ball of L1(e−ρt), when the criterion is to maximize . Since the function u is concave, this criterion is upper semicontinuous for the weak topology σ(L1, L∞). If the set of feasible consumptions is compact for this topology, then there exists a solution to our optimal growth model. Hence, we have to check that the Dunford-Pettis criterion holds for the feasible consumptions set, since a closed ball of L1(e−ρt) is not compact for the weak topology σ(L1, L∞).
APPENDIX
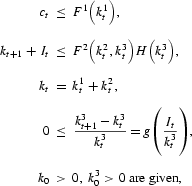
Proof of Proposition 2. Choose k* such that
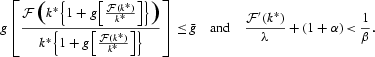
Since
is increasing by Lemma 1,
, and (1+α)β<1 (see Assumption 6), such a k* exists. For k0<k*, let there exist a strictly increasing optimal path. We have the Euler equation given as
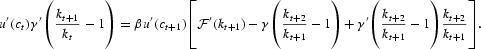
Our claim is that there exists t such that kt+1<k* and kt+2[ges ]k*. If not, we always have kt<k*, ∀t. Then, kt→ks[ges ]k0>0 and
with
due to Euler equation.
Note that we have
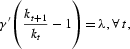
as
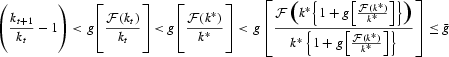
and γ(x)=λx for
according to Assumption 7. However, since
is convex (see Lemma 1) and
leads to a contradiction. Hence, there exists t such that kt+1<k* and kt+2[ges ]k*.
In what follows, consider a path
converging to zero and let
be the point such that
and
.
From t=0 to
, we have
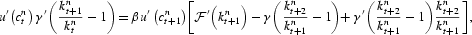
which reduces to
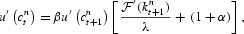
as
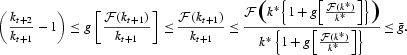
Hence,
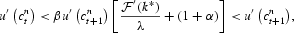
so that
. Now, letting
converges to
and
converges to
. By the upper semicontinuity of
. Since
, from Proposition 1,
.
Then
. Following from Inada condition we have that
on the one hand. But,
. Then,
must converge to zero on the other hand—a contradiction.
Hence, for k0 small enough, (k0, k0, …k0…) is the unique optimal path from k0.
Proof of Proposition 3. Choose k** such that
. Our claim is that if k0>k**, then any optimal path is strictly increasing and grows without bound. To prove this, we will first show that for any k0>k**, the path
is not optimal. Then, we will show that any optimal path is strictly increasing and no optimal path from
k0>k** converges to a steady state.
- Consider the path that is feasible from . Since , there exists ε>0 such that . Then, for k1 [colone ] k0+ε and kt [colone ] k1, ∀t[les ]1, we have and , which is . Thus, there exists ε>0 such that is feasible from k0. We will show that such a path increases the value of U.
Then,
Since limε→0k0/εγ(ε/k0)=γ′(0)=λ, is increasing and k0>k**, we have . Thus, ∃ε>0 such that , concluding that is not optimal.
- If there were an optimal path such that k1=k0, then as the value function verifies the Bellman equation,
the path would then be optimal, which is impossible. So, necessarily, k1>k0. Similarly, what follows is that ∀t, kt+1>kt.
- The proof relies on the Euler equation. Since kt is strictly increasing, limt→∞kt exists. Suppose on the contrary that kt converges to ks<+∞. Then, we would have . However, and ks>k**: a contradiction, since is increasing. So, kt diverges to +∞, inducing that per-capita output grows without bound.
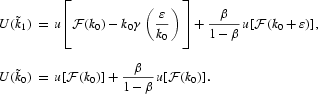
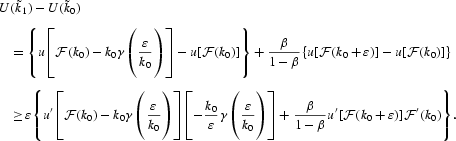
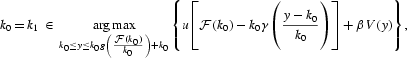
Proof of Proposition 4. If k0>k**, from Proposition 3, any optimal path from k0 will converge to +∞. Consider the case where k0<k**. Let {kt} be an optimal path from k0 and assume that it converges to k**. This optimal path must be increasing and bounded above by k**. There exists T0 such that
and hence,
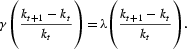
The optimal consumption, for t[ges ]T0 will be
. We also have ∀t[ges ]T0,
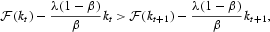
because the function
is decreasing when k is close to k** and k<k**. The following inequality holds:
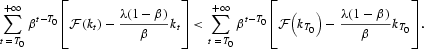
However, we know that
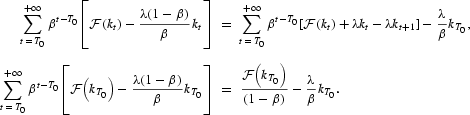
Thus,
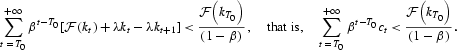
By Jensen's inequality, we have
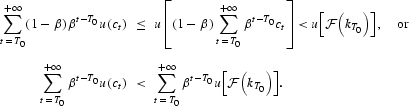
This means that the utility of the stationary path
for t[ges ]T0 is better than the utility from T0 of the optimal path—a contradiction.
We thank Raouf Boucekkine and an anonymous referee for helpful comments and suggestions. The second author acknowledges the support of “Actions Recherches Concerte” 99/04-235. This paper was written while the first author visited IRES and CORE, Université Catholique de Louvain.
