1. Introduction
Ship radars are increasingly being used to observe bird movements because of their high resolution and relatively easy handling (Williams Reference Williams1984, Cooper Reference Cooper, Day, Ritchie and Cranor1991, Harmata et al. Reference Harmata, Podruzny, Zelenak and Morrison1999, Hueppop et al. Reference Hueppop, Exo and Garthe2002). In contrast to radars of higher quality, such as military radars, they are easy to transport and are less expensive. However, with any radar, the problem of quantification of bird migration arises. One needs to know the air volume surveyed by the radar. This is influenced by the fact that with the increase of distance from the radar, the volume of the radar beam increases, the fact that the decrease of received power follows the R4-law, the dependence of the antenna diagram, the respective detection range of the species studied and, last but not least, the variability of the radar cross section following aspect changes and wing-beat pattern of birds (Eastwood Reference Eastwood1967). The range for specified size groups of bird species with common wing-beat patterns and for a single species such as the swift can be determined by X-band tracking radars (Bloch et al. Reference Bloch, Bruderer and Steiner1981, Gasteren et al. Reference Gasteren, van Bell and Buurma2002, Bäckman & Alerstam 2001). However, the maximum range of ship radar detection against target sizes of birds has not yet been determined. This is of crucial importance to decide up to what distance the data are reliable.
There is an important distinction between the nominal and the operational beam width of a radar beam. The nominal beam width is the angle between the two points at which the signal falls by 3 dB compared to the centre of the beam. The operational beam width of the radar is the angle up to which you can detect the study object by the radar; this angle depends on the characteristics of the target and the settings of the radar. Bruderer et al. (Reference Bruderer, Steuri and Baumgartner1995) calibrated the operational beam width by comparing the bird density detected by the tracking radar with that seen by an infrared camera. Knowing the detection range and the beam width of the infrared camera and the nominal angle of the radar, quantities detected by radar were compared to those recorded by the infrared camera. Direct measurements of the operational angle of the radar beam for bird targets are still missing. Since the radar cross sections of song birds are known (Bruderer & Joss Reference Bruderer and Joss1969), we decided to measure the beam width using metal spheres to represent the radar cross section of songbirds.
The huge vertical beam width of a horizontally rotating ship's radar has the advantage of surveying movements in a large section of air space. However, one does not get information on the height of a target. In order to measure the exact position where a target is detectable by the radar, it is necessary to independently determine its position by other instruments. We lifted our targets by a captive balloon and measured their position with theodolites.
Modern radars no longer show the raw signal on the radar display because they work through filters that influence the echo size and intensity. Thus no further conclusions can be obtained from the echo intensity regarding the detectability of targets at different distances. Therefore the detection limit has to be addressed directly by moving the target continually until its signal disappears from the display.
In this paper, we present our experimental approach in detail, in order to facilitate calibration experiments for fellow researchers using different types of radar equipment.
2. Material and Methods
2.1. Study Site
The experiments were performed in calm weather conditions from 27 July to 10 August 2004 at the military drilling ground of Baumholder (49° 40′ 22″N, 7° 28′ 06″W), situated near Idar-Oberstein (Rheinland-Pfalz) and 70 km SW of Mainz (Germany). The radar was installed on the elevated platform of an army shooting range which allowed a free view to a distance of 1400 m and displayed only a minimum of ground clutter.
2.2. The Equipment
We used an X-band fan beam radar with an output power of 25 KW (Furuno Fr-2125) mounted on an iron stand fixed to the ground. The antenna had a length of 2 m, and the rotation velocity was set to 24 times per minute. The radar worked at a pulse repetition rate (PRR) of 3000 Hz and a pulse length of 0·08 μs. Thus, per one degree 20·82 pulses were sent out for each degree of revolution. This value approximates the 25 pulses per target recommended for ornithological studies (Buurma & Bruderer Reference Buurma and Bruderer1990). The beam had a nominal vertical beam width of 20° and a horizontal of 1·23°. The minimum power received by the radar necessary to give an echo on the display amounted to 6 dB μV (this corresponds to 8·0×10−14W according to http://ewhdbks.mugu.navy.mil.fieldint.html) (sensitivity of the receiver). The gain was set to 100%, the rain filter was switched off and the Sensitivity Time Control (STC) was set to the automatic setting. This was the setting we used in previous bird observations.
Our test objects were hollow spheres of brass coated by a copper layer of 10 μm. They had diameters of 25 and 30 mm. As these sizes are in the resonance area, their shadow cross-section does not correspond to their radar cross-section (Göbel Reference Göbel2001). The sphere of 25 mm diameter corresponds to a radar cross section of 9·006 cm2 and the sphere of 30 mm diameter to a radar cross section of 3·58 cm2 (Skolnik Reference Skolnik1988) (Table 1). According to Bruderer & Joss (Reference Bruderer1969) the average radar cross section of songbirds amounts to 3–4 cm2 although it may vary from 2 cm2 up to 10 cm2. Variations in the radar cross section occur according to the wing-beat pattern and to the view of a bird, with the lateral view being biggest (Edwards & Houghton Reference Edwards and Houghton1959).
Table 1. The relation of the radar cross section to the shadow cross section and the diameter of a sphere. Radar cross sections were calculated according to Skolnik (Reference Skolnik1988).

The size of the balloon had been chosen according to the load it had to carry. We worked with a weather balloon of latex with a diameter of 1 to 1·2 m when filled. Its weight amounted to 200 g. The strength of the captive line of the balloon had been chosen according to the forces that were expected to tear at it. We worked with a fishing line as light as possible of 1000 m length and a tear strength of 35 kg.
The fishing line was put to a coil reel with a strap that enabled the balloon leader to hang the strap around his or her neck and wind it in front of the body. In order to stabilise the sphere in choppy wind conditions, we had provided two further coil reels. Thus, the sphere could be fixed by three lines. The sphere to be tested was knotted into the captive line at one and a half metres below the balloon. The balloon made of latex produced an insignificant reflection compared to the metal spheres. We provided helium in order to fill the balloon with about 900 li each time. The position of the sphere was measured by theodolites with electronic readout, which allowed measurements of horizontal and vertical angles. Distances were measured with the help of a laser range finder.
2.3. Strategy to find the echo of a sphere on the radar display
At first, the coordinates of the radar position had to be saved to the memory of a Global Positioning System (GPS). Then, the sphere was brought to the working area (where no ground clutter could be seen at the display). Next, distance and direction of the sphere to the radar was recorded by GPS and communicated by a wireless communication set to the person at the radar. These measurements were converted to the position on the display, where the echo of the sphere had to be expected. If we were not yet sure about the position of the echo of the sphere at the display, we asked the balloon holder to quickly walk in a determined direction or measured the position of the sphere simultaneously by the theodolites.
2.4. Determining the upper borderline of the radar beam and the maximum range
The sphere was brought to the intended direction and distance. It was set lower than the height of the nominal beam width of the beam. A graph showed height and distance corresponding to the nominal beam width. After detection of the echo at the display, the balloon was slowly let up. We observed the echo on the display until it got weak. At this moment, the balloon was fixed and the angles were measured simultaneously by the theodolites. These measurements were repeated at other ranges.
The theoretical range at which an object of a certain size can be detected was calculated by the radar equation:
where N s is the power output of the radar, G the antenna gain, λ the wavelength, σeff the radar cross section of the target and N Emin the minimum power received by the radar (Eastwood Reference Eastwood1967, Becker & van Raden Reference Becker and van Raden1985). The gain amounted to 311·35. In practice, we proceeded as follows to measure the maximum range: at about the distance of 700 m, the sphere was elevated to a height where it is in the optimal detection area (100 to 350 m). After detection of the echo at the display, the sphere was brought to greater distances. At the display, we followed the echo until the detection faded. The position of the sphere was measured immediately by the two theodolites. As the beam width approaches zero at longer ranges, at maximum detection range, the target is detectable only when it is exactly on the beam axis. As birds migrate at different heights, this value does not correspond to the average maximum detectable range of bird migration. Therefore, we measured the maximum range of detection at different heights.
3. RESULTS
3.1. Operational beam width
We tested whether the operational beam width differs from the nominal beam width. We used copper coated hollow spheres with a radar cross section of σ=3·58 cm2 and σ=9·006 cm2 and measured the angle at which the echo of the sphere got faint at the display.
From the 3·58 cm2 sphere, we got faint reflections at distances between 500 m and 1150 m and at heights between 100 and 350 m. The height of the operational beam width increased linearly with increasing distances (y=0·3048x, R2=0·4283, n=19) (Figure 1). This corresponded to an operational beam width of 16·95°. As the nominal beam width amounted to 20°, the operational beam width is 3° degrees smaller than the nominal beam width. We expect that full detection will be achieved at smaller angles. The measurements were recorded between 500 and 850 m distance and at heights between 100 and 200 m. The linear function of the beam width amounted to y=0·229x (R2=0·3942, n=9) (Figure 2). This corresponded to an operational beam width of 12·89°, thus confirming the expectation that good detection values are achieved at a smaller angle than the values of faint detection and much smaller than the nominal beam width.

Figure 1. Beam width (faint detection) at which a sphere of a radar cross section σ=3·58 cm2 could be detected. The linear function: y=0·3048 x (R2=0·3942, n=19).

Figure 2. Good detection of a sphere of σ=3·58 cm2. The linear function: y=0·229x (R2=0·3942, n=9).
We tested a sphere of a radar cross section of 9·006 cm2 expecting that the operational angle for this sphere would be bigger than for the sphere of 3·58 cm2. We got faint reflections between 150 m and 300 m height and between 400 and 800 m distance. The linear function of the operational beam width amounted to y=0·3493x (R2=0·1866, n=6) (Figure 3). This corresponded to an angle of 19·25°, thus confirming the expectation that this angle is bigger than of the sphere of the smaller radar cross section. The difference of detection range between a 3·58 cm2 and a 9·006 cm2 cross section was 2·3°.

Figure 3. Beam width (faint detection) at which a radar cross section of σ=9·006 cm2 radar cross section could be detected. The linear function: y=0·3493x (R2=0·1866, n=6).

Figure 4. Maximum range at which the sphere of σ=3·58 cm2 could be detected. Average maximum range amounted to 1121±138 m (n=6).
Under the assumption that a linear dependency exists between the radar cross section and the operational angle, other operational angles can be extrapolated. The linear function was determined by the operational beam width of the cross section of 3·58 cm2 and of 9·006 cm2 (y=0·424x+15·43). According to this equation, the operational beam width of the most common radar cross sections for songbirds (3 and 4 cm2) would be between 16·70° and 17·13°. The operational beam width for the minimum cross section (2 cm2) would amount to 16·28° and of the maximum (10 cm2) to 19·67° (Table 2).
Table 2. The extrapolated operational beam width for several radar cross sections.

3.2. Maximum range
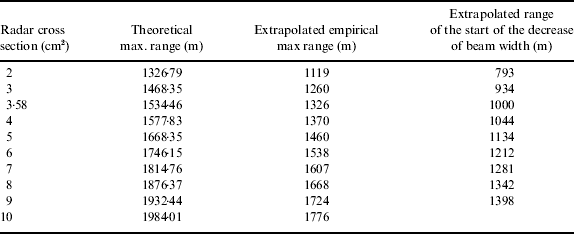
According to the radar equation the maximum distance at which songbirds with their smallest aspects (σ=2 cm2) and their biggest aspects (σ=10 cm2) could be detected was 1327 m and 1984 m respectively (Table 3). The calculated range for a radar cross section of 3·58 cm2 amounted to 1534 m. The maximum range, at which the reflection of this size of sphere could be detected, was 1326 m (Figure 4). The distance from where a decrease of the beam width was discernible amounted to about 1000 m. We assumed that the difference between these values and the theoretical maximum range is similar for other radar cross sections and extrapolated the other values accordingly. One would expect to detect cross sections of typical songbirds (3–4 cm2) on the beam axis up to distances between 1500 and 1600 m, but at differing heights to at most 1000 m. One would expect the smallest songbird radar cross section (2 cm2) to be detected up to 1300 m distance and 800 m in height and the biggest songbird radar cross section (10 cm2) up to a distance of 1800 m and 1450 m respectively.
Table 3. The theoretical and the extrapolated empirical maximum range for different radar cross sections.
4. DISCUSSION
As modern radars do not show the raw signal on the radar display, the operational beam width and the maximum range have to be calibrated by direct measurements. These measurements are essential for quantitative radar studies on bird movements. Therefore, we give all information necessary to repeat the measurements for any other radar and target size. The measurements were made using a 25 KW ship radar.
We measured the operational beam width and the maximum range for metal spheres of the radar cross section of songbirds. These measurements are the basis for any quantitative analysis of bird movements. The maximum range of detection is important to know in order to avoid a bias of the frequency distribution of the directions: outside of the detection range of an average sized songbird, birds in side view can still be detected. Thus, only birds flying in a certain direction can be detected. Another bias would be caused by the fact that at larger distances only bigger birds would be detected.
We found that on average the operational beam width of songbirds is smaller than the nominal angle. We concluded that it amounted to 17°, thus deviating from the nominal angle by about 3°. These findings are in contrast to the situation with a tracking radar where the operational beam width seemed to be twice the nominal beam width for songbirds (Bruderer & Liechti Reference Bruderer and Liechti1994). However, considering all possible views of a songbird from ahead to side view and to tail view the operational angle varies at least between 16° and 20°. That means that the largest cross sections of songbirds can be detected at exactly the size of the nominal angle. On average, the maximum range of this radar for medium sized songbirds off the beam axis amounted to 1000 m. It follows that birds which are seen by the radar from in front or tail on, will disappear from the radar display at smaller distances, while birds in side view will be detected at much longer distances.
The limitations of the present study are that ground clutter did not allow measuring the upper detection border at distances less than 400 m. For all other criteria, the chosen site was the best choice within the military drill ground. More measurements would allow a statistical evaluation of the maximal range and the determination of the function of the curvature of the decrease of the beam width at longer ranges. Budget reasons restricted this study to only two sizes of spheres and to a tight time frame.
A ship radar has the big advantage of being transportable to remote locations and to be the least expensive radar. The adaptation of the concept to other bird sizes, to other nominal beam widths or another type of radar could easily be performed. The costs for the experiment were reasonable. Plan to do the experiments within four to six days in calm weather. If one uses heavier spheres, a bigger balloon has to be chosen. We regard the method as reliable. Only modest modifications should be needed for other radar types and other target sizes.
ACKNOWLEDGEMENTS
We wish to express our sincere thanks to K. Böhning-Gaese for giving the opportunity to perform this study in her working-group. We thank all members of the team comprising K. Scheelke, H. Ullrich, D. Berens, R. Berens, C. Braun, M. Theobald, R. Raiss, J. Drögemüller, N. Gerhardt und S. Junker for their great effort in the field. We are grateful to H. Ullrich for the development of a tool which allowed us to convert the angle under which the radar is seen from the balloon into the angle of the echo on the display. We wish to express our thanks to the staff of the German Research Association (DFG) (H.-J. Bode, O. Hammerstein, P. Augustin), of Ferropilot (W. Luessenhoff), of Optimare (T. Hengstermann, I. Richter), to M. Laub and O. Saul of the military drill ground of Baumholder, to Mr. Hartnauer, Meybauer and Sanftleben of the military ground of Elpersbüttel, to the airport of Bremerhaven, to Mr. Klonowski from the University of Applied Sciences of Mainz for helping out with theodolites, to S. Mitra, B. Friedrich and L. Schütz (Institute of Physics of the Atmosphere) and to the German Weather Forecast (DWD) for their support. We thank two anonymous referees for commenting on a former version of the manuscript and to R. Raiss for improving the English. This study was supported by the German Research Association (DFG).









