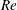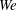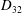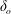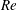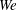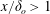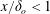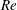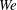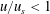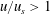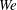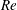1 Introduction
Sprays are complex droplet-laden multiphase flows. One source of complexity is the fact that spray formation cannot be attributed to a single physical breakup mechanism. Bulk liquid is transformed into a large number of drops by an atomizer via various mechanisms. While primary atomization is responsible for the creation of drops from a precursor liquid sheet (Gorokhovski & Herrmann Reference Gorokhovski and Herrmann2008), secondary atomization processes create additional drops from fragmentation of larger blobs (Guildenbecher, López-Rivera & Sojka Reference Guildenbecher, López-Rivera and Sojka2009). Each of these processes are governed by different scaling laws (Lin & Reitz Reference Lin and Reitz1998; Villermaux Reference Villermaux2007). For example, drops whose size is of the same order of magnitude as the precursor sheet thickness are likely to be formed through the instability route (Panchagnula, Sojka & Santangelo Reference Panchagnula, Sojka and Santangelo1996). Drops which are much smaller than the sheet thickness are formed due to shear at the liquid–air interface (Guildenbecher et al. Reference Guildenbecher, López-Rivera and Sojka2009). The statistical characteristics of the joint drop size–velocity probability density distributions from these two sources have been shown to be different by Babinsky & Sojka (Reference Babinsky and Sojka2002). However, attempts to model drop size–velocity distributions at the ‘spray’ level have relied on fitting one mathematical form to the entire distribution (Marmottant & Villermaux Reference Marmottant and Villermaux2004). We will suggest from our experiments reported herein that different pieces of the joint size–velocity distribution need to be modelled differently. We will also suggest a choice of length and velocity scales that can be used to distinguish pieces of the joint size–velocity distribution that require different treatment.
Another aspect of sprays that has not attracted due attention is dynamical similarity. Dynamical similarity in single-phase flows has been well studied (Hardalupas, Taylor & Whitelaw Reference Hardalupas, Taylor and Whitelaw1989; Longmire & Eaton Reference Longmire and Eaton1992). It is well known that velocity profiles in single-phase jets exhibit universal behaviour. Any investigation of these phenomena begins with the identification of an appropriate choice of length and time scales that would in turn result in dynamically similar flow structures (when scaled). In the case of droplet-laden jets (sprays), the extent to which such similarity will extend is not widely discussed in the literature. From our experiments, we will show that dynamical similarity in pressure swirl sprays could, in fact, extend even to higher-order moments of the joint size–velocity distribution.
Correlations (Lefebvre Reference Lefebvre1989; Tratnig & Brenn Reference Tratnig and Brenn2010) or physics-based arguments (Villermaux Reference Villermaux2007) have been the recourse towards realizing predictive tools for spray performance, especially drop size spectra. However, both these classes of arguments rely on an appropriate choice of length scale. In this context, it is well known that viscous effects are important at low values of Reynolds number (
![]() $Re$
), while inviscid theory is sufficient at high
$Re$
), while inviscid theory is sufficient at high
![]() $Re$
. An objective of this study is to quantitatively isolate the conditions under which liquid sheet thickness (from inviscid calculations) is sufficient from those when boundary layer thickness becomes the determining length scale of spray performance. Towards this end, a comprehensive study of pressure swirl sprays in the Reynolds number (
$Re$
. An objective of this study is to quantitatively isolate the conditions under which liquid sheet thickness (from inviscid calculations) is sufficient from those when boundary layer thickness becomes the determining length scale of spray performance. Towards this end, a comprehensive study of pressure swirl sprays in the Reynolds number (
![]() $Re$
) and Weber number (
$Re$
) and Weber number (
![]() $We$
) space has been undertaken. We report experiments spanning approximately one-and-a-half decades of both
$We$
) space has been undertaken. We report experiments spanning approximately one-and-a-half decades of both
![]() $Re$
and
$Re$
and
![]() $We$
, where the effect of each parameter can be independently isolated. In order to span this range of dimensionless parameters, we have employed a cohort of four geometrically similar atomizers.
$We$
, where the effect of each parameter can be independently isolated. In order to span this range of dimensionless parameters, we have employed a cohort of four geometrically similar atomizers.
This experimental study is also motivated by engineering applications of the devices that we have developed and fabricated. In many spray applications, miniaturization of atomizers is emerging as a desirable objective. While miniaturization has been attempted in the past (Simmons & Harvey Reference Simmons and Harvey1995), it comes with a heavy viscous loss penalty, since the miniaturized devices would operate at low
![]() $Re$
(Lefebvre Reference Lefebvre1989). On the related note, a high-turndown device (where the ratio of the highest operable to the lowest operable flow rate is greater than 10) has eluded designers. A possible solution to all three problems mentioned above could be to exploit technological gains in micro-electromechanical systems (MEMS) fabrication to design and develop a micromachined atomizer element. Subsequently, it is possible to operate an array of elements to create a high-quality spray while achieving both high turndown as well as low pressure loss. One of the pressure swirl atomizer devices employed in this study explores this proposition.
$Re$
(Lefebvre Reference Lefebvre1989). On the related note, a high-turndown device (where the ratio of the highest operable to the lowest operable flow rate is greater than 10) has eluded designers. A possible solution to all three problems mentioned above could be to exploit technological gains in micro-electromechanical systems (MEMS) fabrication to design and develop a micromachined atomizer element. Subsequently, it is possible to operate an array of elements to create a high-quality spray while achieving both high turndown as well as low pressure loss. One of the pressure swirl atomizer devices employed in this study explores this proposition.
The basic design procedure for macroscale pressure swirl atomizers is well developed (Bayvel & Orzechowski Reference Bayvel and Orzechowski1993). Simmons & Harvey (Reference Simmons and Harvey1995) have explained a method to design and manufacture microscale pressure swirl atomizers from a thin sheet of material. Silicon microscale atomizers have also been successfully demonstrated by Singh et al. (Reference Singh, Mehregany, Phillips and Harvey1998). Rajan et al. (Reference Rajan, Mehregany, Zorman, Stefanescu and Kicher1999) have demonstrated microscale silicon carbide (SiC) fuel atomizers for gas turbine engines. Fabrication complexities associated with microscale atomizers were discussed by Benjamin & Harvey (Reference Benjamin and Harvey1996). However, a scientific study of the dynamics of microscale sprays from the viewpoint of what makes them different has not been reported in the literature. We are motivated by this lacuna both to develop new designs for microscale atomizers (Dhivyaraja et al. Reference Dhivyaraja, Gaddes, Panchagnula and Tadigadapa2015) as well as to discover the physics of microsprays.
In this paper we will specifically address the following questions:
(i) What is the extent to which dynamical similarity will extend in the case of pressure swirl sprays? Is it possible that the drop size and velocity spectra exhibit universal probability density functions?
(ii) Is the mechanism of spray formation in microscale atomizers the same as in conventional macroscale devices?
The paper is organized as follows. In § 2, theoretical analyses of pressure swirl atomizer internal flow using both inviscid as well as viscous approaches are outlined. Section 3 presents the details of pressure swirl atomizer geometry and its fabrication methodologies (MEMS and additive manufacturing), experimental methods and test set-up. In § 4, results from the current study are presented in detail. Section 4.1 presents macroscale results such as flow rate scaling. In § 4.2, microscale results such as radial variation of Sauter mean diameter (
![]() $D_{32}$
), axial velocity (
$D_{32}$
), axial velocity (
![]() $u$
), drop size distribution and drop velocity distribution are discussed. In § 4.3, generation of droplets from a liquid sheet and its associated breakup mechanisms are discussed. An analysis of the high-speed images based on a proper orthogonal decomposition (POD) is discussed in § 4.4. Section 5 discusses the impact of the key findings in this paper and presents a broad overview of their potential applications. Finally, § 6 presents a summary of the research along with key conclusions.
$u$
), drop size distribution and drop velocity distribution are discussed. In § 4.3, generation of droplets from a liquid sheet and its associated breakup mechanisms are discussed. An analysis of the high-speed images based on a proper orthogonal decomposition (POD) is discussed in § 4.4. Section 5 discusses the impact of the key findings in this paper and presents a broad overview of their potential applications. Finally, § 6 presents a summary of the research along with key conclusions.
2 Theoretical analysis of the nozzle internal flow
The drop size and velocity spectra in a spray are directly influenced by the fluid mechanics inside the atomizer swirl chamber. This internal flow has been analysed theoretically using both inviscid as well as viscous approaches. We would like to identify dimensionless parameter regimes where the length scales obtained from the inviscid analysis are sufficient to predict drop size spectra. In addition, we would also like to identify regimes where viscous effects cannot be ignored and hence a length scale arising from such viscous effects is required. We will begin by first discussing the two analytical approaches briefly.
2.1 Inviscid analysis
In this approach, originally due to Taylor (Reference Taylor1948), the flow inside the swirl chamber is treated as a superposition of a potential swirl vortex and a radial sink flow. The liquid sheet thickness at the nozzle exit can then be obtained from the principle of flow rate maximization, since the sheet thickness is fluid mechanically determined by a balance between the pressure and centrifugal swirl forces. In order to mathematically delineate the model, an atomizer geometry constant (
![]() ${\mathcal{K}}$
) given by
${\mathcal{K}}$
) given by
is first defined. Here,
![]() $A_{p}$
is the area of the inlet ports into the swirl chamber,
$A_{p}$
is the area of the inlet ports into the swirl chamber,
![]() $D_{s}$
is the swirl chamber diameter and
$D_{s}$
is the swirl chamber diameter and
![]() $D_{o}$
is the exit orifice diameter. These features are schematically shown later in figure 2(d). Following Giffen & Muraszew (Reference Giffen and Muraszew1953) and Lefebvre & Suyari (Reference Lefebvre and Suyari1986), the liquid sheet thickness (
$D_{o}$
is the exit orifice diameter. These features are schematically shown later in figure 2(d). Following Giffen & Muraszew (Reference Giffen and Muraszew1953) and Lefebvre & Suyari (Reference Lefebvre and Suyari1986), the liquid sheet thickness (
![]() $t_{s}$
) and
$t_{s}$
) and
![]() ${\mathcal{K}}$
are related by
${\mathcal{K}}$
are related by
where
![]() $X$
is the fraction of the exit orifice area occupied by the air core, which is given by
$X$
is the fraction of the exit orifice area occupied by the air core, which is given by
As can be seen from equations (2.1)–(2.3),
![]() ${\mathcal{K}}$
and the dimensionless sheet thickness (
${\mathcal{K}}$
and the dimensionless sheet thickness (
![]() $t_{s}/D_{o}$
) are uniquely related. For a given
$t_{s}/D_{o}$
) are uniquely related. For a given
![]() ${\mathcal{K}}$
, one could solve the cubic equation (2.2) to find a value for
${\mathcal{K}}$
, one could solve the cubic equation (2.2) to find a value for
![]() $X$
. Equation (2.3) can then be used to solve for
$X$
. Equation (2.3) can then be used to solve for
![]() $t_{s}/D_{o}$
. For
$t_{s}/D_{o}$
. For
![]() $t_{s}/D_{o}\ll 1$
, an explicit relation can be written as
$t_{s}/D_{o}\ll 1$
, an explicit relation can be written as
The liquid sheet thickness at the exit (
![]() $t_{s}$
) is therefore a length scale associated with the spray formation process. One could correspondingly define a liquid sheet velocity scale (
$t_{s}$
) is therefore a length scale associated with the spray formation process. One could correspondingly define a liquid sheet velocity scale (
![]() $u_{s}$
) given by
$u_{s}$
) given by
![]() $u_{s}=Q/\unicode[STIX]{x03C0}D_{o}t_{s}$
. If the spray performance, viz., drop size and velocity spectra, scale with these quantities, one can assume that viscous effects in the nozzle have an insignificant effect on the spray characteristics.
$u_{s}=Q/\unicode[STIX]{x03C0}D_{o}t_{s}$
. If the spray performance, viz., drop size and velocity spectra, scale with these quantities, one can assume that viscous effects in the nozzle have an insignificant effect on the spray characteristics.
We will experimentally explore the effect of
![]() $Re$
on spray performance with the objective of identifying a critical value of
$Re$
on spray performance with the objective of identifying a critical value of
![]() $Re$
where inviscid scaling is likely to break down. Towards this end, we will define
$Re$
where inviscid scaling is likely to break down. Towards this end, we will define
where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity. Alternatively,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity. Alternatively,
![]() $Re=Q/\unicode[STIX]{x03C0}D_{o}\unicode[STIX]{x1D708}$
, where
$Re=Q/\unicode[STIX]{x03C0}D_{o}\unicode[STIX]{x1D708}$
, where
![]() $Q$
is the volume flow rate.
$Q$
is the volume flow rate.
2.2 Viscous analysis
A correction to the inviscid sheet thickness has been proposed by Rizk & Lefebvre (Reference Rizk and Lefebvre1985) based on semi-empirical arguments. Their equation for liquid sheet thickness
![]() $t_{v}$
at the exit can be written in our nomenclature as
$t_{v}$
at the exit can be written in our nomenclature as
where
![]() $\unicode[STIX]{x1D70C}$
is the liquid density,
$\unicode[STIX]{x1D70C}$
is the liquid density,
![]() $\overline{\unicode[STIX]{x0394}p}=\unicode[STIX]{x0394}pD_{o}^{2}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{2}$
is a dimensionless pressure drop and
$\overline{\unicode[STIX]{x0394}p}=\unicode[STIX]{x0394}pD_{o}^{2}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{2}$
is a dimensionless pressure drop and
![]() $\unicode[STIX]{x0394}p$
is the dimensional pressure drop across the atomizer. Based on a comparison of the sheet thickness predicted by (2.4) and (2.6), it was found that (2.6) is valid for
$\unicode[STIX]{x0394}p$
is the dimensional pressure drop across the atomizer. Based on a comparison of the sheet thickness predicted by (2.4) and (2.6), it was found that (2.6) is valid for
![]() $Re<10^{4}$
.
$Re<10^{4}$
.
2.3 Three-dimensional boundary layer analysis
The previously described inviscid approach ignores the presence of the three-dimensional boundary layer at the walls of the swirl chamber formed due to the action of a swirling sink flow. Binnie & Harris (Reference Binnie and Harris1950), Taylor (Reference Taylor1950), Bloor & Ingham (Reference Bloor and Ingham1977), Dumouchel et al. (Reference Dumouchel, Bloor, Dombrowski, Ingham and Ledoux1992) and more recently Amini (Reference Amini2016) have suggested that this is an important cause of spray performance variation. They all suggested that a strongly swirling flow field induces a radial velocity overshoot in the boundary layer, which in turn plays a key role in determining the dynamics of the liquid sheet exiting the nozzle. However, this has also been a source of disagreement in the literature (Taylor Reference Taylor1950). While Taylor (Reference Taylor1950) suggested that the radial velocity overshoot could be as high as
![]() $500\,\%$
, Binnie & Harris (Reference Binnie and Harris1950) found that Taylor’s conclusion was possibly incorrect due to the fact that he ignored the radial velocity field in the potential flow region. It was not until Bloor & Ingham (Reference Bloor and Ingham1977) that a theoretically consistent momentum integral formulation based on the Pohlhausen approximation of the three-dimensional boundary layer was developed. In this approach, both the radial velocity overshoot as well as the wall shear stress are accurately predicted. Their approach has also been validated experimentally by Dumouchel et al. (Reference Dumouchel, Bloor, Dombrowski, Ingham and Ledoux1992) and computationally by Amini (Reference Amini2016). We will use the Bloor–Ingham formulation to numerically calculate the boundary layer thickness and velocity profiles, specific to our cases. We refer the reader to Bloor & Ingham (Reference Bloor and Ingham1977) and their equations (14)–(16) for the mathematical form of the equations. In this context, Lasheras, Villermaux & Hopfinger (Reference Lasheras, Villermaux and Hopfinger1998) as well as Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000) had suggested that the boundary layer plays a significant role in spray formation. The influence of gas turbulence on the air–water mixing boundary layer has also been studied previously by Matas et al. (Reference Matas, Marty, Dem and Cartellier2015). However, its relevance as a length scale governing drop size distributions has not been investigated in the literature.
$500\,\%$
, Binnie & Harris (Reference Binnie and Harris1950) found that Taylor’s conclusion was possibly incorrect due to the fact that he ignored the radial velocity field in the potential flow region. It was not until Bloor & Ingham (Reference Bloor and Ingham1977) that a theoretically consistent momentum integral formulation based on the Pohlhausen approximation of the three-dimensional boundary layer was developed. In this approach, both the radial velocity overshoot as well as the wall shear stress are accurately predicted. Their approach has also been validated experimentally by Dumouchel et al. (Reference Dumouchel, Bloor, Dombrowski, Ingham and Ledoux1992) and computationally by Amini (Reference Amini2016). We will use the Bloor–Ingham formulation to numerically calculate the boundary layer thickness and velocity profiles, specific to our cases. We refer the reader to Bloor & Ingham (Reference Bloor and Ingham1977) and their equations (14)–(16) for the mathematical form of the equations. In this context, Lasheras, Villermaux & Hopfinger (Reference Lasheras, Villermaux and Hopfinger1998) as well as Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000) had suggested that the boundary layer plays a significant role in spray formation. The influence of gas turbulence on the air–water mixing boundary layer has also been studied previously by Matas et al. (Reference Matas, Marty, Dem and Cartellier2015). However, its relevance as a length scale governing drop size distributions has not been investigated in the literature.

Figure 1. (a) Plot of the boundary layer three-dimensional velocity profile at the atomizer exit for
![]() $Re=2760$
. Here,
$Re=2760$
. Here,
![]() $U_{\unicode[STIX]{x1D703}}$
is the tangential or swirl velocity,
$U_{\unicode[STIX]{x1D703}}$
is the tangential or swirl velocity,
![]() $U_{r}$
is the radial velocity and
$U_{r}$
is the radial velocity and
![]() $y$
is the boundary layer thickness coordinate to indicate the boundary layer velocity profiles inside the swirl chamber. The resultant velocity is also shown in black arrows. The radial velocity profile shows an overshoot inside the boundary layer that is approximately
$y$
is the boundary layer thickness coordinate to indicate the boundary layer velocity profiles inside the swirl chamber. The resultant velocity is also shown in black arrows. The radial velocity profile shows an overshoot inside the boundary layer that is approximately
![]() $200\,\%$
of the free-stream radial velocity. In the near-wall region, radial motion is dominant while the swirl component of the velocity dominates the flow towards the edge of the boundary layer. (b) Plot of dimensionless boundary layer thickness (
$200\,\%$
of the free-stream radial velocity. In the near-wall region, radial motion is dominant while the swirl component of the velocity dominates the flow towards the edge of the boundary layer. (b) Plot of dimensionless boundary layer thickness (
![]() $\overline{\unicode[STIX]{x1D6FF}_{0}}$
) at the atomizer exit (
$\overline{\unicode[STIX]{x1D6FF}_{0}}$
) at the atomizer exit (
![]() $\unicode[STIX]{x1D6FF}_{o}/t_{s}$
and
$\unicode[STIX]{x1D6FF}_{o}/t_{s}$
and
![]() $\unicode[STIX]{x1D6FF}_{o}/t_{v}$
) as a function of
$\unicode[STIX]{x1D6FF}_{o}/t_{v}$
) as a function of
![]() $Re$
. The boundary layer thickness (
$Re$
. The boundary layer thickness (
![]() $t_{s}$
) is comparable in thickness to the liquid sheet for low
$t_{s}$
) is comparable in thickness to the liquid sheet for low
![]() $Re$
. The experimental cases and data taken are also shown in this figure. Test 1 are cases where flow rate, spray cone angle and sheet flapping dynamics are measured. Test 2 are cases where local drop size and velocity measurements are also made in addition to those measured in test 1.
$Re$
. The experimental cases and data taken are also shown in this figure. Test 1 are cases where flow rate, spray cone angle and sheet flapping dynamics are measured. Test 2 are cases where local drop size and velocity measurements are also made in addition to those measured in test 1.
Figure 1(a) shows a vectorial representation of the tangential and radial velocity profiles at the end of the swirl chamber (near the exit orifice) for one of the experimental cases considered herein. Firstly, the free-stream swirl velocity magnitude is
![]() ${\sim}2.5$
times higher than the free-stream radial velocity at the exit orifice. As can be seen from figure 1(a), the overshoot in the radial velocity profile resulting from the swirling flow is approximately
${\sim}2.5$
times higher than the free-stream radial velocity at the exit orifice. As can be seen from figure 1(a), the overshoot in the radial velocity profile resulting from the swirling flow is approximately
![]() $200\,\%$
of the mean radial velocity at that location due to the strongly swirling nature of the flow. In addition, the three-dimensional nature of the boundary layer is clearly visible. Finally, while the outer flow is strongly swirling, the flow near the wall shows a strong radial motion. In other words, a liquid sheet exiting the injector has significant gradients in the velocity profile due to this boundary layer.
$200\,\%$
of the mean radial velocity at that location due to the strongly swirling nature of the flow. In addition, the three-dimensional nature of the boundary layer is clearly visible. Finally, while the outer flow is strongly swirling, the flow near the wall shows a strong radial motion. In other words, a liquid sheet exiting the injector has significant gradients in the velocity profile due to this boundary layer.
In order to quantify the viscous effects on the liquid sheet formation process, we compare the boundary layer thickness at the end of the swirl chamber (
![]() $\unicode[STIX]{x1D6FF}_{o}$
) to the liquid sheet thickness at the nozzle exit obtained from an inviscid calculation (
$\unicode[STIX]{x1D6FF}_{o}$
) to the liquid sheet thickness at the nozzle exit obtained from an inviscid calculation (
![]() $t_{s}$
) and viscous calculation (
$t_{s}$
) and viscous calculation (
![]() $t_{v}$
). Figure 1(b) is a plot of the dimensionless boundary layer thickness (
$t_{v}$
). Figure 1(b) is a plot of the dimensionless boundary layer thickness (
![]() $\overline{\unicode[STIX]{x1D6FF}_{o}}$
) as a function of
$\overline{\unicode[STIX]{x1D6FF}_{o}}$
) as a function of
![]() $Re$
. As expected, for
$Re$
. As expected, for
![]() $\unicode[STIX]{x1D6FF}_{o}/t_{s}\sim Re^{-1/2}$
and
$\unicode[STIX]{x1D6FF}_{o}/t_{s}\sim Re^{-1/2}$
and
![]() $\unicode[STIX]{x1D6FF}_{o}/t_{v}\sim Re^{-1/5}$
the boundary layer is comparable in thickness (
$\unicode[STIX]{x1D6FF}_{o}/t_{v}\sim Re^{-1/5}$
the boundary layer is comparable in thickness (
![]() $t_{s}$
) to the liquid sheet for low
$t_{s}$
) to the liquid sheet for low
![]() $Re$
. As
$Re$
. As
![]() $Re$
increases,
$Re$
increases,
![]() $\unicode[STIX]{x1D6FF}_{o}/t_{s}$
decreases. For
$\unicode[STIX]{x1D6FF}_{o}/t_{s}$
decreases. For
![]() $Re>1000$
, which has been suggested by Rizk & Lefebvre (Reference Rizk and Lefebvre1985) as a critical
$Re>1000$
, which has been suggested by Rizk & Lefebvre (Reference Rizk and Lefebvre1985) as a critical
![]() $Re$
value,
$Re$
value,
![]() $\unicode[STIX]{x1D6FF}_{o}/t_{s}<0.3$
. Therefore, one could expect that the liquid sheet exiting a nozzle is less influenced by viscous effects at high
$\unicode[STIX]{x1D6FF}_{o}/t_{s}<0.3$
. Therefore, one could expect that the liquid sheet exiting a nozzle is less influenced by viscous effects at high
![]() $Re$
. Under this condition, the scales obtained from inviscid analysis (
$Re$
. Under this condition, the scales obtained from inviscid analysis (
![]() $t_{s}$
) could be sufficient to scale performance for high-
$t_{s}$
) could be sufficient to scale performance for high-
![]() $Re$
sprays. However, for
$Re$
sprays. However, for
![]() $Re<1000$
, two possible length scales could be appropriate: the boundary layer thickness at the nozzle exit (
$Re<1000$
, two possible length scales could be appropriate: the boundary layer thickness at the nozzle exit (
![]() $\unicode[STIX]{x1D6FF}_{o}$
), or the liquid sheet thickness including the effect of viscosity (
$\unicode[STIX]{x1D6FF}_{o}$
), or the liquid sheet thickness including the effect of viscosity (
![]() $t_{v}$
), calculated in (2.6). We will experimentally test both these propositions.
$t_{v}$
), calculated in (2.6). We will experimentally test both these propositions.
3 Experimental methods
3.1 Atomizer geometry
We would like to study the proposition of dynamical similarity in pressure swirl sprays and study the competition between inviscid and viscous effects. The symbols indicated in figure 1(b) show all the different values of
![]() $Re$
at which experiments have been performed. As can be seen,
$Re$
at which experiments have been performed. As can be seen,
![]() $Re$
values range over at least a factor of
$Re$
values range over at least a factor of
![]() $15$
between the lowest and highest
$15$
between the lowest and highest
![]() $Re$
values. This in itself required a rather unconventional approach to fabricating the experimental devices to be used. The devices will need to produce a fully open conical liquid sheet at low
$Re$
values. This in itself required a rather unconventional approach to fabricating the experimental devices to be used. The devices will need to produce a fully open conical liquid sheet at low
![]() $Re$
values, while allowing for fluid dynamic interrogation tools (viz., high-speed imaging, phase Doppler interferometry (PDI), etc.) to remain usable in high-
$Re$
values, while allowing for fluid dynamic interrogation tools (viz., high-speed imaging, phase Doppler interferometry (PDI), etc.) to remain usable in high-
![]() $Re$
sprays. The experimental devices are designed and fabricated bearing this objective in mind. The smallest device was required to be fabricated using MEMS technology out of silicon and glass, owing to the very low flow rates required for the experiments, while ensuring a good spray.
$Re$
sprays. The experimental devices are designed and fabricated bearing this objective in mind. The smallest device was required to be fabricated using MEMS technology out of silicon and glass, owing to the very low flow rates required for the experiments, while ensuring a good spray.
An unconventional pressure swirl atomizer design has been employed in this study. Unlike in conventional designs, all angular features have been maintained at
![]() $90^{\circ }$
bearing MEMS fabrication limitations in mind (Simmons & Harvey Reference Simmons and Harvey1995). As a result, the working fluid will encounter sharp features inside the atomizer. As we will see, the atomizer is capable of producing a uniform conical liquid sheet from the exit orifice in spite of this design constraint. In this study we have employed four atomizers of the same design but geometrically scaled in size from a base dimension. The four atomizers are designated as
$90^{\circ }$
bearing MEMS fabrication limitations in mind (Simmons & Harvey Reference Simmons and Harvey1995). As a result, the working fluid will encounter sharp features inside the atomizer. As we will see, the atomizer is capable of producing a uniform conical liquid sheet from the exit orifice in spite of this design constraint. In this study we have employed four atomizers of the same design but geometrically scaled in size from a base dimension. The four atomizers are designated as
![]() $1$
x,
$1$
x,
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x. Figure 2(a) shows a photograph of the four atomizers used in this study. Appendix A includes the details of the geometrical dimensions of all the atomizers used in the study.
$10$
x. Figure 2(a) shows a photograph of the four atomizers used in this study. Appendix A includes the details of the geometrical dimensions of all the atomizers used in the study.

Figure 2. (a) Photographs of the geometrically similar atomizers used in this study: (i)
![]() $1$
x, (ii)
$1$
x, (ii)
![]() $3$
x, (iii)
$3$
x, (iii)
![]() $5$
x and (iv)
$5$
x and (iv)
![]() $10$
x. The
$10$
x. The
![]() $1$
x atomizer was fabricated from silicon and glass using MEMS technology. The other atomizers were fabricated using the additive manufacturing technique. (b) A magnified view of the
$1$
x atomizer was fabricated from silicon and glass using MEMS technology. The other atomizers were fabricated using the additive manufacturing technique. (b) A magnified view of the
![]() $1$
x atomizer. (c) A graphical illustration of the MEMS fabrication process of the micro-atomizer. (d) A schematic showing the design parameters: exit orifice diameter (
$1$
x atomizer. (c) A graphical illustration of the MEMS fabrication process of the micro-atomizer. (d) A schematic showing the design parameters: exit orifice diameter (
![]() $D_{o}$
), swirl chamber diameter (
$D_{o}$
), swirl chamber diameter (
![]() $D_{s}$
), length of the exit orifice (
$D_{s}$
), length of the exit orifice (
![]() $L_{o}$
), length of the swirl chamber (
$L_{o}$
), length of the swirl chamber (
![]() $L_{s}$
), length of the inlet port (
$L_{s}$
), length of the inlet port (
![]() $L_{p}$
) and width of the inlet port (
$L_{p}$
) and width of the inlet port (
![]() $W_{p}$
).
$W_{p}$
).
The atomizer shown in figure 2(a)(i) (shown to a larger scale in figure 2
b) is considered the base design and is referred to as the
![]() $1$
x atomizer. The
$1$
x atomizer. The
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x atomizers are designed such that every linear dimension in the
$10$
x atomizers are designed such that every linear dimension in the
![]() $1$
x atomizer is scaled by a factor of
$1$
x atomizer is scaled by a factor of
![]() $3$
,
$3$
,
![]() $5$
and
$5$
and
![]() $10$
, respectively. These atomizers are shown in figure 2(a)(ii–iv). The choice of four atomizers is motivated by a desire to investigate dynamical similarity over a wide range of Reynolds numbers (
$10$
, respectively. These atomizers are shown in figure 2(a)(ii–iv). The choice of four atomizers is motivated by a desire to investigate dynamical similarity over a wide range of Reynolds numbers (
![]() $Re$
) spanning a factor of
$Re$
) spanning a factor of
![]() $15$
. One of the experimental complexities in this process arises from the fact that the flow rate scales approximately as
$15$
. One of the experimental complexities in this process arises from the fact that the flow rate scales approximately as
![]() $\sqrt{\unicode[STIX]{x0394}p}$
. In other words, a factor of
$\sqrt{\unicode[STIX]{x0394}p}$
. In other words, a factor of
![]() $15$
change in
$15$
change in
![]() $Re$
would require a factor of
$Re$
would require a factor of
![]() $225$
increase in
$225$
increase in
![]() $\unicode[STIX]{x0394}p$
. In addition, as
$\unicode[STIX]{x0394}p$
. In addition, as
![]() $\unicode[STIX]{x0394}p$
increases on the same injector, the flow rates increase and, as a result, the associated flow time scales decrease quite rapidly. This will render commercially available high-speed shadowgraphy insufficient to resolve the liquid sheet dynamics at the nozzle exit. Therefore, in order to span a wide range of
$\unicode[STIX]{x0394}p$
increases on the same injector, the flow rates increase and, as a result, the associated flow time scales decrease quite rapidly. This will render commercially available high-speed shadowgraphy insufficient to resolve the liquid sheet dynamics at the nozzle exit. Therefore, in order to span a wide range of
![]() $Re$
in the experiments while obtaining well-resolved high-speed video images, we have employed a cohort of four geometrically similar atomizers scaled up a factor of
$Re$
in the experiments while obtaining well-resolved high-speed video images, we have employed a cohort of four geometrically similar atomizers scaled up a factor of
![]() $10$
from the smallest to the largest. We found it useful to rely on MEMS fabrication technology for the smallest atomizer in order to ensure that dimensionless surface roughness also remains somewhat similar between the four atomizers.
$10$
from the smallest to the largest. We found it useful to rely on MEMS fabrication technology for the smallest atomizer in order to ensure that dimensionless surface roughness also remains somewhat similar between the four atomizers.
The base model
![]() $1$
x is a microscale atomizer that has been fabricated using MEMS fabrication technology. The
$1$
x is a microscale atomizer that has been fabricated using MEMS fabrication technology. The
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x models are macroscale atomizers that were made using an additive manufacturing technology. The atomizer design parameters are chosen based on the procedure discussed by Rajan et al. (Reference Rajan, Mehregany, Zorman, Stefanescu and Kicher1999). These parameters are shown in figure 2(d). The length of the inlet port (
$10$
x models are macroscale atomizers that were made using an additive manufacturing technology. The atomizer design parameters are chosen based on the procedure discussed by Rajan et al. (Reference Rajan, Mehregany, Zorman, Stefanescu and Kicher1999). These parameters are shown in figure 2(d). The length of the inlet port (
![]() $L_{p}$
) was scaled linearly in the
$L_{p}$
) was scaled linearly in the
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x designs but not in the
$10$
x designs but not in the
![]() $1$
x design due to packaging limitations. As discussed by Lefebvre (Reference Lefebvre1989), the length of the inlet port has a minor effect on the spray performance. Finally, the atomizer constant (
$1$
x design due to packaging limitations. As discussed by Lefebvre (Reference Lefebvre1989), the length of the inlet port has a minor effect on the spray performance. Finally, the atomizer constant (
![]() ${\mathcal{K}}$
) defined in (2.1) was maintained constant at
${\mathcal{K}}$
) defined in (2.1) was maintained constant at
![]() ${\mathcal{K}}=0.09$
in all four atomizers. As a result, the dimensionless sheet thickness from (2.4) is given by
${\mathcal{K}}=0.09$
in all four atomizers. As a result, the dimensionless sheet thickness from (2.4) is given by
![]() $t_{s}/D_{o}\approx 0.0663$
for all the atomizers employed in this study.
$t_{s}/D_{o}\approx 0.0663$
for all the atomizers employed in this study.
3.2 Device fabrication
The devices used in this study were fabricated using two approaches: (i) MEMS fabrication technology and (ii) additive manufacturing technology. The design of the atomizer was created using AutoCAD® and the digital images were then converted into optical mask files for photolithography.
The micro-atomizer shown in figure 2(b) is fabricated from a multilayer stack of Borofloat® and silicon as detailed in the cross-sectional views in figure 2(c)(i–iv). First, the swirler and annulus features were etched
![]() $100~\unicode[STIX]{x03BC}\text{m}$
deep into a
$100~\unicode[STIX]{x03BC}\text{m}$
deep into a
![]() $450~\unicode[STIX]{x03BC}\text{m}$
thick double-sided polished silicon wafer as seen in the cross-sectional view in figure 2(c)(i). This was accomplished by patterning a positive photoresist and using it as a mask in an anisotropic deep reactive ion etch (DRIE) process by cycling sulfur hexafluoride (SF
$450~\unicode[STIX]{x03BC}\text{m}$
thick double-sided polished silicon wafer as seen in the cross-sectional view in figure 2(c)(i). This was accomplished by patterning a positive photoresist and using it as a mask in an anisotropic deep reactive ion etch (DRIE) process by cycling sulfur hexafluoride (SF
![]() $_{6}$
), octafluorocyclobutane (C
$_{6}$
), octafluorocyclobutane (C
![]() $_{4}$
F
$_{4}$
F
![]() $_{8}$
) and oxygen (O
$_{8}$
) and oxygen (O
![]() $_{2}$
) (Laermer et al.
Reference Laermer, Schilp, Funk and Offenberg1999). The photoresist was stripped with MicroChem® Remover PG at
$_{2}$
) (Laermer et al.
Reference Laermer, Schilp, Funk and Offenberg1999). The photoresist was stripped with MicroChem® Remover PG at
![]() $70\,^{\circ }\text{C}$
for 15 min, followed by an acid strip using Cyantek Nano-Strip® at
$70\,^{\circ }\text{C}$
for 15 min, followed by an acid strip using Cyantek Nano-Strip® at
![]() $70\,^{\circ }\text{C}$
for 10 min. Next, two
$70\,^{\circ }\text{C}$
for 10 min. Next, two
![]() $100~\unicode[STIX]{x03BC}\text{m}$
thick Borofloat 33 were anodically bonded to both sides of the etched silicon (on the inlet and outlet side). To create the outlet holes in the Borofloat, as seen in the top view and cross-section of figure 2(c)(ii), the Borofloat was first thinned to
$100~\unicode[STIX]{x03BC}\text{m}$
thick Borofloat 33 were anodically bonded to both sides of the etched silicon (on the inlet and outlet side). To create the outlet holes in the Borofloat, as seen in the top view and cross-section of figure 2(c)(ii), the Borofloat was first thinned to
![]() $50~\unicode[STIX]{x03BC}\text{m}$
using
$50~\unicode[STIX]{x03BC}\text{m}$
using
![]() $49\,\%$
hydrofluoric acid (HF). Next, a 20 nm thick chromium (Cr) and 120 nm thick gold (Au) layers were evaporated onto the Borofloat bonded to the outlet side to act as a seed layer for electroplating. The outlet holes illustrated in figure 2(c)(iii) were patterned on a negative photoresist layer and an
$49\,\%$
hydrofluoric acid (HF). Next, a 20 nm thick chromium (Cr) and 120 nm thick gold (Au) layers were evaporated onto the Borofloat bonded to the outlet side to act as a seed layer for electroplating. The outlet holes illustrated in figure 2(c)(iii) were patterned on a negative photoresist layer and an
![]() $8~\unicode[STIX]{x03BC}\text{m}$
nickel (Ni) hardmask is electroplated on the exposed Cr/Au electroplate seed layer.
$8~\unicode[STIX]{x03BC}\text{m}$
nickel (Ni) hardmask is electroplated on the exposed Cr/Au electroplate seed layer.
The photoresist was stripped using Remover PG at
![]() $70\,^{\circ }\text{C}$
for 15 min. An argon (Ar)/SF
$70\,^{\circ }\text{C}$
for 15 min. An argon (Ar)/SF
![]() $_{6}$
dry etch process selectively etches the
$_{6}$
dry etch process selectively etches the
![]() $50~\unicode[STIX]{x03BC}\text{m}$
of Borofloat where there are openings in the Ni mask to create the inlet holes. The Ni, Au and Cr layers were stripped using Transene® nickel etchant type 1, Transene gold etchant trifluoroacetic acid (TFA) and Transene chrome etchant 1020, respectively. Next, the outlet-side Borofloat was used as a hardmask to etch through the remaining
$50~\unicode[STIX]{x03BC}\text{m}$
of Borofloat where there are openings in the Ni mask to create the inlet holes. The Ni, Au and Cr layers were stripped using Transene® nickel etchant type 1, Transene gold etchant trifluoroacetic acid (TFA) and Transene chrome etchant 1020, respectively. Next, the outlet-side Borofloat was used as a hardmask to etch through the remaining
![]() $350~\unicode[STIX]{x03BC}\text{m}$
of silicon to connect to the swirler using DRIE, as illustrated in figure 2(c)(iii). Finally, the inlet holes, seen in top view and cross-section of figure 2(c)(iv), were created using the same Ni hardmask process as described for the outlet holes. High-temperature REVALPHA® thermal release tape is placed on the outlet side to prevent helium (He) cooling pressure loss in the plasma etcher once the inlet and outlet holes are connected. The tape is released on a hotplate after the etching is complete and the Ni–Au–Cr is stripped using the same chemicals as described for the outlet etch. The Borofloat on the outlet side is not required for the micro-atomizer to function, but provides addition mechanical strength enabling higher supply pressure tolerance as compared to a device without a Borofloat layer bonded to the outlet side (Dhivyaraja et al.
Reference Dhivyaraja, Gaddes, Panchagnula and Tadigadapa2015).
$350~\unicode[STIX]{x03BC}\text{m}$
of silicon to connect to the swirler using DRIE, as illustrated in figure 2(c)(iii). Finally, the inlet holes, seen in top view and cross-section of figure 2(c)(iv), were created using the same Ni hardmask process as described for the outlet holes. High-temperature REVALPHA® thermal release tape is placed on the outlet side to prevent helium (He) cooling pressure loss in the plasma etcher once the inlet and outlet holes are connected. The tape is released on a hotplate after the etching is complete and the Ni–Au–Cr is stripped using the same chemicals as described for the outlet etch. The Borofloat on the outlet side is not required for the micro-atomizer to function, but provides addition mechanical strength enabling higher supply pressure tolerance as compared to a device without a Borofloat layer bonded to the outlet side (Dhivyaraja et al.
Reference Dhivyaraja, Gaddes, Panchagnula and Tadigadapa2015).
Additive manufacturing is a material addition process that relies on dropwise deposition of a liquid polymer (Chua, Leong & Lim Reference Chua, Leong and Lim2010). The technology is commonly known as three-dimensional (3D) printing. Initially the design of the atomizers was created using the CAD software, SolidWorks®. The designed model was then converted into a format that can be interpreted by the printer. The printing was accomplished by depositing material layer by layer. Each layer was less than
![]() $100~\unicode[STIX]{x03BC}\text{m}$
in thickness. Poly(methyl methacrylate) (PMMA), commercially available as ViroWhite®, was used for fabricating the
$100~\unicode[STIX]{x03BC}\text{m}$
in thickness. Poly(methyl methacrylate) (PMMA), commercially available as ViroWhite®, was used for fabricating the
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x atomizers. Figure 2(a)(ii–iv) shows photographs of the atomizers fabricated by additive manufacturing technologies. The geometric dimensions of the atomizers used in this study are presented in appendix A. The relative roughness was in all cases less than
$10$
x atomizers. Figure 2(a)(ii–iv) shows photographs of the atomizers fabricated by additive manufacturing technologies. The geometric dimensions of the atomizers used in this study are presented in appendix A. The relative roughness was in all cases less than
![]() $10^{-3}$
. At these values, the boundary layer characteristics are unlikely to be affected by roughness.
$10^{-3}$
. At these values, the boundary layer characteristics are unlikely to be affected by roughness.
3.3 Experimental test set-up and diagnostics

Figure 3. (a) Schematic of the test set-up for liquid delivery (top) and the radial locations where PDI measurements were made (bottom). (b) A plot in
![]() $Re$
–
$Re$
–
![]() $We$
space showing the experimental parametric conditions. The open and closed symbols represent the conditions at which the atomizer produced a fully open conical liquid sheet and a swirling water bell, respectively. The dashed lines indicate the critical
$We$
space showing the experimental parametric conditions. The open and closed symbols represent the conditions at which the atomizer produced a fully open conical liquid sheet and a swirling water bell, respectively. The dashed lines indicate the critical
![]() $Re$
and
$Re$
and
![]() $We$
conditions to achieve a fully open conical liquid sheet.
$We$
conditions to achieve a fully open conical liquid sheet.
A spray test rig capable of delivering the working fluid at a supply pressure up to 30 bar was designed and assembled. A schematic of the rig is shown in figure 3(a). Water was used as the working fluid. The supply pressure to the atomizer was controlled and the mass flow rate is measured. The flow rate was reproducible to within
![]() $\pm 1.5\,\%$
. In addition, the joint drop size and axial velocity distribution as well as volume flux were measured using an Artium® Phase Doppler Interferometer. The PDI system is capable of measuring drop sizes from
$\pm 1.5\,\%$
. In addition, the joint drop size and axial velocity distribution as well as volume flux were measured using an Artium® Phase Doppler Interferometer. The PDI system is capable of measuring drop sizes from
![]() $0.5~\unicode[STIX]{x03BC}\text{m}$
to
$0.5~\unicode[STIX]{x03BC}\text{m}$
to
![]() $1500~\unicode[STIX]{x03BC}\text{m}$
with an estimated accuracy
$1500~\unicode[STIX]{x03BC}\text{m}$
with an estimated accuracy
![]() $\pm 0.5~\unicode[STIX]{x03BC}\text{m}$
and axial velocity from
$\pm 0.5~\unicode[STIX]{x03BC}\text{m}$
and axial velocity from
![]() $-100~\text{m}~\text{s}^{-1}$
to
$-100~\text{m}~\text{s}^{-1}$
to
![]() $200~\text{m}~\text{s}^{-1}$
with estimated accuracy of
$200~\text{m}~\text{s}^{-1}$
with estimated accuracy of
![]() $\pm 0.2\,\%$
. In excess of 10 000 droplets were sampled at each radial location to construct the size–velocity distributions. The drop size measurements were performed at an axial location greater than the breakup length of the liquid sheet, where it was ensured that no ligaments were present. Care was taken to ensure that the PDI phase and drop size validation was always above
$\pm 0.2\,\%$
. In excess of 10 000 droplets were sampled at each radial location to construct the size–velocity distributions. The drop size measurements were performed at an axial location greater than the breakup length of the liquid sheet, where it was ensured that no ligaments were present. Care was taken to ensure that the PDI phase and drop size validation was always above
![]() $95\,\%$
, which implied that most of the drops were inside the measurement range of the instrument. A detailed description of the experimental set-up and test procedure are provided in appendix B.
$95\,\%$
, which implied that most of the drops were inside the measurement range of the instrument. A detailed description of the experimental set-up and test procedure are provided in appendix B.
In order to study the near-nozzle breakup region, high-speed imaging was utilized. A Photron Fastcam® operated at a maximum frame rate of 50 000 frames per second (f.p.s.) was used in the shadowgraphy mode. A synchronized strobe light source and a light sheet diffuser were placed behind the spray to ensure uniform illumination. In addition, a variable focal length lens was used to create a focused image of the spray. The mean cone angle of the spray as well as its fluctuation were calculated from the set of instantaneous spray images (0.1 s of data) obtained from the high-speed video. Finally, the images from the high-speed videos were analysed using POD to study the dynamical characteristics of the spray.
The test conditions examined during this study are depicted graphically in figure 3(b), which is a regime map in
![]() $Re$
–
$Re$
–
![]() $We$
space depicting the experimental conditions (symbols). We define
$We$
space depicting the experimental conditions (symbols). We define
![]() $We=\unicode[STIX]{x1D70C}u_{s}^{2}t_{s}/\unicode[STIX]{x1D70E}$
, where
$We=\unicode[STIX]{x1D70C}u_{s}^{2}t_{s}/\unicode[STIX]{x1D70E}$
, where
![]() $\unicode[STIX]{x1D70C}$
is the liquid density and
$\unicode[STIX]{x1D70C}$
is the liquid density and
![]() $\unicode[STIX]{x1D70E}$
is the surface tension. A spray where a fully open conical liquid sheet was observed at the exit of the atomizer is defined as a ‘good’ spray. The parameter regime where a good spray is observed is shown by the dashed lines in figure 3(b). As can be seen, a critical
$\unicode[STIX]{x1D70E}$
is the surface tension. A spray where a fully open conical liquid sheet was observed at the exit of the atomizer is defined as a ‘good’ spray. The parameter regime where a good spray is observed is shown by the dashed lines in figure 3(b). As can be seen, a critical
![]() $Re\approx 500$
and a critical
$Re\approx 500$
and a critical
![]() $We\approx 50$
are required before a fully open conical liquid sheet is observed. The set of four injectors allows us to systematically study the effect of
$We\approx 50$
are required before a fully open conical liquid sheet is observed. The set of four injectors allows us to systematically study the effect of
![]() $Re$
or
$Re$
or
![]() $We$
independently, while maintaining the other parameters constant.
$We$
independently, while maintaining the other parameters constant.
4 Results
We will classify the results into macroscale and microscale results. Macroscale results will discuss flow rate (
![]() $Q$
) as well as a qualitative description of the near-nozzle breakup structure. Microscale results will comprise radial variation of Sauter mean diameter (
$Q$
) as well as a qualitative description of the near-nozzle breakup structure. Microscale results will comprise radial variation of Sauter mean diameter (
![]() $D_{32}$
), axial velocity (
$D_{32}$
), axial velocity (
![]() $u$
), drop size distributions, drop velocity distributions as well as dynamical frequency (
$u$
), drop size distributions, drop velocity distributions as well as dynamical frequency (
![]() $\unicode[STIX]{x1D6FA}$
) obtained from the POD.
$\unicode[STIX]{x1D6FA}$
) obtained from the POD.
4.1 Macroscale results

Figure 4. (a) Plot of the flow rate
![]() $Q$
(l min
$Q$
(l min
![]() $^{-1}$
) as a function of dimensional supply pressure
$^{-1}$
) as a function of dimensional supply pressure
![]() $\unicode[STIX]{x0394}p$
(bar) for all the atomizers. (b) Plot of dimensionless flow rate
$\unicode[STIX]{x0394}p$
(bar) for all the atomizers. (b) Plot of dimensionless flow rate
![]() $Re$
as a function of dimensionless supply pressure
$Re$
as a function of dimensionless supply pressure
![]() $\overline{\unicode[STIX]{x0394}p}$
. It can be seen that
$\overline{\unicode[STIX]{x0394}p}$
. It can be seen that
![]() $Re\sim \overline{\unicode[STIX]{x0394}p}^{\unicode[STIX]{x1D6FC}}$
with
$Re\sim \overline{\unicode[STIX]{x0394}p}^{\unicode[STIX]{x1D6FC}}$
with
![]() $R^{2}>0.99$
. Here,
$R^{2}>0.99$
. Here,
![]() $\unicode[STIX]{x1D6FC}=0.46\pm 0.009$
with
$\unicode[STIX]{x1D6FC}=0.46\pm 0.009$
with
![]() $99.7\,\%$
confidence. For reference
$99.7\,\%$
confidence. For reference
![]() $Re\sim \sqrt{\overline{\unicode[STIX]{x0394}p}}$
is also plotted. The value
$Re\sim \sqrt{\overline{\unicode[STIX]{x0394}p}}$
is also plotted. The value
![]() $\unicode[STIX]{x1D6FC}=0.46$
is a better estimate than
$\unicode[STIX]{x1D6FC}=0.46$
is a better estimate than
![]() $1/2$
for these data over
$1/2$
for these data over
![]() $Re$
varying by a factor of
$Re$
varying by a factor of
![]() $15$
.
$15$
.
Figure 4(a) shows the variation of volume flow rate (
![]() $Q$
, l min
$Q$
, l min
![]() $^{-1}$
) for all the atomizers at varying supply pressure conditions (
$^{-1}$
) for all the atomizers at varying supply pressure conditions (
![]() $\unicode[STIX]{x0394}p$
, bar). Firstly, it can be observed that the atomizer flow rate increases as the supply pressure increases. In addition, as the atomizer scale increases from
$\unicode[STIX]{x0394}p$
, bar). Firstly, it can be observed that the atomizer flow rate increases as the supply pressure increases. In addition, as the atomizer scale increases from
![]() $1$
x to
$1$
x to
![]() $10$
x, the flow rate at a constant supply pressure also increases. Figure 4(b) shows the data from figure 4(a) plotted in non-dimensional terms as
$10$
x, the flow rate at a constant supply pressure also increases. Figure 4(b) shows the data from figure 4(a) plotted in non-dimensional terms as
![]() $Re$
versus
$Re$
versus
![]() $\overline{\unicode[STIX]{x0394}p}$
, by defining a dimensionless pressure
$\overline{\unicode[STIX]{x0394}p}$
, by defining a dimensionless pressure
![]() $\overline{\unicode[STIX]{x0394}p}=\unicode[STIX]{x0394}p\,D_{o}^{2}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{2}$
and
$\overline{\unicode[STIX]{x0394}p}=\unicode[STIX]{x0394}p\,D_{o}^{2}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{2}$
and
![]() $Re$
is calculated from equation (2.5).
$Re$
is calculated from equation (2.5).
Experiments were carried out on different atomizers operating such that the same dimensionless supply pressure conditions were achieved. As expected, they yield the same dimensionless flow rate (
![]() $Re$
) for all atomizer scales. In addition, the data over dimensionless supply pressures varying over three orders of magnitude collapse onto one power-law curve for all the atomizers. It is no surprise that the Weber number (
$Re$
) for all atomizer scales. In addition, the data over dimensionless supply pressures varying over three orders of magnitude collapse onto one power-law curve for all the atomizers. It is no surprise that the Weber number (
![]() $We$
) plays no role in this scaling process; data corresponding to multiple
$We$
) plays no role in this scaling process; data corresponding to multiple
![]() $We$
at a constant
$We$
at a constant
![]() $Re$
collapse to one point. A Froude number,
$Re$
collapse to one point. A Froude number,
![]() $Fr=u_{s}/\sqrt{gD_{o}}$
, where
$Fr=u_{s}/\sqrt{gD_{o}}$
, where
![]() $g$
is acceleration due to gravity, is calculated for the range of sprays considered. It was observed that
$g$
is acceleration due to gravity, is calculated for the range of sprays considered. It was observed that
![]() $Fr$
ranged from 9 to 307, indicating that the effect of gravitational force on the spray is negligible.
$Fr$
ranged from 9 to 307, indicating that the effect of gravitational force on the spray is negligible.
A best fit of the data was generated using the maximum likelihood estimation technique (Coles Reference Coles2001). As can be seen from figure 4(b), the flow rate data collapse onto one curve for different values of
![]() $\overline{\unicode[STIX]{x0394}p}$
, given by
$\overline{\unicode[STIX]{x0394}p}$
, given by
![]() $Re\sim \overline{\unicode[STIX]{x0394}p}^{\unicode[STIX]{x1D6FC}}$
, where
$Re\sim \overline{\unicode[STIX]{x0394}p}^{\unicode[STIX]{x1D6FC}}$
, where
![]() $\unicode[STIX]{x1D6FC}=0.46\pm 0.009$
. The error bounds on the power-law exponent are
$\unicode[STIX]{x1D6FC}=0.46\pm 0.009$
. The error bounds on the power-law exponent are
![]() $\pm 0.009$
with
$\pm 0.009$
with
![]() $99.7\,\%$
confidence, clearly suggesting that
$99.7\,\%$
confidence, clearly suggesting that
![]() $0.5$
is outside the confidence bounds. Most standard textbooks report that the flow rate of the atomizer varies as the square root of the supply pressure (Lefebvre Reference Lefebvre1989; Bayvel & Orzechowski Reference Bayvel and Orzechowski1993). We would like to suggest that
$0.5$
is outside the confidence bounds. Most standard textbooks report that the flow rate of the atomizer varies as the square root of the supply pressure (Lefebvre Reference Lefebvre1989; Bayvel & Orzechowski Reference Bayvel and Orzechowski1993). We would like to suggest that
![]() $0.46$
is a more accurate exponent to determine the actual flow rate variation in pressure swirl atomizers. The percentage error between the two exponents –
$0.46$
is a more accurate exponent to determine the actual flow rate variation in pressure swirl atomizers. The percentage error between the two exponents –
![]() $0.5$
and
$0.5$
and
![]() $0.46$
– could be significant in many instances. For example, as we attempt to approach the limits of low or high flow rates, such as in the current case, this difference in the exponents could play a major role. Finally, the exponent from figure 4(b) was derived based on measurements over three orders of magnitude variation in the dimensionless pressure. Based on the above discussion, we would also like to suggest that a more accurate definition of a dimensionless flow number (
$0.46$
– could be significant in many instances. For example, as we attempt to approach the limits of low or high flow rates, such as in the current case, this difference in the exponents could play a major role. Finally, the exponent from figure 4(b) was derived based on measurements over three orders of magnitude variation in the dimensionless pressure. Based on the above discussion, we would also like to suggest that a more accurate definition of a dimensionless flow number (
![]() $FN$
) for pressure swirl atomizers is
$FN$
) for pressure swirl atomizers is
![]() $FN=Re/\overline{\unicode[STIX]{x0394}p}^{0.46}$
. It was observed that
$FN=Re/\overline{\unicode[STIX]{x0394}p}^{0.46}$
. It was observed that
![]() $FN=0.067\pm 0.016$
for our design and is independent of the atomizer scale. The pressure drop in the inlet ports was independently calculated using the friction factor approach. From these calculations, it was found that at least 50 % of the pressure drop (typically 80 %) occurred in the swirl chamber, with the remaining pressure drop occurring in the inlet ports. This again confirms that the flow rate is governed more by the air core dynamics than by the viscous losses in the inlet port.
$FN=0.067\pm 0.016$
for our design and is independent of the atomizer scale. The pressure drop in the inlet ports was independently calculated using the friction factor approach. From these calculations, it was found that at least 50 % of the pressure drop (typically 80 %) occurred in the swirl chamber, with the remaining pressure drop occurring in the inlet ports. This again confirms that the flow rate is governed more by the air core dynamics than by the viscous losses in the inlet port.
The physical reason for the deviation of the exponent from
![]() $0.5$
lies in the fact that the ‘square-root law’ was originally derived for flow through an orifice (Lefebvre Reference Lefebvre1989) and is appropriate in instances where the cross-sectional area available to the flow is constant. For example, diesel injectors have been shown to follow such scaling (Payri et al.
Reference Payri, Bermudez, Payri and Salvador2004). In the case of pressure swirl atomizers, the effective cross-sectional area available to the flow is a function of the flow rate. This is due to the presence of an air core at the atomizer exit (Lefebvre Reference Lefebvre1989) and therefore it should not be expected that the flow rate scales as the square root of the supply pressure. Several studies have analysed the effect of
$0.5$
lies in the fact that the ‘square-root law’ was originally derived for flow through an orifice (Lefebvre Reference Lefebvre1989) and is appropriate in instances where the cross-sectional area available to the flow is constant. For example, diesel injectors have been shown to follow such scaling (Payri et al.
Reference Payri, Bermudez, Payri and Salvador2004). In the case of pressure swirl atomizers, the effective cross-sectional area available to the flow is a function of the flow rate. This is due to the presence of an air core at the atomizer exit (Lefebvre Reference Lefebvre1989) and therefore it should not be expected that the flow rate scales as the square root of the supply pressure. Several studies have analysed the effect of
![]() $Re$
on the air core relative diameter. For example, Halder, Dash & Som (Reference Halder, Dash and Som2002), Som (Reference Som2012) and Amini (Reference Amini2016) have observed that the air core relative diameter increases slightly as
$Re$
on the air core relative diameter. For example, Halder, Dash & Som (Reference Halder, Dash and Som2002), Som (Reference Som2012) and Amini (Reference Amini2016) have observed that the air core relative diameter increases slightly as
![]() $Re$
increases. Amini (Reference Amini2016) has reported that
$Re$
increases. Amini (Reference Amini2016) has reported that
![]() $d_{a}/D_{o}\sim Re^{0.1}$
. Owing to this, the effective cross-sectional area available to the liquid is reduced. As a result, the flow rate varies with a power-law exponent less than
$d_{a}/D_{o}\sim Re^{0.1}$
. Owing to this, the effective cross-sectional area available to the liquid is reduced. As a result, the flow rate varies with a power-law exponent less than
![]() $0.5$
.
$0.5$
.

Figure 5. Instantaneous photographs of the spray from different atomizers, all operated at
![]() $Re\approx 1035$
: (a)
$Re\approx 1035$
: (a)
![]() $We=206$
from the
$We=206$
from the
![]() $3$
x, (b)
$3$
x, (b)
![]() $We=122$
from the
$We=122$
from the
![]() $5$
x and (c)
$5$
x and (c)
![]() $We=64$
using the
$We=64$
using the
![]() $10$
x atomizer. Each image shows a scaled area which is
$10$
x atomizer. Each image shows a scaled area which is
![]() $13.5D_{o}\times 27D_{o}$
. The scale bar shown in all images corresponds to 8 mm. The scaled breakup length (in
$13.5D_{o}\times 27D_{o}$
. The scale bar shown in all images corresponds to 8 mm. The scaled breakup length (in
![]() $D_{o}$
units) in all cases is relatively independent of
$D_{o}$
units) in all cases is relatively independent of
![]() $We$
at this value of
$We$
at this value of
![]() $Re$
.
$Re$
.
We next discuss the near-nozzle flow structure in each of the atomizers obtained using high-speed imaging at 10 000 f.p.s. Figure 5(a–c) shows photographs of the near-nozzle breakup structure for the
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x sprays all showing a region
$10$
x sprays all showing a region
![]() $z/D_{o}\times r/D_{o}=13.5\times 27$
. Here
$z/D_{o}\times r/D_{o}=13.5\times 27$
. Here
![]() $r$
and
$r$
and
![]() $z$
are the radial and axial coordinates as shown in figure 3(a). In other words, the field of view in all these images was scaled with
$z$
are the radial and axial coordinates as shown in figure 3(a). In other words, the field of view in all these images was scaled with
![]() $D_{o}$
. All such images were obtained at the constant spray condition,
$D_{o}$
. All such images were obtained at the constant spray condition,
![]() $Re\sim 1035$
, but varying
$Re\sim 1035$
, but varying
![]() $We$
as (
$We$
as (
![]() $206,122,64$
). Firstly, it can be observed that the spray cone angles as well as the breakup lengths for these three sprays are nearly the same and independent of
$206,122,64$
). Firstly, it can be observed that the spray cone angles as well as the breakup lengths for these three sprays are nearly the same and independent of
![]() $We$
. Secondly, it can be observed that the wavelength of the observed waves in figure 5(c) for the
$We$
. Secondly, it can be observed that the wavelength of the observed waves in figure 5(c) for the
![]() $10$
x spray is finer than that observed in figure 5(a,b) for the
$10$
x spray is finer than that observed in figure 5(a,b) for the
![]() $5$
x and
$5$
x and
![]() $3$
x sprays. In conclusion, it can be seen from these images that
$3$
x sprays. In conclusion, it can be seen from these images that
![]() $We$
(again) plays only a minor role in determining the dynamical structure of the liquid sheet. We will revisit these three sprays again when we discuss the unsteady characteristics analysed using POD in § 4.4.
$We$
(again) plays only a minor role in determining the dynamical structure of the liquid sheet. We will revisit these three sprays again when we discuss the unsteady characteristics analysed using POD in § 4.4.
4.2 Microscale results
Drop size and velocity spectra were measured on all sprays using PDI for the different atomizers and at varying
![]() $Re$
and
$Re$
and
![]() $We$
. These measurements were made at various equally spaced radial locations in the midplane of the spray. All measurements were made at a fixed dimensionless downstream location (
$We$
. These measurements were made at various equally spaced radial locations in the midplane of the spray. All measurements were made at a fixed dimensionless downstream location (
![]() $\overline{z}=z/D_{o}=19$
). A schematic showing the measurement locations is shown in figure 3(a). We will begin with a discussion of the liquid-flux-based and number-flux-based global Sauter mean diameter calculated for the different operating conditions and listed in table 1. These values were calculated following the approach proposed by Tratnig & Brenn (Reference Tratnig and Brenn2010). A regression analysis of these data showed that the qualitative variation of
$\overline{z}=z/D_{o}=19$
). A schematic showing the measurement locations is shown in figure 3(a). We will begin with a discussion of the liquid-flux-based and number-flux-based global Sauter mean diameter calculated for the different operating conditions and listed in table 1. These values were calculated following the approach proposed by Tratnig & Brenn (Reference Tratnig and Brenn2010). A regression analysis of these data showed that the qualitative variation of
![]() $D_{32}$
with both
$D_{32}$
with both
![]() $Re$
and
$Re$
and
![]() $We$
follows the previous literature.
$We$
follows the previous literature.
Table 1. Spatially averaged Sauter mean diameter for different flow conditions.

As mentioned before, we are interested in investigating if the spatial structure of mean drop size and velocity distributions in a spray exhibits dynamical similarity. In addition, we are interested in identifying the parameter space where viscous effects inside the injector affect the drop size spectrum in the spray. For this purpose, we define a similarity variable
The above choice of
![]() $\unicode[STIX]{x1D701}$
is motivated by the similarity variable for a round jet
$\unicode[STIX]{x1D701}$
is motivated by the similarity variable for a round jet
![]() $r/z$
, but has been modified for the fact that spray cone angle can vary unlike in a round turbulent jet. Here,
$r/z$
, but has been modified for the fact that spray cone angle can vary unlike in a round turbulent jet. Here,
![]() $\unicode[STIX]{x1D703}_{m}$
is the half cone angle of the spray; and
$\unicode[STIX]{x1D703}_{m}$
is the half cone angle of the spray; and
![]() $z\tan \unicode[STIX]{x1D703}_{m}$
is the radial distance to the edge of the spray, which implies that
$z\tan \unicode[STIX]{x1D703}_{m}$
is the radial distance to the edge of the spray, which implies that
![]() $|\unicode[STIX]{x1D701}|=1$
denotes the spray edge. In effect,
$|\unicode[STIX]{x1D701}|=1$
denotes the spray edge. In effect,
![]() $\unicode[STIX]{x1D701}$
represents the fractional radial distance to the edge of the spray at a given
$\unicode[STIX]{x1D701}$
represents the fractional radial distance to the edge of the spray at a given
![]() $z$
location allowing both positive and negative values to denote the two spray edges visible to the camera.
$z$
location allowing both positive and negative values to denote the two spray edges visible to the camera.

Figure 6. (a) Plot of dimensionless Sauter mean diameter (
![]() $D_{32}/t_{v}$
) versus
$D_{32}/t_{v}$
) versus
![]() $\unicode[STIX]{x1D701}$
with the viscous liquid sheet thickness (
$\unicode[STIX]{x1D701}$
with the viscous liquid sheet thickness (
![]() $t_{v}$
) chosen as the length scale. (b) Plot of dimensionless Sauter mean diameter (
$t_{v}$
) chosen as the length scale. (b) Plot of dimensionless Sauter mean diameter (
![]() $D_{32}/\unicode[STIX]{x1D6FF}_{o}$
) versus
$D_{32}/\unicode[STIX]{x1D6FF}_{o}$
) versus
![]() $\unicode[STIX]{x1D701}$
with the exit boundary layer thickness (
$\unicode[STIX]{x1D701}$
with the exit boundary layer thickness (
![]() $\unicode[STIX]{x1D6FF}_{o}$
) chosen as the length scale. The legend represents the
$\unicode[STIX]{x1D6FF}_{o}$
) chosen as the length scale. The legend represents the
![]() $(Re,We)$
corresponding to each dataset, and the same legend applies to both panels. All data were obtained at
$(Re,We)$
corresponding to each dataset, and the same legend applies to both panels. All data were obtained at
![]() $\overline{z}=19$
. In (a), the profiles for various flow conditions nearly collapse onto a single curve, except for the data corresponding to
$\overline{z}=19$
. In (a), the profiles for various flow conditions nearly collapse onto a single curve, except for the data corresponding to
![]() $(Re,We)$
$(Re,We)$
![]() $=$
(364,76). This shows that the inviscid length scale is not appropriate for
$=$
(364,76). This shows that the inviscid length scale is not appropriate for
![]() $Re\leqslant 1000$
. In (b), all profiles for various flow conditions nearly collapse onto a single curve for
$Re\leqslant 1000$
. In (b), all profiles for various flow conditions nearly collapse onto a single curve for
![]() $|\unicode[STIX]{x1D701}|<1/2$
. It appears that
$|\unicode[STIX]{x1D701}|<1/2$
. It appears that
![]() $\unicode[STIX]{x1D6FF}_{o}$
is a suitable length scale for
$\unicode[STIX]{x1D6FF}_{o}$
is a suitable length scale for
![]() $Re$
.
$Re$
.
Figure 6(a) presents the Sauter mean diameter non-dimensionalized using the viscous length scale (
![]() $t_{v}$
). The corresponding dimensional data are presented in appendix C for completeness. Figure 6(a) presents a plot of
$t_{v}$
). The corresponding dimensional data are presented in appendix C for completeness. Figure 6(a) presents a plot of
![]() $\overline{D_{32}}=D_{32}/t_{v}$
versus
$\overline{D_{32}}=D_{32}/t_{v}$
versus
![]() $\unicode[STIX]{x1D701}$
for all operating conditions considered. It can be seen that the scaled
$\unicode[STIX]{x1D701}$
for all operating conditions considered. It can be seen that the scaled
![]() $\overline{D_{32}}$
data generally collapse onto a single curve over the range of atomizer length scales,
$\overline{D_{32}}$
data generally collapse onto a single curve over the range of atomizer length scales,
![]() $Re$
and
$Re$
and
![]() $We$
considered. This indicates that
$We$
considered. This indicates that
![]() $\overline{D_{32}}$
exhibits self-similar behaviour. Upon closer examination, one can observe that, in the region defined by
$\overline{D_{32}}$
exhibits self-similar behaviour. Upon closer examination, one can observe that, in the region defined by
![]() $|\unicode[STIX]{x1D701}|\leqslant 0.5$
, the data collapse is nearly perfect, except for the data corresponding to the
$|\unicode[STIX]{x1D701}|\leqslant 0.5$
, the data collapse is nearly perfect, except for the data corresponding to the
![]() $1$
x atomizer (which happens to be for a low
$1$
x atomizer (which happens to be for a low
![]() $Re=364$
).
$Re=364$
).
Figure 6(b) is similar to figure 6(a) except that the boundary layer thickness at the nozzle exit (
![]() $\unicode[STIX]{x1D6FF}_{o}$
), as calculated from the Bloor–Ingham theoretical boundary layer analysis, is chosen as the length scale. As can be seen from figure 6(b), the data for the low-
$\unicode[STIX]{x1D6FF}_{o}$
), as calculated from the Bloor–Ingham theoretical boundary layer analysis, is chosen as the length scale. As can be seen from figure 6(b), the data for the low-
![]() $Re$
spray show a much better collapse along with the other high-
$Re$
spray show a much better collapse along with the other high-
![]() $Re$
data. From figure 6(a,b), one can conclude that
$Re$
data. From figure 6(a,b), one can conclude that
![]() $\unicode[STIX]{x1D6FF}_{o}$
is a better choice of length scale if the obligation is to choose a scale that will apply over a wider range of
$\unicode[STIX]{x1D6FF}_{o}$
is a better choice of length scale if the obligation is to choose a scale that will apply over a wider range of
![]() $Re$
.
$Re$
.
In figure 6(a,b), the data do not collapse for
![]() $|\unicode[STIX]{x1D701}|>0.5$
, since this region is approaching the edge of the spray. In this region, there is a dependence of the scaled
$|\unicode[STIX]{x1D701}|>0.5$
, since this region is approaching the edge of the spray. In this region, there is a dependence of the scaled
![]() $\overline{D_{32}}$
with
$\overline{D_{32}}$
with
![]() $Re$
. In other words, a central core region of the spray can be identified where the scaled
$Re$
. In other words, a central core region of the spray can be identified where the scaled
![]() $\overline{D_{32}}$
shows self-similar behaviour following the predictions of Kostoglou (Reference Kostoglou2003) and Rayapati et al. (Reference Rayapati, Bhamidipati, Peddieson and Panchagnula2010). From this observation, one can write a self-similar radial Sauter mean diameter profile for pressure swirl sprays as
$\overline{D_{32}}$
shows self-similar behaviour following the predictions of Kostoglou (Reference Kostoglou2003) and Rayapati et al. (Reference Rayapati, Bhamidipati, Peddieson and Panchagnula2010). From this observation, one can write a self-similar radial Sauter mean diameter profile for pressure swirl sprays as
![]() $D_{32}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D6FF}_{o}h(\unicode[STIX]{x1D701})$
. Here,
$D_{32}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D6FF}_{o}h(\unicode[STIX]{x1D701})$
. Here,
![]() $h(\unicode[STIX]{x1D701})$
is a function that defines the self-similar variation of
$h(\unicode[STIX]{x1D701})$
is a function that defines the self-similar variation of
![]() $\overline{D_{32}}$
as shown in figure 6(b). The number flux and the volume flux information is observed in the region
$\overline{D_{32}}$
as shown in figure 6(b). The number flux and the volume flux information is observed in the region
![]() $|\unicode[STIX]{x1D701}|\leqslant 0.5$
, which is the central region of the spray consisting of a very high number flux of small drops effectively resulting in a low volume flux. This is the region where similarity arguments hold and not in the outer region
$|\unicode[STIX]{x1D701}|\leqslant 0.5$
, which is the central region of the spray consisting of a very high number flux of small drops effectively resulting in a low volume flux. This is the region where similarity arguments hold and not in the outer region
![]() $|\unicode[STIX]{x1D701}|>0.5$
.
$|\unicode[STIX]{x1D701}|>0.5$
.
The self-similarity exhibited by the
![]() $D_{32}/\unicode[STIX]{x1D6FF}_{o}$
profiles in the
$D_{32}/\unicode[STIX]{x1D6FF}_{o}$
profiles in the
![]() $\unicode[STIX]{x1D701}$
coordinate is novel, interesting and deserves discussion. In many ways, a pressure swirl spray appears to be analogous to an annular gas jet, where an inner mixing zone contains a toroidal vortex which is responsible for mass being transported towards the centreline (Ko & Chan Reference Ko and Chan1978). Since pressure swirl sprays are generally hollow-cone, the inward radial droplet transport into the core region is fluid dynamically induced. Therefore, it is reasonable to expect self-similar mean droplet size profiles in this region.
$\unicode[STIX]{x1D701}$
coordinate is novel, interesting and deserves discussion. In many ways, a pressure swirl spray appears to be analogous to an annular gas jet, where an inner mixing zone contains a toroidal vortex which is responsible for mass being transported towards the centreline (Ko & Chan Reference Ko and Chan1978). Since pressure swirl sprays are generally hollow-cone, the inward radial droplet transport into the core region is fluid dynamically induced. Therefore, it is reasonable to expect self-similar mean droplet size profiles in this region.

Figure 7. Plot of number flux and volume flux versus radial location for
![]() $(Re,We)=(1029,122)$
(a) and
$(Re,We)=(1029,122)$
(a) and
![]() $(1057,64)$
(b). The PDI measurements are captured from the centre of the spray to the edge. The number flux will be a maximum in the spray centre where the volume flux is a minimum. This indicates that the core region of the spray consists of a large number of small drops. PDI measurements are performed by traversing up to where the number flux drops to a value less than
$(1057,64)$
(b). The PDI measurements are captured from the centre of the spray to the edge. The number flux will be a maximum in the spray centre where the volume flux is a minimum. This indicates that the core region of the spray consists of a large number of small drops. PDI measurements are performed by traversing up to where the number flux drops to a value less than
![]() $100~\text{s}^{-1}$
.
$100~\text{s}^{-1}$
.
The scaling in figure 6 is most appropriate only for
![]() $|\unicode[STIX]{x1D701}|<1/2$
. Outside this region, it is likely that ballistic motion of large drops will be responsible for breakdown of similarity. This conclusion is also supported by comparing the number flux to volume flux presented in figure 7 for two different operating conditions. Figure 7 shows a plot of number flux (
$|\unicode[STIX]{x1D701}|<1/2$
. Outside this region, it is likely that ballistic motion of large drops will be responsible for breakdown of similarity. This conclusion is also supported by comparing the number flux to volume flux presented in figure 7 for two different operating conditions. Figure 7 shows a plot of number flux (
![]() ${\dot{n}}$
) and volume flux (
${\dot{n}}$
) and volume flux (
![]() $\dot{q}^{\prime \prime }$
) versus
$\dot{q}^{\prime \prime }$
) versus
![]() $r$
for two representative
$r$
for two representative
![]() $Re$
and
$Re$
and
![]() $We$
cases. As can be inferred from figure 7, the core region of the spray where the similarity is most clearly observed consists of large numbers of small droplets. Since the small drops in the spray are likely to show ‘diffusive’ behaviour, it is likely that similarity is observed in this part of the spray. The discussion pertaining to figure 6 suggests that similarity is only restricted to
$We$
cases. As can be inferred from figure 7, the core region of the spray where the similarity is most clearly observed consists of large numbers of small droplets. Since the small drops in the spray are likely to show ‘diffusive’ behaviour, it is likely that similarity is observed in this part of the spray. The discussion pertaining to figure 6 suggests that similarity is only restricted to
![]() $|\unicode[STIX]{x1D701}|<1/2$
. When droplet ballistic motion dominates spray transport, the scaling in (4.1) is likely to break down.
$|\unicode[STIX]{x1D701}|<1/2$
. When droplet ballistic motion dominates spray transport, the scaling in (4.1) is likely to break down.
We will next discuss drop size distributions and their characteristics. As is well known, PDI yields joint drop size–velocity probability density function (p.d.f.) information at one sampling location. Therefore, when one performs several such pointwise measurements in a spray, it is not clear which of the points is representative of the nozzle performance. In contrast, it would be more useful to characterize a global size–velocity p.d.f. as though one were sampling all drops at an entire cross-sectional axial location. Such a p.d.f. would be insensitive to external factors and, more importantly, would be a direct measure of the nozzle performance. In this study, we use the approach suggested by Tratnig & Brenn (Reference Tratnig and Brenn2010) to calculate such a global p.d.f. Assuming symmetry, a given radial location of the probe can be construed to represent half the annular slice of the spray as shown in figure 3(a). Following Tratnig & Brenn (Reference Tratnig and Brenn2010), we calculate a dimensionless global joint particle size–velocity number p.d.f.,
![]() $g(\overline{x},\overline{u})$
, at a given axial location. Here,
$g(\overline{x},\overline{u})$
, at a given axial location. Here,
![]() $\overline{x}$
is a dimensionless particle size and
$\overline{x}$
is a dimensionless particle size and
![]() $\overline{u}$
is a dimensionless axial velocity component given by
$\overline{u}$
is a dimensionless axial velocity component given by
![]() $\overline{u}=u/u_{s}$
;
$\overline{u}=u/u_{s}$
;
![]() $g$
is computed based on the number flux density of drops
$g$
is computed based on the number flux density of drops
![]() ${\dot{n}}(\overline{x},\overline{u};r)$
. In other words,
${\dot{n}}(\overline{x},\overline{u};r)$
. In other words,
![]() ${\dot{n}}(\overline{x},\overline{u};r)\,\text{d}\overline{x}\,\text{d}\overline{u}\,\text{d}t$
is the number of drops of dimensionless size in the range
${\dot{n}}(\overline{x},\overline{u};r)\,\text{d}\overline{x}\,\text{d}\overline{u}\,\text{d}t$
is the number of drops of dimensionless size in the range
![]() $(\overline{x},\overline{x}+\text{d}\overline{x})$
and dimensionless axial velocity magnitude in the range
$(\overline{x},\overline{x}+\text{d}\overline{x})$
and dimensionless axial velocity magnitude in the range
![]() $(\overline{u},\overline{u}+\text{d}\overline{u})$
at a radial location
$(\overline{u},\overline{u}+\text{d}\overline{u})$
at a radial location
![]() $r$
in a time interval (
$r$
in a time interval (
![]() $\text{d}t$
). Mathematically,
$\text{d}t$
). Mathematically,
![]() $g(\overline{x},\overline{u})$
can be computed as
$g(\overline{x},\overline{u})$
can be computed as
 $$\begin{eqnarray}g(\overline{x},\overline{u})=\frac{\displaystyle \int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u};r)2\unicode[STIX]{x03C0}r\,\text{d}r}{\displaystyle \int _{0}^{\infty }\int _{-\infty }^{\infty }\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u};r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}\,\text{d}\overline{x}}.\end{eqnarray}$$
$$\begin{eqnarray}g(\overline{x},\overline{u})=\frac{\displaystyle \int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u};r)2\unicode[STIX]{x03C0}r\,\text{d}r}{\displaystyle \int _{0}^{\infty }\int _{-\infty }^{\infty }\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u};r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}\,\text{d}\overline{x}}.\end{eqnarray}$$
The global p.d.f. presented in equation (4.2) is a number-flux-based reconstruction from pointwise PDI data. An analogous volume-flux-based reconstruction can also be invoked. These p.d.f.s describe the joint drop size and velocity spectrum at a given axial location. This p.d.f. would change from one given axial location to another only if significant drop coalescence or secondary atomization were present. In other words, mere rearrangement of drops between radial or azimuthal locations in the spray would not alter
![]() $g(\overline{x},\overline{u})$
. The limits of numerical integration were chosen such that at least
$g(\overline{x},\overline{u})$
. The limits of numerical integration were chosen such that at least
![]() $99.99\,\%$
of the drops were included in the p.d.f. computation. In addition, as can be seen from figure 7,
$99.99\,\%$
of the drops were included in the p.d.f. computation. In addition, as can be seen from figure 7,
![]() ${\dot{n}}$
(as well as
${\dot{n}}$
(as well as
![]() $\dot{q}^{\prime \prime }$
) decreases exponentially as a function of radial location. Since
$\dot{q}^{\prime \prime }$
) decreases exponentially as a function of radial location. Since
![]() ${\dot{n}}\sim \text{e}^{-r}$
, the integral in (4.2) which is weighted by
${\dot{n}}\sim \text{e}^{-r}$
, the integral in (4.2) which is weighted by
![]() ${\dot{n}}r$
converges rapidly. From the measurement process, we have ensured that the global p.d.f.s contain at least 99.99 % of the droplets in the spray both by number and by volume. Finally, the outermost radial location for each
${\dot{n}}r$
converges rapidly. From the measurement process, we have ensured that the global p.d.f.s contain at least 99.99 % of the droplets in the spray both by number and by volume. Finally, the outermost radial location for each
![]() $(Re,We)$
pair was chosen such that at least 99.99 % of the drops were sampled in each case.
$(Re,We)$
pair was chosen such that at least 99.99 % of the drops were sampled in each case.
The marginal p.d.f.s of the joint size–velocity p.d.f. in each of the dimensionless coordinates (size,
![]() $\overline{x}$
, and axial velocity,
$\overline{x}$
, and axial velocity,
![]() $\overline{u}$
) are given by
$\overline{u}$
) are given by
![]() ${\mathcal{X}}(\overline{x})$
and
${\mathcal{X}}(\overline{x})$
and
![]() ${\mathcal{U}}(\overline{u})$
, respectively. These p.d.f.s can be obtained from (4.2) as
${\mathcal{U}}(\overline{u})$
, respectively. These p.d.f.s can be obtained from (4.2) as
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{X}}_{s}(\overline{x})=\frac{\displaystyle \int _{-\infty }^{\overline{u}_{s}}\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}}{\displaystyle \int _{0}^{\infty }\int _{-\infty }^{\overline{u}_{s}}\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}\,\text{d}\overline{x}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{X}}_{s}(\overline{x})=\frac{\displaystyle \int _{-\infty }^{\overline{u}_{s}}\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}}{\displaystyle \int _{0}^{\infty }\int _{-\infty }^{\overline{u}_{s}}\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}\,\text{d}\overline{x}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{X}}_{m}(\overline{x})=\frac{\displaystyle \int _{\overline{u}_{s}}^{\overline{u}_{m}}\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}}{\displaystyle \int _{0}^{\infty }\int _{\overline{u}_{s}}^{\overline{u}_{m}}\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}\,\text{d}\overline{x}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{X}}_{m}(\overline{x})=\frac{\displaystyle \int _{\overline{u}_{s}}^{\overline{u}_{m}}\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}}{\displaystyle \int _{0}^{\infty }\int _{\overline{u}_{s}}^{\overline{u}_{m}}\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}\,\text{d}\overline{x}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{X}}_{f}(\overline{x})=\frac{\displaystyle \int _{\overline{u}_{m}}^{\infty }\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}}{\displaystyle \int _{0}^{\infty }\int _{\overline{u}_{m}}^{\infty }\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}\,\text{d}\overline{x}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{X}}_{f}(\overline{x})=\frac{\displaystyle \int _{\overline{u}_{m}}^{\infty }\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}}{\displaystyle \int _{0}^{\infty }\int _{\overline{u}_{m}}^{\infty }\int _{0}^{\infty }{\dot{n}}(\overline{x},\overline{u},r)2\unicode[STIX]{x03C0}r\,\text{d}r\,\text{d}\overline{u}\,\text{d}\overline{x}}. & \displaystyle\end{eqnarray}$$

Figure 8. Plot of the scaled global p.d.f. of (a) drop size (
![]() $x$
) scaled by viscous length scale
$x$
) scaled by viscous length scale
![]() $(t_{v})$
based on (2.6), (b) drop size (
$(t_{v})$
based on (2.6), (b) drop size (
![]() $x$
) scaled by boundary layer thickness
$x$
) scaled by boundary layer thickness
![]() $(\unicode[STIX]{x1D6FF}_{o})$
calculated analytically from Bloor–Ingham analysis for each
$(\unicode[STIX]{x1D6FF}_{o})$
calculated analytically from Bloor–Ingham analysis for each
![]() $(Re,We)$
and (c) drop size (
$(Re,We)$
and (c) drop size (
![]() $x$
) scaled by
$x$
) scaled by
![]() $D_{32}$
calculated for each p.d.f. The legend, which is the same for all panels, shows
$D_{32}$
calculated for each p.d.f. The legend, which is the same for all panels, shows
![]() $(Re,We)$
for each dataset. The scaled drop size p.d.f. based on the boundary layer thickness as well as
$(Re,We)$
for each dataset. The scaled drop size p.d.f. based on the boundary layer thickness as well as
![]() $D_{32}$
show a universal behaviour especially for
$D_{32}$
show a universal behaviour especially for
![]() $x/\unicode[STIX]{x1D6FF}_{o}$
and
$x/\unicode[STIX]{x1D6FF}_{o}$
and
![]() $x/D_{32}>1$
.
$x/D_{32}>1$
.
In order to compare drop size p.d.f.s from different atomizers, we define an appropriately non-dimensionalized
![]() $\overline{x}$
. Figure 8(a) is a plot of the scaled global drop size p.d.f.,
$\overline{x}$
. Figure 8(a) is a plot of the scaled global drop size p.d.f.,
![]() ${\mathcal{X}}(\overline{x})$
, versus
${\mathcal{X}}(\overline{x})$
, versus
![]() $\overline{x}$
with
$\overline{x}$
with
![]() $t_{v}$
(the viscous liquid sheet thickness) chosen as the length scale for non-dimensionalization (
$t_{v}$
(the viscous liquid sheet thickness) chosen as the length scale for non-dimensionalization (
![]() $\overline{x}=x/t_{v}$
). The scaled drop size distribution for the
$\overline{x}=x/t_{v}$
). The scaled drop size distribution for the
![]() $1$
x spray indicates coarser atomization (in relation to
$1$
x spray indicates coarser atomization (in relation to
![]() $t_{v}$
), even though the absolute p.d.f. (in
$t_{v}$
), even though the absolute p.d.f. (in
![]() $\unicode[STIX]{x03BC}\text{m}$
) indicated a finely atomized spray (see appendix C for details). As can be observed from figure 8(a), the p.d.f.s for
$\unicode[STIX]{x03BC}\text{m}$
) indicated a finely atomized spray (see appendix C for details). As can be observed from figure 8(a), the p.d.f.s for
![]() $Re>1000$
show good collapse and the data for low
$Re>1000$
show good collapse and the data for low
![]() $Re$
show improvement especially for
$Re$
show improvement especially for
![]() $x/t_{v}>0.5$
. Again for
$x/t_{v}>0.5$
. Again for
![]() $x/t_{v}<0.2$
, the p.d.f.s show
$x/t_{v}<0.2$
, the p.d.f.s show
![]() $Re$
dependence. This indicates that viscous effects cannot be ignored at low
$Re$
dependence. This indicates that viscous effects cannot be ignored at low
![]() $Re$
.
$Re$
.
Figure 8(b) is again a plot of the same p.d.f.,
![]() ${\mathcal{X}}(\overline{x})$
versus
${\mathcal{X}}(\overline{x})$
versus
![]() $\overline{x}$
, but with a different length scale for non-dimensionalization. Here,
$\overline{x}$
, but with a different length scale for non-dimensionalization. Here,
![]() $\unicode[STIX]{x1D6FF}_{o}$
is calculated analytically from the Bloor–Ingham analysis and chosen as the length scale. Consequently,
$\unicode[STIX]{x1D6FF}_{o}$
is calculated analytically from the Bloor–Ingham analysis and chosen as the length scale. Consequently,
![]() $\overline{x}=x/\unicode[STIX]{x1D6FF}_{o}$
. As can be observed from this figure, the p.d.f.s for all
$\overline{x}=x/\unicode[STIX]{x1D6FF}_{o}$
. As can be observed from this figure, the p.d.f.s for all
![]() $Re$
, including the low-
$Re$
, including the low-
![]() $Re$
spray, collapse onto a single curve for
$Re$
spray, collapse onto a single curve for
![]() $x/\unicode[STIX]{x1D6FF}_{o}>1$
. For
$x/\unicode[STIX]{x1D6FF}_{o}>1$
. For
![]() $x/\unicode[STIX]{x1D6FF}_{o}<1$
, the p.d.f.s show
$x/\unicode[STIX]{x1D6FF}_{o}<1$
, the p.d.f.s show
![]() $Re$
dependence, where smaller drops are increasingly probable for larger
$Re$
dependence, where smaller drops are increasingly probable for larger
![]() $Re$
. This implies that drops in the spray smaller than the boundary layer thickness (
$Re$
. This implies that drops in the spray smaller than the boundary layer thickness (
![]() $\unicode[STIX]{x1D6FF}_{o}$
) are formed from a different physical process, such as secondary breakup, and hence do not collapse with
$\unicode[STIX]{x1D6FF}_{o}$
) are formed from a different physical process, such as secondary breakup, and hence do not collapse with
![]() $\unicode[STIX]{x1D6FF}_{o}$
as the length scale. Therefore, we would like to suggest that models of drop size distribution should take this difference in physics into account by invoking two piecewise models, one each for
$\unicode[STIX]{x1D6FF}_{o}$
as the length scale. Therefore, we would like to suggest that models of drop size distribution should take this difference in physics into account by invoking two piecewise models, one each for
![]() $x/\unicode[STIX]{x1D6FF}_{o}>1$
and
$x/\unicode[STIX]{x1D6FF}_{o}>1$
and
![]() $x/\unicode[STIX]{x1D6FF}_{o}<1$
. To the best of our knowledge, this is the first report where experimentally measured mean drop size as well as drop size p.d.f.s have both been shown to be dynamically similar and to exhibit universal scaling. Figure 8(c) is a plot of the p.d.f. of
$x/\unicode[STIX]{x1D6FF}_{o}<1$
. To the best of our knowledge, this is the first report where experimentally measured mean drop size as well as drop size p.d.f.s have both been shown to be dynamically similar and to exhibit universal scaling. Figure 8(c) is a plot of the p.d.f. of
![]() $x/D_{32}$
. Interestingly, again, one can observe behaviour similar to that in figure 8(b).
$x/D_{32}$
. Interestingly, again, one can observe behaviour similar to that in figure 8(b).
It may be recalled that
![]() ${\mathcal{X}}(\overline{x})$
is the global drop size p.d.f. at an axial location
${\mathcal{X}}(\overline{x})$
is the global drop size p.d.f. at an axial location
![]() $z/D_{o}=19$
. If secondary atomization and coalescence are insignificant after this axial location, this drop size p.d.f. is likely to remain unchanged as a function of axial distance. Therefore, the universality of the collapse shown in figure 8(b,c) is even more profound in that a distribution constructed from these experimental data represents a universal representation of the drop size p.d.f. in a pressure swirl spray, which is insensitive to both
$z/D_{o}=19$
. If secondary atomization and coalescence are insignificant after this axial location, this drop size p.d.f. is likely to remain unchanged as a function of axial distance. Therefore, the universality of the collapse shown in figure 8(b,c) is even more profound in that a distribution constructed from these experimental data represents a universal representation of the drop size p.d.f. in a pressure swirl spray, which is insensitive to both
![]() $Re$
and axial location. We refrain from suggesting a particular mathematical form of this distribution, as that discussion will distract the reader from our primary emphasis of showing universality. In conclusion, we would like to argue that
$Re$
and axial location. We refrain from suggesting a particular mathematical form of this distribution, as that discussion will distract the reader from our primary emphasis of showing universality. In conclusion, we would like to argue that
![]() $\unicode[STIX]{x1D6FF}_{o}$
, the boundary layer thickness at the nozzle exit, plays a key role in determining the liquid sheet thickness and therefore the global drop size spectrum in a spray. It is gratifying to see that p.d.f.s of
$\unicode[STIX]{x1D6FF}_{o}$
, the boundary layer thickness at the nozzle exit, plays a key role in determining the liquid sheet thickness and therefore the global drop size spectrum in a spray. It is gratifying to see that p.d.f.s of
![]() $x/D_{32}$
also show self-similarity, but p.d.f.s of
$x/D_{32}$
also show self-similarity, but p.d.f.s of
![]() $x/\unicode[STIX]{x1D6FF}_{o}$
(with
$x/\unicode[STIX]{x1D6FF}_{o}$
(with
![]() $\unicode[STIX]{x1D6FF}_{o}$
calculated analytically) showing similarity offers a route to predict the p.d.f. from first principles.
$\unicode[STIX]{x1D6FF}_{o}$
calculated analytically) showing similarity offers a route to predict the p.d.f. from first principles.
The length scale choice, as has been discussed before, can be either a sheet thickness or a boundary layer thickness. The sheet thickness, in turn, can be calculated purely based on the atomizer’s geometrical parameters which does not include the effect of viscosity or can be calculated after including the effect of viscosity. For low
![]() $Re$
values, the sheet thickness is influenced by viscosity. In other words, the sheet thickness is greater due to the viscous boundary layer and hence results in lower mean axial velocity of the liquid sheet. In addition, at low
$Re$
values, the sheet thickness is influenced by viscosity. In other words, the sheet thickness is greater due to the viscous boundary layer and hence results in lower mean axial velocity of the liquid sheet. In addition, at low
![]() $Re$
, the effect of viscosity delays the breakup process. It has been argued by Lefebvre & Suyari (Reference Lefebvre and Suyari1986) that for
$Re$
, the effect of viscosity delays the breakup process. It has been argued by Lefebvre & Suyari (Reference Lefebvre and Suyari1986) that for
![]() $Re>1000$
(in our nomenclature), the experimental sheet thickness is likely to be close to the inviscid sheet thickness. The critical value of
$Re>1000$
(in our nomenclature), the experimental sheet thickness is likely to be close to the inviscid sheet thickness. The critical value of
![]() $Re$
, identified from our experiments, agrees with this prediction of Lefebvre & Suyari (Reference Lefebvre and Suyari1986). We find that the probability of finding smaller drops appears to be sensitive to
$Re$
, identified from our experiments, agrees with this prediction of Lefebvre & Suyari (Reference Lefebvre and Suyari1986). We find that the probability of finding smaller drops appears to be sensitive to
![]() $Re$
and
$Re$
and
![]() $We$
. In other words,
$We$
. In other words,
![]() $\unicode[STIX]{x1D6FF}_{0}$
appears to provide a distinguishing scale that can, in fact, be used to define ‘large’ and ‘small’ drops from the point of view of universality of the p.d.f.
$\unicode[STIX]{x1D6FF}_{0}$
appears to provide a distinguishing scale that can, in fact, be used to define ‘large’ and ‘small’ drops from the point of view of universality of the p.d.f.

Figure 9. (a) Plot of scaled mean velocity,
![]() $\overline{u}=u/u_{v}$
, versus
$\overline{u}=u/u_{v}$
, versus
![]() $\unicode[STIX]{x1D701}$
. The data show universal scaling especially for
$\unicode[STIX]{x1D701}$
. The data show universal scaling especially for
![]() $|\unicode[STIX]{x1D701}|<1/2$
. (b) Plot of the global scaled drop velocity p.d.f. The drops are divided into three quartiles denoted by
$|\unicode[STIX]{x1D701}|<1/2$
. (b) Plot of the global scaled drop velocity p.d.f. The drops are divided into three quartiles denoted by
![]() $S$
,
$S$
,
![]() $M$
and
$M$
and
![]() $F$
indicating slow-, medium- and fast-moving drops. (c) Plot of scaled volume flux
$F$
indicating slow-, medium- and fast-moving drops. (c) Plot of scaled volume flux
![]() $\dot{q}^{\prime \prime }/u_{v}$
versus
$\dot{q}^{\prime \prime }/u_{v}$
versus
![]() $\unicode[STIX]{x1D701}$
. Inset in (c) shows the same data plotted in log scale. The legend shows
$\unicode[STIX]{x1D701}$
. Inset in (c) shows the same data plotted in log scale. The legend shows
![]() $(Re,We)$
for each dataset, and is the same for all panels. The p.d.f. in (b) exhibits an asymmetry towards slower-moving drops. Also, the data collapse around a universal p.d.f., especially for
$(Re,We)$
for each dataset, and is the same for all panels. The p.d.f. in (b) exhibits an asymmetry towards slower-moving drops. Also, the data collapse around a universal p.d.f., especially for
![]() $\overline{u}<1$
.
$\overline{u}<1$
.
We will next discuss the behaviour of the drop velocity spectra. Figure 9(a) is a plot of the dimensionless mean axial velocity
![]() $\overline{u}$
versus
$\overline{u}$
versus
![]() $\unicode[STIX]{x1D701}$
. Here,
$\unicode[STIX]{x1D701}$
. Here,
![]() $\overline{u}=u/u_{v}$
. This choice stems from the expectation that the droplet axial velocity
$\overline{u}=u/u_{v}$
. This choice stems from the expectation that the droplet axial velocity
![]() $u$
scales with
$u$
scales with
![]() $u_{v}=Q/\unicode[STIX]{x03C0}D_{o}t_{v}$
, which is a velocity scale associated with the viscous liquid sheet effusing from the nozzle. Figure 9(a) contains data from several atomizers and for multiple values of
$u_{v}=Q/\unicode[STIX]{x03C0}D_{o}t_{v}$
, which is a velocity scale associated with the viscous liquid sheet effusing from the nozzle. Figure 9(a) contains data from several atomizers and for multiple values of
![]() $Re$
. As can be observed from figure 9(a), the data appear to show dynamical similarity. In addition, it can be observed that the scaled axial velocity shows a central core (
$Re$
. As can be observed from figure 9(a), the data appear to show dynamical similarity. In addition, it can be observed that the scaled axial velocity shows a central core (
![]() $|\unicode[STIX]{x1D701}|<1/2$
) that is moving slower than the drops near the edge. From the above, we can conclude that
$|\unicode[STIX]{x1D701}|<1/2$
) that is moving slower than the drops near the edge. From the above, we can conclude that
![]() $\overline{u}$
is generally a function of
$\overline{u}$
is generally a function of
![]() $\unicode[STIX]{x1D701}$
. As can be seen in figure 9(a), the droplet mean velocity is maximum near the edge of the spray (
$\unicode[STIX]{x1D701}$
. As can be seen in figure 9(a), the droplet mean velocity is maximum near the edge of the spray (
![]() $|\unicode[STIX]{x1D701}|=1$
) and minimum near
$|\unicode[STIX]{x1D701}|=1$
) and minimum near
![]() $\unicode[STIX]{x1D701}=0$
, indicating hollow cone behaviour. On a related note, effervescent sprays as well as many other sprays have been shown to exhibit self-similar mean velocity profiles (Panchagnula & Sojka Reference Panchagnula and Sojka1999; De Vega, Rodríguez & Lecuoa Reference De Vega, Rodríguez and Lecuoa2000).
$\unicode[STIX]{x1D701}=0$
, indicating hollow cone behaviour. On a related note, effervescent sprays as well as many other sprays have been shown to exhibit self-similar mean velocity profiles (Panchagnula & Sojka Reference Panchagnula and Sojka1999; De Vega, Rodríguez & Lecuoa Reference De Vega, Rodríguez and Lecuoa2000).
Velocity profile similarity has been discussed in the context of single-phase jets, which (in that case) implies both flux and advection velocity similarity. However, in the case of sprays, dispersed phase flux is different from drop velocity owing to spatially varying volume fraction. In order to demonstrate flux scaling, figure 9(c) is presented. Figure 9(c) is a plot of the dimensionless mean volume flux
![]() $\dot{q}^{\prime \prime }/u_{v}$
versus
$\dot{q}^{\prime \prime }/u_{v}$
versus
![]() $\unicode[STIX]{x1D701}$
. Here
$\unicode[STIX]{x1D701}$
. Here
![]() $\dot{q}^{\prime \prime }$
(
$\dot{q}^{\prime \prime }$
(
![]() $\text{cm}^{3}~\text{cm}^{-2}~\text{s}^{-1}$
) is the mean liquid volume flux. As can be seen from this figure, the data show reasonable similarity scaling especially for
$\text{cm}^{3}~\text{cm}^{-2}~\text{s}^{-1}$
) is the mean liquid volume flux. As can be seen from this figure, the data show reasonable similarity scaling especially for
![]() $|\unicode[STIX]{x1D701}|<1/2$
given that PDI flux measurements are known to be noisy. The scaling is not as clean as in a gas jet. In addition, the data do not scale for
$|\unicode[STIX]{x1D701}|<1/2$
given that PDI flux measurements are known to be noisy. The scaling is not as clean as in a gas jet. In addition, the data do not scale for
![]() $|\unicode[STIX]{x1D701}|>1/2$
owing to the fact that this region could involve large drops exhibiting ballistic motion. The scaling is most appropriate when studying the inner core region and liquid flux distribution is a better parameter to demonstrate similarity. The dimensional mean volume flux versus radial location information is added in appendix C.
$|\unicode[STIX]{x1D701}|>1/2$
owing to the fact that this region could involve large drops exhibiting ballistic motion. The scaling is most appropriate when studying the inner core region and liquid flux distribution is a better parameter to demonstrate similarity. The dimensional mean volume flux versus radial location information is added in appendix C.
The continuous phase motion in the central core region is in fact induced by the droplet motion at
![]() $|\unicode[STIX]{x1D701}|=1$
. In that sense, the central core region of a pressure swirl spray is conceptually similar to a wake. Most of the droplets at source are injected into a region near
$|\unicode[STIX]{x1D701}|=1$
. In that sense, the central core region of a pressure swirl spray is conceptually similar to a wake. Most of the droplets at source are injected into a region near
![]() $|\unicode[STIX]{x1D701}|=1$
. The droplets are then transported into the core region (
$|\unicode[STIX]{x1D701}|=1$
. The droplets are then transported into the core region (
![]() $|\unicode[STIX]{x1D701}|<1/2$
) by the continuous phase. The variation of the mean droplet size in this central core region is therefore governed by an ‘advection–diffusion’ process, where the particle diffusivity has a size dependence (Kostoglou Reference Kostoglou2003). In the absence of particle inertia, it is expected that such a random walk process could be responsible for droplet transport. This could be a reason for the self-similarity exhibited by
$|\unicode[STIX]{x1D701}|<1/2$
) by the continuous phase. The variation of the mean droplet size in this central core region is therefore governed by an ‘advection–diffusion’ process, where the particle diffusivity has a size dependence (Kostoglou Reference Kostoglou2003). In the absence of particle inertia, it is expected that such a random walk process could be responsible for droplet transport. This could be a reason for the self-similarity exhibited by
![]() $\overline{D_{32}}$
and drop size p.d.f. discussed in the context of figure 6.
$\overline{D_{32}}$
and drop size p.d.f. discussed in the context of figure 6.
Figure 9(b) presents a plot of the scaled axial velocity p.d.f.,
![]() ${\mathcal{U}}(\overline{u})$
, for the different cases considered. As can be seen from this figure, all the data (including the data from the
${\mathcal{U}}(\overline{u})$
, for the different cases considered. As can be seen from this figure, all the data (including the data from the
![]() $1$
x spray) collapse onto a single curve for
$1$
x spray) collapse onto a single curve for
![]() $\overline{u}<1$
. Secondly, the velocity p.d.f. curves exhibit significant non-Gaussian behaviour in the form of skewness towards slower velocities. The various datasets appear to show differences for
$\overline{u}<1$
. Secondly, the velocity p.d.f. curves exhibit significant non-Gaussian behaviour in the form of skewness towards slower velocities. The various datasets appear to show differences for
![]() $\overline{u}>1$
. This implies that drops moving slower than the parent liquid sheet exhibit a scaling independent of
$\overline{u}>1$
. This implies that drops moving slower than the parent liquid sheet exhibit a scaling independent of
![]() $Re$
and
$Re$
and
![]() $We$
. However, for drops whose axial velocity is greater than the liquid sheet velocity, i.e. for
$We$
. However, for drops whose axial velocity is greater than the liquid sheet velocity, i.e. for
![]() $u/u_{v}>1$
, remnant effects of both
$u/u_{v}>1$
, remnant effects of both
![]() $Re$
and
$Re$
and
![]() $We$
persist in the p.d.f. This, again, implies that the physical mechanism that created drops which move faster than the parent liquid sheet (in spite of drag forces which attempt to slow these drops) is different. This implies, again, that two piecewise models of the p.d.f. are required – one for
$We$
persist in the p.d.f. This, again, implies that the physical mechanism that created drops which move faster than the parent liquid sheet (in spite of drag forces which attempt to slow these drops) is different. This implies, again, that two piecewise models of the p.d.f. are required – one for
![]() $u/u_{v}<1$
and second for
$u/u_{v}<1$
and second for
![]() $u/u_{v}>1$
. The differences in the drop size p.d.f. curves in figure 8(a) for
$u/u_{v}>1$
. The differences in the drop size p.d.f. curves in figure 8(a) for
![]() $x/t_{v}>1$
are related to the differences in the velocity p.d.f. curves in figure 9(b), since large drops are typically moving faster. The fact that both drop size and velocity marginal p.d.f.s shown in figures 8(b) and 9(b) collapse onto a universal curve points to a conclusion that dynamical similarity in sprays can be extended to model even microscale characteristics, if appropriate scales are chosen.
$x/t_{v}>1$
are related to the differences in the velocity p.d.f. curves in figure 9(b), since large drops are typically moving faster. The fact that both drop size and velocity marginal p.d.f.s shown in figures 8(b) and 9(b) collapse onto a universal curve points to a conclusion that dynamical similarity in sprays can be extended to model even microscale characteristics, if appropriate scales are chosen.

Figure 10. Plots of scaled global drop size p.d.f. conditioned on velocity. The legend shows
![]() $(Re,We)$
for each dataset, and is the same for all panels. Panels (a), (b) and (c) show plots with boundary layer thickness
$(Re,We)$
for each dataset, and is the same for all panels. Panels (a), (b) and (c) show plots with boundary layer thickness
![]() $\unicode[STIX]{x1D6FF}_{o}$
chosen as the length scale and represent slow-, medium- and fast-moving drops, respectively. The p.d.f. for the faster[moving drops in (c) exhibits universal behaviour independent of the values of
$\unicode[STIX]{x1D6FF}_{o}$
chosen as the length scale and represent slow-, medium- and fast-moving drops, respectively. The p.d.f. for the faster[moving drops in (c) exhibits universal behaviour independent of the values of
![]() $(Re,We)$
.
$(Re,We)$
.
As mentioned before,
![]() $g(\overline{x},\overline{u})$
is a joint size–velocity p.d.f. that contains information about the size–velocity correlation. In order to analyse the magnitude of this correlation, we plot a drop size p.d.f. conditioned on velocity, which was earlier defined in equation (4.4). Figure 10(a–c) shows plots of
$g(\overline{x},\overline{u})$
is a joint size–velocity p.d.f. that contains information about the size–velocity correlation. In order to analyse the magnitude of this correlation, we plot a drop size p.d.f. conditioned on velocity, which was earlier defined in equation (4.4). Figure 10(a–c) shows plots of
![]() ${\mathcal{X}}_{s}(\overline{x})$
,
${\mathcal{X}}_{s}(\overline{x})$
,
![]() ${\mathcal{X}}_{m}(\overline{x})$
and
${\mathcal{X}}_{m}(\overline{x})$
and
![]() ${\mathcal{X}}_{f}(\overline{x})$
, respectively, with
${\mathcal{X}}_{f}(\overline{x})$
, respectively, with
![]() $\unicode[STIX]{x1D6FF}_{o}$
chosen as the length scale for non-dimensionalization (
$\unicode[STIX]{x1D6FF}_{o}$
chosen as the length scale for non-dimensionalization (
![]() $\overline{x}=x/\unicode[STIX]{x1D6FF}_{o}$
).
$\overline{x}=x/\unicode[STIX]{x1D6FF}_{o}$
).
As can be seen from these figures, the data for even the low-
![]() $Re$
,
$Re$
,
![]() $1$
x spray also collapse onto the other data for high
$1$
x spray also collapse onto the other data for high
![]() $Re$
, especially for
$Re$
, especially for
![]() $x/\unicode[STIX]{x1D6FF}_{o}>1$
. In other words, drops larger than the boundary layer thickness exhibit similarity with increase in
$x/\unicode[STIX]{x1D6FF}_{o}>1$
. In other words, drops larger than the boundary layer thickness exhibit similarity with increase in
![]() $Re$
. However, minor differences are observable for all the p.d.f.s, especially for
$Re$
. However, minor differences are observable for all the p.d.f.s, especially for
![]() $x/\unicode[STIX]{x1D6FF}_{o}<1$
and in the case of slow-moving drops,
$x/\unicode[STIX]{x1D6FF}_{o}<1$
and in the case of slow-moving drops,
![]() ${\mathcal{X}}_{s}(\overline{x})$
shown in figure 10(a). On the other hand, the collapse is nearly perfect for the fast-moving drops,
${\mathcal{X}}_{s}(\overline{x})$
shown in figure 10(a). On the other hand, the collapse is nearly perfect for the fast-moving drops,
![]() ${\mathcal{X}}_{f}(\overline{x})$
in figure 10(c). For
${\mathcal{X}}_{f}(\overline{x})$
in figure 10(c). For
![]() $x/\unicode[STIX]{x1D6FF}_{o}<1$
, i.e. drops smaller than the boundary layer thickness, the physical mechanism causing their formation, and hence the scaling with
$x/\unicode[STIX]{x1D6FF}_{o}<1$
, i.e. drops smaller than the boundary layer thickness, the physical mechanism causing their formation, and hence the scaling with
![]() $Re$
, could be different. This adds another hitherto unknown dimension to the literature on dynamical similarity in sprays, in that conditional p.d.f.s of drop size also exhibit universal behaviour over a wide range of
$Re$
, could be different. This adds another hitherto unknown dimension to the literature on dynamical similarity in sprays, in that conditional p.d.f.s of drop size also exhibit universal behaviour over a wide range of
![]() $Re$
, if the drop size is scaled by
$Re$
, if the drop size is scaled by
![]() $\unicode[STIX]{x1D6FF}_{o}$
and velocity by
$\unicode[STIX]{x1D6FF}_{o}$
and velocity by
![]() $u_{s}$
. The universal collapse is most (least) evident from the conditional p.d.f. of the fastest (slowest) quartile of drops in figure 10(a,c). This further corroborates the residual
$u_{s}$
. The universal collapse is most (least) evident from the conditional p.d.f. of the fastest (slowest) quartile of drops in figure 10(a,c). This further corroborates the residual
![]() $Re$
and
$Re$
and
![]() $We$
effect observed for the smaller drops (which are also the slowest) in figure 8(c).
$We$
effect observed for the smaller drops (which are also the slowest) in figure 8(c).
We have calculated the distribution of Stokes number
![]() $(Stk)$
in the spray for each condition as an alternative means of classifying drops based on their response time. It was observed that
$(Stk)$
in the spray for each condition as an alternative means of classifying drops based on their response time. It was observed that
![]() $Stk\ll 1$
in all cases. The reason for this fact lies in the physics that the air flow in these sprays is induced by diffusion of liquid momentum to a less dense phase and therefore the two phases are more or less in equilibrium. In contrast, air-blast sprays are fundamentally different. The near-nozzle flow structures such as breakup length, liquid film thickness and sheet frequency have been investigated by Déjean, Berthoumieu & Gajan (Reference Déjean, Berthoumieu and Gajan2016a
,Reference Déjean, Berthoumieu and Gajan
b
) in the context of planar air-blast sprays. In contrast to the present study, local droplet Stokes number could play a significant role in such air-blast sprays where the drops and air are not necessarily in local equilibrium.
$Stk\ll 1$
in all cases. The reason for this fact lies in the physics that the air flow in these sprays is induced by diffusion of liquid momentum to a less dense phase and therefore the two phases are more or less in equilibrium. In contrast, air-blast sprays are fundamentally different. The near-nozzle flow structures such as breakup length, liquid film thickness and sheet frequency have been investigated by Déjean, Berthoumieu & Gajan (Reference Déjean, Berthoumieu and Gajan2016a
,Reference Déjean, Berthoumieu and Gajan
b
) in the context of planar air-blast sprays. In contrast to the present study, local droplet Stokes number could play a significant role in such air-blast sprays where the drops and air are not necessarily in local equilibrium.
4.3 Mechanisms of droplet generation

Figure 11. Instantaneous image from an
![]() $Re=1364$
and
$Re=1364$
and
![]() $We=214$
spray. Inset images show magnified views of regions (a) and (b). Shear-induced breakup can be observed in region (a) while Kelvin–Helmholtz–Rayleigh–Taylor (KH–RT) instability-induced breakup can be observed in region (b).
$We=214$
spray. Inset images show magnified views of regions (a) and (b). Shear-induced breakup can be observed in region (a) while Kelvin–Helmholtz–Rayleigh–Taylor (KH–RT) instability-induced breakup can be observed in region (b).
We have shown that the scaled probability distribution of large drops is insensitive to
![]() $Re$
and
$Re$
and
![]() $We$
, while that of the small drops is. Several different drop formation mechanisms have been proposed in the literature; the reader is referred to a recent review article by Villermaux (Reference Villermaux2007) for a comprehensive discussion. We will herein briefly present qualitative experimental evidence that at least two mechanisms of breakup – one that results in large drops and the other that results in small drops – occur simultaneously in our experiments.
$We$
, while that of the small drops is. Several different drop formation mechanisms have been proposed in the literature; the reader is referred to a recent review article by Villermaux (Reference Villermaux2007) for a comprehensive discussion. We will herein briefly present qualitative experimental evidence that at least two mechanisms of breakup – one that results in large drops and the other that results in small drops – occur simultaneously in our experiments.
Figure 11 depicts an instantaneous image obtained from a spray at
![]() $Re=1364$
and
$Re=1364$
and
![]() $We=214$
. Importantly, two regions are magnified and shown as insets. The inset (a) shows ligaments being formed from the surface of an intact liquid sheet, which will likely result in small drops. These drops are typically smaller than the boundary layer thickness. The mechanism associated with the formation of these drops has been widely discussed in the literature as being one originating from shear (see Lasheras et al.
Reference Lasheras, Villermaux and Hopfinger1998). In contrast, the inset (b) shows drops forming from the disintegration of a flapping edge of the liquid sheet. This Kelvin–Helmholtz–Rayleigh–Taylor (KH–RT) based mechanism creates large drops, typically much bigger than the boundary layer thickness.
$We=214$
. Importantly, two regions are magnified and shown as insets. The inset (a) shows ligaments being formed from the surface of an intact liquid sheet, which will likely result in small drops. These drops are typically smaller than the boundary layer thickness. The mechanism associated with the formation of these drops has been widely discussed in the literature as being one originating from shear (see Lasheras et al.
Reference Lasheras, Villermaux and Hopfinger1998). In contrast, the inset (b) shows drops forming from the disintegration of a flapping edge of the liquid sheet. This Kelvin–Helmholtz–Rayleigh–Taylor (KH–RT) based mechanism creates large drops, typically much bigger than the boundary layer thickness.
![]() $Re$
and
$Re$
and
![]() $We$
are dimensionless numbers based on the bulk flow properties and known to govern the liquid sheet flapping dynamics and the probability of finding large drops. In contrast, the smaller drops form from shear-induced K–H instability at the liquid free surface. These two mechanisms are known to exhibit different scaling behaviour (Lasheras et al.
Reference Lasheras, Villermaux and Hopfinger1998) and will therefore result in different scaled probabilities of finding large and small drops.
$We$
are dimensionless numbers based on the bulk flow properties and known to govern the liquid sheet flapping dynamics and the probability of finding large drops. In contrast, the smaller drops form from shear-induced K–H instability at the liquid free surface. These two mechanisms are known to exhibit different scaling behaviour (Lasheras et al.
Reference Lasheras, Villermaux and Hopfinger1998) and will therefore result in different scaled probabilities of finding large and small drops.
4.4 Dynamical modes of the liquid sheet
We have shown scaling of flow rate, mean drop size, mean axial velocity as well as drop size and velocity p.d.f.s with the appropriate scale choices. These quantities are time-averaged and hence can be construed as steady-state measures of the spray. In contrast, high-speed shadowgraph images captured in the experiments contain information about the unsteadiness. In order to analyse the scaling behaviour of the dynamical aspects of a spray, we treat a video of the spray as a time series of spray structures represented in individual images. POD is used to identify the dominant spatial modes in the spray as well as temporal frequencies.
The POD technique is widely used to identify the dominant dynamical structures in the flow field (Sampath & Chakravarthy Reference Sampath and Chakravarthy2014; Rajamanickam & Basu Reference Rajamanickam and Basu2017). A comprehensive overview of the technique is available in Chatterjee (Reference Chatterjee2000). For the purpose of this study, a variation of POD for image analysis introduced by Sirovich (Reference Sirovich1987) was employed. In this method, the high-speed shadowgraph video of a spray is converted into a set of images. Each instantaneous
![]() $m\times n$
pixels image contains information about the spatial variation of the drops in the flow field as grey scale intensity and is assembled into a column vector. The column vectors corresponding to successive time steps are assembled into a matrix
$m\times n$
pixels image contains information about the spatial variation of the drops in the flow field as grey scale intensity and is assembled into a column vector. The column vectors corresponding to successive time steps are assembled into a matrix
![]() $\unicode[STIX]{x1D63C}$
which is of size
$\unicode[STIX]{x1D63C}$
which is of size
![]() $mn\times N$
, where
$mn\times N$
, where
![]() $N$
is the number of time instants sampled. In the POD method, one is interested in identifying the singular values of this matrix
$N$
is the number of time instants sampled. In the POD method, one is interested in identifying the singular values of this matrix
![]() $\unicode[STIX]{x1D63C}$
, as well as its spatial modes or basis functions from the space–time series data captured in the high-speed shadowgraph imaging experiments. The singular value decomposition (SVD) (Alter, Brown & Botstein Reference Alter, Brown and Botstein2000) of matrix
$\unicode[STIX]{x1D63C}$
, as well as its spatial modes or basis functions from the space–time series data captured in the high-speed shadowgraph imaging experiments. The singular value decomposition (SVD) (Alter, Brown & Botstein Reference Alter, Brown and Botstein2000) of matrix
![]() $\unicode[STIX]{x1D63C}$
has the form
$\unicode[STIX]{x1D63C}$
has the form
where
![]() $\unicode[STIX]{x1D650}$
is an
$\unicode[STIX]{x1D650}$
is an
![]() $mn\times N$
matrix containing the spatial mode information and
$mn\times N$
matrix containing the spatial mode information and
![]() $\unicode[STIX]{x1D651}$
is an
$\unicode[STIX]{x1D651}$
is an
![]() $N\times N$
matrix containing the temporal mode information corresponding to each spatial mode. The energy content of each mode is calculated from the singular values which are the diagonal elements of
$N\times N$
matrix containing the temporal mode information corresponding to each spatial mode. The energy content of each mode is calculated from the singular values which are the diagonal elements of
![]() $\unicode[STIX]{x1D72E}$
. A Fourier transform of the temporal mode
$\unicode[STIX]{x1D72E}$
. A Fourier transform of the temporal mode
![]() $\unicode[STIX]{x1D651}$
is performed to identify the dominant frequency of a particular spatial mode. We are interested in understanding the two most dominant spatial modes in each spray at the same dimensionless flow conditions. The first mode (mode
$\unicode[STIX]{x1D651}$
is performed to identify the dominant frequency of a particular spatial mode. We are interested in understanding the two most dominant spatial modes in each spray at the same dimensionless flow conditions. The first mode (mode
![]() $0$
) is usually the time-averaged steady state and the second mode (mode
$0$
) is usually the time-averaged steady state and the second mode (mode
![]() $1$
) corresponds to the most energetic unsteady mode. A power spectral density (PSD) plot is then constructed to identify the dominant temporal frequency in the image sequence.
$1$
) corresponds to the most energetic unsteady mode. A power spectral density (PSD) plot is then constructed to identify the dominant temporal frequency in the image sequence.

Figure 12. Contour plots of the mode shapes obtained from POD for
![]() $Re\approx 1035$
but varying values of
$Re\approx 1035$
but varying values of
![]() $We$
. The steady mode (mode 0) is shown for: (a)
$We$
. The steady mode (mode 0) is shown for: (a)
![]() $We=135$
obtained using
$We=135$
obtained using
![]() $3$
x, (b)
$3$
x, (b)
![]() $We=79$
obtained using
$We=79$
obtained using
![]() $5$
x and (c)
$5$
x and (c)
![]() $We=42$
obtained using
$We=42$
obtained using
![]() $10$
x. The first unsteady mode (mode 1) is shown for: (d)
$10$
x. The first unsteady mode (mode 1) is shown for: (d)
![]() $We=135$
obtained using
$We=135$
obtained using
![]() $3$
x, (e)
$3$
x, (e)
![]() $We=79$
obtained using
$We=79$
obtained using
![]() $5$
x and (f)
$5$
x and (f)
![]() $We=42$
obtained using
$We=42$
obtained using
![]() $10$
x. Each image has a scaled window size of
$10$
x. Each image has a scaled window size of
![]() $27D_{o}\times 13.5D_{o}$
. The wavelength associated with the antisymmetric flapping motion of the liquid sheet is shown in (f). The
$27D_{o}\times 13.5D_{o}$
. The wavelength associated with the antisymmetric flapping motion of the liquid sheet is shown in (f). The
![]() $\unicode[STIX]{x1D706}/D_{o}$
value was observed to be approximately the same (
$\unicode[STIX]{x1D706}/D_{o}$
value was observed to be approximately the same (
![]() ${\approx}6$
) in (d–f). This value is close to the theoretical predictions from linear stability analysis of Xianguo & Tankin (Reference Xianguo and Tankin1991).
${\approx}6$
) in (d–f). This value is close to the theoretical predictions from linear stability analysis of Xianguo & Tankin (Reference Xianguo and Tankin1991).
Figure 12 shows contour plots of the dominant spatial modes in the
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x spray at
$10$
x spray at
![]() $Re\approx 1000$
. The values of
$Re\approx 1000$
. The values of
![]() $We$
for each case are indicated in the caption. Each image shows the same dimensionless spatial region of
$We$
for each case are indicated in the caption. Each image shows the same dimensionless spatial region of
![]() $27D_{o}\times 13.5D_{o}$
in width and height. Figure 12(a–c) depicts the mode 0 in the three sprays, which is the time-averaged steady mode. In all three cases, this was the most dominant spatial structure in the spray as identified from the POD analysis. It can be seen that these contour plots are nearly identical, implying that the breakup length scales as
$27D_{o}\times 13.5D_{o}$
in width and height. Figure 12(a–c) depicts the mode 0 in the three sprays, which is the time-averaged steady mode. In all three cases, this was the most dominant spatial structure in the spray as identified from the POD analysis. It can be seen that these contour plots are nearly identical, implying that the breakup length scales as
![]() $D_{o}$
and is independent of
$D_{o}$
and is independent of
![]() $We$
at this value of
$We$
at this value of
![]() $Re$
.
$Re$
.
Figure 12(d–f) depicts the second most energy-containing unsteady mode (referred to as mode 1). As can be seen from these images, the flapping motion of the conical liquid sheet exiting the spray atomizer is well represented. The wavelength of the propagating wave can be estimated from the distance along the sheet between the centres of red and blue contour regions. It can be seen that this wavelength is approximately the same in all the three images in figure 12(d–f). Since each image represents the same dimensionless field of view, it can be concluded that the dimensionless wavelength (
![]() $\unicode[STIX]{x1D706}/D_{0}$
) associated with the flapping motion is approximately the same. In addition, the wavelength in figure 12(e) is within
$\unicode[STIX]{x1D706}/D_{0}$
) associated with the flapping motion is approximately the same. In addition, the wavelength in figure 12(e) is within
![]() $20\,\%$
of the theoretical prediction of Xianguo & Tankin (Reference Xianguo and Tankin1991) from a linear stability analysis of a planar liquid sheet. We have also measured the wavelength for a single atomizer at several
$20\,\%$
of the theoretical prediction of Xianguo & Tankin (Reference Xianguo and Tankin1991) from a linear stability analysis of a planar liquid sheet. We have also measured the wavelength for a single atomizer at several
![]() $Re$
conditions for
$Re$
conditions for
![]() $Re>1000$
. From these measurements, we have seen that the dimensionless wavelength appears to be relatively independent of
$Re>1000$
. From these measurements, we have seen that the dimensionless wavelength appears to be relatively independent of
![]() $Re$
for all these cases, again implying that inviscid theory is sufficient. The flapping motion of the liquid sheet shows nearly similar spatial characteristics in terms of the shape of the most energetic unsteady mode.
$Re$
for all these cases, again implying that inviscid theory is sufficient. The flapping motion of the liquid sheet shows nearly similar spatial characteristics in terms of the shape of the most energetic unsteady mode.
The phase difference between the left and right edges of the conical liquid sheet in figure 12(d–f) is also a point to note. Let us consider figure 12(f), for an example. A horizontal line through the image at approximately half the height in the image would pass through a red region on the left-hand edge and a blue region on the right-hand edge of the conical liquid sheet. Since these POD modes are derived from instantaneous snapshots, the red and blue correspond to the presence and absence of the liquid sheet at that point in the image, respectively. Therefore, the liquid sheet appears to be oscillating such that the left edge and the right edge of the spray are out of phase. This implies that the most dominant unsteady mode is antisymmetric, as has been pointed out by Shen & Li (Reference Shen and Li1996).

Figure 13. (a) Plot of dimensional dominant liquid sheet flapping frequency (
![]() $\unicode[STIX]{x1D6FA}$
) of the most energetic unsteady mode (mode 1) as a function of the dimensional flow rate (
$\unicode[STIX]{x1D6FA}$
) of the most energetic unsteady mode (mode 1) as a function of the dimensional flow rate (
![]() $Q$
) for the
$Q$
) for the
![]() $1$
x,
$1$
x,
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x atomizers. The inset in (a) shows the PSD plot for one case. The dominant flapping frequency is identified from this PSD plot. It is observed that above a critical value of
$10$
x atomizers. The inset in (a) shows the PSD plot for one case. The dominant flapping frequency is identified from this PSD plot. It is observed that above a critical value of
![]() $Re>1000$
, the liquid sheet exhibits a second peak in the PSD plot (see inset in b). The frequencies corresponding to the second peak are shown using open symbols. (b) Plot of Strouhal number versus Reynolds number calculated from the data in (a). The grey region indicates the accuracy of measurement of
$Re>1000$
, the liquid sheet exhibits a second peak in the PSD plot (see inset in b). The frequencies corresponding to the second peak are shown using open symbols. (b) Plot of Strouhal number versus Reynolds number calculated from the data in (a). The grey region indicates the accuracy of measurement of
![]() $St$
;
$St$
;
![]() $St$
is nearly constant and independent of
$St$
is nearly constant and independent of
![]() $Re$
for
$Re$
for
![]() $Re>1000$
.
$Re>1000$
.
We are next interested in the most dominant frequency associated with the sheet flapping motion. Information pertaining to the time variation of the modal amplitude is contained in the
![]() $\unicode[STIX]{x1D651}^{\text{T}}$
matrix in (4.5). The PSD is then calculated from
$\unicode[STIX]{x1D651}^{\text{T}}$
matrix in (4.5). The PSD is then calculated from
![]() $V$
. The frequency corresponding to a maximum power in the PSD (
$V$
. The frequency corresponding to a maximum power in the PSD (
![]() $\unicode[STIX]{x1D6FA}$
) is identified for each case. See the inset of figure 13(a) for a plot of the PSD for one case, also depicting the peak frequency (
$\unicode[STIX]{x1D6FA}$
) is identified for each case. See the inset of figure 13(a) for a plot of the PSD for one case, also depicting the peak frequency (
![]() $\unicode[STIX]{x1D6FA}$
). In order to quantify the error in the peak frequency, we have performed the POD analysis on multiple subsets of the images. The repeatability error in the peak frequency from at least 10 different subset realizations of the experimental data was less than
$\unicode[STIX]{x1D6FA}$
). In order to quantify the error in the peak frequency, we have performed the POD analysis on multiple subsets of the images. The repeatability error in the peak frequency from at least 10 different subset realizations of the experimental data was less than
![]() $5\,\%$
.
$5\,\%$
.
Figure 13(a) shows a plot of the most dominant dimensional flapping frequency (
![]() $\unicode[STIX]{x1D6FA}$
) as a function of the dimensional flow rate
$\unicode[STIX]{x1D6FA}$
) as a function of the dimensional flow rate
![]() $Q$
for the
$Q$
for the
![]() $1$
x,
$1$
x,
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x atomizers. Firstly, it can be observed that, for a given atomizer,
$10$
x atomizers. Firstly, it can be observed that, for a given atomizer,
![]() $\unicode[STIX]{x1D6FA}$
increases with increasing
$\unicode[STIX]{x1D6FA}$
increases with increasing
![]() $Q$
. In addition, as the scale of the atomizer decreases, the dimensional flapping frequency increases sharply. It is particularly noteworthy that the dimensional flapping frequencies in the
$Q$
. In addition, as the scale of the atomizer decreases, the dimensional flapping frequency increases sharply. It is particularly noteworthy that the dimensional flapping frequencies in the
![]() $1$
x case are between
$1$
x case are between
![]() $3$
and 10 kHz. We would like to reiterate that the high-speed camera was operated at 50 000 f.p.s. for this case, in order to resolve motion at this frequency.
$3$
and 10 kHz. We would like to reiterate that the high-speed camera was operated at 50 000 f.p.s. for this case, in order to resolve motion at this frequency.
Figure 13(b) is a plot of the data in figure 13(a) in a dimensionless framework. In figure 13(b) we plot
![]() $St$
versus
$St$
versus
![]() $Re$
, where
$Re$
, where
![]() $St=\unicode[STIX]{x1D6FA}t_{s}/u_{s}$
. As can be observed from this figure,
$St=\unicode[STIX]{x1D6FA}t_{s}/u_{s}$
. As can be observed from this figure,
![]() $St$
initially increases with
$St$
initially increases with
![]() $Re$
. At low
$Re$
. At low
![]() $Re$
, it appears that viscous effects cause the dimensionless flapping frequency to be less than that obtained under high-
$Re$
, it appears that viscous effects cause the dimensionless flapping frequency to be less than that obtained under high-
![]() $Re$
conditions. At high-
$Re$
conditions. At high-
![]() $Re$
conditions,
$Re$
conditions,
![]() $St\sim 2\times 10^{-3}$
and is approximately constant. This order of magnitude of
$St\sim 2\times 10^{-3}$
and is approximately constant. This order of magnitude of
![]() $St$
has also been observed in experiments on air-blast sprays by Wahono et al. (Reference Wahono, Honnery, Soria and Ghojel2008).
$St$
has also been observed in experiments on air-blast sprays by Wahono et al. (Reference Wahono, Honnery, Soria and Ghojel2008).
For
![]() $Re>1500$
, an interesting feature is observed in the flapping dynamics. For these cases, a second non-harmonic higher-frequency peak in the PSD was observed (see inset in figure 13
b). While a second sharp peak is observed at
$Re>1500$
, an interesting feature is observed in the flapping dynamics. For these cases, a second non-harmonic higher-frequency peak in the PSD was observed (see inset in figure 13
b). While a second sharp peak is observed at
![]() $\unicode[STIX]{x1D6FA}=1067~\text{Hz}$
, it is still of a lower energy than the dominant peak at
$\unicode[STIX]{x1D6FA}=1067~\text{Hz}$
, it is still of a lower energy than the dominant peak at
![]() $\unicode[STIX]{x1D6FA}=343~\text{Hz}$
. The
$\unicode[STIX]{x1D6FA}=343~\text{Hz}$
. The
![]() $St$
corresponding to these higher frequencies is also indicated in figure 13(b) as open symbols. Except for a case
$St$
corresponding to these higher frequencies is also indicated in figure 13(b) as open symbols. Except for a case
![]() $Re\approx 2000$
, the
$Re\approx 2000$
, the
![]() $St$
corresponding to the lower frequency always has a greater energy. In both cases of
$St$
corresponding to the lower frequency always has a greater energy. In both cases of
![]() $St$
(based on either high or low frequency)
$St$
(based on either high or low frequency)
![]() $St$
appears to be independent of
$St$
appears to be independent of
![]() $Re$
, for
$Re$
, for
![]() $Re>1500$
. Finally, the difference in the magnitudes of the energies between the two peak frequencies is observed to decrease with increasing
$Re>1500$
. Finally, the difference in the magnitudes of the energies between the two peak frequencies is observed to decrease with increasing
![]() $Re$
. This implies that a critical value of
$Re$
. This implies that a critical value of
![]() $Re$
could exist where a crossover may occur to the higher-
$Re$
could exist where a crossover may occur to the higher-
![]() $St$
mode. Similar dynamics has been observed for vortex shedding behind a cylinder by Bearman (Reference Bearman1969) where he showed that the higher value of
$St$
mode. Similar dynamics has been observed for vortex shedding behind a cylinder by Bearman (Reference Bearman1969) where he showed that the higher value of
![]() $St$
is approximately
$St$
is approximately
![]() $2.5$
times the lower
$2.5$
times the lower
![]() $St$
value. As Bearman (Reference Bearman1969) suggests, it is likely that beyond a critical value of
$St$
value. As Bearman (Reference Bearman1969) suggests, it is likely that beyond a critical value of
![]() $Re$
, the vortex shedding dynamics transitions to a ‘supercritical’ regime. The present results appear to suggest a similar transition in the case of a flapping liquid sheet.
$Re$
, the vortex shedding dynamics transitions to a ‘supercritical’ regime. The present results appear to suggest a similar transition in the case of a flapping liquid sheet.
5 Discussion
Pressure swirl injectors exhibit extremely complex three-dimensional boundary layer behaviour. As we have shown, drop size spectra show good scaling when the boundary layer thickness at the nozzle exit (
![]() $\unicode[STIX]{x1D6FF}_{o}$
) is chosen as the length scale. Specifically, drops greater than the boundary layer thickness exhibit similar behaviour, while drops smaller than this boundary layer thickness show a remnant effect of both
$\unicode[STIX]{x1D6FF}_{o}$
) is chosen as the length scale. Specifically, drops greater than the boundary layer thickness exhibit similar behaviour, while drops smaller than this boundary layer thickness show a remnant effect of both
![]() $Re$
and
$Re$
and
![]() $We$
. This could be due to the fact that the physical mechanisms associated with the formation of these drops is different from that associated with forming the larger drops. Finally, we would like to point out from figure 1(b) that
$We$
. This could be due to the fact that the physical mechanisms associated with the formation of these drops is different from that associated with forming the larger drops. Finally, we would like to point out from figure 1(b) that
![]() $\unicode[STIX]{x1D6FF}_{o}/t_{s}\sim Re^{-1/2}$
. From equation (2.4), this also implies that
$\unicode[STIX]{x1D6FF}_{o}/t_{s}\sim Re^{-1/2}$
. From equation (2.4), this also implies that
![]() $\unicode[STIX]{x1D6FF}_{o}/D_{o}\sim Re^{-1/2}$
. Therefore, for
$\unicode[STIX]{x1D6FF}_{o}/D_{o}\sim Re^{-1/2}$
. Therefore, for
![]() $Re>1000$
, which we have identified as a critical value of
$Re>1000$
, which we have identified as a critical value of
![]() $Re$
from the data presented in this paper, it is possible that drop size spectra are independent of
$Re$
from the data presented in this paper, it is possible that drop size spectra are independent of
![]() $Re$
.
$Re$
.
From a reading of the data presented in figures 8(c) and 9(b) as well as from figure 10(a,c), one can observe that the drop size p.d.f. could admit a universal description only for the larger drops. Similarly, the velocity spectrum exhibits a universal p.d.f. only for the slower-moving drops. In other words, the data from the larger drops (which are also the faster-moving ones in the spray) collapse around a universal scaled drop size p.d.f., but a Reynolds-number-dependent scaled velocity p.d.f. Also, the data from the smaller drops (which are also the slower-moving ones in the spray) collapse around a universal scaled velocity p.d.f., but a Reynolds-number-dependent scaled drop size p.d.f.
An intended windfall of this work are the experimental MEMS-based spray devices that we have fabricated to perform the high-
![]() $We$
, low-
$We$
, low-
![]() $Re$
set of experiments. These devices produce a finely atomized spray at reasonably low supply pressures and flow rates. The effect of miniaturization in these spray devices appears to produce a twofold impact. Firstly, we observed that the variability in the cone angle appears to be much higher in the case of the
$Re$
set of experiments. These devices produce a finely atomized spray at reasonably low supply pressures and flow rates. The effect of miniaturization in these spray devices appears to produce a twofold impact. Firstly, we observed that the variability in the cone angle appears to be much higher in the case of the
![]() $1$
x microspray in comparison with the other sprays for similar
$1$
x microspray in comparison with the other sprays for similar
![]() $Re$
. This points to the fact that a scaled flapping amplitude
$Re$
. This points to the fact that a scaled flapping amplitude
![]() ${\mathcal{A}}/D_{o}$
associated with the flapping motion of the liquid sheet is much higher in the case of the
${\mathcal{A}}/D_{o}$
associated with the flapping motion of the liquid sheet is much higher in the case of the
![]() $1$
x microspray when compared to the
$1$
x microspray when compared to the
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x sprays. Secondly, as can be seen from figure 13(a), the flapping frequency of the
$10$
x sprays. Secondly, as can be seen from figure 13(a), the flapping frequency of the
![]() $1$
x microspray is also much higher than in the case of the other sprays. This implies that the acceleration induced by the flapping motion
$1$
x microspray is also much higher than in the case of the other sprays. This implies that the acceleration induced by the flapping motion
![]() ${\mathcal{A}}\unicode[STIX]{x1D6FA}^{2}$
is a source of an amplified destabilizing force for the parasitic Rayleigh–Taylor (RT) instability. This force is characterized by a Bond number,
${\mathcal{A}}\unicode[STIX]{x1D6FA}^{2}$
is a source of an amplified destabilizing force for the parasitic Rayleigh–Taylor (RT) instability. This force is characterized by a Bond number,
![]() $Bo=\unicode[STIX]{x1D70C}_{l}{\mathcal{A}}\unicode[STIX]{x1D6FA}^{2}D_{o}^{2}/\unicode[STIX]{x1D70E}$
. As discussed by Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000) as well as by Vadivukkarasan & Panchagnula (Reference Vadivukkarasan and Panchagnula2016, Reference Vadivukkarasan and Panchagnula2017), an accelerating interface with a density difference is unstable to transverse modes. While Kelvin–Helmholtz (KH) instability gives rise to the flapping motion, it is the parasitic RT instability that is finally responsible for atomization. It appears that these microscale atomizers operate in an hitherto unexplored and rather unconventional, high
$Bo=\unicode[STIX]{x1D70C}_{l}{\mathcal{A}}\unicode[STIX]{x1D6FA}^{2}D_{o}^{2}/\unicode[STIX]{x1D70E}$
. As discussed by Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000) as well as by Vadivukkarasan & Panchagnula (Reference Vadivukkarasan and Panchagnula2016, Reference Vadivukkarasan and Panchagnula2017), an accelerating interface with a density difference is unstable to transverse modes. While Kelvin–Helmholtz (KH) instability gives rise to the flapping motion, it is the parasitic RT instability that is finally responsible for atomization. It appears that these microscale atomizers operate in an hitherto unexplored and rather unconventional, high
![]() $Bo$
, low
$Bo$
, low
![]() $Re$
regime. This regime of operation could produce disproportionate benefits by significantly enhancing the parasitic Rayleigh–Taylor instability. For example, one could externally excite the liquid sheet near its natural frequency in a MEMS atomizer to produce a finely atomized spray without significant viscous pressure loss.
$Re$
regime. This regime of operation could produce disproportionate benefits by significantly enhancing the parasitic Rayleigh–Taylor instability. For example, one could externally excite the liquid sheet near its natural frequency in a MEMS atomizer to produce a finely atomized spray without significant viscous pressure loss.
6 Summary and conclusions
We have presented an experimental study of geometrically similar atomizers ranging in size by a factor of
![]() $10$
. The objective of this study was to investigate the effect of various choices of length scales in determining the performance of a range of pressure swirl atomizers. We have fabricated these atomizers using MEMS fabrication methods as well as additive manufacturing (3D printing) methods. We have used water as the test fluid and studied the spray characteristics using phase Doppler interferometry (PDI) as well as high-speed imaging. From these studies, we show that the dimensionless flow rate (
$10$
. The objective of this study was to investigate the effect of various choices of length scales in determining the performance of a range of pressure swirl atomizers. We have fabricated these atomizers using MEMS fabrication methods as well as additive manufacturing (3D printing) methods. We have used water as the test fluid and studied the spray characteristics using phase Doppler interferometry (PDI) as well as high-speed imaging. From these studies, we show that the dimensionless flow rate (
![]() $Re$
) in all cases scales with the dimensionless supply pressure (
$Re$
) in all cases scales with the dimensionless supply pressure (
![]() $\overline{\unicode[STIX]{x0394}p}$
). In this context, we show a new scaling law for pressure swirl atomizers that
$\overline{\unicode[STIX]{x0394}p}$
). In this context, we show a new scaling law for pressure swirl atomizers that
![]() $Re\sim \overline{\unicode[STIX]{x0394}p}^{0.46}$
. This correction (in relation to the usually used
$Re\sim \overline{\unicode[STIX]{x0394}p}^{0.46}$
. This correction (in relation to the usually used
![]() $\sqrt{\overline{\unicode[STIX]{x0394}p}}$
) becomes significant for either high mass flow rate or microscale sprays.
$\sqrt{\overline{\unicode[STIX]{x0394}p}}$
) becomes significant for either high mass flow rate or microscale sprays.
PDI is used to measure drop size and velocity spectra in the spray. The dimensionless mean drop size is shown to scale with dimensionless radial location. More specifically, we show that the mean drop sizes in these sprays appear to exhibit self-similarity when
![]() $\unicode[STIX]{x1D701}=r/(z\tan \unicode[STIX]{x1D703}_{m})$
is chosen as the similarity variable. With this choice, we show that the scaled
$\unicode[STIX]{x1D701}=r/(z\tan \unicode[STIX]{x1D703}_{m})$
is chosen as the similarity variable. With this choice, we show that the scaled
![]() $D_{32}$
for a range of
$D_{32}$
for a range of
![]() $Re$
appear to collapse onto one universal curve. The variation of
$Re$
appear to collapse onto one universal curve. The variation of
![]() $D_{32}$
in these sprays appears to show a self-similar central core for
$D_{32}$
in these sprays appears to show a self-similar central core for
![]() $|\unicode[STIX]{x1D701}|<1/2$
and a region where
$|\unicode[STIX]{x1D701}|<1/2$
and a region where
![]() $Re$
effects cannot be ignored outside this region. In this context, several researchers have shown that mean velocity profiles show self-similar behaviour, but this is the first report of self-similar behaviour in mean drop size and liquid volume flux.
$Re$
effects cannot be ignored outside this region. In this context, several researchers have shown that mean velocity profiles show self-similar behaviour, but this is the first report of self-similar behaviour in mean drop size and liquid volume flux.
The pointwise PDI measurements of the joint size–velocity p.d.f. at various radial locations in the spray are used to calculate a global size–velocity p.d.f. The global p.d.f. represents a flux-based p.d.f. of all drops that cross a certain axial location. We show that the boundary layer thickness at the nozzle exit is an important length scale that determines the downstream drop size distributions. In this context, we show that the drop size p.d.f. exhibits universal scaling for drops of size greater than this boundary layer thickness. For drops smaller than this boundary layer thickness, remnant Reynolds- and Weber-number effects are evident, indicating that the underlying physics is different for these two classes of drops.
We use proper orthogonal decomposition to analyse the dynamical modes that occur in these sprays. Using this analysis, we show that the dimensionless wavelength associated with the flapping motion is nearly the same for
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x sprays, spanning a wide range of Weber numbers. In addition, we show that the temporal frequency associated with the most energetic dynamical mode is greater in the case of
$10$
x sprays, spanning a wide range of Weber numbers. In addition, we show that the temporal frequency associated with the most energetic dynamical mode is greater in the case of
![]() $1$
x than in the other atomizers. However, when scaled as a Strouhal number, we show that the Strouhal number initially increases with increase in
$1$
x than in the other atomizers. However, when scaled as a Strouhal number, we show that the Strouhal number initially increases with increase in
![]() $Re$
, but remains constant for large values of the Reynolds number. Beyond a critical
$Re$
, but remains constant for large values of the Reynolds number. Beyond a critical
![]() $Re$
,
$Re$
,
![]() $St$
appears to show a sharp transition to a supercritical regime. This unusually high flapping frequency of the liquid sheet opens a new route to creating a finely atomized spray, where parasitic Rayleigh–Taylor instability is exploited as the main source of atomization energy.
$St$
appears to show a sharp transition to a supercritical regime. This unusually high flapping frequency of the liquid sheet opens a new route to creating a finely atomized spray, where parasitic Rayleigh–Taylor instability is exploited as the main source of atomization energy.
Acknowledgements
This work was supported in part by grants from National Center for Combustion Research and Development (NCCRD), Indian Institute of Technology Madras, India, and the University Office of Global Programs, Penn State University, USA. K.D. would like to acknowledge support from the Prime Minister’s Fellowship Scheme for doctoral research from partnership between Science and Engineering Research Board (SERB), Department of Science and Technology (DST), Government of India, and Eaton Technology Pvt Ltd., India, facilitated by the Confederation of Indian Industry (CII).
Appendix A. Geometric details of atomizers
Table 2. The dimensions of the four atomizers used in the study.

Table 2 lists the absolute dimensions of the cohort of atomizers employed in this study. Figure 2(d) represents a graphical description of the dimensional features of the atomizer.
A.1 Accuracy of the manufacturing processes
A Stratasys® EDEN 350 V® poly-jet additive manufacturing machine has been used to build the
![]() $3$
x,
$3$
x,
![]() $5$
x and
$5$
x and
![]() $10$
x atomizers. The atomizers were built with the photopolymer Vero Clear Fullcure 720 model material supplied by Stratasys. The poly-jet additive manufacturing machine is capable of building a layer of minimum thickness of
$10$
x atomizers. The atomizers were built with the photopolymer Vero Clear Fullcure 720 model material supplied by Stratasys. The poly-jet additive manufacturing machine is capable of building a layer of minimum thickness of
![]() $16~\unicode[STIX]{x03BC}\text{m}$
with the glossy surface finish of 300 dpi at a local surface orientation of
$16~\unicode[STIX]{x03BC}\text{m}$
with the glossy surface finish of 300 dpi at a local surface orientation of
![]() $0^{\circ }$
. The surface roughness on parts printed using a poly-jet additive manufacturing system was less than
$0^{\circ }$
. The surface roughness on parts printed using a poly-jet additive manufacturing system was less than
![]() $3~\unicode[STIX]{x03BC}\text{m}$
(Kumar & Kumar Reference Kumar and Kumar2015). The
$3~\unicode[STIX]{x03BC}\text{m}$
(Kumar & Kumar Reference Kumar and Kumar2015). The
![]() $3$
x atomizer (which is the smallest of the additive manufactured parts) was 3.6 mm. Therefore, it can be estimated that the relative surface roughness in these parts is less than
$3$
x atomizer (which is the smallest of the additive manufactured parts) was 3.6 mm. Therefore, it can be estimated that the relative surface roughness in these parts is less than
![]() $10^{-3}$
. At these low values of relative roughness and low values of
$10^{-3}$
. At these low values of relative roughness and low values of
![]() $Re\sim 10^{3}$
, the boundary layer is unlikely to be affected by roughness.
$Re\sim 10^{3}$
, the boundary layer is unlikely to be affected by roughness.
The
![]() $1$
x atomizer was fabricated by MEMS technology. A silicon wafer is used to make the microscale atomizer. The surface roughness on parts etched using MEMS technology is less than 30 nm. The smallest feature in the
$1$
x atomizer was fabricated by MEMS technology. A silicon wafer is used to make the microscale atomizer. The surface roughness on parts etched using MEMS technology is less than 30 nm. The smallest feature in the
![]() $1$
x atomizer is
$1$
x atomizer is
![]() $100~\unicode[STIX]{x03BC}\text{m}$
. The relative surface roughness is
$100~\unicode[STIX]{x03BC}\text{m}$
. The relative surface roughness is
![]() $10^{-4}$
. The above conclusion holds for this case as well.
$10^{-4}$
. The above conclusion holds for this case as well.
A.2 Flow rate reproducibility
Each experimental trial was repeated at least three times to verify reproducibility. In this study the flow was controlled with the help of a needle valve and the pressure was set based on the digital pressure gauge fixed at the atomizer inlet. The digital pressure gauge was calibrated regularly, with the master gauge based on standards. The digital pressure gauge was rated to operate up to millibar accuracy. All the experiments were performed once the digital pressure gauge value reached a stable reading. The supply pressure operating condition and the flow rate was reproducible to within
![]() $\pm 1.5\,\%$
in all cases.
$\pm 1.5\,\%$
in all cases.
Appendix B. Experimental set-up details and error quantification
B.1 PDI measurements

Figure 14. A schematic of the PDI set-up used for drop size and velocity measurements. The traverse system is used to move the PDI to various radial locations for performing measurements.
An Artium PDI system is used in the forward scatter mode to measure the drop size and velocity. The schematic of the PDI set-up is shown in figure 14. Phase calibration is performed periodically to ensure that no unexpected phase delay occurs due to electronic components. As is well known, accurate size measurements depend heavily on the phase difference between the photo-detectors. As an additional precautionary measure, auto set-up is enabled. Auto set-up is the unique feature in the Artium PDI system which samples the real spray (maximum of 1000 signals) for the purpose of establishing the optimum settings for the signal processor. This enables that the gain setting is customized for each setting to maximize the range of droplets that can be measured. More detailed information is provided in Artium Technologies (2015).
For a typical measurement, the static range of diameters that could be accurately measured by the PDI system was
![]() $1$
to
$1$
to
![]() $647.9~\unicode[STIX]{x03BC}\text{m}$
. The static range of measurable diameters varies by varying the processor and the optical settings and was noted for each measurement. Table 3 has the information of optical setting of transmitter and receiver.
$647.9~\unicode[STIX]{x03BC}\text{m}$
. The static range of measurable diameters varies by varying the processor and the optical settings and was noted for each measurement. Table 3 has the information of optical setting of transmitter and receiver.

Figure 15. The cone angle
![]() $2\unicode[STIX]{x1D703}$
variation with
$2\unicode[STIX]{x1D703}$
variation with
![]() $Re$
is shown with the standard deviation.
$Re$
is shown with the standard deviation.
Table 3. PDI system optical settings.

B.2 High-speed imaging
We captured at 10 000 f.p.s. and used 1000 images (0.1 s) data to identify the spray characteristics. Two main spray characteristics were calculated from these images. The spray cone angle was calculated using a built-in edge detection algorithm in MATLAB (Otsu Reference Otsu1979). From the detected edge radial location, the cone angle was calculated from trigonometry. Figure 15 is a plot of the spray cone angle versus
![]() $Re$
with the experimental frame-to-frame variation shown as error bars. As can be seen, the variability in spray cone angle decreases as
$Re$
with the experimental frame-to-frame variation shown as error bars. As can be seen, the variability in spray cone angle decreases as
![]() $Re$
increases.
$Re$
increases.
Appendix C. Drop size, velocity, volume and number flux data
The dimensional mean drop size and axial velocity distribution along the radial location are shown in figure 16, the dimensional global drop size and velocity p.d.f. are shown in figure 17.

Figure 16. (a) Plot of Sauter mean diameter,
![]() $D_{32}$
, versus radial location,
$D_{32}$
, versus radial location,
![]() $r$
. (b) Plot of mean axial velocity,
$r$
. (b) Plot of mean axial velocity,
![]() $u$
, versus radial location,
$u$
, versus radial location,
![]() $r$
. (c) Plot of liquid volume flux,
$r$
. (c) Plot of liquid volume flux,
![]() $\dot{q}^{\prime \prime }$
, versus radial location,
$\dot{q}^{\prime \prime }$
, versus radial location,
![]() $r$
. The legend represents
$r$
. The legend represents
![]() $(Re,We)$
corresponding to each dataset, and applies to all panels. The dimensional pressure and nozzle used for each data series are: ▫, 7 bar, 1x; ♢, 8.3 bar, 3x; ▵, 3 bar, 5x;
$(Re,We)$
corresponding to each dataset, and applies to all panels. The dimensional pressure and nozzle used for each data series are: ▫, 7 bar, 1x; ♢, 8.3 bar, 3x; ▵, 3 bar, 5x;
![]() $\times$
, 5 bar, 5x; ○, 0.75 bar, 10x; ▿, 1.25 bar, 10x.
$\times$
, 5 bar, 5x; ○, 0.75 bar, 10x; ▿, 1.25 bar, 10x.

Figure 17. Plot of global p.d.f. of (a) drop size
![]() $x$
and (b) drop velocity
$x$
and (b) drop velocity
![]() $u$
for different
$u$
for different
![]() $Re$
and
$Re$
and
![]() $We$
. The legend shows the
$We$
. The legend shows the
![]() $(Re,We)$
for each dataset. The dimensional conditions for each dataset are the same as in figure 16.
$(Re,We)$
for each dataset. The dimensional conditions for each dataset are the same as in figure 16.
Figure 16(a) shows a plot of the mean drop size variation as a function of radial location for different geometrically scaled pressure swirl atomizers operating over a range of Reynolds numbers (
![]() $Re$
). Firstly, it can be observed that the profiles for various flow conditions follow a similar trend and it is observed from figure 16(a) that
$Re$
). Firstly, it can be observed that the profiles for various flow conditions follow a similar trend and it is observed from figure 16(a) that
![]() $D_{32}$
exhibits a maximum near the edge of the spray and a minimum near the spray centre. Figure 16(b) shows a plot of the mean axial velocity variation along the radial location for different geometrically scaled pressure swirl atomizers operating over a range of
$D_{32}$
exhibits a maximum near the edge of the spray and a minimum near the spray centre. Figure 16(b) shows a plot of the mean axial velocity variation along the radial location for different geometrically scaled pressure swirl atomizers operating over a range of
![]() $Re$
. It can be observed from this figure that the profiles for various flow conditions follow a similar trend.
$Re$
. It can be observed from this figure that the profiles for various flow conditions follow a similar trend.
Figure 17(a) shows a plot of the global drop size p.d.f.,
![]() ${\mathcal{X}}(x)$
(
${\mathcal{X}}(x)$
(
![]() $\unicode[STIX]{x03BC}\text{m}^{-1}$
). It is observed that the width of the distribution is large for the
$\unicode[STIX]{x03BC}\text{m}^{-1}$
). It is observed that the width of the distribution is large for the
![]() $10$
x (
$10$
x (
![]() $\times$
) spray compared to the
$\times$
) spray compared to the
![]() $3$
x (♢) and
$3$
x (♢) and
![]() $5$
x (▵) sprays operated at almost the same
$5$
x (▵) sprays operated at almost the same
![]() $Re$
. Figure 17(b) shows a plot of the global drop velocity p.d.f.,
$Re$
. Figure 17(b) shows a plot of the global drop velocity p.d.f.,
![]() ${\mathcal{U}}(u)$
(
${\mathcal{U}}(u)$
(
![]() $(\text{m}~\text{s}^{-1})^{-1}$
).
$(\text{m}~\text{s}^{-1})^{-1}$
).