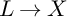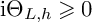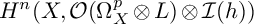1 Introduction.
Let X be a complex projective manifold of dimension n and let
$L\rightarrow X$
be a holomorphic line bundle over X. Bogomolov [Reference Bogomolov1], [Reference Bogomolov2] proved that
$$\begin{align*}H^0\left(X,\mathcal{O}\left(\Omega^p_X\otimes L^{-1}\right)\right)=0,\end{align*}$$
for
$p<\kappa (L)$
, where
$\kappa (L)$
denotes the Kodaira–Iitaka dimension of L. Equivalently, we have
$$\begin{align*}H^n\left(X,\mathcal{O}\left(\Omega^p_X\otimes L\right)\right)=0\end{align*}$$
for
$p\geqslant n-\kappa (L)+1$
. There are many generalizations of the Bogomolov vanishing theorem, cf. [Reference Boucksom3], [Reference Esnault and Viehweg11], [Reference Graf12], [Reference Mourougane14], [Reference Shiffman and Sommese15], [Reference Wu17], etc.
In recent years, there has been a growing interest in the study of singular (Hermitian) metrics for holomorphic line bundles. Vanishing theorems with multiplier ideal sheaves play important roles in several complex variables and complex geometry.
Recently, Watanabe [Reference Watanabe16] proved that if L is a holomorphic line bundle over a projective manifold X of dimension n equipped with a Kähler metric
$\omega $
, and if h is a singular Hermitian metric of L such that
$\mathrm {i}\Theta _{L,h}\geqslant \varepsilon \omega $
in the sense of currents for some
$\varepsilon>0$
, then
$$\begin{align*}H^n\left(X,\mathcal O\left(\Omega^p_X\otimes L\right)\otimes \mathcal I\left(h\right)\right)=0,\end{align*}$$
for
$p>0$
, where
$\mathcal I(h)$
is the multiplier ideal sheaf associated to the singular metric h.
Note that in Watanabe’s theorem, the line bundle is assumed to be big, and the manifold is assumed to be projective.
In this paper, we prove the following Bogomolov-type vanishing theorem for pseudoeffective line bundles over compact Kähler manifolds.
Theorem 1.1. Let X be a compact Kähler manifold of dimension n. Let
$L \rightarrow X$
be a holomorphic line bundle equipped with a singular metric h with
$$\begin{align*}\mathrm{i}\Theta_{L, h}\geqslant 0, \end{align*}$$
in the sense of currents, and let
$\operatorname {nd} (L, h)$
denote the numerical dimension of
$(L, h)$
. Then
$$\begin{align*}H^n\left(X,\mathcal O\left(\Omega^p_X\otimes L\right)\otimes \mathcal I(h)\right)=0, \end{align*}$$
for
$p \geqslant n - \operatorname {nd}(L, h) + 1$
.
The definition of
$\operatorname {nd}(L,h)$
(see Definition 2.1) is given in [Reference Cao4].
The idea of the proof draws inspiration from the works of Cao [Reference Cao4], Demailly-Peternell [Reference Demailly and Peternell9], and Watanabe [Reference Watanabe16], as well as the solution of Demailly’s strong openness conjecture by Guan and Zhou [Reference Guan and Zhou13].
As applications, one can find a singular metric h on L through the Kodaira–Iitaka map, such that
$\kappa (L)\leqslant \operatorname {nd} (L,h)$
, thus Theorem 1.1 covers the Bogomolov vanishing theorem. Meanwhile, if
$\mathrm {i}\Theta _{L,h}\geqslant \varepsilon \omega $
for some
$\varepsilon>0$
, then
$\operatorname {nd}(L,h)=n$
, thus Theorem 1.1 also implies Watanabe’s result.
The structure of the present paper is as follows. In §2, we introduce the numerical dimension
$\operatorname {nd}(L,h)$
. In §3, we prove an
$L^2$
-estimate for the
$\bar \partial $
-equation related to the numerical dimension
$\operatorname {nd}(L,h)$
. In §4, we prepare a criterion of the vanishing of cohomology class in the Čech cohomology group. In §5, we complete the proof of Theorem 1.1. In §6, we show that Theorem 1.1 implies the Bogomolov vanishing theorem.
2 Numerical dimension.
Let
$\theta +dd^c\varphi $
be a closed positive current on a compact Kähler manifold
$(X,\omega )$
, where
$\theta $
is a smooth form and
$\varphi $
is a quasi-plurisubharmonic function on X. From [Reference Demailly, Peternell and Schneider10, Th. 2.2.1], there is a quasi-equisingular approximation
$\{\varphi _k\}$
of
$\varphi $
for the current
$\theta +dd^c\varphi $
, such that
-
• the sequence
$\{\varphi _k\}$
converges to
$\varphi $
in
$L^1$
topology and
$\theta +dd^c\varphi _k\geqslant -\tau _k\omega $
for some constants
$\tau _k\rightarrow 0$
as
$k\rightarrow \infty $
; -
• all the
$\varphi _k$
has analytic singularities and
$\varphi _k$
is less singular than
$\varphi _{k+1}$
, i.e.,
$\varphi _{k+1}\leqslant \varphi _{k}+O(1)$
; -
• for any
$\delta>0$
and
$m\in \mathbb N$
, there exists
$k_0(\delta ,m)\in \mathbb N$
such that
$\mathcal I(m(1+\delta )\varphi _k)\subset \mathcal I(m\varphi )$
for every
$k\geqslant k_0(\delta ,m)$
.
Let
$T_1=\theta _1+dd^c\varphi _1,\cdots , T_k=\theta _k+dd^c\varphi _k$
be closed positive
$(1,1)$
-currents on a compact Kähler manifold X. In [Reference Cao4], it is proved that one can define a cohomological product
$$\begin{align*}\langle T_1\wedge\cdots\wedge T_k\rangle\in H^{k,k}_{\geqslant 0}(X),\end{align*}$$
such that for all
$u\in H^{n-k,n-k}(X)$
,
where
$\{\varphi _{i,j} \}_{j=1}^{\infty }$
is a quasi-equisingular approximation of
$\varphi _i$
and
$(\theta _i+dd^c\varphi _{i,j})_{ac}$
is the absolute continuous part of the Lebesgue decomposition of the current
$\theta _i+dd^c\varphi _{i,j}$
. The key point of the product is that the above limit exists and does not depend on the choice of the quasi-equisingular approximation.
Definition 2.1 [Reference Cao4].
Let L be a holomorphic line bundle on a compact Kähler manifold X and h a singular metric on L. The numerical dimension
$\operatorname {nd}(L,h)$
is defined to be the largest
$v\in \mathbb N$
such that
$\langle (\mathrm {i}\Theta _{L,h})^v\rangle \neq 0$
.
3
$L^2$
-estimates.
In this section, we prove an
$L^2$
-estimate which is inspired by [Reference Cao4]. We need the following
Lemma 3.1. Let X be a complex manifold of dimension n, and let
$\omega $
,
$\gamma $
be Hermitian metrics on X such that
$\gamma \geqslant \omega $
. Let
$(L,h)\rightarrow X$
be a holomorphic Hermitian line bundle on X. Then for every L-valued
$(p, n)$
form u, we have
$$\begin{align*}| u |_{h, \gamma}^2 d V_{\gamma} \leqslant | u |^2_{h, \omega} d V_{\omega}. \end{align*}$$
If
$\mathrm {i}\theta \in C^{\infty }_{1, 1} (M, \mathrm {Herm} (L, L))$
is positive, we have
$$\begin{align*}\langle [\mathrm{i}\theta, \Lambda_{\gamma}]^{- 1} u, u \rangle_{h, \gamma} d V_{\gamma} \leqslant \langle [\mathrm{i}\theta, \Lambda_{\omega}]^{- 1} u, u \rangle_{h, \omega} d V_{\omega}, \end{align*}$$
where
$\Lambda _{\gamma }$
and
$\Lambda _{\omega }$
are the adjoint operators of
$L_{\gamma }=\gamma \wedge \cdot $
and
$L_{\omega }=\omega \wedge \cdot $
, respectively.
The above result is essentially the same as [Reference Demailly7, Lem. 6.3 of Chap. VIII] by taking a conjugate and [Reference Watanabe16, Lem. 2.2]. For the sake of completeness, we include the detail here.
Proof. The proof is quite standard. For the reader’s convenient, we provide the details here. Let
$x_0 \in X$
be an arbitrary point and choose a coordinate chart
$(U, z) $
centered at
$x_0$
such that
$$\begin{align*}\omega = \mathrm{i} \sum_{1 \leqslant j \leqslant n} d z_j \wedge d \bar{z}_j, \quad \gamma = \mathrm{i} \sum_{1 \leqslant j \leqslant n} \gamma_j d z_j \wedge d \bar{z}_j, \end{align*}$$
at
$x_0$
, where
$\gamma _j \geqslant 1$
,
$j = 1, 2, \cdots , n$
are the eigenvalues of
$\gamma $
with respect to
$\omega $
. For a multi-index K, let
$\gamma _K = \prod _{j \in K} \gamma _j$
. For any L-valued
$(p, n)$
form
$u = \sum _K u_K d z_K \wedge d \bar {z} \otimes e$
with e the local frame of L and
$d \bar {z} = d \bar {z}_1 \wedge \cdots \wedge d \bar {z}_n$
,
$| K | = p$
, arranged in increasing order, one has
$$\begin{align*}| u |_{h, \gamma}^2 d V_{\gamma} = \sum_K \frac{1}{\gamma_K} | u_K |^2 | e |^2_h d V_{\omega} \leqslant \sum_K | u_K |^2 | e |^2_h d V_{\omega} = | u |^2_{h, \omega} d V_{\omega} , \end{align*}$$
at the point
$x_0$
. We extend the definition of
$u_{jI}$
to nonincreasing multi-indices
$jI$
by deciding that
$u_{jI}=0$
if
$jI$
contains identical components repeated and
$u_{jI}$
is alternate in
$jI$
. Let us write
$$\begin{align*}\mathrm{i}\theta = \mathrm{i} \sum_{j k} c_{j \bar{k}} dz_{j} \wedge d\bar{z}_{k}, \end{align*}$$
and
$$\begin{align*}\widehat{d \bar{z}_j}=d\bar{z}_1\wedge\cdots\wedge d\bar{z}_{j-1}\wedge d\bar{z}_{j+1}\wedge\cdots\wedge d\bar{z}_n. \end{align*}$$
Then one can check that
$$\begin{align*}\Lambda_{\gamma} u = \mathrm{i} \sum_{j, | I | = p - 1} (- 1)^{p + j - 1} \frac{1}{\gamma_j} u_{j I} d z_I \wedge (\widehat{d \bar{z}_j}) \otimes e, \end{align*}$$
$$\begin{align*}[\mathrm{i}\theta, \Lambda_{\gamma}] u = \sum_{| I | = p - 1} \sum_{j, k} \frac{1}{\gamma_k} c_{j \bar{k}} u_{k I} d z_{j I} \wedge d \bar{z} \otimes e, \end{align*}$$
and thus
$$ \begin{align*} \langle [\mathrm{i}\theta, \Lambda_{\gamma}] u, u \rangle_{h, \gamma} & = \frac{1}{\gamma_1 \gamma_2 \cdots \gamma_n} \sum_{| I | = p - 1} \frac{1}{\gamma_I} \sum_{j, k} \frac{1}{\gamma_j \gamma_k} c_{j \bar{k}} u_{k I} \bar{ u}_{j I}\\ & \geqslant \gamma_1 \gamma_2 \cdots \gamma_n \langle [\mathrm{i}\theta, \Lambda_{\omega}] S_{\gamma} u, S_{\gamma} u \rangle_{h, \omega}, \end{align*} $$
where
$S_{\gamma } u = \sum \frac {1}{\gamma _1 \gamma _2 \cdots \gamma _n \gamma _K} u_K d z_K \wedge d \bar {z} \otimes e$
. Therefore,
$$ \begin{align*} | \langle u, v \rangle_{h, \gamma} |^2 & = | \langle u, S_{\gamma} v \rangle_{h, \omega} |^2\\ & \leqslant \langle [\mathrm{i}\theta, \Lambda_{\omega}]^{- 1} u, u \rangle_{h, \omega} \langle [\mathrm{i}\theta, \Lambda_{\omega}] S_{\gamma} v, S_{\gamma} v \rangle_{h, \omega}\\ & \leqslant \frac{1}{\gamma_1 \gamma_2 \cdots \gamma_n} \langle [i \theta, \Lambda_{\omega}]^{- 1} u, u \rangle_{h, \omega} \langle [i \theta, \Lambda_{\gamma}] v, v \rangle_{h, \gamma}. \end{align*} $$
Let
$v = [\mathrm {i}\theta , \Lambda _{\gamma }]^{- 1} u$
, it follows that
$$\begin{align*}\langle [\mathrm{i}\theta, \Lambda_{\gamma}]^{- 1} u, u \rangle_{h, \gamma} d V_{\gamma} \leqslant \langle [\mathrm{i}\theta, \Lambda_{\omega}]^{- 1} u, u \rangle_{h, \omega} d V_{\omega}. \end{align*}$$
Proposition 3.2. Let
$(X,\omega )$
be a compact Kähler manifold of dimension n, and let
$L \rightarrow X$
be a holomorphic line bundle over X equipped with a singular metric h, which is smooth outside a subvariety
$Z \subset X$
. Assume further that
$$\begin{align*}\mathrm{i}\Theta_{L, h} \geqslant - \varepsilon \omega, \end{align*}$$
on
$X\setminus Z$
. Let
$\lambda _1 \leqslant \lambda _2 \leqslant \cdots \leqslant \lambda _n$
be the eigenvalues of
$\mathrm {i}\Theta _{L, h}$
with respect to
$\omega $
. Then for any L-valued
$(p, n)$
form f with
$$\begin{align*}\int_X | f |^2_{h, \omega} d V_{\omega} < \infty , \end{align*}$$
there exists u and v such that
$$\begin{align*}f = \bar{\partial} u + v, \end{align*}$$
and
$$\begin{align*}\int_X | u |^2_{h, \omega} d V_{\omega} + \frac{1}{2 p \varepsilon} \int_X | v |^2_{h, \omega} d V_{\omega} \leqslant \int_X \frac{1}{\lambda_1 + \lambda_2 + \cdots + \lambda_p + 2 p \varepsilon} | f |^2_{h, \omega} d V_{\omega}. \end{align*}$$
Proof. By [Reference Demailly5],
$X\setminus Z$
admits a complete Kähler metric
$\omega _1$
. Set
$\omega _{\delta } := \omega + \delta \omega _1$
. It is a complete Kähler metric on
$X\setminus Z$
for every
$\delta>0$
. Denote by
$\langle \! \langle \cdot , \cdot \rangle \! \rangle _{h, \delta }$
the global inner product defined by h and
$\omega _{\delta }$
, and
$\| \cdot \|_{h, \delta }$
the norm induced by this inner product. The completion of the space of smooth, compact-supported L-valued
$(p,q)$
forms with respect to the norm
$\| \cdot \|_{h,\omega _{\delta }}$
is
$L^2_{(p,q)}(X\setminus Z,L,h,\omega _{\delta })$
, whose elements are
$L^2$
integrable L-valued
$(p,q)$
forms with measurable coefficients. Therefore, the operator
$\bar {\partial }$
can be extended to an densely defined closed unbounded operator from
$L^2_{(p,q)}(X\setminus Z,L,h,\omega _{\delta })$
to
$L^2_{(p,q+1)}(X\setminus Z,L,h,\omega _{\delta })$
, and
$u\in \operatorname {Dom}\bar {\partial }$
if u and
$\bar {\partial }u$
are square integrable on X. Denote by
$\bar {\partial }^{\ast }$
the adjoint operator of
$\bar {\partial }$
and
$\operatorname {Dom}\bar {\partial }^{\ast }$
the domain of
$\bar {\partial }^{\ast }$
. There exists an orthogonal decomposition
$$\begin{align*}L^2_{(p,q)}(X\setminus Z,L,h,\omega_\delta)=\operatorname{Ker}\bar{\partial}\oplus \overline{\operatorname{Im}\bar{\partial}^{\ast}}. \end{align*}$$
Let s be a
$\bar {\partial }$
-closed L-valued
$(p, n)$
form with coefficients in
$C^{\infty }_c (X\setminus Z)$
. Then the Bochner–Kodaira–Nakano equality reads
$$\begin{align*}\| \bar{\partial}^{\ast} s \|^2{}_{h, \delta} + \|\bar{\partial} s \|^2{}_{h, \delta} = \langle \! \langle [\mathrm{i}\Theta_{L, h}, \Lambda_{\omega_{\delta}}] s, s \rangle \! \rangle_{h, \delta} + \| D's \|^2{}_{h, \delta} + \|D^{\prime\ast} s \|^2_{h, \delta}, \end{align*}$$
where
$D'$
is the
$(1,0)$
part of the Chern connection. Let
$\lambda _{1,\delta } \leqslant \lambda _{2,\delta } \leqslant \cdots \leqslant \lambda _{n,\delta } $
be the eigenvalues of
$\mathrm {i}\Theta _{L, h}$
with respect to
$\omega _{\delta }$
. It follows that
$$\begin{align*}\| \bar{\partial}^{\ast} s \|^2_{h, \delta} \geqslant \int_{X\setminus Z} (\lambda_{1,\delta} + \lambda_{2,\delta} + \cdots + \lambda_{p,\delta}) \left| s \right|{}^2_{h, \delta} d V_{\omega_\delta}, \end{align*}$$
therefore,
$$\begin{align*}\|\bar{\partial}^{\ast} s \|_{h, \delta}^2 + 2 p \varepsilon \| s \|^2_{h, \delta}\geqslant\int_{X\setminus Z} (\lambda_{1,\delta} + \lambda_{2,\delta} + \cdots + \lambda_{p,\delta} + 2 p \varepsilon) \left| s \right|{}^2_{h, \delta} d V_{\omega_\delta}. \end{align*}$$
Since the space of smooth, compactly supported L-valued
$(p, n)$
forms on
$X\setminus Z$
is dense in
$L^2_{(p,n)}(X\setminus Z,L,h,\omega _{\delta })$
, the above inequality holds true for
$s\in L^2_{(p,n)}(X\setminus Z,L,h,\omega _{\delta })\cap \mbox {Dom~}\bar \partial ^*$
. Therefore, for
$s\in L^2_{(p,n)}(X\setminus Z,L,h,\omega _{\delta })\cap \mbox {Dom~}\bar \partial ^*$
and
$f \in \operatorname {Ker} \bar {\partial }$
, one can obtain
$$ \begin{align*} & \left| \langle \! \langle f, s \rangle \! \rangle_{h, \delta} \right|{}^2\\ & \quad\leqslant \int_{X\setminus Z} \frac{1}{\lambda_{1,\delta} + \lambda_{2,\delta} + \cdots + \lambda_{p,\delta} + 2 p \varepsilon} \left| f \right|{}^2_{h, \delta} d V_{\omega_\delta}\\ &\qquad\cdot \int_{X\setminus Z} (\lambda_{1,\delta} + \lambda_{2,\delta} + \cdots + \lambda_{p,\delta} + 2 p \varepsilon) \left| s \right|{}^2_{h, \delta} d V_{\omega_\delta}\\ & \quad\leqslant \left( \int_{X\setminus Z} \frac{1}{\lambda_{1,\delta} + \lambda_{2,\delta} + \cdots + \lambda_{p,\delta} + 2 p \varepsilon} \left| f \right|{}^2_{h, \delta} d V_{\omega_\delta} \right) \cdot \left(\| \bar{\partial}^{\ast} s \|_{h, \delta}^2 + 2 p \varepsilon \| s \|^2_{h, \delta}\right). \end{align*} $$
Thanks to the Hahn–Banach theorem and the Riesz representation theorem, there exists
$u_{\delta }$
and
$v_{\delta }$
such that
$$\begin{align*}\langle \! \langle f, s \rangle \! \rangle_{h, \delta} = \langle \! \langle u_{\delta}, \bar{\partial}^{\ast} s \rangle \! \rangle_{h, \delta} + \langle \! \langle v_{\delta}, s \rangle \! \rangle_{h, \delta},\end{align*}$$
and
$$ \begin{align} \| u_{\delta} \|^2_{h, \delta} + \frac{1}{2 p \varepsilon} \| v_{\delta} \|^2_{h, \delta} \leqslant \int_{X\setminus Z} \frac{1}{\lambda_{1,\delta} + \lambda_{2,\delta} + \cdots + \lambda_{p,\delta} + 2 p \varepsilon} | f |^2_{h, \delta} d V_{\omega_\delta}. \end{align} $$
Therefore,
$$\begin{align*}f = \bar{\partial} u_{\delta} + v_{\delta}.\end{align*}$$
By applying the positive curvature
$i\Theta _{L,h}+2\varepsilon \omega $
to Lemma 3.1, it follows from inequality (3.1) that
$$\begin{align*}\| u_{\delta} \|^2_{h, \delta} + \frac{1}{2 p \varepsilon} \| v_{\delta} \|^2_{h, \delta} \leqslant \int_{X\setminus Z} \frac{1}{\lambda_1 + \lambda_2 + \cdots + \lambda_p + 2 p \varepsilon} | f |^2_{h, \omega} d V_{\omega}, \end{align*}$$
which implies that
$\{ u_{\delta } \}_{\delta }$
and
$\{ v_{\delta } \}_{\delta }$
are bounded in
$L^2$
norms on every compact subset of
${X\setminus Z}$
. Thus, there are subsequences of
$\{ u_{\delta } \}_{\delta }$
and
$\{ v_{\delta } \}_{\delta }$
, which weakly converge to u and v on
$X\setminus Z$
, such that
$$\begin{align*}f = \bar{\partial} u + v, \end{align*}$$
and
$$\begin{align*}\| u \|^2_{h, \omega} + \frac{1}{2 p \varepsilon} \| v \|^2_{h, \omega} \leqslant \int_{X\setminus Z} \frac{1}{\lambda_1 + \lambda_2 + \cdots + \lambda_p + 2 p \varepsilon} | f |^2_{h, \omega} d V_{\omega}. \end{align*}$$
By the extension theorem in [Reference Demailly6, Lem. 11.10], we complete the proof.
Guan–Zhou’s solution to Demailly’s strong openness conjecture [Reference Guan and Zhou13] plays a crucial role in the proof of Theorem 1.1.
Theorem 3.3 [Reference Guan and Zhou13, Th. 1.1].
Let
$\varphi $
be a negative plurisubharmonic function on the unit polydisc
$\Delta ^n\subset \mathbb {C}^n$
. Suppose f is a holomorphic function on
$\Delta ^n$
, which satisfies
$$\begin{align*}\int_{\Delta^n}|f|^2e^{-\varphi}d V_n<+\infty, \end{align*}$$
where
$dV_n$
is the Lebesgue measure on
$\mathbb {C}^n$
. Then for
$r\in (0,1)$
, there exists
$s>0$
such that
$$\begin{align*}\int_{\Delta^n_r}|f|^2e^{-(1+s)\varphi}d V_n<+\infty, \end{align*}$$
where
$\Delta ^n_r=\{z\in \mathbb {C}^n:|z_k|<r,k=1,\cdots ,n\}$
.
It follows from the strong openness property (Theorem 3.3) and [Reference Cao4, Lem. 5.9] that a singular metric for a holomorphic line bundle admits a good regularization.
Lemma 3.4 [Reference Cao4, Lem. 5.9], [Reference Guan and Zhou13, Th. 1.1],[Reference Demailly8, Prop. 5.1].
Let
$(L, h)$
be a pesudo-effective line bundle over a compact Kähler manifold
$(X, \omega )$
of dimension n and
$p \geqslant n - \operatorname {nd} (L, h) + 1$
be an integer. Fix an arbitrary smooth Hermitian metric
$h_0$
of L, and denote by
$\mathrm {i} \Theta _{L,h_0}$
the curvature of
$h_0$
. Let
$h=h_0e^{-2\varphi }$
, with
$\varphi $
a quasi-plurisubharmonic function on X, such that
$\mathrm {i} \Theta _{L,h_0}+\mathrm {i}\partial \bar {\partial }\varphi \geqslant 0$
in the sense of currents. Then there exists a sequence of functions
$\{ \hat {\varphi }_k \}_{k = 1}^{\infty }$
on X satisfying the following properties.
-
1.
$\mathcal {I} (\hat {\varphi }_k) = \mathcal {I} (\varphi )$
for all
$k \in \mathbb {N}$
. -
2.
$\hat {\varphi }_k \leqslant 0$
on X. -
3. Let
$\lambda _{1, k} \leqslant \lambda _{2, k} \leqslant \cdots \leqslant \lambda _{n.k}$
be the eigenvalues of
$\mathrm {i}\Theta _{L, h_0e^{-2 \hat {\varphi }_k}}$
with respect to the base metric
$\omega $
. Then there exist two sequences
$\tau _k \rightarrow 0$
and
$\varepsilon _k \rightarrow 0$
such that
$$\begin{align*}\varepsilon_k \gg \tau_k + \frac{1}{k}, \quad \lambda_{1, k} (x) \geqslant - \varepsilon_k - \frac{C}{k} - \tau_k, \end{align*}$$
for all
$x \in X$
and
$k \in \mathbb {N}$
, where C is a constant independent of k. -
4. We can choose
$\beta> 0$
and
$0 < \alpha < 1$
independent of k such that for every k, there exists an open subset
$U_k$
of X satisfying
$$\begin{align*}\operatorname{vol} (U_k) \leqslant \varepsilon^{\beta}_k, \end{align*}$$
and
$$\begin{align*}\lambda_{p, k} + 2 \varepsilon_k \geqslant \varepsilon_k^{\alpha}, \end{align*}$$
on
$X\setminus U_k$
.
Lemma 3.5 [Reference Cao4, Lem. 5.10].
Let
$\varphi $
and
$\hat \varphi _k$
be as in Lemma 3.4. Let f be a local section of
$\mathcal {O}(\Omega _X^p \otimes L) \otimes \mathcal {I} (\varphi )$
over an open subset
$V \subset X$
. Then for any relatively compact open subset
$U\Subset V$
, there exists
$s>0$
such that for k large enough,
$$\begin{align*}\int_U | f |^2 e^{- 2 \hat{\varphi}_k} dV_{\omega} \leqslant C_{\| f \|_{L^{\infty}}} \cdot \left( \int_U | f |^2 e^{- 2 (1 + s) \varphi} dV_{\omega} \right)^{1 / (1 + s)}, \end{align*}$$
where
$C_{\| f \|_{L^{\infty }}}$
is a constant depending only on
$\| f \|_{L^{\infty }}$
.
By Guan–Zhou’s solution to Demailly’s strong openness conjecture (Theorem 3.3), we may assume that
$|f|^2e^{-2(1+s)\varphi }$
in Lemma 3.5 is integrable on U with respect to
$d V_{\omega }$
.
Theorem 3.6. Let
$(X, \omega )$
be a compact Kähler manifold of dimension n, and let
$(L, h) \rightarrow X$
be a holomorphic line bundle equipped with a singular metric h satisfying
$\mathrm {i}\Theta _{L, h} \geqslant 0$
in the sense of currents. Denote by
$\operatorname {nd} (L, h)$
the numerical dimension of
$(L, h)$
, and let
$p \geqslant n -\operatorname {nd}(L, h) + 1$
be an integer. Fix a smooth metric
$h_0$
on L and write
$h = h_0 e^{- 2 \varphi }$
. Let
$\{ \hat {\varphi }_k \}_{k = 1}^{\infty }$
be the sequence of functions in Lemma 3.4. Then for any smooth
$f \in L^2_{p, n} (X, L, h, \omega ) $
, there exists
$u_k$
and
$v_k$
such that
$$\begin{align*}f = \bar{\partial} u_k + v_k, \end{align*}$$
with
$$ \begin{align} & \int_X | u_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} + \frac{1}{2 p \varepsilon_k} \int_X | v_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} \nonumber\\ &\quad\leqslant \int_X \frac{1}{\lambda_{1, k} + \lambda_{2, k} + \cdots + \lambda_{p, k} + 2 p \varepsilon_k} | f |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega}, \end{align} $$
and
$$ \begin{align} \lim_{k \rightarrow \infty} \int_X | v_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} = 0. \end{align} $$
Proof. By Theorem 3.3 and the compactness of X, there exists
$s> 0$
such that
$$\begin{align*}\int_X | f |^2_{h_0, \omega} e^{- 2 (1 + s) \varphi} d V_\omega< \infty. \end{align*}$$
It follows from Lemma 3.5 that for any open set U,
$$ \begin{align} \int_U | f |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} dV_{\omega} \leqslant C_{\| f \|_{L^{\infty}}} \cdot \left(\int_U | f |^2_{h_0, \omega} e^{- 2 (1 + s) \varphi} d V_{\omega} \right)^{\frac{1}{1+s}}. \end{align} $$
From Lemma 3.4 (c), we may assume
$\lambda _{1, k} + 2 \varepsilon _k> 0$
and by Proposition 3.2, there exists
$u_k$
and
$v_k$
such that
$$\begin{align*}f = \bar{\partial} u_k + v_k, \end{align*}$$
and
$$ \begin{align*} & \int_X | u_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} + \frac{1}{2 p \varepsilon_k} \int_X | v_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega}\\ &\quad \leqslant \int_X \frac{1}{\lambda_{1, k} + \lambda_{2, k} + \cdots + \lambda_{p, k} + 2 p \varepsilon_k} | f |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega}. \end{align*} $$
It remains to verify that
$$\begin{align*}\lim_{k \rightarrow \infty} \int_X | v_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} = 0. \end{align*}$$
From the estimate (3.2), we have
$$ \begin{align*} & \int_X | u_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} + \frac{1}{2 p \varepsilon_k} \int_X | v_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega}\\ & \quad \leqslant \int_X \frac{1}{\lambda_{1, k} + \lambda_{2, k} + \cdots + \lambda_{p, k} + 2 p \varepsilon_k} | f |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega}\\ &\quad \leqslant \int_{X\setminus U_k} \frac{1}{\varepsilon_k^{\alpha}} | f |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} + \int_{U_k} \frac{1}{C_1 \varepsilon_k} | f |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega}, \end{align*} $$
where the constant
$C_1$
is independent of k and the second inequality follows from the properties (c) and (d) of Lemma 3.4. Therefore, one has
$$ \begin{align*} \int_X | v_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} \leqslant & 2 p \varepsilon_k^{1 - \alpha} \int_{X\setminus U_k} | f |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} + \frac{2 p}{C_1} \int_{U_k} | f |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega}. \end{align*} $$
Since
$\operatorname {vol }(U_k) \rightarrow 0$
as
$k \rightarrow \infty $
, it follows from the inequality (3.4) that the second term of the above inequality tends to zero as
$k \rightarrow \infty $
. Again by the inequality (3.4), the first term of the above inequality tends to zero as
$k \rightarrow \infty $
since
$\varepsilon _k \rightarrow 0$
and
$\alpha \in (0, 1)$
.
4 Čech cohomology.
Let X be a compact complex manifold of dimension n, and let
$L \rightarrow X$
be a holomorphic line bundle equipped with a singular metric h such that
$\mathrm {i} \Theta _{L, h} \geqslant 0$
in the sense of currents. Denote by
$\mathcal {U} = \{ U_{\alpha } \}_{\alpha \in I}$
a Stein covering of X and set
$$\begin{align*}U_{\alpha_0 \alpha_1 \cdots \alpha_q} = U_{\alpha_0} \cap U_{\alpha_1} \cap \cdots \cap U_{\alpha_q}. \end{align*}$$
Denote by
$\check {C}^q (\mathcal {U}, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
the Čech q-cochain of
$\mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h )$
. For
${u \in \check {C}^q (\mathcal {U}, \mathcal {O}(\Omega ^p_X \otimes L)\otimes \mathcal {I} ( h ))}$
, denote by
$u_{\alpha _0 \alpha _1 \cdots \alpha _q}$
its component on
$U_{\alpha _0 \alpha _1 \cdots \alpha _q}$
. Let
$$\begin{align*}\delta^q : \check{C}^{q} (\mathcal{U}, \mathcal{O}(\Omega^p_X \otimes L) \otimes \mathcal{I} (h)) \rightarrow \check{C}^{q+1} (\mathcal{U}, \mathcal{O}(\Omega^p_X \otimes L) \otimes \mathcal{I} (h)), \end{align*}$$
be the Čech operator and 
. It is proved in [Reference Cao4, Lem. 5.8] that
$\check {C}^q (\mathcal {U}, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
is a Fréchet space equipped with semi-norms defined by the
$L^2$
-integration on relatively compact subsets. The following result is obtained in [Reference Cao4] for
$u\in \check {H}^p(\mathcal U ,\mathcal {O}(K_X\otimes L)\otimes \mathcal {I}(\varphi ))$
. With the same method, it holds true for
$u\in \check {H}^q (X, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} (h))$
as well. For the sake of completeness, we include the proof here.
Lemma 4.1 [Reference Cao4, Lem. 5.8].
Let
$(X, \omega )$
be a compact complex manifold, and let
$L \rightarrow X$
be a holomorphic line bundle equipped with a singular metric h such that
$\mathrm {i} \Theta _{L, h} \geqslant 0$
in the sense of currents. Let
$\mathcal U=\{ U_{\alpha } \}_{\alpha \in I}$
be a Stein covering of X. Let u be an element in
$\check {H}^q (X, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} (h))$
. If there exists a sequence
$\{ v_k \} \subset \check {C}^q (\mathcal {U}, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
in cohomology class u such that
$$\begin{align*}\lim_{k \rightarrow \infty} \int_{U_{\alpha_0 \alpha_1 \cdots \alpha_q}} | v_{k, \alpha_0 \alpha_1 \cdots \alpha_q} |^2_{h_{0,} \omega} d V_{\omega} =0, \end{align*}$$
where
$h_0$
in the above equality is a fixed smooth metric on L, then
$u=0$
in
$\check {H}^q (X, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
.
Proof. The proof is due to [Reference Cao4]. Combining Guan-Zhou’s strong openness of the multiplier ideal sheaves and the proof of Cao, we can see that
$\check {C}^q (\mathcal {U}, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
is a Fréchet space, equipped with a family of semi-norms defined by
$$\begin{align*}\sum_{\alpha_0\cdots\alpha_q}\int_{V_{\alpha_0\cdots\alpha_q}}|u|^2\omega^n, \mbox{ for any open set } V_{\alpha_0\cdots\alpha_q}\Subset U_{\alpha_0\cdots\alpha_q}.\end{align*}$$
Then the Čech operator is continuous and its Kernel
$\check {Z}^q (\mathcal {U}, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
is also a Fréchet space. Therefore the boundary morphism
$$\begin{align*}\delta^{q-1} : \check{C}^{q - 1} (\mathcal{U}, \mathcal{O}(\Omega^p_X \otimes L) \otimes \mathcal{I} ( h )) \rightarrow \check{Z}^q (\mathcal{U}, \mathcal{O}(\Omega^p_X \otimes L ) \otimes\mathcal{I} ( h )), \end{align*}$$
is continuous.
Since X is compact, the cokernel of
$\delta ^{q-1}$
, i.e.,
$\check {H}^q (X, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
, is of finite dimension and thus the image of
$\delta ^{q-1}$
is closed. Thus the quotient morphism
$$\begin{align*}\operatorname{pr} : \check{Z}^q (\mathcal{U}, \mathcal{O}(\Omega^p_X \otimes L )\otimes \mathcal{I} ( h )) \rightarrow \check{H}^q (\mathcal U, \mathcal{O}(\Omega^p_X \otimes L) \otimes \mathcal{I} ( h )), \end{align*}$$
is continuous. Therefore the equation
$$\begin{align*}\lim_{k \rightarrow \infty} \int_{U_{\alpha_0 \alpha_1 \cdots \alpha_q}} | v_{k, \alpha_0 \alpha_1 \cdots \alpha_q} |^2_{h_0,\omega} d V_{\omega} = 0, \end{align*}$$
implies
$\{ v_k \}_{k = 1}^{\infty }$
tends to
$0$
in
$\check {Z}^q (\mathcal {U}, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
and hence
$$\begin{align*}\lim_{k \rightarrow \infty} \operatorname{pr} (v_k) = 0 \in \check{H}^q (\mathcal U, \mathcal{O}(\Omega^p_X \otimes L) \otimes \mathcal{I} ( h )). \end{align*}$$
Since
$\operatorname { pr }(v_k)=u \in \check {H}^q (\mathcal U, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
, it implies that
$u=0$
in
$\check {H}^q (\mathcal U , \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
.
5 Proof of Theorem 1.1.
Let
$\mathcal {L}_{(L, h)}^{p, q}$
be the sheaf of germs of L-valued
$(p, q)$
forms u with measurable coefficients such that both
$| u |^2_{h, \omega }$
and
$| \bar {\partial } u |^2_{h, \omega }$
are locally integrable. Consider the following exact sequence
$$ \begin{align*} &0 \rightarrow\operatorname{Ker} \bar{\partial}_0 \rightarrow \mathcal{L}_{(L, h)}^{p, 0} \xrightarrow{\bar{\partial}_0} \mathcal{L}_{(L, h)}^{p, 1} \xrightarrow{\bar{\partial}_1} \cdots \xrightarrow{\bar{\partial} _{n-1}} \mathcal{L}_{(L, h)}^{p, n} \longrightarrow 0. \end{align*} $$
By the proof of [Reference Watanabe16, Th. 1.1], it follows from Dolbeault–Grothendieck’s lemma [Reference Demailly7, Chap. I] that
$$\begin{align*}\operatorname{Ker} \bar{\partial}_0 = \mathcal{O} (\Omega^p_X \otimes L) \otimes \mathcal{I} ( h ), \end{align*}$$
and by using the above with Hörmander’s
$L^2$
-estimate, one has the following isomorphism:
$$\begin{align*}H^q (X, \mathcal{O} (\Omega^p_X \otimes L) \otimes \mathcal{I} ( h )) \cong H^q \left(\Gamma \left(X, \mathcal{L}_{(L, h)}^{p, \bullet}\right)\right). \end{align*}$$
Fix a smooth metric
$h_{0}$
on L, then we can write
$h = h_{0} e^{- 2 \varphi }$
for some quasi-plurisubharmonic function
$\varphi $
on X. By Lemma 3.4, one has
$\mathcal {I} ( h ) = \mathcal {I} (h_0 e^{- 2 \varphi }) = \mathcal {I} (h_0 e^{- 2 \hat {\varphi }_k})$
for all k. Here we use the same notations as in Lemma 3.4. Then
$$\begin{align*}H^q (X, \mathcal{O}(\Omega^p_X \otimes L )\otimes \mathcal{I} ( h )) \cong H^q \left( \Gamma \left( X, \mathcal{L}_{(L, h_0 e^{- 2 \hat{\varphi}_k})}^{p, \bullet} \right) \right), \end{align*}$$
for all
$k \in \mathbb {N}$
.
Now assume that
$p \geqslant n - \operatorname {nd} (L, h) + 1$
and
$q = n$
. Let
$\mathcal {U} = \{ U_{\alpha } \}_{\alpha \in I}$
be a Stein covering of X. Using partition of unity, every cohomology
$\alpha \in H^q (X, \mathcal {O}(\Omega ^p_X \otimes L )\otimes \mathcal {I} ( h ))$
can be represented by a smooth L-valued
$(p, n)$
form
$f \in L^2_{p, n} (X, L, h, \omega )$
via the de Rham–Weil isomorphism. By Proposition 3.6, there exists
$u_k$
and
$v_k$
which satisfies the equation
$f = \bar {\partial } u_k + v_k$
and the estimates (3.2) and (3.3).
By solving
$\bar {\partial }$
-equations, we can get a n-cocycle
$$\begin{align*}\{ v_{k, \alpha_0 \alpha_1 \cdots \alpha_n} \} \in \check{Z}^n (\mathcal{U}, \mathcal{O}(\Omega^p_X \otimes L) \otimes \mathcal{I} ( h )), \end{align*}$$
with the following estimate
$$ \begin{align} \int_{U_{\alpha_0 \alpha_1 \cdots \alpha_n}} | v_{k, \alpha_0 \alpha_1 \cdots \alpha_n} |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega} \leqslant C \int_X | v_k |^2_{h_0, \omega} e^{- 2 \hat{\varphi}_k} d V_{\omega}, \end{align} $$
where the constant C is independent of k. Moreover, under the de Rham-Weil isomorphism
$$\begin{align*}H^n \left(\Gamma\left(X, \mathcal{L}_{(L, h_0 e^{- 2 \hat{\varphi}_k})}^{p, \bullet}\right)\right) \cong \check{H}^n (X, \mathcal{O}(\Omega^p_X \otimes L) \otimes \mathcal{I} ( h )), \end{align*}$$
the cohomology class of
$\{ v_{k, \alpha _0 \alpha _1 \cdots \alpha _n} \}$
in
$\check {H}^n (X, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
corresponds to the cohomology of
$v_{k}$
in
$H^n \left (\Gamma \left (X, \mathcal {L}_{(L, h_0 e^{- 2 \hat {\varphi }_k})}^{p, \bullet }\right )\right )$
. From the equation
$f = \bar {\partial } u_k + v_k$
, we know that f and
$v_{k}$
are in the same cohomology class and which corresponds to the cohomology class of
$\alpha \in H^n (X, \mathcal {O}(\Omega ^p_X \otimes L )\otimes \mathcal {I} ( h ))$
By properties (b) of Lemma 3.4,
$\hat {\varphi }_k$
is uniformly upper bounded on X. Then it follows from the estimate (5.1) and (3.3) that
$$\begin{align*}\int_{U_{\alpha_0 \alpha_1 \cdots \alpha_n}} | v_{k, \alpha_0 \alpha_1 \cdots \alpha_n} |^2_{h_0, \omega} d V_{\omega} \rightarrow 0. \end{align*}$$
Then we can conclude that the cohomology class of
$\{ v_{k, \alpha _0 \alpha _1 \cdots \alpha _n} \}$
in
$\check {H}^n (X, \mathcal {O}(\Omega ^p_X \otimes L) \otimes \mathcal {I} ( h ))$
is zero by Lemma 4.1. Hence, the cohomology class
$\alpha = 0$
in
$H^n (X, \mathcal {O}(\Omega ^p_X \otimes L )\otimes \mathcal {I} ( h ))$
. We thus proved that
$$\begin{align*}0= H^n \left(\Gamma \left(X, \mathcal{L}_{(L, h)}^{p, \bullet}\right)\right) \cong H^n (X, \mathcal{O}(\Omega^p_X \otimes L) \otimes \mathcal{I} ( h )), \end{align*}$$
for
$p \geqslant n - \operatorname {nd} (L, h) + 1$
.
6 A new proof of the Bogomolov vanishing theorem.
Another important concept is the Kodaira-Iitaka dimension. Let L be a holomorphic line bundle over a compact complex manifold. For each positive integer
$m\geqslant 1$
, let
$s_0, \cdots , s_N$
be a basis of
$H^0(X,mL)$
. Consider the Kodaira-Iitaka map
$$\begin{align*}\Phi_{m}: X \setminus B_{m} \longrightarrow \mathbb{P}^N = P \left(H^0 (X, m L)^{\ast}\right), \quad x\mapsto[s_0(x):\cdots:s_N(x)], \end{align*}$$
defined by
$s_0, \cdots , s_N$
, where
$B_{m} = \bigcap _{i=0}^{N} s_{i}^{-1}(0)$
is the base locus of the linear system
$| mL |$
. There is a canonical commutative diagram
Moreover, the holomorphic map
$\Phi _{m}$
can be extended to a meromorphic map
$\Phi _{m}: X \dashrightarrow \mathbb {P}^{N}$
. Denote by
$Y_{m} \subset \mathbb {P}^{N}$
the image of the meromorphic map
$\Phi _m$
. The Kodaira-Iitaka dimension
$\kappa (L)$
of L is defined to be
$$\begin{align*}\sup\{\dim Y_m:m\geqslant 1\}. \end{align*}$$
In the case
$H^0(X,mL)=0$
for all
$m\geq 1$
, we set
$\kappa (L)=-\infty $
. It is clear that
$\kappa (L)\leqslant \dim X$
.
Lemma 6.1. Let X be a compact Kähler manifold and
$L \rightarrow X$
a holomorphic line bundle over X. Then there exists a singular metric h on L such that the Kodaira dimension
$\kappa (L) \leqslant \operatorname {nd} (L, h)$
.
Proof. With the notations as above, we may assume that
$\kappa ( L ) = \dim Y_{m} \geqslant 0$
for some
$m \geqslant 1$
. Denote by
$j : Y_{m} \rightarrow \mathbb {P}^{N}$
the natural inclusion map. Then
$\Phi _{m}$
can be written as the composition
$$\begin{align*}X \setminus B_{m} \xrightarrow{\Psi_{m}} Y_{m} \xrightarrow{j} \mathbb{P}^{N}, \end{align*}$$
where
$\Psi _{m}$
is induced by
$\Phi _{m}$
. In this case, we have
$$\begin{align*}\left. L^m \right|{}_{X \setminus B_{m}} = \Phi_{m}^{\ast} \mathcal{O} ( 1 ) = \Psi_{m}^{\ast} \left( j^{\ast} \mathcal{O} ( 1 ) \right). \end{align*}$$
Denote by
$h_{\mathrm {can}}$
the metric on
$\mathcal {O} (1)$
defined by
$$\begin{align*}e^{- \log (| z_0 |^2 + \cdots + | z_N |^2)}, \end{align*}$$
where
$[z_0: \cdots : z_N]$
is the homogeneous coordinate of
$\mathbb {P}^N$
. Its curvature
$\mathrm {i}\Theta _{\mathcal {O} (1), h_{\mathrm {can}}}$
is nothing but the Fubini-Study metric. It follows that the line bundle
$j^{\ast } \mathcal {O} (1) \rightarrow Y_m$
is ample, and on the regular part
$(Y_m)_{\mathrm {reg}}$
of
$Y_m$
, the curvature of the pull back metric
$j^{\ast } h_{\mathrm {can}}$
on
$j^{\ast } \mathcal {O} ( 1 )$
is positive. Since
$\Phi _m : X\setminus B_{m} \rightarrow Y_m$
has dense image, there exists a point
$x_0 \in X\setminus B_{m}$
such that
$y_0 = \Phi _m (x_0) \in (Y_m)_{\mathrm {reg}}$
and the rank of
$(\Phi _m)_{\ast }$
at
$x_0$
is
$\dim Y_m$
.
Define a metric
$h = e^{- \varphi }$
on
$L \rightarrow X$
by local weight
$$\begin{align*}\varphi = \frac{1}{m}\log (| s_0 |^2 + \cdots + | s_N |^2). \end{align*}$$
Then
$\varphi $
admits analytic singularities and the curvature
$\mathrm {i} \Theta _{L, h} \geqslant 0$
in the sense of current. Since
$\Phi _m = j \circ \Psi _m$
and
$h = \Phi _m^{\ast } h_{\mathrm {can}} = \Psi _m^{\ast } j^{\ast } h_{\mathrm {can}}$
, on
$X\setminus B_{m}$
, one has
$$\begin{align*}m\mathrm{i}\Theta_{L, h} = \Psi_{m}^{\ast} \left(\mathrm{i}\Theta_{\mathcal{O} (1), j^{\ast}h_{\mathrm{can}}}\right). \end{align*}$$
Moreover,
$\mathrm {i}\Theta _{\mathcal {O} (1), j^{\ast }h_{\mathrm {can}}}> 0$
and
$\Psi _m$
is a submersion near
$x_0$
. So the number of positive eigenvalues of
$\mathrm {i}\Theta _{L, h}$
is
$\kappa ( L )$
near
$x_0$
. It then follows that
$$\begin{align*}(\mathrm{i}\Theta_{L, h})^{\kappa ( L )} \wedge \omega^{n - \kappa ( L )}> 0, \end{align*}$$
near
$x_0$
. Therefore, by the definition of
$\operatorname {nd} ( L, h )$
, we get that
$$\begin{align*}\kappa (L) \leqslant \operatorname{nd} (L, h). \end{align*}$$
Bogomolov vanishing theorem can be deduced from Theorem 1.1 as follows: Let h be the singular metric on L constructed in Lemma 6.1. In this case, we have
$\kappa ( L ) \leqslant \operatorname {nd} ( L , h )$
. Consider the following exact sequence
$$ \begin{align*}& \cdots \rightarrow H^n (X, \mathcal{O} (\Omega^p_X \otimes L) \otimes \mathcal{I} \left(h\right)) \rightarrow H^n (X, \mathcal{O}(\Omega_X^p \otimes L))\\&\quad \rightarrow H^n \left(V (\mathcal{I} (h)), \mathcal{O}(\Omega^p_n \otimes L) |_{V (\mathcal{I} (h))}\right) \rightarrow \cdots, \end{align*} $$
where
$V ( \mathcal {I} (h))$
is the complex analytic subspace defined by
$\mathcal {I} (h)$
. By Theorem 1.1, we have
$$\begin{align*}H^n (X, \mathcal{O} (\Omega^p_X \otimes L) \otimes \mathcal{I} (h)) = 0. \end{align*}$$
for
$p \geqslant n - \operatorname {nd} ( L , h ) + 1$
. However,
$$\begin{align*}H^n \left(V (\mathcal{I} ( h )), \mathcal{O}\left.\left(\Omega^p_X \otimes L\right) \right|{}_{V (\mathcal{I} ( h ))}\right) = 0, \end{align*}$$
since
$\dim V (\mathcal {I} ( h ))<n$
. It follows that
$$\begin{align*}H^n \left(X, \mathcal{O}\left(\Omega_X^p \otimes L\right)\right) = 0 \quad \text{for} \quad p \geqslant n - \operatorname{nd} ( L , h ) + 1. \end{align*}$$
By construction,
$\kappa ( L ) \leqslant \operatorname {nd} ( L , h )$
, so we can conclude that
$$\begin{align*}H^n \left(X, \mathcal{O}\left(\Omega_X^p \otimes L\right)\right) = 0 \quad \text{for} \quad p \geqslant n - \kappa (L) + 1. \end{align*}$$
Remark 6.2. Let
$L \rightarrow X$
be a holomorphic line bundle over a compact complex manifold. If X is in the Fujiki class, i.e. X admits a Kähler modification
$\pi : Y \rightarrow X$
, then the Bogomolov vanishing theorem is also valid. In fact,
$$\begin{align*}H^{0} \left( X, \Omega_{X}^{p} \otimes L^{-1} \right) \subset H^{0} \left( Y, \Omega_{Y}^{p} \otimes \pi^{\ast}L^{-1} \right) = 0 \quad \text{for} \quad p < \kappa (\pi^{\ast} L) = \kappa (L). \end{align*}$$
Remark 6.3. Let X be a complex Kähler manifold, Y an irreducible complex space and
$F: X \rightarrow Y$
a proper surjective holomorphic map. Let
$L \rightarrow X$
be a holomorphic line bundle. It is well-known that there exists an analytic subset
$Z \subset Y$
such that
$F|_{X \setminus F^{-1}(Z)}: X \setminus F^{-1}(Z) \rightarrow Y \setminus Z$
is a proper submersion. Then one has
$$\begin{align*}F_{\ast} \left( \Omega_{X}^{p} \otimes L^{-1} \right) = 0 \quad \text {for} \quad p < \max_{b \in Y \setminus Z} \kappa \left( L|_{F^{-1}(b)} \right). \end{align*}$$
This is an immediate consequence of the classical Bogomolov vanishing theorem since the coherent sheaf
$F_{\ast } \left ( \Omega _{X}^{p} \otimes L^{-1} \right )$
is torsion free.
Acknowledgments
This research was supported by National Key Research and Development Program of China (Nos. 2021YFA1002600, 2021YFA1003100). The authors are partially supported respectively by National Natural Science Foundation of China (Nos.12271057, 12201060, 12071485, 12071035, 12288201). The fourth author was partially supported by the Fundamental Research Funds for the Central Universities.
