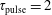1 Introduction
Much attention is being devoted to high pressure non-equilibrium plasmas due to their importance for many technological applications. In particular, nanopulse atmospheric discharges are widely investigated either in the one pulse modality or in repetitive nanopulsed discharges. The experimental characterization of one pulse and multipulse discharges is well developed mostly due to the their relatively easy realization.
The chemical kinetics either in the discharge or in the post-discharge is usually decoupled from the electron component, a hypothesis which can be open to question especially in the post-discharge regime. Vibrational–chemical modelling of CO and mixtures of CO2/CO molecules have been developed for aerospace applications not considering the electron induced processes (see Kosareva & Nagnibeda Reference Kosareva and Nagnibeda2017; Mishina & Kustova Reference Mishina and Kustova2017).
The coupling between EEDF and excited state kinetics has a long history as can be appreciated by looking at different reviews and monographies on the subject (Cacciatore et al. Reference Cacciatore, Capitelli, De Benedictis, Dilonardo and Gorse1986; Capitelli et al. Reference Capitelli, Ferreira, Gordiets and Osipov2000, Reference Capitelli, Celiberto, Colonna, Esposito, Gorse, Hassouni, Laricchiuta and Longo2016) in general dealing with moderate pressure conditions (Torr regime).
High pressure nanosecond pulse discharges followed by a long afterglow have been investigated for nitrogen, emphasizing the dependence of the electron energy distribution function on the concentrations of electronically excited states. Indeed, superelastic electronic collisions of cold electrons with metastable states were responsible of the formation of structures in EEDF (Gorse et al. Reference Gorse, Paniccia, Bretagne and Capitelli1986; Colonna et al. Reference Colonna, Laporta, Celiberto, Capitelli and Tennison2015). In these studies, vibrationally excited molecules play a minor role in affecting the plasma kinetics due to the fact that the short pulse considered is unable to create a large concentration of vibrationally excited states. The situation changes when modulating the duration of the pulse as well as the time between one pulse and the next as recently shown in the case of atmospheric hydrogen plasmas (Colonna et al. Reference Colonna, Laporta, Celiberto, Capitelli and Tennison2015; Colonna, D’Ammando & Pietanza Reference Colonna, D’Ammando and Pietanza2017a ).
Very recently, nanosecond discharges were also studied for the CO2 system for conditions similar to those occurring in dielectric barrier discharges (DBD) (Capitelli et al. Reference Capitelli, Colonna, D’Ammando and Pietanza2017a ).
In the present paper, we consider one pulse nanosecond discharge and corresponding afterglow in reacting CO. The choice of CO is justified by the importance of this system in different applications including the infrared CO laser as well as the possibility of creating micro and nano carbon materials when the corresponding discharge produces a long plateaux in the vibrational distribution function (Mori & Suzuki Reference Mori and Suzuki2009; Belov et al. Reference Belov, Vanneste, Aghaee, Paulussen and Bogaerts2017). Moreover, the kinetics of CO under non-equilibrium plasma conditions is of primary importance in CO2 discharges when the dissociation of CO2 produces important quantities of CO. This problem, largely underestimated by the recent efforts in the activation of CO2 by cold plasmas (Kozak & Bogaerts Reference Kozak and Bogaerts2014, Reference Kozak and Bogaerts2015; Pietanza et al. Reference Pietanza, Colonna, D’Ammando, Laricchiuta and Capitelli2015; Bogaerts et al. Reference Bogaerts, Wang, Berthelot and Guerra2016; Pietanza et al. Reference Pietanza, Colonna, D’Ammando and Capitelli2017a ), can be solved by inserting in the CO2 system a robust plasma kinetics describing the CO reacting system.
The state to state plasma kinetics of CO has been recently re-examined (see Pietanza, Colonna & Capitelli Reference Pietanza, Colonna and Capitelli2017b ) for conditions typical of moderate pressure microwave discharges, taking into account the efforts made in the past by Gorse, Cacciatore & Capitelli (Reference Gorse, Cacciatore and Capitelli1984a ), Gorse & Capitelli (Reference Gorse and Capitelli1984b ).
The new model contains several important improvements with respect to the past attempts either in the quality of cross-sections of elementary processes or in the plasma kinetic model describing the activation of CO. In particular, the electron-impact resonant vibration excitation processes in CO (the electron–vibration (e–V) processes) are nowadays well described thanks to the large effort made by Laporta et al. (Reference Laporta, Cassidy, Tennyson and Celiberto2012), Laporta, Tennyson & Celiberto (Reference Laporta, Tennyson and Celiberto2016). These new data can be used instead of the assumption of e–V linking only the first 10 CO vibrational levels Gorse, Cacciatore & Capitelli Reference Gorse, Cacciatore and Capitelli1984a
; Gorse & Capitelli Reference Gorse and Capitelli1984b
. These processes can be important for very short pulses when the e–V collisions from
$v=0$
dominate other processes in the formation of the vibrational distribution function of CO. Another important improvement is the new activation energy value of the Boudouard reactions, i.e.
$E_{a}=8.3$
eV calculated by Barreto et al. (Reference Barreto, De O. Euclides, Albernaz, Aquilanti, Capitelli, Grossi, Lombardi, Macheret and Palazzetti2017), instead of 6 eV used in Gorse, Cacciatore & Capitelli Reference Gorse, Cacciatore and Capitelli1984a
; Gorse & Capitelli Reference Gorse and Capitelli1984b
and 11.3 eV in Essenhigh et al. (Reference Essenhigh, Utkin, Bernard, Adamovich and Rich2006), which affects either the formation of CO2 in pure CO discharges or the deactivation of the plateau in the vibrational distribution of CO.
On the other hand, the present kinetic model considers the presence of metastable excited states of CO and corresponding C and O atoms produced in the discharge, which are able to form a large number of structures in the EEDF in the post-discharge regime as a result of superelastic electronic collisions, not considered in Gorse & Capitelli (Reference Gorse, Cacciatore and Capitelli1984a ,Reference Gorse and Capitelli b ).
The paper is divided into 4 sections. After the introduction, § 2 describes the model, § 3 reports the results obtained by changing the initial conditions of the discharge, § 4 reports conclusions and perspectives. Explicit expressions of the dissociation rates are reported in an appendix A at the end of the paper.
2 The model
The model is based on the solution of a zero-dimensional time dependent Boltzmann equation for the electrons coupled to the non-equilibrium vibrational and electronic excited state kinetics of the CO molecule with a simple dissociation and ionization kinetics describing the plasma mixture (Capitelli et al. Reference Capitelli, Colonna, D’Ammando and Pietanza2017a ,Reference Capitelli, Colonna, D’Ammando, Hassouni, Laricchiuta and Pietanza b ; Pietanza et al. Reference Pietanza, Colonna, D’Ammando and Capitelli2017c ).
The electron Boltzmann equation is coupled in this case to the non-equilibrium vibrational kinetics of the CO levels, to the kinetics of electronically excited states of CO, C and O species, to the dissociation–recombination kinetics, to the ionization–recombination kinetics. All the kinetics are self-consistently solved in a time dependent manner.
The electron Boltzmann equation can be written in the following compact form
$$\begin{eqnarray}\frac{\text{d}n(\unicode[STIX]{x1D700},t)}{\text{d}t}=-\frac{\text{d}J_{E}}{\text{d}\unicode[STIX]{x1D700}}-\frac{\text{d}J_{\text{el}}}{\text{d}\unicode[STIX]{x1D700}}-\frac{\text{d}J_{\text{e}{-}\text{e}}}{\text{d}\unicode[STIX]{x1D700}}+S_{\text{in}}+S_{\text{sup}},\end{eqnarray}$$
where
$n(\unicode[STIX]{x1D700},t)$
represents the number of electrons in the energy range
$\unicode[STIX]{x1D700}$
to
$\unicode[STIX]{x1D700}+\text{d}\unicode[STIX]{x1D700}$
, linked to the EEDF
$f(\unicode[STIX]{x1D700},t)$
by
$$\begin{eqnarray}f(\unicode[STIX]{x1D700},t)=\frac{n(\unicode[STIX]{x1D716},t)}{N_{e}(t)}\unicode[STIX]{x1D700}^{-1/2},\end{eqnarray}$$
with the normalization condition
$$\begin{eqnarray}N_{e}(t)=\int _{0}^{\infty }n(\unicode[STIX]{x1D700},t)\,\text{d}\unicode[STIX]{x1D700},\quad \int _{0}^{\infty }f(\unicode[STIX]{x1D700},t)\,\text{d}\unicode[STIX]{x1D700}=1,\end{eqnarray}$$
where
$N_{e}(t)$
is the instantaneous electron number density.
The first three terms on the right-hand side of (2.1) correspond to fluxes
$J$
along the electron energy axis due to, respectively, the electric field
$\text{d}J_{E}/\text{d}\unicode[STIX]{x1D700}$
, the elastic electron–molecule collisions
$\text{d}J_{\text{el}}/\text{d}\unicode[STIX]{x1D700}$
and the electron–electron (e–e) collisions
$\text{d}J_{\text{e}{-}\text{e}}/\text{d}\unicode[STIX]{x1D700}$
. The sources terms
$S$
are due to inelastic collisions including electronic excitation, dissociation and ionization processes
$S_{\text{in}}$
, while the last term
$S_{\text{sup}}$
denotes superelastic collisions involving electrons and vibrationally and electronically excited states.
Explicit expressions of the different terms in (2.1) can be found in a number of papers (Rockwood Reference Rockwood1973; Capitelli et al. Reference Capitelli, Celiberto, Colonna, Esposito, Gorse, Hassouni, Laricchiuta and Longo2016).
The plasma mixture considered is composed of the following species: CO, CO2, C, O, CO+, CO2 +, C+, O+ and e-.
Figure 1. Schematic representation of the (a) CO and (b) C and O energy level diagrams.
The energy level diagrams of CO, C and O are schematically represented in figure 1. The CO molecule has 80 vibrational levels in the ground electronic state (
$X^{1}\unicode[STIX]{x1D6F4}^{+}$
), whose energies, calculated in the anharmonic oscillator approximation, have been taken from the work of Laporta et al. (Reference Laporta, Tennyson and Celiberto2016), together with the dissociation energy value of 11.128 eV (CO → C(3P) + O(3P)). Several singlet and triplet CO electronic excited states have been considered, in particular, three triplet states,
$a^{3}\unicode[STIX]{x1D6F1}$
(6.006 eV),
$a^{\prime 3}\unicode[STIX]{x1D6F4}^{+}$
(6.863),
$b^{3}\unicode[STIX]{x1D6F4}^{+}$
(10.40 eV) and four singlet states,
$A^{1}\unicode[STIX]{x1D6F1}$
(8.03 eV),
$B^{1}\unicode[STIX]{x1D6F4}^{+}$
(10.78 eV),
$C^{1}\unicode[STIX]{x1D6F4}^{+}$
(11.40 eV),
$E^{1}\unicode[STIX]{x1D6F4}^{+}$
(11.52 eV).
For C and O atoms, only four and five electronic levels are accounted for, see figure 1(b), which from now on will be labelled as C(3P), C(1D), C(1S), C(5S0) and O(3P), O(1D), O(1S), O(3S) and O(5S), respectively. Their energies have been taken from the National Institute of Standards and Technology (NIST) Atomic Spectra Database.
The electron-impact cross-sections entering in the Boltzmann equation are those corresponding to the processes listed in table 1, together with the corresponding sources and discussed in a recent paper on the application of the model to microwave plasmas and afterglows (Pietanza et al. Reference Pietanza, Colonna and Capitelli2017b ). The most important improvement with respect to the current literature is a complete set of electron-impact resonant vibration excitation cross-sections linking all the vibrational levels of CO (see processes e–VRes in table 1) as well as the consideration of the resonant dissociation cross-sections depending on the vibrational levels of CO (see process DRes(v) in table 1).
Table 1. Electron-impact processes: momentum transfer (MT), ionization (I), excitation and deexcitation of CO electronically excited states, assumed as metastable states (Met), dissociation (D), vibrational excitation (e–V), excitation and deexcitation of C and O excited states (e–C, e–O).
2.1 CO plasma chemistry
In the model, the following two reactive channels assisted by vibrational excitation (pure vibrational mechanisms, PVM) are accounted for:
-
(1) direct dissociation (PVM1)
(2.1.1)
$$\begin{eqnarray}\text{CO}(v)+M\rightarrow \text{C}+\text{O}+\text{M}.\end{eqnarray}$$
-
(2) Boudouard or disproportionation reaction (PVM2)
(2.1.2)
$$\begin{eqnarray}\text{CO}(v)+\text{CO}(w)\rightarrow \text{CO}_{2}+\text{C}.\end{eqnarray}$$
The equation for the PVM1 and PVM2 rate coefficients, can be found in the appendix A and have been derived from Essenhigh et al. (Reference Essenhigh, Utkin, Bernard, Adamovich and Rich2006) and Pietanza et al. (Reference Pietanza, Colonna and Capitelli2017b ). The activation energy of process (2.1.2) has been considered equal to 8.3 eV from the work of Barreto et al. (Reference Barreto, De O. Euclides, Albernaz, Aquilanti, Capitelli, Grossi, Lombardi, Macheret and Palazzetti2017).
The two PVM mechanisms can have an important role especially in microwave (MW) discharge and post-discharge conditions, while in nanopulse atmospheric discharges, dissociation occurs mainly through direct electron-impact mechanisms (DEM) as will be discussed in the present work (see also Capitelli et al. Reference Capitelli, Colonna, D’Ammando and Pietanza2017a ), i.e. through the following process
$$\begin{eqnarray}e+\text{CO}(v)\leftrightarrow e+\text{C}+\text{O}.\end{eqnarray}$$
Electron-impact ionization of CO, C and O is also considered, i.e.
$$\begin{eqnarray}e+\text{CO}(v)\leftrightarrow e+\text{CO}^{+}+e\end{eqnarray}$$
$$\begin{eqnarray}e+\text{C}(\text{}^{3}\text{P})\leftrightarrow e+\text{C}^{+}\end{eqnarray}$$
$$\begin{eqnarray}e+\text{O}(\text{}^{3}\text{P})\leftrightarrow e+\text{O}^{+}.\end{eqnarray}$$
The electron-impact rates of processes (2.1.3)–(2.1.6) are calculated from the corresponding cross-sections
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D700})$
, used for the Boltzmann equation, the EEDF
$f(\unicode[STIX]{x1D700})$
and the electron velocity
$v(\unicode[STIX]{x1D700})$
by integrating over the electron energy
$\unicode[STIX]{x1D700}$
$$\begin{eqnarray}K=\int _{E_{t}}v(\unicode[STIX]{x1D700})\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D700})f(\unicode[STIX]{x1D700})\,\text{d}\unicode[STIX]{x1D700}.\end{eqnarray}$$
The formed C and O atoms, produced through both the PVM (see (2.1.1)) and DEM (see (2.1.3)) dissociation mechanisms, are allowed to recombine according to the process
$$\begin{eqnarray}\text{C}+\text{O}+\text{M}\rightarrow \text{CO}+\text{M}.\end{eqnarray}$$
Finally, CO+ losses occur mainly by the dissociative recombination process
$$\begin{eqnarray}\text{CO}^{+}+e\rightarrow \text{C}+\text{O}.\end{eqnarray}$$
The rate of processes (2.1.8) and (2.1.9) are taken from Kozak & Bogaerts (Reference Kozak and Bogaerts2014).
2.2 CO vibrational kinetics
The CO vibrational distribution function (VDF) is obtained by the solution of a coupled system of differential equations, one equation for each vibrational level, of the kind
$$\begin{eqnarray}\displaystyle \frac{\text{d}N_{v}}{\text{d}t} & = & \displaystyle \left(\frac{\text{d}N_{v}}{\text{d}t}\right)_{\text{e}{-}\text{V}}+\left(\frac{\text{d}N_{v}}{\text{d}t}\right)_{\text{e}{-}\text{D}}+\left(\frac{\text{d}N_{v}}{\text{d}t}\right)_{\text{e}{-}\text{I}}+\left(\frac{\text{d}N_{v}}{\text{d}t}\right)_{\text{PVM}}\nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{\text{d}N_{v}}{\text{d}t}\right)_{\text{V}{-}\text{V}}+\left(\frac{\text{d}N_{v}}{\text{d}t}\right)_{\text{V}{-}\text{T}}+\left(\frac{\text{d}N_{v}}{\text{d}t}\right)_{\text{SE}},\end{eqnarray}$$
where e–V, e–D and e–I contributions correspond, respectively, to the electron-impact resonant vibrational excitation processes (e–VRes), to the two contributions of direct (DDir) and resonant (DRes) dissociation processes and to ionization (ICO) processes listed in table 1. The PVM term corresponds to the contribution of dissociation induced by vibrational excitation due to both direct dissociation (2.1.1) and the Boudouard process (2.1.2). The last terms (V–V, V–T and SE) correspond to the following energy-exchange processes:
-
(1) V–V (vibration–vibration)
(2.2.2)
$$\begin{eqnarray}\text{CO}(v)+\text{CO}(w)\leftrightarrow \text{CO}(v-1)+\text{CO}(w+1)+\unicode[STIX]{x0394}\unicode[STIX]{x1D700}.\end{eqnarray}$$
-
(2) V–T (vibration–translation) by CO
(2.2.3)
$$\begin{eqnarray}\text{CO}(v)+\text{CO}\leftrightarrow \text{CO}(v-1)+\text{CO}+\unicode[STIX]{x0394}\unicode[STIX]{x1D700}_{T}.\end{eqnarray}$$
-
(3) V–T by C, O
(2.2.4)
$$\begin{eqnarray}\text{CO}(v)+\text{C}\leftrightarrow \text{CO}(v-1)+\text{C}+\unicode[STIX]{x0394}\unicode[STIX]{x1D700}_{T}\end{eqnarray}$$
(2.2.5)
$$\begin{eqnarray}\text{CO}(v)+\text{O}\leftrightarrow \text{CO}(v-1)+\text{O}+\unicode[STIX]{x0394}\unicode[STIX]{x1D700}_{T}.\end{eqnarray}$$
-
(4) SE (spontaneous emission)
(2.2.6)
$$\begin{eqnarray}\text{CO}(v)\leftrightarrow \text{CO}(w)+h\unicode[STIX]{x1D708}_{vw}.\end{eqnarray}$$
The different rate coefficients are discussed by Pietanza et al. (Reference Pietanza, Colonna and Capitelli2017b ).
3 Results
In this section, we report the results obtained by applying the model to different discharge and post-discharge conditions. In particular, two different initial discharge conditions have been selected considering applied reduced field E/N and pulse durations
$\unicode[STIX]{x1D70F}_{\text{pulse}}$
values of 200 Td, 2 ns and 130 Td 50 ns with different post-discharge times in the ms regime. On the other hand, pressure (1 atm) and gas temperature (
$T_{\text{gas}}=500$
K) are kept constant in all the numerical examples. The selected examples are sufficient to understand the non-equilibrium effects in both EEDF and VDF.
3.1 Case study 1
The following initial conditions are selected
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=200$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=2$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=10$
ms. Before examining the results, we want to anticipate that these E/N and
$\unicode[STIX]{x1D70F}_{\text{pulse}}$
values minimize the input of vibrational quanta in the CO molecule, i.e. the increase of the corresponding macroscopic vibrational temperature of CO (
$T_{\text{v}{-}\text{CO}}$
) is expected to be very small. On the other hand, the EEDF in the discharge will reach a quasistationary condition in times much less than the pulse duration.
We expect a minor role of vibrational superelastic collisions in the EEDF due to the corresponding low vibrational temperature. In addition, during the discharge, the superelastic electronic collisions should have a limited effect on the EEDF because the high electron temperature controlled by the high E/N value is such to hide the peaks formed by these collisions, the reverse will be in post-discharge conditions.
These observations are confirmed by inspection of the typical relaxation times for the present condition reported in the following table (table 2), which represent, in order, the time to achieve a quasistationary EEDF (
$\unicode[STIX]{x1D70F}_{\text{EEDF}}$
), the characteristic time to pump the vibrational energy in the system (
$\unicode[STIX]{x1D70F}_{\text{e}{-}\text{V}}$
), the time of V–V energy-exchange processes (
$\unicode[STIX]{x1D70F}_{\text{V}{-}\text{V}}$
) and the time of V–T relaxation by CO (
$\unicode[STIX]{x1D70F}_{\text{V}{-}\text{T}(\text{CO})}$
) and by C and O (
$\unicode[STIX]{x1D70F}_{\text{V}{-}\text{T}(\text{C},\text{O})}$
). Such relaxation times are calculated from the corresponding rates linking the ground and the first vibrational level.
Table 2. Characteristic times evaluated at the end of the pulse (
$\unicode[STIX]{x1D70F}_{\text{pulse}}=2$
ns) when the electron density is approximatley
$2.2\times 10^{14}~\text{cm}^{-3}$
.
From table 2, we can see that
$\unicode[STIX]{x1D70F}_{\text{e}{-}\text{V}}>\unicode[STIX]{x1D70F}_{\text{pulse}}$
implying a very small vibrational pumping in the system. This is indeed the case as can be observed from figure 2(a), where the 0–1 vibrational temperature of CO and the electron temperature are reported as a function of time in the discharge and post-discharge conditions.
Figure 2. (a) Temperature and (b) molar fraction time evolution in case study 1 (
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=200$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=2$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=10$
ms).
We observe that the vibrational temperature of CO presents a very small increase from 500 to 640 K, while the electron temperature soon reaches a quasistationary value of approximately 30 000 K, in the so-called cold gas approximation. In this case, under discharge conditions, superelastic vibrational collisions are practically absent, while superelastic electronic collisions are hidden by the heating of EEDF by the applied E/N value, as already anticipated. In the post-discharge conditions, we can observe an abrupt decrease of electron temperature following the turning off of the electric field. Figure 2(b), on the other hand, reports the concentration of the different species under discharge and post-discharge conditions. We can observe an increase of approximately an order of magnitude in the electron density under discharge conditions, followed by its rapid decrease in the post-discharge due to the dissociative recombination process with CO+. Carbon and oxygen atom concentrations formed under discharge conditions by direct electron-impact collisions keep their values in the post-discharge up to 10 ms, starting to decrease for
$t>10$
ms as a result of the recombination process (2.1.8). C+ and O+ species start being relatively important in the post-discharge for
$t>1$
ms.
The vibrational distribution for this case study is reported in figure 3 as a function of time in (a) discharge and (b) post-discharge conditions. Under discharge conditions, the VDF is controlled by e–V transition over the whole vibrational ladder, i.e. by the process e–VRes in table 1. The corresponding rates decrease with increasing
$v_{f}$
generating the form reported in figure 3(a). Once the VDF tail is sufficiently pumped by e–V processes, for
$t>10$
ns, only a small depletion of the VDF tail for
$v>60$
is observed due to the effect of the direct dissociation process (2.1.1), while the contribution of the Boudouard process, which acts in an intermediate range of
$v$
values (
$v>20$
), is hidden by the dominance of e–V processes.
During the post-discharge, see figure 3(b), the quanta introduced by e–V processes are, to a given extent, redistributed by V–V processes and then deactivated by V–T ones. In any case, the corresponding plateaux present a molar fraction of
$10^{-7}$
, insufficient to activate pure vibrational mechanisms in the dissociation process.
Figure 3. Vibrational distribution function in (a) discharge and (b) post-discharge conditions for case study 1 (
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=200$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=2$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=10$
ms).
Figure 4. Electron energy distribution function in (a) discharge and (b) post-discharge conditions for case study 1 (
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=200$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=2$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=10$
ms).
Figure 4 presents the corresponding time dependent EEDF. Under discharge conditions (figure 4 a) the EEDF rapidly reaches a quasistationary condition characterized by a quasi-Maxwellian distribution function. More interesting is the behaviour of the EEDF post-discharge, which is governed by the repetition of different peaks due to the superelastic electronic collisions of CO metastables and cold electrons, confirming the parametric study of Gorse et al. (Reference Gorse, Paniccia, Bretagne and Capitelli1986). In the present study, the concentration of CO electronically excited states is calculated as a result of pumping and deactivation by electron-impact collisions (see MetCO processes in table 1), disregarding optical and quenching processes. The peaks reported in figure 4(b) reflect the threshold energies of the CO electronically excited states considered in the present work, which are more numerous than the choice of Gorse et al. (Reference Gorse, Paniccia, Bretagne and Capitelli1986). It should be noted that the role of electronic states becomes evident when the reduced electric field is turned off, determining a very cold EEDF in the low energy zone, thus allowing to the considered excited states to manifest the role of superelastic electronic collisions in forming repetitive structures in the EEDF. In addition, the numerous CO electronic excited states inserted in the Boltzmann equation form a quasicontinuous sequence of maxima in the EEDF.
In figure 5, we report the CO dissociation rates due to the different reactive channels as a function of the vibrational temperature in (a) discharge and (b) post-discharge conditions. In particular, we report the rate of the direct electron impact dissociation process DEM (see process in (2.1.3)), resonant dissociation process (RES) (see process DRes in table 1) and pure vibrational mechanisms of direct dissociation PVM1 (see process in (2.1.1)) and Boudouard process PVM2 (see process in (2.1.2)). The explicit rate expressions can be found in Pietanza et al. (Reference Pietanza, Colonna and Capitelli2017b ) (see also the appendix A). As we can note, the plasma kinetics is dominated by direct dissociation electron-impact mechanisms, since the corresponding DEM rates are larger than the PVM1 and PVM2 ones, the difference decreasing in the post-discharge.
Figure 5. Dissociation rates (
$\text{cm}^{3}~\text{s}^{-1}$
) as a function of the vibrational temperature in (a) discharge and (b) post-discharge conditions for case study 1 (
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=200$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=2$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=10$
ms).
3.2 Case study 2
The selected conditions change in
$\text{E/N}=130$
Td and
$\unicode[STIX]{x1D70F}_{\text{pulse}}=50$
ns, implying a larger vibrational energy pumping as compared with the previous case. The relevant results qualitatively follow those reported in the previous case, as can be observed by looking at the corresponding figures (see figures 6–9). In this case, however, the vibrational temperature of CO increases up to 1400 K (see figure 6
a), enhancing the electron temperature at the end of the pulse as a consequence of superelastic vibrational collisions (see the peak in
$T_{\text{e}}$
at the end of the pulse). The trend of the electron and C and O molar fractions follow the previous ones also from a quantitative point of view (compare figures 6
b and 2
b). Their molar fractions reach a value of
$10^{-4}$
against
$10^{-5}$
obtained in the first case, the pulse duration being more important than the choice of E/N value in increasing the molar fraction of C and O atoms. The electron molar densities are very similar in the two cases because a sort of compensation exists between E/N value and pulse duration for the two case studies, i.e. the increase of ionization rates with E/N in case 1 is compensated for by the increase of rates due to the increase of the pulse duration in case 2.
Figure 6. (a) Temperature and (b) molar fraction time evolution in case study 2 (
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=130$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=50$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=4$
ms).
Figure 7. Vibrational distribution function in (a) discharge and (b) post-discharge conditions for the case study 2 (
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=130$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=50$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=4$
ms).
Figure 8. Electron energy distribution function in (a) discharge and (b) post-discharge conditions for case study 1 (
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=130$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=50$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=4$
ms).
Figure 9. Dissociation rates (
$\text{cm}^{3}~\text{s}^{-1}$
) as a function of the vibrational temperature in (a) discharge and (b) post-discharge conditions for case study 2 (
$T_{\text{gas}}=500$
K,
$p=1$
atm,
$\text{E/N}=130$
Td,
$\unicode[STIX]{x1D70F}_{\text{pulse}}=50$
ns,
$\unicode[STIX]{x1D70F}_{\text{afterglow}}=4$
ms).
The characteristic times reported in table 3 for this case study are very similar to those reported for case study 1 (table 2), the major difference being the increase of vibrational temperature in this case as well as the higher production of C and O atoms due to the long pulse duration.
Table 3. Characteristic times evaluated at the end of the pulse (
$\unicode[STIX]{x1D70F}_{\text{pulse}}=50$
ns) when the electron density is approximately
$2\times 10^{15}~\text{cm}^{-3}$
.
Qualitatively, the time evolution of the VDF under discharge and post-discharge conditions is similar to the results of previous case even though quantitatively the VDF, in the new case, is orders of magnitude higher than the 2 ns/200 Td case, both in discharge and post-discharge conditions, i.e. the pulse duration is more effective than E/N in increasing the input of vibrational quanta in the vibrational ladder. The reverse is observed for EEDF in both discharge and post-discharge conditions. In both cases, the EEDF at 200 Td is more populated than the corresponding values at 130 Td, i.e. the reduced electric field is predominant in forming the EEDF, the pulse duration is not active enough in the pumping of the electronically excited states. As a result, the EEDF in the post-discharge regime is more populated than in the first case study.
Finally, by looking to figure 9, where the dissociation rates are reported for this second case study, it is clear that PVM rates, in particular the one corresponding to the Boudouard process (PVM2), are increased with respect to case study 1, due to the higher vibrational excitation, which start approaching the DEM rates. Also in this case, the DEM rates remain higher that the PVM ones.
4 Conclusions and perspectives
The present results indicate the importance of the pulse duration in increasing the population of vibrational excited states and their role in affecting the PVM mechanisms in the activation of CO. In the 2 ns/200 Td discharge conditions, we observe that the plasma chemistry is governed by the electron-impact processes. In addition, the population of electronically excited states becomes essential in shaping the EEDF in the post-discharge. This last behaviour is also present in the post-discharge of a 50 ns/130 Td pulse discharge; in this case, however, PVM rates start to approach the DEM ones. This behaviour becomes essential in the microwave discharges, as shown in Pietanza et al. (Reference Pietanza, Colonna and Capitelli2017b ).
The reported results can be used as a guide to choose the initial conditions in nanopulsed repetitive discharges, in particular the duration of each pulse and the time between the different pulses.
An interesting aspect of the results presented in figures 2–5 is their qualitative and quantitative similarity with the corresponding ones reported by Capitelli et al. (Reference Capitelli, Colonna, D’Ammando and Pietanza2017a ) for the same conditions as case 1 in CO2 discharge and post-discharge conditions. In the CO2 case, the molar fraction and VDF of CO2 present a time dependent behaviour similar to that of CO, shown in the present case study 1. This can be observed by comparing the results of figures 2–5 of the present paper and the corresponding figures 9–12 in Capitelli et al. (Reference Capitelli, Colonna, D’Ammando and Pietanza2017a ). The similarity in the trends emphasizes the necessity of considering vibrational excitation of CO with the same accuracy as that of CO2, in the context of the CO2 plasma activation problem. In the post-discharge of the CO system (figure 4 b), we observe a more structured EEDF than in the CO2 case (see figure 11b in Capitelli et al. Reference Capitelli, Colonna, D’Ammando and Pietanza2017a ), which could have some role in the global kinetics of CO2. Of course, the introduction of the whole CO vibrational kinetics in the corresponding one for CO2 increases the computational time especially for higher-dimensional model (one, two and three dimensions).
An alternative could be to use reduction approaches to simplify the global kinetics, as recently proposed by Colonna et al. (Reference Colonna, Armenise, Bruno and Capitelli2006) for the activation of diatomic molecules, based on the kinetics of the last vibrational bound state. This model could be applied when the so-called ladder climbing model (Capitelli, Dilonardo & Molinari Reference Capitelli, Dilonardo and Molinari1977; Capitelli, Colonna & Esposito Reference Capitelli, Colonna and Esposito2004) can be used for describing the dissociation of the molecule, as also reported (to a given extent) in the CO2 case by Peeremboom, Khaj & Degrez (Reference Peeremboom, Khaj and Degrez2017).
In the case of CO, this model cannot be applied because the last bound level is scarcely populated and the PVM2 mechanism needs the opening of a reaction involving an intermediate level, this situation being present under many situations of cold plasmas (see for example Colonna et al. Reference Colonna, Tuttafesta, Capitelli and Giordano1999). This means that the reduction theory of Colonna et al. (Reference Colonna, Armenise, Bruno and Capitelli2006) should be refined to introduce a series of levels which typically mime the opening of reactive channels.
The other conclusion of the present paper is the role of the metastable electronic states of CO in forming structures in EEDF, as a consequence of the superelastic collisions of these states with cold electrons. We can anticipate that these processes will occur also in the CO2 mixture producing CO with large consequences on the corresponding EEDF and more in general on the plasma kinetics. As a perspective, we will introduce a more robust kinetics for these metastable states. In the present approach, the population and depopulation of excited states are due to electron collisions, neglecting optical decay and quenching reactions. Taking these reactions into account (see for example Colonna & Capitelli Reference Colonna and Capitelli2001; Colonna et al. Reference Colonna, Pietanza, D’Ammando, Celiberto, Capitelli and Laricchiuta2017b ), including the redistribution of electronic energy after the quenching process (Pietanza et al. Reference Pietanza, Colonna and Capitelli2017b ), will probably introduce a new scenario in the form of EEDF and VDF in the post-discharge. In this context, the models developed for describing CO shock wave flow should be also taken into account (Aliat, Chikhaoui & Kustova Reference Aliat, Chikhaoui and Kustova2003, Reference Aliat, Chikhaoui and Kustova2005). In addition, the theoretical dissociative–recombination rates of process (2.1.9) by Mezei et al. (Reference Mezei, Backodissa-Kiminou, Tudorache, Morel, Chakrabarti, Motapon, Dulieu, Robert, Tchang-Brillet and Bultel2015), including the calculated branching ratios to the formed electronically excited states of C and O atoms, should be considered. The relevant cross-sections and rates depend on the initial vibrational state of the CO+ ions adding new complexity to the whole kinetics at the moment beyond the aim of the present work.
Finally, the present results can be also considered to be a possible guide for the understanding of the behaviour of DBD discharges, which present more complicated spatio-temporal profiles of E/N (see for example Levko, Paschulli & Raja Reference Levko, Paschulli and Raja2017). In particular, the time dependent streamers are characterized by duration times ranging from the sub-nanosecond to several nano-second level and an electron density of
$10^{14}$
–
$10^{15}~\text{cm}^{-3}$
. Under these conditions, not too far from those reported in cases 1 and 2, we can expect a minor importance of the vibrational kinetics in affecting the EEDF especially for sub-nanosecond streamers. On the contrary, in both regimes, the EEDF keeps a memory of the electronic excited states, especially in the spatial zone characterized by a low reduced electric field.
Acknowledgement
This work is dedicated to Professor F. Pegoraro for his important contributions to the physics of collisionless plasmas.
Appendix A
The direct electron-impact dissociation rate (DEM) and the resonant dissociation rate (RES) are calculated by taking into account the contribution to dissociation from all the CO vibrational levels v, according to
$$\begin{eqnarray}\displaystyle & \displaystyle \text{DEM}=\mathop{\sum }_{v}k_{D}^{\text{dir}}(v)(E/N,f_{v},x_{E_{i}},x_{e},x_{\text{C}},x_{\text{O}},x_{\text{C}^{+}},x_{\text{O}^{+}})f_{v} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{RES}=\mathop{\sum }_{v}k_{D}^{\text{Res}}(v)(E/N,f_{v},x_{E_{i}},x_{e},x_{\text{C}},x_{\text{O}},x_{\text{C}^{+}},x_{\text{O}^{+}})f_{v}, & \displaystyle\end{eqnarray}$$
where
$f_{v}$
is the molar fraction of the vth vibrational level and
$k_{D}^{\text{dir}}(v)$
and
$k_{D}^{\text{Res}}(v)$
are the rates for direct and resonant dissociation from the v level (i.e. the rates of processes Ddir(v) and DRes(v) in table 1).
$k_{D}^{\text{dir}}(v)$
and
$k_{D}^{\text{Res}}(v)$
are calculated from the EEDF and the corresponding cross-sections by using (2.1.7) and thus depend indirectly also on E/N,
$f_{v}$
and
$x_{E_{i}}$
,
$x_{e}$
,
$x_{\text{C}}$
,
$x_{\text{O}}$
,
$x_{\text{C}^{+}}$
,
$x_{\text{O}^{+}}$
, which are, respectively, the molar fractions of CO electronic excited states, electrons, C, O, C+ and O+.
The two PVM rates for direct dissociation and Boudouard process can be calculated by
$$\begin{eqnarray}\displaystyle & \displaystyle \text{PVM}_{1}=\frac{n_{\text{CO}}}{n_{e}}\mathop{\sum }_{v}k_{D}^{\text{direct}}(v)(\unicode[STIX]{x1D6FC},T_{\text{gas}})f_{v} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{PVM}_{2}=\frac{n_{\text{CO}}}{n_{e}}\mathop{\sum }_{v,w}k_{D}^{\text{Boud}}(v,w)(E_{a},T_{\text{gas}})f_{v}\,f_{w}, & \displaystyle\end{eqnarray}$$
where
$k_{D}^{\text{direct}}(v)$
and
$k_{D}^{\text{Boud}}(v,w)$
are the rate of processes (2.1.1) and (2.1.2).
$k_{D}^{\text{direct}}(v)$
is calculated from the corresponding rate from the ground state
$k_{D}^{\text{direct}}(0)$
, taken from Macdonald et al. (Reference Macdonald, Munafo’, Johnston and Panesi2016), by applying the Fridman–Macheret
$\unicode[STIX]{x1D6FC}$
-model (see Fridman Reference Fridman2008), i.e.
$$\begin{eqnarray}k_{D}^{\text{direct}}(v)=k_{D}^{\text{direct}}(0)\exp (\unicode[STIX]{x1D6FC}E_{v}/T_{\text{gas}}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}$
(assumed equal to 1, as for strongly endothermic reactions) is a parameter that determines the efficiency of vibrational energy in lowering the reaction barrier of the ground state dissociation process.
$k_{D}^{\text{Boud}}(v,w)$
, instead, is calculated from Essenhigh et al. (Reference Essenhigh, Utkin, Bernard, Adamovich and Rich2006), strongly depending on the chosen activation energy
$E_{a}$
value.
