INTRODUCTION
The Memory Scanning Test (MST) was introduced by Sternberg in 1966 (Sternberg, Reference Sternberg1966). In the MST, a set of one to six different random digits (called the ‘positive set’) needs to be memorized. After a short delay, a test probe of one digit is presented after which the testee has to decide as fast as possible whether or not the test probe was a member of the positive set. This procedure is repeated multiple times with either the same or a different positive set (fixed-set procedure and varied-set procedure, respectively). The processing that occurs in the MST consists of four, supposedly additive, independent phases: (a) encoding of the stimulus, (b) working memory scanning, (c) binary decision about the nature of the response, and (d) response organization and execution (Sternberg, Reference Sternberg1975). The MST paradigm allows for distinguishing memory (stage b) and non-memory stages (stages a, c, and d). The slope of the line that is obtained by regressing the response times on the set size provides a measure of the speed of memory scanning; and the intercept provides an estimate of the time needed to complete the non-memory stages. Due to its firm theoretical paradigm, the MST has become a popular task for studying information processing in working memory in different scientific settings. However, the use of the MST in the clinic has been very limited until now. This is, at least in part, attributable to the fact that certain test characteristics of the MST hamper routine administration in a clinical setting. First, in the generic test paradigm, a computer is needed to present the stimuli and to record the responses. Secondly, the administration time of the MST is long. Thirdly, the test is too difficult for certain clinical populations and, finally, the main outcome scores of the MST are difficult to compute.
Brand & Jolles (Reference Brand and Jolles1987) developed a paper and pencil version of the MST (P&P MST) to overcome these problems. In this test, the participant is shown a sheet of paper that depicts a positive set of one to four letters. This sheet is replaced after 5 seconds by a test sheet that contains a matrix of 120 letters (for an example, see Fig. 1). The participant is instructed to cross out the letters that were in the positive set. The P&P MST is more suitable for use in clinical settings than the original MST for several reasons. First, the test is in a paper and pencil format, so no computer is needed to present the stimuli or to record the responses. Paper and pencil test versions are often preferred to computer-based tests in the clinic because computers are not always available. Also, many testees are not familiar with computers (e.g. older and poorly educated people) which may affect their test performance adversely. Secondly, the administration of the P&P MST takes only about 5 minutes. Brief tests are preferred by clinicians because many people who are typically referred for cognitive evaluation (i.e. people with suspected or known brain dysfunction) are not able to undergo long test sessions. Thirdly, the P&P MST is less difficult than the original MST because the maximum size of the positive set is only four items instead of the six used in the original. Previous research has indicated that memory span sizes greater than four may be particularly difficult for people with cognitive disorders such as mild and moderate dementia (Storandt et al. Reference Storandt, Botwinick, Danziger, Berg and Hughes1984). Thus, it is important to limit the size of the positive set to four items because otherwise administration of the test would not be feasible in certain clinical populations. Fourthly, a simplified scoring system was devised for the P&P MST because the main outcome variables of the original MST are difficult to compute. The time needed to complete the P&P MST Trial 1 served as the intercept measure because it reflects the response latency with a memory load of one item. The rate of working memory scanning (i.e. the slope) was quantified by calculating the average increase in the time needed to complete a test form per item extra in working memory.

Fig. 1. An example of the stimulus material for the Paper & Pencil Memory Scanning Test (Trial 3): sheet with the positive set (left) and test sheet (right). The stimulus material is presented here on a reduced scale. The true size of both sheets is 11·69 in ×8·26 in (29·70×20·99 cm).
Having a Sternberg paradigm-based test available for use in the clinic may be of advantage for many clinicians. For example, Ferraro & Balota (Reference Ferraro and Balota1999) found that the speed of the memory scanning (slope) and non-memory (intercept) stages of the MST were reduced in healthy older people relative to younger people. People with Alzheimer dementia showed impaired memory and non-memory stages compared with non-demented age-matched controls (Ferraro & Balota, Reference Ferraro and Balota1999). Naus and colleagues (Reference Naus, Cermak and DeLuca1977) showed similar deficits in people with Korsakoff amnesia. The memory scanning rate of non-demented Parkinson's disease patients did not differ from controls, but their non-memory processing was slower (Poewe et al. Reference Poewe, Berger, Benke and Schelosky1991). Archibald & Fisk (Reference Archibald and Fisk2000) found that both relapsing-remitting and secondary-progressive multiple sclerosis patients showed a reduced working memory scanning speed relative to controls, whilst the non-memory phases in the MST were only impaired for the secondary-progressive multiple sclerosis patients. Thus, several studies suggest that the MST may be a useful test in the clinic, for example from a diagnostic viewpoint. As noted by Archibald & Fisk (Reference Archibald and Fisk2000), a problem with the original MST is that there are no normative data available for it. Normative data provide an empirical frame of reference that is essential for evaluating an individual's cognitive functions (Capitani, Reference Capitani1997). Indeed, an understanding of what constitutes ‘normal’ performance is needed before an opinion can be given about an individual's cognitive strengths and weaknesses (Mitrushina et al. Reference Mitrushina, Boon and D'Elia1999). The lack of normative data for the original MST is most likely related to the fact that using the test is difficult in the clinic, as discussed above. The aim of our study was to present normative data for the P&P MST, a Sternberg paradigm-based test that was especially developed for use in the clinic. In order to establish reliable normative data, the P&P MST was administered to a very large sample of cognitively intact people aged between 24 and 81 (n=1839). We established norms for the intercept and slope measures of the P&P MST, and evaluated whether the ‘original’ and simplified procedures of calculating the slope and intercept measures yielded clinically relevant differences in the interpretation of the P&P MST performance.
Method
Participants
The data were derived from the Maastricht Aging Study (MAAS), a prospective study into the determinants of cognitive ageing. The MAAS sample has been described in detail elsewhere (Jolles et al. Reference Jolles, Houx, Van Boxtel and Ponds1995). Briefly, a large group of cognitively intact people aged between 24 and 81 underwent various cognitive tests and medical examinations. The P&P MST was administered to 1839 people. The data of 29 participants were excluded from the analyses for the following reasons: a score below 24 on the Mini-Mental State Examination (Folstein et al. Reference Folstein, Folstein and McHugh1975; n=13), the occurrence of technical problems during test administration (n=3), refusal or lack of motivation of the participant (n=4), and physical or cognitive limitations that obstructed test administration (n=9). Basic descriptive data for the sample are provided in Table 1. The ethnic background of all participants was Caucasian, and all participants were native Dutch speakers. Level of education (LE) was measured by classifying formal schooling into three groups – those with at most primary education (LE low), those with junior vocational training (LE average), and those with senior vocational or university training (LE high). This LE system is often used in The Netherlands (De Bie, Reference De Bie1987) and is comparable with the International Standard Classification of Education (UNESCO, 1976). LE low, LE average and LE high corresponded with an average of 8·59, 11·41 and 15·26 years of full-time education in the sample (s.d.=1·93, 2·50 and 3·32), respectively.
Table 1. Descriptive characteristics of the sample that was administered the P&P MST (n=1810)
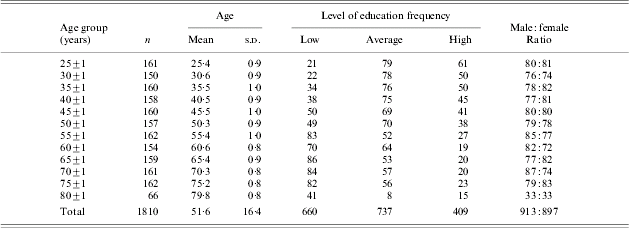
Data on level of education were missing for four participants.
P&P MST, Paper and pencil memory scanning test.
Procedure and instruments
The P&P MST was administered individually at the neuropsychological laboratory of the Brain & Behaviour Institute, Maastricht, The Netherlands. The P&P MST consists of four trials, in which the positive set contains 1, 2, 3 and 4 letters (i.e. ‘H’, ‘N R’, ‘Q W K’, and ‘S Z X P’, respectively). The administration of each trial of the P&P MST consists of two parts. In the first part, a white sheet of paper [portrait-oriented A4 format, 11·69×8·26 inch (29·70×20·99 cm)] that depicts the positive set in the centre of the sheet is shown to the participant for 5 seconds. In the second part, the sheet with the positive set is replaced by the actual test sheet. This sheet presents a matrix of 10×12 items printed on a sheet of white paper (portrait-oriented A4 format). Twenty items are ‘targets’ (i.e. items that were part of the positive set) and the remaining 100 items are ‘distractors’ (i.e. items that were not part of the positive set). All items are printed in black ink in capital letters (font size 12). An example of both sheets is given in Fig. 1. The participants were instructed to memorize the item(s) of the positive set in the first part. In the second part, they were asked to scan the test sheet line by line from left to right and cross out all the targets with a pencil as quickly and accurately as possible. There was no time limit to complete a sheet. The times needed to complete each test sheet were recorded (in seconds), as well as the number of omissions (i.e. the number of targets that were not crossed out) and errors (i.e. the number of distractors that were crossed out).
A practice trial was administered prior to the four test trials to make sure that the participants understood the test instructions. The positive set contained a non-letter symbol (i.e. ‘&’) in the practice trial. The administration order of the test trials was fixed for all participants: the trial with a positive set of one letter was always administered first, followed by the trials with a positive set of two, three and four letters. These trials will be referred to as Trial 1, Trial 2, Trial 3 and Trial 4, respectively.
We used two methods to calculate the slope and intercept measures. The first method is equivalent to the method used in the original MST paradigm, and consists of regressing the response times on the set size. In this method, the slope provides a measure of the speed of memory scanning, and the intercept provides an estimate of the time needed to complete the non-memory stages (note that the 1-intercept is calculated, i.e. the estimated response latency with a memory load of only one item). In the second method, the Trial 1 time served as the intercept score. The slope was calculated as [(Trial 2 time−Trial 1 time)+(Trial 3 time−Trial 2 time)+(Trial 4 time−Trial 3 time)]/3, which can be simplified to (Trial 4 time−Trial 1 time)/3 by basic algebraic operations. The intercept and slope measures that were calculated by using the original MST method will be referred to by adding the subscript o (i.e. Intercepto and Slopeo); the subscript s is used to indicate that the simplified calculation method was used (i.e. Intercepts and Slopes).
Statistical analyses
Multiple linear regression analysis was used to determine which variables were predictive for the P&P MST scores. The raw test scores were square-root-transformed because preliminary data analyses showed that the residuals were positively skewed before transformation of the scores (data not shown). The P&P MST square-root-transformed scores were regressed on age, age2 (which enables modelling of quadratic age associations), gender, level of education and all possible two-way interactions. To take speed–accuracy trade-offs into account, we also added the number of omissions made in Trial 1 as a predictor in the √Intercepto and √Intercepts models. The Trial 1, Trial 2, Trial 3 and Trial 4 omissions were added as extra predictors in the √Slopeo and √Slopes models. These corrections were made because people who make many omissions were expected to complete the test trials faster compared with people who work more accurately and make fewer omissions. Note that there is no correction for errors required because the effects of errors are already reflected in the time scores indirectly (i.e. crossing out a distractor costs time).
The coding of the predictors to be used in the regression models was as follows. Age was centred (age=calendar age−50) before computing the quadratic terms and interactions to avoid multicollinearity (Marquardt, Reference Marquardt1980). Gender was dummy-coded with male=1 and female=0. Level of education (LE) was dummy-coded with two dummies (LE low and LE high) and LE average as the reference category. The number of omissions made in Trial 1, Trial 2, Trial 3, and Trial 4 were dummy-coded after a median split. The dummy-coded omission variables are referred to by adding the subscript d. Coding was as follows: Trial 1 omissionsd=1 if Trial 1 omissions⩾1, 0 if Trial 1 omissions<1; Trial 2 omissionsd=1 if Trial 2 omissions⩾2, 0 if Trial 2 omissions<2; Trial 3 omissionsd=1 if Trial 3 omissions⩾2, 0 if Trial 3 omissions<2; Trial 4 omissionsd=1 if Trial 4 omissions⩾3, 0 if Trial 4 omissions<3.
The full models (including all predictors) were then reduced stepwise by eliminating the least significant predictor if its two-tailed p value was above 0·005. This procedure is described in detail elsewhere (Van Breukelen & Vlaeyen, Reference Van Breukelen and Vlaeyen2005). We tested the assumptions of homoscedasticity, normal distribution of the residuals, absence of multicollinearity and absence of ‘influential cases’. Homoscedasticity was evaluated by grouping participants into quartiles of the predicted scores and applying the Levene test to the residuals. Normal distribution of the standardized residuals was checked by conducting Kolmogorov–Smirnov tests on the residual values. The occurrence of multicollinearity was checked by calculating the Variance Inflation Factors (VIFs), which should not exceed 10 (Belsley et al. Reference Belsley, Kuh and Welsch1980). Cook's distances were calculated to identify possible influential cases (Cook & Weisberg, Reference Cook and Weisberg1982). Normative data are provided by converting the square-root-transformed P&P MST scores into standardized residuals in three steps. First, the predicted P&P MST scores of a test subject are calculated by using the final regression models (predicted score=B 0+B 1X 1+ … +B nX n). Second, the residuals are calculated (e i=−[observed score−predicted score]). Note that the residual is prefaced by a negative sign as a higher P&P MST score reflects poor performance and a lower score indicates good performance. Third, the residuals are standardized (Z i=e i/s.d.[residual]). The standardized residuals are then interpreted as percentiles via a Z-distribution table with cumulative probabilities (if the model assumption of normality of the residuals was met), or via a table with the observed distribution of the residuals of the normative sample (if the standardized residuals were not normally distributed). As the three-step procedure to norm a person's P&P MST scores requires quite some calculation, we also established normative tables that require no calculation at all to evaluate a person's scores.
Percentages of agreement and Kappa coefficients (Cohen, Reference Cohen1960) were computed to evaluate the extent to which the original and simplified methods of calculating the Intercept and Slope measures yielded comparable results when the 5th percentile was used as a cut-off to distinguish impairment from normal performance. Kappa is the proportion of agreement that exceeds the amount of agreement that can occur by chance (Cohen, Reference Cohen1960). Kappa values below 0·40 are poor, values of 0·40–0·60 suggest fair agreement, values of 0·60–0·75 represent good agreement, and values above 0·75 indicate excellent agreement (Watkins & Pacheco, Reference Watkins and Pacheco2000). In addition, agreement was also evaluated by computing the correlations between the standardized Intercept and Slope measures calculated using the original and the simplified methods (i.e. r[Z(√Intercepto), Z(√Intercepts)] and r[Z(√Slopeo), Z(√Slopes)]).
All analyses were performed using the SPSS 11.5 for Windows software package. The level of α error was set to 0·005 for all analyses.
Results
Normative models
The final regression models for the P&P MST scores are presented in Table 2. There was no serious influence of outliers (maximum Cook's distance equalled 0·039) or multicollinearity (maximum VIF=2·230) observed for these models. The Levene test rejected homogeneity of variance for all models (p<0·005). The standard deviations of the residuals increased as a function of increasing predicted scores. Normally distributed residuals were observed for the √Intercepto model, but the residuals for the other models were not normally distributed (p's of the Kolmogorov–Smirnov Z's<0·005).
Table 2. Final multiple linear regression models for the P&P MST scores

P&P MST, Paper and pencil memory scanning test. LE: level of education; Trial 4 omissionsd: number of omissions in Trial 4 ⩾3=1, number of omissions in Trial 4<3=0. Coding of the predictors: Age=calendar age−50; Age2=(calendar age−50)2; Gender: Male=1, Female=0; LE low: low educational level=1, average or high educational level=0; LE high: high educational level=1, low or average educational level=0.
* p<0·005, ** p<0·001.
The √Intercepto and √Intercepts scores were affected by Age, Age2, and LE. Older and poorly educated participants were outperformed by their younger and better educated counterparts. Age, Gender, LE, and Trial 4 omissionsd affected the √Slopeo and √Slopes scores. Participants with a lower level of education performed more poorly than participants with a higher level of education. There was a significant Age×Gender interaction: females outperformed males until the age of about 55, whilst this relationship was reversed for people older than 55 (Fig. 2). People who made three or more omissions in Trial 4 obtained lower √Slopeo and √Slopes scores than people who made fewer than three omissions (note that a lower score reflects a better performance).

Fig. 2. Predicted √Slopeo (left) and √Slopes (right) scores for people with an average educational level who made fewer than four omissions in Trial 4, as a function of age and gender. ––■––, Females; - -◊- -, males.
The P&P MST scores are normed by first calculating the predicted scores using the regression models in Table 2. Next, the residuals for each score are calculated (e i=−[observed score−predicted score]) and standardized (Z i=e i/s.d.[residual]). As heteroscedasticity was observed, the s.d.(residual)s per quartile of the predicted scores should be used to standardize the residual scores (see Table A1, available in online version of paper). The resulting Z values are interpreted by using a standard normal distribution table with cumulative percentages for the √Intercepto score (because the residuals of the model of this score were normally distributed), or by using the distribution of the observed residuals with their cumulative percentages for the √Intercepto, √Slopeo and √Slopes scores (because the residuals of the models of these scores were not normally distributed). This table is provided online (Table A2, available online).
Comparison between the original and simplified methods of scoring the P&P MST
When percentile 5 is used as a clinical cut-off, there is agreement in 96·3% of the cases for the Intercept scores (Cohen's Kappa=0·644) and in 98·9% of the cases for the Slope scores (Cohen's Kappa=0·908). The correlations between the standardized Intercept and Slope measures that were calculated using the original and the simplified methods (i.e. r[Z(√Intercepto), Z(√Intercepts)] and r[Z(√Slopeo), Z(√Slopes)]) equalled 0·854 and 0·991, respectively (p<0·001). These results suggest that the differences between the original and simplified methods of calculating the Intercept and Slope scores are rather small and are not likely to cause important differences in the clinical interpretation of the P&P MST performance.
User-friendly normative tables
Regression-based norming has some important methodological advantages compared with a ‘traditional’ normative approach (Van Breukelen & Vlaeyen, Reference Van Breukelen and Vlaeyen2005), but a disadvantage of this method is that the three-step normative method described above is cumbersome and not user-friendly. This problem can be solved by providing normative tables that are based on Table 2. These tables allow the clinician to evaluate a person's P&P MST scores without having to conduct any calculations whatsoever, but this is at the cost of some accuracy (i.e. interpolation is needed when a person's raw test score falls between two tabulated values). Table 3 presents the norms for the raw Intercepts P&P MST score. The normative table for the Slopes score is provided online (Table A3). We provided normative tables for the Intercepts and Slopes measures rather than for the Intercepto and Slopeo scores because most clinicians may be expected to use the simplified method to calculate these scores. Note that the normative tables present norms for the raw Intercepts and Slopes scores (i.e. not for the square-root-transformed scores), also in view of increasing the user-friendliness of the norms.
Table 3. Normative table for the raw P&P MST Intercepts score stratified by age and level of education

LE, Level of education; Cum. prob.: cumulative probability.
For example, the P&P MST was administered to a 45-year-old poorly educated woman. It took her 26s, 36s, 46s, and 60s to complete Trials 1–4. No omissions were made in any of the four test trials. The Intercepts score equals 26, the Slopes measure equals 11·3 ([60−26]/3). A raw Intercepts score of 26 falls into the range of percentile 25–50 (see Table 3), a raw Slopes score of 11·3 (=[60−26]/3) falls into the range of percentile 50–75 (see Table A3, online). Thus, the speed of the memory scanning and non-memory processing appears normal for this woman.
Discussion
The aim of the present study was to establish normative data for a new Sternberg paradigm-based test that was especially developed for use in the clinic, the P&P MST. We used a regression-based normative approach to derive norms for the memory scanning (√Slopeo and √Slopes) and non-memory (√Intercepto and √Intercepts) processing phases. The results showed that both the Slope and the Intercept measures increased as a function of age, suggesting that ageing affects all components of information processing involved in the P&P MST. Similar age effects were also seen in studies with the original MST (e.g. Wickens et al. Reference Wickens, Braune and Stokes1987; Ferraro & Balota, Reference Ferraro and Balota1999). Education also affected both the memory scanning and the non-memory processing phases involved in the P&P MST, with the effects of LE low compared with the effects of LE average being larger than the effects of LE high. This result is consistent with the brain reserve hypothesis (i.e. that people with less education are more vulnerable to age-related cognitive decline and brain pathology; Stern et al. Reference Stern, Zarahn, Hilton, Flynn, DeLaPaz and Rakitin2003). Gender did not affect the non-memory processing stages in the P&P MST, but influenced the speed of memory scanning. An Age×Gender interaction was observed, suggesting that females under 55 scanned working memory faster than males, and vice versa for people over 55 (see Fig. 2). To the best of our knowledge, no other studies using a Sternberg-based task have investigated Age×Gender interactions, but Meinz & Salthouse (Reference Meinz and Salthouse1998) reported that the age-related decline in other cognitive tests of measures of speed was smaller for males than females.
We used two scoring procedures to quantify the memory (Slope) and non-memory (Intercept) processing phases involved in the P&P MST. The scores that were calculated by using the original versus the simplified procedures were influenced by the same independent variables, and the regression-weights of these predictors were very similar (see B's in Table 2). The clinical agreement between both scoring methods was at least 96% when percentile 5 was used as a clinical cut-off. Kappa was at least 0·64, indicating good agreement. High positive correlations were found between the standardized Intercept and Slope measures that were calculated using the original and the simplified scoring methods (p<0·001). These results justify using the simplified procedure instead of the original method. Therefore we provided normative tables for the Intercepts and Slopes measures. Note that the normative table for the Slopes measure was stratified by the Trial 4 omissionsd variable in addition to the stratification by the demographical variables (in view of the significant influence of this variable on the √Slopes measure; see Table 2).
This brings us to some general remarks and limitations of this study. First, the sample was Dutch-speaking and Caucasian. It is unknown to what extent language or culture affects P&P MST performance. The generalizability of our norms to non-Western populations seems limited because these people are not familiar with the Western alphabet. Møller et al. (Reference Møller, Cluitmans, Rasmussen, Houx, Rasmussen, Canet, Rabbitt, Jolles, Larsen, Hanning, Langeron, Johnson, Lauven, Kristensen, Biedler, van Beem, Fraidakis, Silverstein, Beneken and Gravenstein1998) evaluated the P&P MST performance of a control sample of people who were aged at least 60 in a study on post-operative cognitive dysfunction. The results suggested that the P&P MST was a culturally robust test in a sample from eight European countries and the USA, but more research is needed to generalize these results. Secondly, the P&P MST uses letters as stimuli instead of the numbers used in the original MST. Although a digit version of the P&P MST has also been developed, we used the letter version because earlier research showed that the linear fit between response time and size of the positive set was higher for the letter version (Brand & Jolles, Reference Brand and Jolles1987). Thirdly, we used a cross-sectional design in the present study. As a consequence, the effects of age on P&P MST performance are confounded by cohort effects. However, this is not a major problem because we were primarily interested in normative trends and a cross-sectional study design is appropriate for such purposes (Hayslip & Panek, Reference Hayslip and Panek1989). Fourthly, the number of omissions made in each trial was dichotomized by a median split for its use as a predictor in the regression models. It is in general not advisable to dichotomize a variable because this results in a loss of measurement information and statistical power (MacCallum et al. Reference MacCallum, Zhang, Preacher and Rucker2002). In the context of normative analyses, however, dichotomization is useful in view of constructing user-friendly normative tables. Indeed, if the semi-continuous raw omission variables were used as predictors in the regression models instead of the dichotomized variables, a large number of normative tables would have to be generated (i.e. a table for people who scored 0 omissions, 1 omission, 2 omissions etc.). Note that we also used the semi-continuous omission measures as predictors in preliminary data-analyses, and that these models did not explain significantly more variance than the models that used dichotomized omission measures (data not shown). Fifthly, the test layout of the P&P MST is similar to that of substitution tasks such as the Digit Symbol Substitution Test (Wechsler, Reference Wechsler1981) or the Letter Digit Substitution Test (Van der Elst et al. Reference Van der Elst, Van Boxtel, Van Breukelen and Jolles2006). It is, however, important to note that the two types of test measure different cognitive functions, despite their apparent similarity. Indeed, substitution tests are essentially measures of general information processing speed that do not involve working memory processes (Van der Elst et al. Reference Van der Elst, Van Boxtel, Van Breukelen and Jolles2006), whereas performance on the P&P MST relies heavily on the speed and efficiency of memory scanning and non-memory scanning processes in working memory.
In summary, the P&P MST distinguishes itself from the ‘original’ MST on some important points: its administration time is short, no computer is needed to administer the test, the size of the largest positive set is within the memory span capacity of people with cognitive disorders, and the scoring procedure is simple. Our aim was to evaluate the range of normal performance of the scores for this test, so that the P&P MST can be widely used by clinicians to assess the information processing in the working memory of people who are referred for cognitive evaluation.
Acknowledgements
The research reported here was supported by the University of Maastricht and the PMS Vijverdal (The Netherlands). We thank all the participants for their cooperation and the test assistants for help with data collection.
DECLARATION OF INTEREST
None.
NOTE
Supplementary information accompanies this paper on the Journal's website (http://journals.cambridge.org).







