The Chairman (Mr D. A. Macleod, F.F.A.): I am going to invite Sandy Sharp, who is one of the authors of tonight’s paper, to give an introduction.

Mr A.C. Sharp, F.I.A. (introducing the paper): The title of the paper is “Difficult risks and capital models” and it is the work of the Extreme Events Working Party. I would like to acknowledge the contribution of all the members of the working party.

This paper concerns itself with capital modelling, but many of the ideas are applicable to modelling in general. I will be giving a high-level summary of the paper and presenting three examples from the paper that we think are important or new.

On Figure 1 we have a high-level description of a model building process.

Figure 1 (Capital) modelling

Section 1 of the paper gives some real and hypothetical examples where capital models have gone wrong. The rest of the paper describes a range of techniques that we think can reduce the chance of capital models going wrong.

Section 2 of the paper concerns judgement in building a capital model, highlighting areas where judgement is required and describing some of the key issues involved.

Some of the decisions or choices are listed in Figure 2, but there are others. We have decisions around which past data to use to base our model; our knowledge and beliefs about the particular problem, and the process of building a model that will allow us to predict the future and make decisions, such as how much capital to hold.

Figure 2 Types of uncertainties

The model is necessarily a simplification. We want the model to be manageable and to run faster than the “real world” that it represents. Regulation exacerbates the problem. Also, the long-term nature of insurance introduces some unique challenges in itself.

So, the first example I would like to present concerns the choices we make when simplifying the real world down to a manageable size. For our model, the process of simplifying involves a huge amount of choice and judgement.

In section 2 of the paper we discuss which risk factors (RFs) to model and the choice of framework for a model. An example of different frameworks would relate to the aggregation methodology: whether to use a correlation matrix or Monte Carlo simulation (Figure 3).

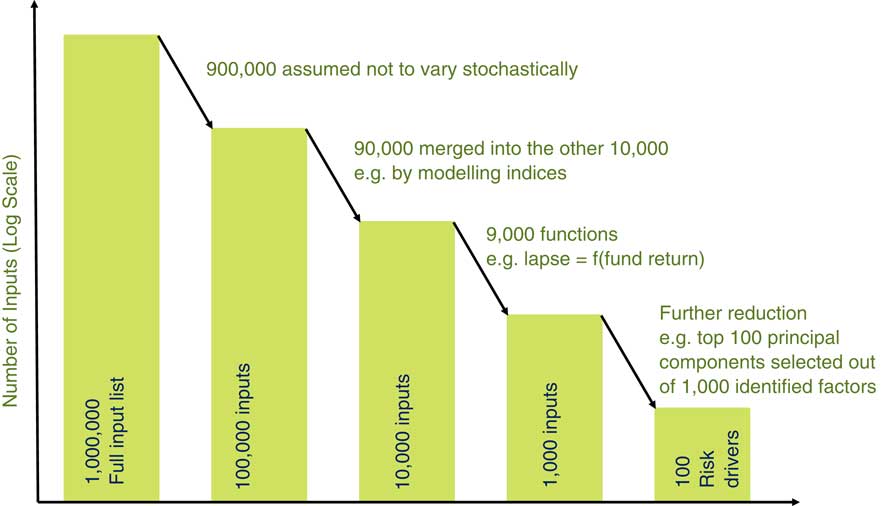
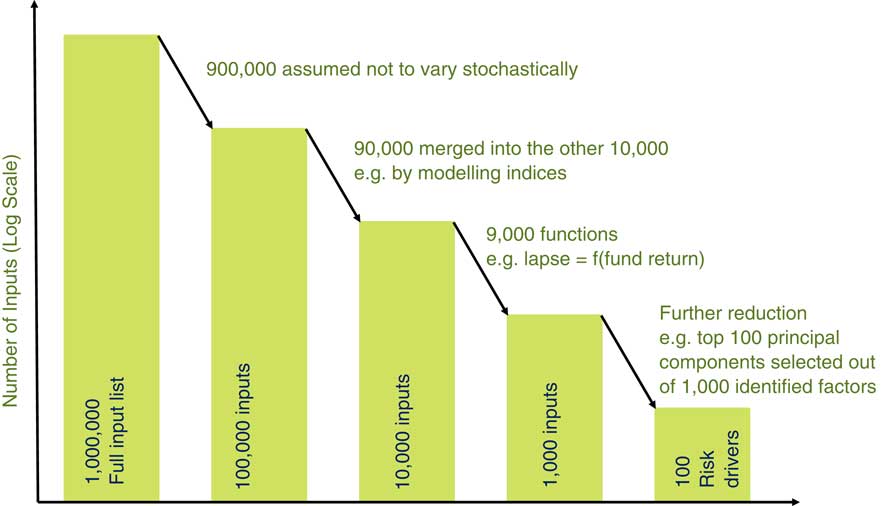
Figure 3 What risk factors to model?

As an illustration, we can consider which RFs to model stochastically. On an average company balance sheet there are over one million data inputs for liabilities. For example, it might have 30 products in each of three countries with each product having 5,000 data points or policies, and with each product depending on several tables: mortality, lapses and expenses. On the asset side the company might have tens of thousands of inputs say one million in total.

We cannot realistically expect to model one million data inputs except by using data reduction. So 90% of the inputs are not modelled stochastically (e.g. we might use a fixed mortality table).

We can also group policy model points and use stock indices for assets. Where two input variables are closely related we can also make one a function of the other (e.g. lapse rates may depend on fund return).

So, after a lot of decisions and by using expert judgement, we end up with 100 RFs for our model from the one million potential RFs. The question is what should we do with the RFs that are in the one million but did not make it to the 100 in our model? Clearly, grossing up by one million over 100 would not be appropriate. But it is hard to argue that no gross up is required. A gross-up factor also incentivises the company to understand the process that led to 100 from one million and improve the process. This process is covered in section 3 of the paper.

Once we have identified the RFs we still have model and parameter risk. These are the two other examples I should like to highlight from the paper. This is now section 4 of the paper.

Let us start with a very simple example. If we know what the true model is, we have an exact distribution of capital and we can read off our calculated percentiles. For example, we initially consider a normal distribution with known mean and variance in Figure 4. We can do a similar calculation for distributions other than normal. For example, in Figure 4, we also consider a t-distribution with 10 degrees of freedom.

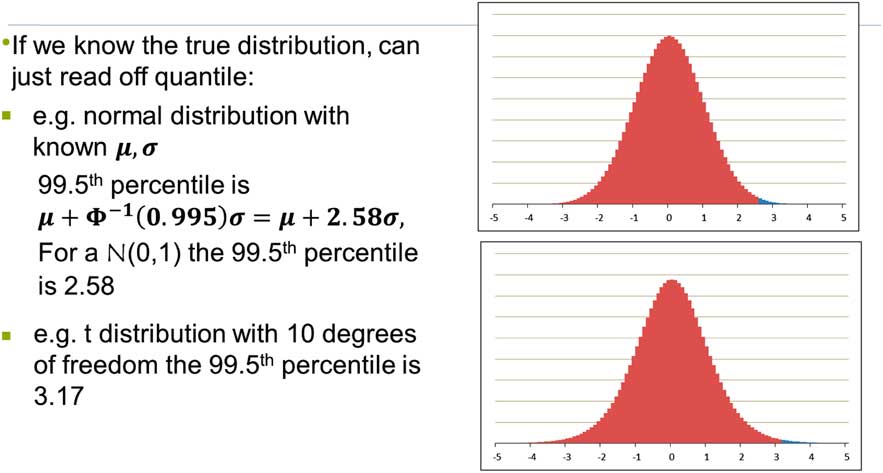
Figure 4 Model certainty

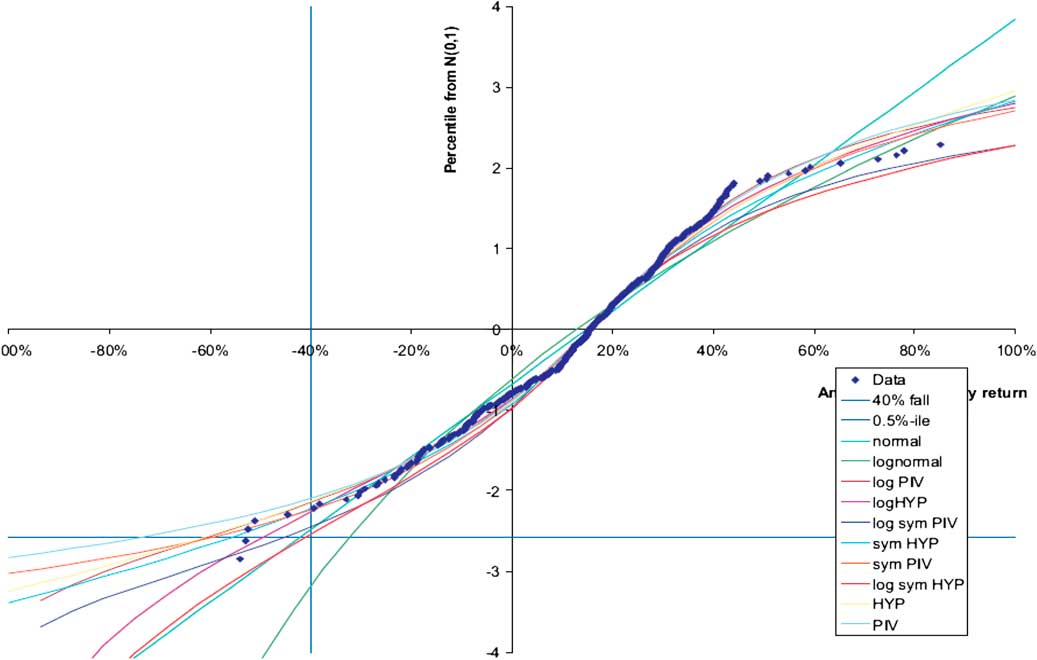
In this very simple example we show the effect of different models (or distributions). Of course, for real problems we do not know the distribution or the parameters. Figure 5 is an example from the 2008 “Modelling extreme market events” paper.

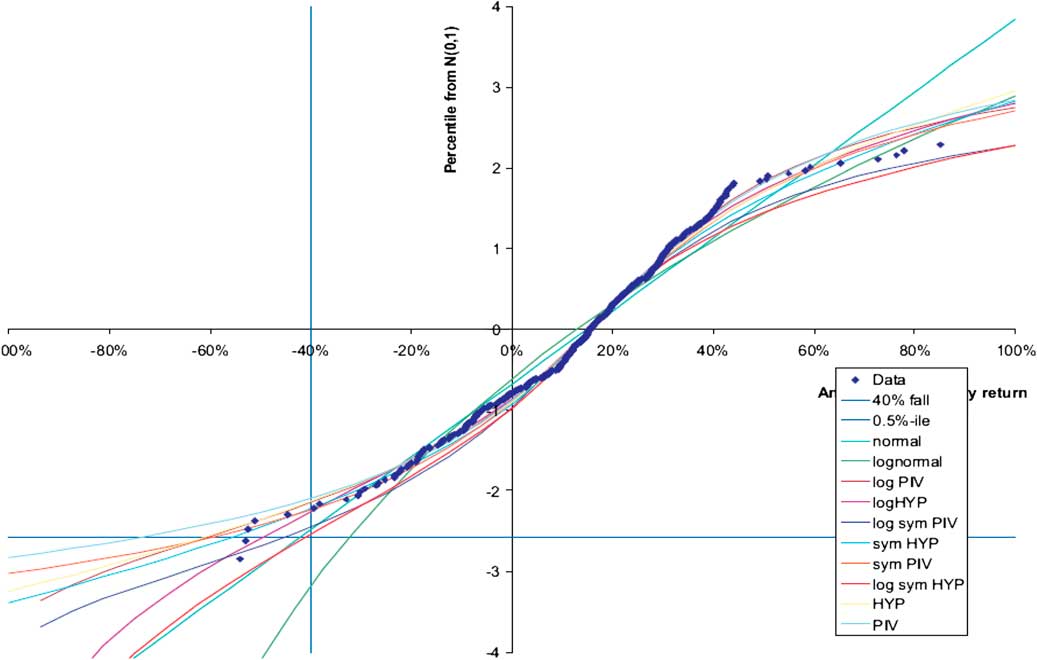
Figure 5 Model uncertainty

This chart is discussed in the 2008 paper in sections 6.4, 6.5 and 6.6. The salient point to note is that different distributions give very different percentile values as seen in the bottom left hand side of the chart but all actually fit most of the data quite well. In the chart there are 38 years of monthly observations of the annual UK equity return using the MSCI index. There are 38 years of data but more than 38 observations since we are including overlapping periods, which itself generates some challenges and again requires judgement to resolve. The actual (overlapping) annual returns are the blobs on the chart plotted in ascending order. These data were fitted to a range of distributions which are listed in the bottom right hand side of Figure 5 and presented in a Q–Q plot. The parameters of each distribution are chosen to give best fit to the data.

In this example, we have a lot of data, a lot more than for most decisions, yet choosing a model for the extreme percentile is hard. The difference between highest and lowest is a factor of 2. For a smaller data set the challenge will be greater.

What this illustrates is that, given particular distributions of data, it is difficult to justify using the model which is most credible, or gives best fit to the data, when there are other possible models. The model with the best fit is not the only model that can describe the data. In the paper we have examined parameter uncertainty and its implications for the capital modeller.

Figure 6 illustrates the third example from the paper.

Figure 6 Allowing for parameter uncertainty

When the model and parameters are known we can calculate capital requirements in a straightforward way. This is the traditional meaning of VaR. When parameters are uncertain there are different possible meanings of VaR. The percentile estimate depends upon the data, the model and the parameters fitted.

Here we consider four possible methods of calculating VaR, allowing for parameter uncertainty.

The first two methods involve finding the best estimate parameter by fitting the model to the data and calculating the capital. This is a very common approach which is called “Substitution” in Figure 6. A variation is to consider an adjustment to the parameter so that it gives us an unbiased estimate of the capital required. This is a Jensen’s inequality effect. This is called “Unbiased” in Figure 6.

These two approaches are not really allowing for parameter uncertainty. Two methods that do allow for parameter uncertainty, to different degrees, are called “Confidence Interval” and “Prediction Interval”, respectively.

The confidence interval is the interval which would, at a given probability level, say 95%, contain the true parameters. Here we are making a large allowance for parameter uncertainty as we construct a parameter at a given confidence level and then look at the 99.5% event given these extreme parameters.

Given a series of historical observations and a probability level, the prediction interval is the interval that contains the next observation at the given probability level. This allows for diversification between the parameter choice and the outcome and will tend to produce a lower capital requirement than the confidence interval approach.

There are more details on both methods in section 4 of the paper.

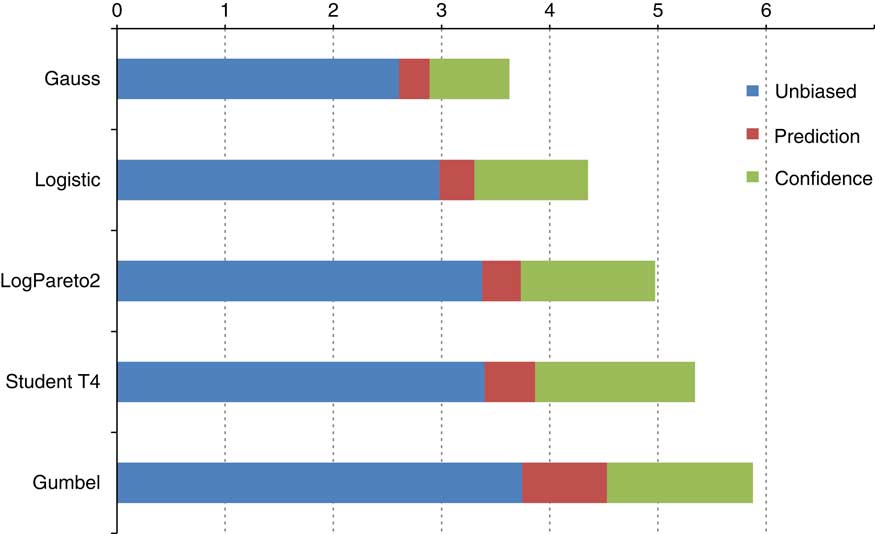
I would like to illustrate the different methods of allowing for parameter uncertainty with a table from the paper in Figure 7. We performed a Monte Carlo exercise to calculate 99.5% intervals for 20 data points from five common distributions.

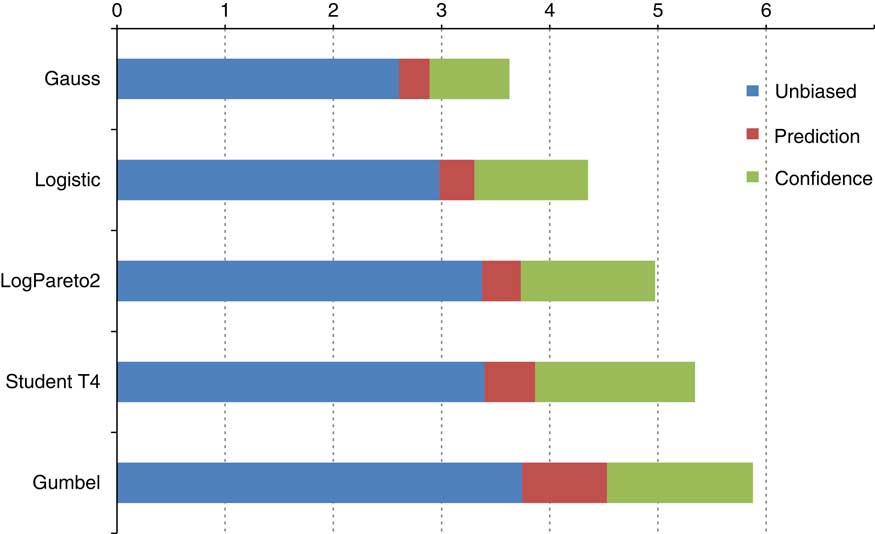
Figure 7 Allowing for model uncertainty

This chart shows the interval size (as a multiple of sample standard deviation). The unbiased estimate is shown in blue and the results from the Prediction and Confidence approaches to parameter uncertainty are shown in red and green. Parameter uncertainty is often missed and there are a range of approaches to allow for it.

Whilst this example has been discussing parameter uncertainty, the use of multiple distributions in Figure 7 allows me to return to model uncertainty. Section 4 of the paper describes an approach to model uncertainty using robust statistics and ambiguity sets. Finally, section 5 of the paper discusses some of the issues raised by the use of proxy models, and appendix A discusses Bayesian methods as a framework for expert judgement.

The Chairman: I would like to introduce some representatives from the working party. We have Sandy Sharp, Laura Johnston and Andrew Smith. With that we will open the debate.

Mr A. J. Clarkson, F.F.A. (opening the discussion): I would like to start by thanking the authors for a very thorough and thought-provoking paper. There are two areas covered in the paper on which I would like to comment.

First, expert judgement and the validation of expert judgement, which is discussed in section 2.2.5. That section notes that a potential validation approach is discussion by an independent panel. If that approach is taken, then I think it is important to be clear about the exact role and responsibilities of that committee. For example, without appropriate care, the existence of such a committee could blur clarity around who is performing an independent second line of defence review. This is particularly true if the committee has a mixture of representatives from both the first and second line of defence. If there are individuals who have particularly strong viewpoints, and whose reward is linked to financial performance metrics, then the dangers are clear. My view is that if such a committee is not purely populated with second line of defence people, which might be challenging given the nature of the skills required, then it should be made clear that the committee is supporting the individual responsible for making the recommendation from a first line of defence perspective. In that scenario, it is acceptable for second line of defence people to sit on the committee so that the committee can, if it wants, take their views into account, but they should not be voting members.

The second area on which I would like to comment is model and parameter risk, which is covered in section 4 of the paper. When considering this topic, I think it is important to be clear whether we are talking about a model to calculate pillar 1 capital requirements or one to calculate pillar 2 capital requirements. In that terminology, I am thinking ahead to Solvency II. In terms of pillar 1 capital requirements I wonder what there is to incentivise the Boards of life companies to include an allowance for model and parameter risk within their Internal Models. To my mind, whether or not this should be included is a matter for the regulators. It is part of the overall consideration of the appropriate capitalisation level for insurers, the answer to which involves political, as well as theoretical, considerations. I have heard views on both sides of the debate about whether the draft Solvency II regulations suggest that allowance for model and parameter risk is required. Consistency is important, and clarification of the requirements would be helpful. Any such clarification should aim to ensure consistency of treatment of Standard Formula and Internal Model companies.

Having said all that, I think it is important that the Board are made aware of whether or not an allowance for model and parameter risk is included within the proposed Internal Model methodology. It would not be appropriate to have no allowance and not to make that clear to them. Turning to pillar 2 capital requirements, this is essentially about how the Board want to run the company, so my earlier comments about the aims of the regulator are no longer relevant. I think the Board have a choice, they could allow for model and parameter risk directly within their assessment of risk and capital requirements.

Alternatively, they could set a higher capital target, or set a higher VaR percentile, than they otherwise would in the knowledge that there is no allowance for model and parameter risk within their modelling.

Personally, I prefer the latter approach in terms of simplicity. I think that has advantages although I do not think that it is appropriate for all companies. It is up to individual judgement whether to adopt that approach. The techniques considered in the paper are a potential approach for assessing the appropriate change in capital target which you might think is appropriate if you do not have direct allowance for model and parameter error.

The Chairman: Would anybody from the working party like to comment?

Mr A. D. Smith (co-author): On the pillar 1 point, I agree with you that clarity would be welcome. The sort of experiment that we have in our minds is of an insurance company potentially failing, policyholders losing out and it turning out that the problem was the models were wrong. Would it be politically acceptable for your European Member of Parliament to stand up and say, “Well, actually, we were not expecting to hold capital against that risk. We hold capital against other sorts of risks but not that one”. At the top political level, that seemed to us to be a rather difficult position to sustain. As you say, it could be that one can interpret the directive not to require an explicit capital requirement. Whether that interpretation is correct would be a legal question.

There is also the wider question of what are we, as a profession, representing in terms of the degree of protection policyholders enjoy? We need to be sure that it is not a misrepresentation. I welcome your comments that we propose disclosing what has not been allowed for in the modelling.

In respect of your points on pillar 2, the danger with an implicit allowance for model and parameter error is that they affect different risks in different ways. So, for example, for longevity most people would say there is a large degree of model and parameter uncertainty and you might need quite a big multiple or quite a big level of confidence to incorporate that factor. It might not be such a big increase for some of the market risks where you have more plentiful data and more consensus. So there is a danger that the relative size of the different risks might be misrepresented if you go for a broad brush scaling up approach. But I do recognise the advantage of such an approach being simpler.

Mr P. O. J. Kelliher, F.I.A.: In sections 2.2.4 and 6.1.1, mention is made that the experts who are making the expert judgement should be sufficiently independent of the calibration process and the capital calculation process. In my experience, the people actually making the judgements in terms of choice of data and choice of distribution are the people who are doing the calibration. A team within the actuarial function will do the actual hard work of the calibrations but will also make the expert judgements. So, I am not sure about that particular point. I think it is more important to have the expert judgements reviewed independently, perhaps by a second-line committee.

That brings me onto a more general issue. We seem to be talking about whether we need to hold extra capital for parameter risk. I wonder whether this particular risk is one that is better addressed by controls, by having a sound model governance process, rather than by holding extra capital.

The amount of capital needed to be held to deal with parameter uncertainty and different distributions could be akin to “how long is a piece of string”? You can have a wide range of answers, as we have noted, in terms of what different distributions and confidence levels can tell you. To my mind, it is more important to have a very robust model governance process, making sure that the Board are aware of all the potential answers and letting them make the choice in terms of the appropriate distribution, rather than adding an additional layer of capital.

That brings me onto controls in general. Model governance, obviously, is an important control. In terms of why models fail, it is partly because we have failures of controls. One example would be the sub-prime crisis. You had models that were clearly unsuitable for assessing sub-prime CDOs, for example, because the appraisal of risks by the rating agencies and by the investment banks themselves failed to pick up on increasing concentration of sub-prime Residential Mortgage-Backed Securities (RMBS) in the underlying portfolio. That is another issue in terms of model uncertainty. We have uncertainty regarding the parameters and choice of distribution, but you can also have step changes in the nature of risk. Even if you had maybe chosen the most appropriate model and allowed for parameter uncertainty in 2001 and 2002, the change in the RMBS concentration level that occurred in the next five years would have invalidated that model. So the important thing is to have a continual process of reviewing the model in the light of the actual risks.

I have one final comment on longevity bias. We seem to be saying that there is some sort of political bias to explain why people underestimate longevity. However, when life insurers go out and talk to the general public and ask them their perceptions of longevity, many studies show that people systematically underestimate their own longevity. That is one of the reasons why annuities are perceived to be such poor value. I suspect that, rather than political bias, the human race in general has a tendency to overstate mortality and underestimate longevity.

Finally, I should like to congratulate the authors on an excellent paper. It builds on the “Modelling extreme market events” paper in 2008. I found that very useful in my work on Solvency II. This paper has added to that body of knowledge.

The Chairman: I think it would be unfair not to invite Mr Anderson to speak about the longevity point.

Mr W. D. B. Anderson, F.I.A.: I agree with Mr Kelliher about people underestimating their own longevity. I want to give you a possible explanation. It is what psychologists call the availability bias. That is, people form judgements, which may not be rational, on the basis of the information that is available to them. One common source of information when it comes to people looking at how long they might live, is simply to look at their peer group. They look at who has died within the cohort of people who have been born at the same time. The deaths of their friends and family make a big personal impression on their thinking. Of course, what they do not recognise is that there is a whole group of other people who have not died and they cannot really conceptualise the long-term longevity trend.

It is just one of a whole series of complex behavioural effects that one finds when you look at the way that people react to views about longevity. Looking at the public sector pension negotiations in which I have been involved, it is absolutely true that all the trade unionists talk about the examples of their members who have died immediately after retirement as a reason why you cannot increase the pension age of the pension scheme. You can argue until you are blue in the face about providing all this other statistical information. This availability bias is really well engrained in their psyche.

The Chairman: Would any other members of the working party like to comment on any of the other points raised by Mr Kelliher?

Dr L. L. Johnston, F.I.A: I should like to say something about the point on expert judgement. A typical “first-line” employee may not volunteer themselves to make the required expert judgements. We should consider what makes someone a valid expert. It is also important that there is a regular control cycle to review all the relevant expert judgements made.

Similarity with the industry is not sufficient for an expert judgement to be valid. Even if other companies are making similar decisions, the judgements should still be subject to internal review and challenge.

Mr Smith: A point was made about firms holding extra capital for parameter and model risk. Let us be clear: we are not saying in this paper that firms need to hold more capital. What we are saying is you ought to be honest about the relationship between the capital you hold and the degree of security that you are offering.

We could imagine a situation where we were more inclusive about some of the risks that we model. Let us be clear that for many of these risks the parameter and model uncertainty are at least as big as the things we are currently modelling explicitly. If we are going to include more risks you could imagine an end point where you actually agreed, subject to negotiation, that you were holding 95% confidence, not 99½%, but you were being more holistic about the risks that were being modelled. What we would like to see is a more defensible relationship between the capital held and the degree of security being claimed.

I am not sure that I really understood the point about addressing parameter risk by controls. The sort of situation that we are looking at, for modelling, say, lapses is that you might have 15 years’ data and there is a limited amount you can infer from this amount of data. Some experts might remember a bit longer but you are still constrained by there being a small amount of data that may or may not be representative of the future.

You could confront the Board with a list of models and ask them to make a choice but that really would not remove the issue that there is not enough data. It does not seem to me that in that case controls are really the answer.

I think there is a much better argument to be made in the case of sub-prime mortgages. My understanding is that there were plenty of individuals within the system who had a reasonably good idea of the risks, which was why they were selling. It is a governance shortcoming if the awareness is there within the organisation but it does not filter up to the top.

The Chairman: A lot of the problem in the sub-prime area was not model risk, it was product risk. It was that the people running the business did not really understand the products that were being sold. Even if you sorted out the model risk that problem would still have existed. Is there an irrationality around decision making that leads to bad decisions?

Mr A. M. Eastwood, F.F.A: I thought this was an excellent paper. I particularly liked the frighteningly plausible hypothetical example described in section 1.1. That in itself is probably instructive reading for any Board that is asked to approve an internal model or an individual capital assessment (ICA), not least because it is readily accessible.

Chapters 3 and onwards I did find more challenging, but they very clearly highlight that there are a lot of other choices that are implicitly made by a Board when agreeing to an internal model that is proposed to it by relevant experts. I am sure you are not suggesting this, Mr Kelliher, but the idea of “Here is a range of answers, Board. Over to you” would fill me with horror. I think that would be abdicating our responsibility to make recommendations as the relevant experts.

What I have not found the time to do is to construct the explanations corresponding to section 1.1, which would provide the accessible explanation of some of the mathematics of chapters 3–5 in the paper that is appropriate to a Board of directors.

I like to think that in my time, which is a few years ago now, I warned Boards that:

• ∙ in approving an ICA there are no answers which can be proved right in this context because we are dealing with a once in 200 years level;

• ∙ for most things there are insufficient data points to confidently calibrate the capital requirements at that kind of level; and

• ∙ in any case, there is no guarantee that the past is an adequate guide to the future.

I have warned them that the allowances for diversification rely on a number of assumptions, which it can be difficult to prove or test, and a huge amount comes down to judgement.

Rightly or wrongly, in making my recommendations, I have taken comfort from benchmarking. The authors hint at that in section 4.3 of the paper and you can see the clear risk of a herd mentality developing in taking comfort from benchmarking. I am a little nervous that perhaps that is where the banks were in the run up to the credit crunch. I would be interested to hear the views of people more expert than me on whether that is indeed where the investment banks were in respect of some of the really extreme events that are quoted in the paper.

I would also appreciate some comments on the relative significance of the judgements made, sometimes implicitly, by a Board when agreeing to an internal model that are commented on in the later chapters of the paper compared with the significant risks that are highlighted in the hypothetical example of section 1.1. Things like legal risk and regulatory risk, particularly the risk of retrospective interpretation of regulations, have probably caused far more pain to the insurance companies than market risk which has been adequately modelled and often hedged.

It would be interesting to hear views on whether I am right in thinking that having a proper look at these operational type risks can be more important than worrying about the niceties of exactly which model you have picked. I note Mr Sharp was saying some equity models can suggest capital requirements a factor of two times those resulting from other equity models, and I would certainly accept that a factor of two on the amount of capital held against equity risk is quite significant in most companies.

Some of the techniques in the paper use lots of maths with which I, for one, am not intimately familiar. How practical are some of these techniques to employ? For example, section 3.3 looks at a couple of grossing-up techniques. One approach involves determining the eigenvalues of different matrices. It seemed to me that it is highly unlikely I am ever going to have the information to do this properly. As Mr Sharp said in his introduction, we do not know what “the real model’ is in practice. Can you take the kind of techniques described in section 3.3 of the paper, apply them in practice and obtain some useful information in that way?

The Chairman: Would anybody from the panel like to respond?

Mr Smith: I will pick up on a couple of points that you made. One was about taking comfort in benchmarking and one about the practicality of some of the mathematical techniques. I think they are related. When you are doing benchmarking, you are taking the historic data that is available and looking at how different experts might interpret that data. That is a technique which, as you say, has dangers associated with herd instincts. On the other hand, it gives some protection against cherry picking where somebody has just opportunistically taken the model that gives the most commercially attractive answer.

But, there is a risk that that it does not pick up, and that the past data have come, by statistical fluke, from a particularly smooth or well-behaved time series. Some of the more mathematical sections describe, with a lot of practical numbers, how, by generating Monte Carlo histories, you can obtain a measure of that element of variability, which is not picked up by benchmarking. These tools are widely used in the statistical world and will be absolutely standard, for example, in medical investigations.

While I recognise that some of the mathematics may be a bit of a hurdle, the risks being modelled are really there. I do not think that people in this room should be ashamed of applying a bit of mathematics to quantify those risks, particularly when that path is well trodden in other disciplines. It is something that we are not doing at the moment and we think it will be helpful for our profession and society at large, if we were able to make more progress in this area.

The Chairman: A question for the working party is what kind of challenges they see for auditors and regulators, in particular, around judgement where there is so much subjectivity. What solutions should regulators or auditors be looking for to rise to the challenges?

Mr Smith: In the paper we have described briefly what auditors are seeking. The key point is that audits are giving assurance on certain aspects but not on others. So, for example, when auditors are looking at judgements, they are seeing whether those judgements are reasonable. That is not a test as to whether other experts could have come up with a different judgement.

When auditors are looking at materiality limits, they are not generally considering different reasonable judgements. Their materiality limit is concerned with actual mistakes like failing to account for tax or expenses, things that are definitely wrong, rather than a difference in view.

I suppose auditors have a similar communication issue to actuaries when they talk about materiality limits. It is easy to think that if somebody has done an audit and signed it off to be accurate to within £10 million, then that means no other answer could be more than £10 million different. Whereas what it actually means is that the aggregate of unintentional mistakes is <£10 million, but there still could be a judgement that could move it by £100 million.

So auditors have this get-out which means there can be large variations in their results. There is a different debate as to whether it is desirable for them to have that get-out.

The other thing about judgement is that quite often we tend to use judgement as a means of rejecting alternative models. We might be in a situation where we have a set of data and there could be a dozen different ways of modelling it, none of which can be disproved by the data because you just do not have enough data. Then we look to judgement effectively to say: “We are going to pick this one”. There are good uses and there are bad uses of judgement. That might be one of the less defensible uses. If there are 12 models that give quite different answers, all of which have some plausibility, you should not be throwing away 11 of them because that is just a loss of information. You get the appearance of having removed the model uncertainty, but you have not really done so, you have just decided to use judgement as an excuse not to measure it.

Mr Anderson: I would like to agree with everything that Mr Smith has said. One of the sentences which jumped out of the page at me in the judgement section is the statement of the obvious that we tend to forget: “the Board is ultimately responsible for all assumptions and judgements”. There is also the true and fair accounting principle to consider.

I was thinking about that when Mr Eastwood was speaking about his counselling of his Board. That also made me think about his question about whether the operational, regulatory and legal risks are more significant than the model risks. If you think about the insurance companies which have suffered fatal or near-fatal disasters, there are some, which I think most people would put largely down to under-reserving problems. An example of this is Independent Insurance, a general insurance company which was probably being a bit too aggressive on the pricing side. The problem here was probably not with the model, but with faulty subjective judgement. The problems with American Insurance Group, discussed in the paper, feel to me more like a model risk situation. It was brought down by the huge business concentration in the London-based manufacturing centre of mis-priced credit default swaps. This was largely a statistical modelling issue.

It is not impossible that we might see a public enquiry into model risk in the future.

Another sobering document which is worth having a look at is the government’s own investigation into what it calls its material models that are used in government decision-making. This was in the wake of the fiasco of the letting of the West Coast rail franchise and the failure to appreciate the time value of money which seems to have confused the Department of Transport in their cost-cutting measures. On the back of that, the government then looked at how many other models used by central government contain embarrassing errors. They just looked at central government departments, so they excluded all the quangos, but they still counted 500 different models which were being used for different things, any one of which could have a malfunction. They have now become real converts to model governance, but it is model governance in a world of austerity. It is an interesting concept and is explained on the Treasury website where there is a list of all 500 models.

Mr J. E. Gill, F.F.A.: A direct follow-up to the point Mr Anderson made on 500 models. Are we now at the point where a legitimate science would be to be modelling “model failure” and building something around that, or is that overly perverse?

A second point that came out of section 2.2.4 for me was that the way that the judgement is elicited might be as important as the judgement itself. I wonder whether the authors have any views on that point.

The Chairman: I agree that, in many cases, it is actually how the model is used, which is more important than how good the model is. There is sometimes an irrationality in decision making of which people are not conscious.

Another thought is that, as a profession, we can look back and see that what was a cutting-edge model 10 years ago may now be obsolete. So, for us there is always a need to keep working on the models as more data becomes available, the economy changes and so on. The points raised in the paper will certainly remain relevant.

I should like to invite the panel, Mr Smith in particular, to respond to the discussion.

Mr Smith: I think we have responded to the points as they were made and I have nothing else to add.

The Chairman: One other point was the cost benefits of using more accurate models. I wonder whether you have any thoughts on using more expert judgement which could be more expensive but which could give you a better answer or remove some of the poorer answers.

Mr Smith: The comment that I would make is the costs and the benefits can be spread in strange ways. The major beneficiaries of insurers holding adequate capital against model risk would be policyholders or the policyholders’ compensation scheme. But they are not necessarily the ones who are going to bear the cost. There certainly needs to be a grown-up discussion about how the costs and the benefits accrue to different parties.

The Chairman: If there are no other comments, I will invite Gordon Wood to close the discussion.

Mr G. C. Wood, F.F.A. (closing the discussion): I have a number of observations tonight and before I touch on them I will add my thanks to the speakers. I thought the paper was a very useful summary of modelling issues, some practical and theoretical techniques and some interesting pitfalls.

In terms of the conversation this evening, there are a few themes on which we touched. Probably the biggest, and most important, was that of judgement. We clearly need expert judgement. I think everybody will agree it is an essential adjunct to the statistics.

There were a number of conversations about how many experts we need and where these experts sit. Mr Clarkson talked about first line versus second line. We did talk about perhaps a dearth of experts, and what were they all doing rather than reviewing or validating?

There were a number of elements in the paper which touched on RFs. Clearly, there are statistical techniques in terms of the principal component analysis and the algorithmic approach is touched on in the paper. The crucial override is many of these need to be augmented by sensible judgement. I personally think there could have been more on the gross-up factors and some of the practical techniques involved. I very much agree with the point about legal hindsight and retrospection. These techniques are absolutely fine for market risk but we cannot ignore the major operational risks and the need to quantify capital and apply controls for operational risks.

There was quite a bit of discussion on various aspects of model and parameter error. We had the usual complaints about the lack of data in the tail, and therefore, in terms of model uncertainty, whether we should use correlation approaches or copula approaches.

One speaker pointed out that the model which is the best fit is not necessarily the best for purpose. We need to look very carefully at the uses of the model and which particular part of the distribution we are going to be using in practice.

Mr Kelliher touched on the fact that capital is not always the answer. That was demonstrated quite clearly in terms of the large range for parameter uncertainty on top of the unbiased estimates.

There was some interesting conversation on the purpose of the model. We talked about the regulatory imperative versus the need to give the Board more appropriate numbers for decision making, specifically with regard to pillar 1 versus pillar 2 in a Solvency II world.

In terms of parameter uncertainty, I was struck by the very striking example about longevity models in section 4.2.1. There were seven quite plausible longevity models, and the annuity value shown was actually below the mean for two of the models but above the 99.5 percentile for two of the models. That certainly brought home to me the potential uncertainty and risks of using models without appropriate judgement being applied.

I was slightly struck by the fact that there was not any discussion on Chapter 5, where I thought the content on proxy models and on spanning errors, for example, was particularly useful. I think proxy models, particularly given the later conversation about cost-benefit analysis, are something that does repay careful attention, certainly within a commercial environment.

In summary, this has been a very useful paper with a very good discussion.

The Chairman: I should like to express my own thanks to the authors, Mr Sharp, Dr Johnston and Mr Smith, and the others who are not here, for an excellent paper. I thought it was very timely and relevant to what we are doing. We will probably have the same discussion in five or ten years’ time when many of the same issues will probably be recurring.

I should like to say thanks very much to Mr Clarkson for his opening remarks, to Mr Wood for his closing remarks and to everyone else who participated in the discussion tonight.