Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-11T15:32:30.187Z Has data issue: false hasContentIssue false
  • English
  • Français

An experimental study of the high Mach number and high initial-amplitude effects on the evolution of the single-mode Richtmyer–Meshkov instability

Published online by Cambridge University Press:  03 March 2004

O. SADOT ,
A. RIKANATI ,
D. ORON ,
G. BEN-DOR  and
D. SHVARTS
O. SADOT
Affiliation:
Department of Physics, Nuclear Research Center–Negev, Beer-Sheva, Israel Department of Mechanical Engineering, Ben Gurion University of the Negev, Beer-Sheva, Israel
A. RIKANATI
Affiliation:
Department of Physics, Nuclear Research Center–Negev, Beer-Sheva, Israel Department of Physics, Ben Gurion University of the Negev, Beer-Sheva, Israel
D. ORON
Affiliation:
Department of Physics, Nuclear Research Center–Negev, Beer-Sheva, Israel Department of Physics of Complex Systems, Weizmann Institute of Science, Rehovot, Israel
G. BEN-DOR
Affiliation:
Department of Mechanical Engineering, Ben Gurion University of the Negev, Beer-Sheva, Israel
D. SHVARTS
Affiliation:
Department of Physics, Nuclear Research Center–Negev, Beer-Sheva, Israel Department of Mechanical Engineering, Ben Gurion University of the Negev, Beer-Sheva, Israel Department of Physics, Ben Gurion University of the Negev, Beer-Sheva, Israel
Rights & Permissions [Opens in a new window]

Abstract

The present article describes an experimental study that is a part of an integrated theoretical (Rikanati et al.2003) and experiential investigation of the Richtmyer–Meshkov (RM) hydrodynamic instability that develops on a perturbed contact surface by a shock wave. The Mach number and the high initial-amplitude effects on the evolution of the single-mode shock-wave-induced instability were studied. To distinguish between the above-mentioned effects, two sets of shock-tube experiments were conducted: high initial amplitudes with a low-Mach incident shock and small amplitude initial conditions with a moderate-Mach incident shock. In the high-amplitude experiments a reduction of the initial velocity with respect to the linear prediction was measured. The results were compared to those predicted by a vorticity deposition model and to previous experiments with moderate and high Mach numbers done by others and good agreement was found. The result suggested that the high initial-amplitude effect is the dominant one rather than the high Mach number effect as suggested by others. In the small amplitude–moderate Mach numbers experiments, a reduction from the impulsive theory was noted at late stages. It is concluded that while high Mach number effect can dramatically change the behavior of the flow at all stages, the high initial-amplitude effect is of minor importance at the late stages. That result is supported by a two-dimensional numerical simulation.

Keywords

Richtmyer–Meshkov instabilityShock-tube experimentsTurbulent mixing
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 3 , July 2003 , pp. 341 - 346
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

The instability mechanism, which appears at an interface between two fluids of different densities when it is accelerated by a shock wave, that is, the Richtmyer–Meshkov (RM) instability, can give rise to turbulent mixing. Recent theoretical work has predicted the evolution of a single-mode perturbation through the linear (see Richtmyer, 1960; Meshkov, 1969), nonlinear (Zhang & Sohn, 1997; Sadot et al., 1998), and late nonlinear stages (Hecht et al., 1994; Alon et al., 1995; Sadot et al., 1998). In those models, after the shock passage the interface can be described by an incompressible evolution of the flow field. For a single-mode perturbation, the instability can be described by the linear stage model, in which a constant velocity characterizes the growth:

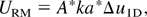
where k is the wave number (2π/λ), A* and a* are the postshock Atwood number and amplitude, respectively, and Δu1D is the one-dimensional postshock interface velocity. a* is equal to a0+, the postshock amplitude for the light to heavy configuration (see Richtmyer, 1960), and to a* = (a0+ + a0−)/2 for the heavy to light configuration (see Meyer & Blewett, 1972), where a0− is the preshock amplitude. The linear stage is followed by a nonlinear stage during which the growth velocity reaches an asymptotic C(A)λ/t behavior where C(A) is a constant that depends on the Atwood number and the dimensionality (for more details, see Hecht et al., 1994; Rikanati et al., 1998). Those models (nonlinear classical models) are applicable when the initial perturbation wavelength is much smaller than the initial amplitude (a0 k << 1) and incompressible flow.

In recent years, efforts have been made to study the evolution of the Richtmyer–Meshkov instability in the case of high Mach numbers. Shock-tube experiments where conducted by Aleshin's research group (Aleshin et al., 1990, 1997) using moderate Mach numbers (2.5–3.5), various initial conditions, and different test gas combinations (He-Xe, Ar-Kr, He-Xe in heavy to light and light to heavy arrangements). In their work, an effort was made to map the behavior for the instability and to quantify the differences between the various regimes. Three regimes were defined as “soft” where the nonlinear theory is applicable, “hard,” and “irregular,” where the nonlinear behavior was observed immediately at the initial stages (shear instabilities and asymmetry between the bubbles and spikes). The hard and irregular regions were distinguished from the soft one by the high Atwood number, high initial-amplitude and high-Mach number (for more details, see Aleshin et al., 1997). A reduction in the initial velocity of the perturbation from the linear velocity predicted by the Richtmyer and Meyer-Blewett models in the light to heavy and heavy to light configurations was observed in the hard and irregular regions.

Dimonte et al. (1996) conducted experiments with higher Mach numbers. The experiments were conducted on the NOVA laser at Lawrence Livermore National Laboratory (LLNL). The focusing of the laser beams into a radiation enclosure (indirect drive configuration) generated shock waves with Mach numbers of M ∼ 15 in Be (ρ = 1.7 g/cc) to foam (ρ = 0.12 g/cc) configurations. In these experiments, the initial amplitudes ranged from a0 k ∼ 0.2 to a0 k ∼ 4, which is well above the applicability limit of the linear models. In some of these experiments with a0 k > 4, large reductions of the initial instability growth velocities from those predicted by the linear classical model were observed, whereas in others with a0 k ≤ 1, the agreement was good. It is commonly assumed that the reduction was due to high Mach number effects (see, e.g., Aleshin et al., 1997; Holmes et al., 1999).

In our theoretical complementary study (see Rikanati et al., 2003) the reduction of the initial instability growth velocity as compared to the predictions of a new nonlinear classical model is presented and two models were introduced and supported by two-dimensional (2D) simulations. The models, which described correctly the reduction, took into account the effect of the high initial amplitude (geometrical effect)—the “vorticity deposition” model—and the shock-interface proximity effect (high Mach number effect)—the “wall” model. It was found that the geometric effect was dominant only at the initial stage. At the late stage, the effect was diminished and the bubble front floated in its asymptotic velocity. The Mach number effect reduced the initial velocity.

In the present study, two sets of shock-tube experiments are reported. One set has large initial amplitudes and low Mach numbers demonstrating the reduction in the initial instability growth velocity as compared to the nonlinear classical model, and gives us to study the late stage evolution with nonlinear initial conditions. The other set has a moderate Mach number of M = 2 and a linear initial amplitude (a0 k < 1) demonstrating the high Mach number effect on the instability at the late nonlinear stages of the flow.

2. EXPERIMENTAL APPARATUS

The experiments were performed in a 5.5-m-long horizontal double-diaphragm shock tube with an 8 cm × 8 cm cross section. A thin membrane separated the two gases (in this kind of experiments, the effect of the membrane is negligible; see Erez et al., 2000). The evolution of the shock-wave-induced mixing zone was measured by recording a series of Schlieren photographs using a Nd:YAG frequency-doubled laser pulsed at intervals of about 20 to 200 μs and a shutterless rotating-prism camera. The photographs were analyzed using a computerized image analysis. Figure 1 is a schematic diagram of the experimental apparatus. To generate a shock wave having a Mach number in the range 1.2–2.0, the driver section was first filled with air or He until it reached the pressure that was required to rupture a 0.14-mm-thick diaphragm consisting of one or two layers of mylar sheet.

The experimental apparatus. A PC controls the diagnostic system. The light source to the Schlieren optical system is a Nd:YAG doubled frequency laser.

The strength and velocity of the shock wave were measured with piezoelectric pressure transducers that were flush mounted on the shock-tube walls. The arrival of the shock wave at the first pressure transducer was used to trigger the diagnostic timing sequence.

A thin membrane was placed between the two investigated gases in the test section. Upon the rupture of this membrane by the shock wave, the mixing process began. Windows were built into the side walls of the test section. Their height spanned the entire 8-cm height of the test section. Their length was 20 cm, beginning at the frame holding the membrane. The gases on both sides of the membrane, in the test section, were at an ambient pressure. The apparatus was controlled by a PC computer system that operated the pneumatic valves and slow rate sensors. The system was equipped with timing and DAQ cards and operated using LabVIEW software.

To investigate the high-initial amplitude effect, a set of experiments with varied a0−k was performed. All the experiments were done with an air/SF6 gas combination (light to heavy combination, Atwood number A = 0.67) and a Mach number of M = 1.2. Table 1 summarizes the initial conditions. The high Mach number study was done using air/SF6 gas combination with M = 2.

The initial amplitude and wavelength of the high initial-amplitude experiments

3. EXPERIMENT RESULTS AND DISCUSSION

3.1. High initial amplitude with small Mach numbers

An experimental verification of the high initial-amplitude dominance in the above experiments was obtained using shock-tube experiments at low Mach numbers (M = 1.2) with saw-tooth initial perturbations of low and high initial amplitudes (a0 k = 0.5–3). A set of Schlieren photographs taken from the shock-tube experiment is shown in Figure 2a. The comparison between the experimental results and our 2D simulation is presented in Figure 2b.

a: Three sets of Schlieren photographs with different initial conditions. The shock travels from right to left. All experiment are done with air to SF6 gases. b: Bubble height in the high initial-amplitude shock-tube experiments.

LEEOR2D, which is a homemade two-dimensional Arbitrary Lagrangian Eulerian (ALE) code, was used. More details about the code can be found in Ofer et al. (1996).

Due to the good agreement between the simulation and the experimental results that can be seen in Figure 2b, the initial bubble velocity for the experimental results (which was not measured due to technical limitations) was assumed to be equal to that predicted by the simulation. It is also evident from Figure 2b that the velocity growth as predicted by the linear classical model (Richtmyer, 1960) does not predict the initial velocity. Note that there is a very good agreement between the experimental results and the predictions of the classical nonlinear model (Alon et al., 1995; Sadot et al., 1998) of the asymptotic evolution (the theoretical predictions were shifted vertically to fit the experimental results).

A comparison of the reduction factor of the initial velocity with predictions of the vorticity deposition model is shown in Figure 3a. As can be seen, very good agreement was achieved, similar to that derived for the moderate and high Mach number experiments. Our results, together with those of Aleshin et al. (1990, 1998) and Dimonte et al. (1996) for moderate and high Mach number experiments, are presented in Figure 3b. As can be seen, the reduction in all of the experiments fit a single curve. (It should be noted that a calculation using the vorticity deposition model produced a similar curve; see Rikanati et al., 2003). The result suggests that the main reduction in those experiments is due to the high-a0 to λ ratio and not the shock wave Mach number.

a: Comparison of the reduction factor between the vorticity deposition model and the shock-tube experiment at M = 1.2. b: Comparison of the results from the present work at low Mach number and Dimonte et al. (1996) and Aleshin et al. (1990) at moderate and high Mach number.

3.2. Small initial amplitude with moderate Mach number

Experiments with an air to SF6 gas combination and shock wave Mach number M = 2 were conducted to investigate the Mach number effect. Schlieren photographs from one of those experiments are presented in Figure 4a. It is seen clearly that the shock wave is in the vicinity of the perturbed interface during a longer time and that the shock reverberation is traveling in a direction tangential to the interface propagation. Due to the tangential traveling of the shock reverberation, the shocks collide and create regions of high and low pressure in front of the bubbles and the spikes alternately. While the high pressure in front of the spike increases the spike growth, the high pressure in front of the bubble reduces the bubble growth and can even cause the bubble tip to drift downstream as is evident in Figure 4b. The results were compared to a full 2D numerical simulation and the same pressure pattern and bubble behavior were observed. This effect does not occur in the low Mach number case. When the shock is weak, the interface travels much slower than the shock, and small pressure fluctuation dissolve quickly. In this case, the evolution of the perturbation is dominated by the inertia and drag. In Figure 4b, initially the bubble rises as predicted by the nonlinear classical theory (Hecht et al., 1994; Sadot et al., 1998) but later on, the bubble is decelerated and is washed downstream due to the pressure, which evolves in front of it. The deceleration and negative velocity effect flattened the tip of the bubble and increased the bubble radius of curvature. Figure 4c (inserted into Fig. 4b) presents the time-dependent radius of curvature of the bubble. Due to the moderate Mach number and to the linear initial conditions, the perturbation evolved initially as predicted by the nonlinear classical model. To the best of the authors' knowledge, a model that predicts the late time bubble evolution in the high Mach number situations does not yet exist.

a: Schlieren photographs from the shock-tube experiment with M = 2 air to SF6 λ = 26 mm, a0 = 3 mm. b: Comparison between the nonlinear model—dashed line (Sadot et al., 1998)—and the high Mach number experiment together with full 2D numerical simulation—full heavy line—and the linear theory—heavy dashed line (Richtmyer, 1960). The reduction from the nonlinear model at late time is clear. c: The bubble radius of curvature versus time.

4. SUMMARY

An attempt was made to understand the effects of the high initial amplitudes and high Mach numbers on the Richtmyer–Meshkov instability evolution. Recent theoretical and experimental studies by Aleshin et al. (1990, 1997) and Dimonte et al. (1996) showed that in some cases there is a reduction in the initial growth velocity with respect to the predictions of the linear model (and likewise the nonlinear classical model). In the present work, combined experimental and theoretical studies reveal two different effects that dominate the instability evolution, the geometric effect and the high Mach number effect. Two sets of shock-tube experiments were conducted to validate these effects by using low Mach number and high initial-amplitude and moderate Mach number and linear initial conditions. The reduction factors that were obtained in the high initial-amplitude experiments were compared to the model predictions and to experimental results of others and good agreement was found. The results suggested that even at high Mach numbers, the geometric effect is the dominant one. It is also shown that at late stages, the asymptotic velocity in the high initial-amplitude experiments is the same as that predicted by the nonlinear classical models. For the case of moderate Mach number experiments with linear initial conditions, no significant reduction was observed because the Mach number was not high enough. However, an irregular asymptotic behavior, namely a negative growth rate, was observed experimentally and numerically. Pressure fluctuations in front of the bubble due to shock reverberation suppress the bubble growth and can even cause a negative growth velocity.

References

REFERENCES

Aleshin, A.N., Lazareva, E.V., Chebotareva, E.I., Sergeev, S.V., & Zaytsev, S.G. (1997). Investigation of the Richtmyer–Meshkov instability induced by the incident and reflected shock wave. Proc. 6th Int. Workshop on Compressible Turbulent Mixing, pp. 1–6. France: IUSTI, Universite de Provence.
Aleshin, A.N., Lazareva, E.V., Zaitsev, S.G, Rozanov, V.B., Gamali, E.G., & Lebo, I.G. (1990). Linear, nonlinear and transient stages in development of Richtmyer–Meshkov instability. Sov. Phys. Dokl. 35, 159–161.Google Scholar
Alon, U., Hecht, J., Ofer, D., & Shvarts, D. (1995). Power laws and similarity of Rayleigh–Taylor and Richtmyer–Meshkov mixing fronts at all density ratios. Phys. Rev. Lett. 74, 534–537.Google Scholar
Dimonte, G., Frerking, C.E., Schneider, M., & Remington, B. (1996). Richtmyer–Meshkov instability with strong radiatively driven shocks. Phys. Plasmas 3, 614–630.Google Scholar
Erez, L., Sadot, O., Levin, L.A., Shvarts, D., & Ben-Dor, G. (2000). Study of the membrane effect on turbulent mixing measurements in shock tubes. Shock Waves 10, 241–251.CrossRefGoogle Scholar
Hecht, J., Alon, U., & Shvarts, D. (1994). Potential flow models of Rayleigh–Taylor and Richtmyer–Meshkov bubble fronts. Phys. Fluids 6, 4019–4030.CrossRefGoogle Scholar
Holmes, R.L., Dimonte, G., Fryxell, B., Gittings, M.L., Grove, J.W., Schneider, M., Sharp, D.H., Velikovich, A.L., Weaver, R.P., & Zhang, Q. (1999). Richtmyer–Meshkov instability growth: Experiment, simulation and theory. J. Fluid Mech. 389, 55–79.CrossRefGoogle Scholar
Meshkov, E.E. (1969). Instability of the interface of two gases by a shock wave. Fluid Dyn. 4, 101–104.Google Scholar
Meyer, K.M., & Blewett, P.J. (1972). Numerical investigation of the stability of a shock-accelerated interface between two fluids. Phys. Fluids 15, 753–759.Google Scholar
Ofer, D., Hecht, J., Alon, U., Shvarts, D., McCrory, R.L., & Verdon, C.P. (1996) Phys. Plasmas 3, 3073.
Richtmyer, R.D. (1960). Taylor instability in shock acceleration of compressible fluids. Comm. Pure Appl. Math. 13, 297–319.CrossRefGoogle Scholar
Rikanati, A., Alon, U., & Shvarts, D. (1998). Vortex model for the nonlinear evolution of the multimode Richtmyer–Meshkov instability at low Atwood numbers. Phys. Rev. E. 58, 7410–7418.CrossRefGoogle Scholar
Rikanati, A., Oron, D., Sadot, O., & Shvarts, D. (2003). High-Mach number and high-initial amplitudes effects on the evolution of the single-mode Richtmyer–Meshkov instability. Phys. Rev. E. 67, 26307–26318.Google Scholar
Sadot, O., Erez, L., Alon, U., Oron, D., Levin, L.A., Erez, G., Ben-Dor, G., & Shvarts, D. (1998). Study of nonlinear evolution of single-mode and two-bubble interaction under Richtmyer–Meshkov instability. Phys. Rev. Lett. 80, 1654–1657.CrossRefGoogle Scholar
Zhang, Q., & Sohn, S.-I. (1997). Padé approximation to an interfacial fluid mixing problem. Appl. Maths Lett. 10, 121–127.CrossRefGoogle Scholar
Figure 0

The experimental apparatus. A PC controls the diagnostic system. The light source to the Schlieren optical system is a Nd:YAG doubled frequency laser.

Figure 1

The initial amplitude and wavelength of the high initial-amplitude experiments

Figure 2

a: Three sets of Schlieren photographs with different initial conditions. The shock travels from right to left. All experiment are done with air to SF6 gases. b: Bubble height in the high initial-amplitude shock-tube experiments.

Figure 3

a: Comparison of the reduction factor between the vorticity deposition model and the shock-tube experiment at M = 1.2. b: Comparison of the results from the present work at low Mach number and Dimonte et al. (1996) and Aleshin et al. (1990) at moderate and high Mach number.

Figure 4

a: Schlieren photographs from the shock-tube experiment with M = 2 air to SF6 λ = 26 mm, a0 = 3 mm. b: Comparison between the nonlinear model—dashed line (Sadot et al., 1998)—and the high Mach number experiment together with full 2D numerical simulation—full heavy line—and the linear theory—heavy dashed line (Richtmyer, 1960). The reduction from the nonlinear model at late time is clear. c: The bubble radius of curvature versus time.