1. Introduction

From the perspective of philosophy of science, investigative procedures in modern economics often appear quite unsatisfactory. As a result, it is tempting to distinguish the laws of economics from those of physics in the following way. The laws of physics are universal and exceptionless; they are exemplars of scientific achievement that other disciplines should aspire to. Not only do the laws of economics admit of exceptions, they apply only under extremely unrealistic assumptions and appeal to equilibrium conditions rarely witnessed in real life. We hedge economic generalizations with the proviso that all other things are equal, or ceteris paribus, for example, “an increase in the price of a commodity X leads, ceteris paribus, to a decrease of the quantity demanded.” Perhaps one day this generalization can be replaced with an explicit, comprehensive law of consumer demand that is exceptionless. As physicist Richard Feynman (Reference Feynman1981) once remarked, “Social science is an example of a science which is not a science. … They follow the forms … but they don’t get any laws. … They haven’t got anywhere yet. … Maybe someday they will.” After all, economics “hasn’t helped us improve our predictive abilities,” which “suggests that it is still far from being a science, and may never be” (Rosenberg and Curtain Reference Rosenberg and Curtain2013). So, it is common to interpret ceteris paribus laws, as Earman and Roberts (Reference Earman and Roberts1999) do, as at best signaling “an embryonic theory on its way to being developed to the point where it makes definite claims about the world” (466).

This essay, alongside objections from Cartwright (1983, Reference Cartwright1999), Woodward (Reference Woodward2000, Reference Woodward2002), and Hoover (Reference Hoover, Chao, Chen and Millstein2013), aims to dislodge the background view underlying this dismissive attitude: that the target of analysis must be treated as an autonomously evolving system. Rather, statements that get called “laws” form a varied group. But when philosophers discuss the laws of dynamical systems, they tend to assume that the primary role of laws is to supply evolutionary principles that carry a target system autonomously from state to state.Footnote ¹ Those laws help generate descriptions of future states of dynamical systems, given initial (and boundary) conditions. The laws of thermodynamics are unlike those; instead, they primarily concern hypothetical manipulations by outside factors under extremely controlled conditions.

I argue that there is a kind of ceteris paribus statement that has an important explanatory role detached from such predictive aims. While this is not a general account of ceteris paribus claims, or of lawhood, I suspect philosophers sometimes neglect this role because they fail to see how such statements diverge from what is typically expected from laws of nature. Ceteris paribus laws are often considered incomplete. But by considering the specific way ceteris paribus clauses, via the equilibrium assumptions they lean on, are regularly deployed in economics, I suggest that these assumptions help us articulate the relevant causal relationships that characterize a specific problem of interest and understand a dynamic system in terms of how efficient its performance is.Footnote ²

This explanatory role is not unique to economic methodology. Conventional thinking about what scientific law looks like treats Newton’s celestial mechanics as exemplary—given some initial conditions, I can predict the future trajectory of celestial bodies over time. In this kind of Newtonian setup, frictional processes do not interfere much with planetary motion. These frictional processes have serious implications, however, if we consider the behavior of steam engines. Friction degrades the potential work a steam engine can perform in a nonnegligible way. The physicist Rudolf Clausius relied on the theoretical Carnot cycle, which traces out the optimal performance of a heat engine that does work and then returns to its original state, to make sense of the entropy concept. It is impossible to get a real steam engine to follow the perfectly controlled path of the cycle so its work capacity will be less than its idealized Carnot counterpart. But an engineer’s appreciation of how well an actual engine is performing compared to what is optimally possible is central to her understanding of the machine’s workings.

After establishing that the use of supply and demand curves is analogous to an engineer’s use of the pathway drawn by the Carnot cycle (sec. 2), I show that the original motivation of ceteris paribus reasoning introduced in Alfred Marshall’s (Reference Marshall1890) Principles of Economics—as part of an (partial) equilibrium methodology—aligns with this interpretation (sec. 3). It still characterizes how an economist today might approach economic problems, such as financial phenomena like the recent 2007 crisis. The substantial similarities between economic and thermodynamic reasoning suggest that ceteris paribus laws are used to (1) articulate the causal constraints on a system and (2) flag loci for possible interventions and manipulations. To accommodate these roles, section 4 offers an account of understanding—understanding in terms of efficient performance—that builds on recent work by Woodward (Reference Woodward2003) on interventionist theories of causation. This contrasts with the popular semantic completer interpretation, which proposes that ceteris paribus clauses stand in for information we have not uncovered yet (but if we did, we would have had laws). Section 5 diagnoses this interpretation as one such misguided attempt to cram the kind of understanding valued by the engineer or the economist into the Newtonian paradigm, forcing explanation into the narrow confines of predicting the temporal behavior of an autonomously evolving system. Rather, ceteris paribus laws, and the equilibrium methodology they lean on, have an explanatory role that is diagnostic and evaluative in nature, allowing us to assess the performance of dynamical systems in terms of efficient performance.

2. Carnot Cycles and Supply-Demand Curves

In the nineteenth century, Clausius attempted to explain what we now call entropy by appealing to the Carnot cycle mentioned in the introduction. The Carnot cycle consists of four reversible processes—processes that could in theory be “reversed” to their initial states with no trace that a change had taken place at all. This implies that at any given time the system is in thermodynamic equilibrium with its surroundings, moving at an infinitely slow pace.Footnote ³ Imagine a piston cylinder, with ideal gas inside, as depicted in figure 1. At the first stage of the cycle (1) we submerge it in a heat reservoir like an infinite vat of water. The gas expands, pushing the piston up and leading to a decrease in pressure. That is, the engine does work. The heat reservoir and the engine remain the same temperature while volume increases. Then, (2) we remove the piston, insulate it so that we lose no heat during transit, and lift the piston as the gas continues to expand. Next, (3) we place the piston cylinder in a cooler reservoir. Then we compress the piston again. Temperature remains the same while pressure increases and volume decreases. The piston cylinder releases heat. Work is done on the engine. In the last step (4) we further compress the piston after removing the cylinder and insulating it in order to raise the temperature, returning it to its initial state before putting it back in the heat bath. Stages 1 and 3 are isothermal processes involving no temperature change. Stages 2 and 4 are adiabatic processes that involve no heat transfer.

Figure 1. Carnot engine.

In a way, the posited stages of a Carnot cycle are all physically absurd and scarcely predictive of any behavior we might ever witness. Gases are not ideal, infinite heat baths do not exist, and there is no way to perfectly insulate things. The system is, paradoxically, both dynamic and yet always at equilibrium. Why undertake this bit of unrealistic reasoning at all? Because we actually do get some empirical information out of this exercise. One consequence is that this Carnot engine represents the upper efficiency limit of any engine that takes in heat and converts it into mechanical work. This limit depends solely on the temperature differential between heat reservoirs. No real engine will do better than the Carnot engine because real engines produce waste heat due to friction.

Nothing a priori tells us what the correct description of a physical system looks like.Footnote ⁴ But by positing a hypothetical external controller that can in principle adjust one variable to see how some other variable will vary (holding all the others constant), we can articulate which pairs of variables are causally tied to one another. Each conjugate pair consists of one extensive variable and one intensive variable—one variable that represents a force and the other the displacement. Volume and pressure are one such pairing (fig. 2).

Figure 2. Pressure-volume diagram for a Carnot engine.

We need such conjugate pairs because they provide the vocabulary to talk about systems and articulate the outlines of the Carnot cycle. Toggle the volume in just such a way, and we thereby adjust the pressure by this much. The behavior of real heat engines will play out in less perfect and more inefficient ways but within these contours.Footnote ⁵ The interior of figure 2 represents the most work that any heat engine will ever be able to do. That is, these illustrated boundaries represent important limits and guidelines on what can and does occur in the real world and so remain crucial in manufacturing and engineering contexts.

Even if it is not in general possible to manufacture actual reversible processes that are at equilibrium, the equilibrium benchmark is still a useful tool, for example, in the study of transport phenomena, which are always irreversible. We can compare our real engine’s behavior to the ideal case, perhaps identifying dimensions along which we could improve. For instance, the suboptimal performance of a real life engine undergoing a process corresponding to the line in figure 1 representing the insulated piston being transferred between heat reservoirs might be due to insufficient insulation.Footnote ⁶ Despite their static nature, those thermodynamic snapshots allow us to investigate dynamical properties. The arrows drawn in figure 1 represent the Carnot engine’s progress through the cycle, essentially representing a succession of variable driven equilibrium states. The idealized machine yields information about the primary processes at work in the real life mechanism and how its performance could be improved via various alterations in design.

These observations provide a robust analogy to equilibrium analysis in economics. Consider the classic so-called law of demand: ceteris paribus, the price of a commodity and the quantity demanded are inversely related, represented in figure 3 by the downward-sloping consumer demand curve. In order to establish this relationship, we ignore changes in the population, in consumers’ preferences and incomes, and in the prices of other goods that would otherwise prevent us from drawing such a nice linear curve. The upward-sloping supply curve represents the combinations of quantities and prices at which a firm is willing to sell a good. In figure 3, both the supply and demand curves intersect to determine the equilibrium price and quantity, p and q.

Figure 3. Supply and demand equilibrium.

Now, suppose that some outside influence affects the supply curve, pushing it to where the dashed line is in figure 4. The new equilibrium price and quantity are at p* and q*. The price is now higher, and the new quantity is lower. We have investigated the pure causal effect of a supply shock. So these ceteris paribus assumptions allow us to characterize equilibrium states for limited markets (fig. 3) and talk about the dynamic behavior of markets in terms of comparative statics (fig. 4).

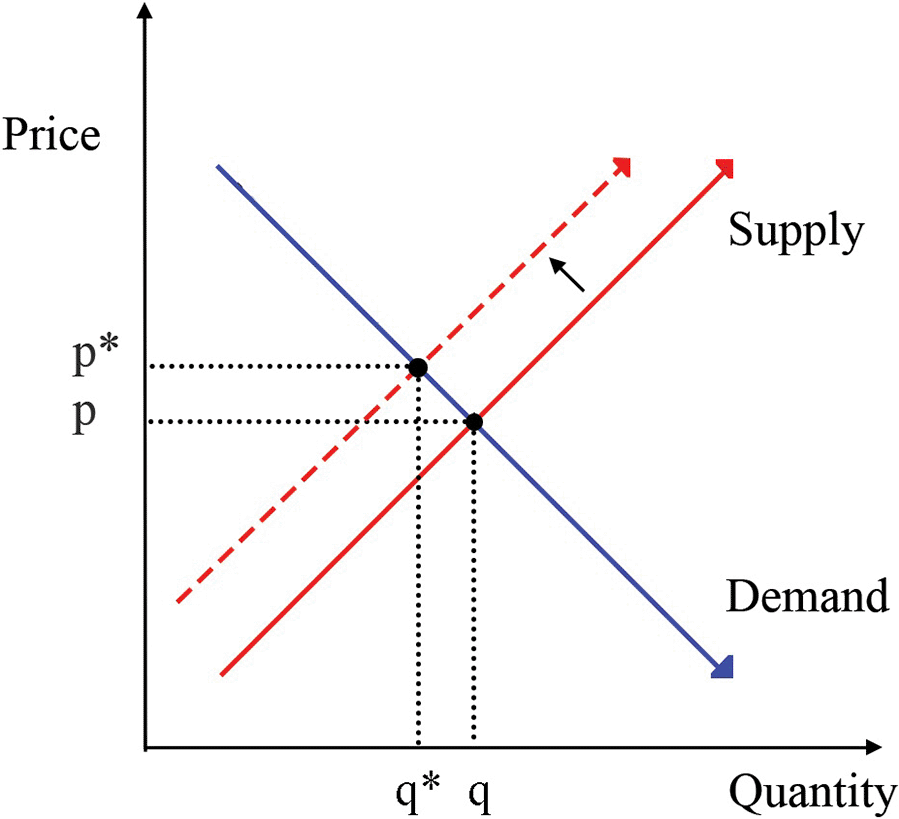
Figure 4. Postsupply shock.

Demand and supply curves are exact analogs of the arrows in figure 1. When economists characterize equilibrium states in order to employ the method of comparative statics, they compare two equilibriums to get a handle on how some feature—such as the price of a product—responds to changes in the market. Tracing out a demand or supply curve itself invokes a hypothetical external controller nudging one variable to see how only one other variable will vary in response (e.g., a rise in a commodity’s price means that consumers are willing to buy less of it). We envision such processes as perfectly smooth adjustments from one equilibrium state to another. In so doing, we ignore how long it would take to reach the new equilibrium, the fluctuations that route might include, and the effects on (and feedback from) outside markets. Doing this ensures that the theoretical change in the target variable is due solely to the external force we subject it to.

This external controller is explicitly invoked in partial equilibrium exercises when we investigate market disturbances. In figure 4, the supply of a commodity (say, widgets) moves downward due to a shock. This could be due to external factors, such as the main widget factory burning to the ground. Alternatively, I might affect the supply curve by downsizing my factory. Both would move the equilibrium price upward. In the meantime, I have put aside various inconveniences to my analysis. For instance, I assume that the new equilibrium state will be reached in fairly short order and that the local widget market that I am considering is sufficiently independent of other gadget markets in the vicinity. But in reality, the economy also exhibits behavior due to “frictions” that impede its functioning.Footnote ⁷ For instance, the price might take time to adjust or end up lower than the calculated equilibrium price.

Selling the new, lower quantity of product at a higher price is efficient in that at this new equilibrium state, nobody can do better without making someone worse off, and all benefits from exchange are realized.Footnote ⁸ If I were to sell or price my commodities somewhere other than at equilibrium, I incur deadweight loss (i.e., social welfare could be improved; fig. 5). Suppose that instead of the equilibrium price (p_eq) and quantity (q_eq), I decide to sell at the price and quantity indicated at price p and quantity q, designated by the black dot in figure 5, perhaps due to a government-mandated price ceiling. The shaded triangle represents the loss in (allocative) efficiency, which is the cost to society due to our failing to meet equilibrium conditions. The result is a widget shortage: consumers are willing to buy more widgets at this price than suppliers are willing to sell, and the overall welfare of society could have been improved without leaving the supplier worse off.

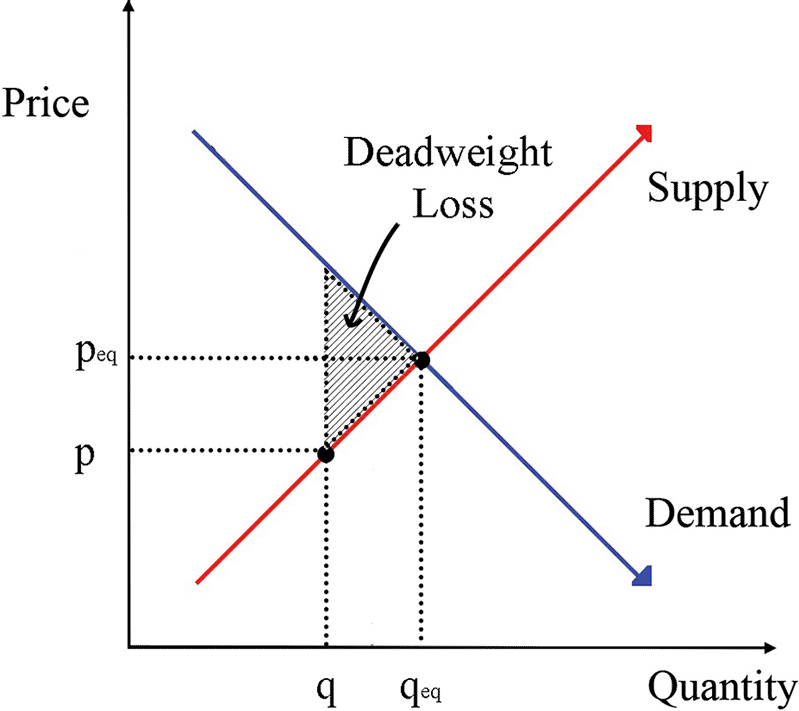
Figure 5. Deadweight loss.

The temperature-entropy diagram functions in much the same way. If an engine’s performance is located somewhere in the interior of the quadrilateral region that is traced out by the legs of a Carnot cycle, that engine is not doing as well as it could be. Similar to deadweight loss, this is a loss in efficiency and represents the amount by which I could be doing better (i.e., do more work). Because these lines set the benchmark for what would be efficient performance, the supply/demand curves represent the limits that we try to approximate as best as we can.

3. A Lesson from History: Alfred Marshall on Ceteris Paribus Provisos

I suggested in the previous section that law-like generalizations in economics such as “an increase in price leads to a decrease in supply” serve as strategic anchors around which we do empirical work in the way that thermodynamic equations do. Ceteris paribus assumptions in economics do the same thing that positing reversible processes does in thermodynamics. And they have been motivated this way since the inception of modern economic thought: this usage is usually associated with Alfred Marshall and his well-known partial equilibrium method. In his original writings, Marshall shows a clear commitment to and appreciation for the function I have argued that both economics and thermodynamics perform.Footnote ⁹

His exploitation of the ceteris paribus pound, where inconveniences to our analysis are kenneled away for the time being, is quite clearly motivated in part by issues of tractability. But he means something more than just making a difficult problem manageable. He acknowledges that the effects of causes may unfold at different rates, so some causes may be less relevant than others in one’s analysis. Changes may occur so rapidly that their effects negate one another within a short period of time (e.g., rapid fluctuations in weather). In addition to factors that cancel one another out, we omit consideration of other interfering factors such as ones that simply take too long to be of current interest. The example of the fish market illustrates the practical questions one considers when making economic decisions, for example, what kind of employment to seek for the next year or two:

Marshall was well aware of the risks posed by holding on to ceteris paribus assumptions for too long; even seemingly negligible fluctuations could accumulate over time (Reference Marshall1890, V.V.20). Impounding has to be done carefully and with good reasons. The target of interest was dynamic behavior during some period of “normal conditions,” left deliberately ambiguous and specifiable only with the help of ceteris paribus restrictions. He intended, although unfortunately never completed, a follow-up second volume to the Principles elaborating on dynamic analysis.

Whatever the fully developed economic theory might have been, Marshall has significant commitments about what science looked like. By his own lights, even a law of physics such as the law of gravitation was “a statement of tendencies” (Marshall Reference Marshall1890, I.III.7). So in principle, economics and physics were doing the same thing; neither should be penned into the caricature of a science that facilitates deductive inferences about future behavior. Even in his last work, Industry and Trade (Reference Marshall1920), published shortly before his death, Marshall disavows this view of science as artificial and only applicable within very controlled environments. “Absolute certainty is possible only in regard to (1) particular individual facts; and (2) deductions by strict reasoning from axiomatic premisses, such as those of pure mathematics. Even sciences, which deal with concrete facts and conditions as definite and immutable as those of physics appear to be, cannot claim certainty over the whole of their area” (673). Both economics and physics state tendencies and can claim only some range of certainty over the “whole of their area.” Physics, Marshall thought, was better in terms of “exactness”Footnote ¹⁰—the statements of physics were less probabilistic than those of economics, which was akin to the “science of the tides” (Reference Marshall1890, I.III.9).Footnote ¹¹ The complexity of economics’ subject matter would, he thought, ultimately require the discipline to move away from the methods of mechanics and take its cue from the biological sciences. “The Mecca of the economist lies in economic biology rather than in economic dynamics. But biological conceptions are more complex than those of mechanics; a volume on Foundations must therefore give a relatively large place to mechanical analogies; and frequent use is made of the term ‘equilibrium,’ which suggests something of statical analogy. … But in fact it is concerned throughout with the forces that cause movement: and its key-note is that of dynamics, rather than statics” (preface, 19).

Not only did biological examples supply analogues for economic phenomena, but biology also provided metaphors for economic science itself. “The modern economic organism is vertebrate; and the science which deals with it should not be invertebrate. It should have that delicacy and sensitiveness of touch which are required for enabling it to adapt itself closely to the real phenomena of the world; but none the less must it have a firm backbone of careful reasoning and analysis” (Marshall Reference Marshall1890, app. B, 46, emphasis mine). If statics is always really a part of dynamics, ceteris paribus reasoning cannot be eliminated from the completed science. Properly conceived, then, ceteris paribus assumptions are fundamental to economic reasoning, and although an economic statement “is not descriptive, nor does it deal constructively with real problems,” it serves as “the theoretical backbone of our knowledge of the causes which govern value” (V.I.4).Footnote ¹²

Like the deployment of reversible processes in thermodynamic reasoning, ceteris paribus assumptions in economic reasoning help establish sets of relevant variables that are in principle dependent on one another. Articulating these variables establishes at the same time the scope of the problem at hand. In thermodynamics, we might establish the maximal efficiency limit of an engine. In economics, we might assess the extent of the effect of an economic perturbation on a particular market (at V.V.18, Marshall [Reference Marshall1890] humorously considers the effect of an influx of artists who insist on being pescatarians on the fishing industry). For Marshall, the idealizations used by economics (and thermodynamics) have a purpose that is not strictly descriptive or predictive. Rather, they have a demarcating role. They help set limits on what is empirically possible, and thus the scope of analysis itself, via articulating the relevant causal relationships for a given problem of interest. Properly conceived, ceteris paribus statements actually aid precise analysis.

4. Scientific Understanding in Terms of Efficiency

Ceteris paribus assumptions flag a methodology that we use to formulate clean answers to causal questions by positing an external (theoretical) controller manipulating one variable at a time, transporting a system from one equilibrium state to another. And while not explicit, the fundamental laws of thermodynamics are grounded on such a methodology. The causal relationships expressed by ceteris paribus laws draw the boundaries of what is empirically possible. Inextricably tied to this constraining role are opportunities for system control and, therefore, what I call understanding in terms of efficiency.Footnote ¹³

In applied contexts, our aim is to identify causal relationships apt for manipulation and the extent to which we can manipulate them in order to achieve desired effects. Notice that even in theoretical contexts, such as formulating the laws of supply and demand or the laws of thermodynamics, we nonetheless formulate them in terms of variable manipulation. Borrowing some terminology from recent work by Woodward (Reference Woodward2003), ceteris paribus assumptions help provide baseline conditions in order to assess how invariant the causal relationships between different variables are. Woodward defines invariance thusly: “When a relationship is invariant under at least some interventions … it is potentially usable in the sense that … if an intervention on X were to occur, this would be a way of manipulating or controlling the value of Y” (16). The problem an economist or an engineer faces is figuring out which Xs and which Ys matter, and to what extent they do. Assessing these relationships requires theoretical interventions that involve changing the value of a single variable and tracking the way it affects some other variable. What the relevant variables are depends on what the problem of interest is, and so they will also depend on how isolated that economic or thermodynamic system is from its surroundings.

So ceteris paribus assumptions partake in a methodology for establishing the maximal invariance of relevant variables with respect to each other and, at the same time, establishing what those variables are. This assessment involves determining which factors may be safely neglected, for example, those small daily weather fluctuations on the fish market. Manufacturing engines does not require our knowing all positions and velocities of the interacting gas particles contained inside. Woodward (Reference Woodward2002) considers an example from neuroscience—a simple Hebbian learning rule expressing the relationship between change in the synaptic weight of a neuron to its pre- and postsynaptic activity.Footnote ¹⁴ While the Hebbian yields causal information, we do not have to spell out all the conditions that hold in order to see that the Hebbian holds. Similarly, we do not have to spell out all the conditions that hold in order to see that the laws of supply/demand can be informative, too.

The knee-jerk reaction is to suspect that something paradoxical is going on here: interventions in the real world are always what we might call “ham-fisted” or “fat-handed”—an intervention will induce an effect along more than one causal path. After all, real interventions involve more than one thing changing, and often several causal processes will mutually interact. Woodward’s interventions are what one might call “surgical” (Pearl Reference Pearl2000) or “immaculate” (Bogen 2004)—the effects of any other variables are ignored or fixed during the hypothetical manipulation.Footnote ¹⁵ So how do we make sense of what actually happens in terms of what would happen?Footnote ¹⁶ My answer is that for many cases in physics and in economics formulating what would happen is prior to the question of what will happen. And it is not necessarily a stepping-stone to answering the question of what will happen; rather, it illuminates ways in which we could in principle be doing better. This is understanding in terms of efficient performance.

Like the pathways of the Carnot cycle, our supply and demand curves draw the boundaries of what counts as most efficient. We compare how we are actually doing against a baseline, as I did when evaluating the deadweight loss from selling widgets at too low a price. Given causal constraints articulated in terms of manipulable causal relations, we then know along what dimensions our system is most efficient and to what extent we fail to achieve efficiency (and so at the same time, what maneuvers are available to us for improvement). A pure decrease in supply pushes the new equilibrium price higher but at lower quantities sold. Comparative static exercises help us diagnose and proffer solutions for problems of inefficiency; for example, we might try to reduce exchange frictions by minimizing transaction costs. Similarly, while we cannot build Carnot engines, we can (and do successfully) try to improve the efficiency of engines, for example, by creating greater temperature differentials or by adjusting the inner workings of the engine to reduce losses due to friction.

Thus, we gain key information about a thermodynamic (or economic) system by considering its progress by way of various patterns of single-variable control, such as those reflected by the four legs of the Carnot cycle (or supply-demand curves). Despite their “idealized” nature, this diagnostic and evaluative role still leaves room for such laws to be empirically useful in more complicated scenarios in which representing multiple variables changing in relation to one another at once remains difficult or elusive (e.g., what happens if we tweak both the temperature and the pressure of a gas at the same time or supply and demand both change). These considerations suggest that partial equilibrium analyses—analyses of processes that are essentially driven by single-variable control—are still importantly useful and may not require a general equilibrium type of analysis (whose scope would be of the whole economy) to be available, even in principle. Idealizing methods that ignore disturbing factors are, thus, effective ways of dealing with complex, dynamic systems.

Equilibrium exercises also have clear, contemporary implications in applied economics and in many cases are successful. Equilibrium analysis is still a dominant strategy in economics, in particular when it comes to matters of policy making. In reaction to financial crises, notably since the 1990s and especially since the 2007 crash, the Federal Reserve conducts an annual review of the banking sector. One thing it checks for is whether the banking sector can absorb large shocks and yet continue operating normally—these are so-called stress tests. If the banking sector is able to withstand economic shocks, disastrous effects on individuals (and other regions of the economy at large) can be curtailed. The analysis is clearly counterfactual—if a crisis were to occur, then we want the economy to be structured in a way as to withstand it. Our aim is not predictive in the strict sense that we should be able to deduce something’s behavior at any point in the future: “Stress tests estimate the exposure, the possible losses and the general reaction of the financial system to a specific event, but not the probability of the event occurring” (Committee on the Global Financial System 2000, 3). Rather, economic policy is often concerned with the question of how to best curtail the effects of financial crises in case one should occur, independently of whether a crisis occurs. They help answer questions such as, “Does this bank have enough capital in reserve in order to continue lending if unemployment rises/equity prices drop/housing prices change/and so on by X%? If not, how much more does it need?”

This methodology establishes some a priori expectation on how driving forces relate to the responses elicited.Footnote ¹⁷ These may not tell us, however, about what will actually happen at any arbitrary moment in the future. A Carnot engine does not tell us much about how an actual engine works, and a partial equilibrium analysis will not tell us exactly how the actual fish market will behave. But these exercises articulate the benchmarks that we might try to approximate, whether it be smoothly functioning engines or resilient markets. The modern worry, as former Treasury Secretary Timothy Geithner (Reference Geithner2014) puts it, is what to do since “financial crises cannot be reliably predicted, so they cannot be reliably prevented.” Ultimately, economists wish to understand how a fluctuating economy behaves so that through suitable controlled interventions, its functioning can be improved. Despite the unpredictability of crises, “governments can do a lot to reduce the damage of financial disasters. … They can reduce the system’s vulnerability of risk, as well as the risk that crises will spiral out of control” (388). The methodology of using ceteris paribus yields understanding in terms of diagnostic causal relationships between salient variables; we use those variable relationships to design and evaluate efficient systems.

5. Against Orthodoxy: Rejecting the Semantic Completer Account

In the previous section, I proposed that ceteris paribus methods serve to articulate relevant causal relationships and so aid us in our understanding a system in terms of how efficiently it can perform. This interpretation accommodates its original intended usage and still persists today in practice but contrasts with the point of view pursued by a large group of prominent philosophers.Footnote ¹⁸ According to one popular understanding of ceteris paribus laws, the semantic completer interpretation, “If A, then ceteris paribus, B” is an abbreviation for “If A and … and … then B.” The ceteris paribus clause is a placeholder for this list of other conditions assumed to hold. But given the similarities with thermodynamics detailed in section 2, looking at a demand curve as representing a deficient species of law would be just as odd as, say, considering the idealized temperature-entropy curves for the Carnot engine as representing a deficient law of thermodynamics. As I have been arguing, the purpose of these idealizations is to articulate variable relationships for diagnostic purposes. Regardless of whether the semantic completer account is ever useful, it gets the motivation for deploying idealizations in the way that economics does quite wrong, and here ceteris paribus is explicitly and systematically used in a way it is not in other sciences.

Fodor (Reference Fodor1991) and Schiffer’s (1991) seminal debate over whether social science statements could count as laws was grounded in a common assumption despite their differing verdicts. This assumption, which has been inherited by contemporary views and complaints like those described in section 1, identifies ceteris paribus statements as problematic because they admit of exceptions. To turn them into robust laws, we would have to undertake the following project. A state such as “desiring cake” can be realized in any number of ways at the neurological level. A lower-level state that instantiates this higher-order one might take the form of “neurons a and b light up and c does not.” We spell out what it would be to desire cake in terms of neurons lighting up, and in addition, we have to rule out other goings-on that may interfere and render the statement false. After all, I often desire cake without following up on this desire. I may have overriding desires that would prevent my pursuing cake, such as a conflicting desire to make it to a department meeting on time. For Fodor, who maintains that there are such things as ceteris paribus laws, this means there are circumstances that in addition to the realizer of “desiring cake”—the comprehensive description of such circumstances is called the “completer”—imply my pursuit of cake. As long as realizers have completers, the statement counts as a law. So suitably filled out, “Desiring cake leads to pursuit of cake” is a law according to this view.

But Fodor’s account will allow too many things to count as laws. Just about anything—even “ceteris paribus, if someone is hungry, she will pursue cake” is a candidate for lawhood.Footnote ¹⁹ Schiffer maintains that generalizations hedged by ceteris paribus clauses are simply not laws at all. Even if the completer could be formulated to yield a true statement, the relevant filler is usually borrowed from the language of a different science than the target one.Footnote ²⁰ Although it does not bar such statements from having explanatory value, Schiffer thinks it does bar them from being proper laws.

Other philosophers eschew the semantic interpretation as the right question to ask. Questions of lawhood are at stake.Footnote ²¹ Earman and Roberts (Reference Earman and Roberts1999) claim that “that there is no distinctively philosophical problem about ceteris paribus, but there is a scientific problem: what is needed is not finer logic chopping but better science” (460). Contra Cartwright (Reference Cartwright1983), they claim that “typical theories from fundamental physics are such that if they were true, there would be precise proviso-free laws” (Earman and Roberts Reference Earman and Roberts1999, 446). So, the statements of the special sciences do not count as laws because ceteris paribus statements need further development. Not only does physics contain real laws, but it has always been the aim of physics to do so: “We also claim that the history of physics and the current practice of physics reveal that it is the goal of physicists to find such strict, proviso free laws” (446). The presence of ceteris paribus indicates that a statement serves as a landmark in a scientific landscape that is yet in progress. Like Earman and Roberts, Smith (Reference Smith2002) agrees it is only at the level of fundamental physics that we have laws that hold without exception; ceteris paribus clauses have no substantive role there.

But, one might suggest that economics is not one of these sciences that is in its early stages. To account for social science statements that seem fairly well developed, Earman, Roberts, and Smith (Reference Earman, Roberts and Smith2002) propose that “there are plenty of important things that indicative-mood sentences can do other than state propositions or facts” (290). It is not merely that they fail to be laws; ceteris paribus claims simply are not meant to be laws in the first place. Perhaps, Earman et al. suggest, they state statistical relationships between well-defined variables. This is not satisfactory for two reasons. First, this is inadequate since our goal is to make sense of causal relations, not mere correlations.Footnote ²² Second, in economic analysis—and in thermodynamics—what we are trying to do is delineate variables, and it is not given that we have well-defined ones.Footnote ²³

Yet other philosophers have taken different strategies that allow for the statements of the social sciences to be invariant under some range of counterfactual scenarios, rather than requiring them to be exceptionless simpliciter. This would both avoid the demand to provide completers as well as leave room for ceteris paribus to perform a role that is substantially law-like. But they often assume a distinction between “more” and “less” fundamental laws depending on how stable or invariant they are, that is, how more or less broadly they hold. So even more permissive accounts of lawhood, such as Mitchell’s (Reference Mitchell2003), do not capture the role that ceteris paribus laws play in disciplines such as economics. Mitchell’s account emphasizes that the distinction between laws of the social sciences and the laws of physics or logic is a matter of a difference not in kind (where one kind counts as law and the others do not) but rather in degree (in terms of regularity). This spectrum is meant to capture the gamut of scientific statements from the law of conservation of energy (fairly close to our notion of a law), Galileo’s law of free fall (further away this notion), Mendel’s law of inheritance (yet even further), all the way to accidental generalizations on the opposite end (Mitchell Reference Mitchell2003, 138–40).

However, the way ceteris paribus assumptions are invoked in the economic and thermodynamic examples discussed does not flag them as occupants on a sliding scale, where some statements are universal or more exceptionless than others. In fact, economic statements hedged by ceteris paribus clauses, such as the laws of supply and demand, are not invariant (or otherwise) just as they are, so the sliding scale metaphor would be inappropriate. They can be used to analyze any part of the economy over any amount of time, depending on what the relevant economic problem is. If anything is invariant (or not), it is particular claims about particular markets. This presupposes having already carved out some particular part of the economy over some period of time. And the scope of interest, insofar as the economy is concerned, is often dictated by questions of economic policy making.

Ultimately, I am not concerned with whether the statements of economics or other social sciences are laws but rather with the assumptions that give rise to this question in the first place. My account emphasizes the purely methodological role ceteris paribus assumptions play instead. They do not indicate that the statement is a special kind of scientific generalization that is entirely different from other things considered to be laws. They are tools for the identification of invariant causal relationships relative to a particular problem. This is at the same time to establish the relevant scope of the problem within which they are invariant, so that we can engineer efficient systems and processes. As we have seen, there is no significant difference in methodology between the idealizations invoked by ceteris paribus assumptions in economics and those sometimes deployed in other sciences such as thermodynamics. While this does not imply that there is no difference between economics and the other sciences, it does suggest that differences cannot be justified by merely pointing at the presence of the ceteris paribus rider.

Completer accounts miss out entirely on this diagnostic kind of understanding in terms of efficiency that is crucial in applications. Instead they try to cram valuable scientific information into a form in which it does not fit. Like my account, a completer account is motivated in part by the fact that what we want to know is the range of circumstances in which a particular generalization holds. But they take ceteris paribus laws to be approximations of—and thus in some way deficient forms of—more general laws. On my account, ceteris paribus laws are not deficient forms of anything, although real life systems may be deficient (i.e., inefficient) when contrasted with them.

6. Concluding Remarks

Discussions in philosophy of science frequently take ceteris paribus assumptions to signal that the law-like statement they figure in is not yet complete. This is orthogonal to the way ceteris paribus assumptions are often actually employed in the discipline in which they appear explicitly the most often (economics), and it obscures the fact that similar strategies are employed in other sciences such as physics.

One might initially think the obvious way to improve predictive accuracy is to treat an idealized model as a useful base case. The received view has it that science progresses by making its way to a more comprehensive and realistic picture by adding those extra details that we missed the first time around. So this may not be the best way to measure the degree to which something succeeds or fails to be a genuine science. The distinction between the laws of thermodynamics and the laws of economics is not a difference in kind since they both involve idealization involving ceteris paribus assumptions, and for the same reasons. They are also not different by degree from one another, because the ceteris paribus rider flags a background methodology—the equilibrium methodology—aimed at constraint and control in both disciplines.

Instead of envisioning science as primarily describing autonomously evolving systems, philosophers of science should approach dynamical systems, including economic and thermodynamic ones, as the kinds of things we can theoretically intervene on. This shift in perspective has dramatic effects: it makes possible an interesting notion of explanation, yet still preserves a sense in which we talk about the dynamical properties of systems without having to give up our static idealizing strategies. We move away from describing and predicting the behavior of autonomously evolving systems to understanding the behavior of systems in terms of the ways they can be manipulated and improved. This recognizes idealizations via ceteris paribus hedging as crucial causal tools that are and can be usefully deployed in sciences quite generally.Footnote ²⁴