The left-invariant sub-Riemannian problem on the group of motions (rototranslations) of a plane SE(2) is considered. In the previous works [Moiseev and Sachkov, ESAIM: COCV, DOI: 10.1051/cocv/2009004; Sachkov, ESAIM: COCV, DOI: 10.1051/cocv/2009031], extremal trajectories were defined, their local and global optimality were studied. In this paper the global structure of the exponential mapping is described. On this basis an explicit characterization of the cut locus and Maxwell set is obtained. The optimal synthesis is constructed.

The optimal control of a mechanical system is of crucial importance in many application areas. Typical examples are the determination of a time-minimal path in vehicle dynamics, a minimal energy trajectory in space mission design, or optimal motion sequences in robotics and biomechanics. In most cases, some sort of discretization of the original, infinite-dimensional optimization problem has to be performed in order to make the problem amenable to computations. The approach proposed in this paper is to directly discretize the variational description of the system's motion. The resulting optimization algorithm lets the discrete solution directly inherit characteristic structural properties from the continuous one like symmetries and integrals of the motion. We show that the DMOC (Discrete Mechanics and Optimal Control) approach is equivalent to a finite difference discretization of Hamilton's equations by a symplectic partitioned Runge-Kutta scheme and employ this fact in order to give a proof of convergence. The numerical performance of DMOC and its relationship to other existing optimal control methods are investigated.

This paper focuses on the analytical properties of the solutions to the continuity equation with non local flow. Our driving examples are a supply chain model and an equation for the description of pedestrian flows. To this aim, we prove the well posedness of weak entropy solutions in a class of equations comprising these models. Then, under further regularity conditions, we prove the differentiability of solutions with respect to the initial datum and characterize this derivative. A necessary condition for the optimality of suitable integral functionals then follows.

We propose a general reduced-order filtering strategy adapted to Unscented Kalman Filtering for any choice of sampling points distribution. This provides tractable filtering algorithms which can be used with large-dimensional systems when the uncertainty space is of reduced size, and these algorithms only invoke the original dynamical and observation operators, namely, they do not require tangent operator computations, which of course is of considerable benefit when nonlinear operators are considered. The algorithms are derived in discrete time as in the classical UKF formalism – well-adapted to time discretized dynamical equations – and then extended into consistent continuous-time versions. This reduced-order filtering approach can be used in particular for the estimation of parameters in large dynamical systems arising from the discretization of partial differential equations, when state estimation can be handled by an adequate Luenberger observer inspired from feedback control. In this case, we give an analysis of the joint state-parameter estimation procedure based on linearized error, and we illustrate the effectiveness of the approach using a test problem inspired from cardiac biomechanics.

The paper represents the first part of a series ofpapers on realization theory of switched systems. Part I presents realization theory of linear switched systems,Part II presents realization theory of bilinear switched systems.More precisely, in Part I necessary and sufficient conditionsare formulated for a family of input-output maps to berealizable by a linear switched system and a characterizationof minimal realizations is presented. The paper treats two types of switched systems.The first one is when all switching sequences are allowed. The second one is when only a subset of switching sequences isadmissible, but within this restricted set the switching times are arbitrary.The paper uses the theory of formal power series to derivethe results on realization theory.

This paper is the second part of a series of papers dealing withrealization theory of switched systems.The current Part II addresses realization theory of bilinear switchedsystems. In Part I [Petreczky, ESAIM: COCV, DOI: 10.1051/cocv/2010014] we presented realizationtheory of linear switched systems.More precisely, in Part II we present necessary and sufficient conditionsfor a family of input-output maps to berealizable by a bilinear switched system, together with a characterizationof minimal realizations.Similarly to Part I, the paper deals with two types of switched systems.The first one is when all switching sequences are allowed. The second one is when only a subset of switching sequences isadmissible, but within this restricted set the switching times are arbitrary.The paper uses the theory of formal power series to derivethe results on realization theory.

We consider higher order functionals of the form

$F[u]=\int\limits_\Omega f(D^mu)\,{\rm d}x \qquad\text{for }u:\mathbb{R}^n\supset\Omega\to\mathbb{R}^N,$

where the integrand $f:{\textstyle \bigodot^m}(\R^{n},\R^{N})\to\mathbb{R}$, m ≥ 1 is strictly quasiconvex and satisfies a non-standard growth condition.More precisely we assume that f fulfills the (p, q)-growth condition

\[\gamma|A|^p\le f(A)\le L(1+|A|^q)\qquad \mbox{for all }A \in {\textstyle \bigodot^m}(\R^{n},\R^{N}),\]

with γ, L > 0 and $1< p \le q<\min\big\{p+\frac1n,\frac{2n-1}{2n-2}p\big\}$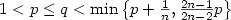. We study minimizers of thefunctional $F[\cdot]$ and prove a partial $C^{m,\alpha}_{\rm loc}$-regularity result.

We prove that the critical points of the 3d nonlinear elasticity functionalon shells of small thickness h and around the mid-surface S of arbitrary geometry, converge as h → 0to the critical points of the vonKármán functional on S, recently proposed in [Lewicka et al., Ann. Scuola Norm. Sup. Pisa Cl. Sci. (to appear)].This result extends the statement in [Müller and Pakzad, Comm. Part. Differ. Equ. 33 (2008) 1018–1032], derived for the case of plates when $S\subset\mathbb{R}^2$.The convergence holds provided the elastic energies of the 3d deformations scale like h4 and the external body forces scale like h3.

We are interested in the feedback stabilization of a fluid flow over a flat plate, around a stationary solution, in the presence of perturbations. More precisely, we want to stabilize the laminar-to-turbulent transition location of a fluid flow over a flat plate. For that we study the Algebraic Riccati Equation (A.R.E.) of a control problem in which the state equation is a doubly degenerate linear parabolic equation. Because of the degenerate character of the state equation, the classical existence results in the literature of solutions to algebraic Riccati equations do not apply to this class of problems. Here taking advantage of the fact that the semigroup of the state equation is exponentially stable and that the observation operator is a Hilbert-Schmidt operator, we are able to prove the existence and uniqueness of solution to the A.R.E. satisfied by the kernel of the operator which associates the 'optimal adjoint state' with the 'optimal state'. In part 2 [Buchot and Raymond, Appl. Math. Res. eXpress (2010) doi:10.1093/amrx/abp007], we study problems in which the feedback law is determined by the solution to the A.R.E. and another nonhomogeneous term satisfying an evolution equation involving nonhomogeneous perturbations of the state equation, and a nonhomogeneous term in the cost functional.


In this paper, the stability of a Timoshenko beam with time delaysin the boundary input is studied. The system is fixed at the leftend, and at the other end there are feedback controllers, in which time delays exist. We prove that this closed loop system iswell-posed. By the complete spectral analysis, we show that there isa sequence of eigenvectors and generalized eigenvectors of thesystem operator that forms a Riesz basis for the state Hilbert space. Hence the system satisfies the spectrum determined growth condition. Then we conclude the exponential stability of the system under certain conditions. Finally, we give some simulations to support our results.


We prove the existence of a principal eigenvalue associated to the∞-Laplacian plus lower order terms and the Neumann boundarycondition in a bounded smooth domain. As an application we getuniqueness and existence results for the Neumann problem and adecay estimate for viscosity solutions of the Neumann evolutionproblem.