Characteristics of the rectangular SIW cavity resonator

Figure 1 depicts the simplified structure of a dielectric-filled rectangular cavity resonator where w, l, and h are the width length, and height of the cavity, ɛ_r and μ_r are relative permittivity and relative permeability of the substrate, respectively. For such a cavity resonator, the height of the cavity is much smaller than the working wavelength. Thus, only TE_m0q mode can be excited. The resonant frequencies of the TE_m0q mode in the cavity are determined by [Reference Pozar24]

(1)$$f_{TEm0q} = \displaystyle{c \over {2\sqrt {\mu _r\varepsilon _r} }}\sqrt {{\left({\displaystyle{m \over w}} \right)}^2 + {\left({\displaystyle{q \over l}} \right)}^2} , \;$$

where c is the light velocity in vacuum, m and q are mode indices in the x- and z-axis directions, respectively. The fundamental resonant mode in a rectangular SIW cavity is TE₁₀₁ mode. The frequency ratio of higher-order resonant mode to the fundamental one is given by

(2)$$\displaystyle{{\,f_{TE_{m0q}}} \over {\,f_{TE_{101}}}} = \sqrt {q^2 + \displaystyle{{m^2-q^2} \over {1 + {( {{w / l}} ) }^2}}} .$$

Fig. 1. Structure of a rectangular cavity resonator.

In equation (2), let m = q, we can get

(3)$$f_{TE_{q0q}} = q\cdot f_{TE_{101}}.$$

It indicates that if a square cavity resonator and a rectangular one have the same fundamental frequency f _TE101, they would also have the same higher resonant mode frequencies for TE₂₀₂ and TE₃₀₃ mode. Figure 2 shows the normalized frequency distribution for a square cavity resonator and a rectangular one. The highest resonant mode in Fig. 2 is chosen to be TE₃₀₃ mode whose resonant frequency is three times the fundamental one. It is due to the fact that the upper stopband of the wide stopband SIW filters in the former literatures is limited to 3f ₀. For a square cavity resonator (w/l = 1), it has 11 resonant modes in Fig. 2. Except for TE₁₀₁, TE₂₀₂, and TE₃₀₃ mode, there are four couples of degenerate modes. The degenerate modes have the same resonant frequencies. For the rectangular cavity resonator (w/l = 2), each couple of degenerate modes in the square one splits into two different frequencies. So the rectangular cavity resonator has more unwanted higher mode resonant frequencies than the square one. Furthermore, a square cavity has a smaller cavity size and higher quality factor than the rectangular cavity with the same fundamental resonant frequency. Thus, the square cavity resonator is more suitable for the wide stopband filter design.

Fig. 2. Normalized frequency distribution for a square cavity resonator (w/l = 1) and a rectangular one (w/l = 2).

Analysis of the coupling structure

Magnetic field distribution of the square cavity resonator

All the resonators in our filter design are magnetically coupled. So the magnetic field distribution of the square cavity resonator is firstly analyzed. Figure 3 shows the magnetic field distribution and resonant frequencies of the first 11 resonant modes of a square cavity resonator. Rectangle A represents the input/output coupling slot. The nodes of the standing wave for TE₂₀₁, TE₂₀₂, TE₂₀₃, and TE₄₀₁ modes appear at the center of rectangle A. On each side of the node, the magnetic fields for those modes have the same amplitude and are 180° out-of-phase. Thus, none of those modes could be excited. In addition, there are two nodes of standing wave for TE₃₀₁, TE₃₀₂, and TE₃₀₃ modes at the location of rectangle A. The coupling to those modes depends on the length of rectangle A. If rectangle A has an appropriate length, the magnetic fields would have the same amplitude and are 180° out-of-phase on each side of the node. Those modes would be weakly coupled to the input/output port. Rectangle B represents the coupling slot on the common metal layer of two vertical adjacent square cavity resonators. It is perpendicular to the magnetic field lines of TE₁₀₂, TE₂₀₂, TE₁₀₃, TE₂₀₃, and TE₁₀₄ modes. So the couplings among those modes are suppressed. Meanwhile, this slot is parallel to the magnetic field lines of the other modes. As a result, the couplings of those modes are stronger. Rectangle C is the location of the post-wall iris. Its center is at the nodes of the standing wave of TE₁₀₂, TE₂₀₂, TE₃₀₂, and TE₁₀₄ modes. The couplings of those modes are suppressed. Similar to the situation of rectangle A, the couplings between TE₁₀₃, TE₂₀₃, and TE₃₀₃ modes depends on the length of rectangle A. Those modes may be weakly coupled if a proper length is achieved. By combing those external and internal coupling structures in the filter design, the couplings of the higher resonant modes in the cavity are suppressed. Only TE₁₀₁ mode can be effectively coupled.

Fig. 3. Magnetic field distribution of the first 11 resonant modes in a square cavity resonator.

Input/output coupling

The feeding structure at port 1 in Fig. 4 is employed in our filter design. At port 1, the microstrip feeding line is magnetically coupled to the cavity resonator through the slot. Port 2 is weakly coupled for extracting the external Q for the feeding structure. This model is simulated by the commercial software ANSYS HFSS 15. With the simulated transmission response, the external Q can be calculated by [Reference Hong and Lancaster25]

(4)$$Q_e = \displaystyle{{\,f_0} \over {\Delta f_{3{\rm dB}}}}, \;$$

where f ₀ is the center frequency of the transmission response, Δf _3dB is the 3 dB bandwidth of the passband. By changing the length of the slot l_s, we can get the design curves for external Q as shown in Fig. 5. Figure 6 shows the wide-band transmission response of the feeding structure and the magnetic field distribution at resonant frequencies. As shown, only TE₁₀₁, TE₁₀₂, TE₁₀₃, TE₃₀₂, TE₁₀₄, and TE₃₀₃ modes are excited. Because the resonant frequencies of TE₁₀₄ and TE₃₀₃ modes are very close to each other while the coupling for TE₃₀₃ mode is stronger than TE₁₀₄ mode, it is difficult to see the peak for the TE₁₀₄ mode. The resonant frequency of TE₁₀₄ mode is estimated by the TE₃₀₃ mode. In Fig. 6, f _TE303 = 25.11 GHz while the frequency ratio of f _TE303 and f _TE104 is 1.029. So we can get f _TE104 = 24.4 GHz.

Fig. 4. Structure for extracting Q_e of different modes.

Fig. 5. Extracted Q_e against the length of the coupling slot.

Fig. 6. Transmission response of the two-port coupled single cavity resonator and the magnetic field distribution at resonant frequencies (l_s = 3 mm).

Coupling through slots

The vertically adjacent resonators are coupled through the slot on the common metal layer as shown in Fig. 7. The distance between the slot and the side is about one-fourth of the side length. The Eigen-mode simulation in HFSS is used to extract the coupling coefficients. The coupling coefficient is calculated by [Reference Hong and Lancaster25]

(5)$$M = \displaystyle{{\,f_{02}^2 -f_{01}^2 } \over {\,f_{02}^2 + f_{01}^2 }}, \;$$

where f ₀₁ and f ₀₂ are the resonant frequencies of the corresponding modes. Figures 8(a) and 8(b) show the extracted coupling coefficients versus the slot length l ₃ for weakly and strongly coupled modes, respectively. It can be found that the coupling coefficients are smaller than 0.008 for the weakly coupled modes no matter how large l ₃ is. Those weakly coupled modes agree well with the former analysis. In Fig. 8(b), when l ₃ changes from 1 to 8 mm, the coupling coefficient for TE₁₀₁ mode has a wide range from 0.001 to 0.05 which may cover a wide range of the filter's corresponding bandwidth. In Fig. 8(a), the curves do not show the exponential feature as the curves in Fig. 8(b). The effect of weak electric coupling cannot be neglected when the magnetic coupling is also very weak. They would cancel each other. When the length of the slot increases, the increment of the electric and magnetic coupling is quite different. Thus, the curves in Fig. 8(a) have different shapes compared with those curves in Fig. 8(b).

Fig. 7. Resonators coupled through slots for extracting the coupling coefficients of different modes.

Fig. 8. Extracted coupling coefficients against the length of the coupling slot, (a) weakly coupled modes, (b) strongly coupled modes.

Coupling through the horizontal aperture

The coupling between two horizontally adjacent resonators is realized by the post-wall formed aperture as shown in Fig. 9. The extracted coupling coefficients versus the aperture width d ₂ for weakly and strongly coupled modes are shown in Figs 10(a) and 10(b), respectively. The coupling coefficients for TE₁₀₂, TE₂₀₂, TE₃₀₂, and TE₁₀₄ modes are smaller than 0.014 which are much lower than those of the strongly coupled modes. It agrees well with the prediction. In addition, TE₁₀₃ and TE₃₀₃ modes are also weakly coupled modes whose coupling coefficients are smaller than 0.008. Although TE₂₀₃ mode is categorized to be strongly coupled mode, it is the smallest one in this category while the coupling coefficients for other strongly coupled modes are all larger than 0.02. The coupling coefficient for TE₁₀₁ mode ranges from 0.022 to 0.054 which may expand by further removing some vias for a wider filter bandwidth or reduce by adding more vias for a narrower filter bandwidth.

Fig. 9. Resonators coupled through the horizontal aperture for extracting the coupling coefficients of different modes.

Fig. 10. Extracted coupling coefficients against the width of the post-wall iris, (a) weakly coupled modes, (b) strongly coupled modes.

Design and measurement of the proposed filter

Figure 11 shows the final configuration of the proposed multilayer SIW filter. It consists of four square SIW cavity resonators. Resonators 1 and 2, as well as resonators 3 and 4 are vertically coupled through the rectangular slots in the middle metal layer. Resonators 2 and 3 are horizontally coupled according to the magnetic post-wall iris. This filter is designed to operate at the center frequency of 8 GHz with a relative bandwidth of 6%. The Chebyshev low-pass prototype with 0.0436 dB ripple is chosen here. The coupling matrix and external Q which satisfy those specifications can be calculated by equations (3.26) and (5.24) in [Reference Hong and Lancaster25]

(6)$$[ M ] = \left[{\matrix{ {0.0483} & 0 & 0 & 0 & 0 \cr 0 & {0.0425} & 0 & 0 & 0 \cr 0 & 0 & {0.0326} & 0 & 0 \cr 0 & 0 & 0 & {0.0425} & 0 \cr 0 & 0 & 0 & 0 & {0.0483} \cr } } \right]$$

(7)$$Q_{ei} = Q_{eo} = 20.02.$$

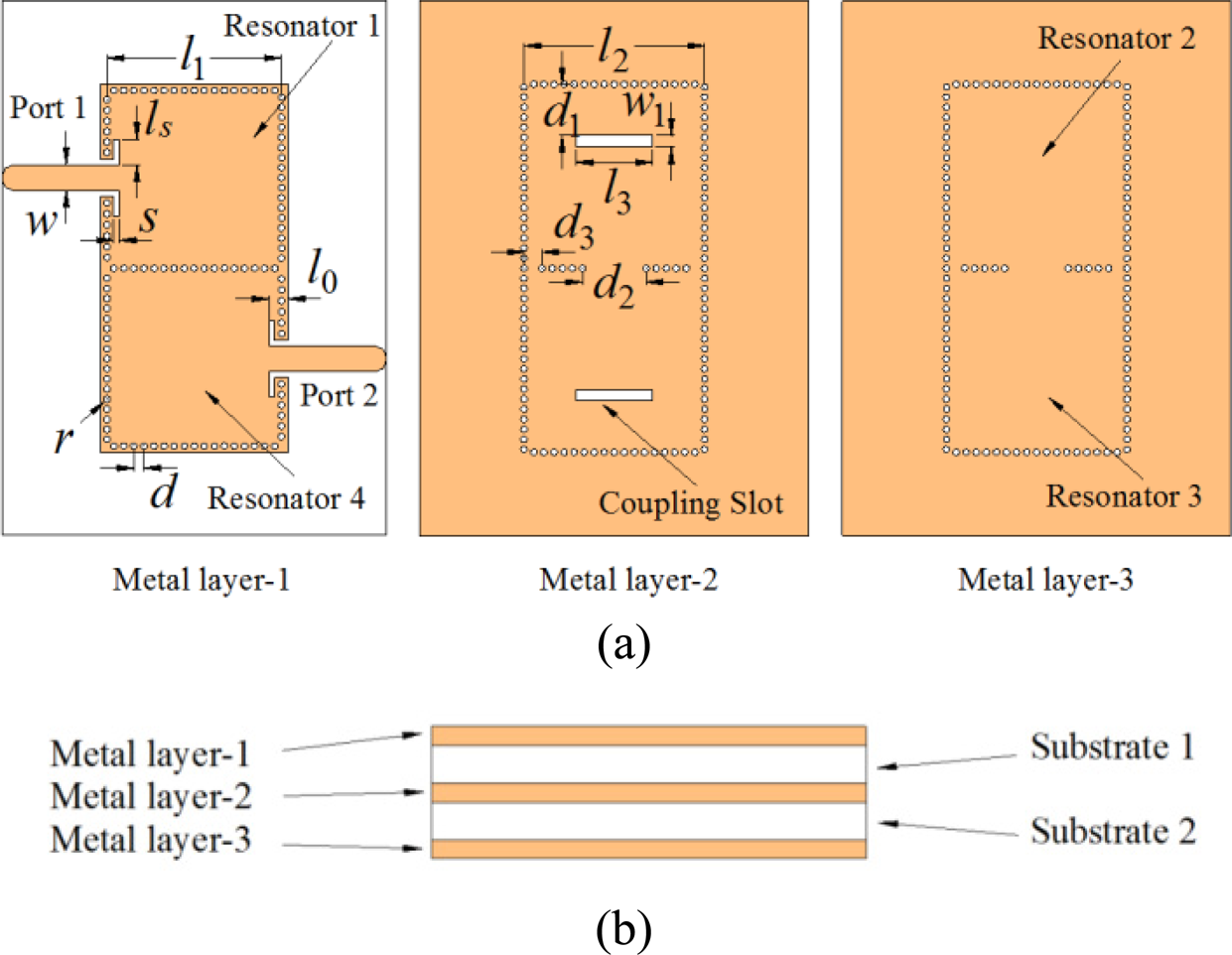
Fig. 11. Structure of the proposed multilayer SIW filter, (a) layout of each metal layer, (b) side view of the filter (l ₀ = 1.7, l ₁ = 15.6, l ₂ = 16.16, l ₃ = 6.84, l_s = 2.26, w = 2.3, w ₁ = 1, s = 0.5, d = 0.9, d ₁ = 4.6, d ₂ = 5.7, d ₃ = 1.63, r = 0.3, unit: mm).

For convenience, the unnormalized coupling coefficient instead of the normalized coupling coefficients is used here because the unnormalized coupling coefficient can be read directly in the figures. The general guidelines for designing the proposed filter are as follows:

1. (1) The F4B substrate (dielectric constant = 2.6, loss tangent = 0.001, substrate thickness = 0.8 mm, copper thickness = 0.018 mm) is chosen for the filter design. The initial dimensions of the square SIW cavity resonator can be decided by the center frequency of the filter according to equation (1). We can get the side length of the resonator which is 16.4 mm. The accurate dimensions can be obtained by the full-wave EM simulator HFSS.

2. (2) According to the required external Q of the filter (Q_e = 20.02), the length of the coupling slot l_s is about 2.5 mm in Fig. 5. Similarly, the required coupling coefficient M ₁₂ = 0.0425 and M ₂₃ = 0.0326, it can be found in Figs 8(b) and 10(b) that the slot length l ₃ is about 7.5 mm and the width of the post-wall iris d ₂ is about 5.75 mm, respectively.

3. (3) Because the introduction of coupling structure and the vias which forms the metal wall would change the resonant frequencies of the resonators and coupling, all the design parameters are tuned to satisfy the filter's specifications.

The final dimensions for the SIW filter after tuning is listed in the caption of Fig. 11. Figure 12 shows the photographs of the fabricated filter. The upper and lower substrates are stacked together by screws. The overall size of the filter is 17.36 mm × 34.12 mm × 1.672 mm. Figure 13(a) shows the narrowband response of the filter. The simulated results show an insertion loss of 2.01 dB at the center frequency 8 GHz and a relative bandwidth of 6%. The measured insertion loss is 2.49 dB at the center frequency 8.02 GHz and the measured relative bandwidth is 6.23%. The measured return loss is better than 12 dB in the whole passband. Figure 13(b) is the simulated and measured wideband response of the filter. As shown, the rejection level of the measured spurious response is better than 20 dB up to 21.92 GHz which is 2.73 times the filter's center frequency. Table 1 compares our design with other reported wide stopband SIW filters. It can be seen that the designs in [Reference Moro, Moscato, Bozzi and Perregrini13, Reference Zhu, Hong, Chen and Wu17, Reference Chu, Guo, Zhang, Xu, Hong and Wu22] have deep stopband suppression better than 45 dB with a suppression bandwidth around 2f ₀. If a compact size is required, the method in [Reference Moro, Moscato, Bozzi and Perregrini13, Reference Shen14, Reference Cheng, Li, Lu and Huang23] is a good choice. Our design has a wider relative bandwidth than most other designs. A wider bandwidth may lead to a stronger coupling of the higher harmonics. But our design shows a wider stopband than most other designs. Compared with [Reference Chu, Guo, Zhang, Xu, Hong and Wu22] whose ports are at different layers, our design has both ports at the same layer which is more convenient for practical use. Moreover, taking advantage of the multilayer technology, the fabricated filter has a smaller size than most other designs.

Fig. 12. Photograph of the fabricated filter, (a) before assembled, (b) after assembled.

Fig. 13. Synthesized, simulated and measured results of the proposed filters (dash dot line: synthesis, dash line: simulation, solid line: measurement), (a) narrowband response, (b) wideband response.

Table 1. Comparison of presented wide stopband SIW filter with other similar designs

Rej. (dB)/S.B.: rejection (dB)/stopband.