1. INTRODUCTION
Receiver Autonomous Integrity Monitoring (RAIM) is a technique whereby a GNSS receiver processor determines the integrity of the GNSS navigation signals using only GNSS signals or GNSS signals augmented with altitude. This determination is achieved by a consistency check among redundant pseudorange measurements. At least one satellite in addition to those required for navigation should be in view for the receiver to perform the RAIM fault detection (FD) function or two additional satellites if the RAIM fault detection and exclusion (FDE) is to be performed (AMC-20-5, 2003). However, it is very common that more satellites are needed for successful FD or FDE due to bad satellite geometry. Moreover, additional satellites may be needed if some of the satellites are obscured by terrain.
RAIM algorithms can be divided into two parts: an algorithm for error detection, which detects the actual satellite failures, and a geometry screening algorithm, which computes error detection performance with regards to specific satellite geometry. By using only the geometry screening algorithm, without the actual pseudorange measurement and error detection, error detection performance can be computed in advance for any given point in time and space. In this way, the RAIM availability prediction can be performed in advance for any flight, and this is, in fact, required by law (AMC-20-5, 2003). For this purpose of predicting RAIM availability, the AUGUR program was created by EUROCONTROL.
At higher altitudes, such as those flown at during the en-route part of flight, terrain masking is of little influence and a fixed mask can be used (usually 5°). However, GPS is also approved as a stand-alone aid for non-precision approaches (NPA), allowing flying at much lower altitudes, thus increasing the probability of RAIM unavailability due to terrain masking in mountainous areas. Furthermore, such RAIM outages cannot be predicted using the conventional RAIM availability prediction algorithms. Of course, fixed mask used by these algorithms can be elevated to a higher value (maximum of 12·5° in AUGUR) but, for example, a mountain can mask satellites up to 20° on one side of the desired flight track and merely 5° on the other side. Fixed mask of 12·5° could, in that case, exclude some satellites that would be visible, and include some satellites that would be invisible in the real-time (actual) situation. Because of this, aerodromes in mountainous areas should employ a variable mask RAIM availability prediction algorithm for fulfilling requirements made by AMC-20-5, 6.2.2 (d) (ii), which states:
“… predictive RAIM or an equivalent prediction tool is used, and the monitoring capability (RAIM or equivalent) is available at the destination aerodrome at the expected time of arrival.”
If it is to be reliable and accurate, this monitoring capability should extend beyond the aerodrome to include the whole approach track. Obviously, monitoring stations cannot be placed along the whole approach track, therefore, accurate simulation must be performed taking into account the terrain elevation model. Computationally, an algorithm including a terrain elevation model is more expensive; however, computers today are more powerful than ever and this task can be easily solved.
2. RAIM OVERVIEW
There are many RAIM algorithms that have been proposed in different papers and literature and all of them are based on checking consistency among redundant pseudorange measurements. Before making any modifications, however small, to the existing algorithms one must understand the way these algorithms work. An overview of all RAIM schemes is beyond the scope of this paper, hence for illustrative purposes, one simple baseline RAIM algorithm will be described. These are the steps of the baseline RAIM algorithm:
1. Ascertain the number of satellites that are visible to the receiver.
2. Calculate the observation matrix.
3. Choose the adequate threshold corresponding to the number of satellites that are visible to the receiver.
4. Determine if the satellite geometry is acceptable.
5. If the satellite geometry is acceptable, calculate the test statistic, otherwise, give appropriate warning to the flight crew.
6. Compare the test statistic to the precomputed threshold and declare ‘failure’ if it is greater.
7. Continue to the next time sample, repeat steps 1 to 6.
Figure 1 shows a standard RAIM algorithm that is used, with some additions, by GPS receivers. For the purpose of RAIM availability prediction this algorithm is not suitable because it requires actual pseudorange measurements which cannot be obtained either in advance or for remote location. Therefore, RAIM availability prediction focuses on the first part of this algorithm, testing predicted satellite geometries and their ability to provide adequate integrity monitoring.

Figure 1. A baseline RAIM algorithm (expanded from Sandstrom Reference Sandstrom2001).
3. COMMON GEOMETRY SCREENING METHODS
Different principles have been proposed for testing if the given satellite geometry provides enough data for successful integrity monitoring. First of all, each satellite geometry must satisfy the minimum number of satellites criterion. For fault detection (FD) the minimum number of satellites is five, and for fault detection and exclusion (FDE) the minimum number of satellites is six. The best known methods for satellite geometry screening are the δHmax method, the Approximate Radial-Error Protected (ARP) method (Parkinson, Reference Parkinson and Spilker1996.) and the HPL method (Kaplan, Reference Kaplan1996).
3.1. δHmax Method
In this method, horizontal dilution of precision (HDOP) is first calculated for a given subset of satellites and called HDOPi. Next, HDOP is calculated for a full satellite least square solution, denoted simply as HDOP (Sandstrom, Reference Sandstrom2001):
If the δH max is beyond the ceiling value for the geometry that is being tested, it is labelled as inadmissible (Parkinson, Reference Parkinson and Spilker1996). It has been shown by (Chin, Reference Chin, Kraemer, Brown, Parkinson and Spilker1996) that this is a very inferior way to do geometry screening due to low correlation of its value and actual RAIM performance parameters. Chin states:
“… we conclude that HDOP maxis not a useful criterion”.
3.2. ARP Method
The ARP method goes one step further than δH max by factoring threshold setting on the test statistic, therefore making possible a simple geometric interpretation of the ARP. By placing deterministic ramp error on the satellite that is most difficult to detect, a typical error trajectory would be as shown in Figure 2. (Brown, Reference Brown1992).

Figure 2. Ramp error trajectory, reproduced from (Brown, Reference Brown1992).
The value of ARP is determined by only two factors, satellite geometry and threshold so it can be easily calculated following these steps (Brown, Reference Brown1992):
1. Determine the observation matrix G.
2. Define matrices A and B as:
(2) (3)
(3)
3. For each satellite in view calculate the value of SLOPE:
(4)
4. Define SLOPEmax as:
(5)
5. Finally,
(6)
If the ARP value is greater than the ARPceiling, which is a pre-computed constant for a specified number of satellites, the satellite geometry must be declared inadmissible.
3.3. HPL Method
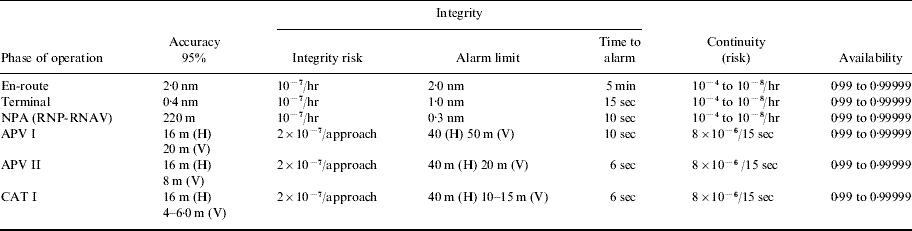
In the Horizontal Protection Limit (HPL) method the RAIM availability prediction is determined by comparing the HPL to the Horizontal Alarm Limit (HAL). HAL has a predefined value for a specific phase of flight, as can be seen from Table 1, alarm limit column.
Table 1. Required Navigational Performance (H-horizontal, V-Vertical).
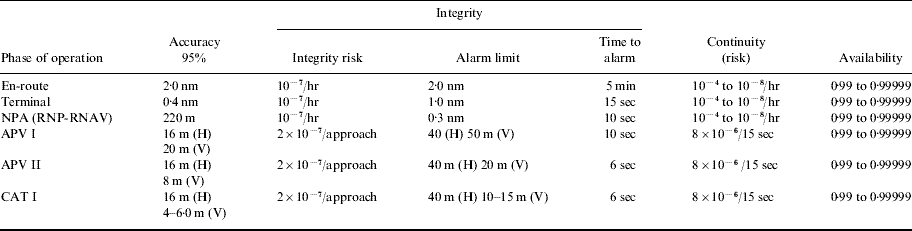
HPL is computed using Equation (7) where p bias is equal to the standard deviation (σ) multiplied by a non centrality parameter (λ) (Equation 8). The non centrality parameter can be defined in terms of the normalised mean (m) of the squared measurement residuals and the number of degrees of freedom (k) (Equation 9), which is itself a number of redundant pseudorange measurements (Equation 10), N being the number of visible satellites (Kaplan, Reference Kaplan1996).
If the HPL, being the minimum detectable error, is greater than HAL, RAIM is declared unavailable because there is a probability that an error may occur which will be greater than HAL but less than HPL and therefore, undetectable.
4. MODIFIED GEOMETRY SCREENING ALGORITHM
The reason for modifying the geometry screening algorithm lies in the fact that not all aerodromes are located in ideal locations. The fact that some aerodromes are situated near, or surrounded by, high mountains, must be recognized and dealt with, especially for those aerodromes at high latitudes (e.g. Norway), where the satellite visibility is already reduced.
This modified geometry screening algorithm is based on the HPL method but its modifications can be applied to any of the geometry screening algorithms. The main significance of this modification is the algorithm's ability to include a terrain elevation model into satellite visibility prediction. Of course, this is not a novel idea, but to the best of the authors' knowledge it has not been addressed yet in this context. Figure 3 shows the proposed variable mask algorithm.

Figure 3. The modified geometry screening algorithm.
5. DIGITAL TERRAIN MODEL
The digital terrain model (DTM) or digital elevation model (DEM) is a digital representation of the Earth's surface topography which can be stored as a raster (grid) or as a triangular irregular network (TIN). Both of these methods have advantages and disadvantages, however, due to the availability and the ease of implementation, raster DEM was used for the simulation performed in this paper. No significant difference in the end result is expected from the use of the TIN.
Another significant DEM property that must be considered is its resolution. As always, the more detailed DEMs provide greater accuracy of the simulation and the higher probability of detecting all relevant terrain features. On the other hand, handling extremely detailed DEMs is computationally more expensive and time consuming. For the purpose of detecting satellite visibility, 3 arc-second resolution DEM was used with points 90 m apart. The greatest possible theoretically undetected terrain feature would therefore be 90×90 m in area and of unknown height. This terrain feature, if it existed and fitted exactly in between sample points, could mask less than 1° of azimuth at the distance of 3 nautical miles; however, the probability of such a feature being undetected is very low. This makes the 3 arc-second DEM suitable but obviously less than perfect. For all real-life applications, the DEM should comply with requirements of DO-201A and TSO-C151b documents.
Great care must be exercised while selecting the DEM segment to be used for a particular aerodrome. Clearly, the whole approach track must be selected along with the surrounding obstacles, on the other hand, too large an area selected will cause points of no significance to be included in the computation, thus unnecessarily slowing it down, while an area too small might exclude significant terrain features. The first matter to be considered is the height of the highest obstacle in the area. By using a 5° mask angle as the lower mask angle limit, it can be easily calculated at what distance the highest obstacle in the area masks less than 5° of elevation. This distance, added to the outer points of the approach track, can then be used as a boundary of the test region. For the purpose of simplification, the nearest rectangular shape can be used. One such DEM section is shown in Figure 4. along with the runway (short black line) and potential GPS NPA safety surfaces (hollow black rectangles). The conventional 5° mask is still used in this algorithm because it eliminates satellites which could give erroneous ranging data due to atmospheric effects.

Figure 4. DEM section showing Dubrovnik airport and potential GPS NPA safety surfaces.
6. DETECTING VISIBLE SATELLITES
This part of the modified geometry screening algorithm can be divided into two sections:
▪ determining which satellites would be visible at a given location and time in ideal conditions, and
▪ determining which of those should be excluded due to the terrain masking them.
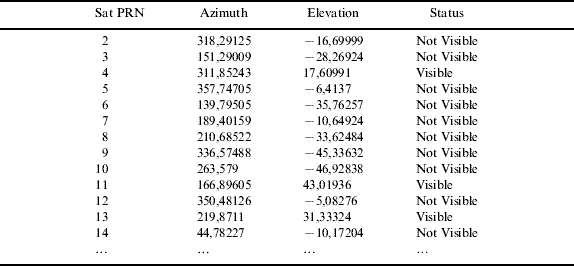
Methods for computing the first section are widespread and easily accessible; therefore, they will not be discussed here. A sample of data produced by these methods can be seen in Table 2. Obviously, the visible satellites are those with positive elevation angles.
Table 2. Sample of satellite visibility data.
For the second section, a terrain elevation profile must be computed, starting from the current test location and going out to each of the satellites. This can be seen in Figure 5(Top), each line being the direction towards each of the ideally visible satellites (elevation above 5°). The length of these profiles should be equal to the distance at which the highest obstacle in the area masks less than 5° of elevation (as in Section 5). The red line in Figure 5(Top) is the azimuth towards the satellite which will be more closely studied in Figures 5(Centre) and 5(Bottom). Figure 5(Centre) shows the terrain elevation profile, directed towards that satellite, expressed as an absolute height above the ellipsoid.

Figure 5. Top: satellite azimuths. Centre: terrain elevation profile. Bottom: terrain elevation profile relative to the test location.
Next, an elevation profile relative to the test location should be computed by using the tangent function. This produces Figure 5(Bottom) which shows the profile expressed as an angle of elevation relative to the test location. It can be seen that the obstacle located around 4 km from the test location masks the highest elevation angle even though it is not the highest obstacle on this profile. It masks roughly 14° of elevation, therefore, if this satellite's elevation is less than 14° it should be excluded from the RAIM prediction algorithm.
This procedure must be repeated for every satellite at each location in space and time. Of course, there are numerous ways to optimize this algorithm. For example, it is safe to assume that RAIM is available at all locations directly above those locations where RAIM is already proved to be available (for that time sample).
7. OBSERVATION MATRIX
The modified geometry screening algorithm started with the list of satellites that are visible at a given point in time and space in ideal conditions (no terrain masking). Next, all satellites masked by the terrain were removed, and now, the observation matrix must be computed. The observation matrix, labelled G in Equation 2, can be calculated using:
![G \equals \left[ {\matrix{ {\alpha _{\setnum{11}} } \tab {\alpha _{\setnum{12}} } \tab {\alpha _{\setnum{13}} } \tab 1 \cr {\alpha _{\setnum{21}} } \tab {\alpha _{\setnum{22}} } \tab {\alpha _{\setnum{23}} } \tab 1 \cr {\alpha _{\setnum{31}} } \tab {\alpha _{\setnum{32}} } \tab {\alpha _{\setnum{33}} } \tab 1 \cr {...} \tab {...} \tab {...} \tab {...} \cr {\alpha _{n\setnum{1}} } \tab {\alpha _{n\setnum{2}} } \tab {\alpha _{n\setnum{3}} } \tab 1 \cr} } \right]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022094933549-0623:S0373463309990294_eqn11.gif?pub-status=live)
Where:
x i, y i, z i – coordinates of the ith satellite
x u, y u, z u – coordinates of the receiver
ρi – range to the ith satellite, can be expressed as:
With the observation matrix computed, the rest of the RAIM availability prediction can be performed using Equations 3 to 10.
8. SIMULATION RESULTS
In order to determine the impact of the modified geometry screening algorithm on the RAIM availability prediction, a series of simulations was performed. Dubrovnik aerodrome (LDDU – Ćilipi) was chosen because of its surrounding terrain which is mountainous to the northeast and flat (sea) to the southwest. This terrain configuration, as seen in Figure 4, is somewhat challenging for satellite detection but not nearly as challenging as some areas around other aerodromes in the world (e.g. Innsbruck – LOWI). The worst case scenario would be an aerodrome in a long valley with approach track descending through that valley.
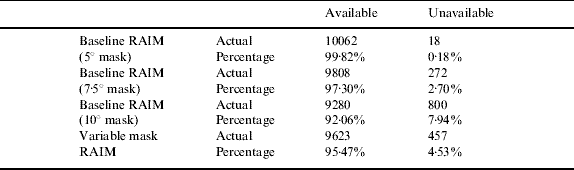
RAIM FDE availability was predicted for the duration of one week using the baseline RAIM algorithm and the variable mask RAIM algorithm. At the time of this simulation, the GPS satellite constellation consisted of 30 satellites. The time step was set to 60 seconds to ensure no RAIM hole would go undetected and the number of time samples was 10 080. The results can be seen in Table 3. As can be seen from the table the degradation in availability is not insignificant. The predicted availability of the variable mask RAIM lies somewhere between 7·5° and 10° masked baseline RAIM for this example. The fixed mask angle could be tuned so that available/unavailable percentages match the variable mask RAIM percentages exactly; however, further simulations showed that this tuned fixed mask angle changes from week to week and, more importantly, actual times at which the RAIM FDE is unavailable do not match.
Table 3. RAIM algorithms compared.

Most of these simulated RAIM outages lasted from 10 to 20 minutes; more than long enough to prevent a GPS non-precision approach. In order to increase the RAIM availability, a more detailed study of the areas affected by RAIM outages must be done. For that purpose a chart similar to the one in Figure 6 should be made. In this figure the large square is the test area and the grey area indicates a RAIM hole. It is possible that a GPS approach in one of the runway directions can be made while one in the opposite direction cannot (which is not the case in this figure). Also, it is possible that one runway is unusable due to RAIM outage while the runway parallel to that one is not.

Figure 6. RAIM outage due to terrain mask.
The shape of the RAIM hole produced by the terrain mask is irregular and therefore completely unpredictable by ordinary means. RAIM availability equipment is usually placed at the aerodrome but it cannot detect a RAIM outage at all the points along the approach track. This is the main reason why these simulations must be performed.
9. EXPERIMENTAL RESULTS
In order to verify simulation results extensive satellite visibility tests were performed at several locations in the vicinity of Dubrovnik aerodrome. The purpose of these tests was to establish the amount of error in predicted times of RAIM outages. Since the time samples were one minute apart, it was logical to believe that the maximum error in predicted times of RAIM outages would also be one minute. Indeed, this was the case for all the performed measurements except one. In that one case the error in predicted time of RAIM outage was one minute and 15 seconds. The existence of an outlier like this proves at least one of the several things:
• error in simulation computations
• error in digital terrain elevation model
• error (or at least a lag) in the receiver signal processing
• more conservative RAIM algorithm used in simulation than the one in the receiver
• unpredictable atmospheric or multipath effects
Even though this question is intriguing and should be more thoroughly investigated, it neither invalidates the concept nor decreases the usefulness of the variable mask RAIM algorithm. The error in predicting the beginning or the end of a RAIM outage can be easily decreased by making shorter intervals between two time samples, however, this will increase the computation time. The solution is to keep an interval of one minute between two samples for detecting the existence of a RAIM hole and then use shorter intervals to define the edges more precisely (e.g. 5 seconds).
10. CONCLUSION
The purpose of this paper was to introduce the possibility of using digital elevation models in the predicting of GPS RAIM availability. Many GPS receivers already have some terrain elevation models installed for the purpose of ground proximity warning. These receivers are also powerful enough to use a variable mask RAIM availability prediction algorithm, therefore, the implementation is merely a point of a software upgrade. For those receivers that are not powerful enough or do not have enough memory to store DEMs for a reasonable number of aerodromes, this kind of RAIM availability prediction should be performed by appropriate air traffic services.
This paper has shown how such an algorithm could be made by modifying existing RAIM availability prediction algorithms and has demonstrated the effect of these modifications on RAIM availability by using it in a real situation. Moreover, experimental measurements were carried out with the purpose of confirming data acquired by simulation.
The authors conclude that a variable mask RAIM availability prediction algorithm is useful, practical and should be applied at all aerodromes in mountainous areas that experience unpredicted RAIM outages. It is also useful as a pre-flight planning tool for anyone wishing to fly GPS NPA.
ACKNOWLEDGMENTS
This research was supported by the Faculty of Transport and Traffic Sciences, project number: 135-1352339-2349.