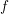1 Introduction
Let 
$\mathscr{X}$ be a projective smooth scheme over the ring 
$\mathscr{O}_{F,S}$ of 
$S$-integers in a number field 
$F$, and let 
$X/F$ be the generic fibre. For each integer 
$i$, one defines the Hodge polygon 
$HP^{i}(X)$ from the Hodge filtration on 
$H_{\text{dR}}^{i}(X/F)$: it is the convex planar graph emanating from the origin in which the line segment of slope 
$a$ appears with multiplicity equal to the Hodge number 
$h^{a,i-a}=\dim _{F}H^{i-a}(X,\unicode[STIX]{x1D6FA}^{a})$. For every 
$\mathfrak{p}$ outside the finite set 
$S$, one also forms the Newton polygon 
$\text{NP}(\operatorname{Frob}_{\mathfrak{p}},H_{\text{cris}}^{i}((\mathscr{X}\otimes _{\mathscr{O}_{F}}k(\mathfrak{p}))/W(k(\mathfrak{p}))))$ using the 
$p$-adic slopes of the crystalline Frobenius. (See § 3.4.)
Katz [Reference KatzKat71, Conjecture 2.9] conjectured, and Mazur proved [Reference MazurMaz73], that the latter lies above the former:
$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}},H_{\text{cris}}^{i}((\mathscr{X}\otimes _{\mathscr{ O}_{F}}k(\mathfrak{p}))/W(k(\mathfrak{p}))))\geqslant HP^{i}(X).\end{eqnarray}$$ When the two coincide, we say that 
$\mathfrak{p}$ is an ordinary prime (in degree 
$i$ for 
$X$), following Mazur. The following conjecture appears to have been first considered by Serre [Reference SerreSer13, no. 133] for abelian varieties 
$X$ (in degree 
$1$).
Conjecture 1.1 (Ordinariness conjecture).
There exists an infinite set of primes 
$\mathfrak{p}$ such that
$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}},H_{\text{cris}}^{i}((\mathscr{X}\otimes _{\mathscr{ O}_{F}}k(\mathfrak{p}))/W(k(\mathfrak{p}))))=HP^{i}(X).\end{eqnarray}$$ This is known to be true for elliptic curves and abelian surfaces by arguments of Katz and of Ogus [Reference OgusOgu82, Proposition 2.7], and for abelian varieties whose endomorphism ring is 
$\mathbb{Z}$ and whose algebraic monodromy group satisfies a condition; see Pink [Reference PinkPin98, §7]. It is also known for all CM abelian varieties.
In this paper we investigate Conjecture 1.1 for the factors of modular Jacobians cut out by cuspforms of weight 
$2$, and provide several methods for finding ordinary primes in them.
More generally, we consider the parts of the intersection cohomology of the Hilbert modular varieties attached to totally real number fields 
$F$ of degree 
$d=[F:\mathbb{Q}]$, cut out by new normalised cuspforms 
$f$ of parallel weight 
$(2,\ldots ,2)$. The ordinariness in this context first appeared as an assumption in the construction of Galois representations by Wiles [Reference WilesWil88], which was later removed by Taylor [Reference TaylorTay89] and by Blasius and Rogawski [Reference Blasius and RogawskiBR93]. However, many of the best results and constructions in Iwasawa and Hida theory at present depend on the existence of ordinary primes in a crucial way, see, among others, the works of Emerton, Pollack and Weston [Reference Emerton, Pollack and WestonEPW06], Ochiai [Reference OchiaiOch06], Nekovář [Reference NekovářNek01], Dimitrov [Reference DimitrovDim13], Skinner and Urban [Reference Skinner and UrbanSU14], and Wan [Reference WanWan15].
Since, at the moment, we lack a satisfactory ‘crystalline’ theory of perverse sheaves or intersection cohomology, we first formulate in § 2 analogues of the Katz conjecture and Conjecture 1.1 for the 
$\ell$-adic étale intersection cohomology of any projective variety 
$X$, where 
$\ell$ is any auxiliary prime. Here we form the Hodge–Tate polygon attached to the Galois representation in place of the Hodge polygon, and the Newton polygon by using the 
$\ell$-adic Frobenius.
These conjectures (Conjectures 2.4 and 2.5) satisfy a basic consistency, in that (a) the Hodge–Tate polygon is independent of the choice of a prime 
$\unicode[STIX]{x1D706}$ of 
$F$ lying over 
$\ell$; and (b) the conjectures are independent of the auxiliary prime 
$\ell$. We prove these statements by using theorems of Gabber (on the independence of 
$\ell$ in the intersection cohomology of complete varieties) [Reference FujiwaraFuj02], Katz and Laumon (on the constructibility properties of certain constructions in derived categories) [Reference Katz and LaumonKL85], André (his theory of motivated cycles) [Reference AndréAnd96] and de Cataldo and Migliorini (on the motivated nature of the decomposition theorem in intersection cohomology) [Reference de Cataldo and MigliorinideCM15].
Let us return to the Hilbert modular varieties and the forms 
$f$. By using either (i) the theorem of de Cataldo and Migliorini in [Reference de Cataldo and MigliorinideCM15] and its rational extension due to Patrikis [Reference PatrikisPat16] or (ii) the recent motivic constructions of Ivorra and Morel [Reference Ivorra and MorelIM19], we construct an intersection motive of 
$X$ which in realisations give the intersection cohomology. Then by lifting the action of the Hecke correspondences on the intersection cohomology to one on the intersection motive (see Proposition 2.2.6), we construct an André motive 
$M(f)$. The conjectures make sense for these submotives, and the consistency mentioned above also holds for them. We denote by 
$K_{f}$ the Hecke field of 
$f$.
We say that a subset 
$\unicode[STIX]{x1D6F4}$ of 
$\text{MaxSpec}(\mathscr{O}_{F})$ is abundant if 
$\unicode[STIX]{x1D6F4}$ has lower (natural) density greater than 
$0$, and that 
$\unicode[STIX]{x1D6F4}$ is principally abundant if there exists a finite extension 
$F^{\prime }/F$ such that the inverse image of 
$\unicode[STIX]{x1D6F4}$ in 
$\text{MaxSpec}(\mathscr{O}_{F^{\prime }})$ has density equal to 
$1$ in 
$F^{\prime }$. In the previous cases where Conjecture 1.1 has been established, in fact a principally abundant set of ordinary primes was found.
By using the construction of the Galois representation attached to 
$f$ and the purity of the intersection cohomology (IH), we first show that 
$M(f)$ satisfies the analogue of the Katz conjecture and that we can push the Newton polygon ‘half way’ to ordinariness in a quantifiable sense, for a principally abundant set of primes. However, in the attempt to push just beyond the half-way threshold, we face an obstruction of ‘geometry of numbers’ type (Minkowski). We show how to overcome this (for a principally abundant set of primes) by using a stronger form of Sato–Tate equidistribution (see § 3.3), but the latter form remains unknown in general.
In order to go further and to obtain unconditional results, we look into (a) ‘multivariate’ variants of the Sato–Tate conjecture in § 3.3 and (b) the interaction between 
$F$ and 
$K_{f}$ in § 3.5. For the latter, we define an invariant, the slope 
$\unicode[STIX]{x1D70E}_{F}(K)\in [0,1]$ of a coefficient number field 
$K$ over a ground number field 
$F$ (see Definition 3.5.4), by using the action of 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ on the set 
$\operatorname{Hom}(K,\overline{\mathbb{Q}})$ of field embeddings. The slope 
$\unicode[STIX]{x1D70E}_{F}(K)$ is 
$0$ if, for example, (1) 
$[K:\mathbb{Q}]$ is a prime not dividing 
$[F:\mathbb{Q}]$; or (2) the Galois group of 
$K/\mathbb{Q}$ is the (full) symmetric group on 
$[K:\mathbb{Q}]$ lettersFootnote 1 and 
$K$ and 
$F$ have coprime discriminants.
Here is a collection of results which follow from the main theorem (Theorem 4.1.1).
Theorem. Let the notation be as above. Then 
$M(f)$ has an abundant set of ordinary primes if at least one of the following conditions is satisfied:
(a)
$[K_{f}^{\circ }:\mathbb{Q}]\leqslant 2$, where $K_{f}^{\circ }$ is the smallest Frobenius field of $f$ in the sense of Ribet (see § 3.2 for the precise definition);(b)
$f$ is of CM type;(c) the slope
$\unicode[STIX]{x1D70E}_{\widetilde{F}}(K_{f})$ is equal to $0$, where $\widetilde{F}$ is the Galois closure of $F$ over $\mathbb{Q}$; or(d) an element of
$\operatorname{Gal}(\overline{\mathbb{Q}}/\widetilde{F})$ has exactly two orbits in $\operatorname{Hom}(K_{f},\overline{\mathbb{Q}})$, the orbits have the same size and $f$ satisfies a strong form of Sato–Tate equidistribution named (RST) in § 3.3.
The statement in (c) follows from the quantitative part (4) of Theorem 4.1.1: the smaller the slope 
$\unicode[STIX]{x1D70E}$, the closer to ordinariness we can push the Newton polygons.
In § 5 we look at the forms 
$f$ with low levels for four number fields 
$F$ of degree 
$d\leqslant 4$, and show that for most 
$f$ under consideration, (a), (b) and (c) provide an abundant set of ordinary primes unconditionally, and that (d) complements them under the strong Sato–Tate condition. We give descriptions of the conditional cases as well as some cases where our methods fall short of yielding abundance of ordinary primes.
Plan. Here are some of the main ingredients and ideas in the text.
In § 2 we show (Theorem 2.2.1) that for André motives, the Hodge polygon consisting of the Hodge numbers in its (transcendental) Betti realisations coincides with the Hodge–Tate polygon consisting of the 
$p$-adic Hodge–Tate weights in the (algebraic) 
$p$-adic étale realisations. This applies in particular to the Hecke isotypic components of the intersection cohomology (motive) of the Hilbert modular varieties.
In § 3 we introduce a few things in preparation for the main theorem in § 4. (a) In § 3.4 we study the partially ordered semiring of Newton polygons; this will be useful in dealing with the tensor induction in Theorem 4.1.1. (b) In § 3.5 we define the notion of slope and bisection in the interaction between the ground field 
$F$ and the coefficient field 
$K$; very roughly speaking, they measure the sizes and shapes of ‘large’ orbits in the Hecke and Frobenius fields. In Theorem 4.1.1, these will be combined with the Chebotarev density theorem and strong forms of the Sato–Tate conjecture.
In § 4 we prove the main theorem (Theorem 4.1.1). Here we make a connection (which to the author’s knowledge is new) between two conjectures on the eigenvalues of the Frobenius elements: namely, the Sato–Tate conjecture on the archimedean properties of the eigenvalues (which in turn is closely linked to the Langlands programme) on the one hand and the ordinariness conjecture on the 
$p$-adic properties (with varying 
$p$) of the eigenvalues on the other hand.
In the final § 6, we formulate analogues of the Katz and the ordinariness conjectures for submotives of the intersection cohomology of more general motivic coefficients, following a suggestion of Katz. In cases where we have good crystalline realisations compatible with the 
$\ell$-adic realisations (which include the non-constant motivic coefficients on Hilbert modular varieties), we verify the Katz conjecture by using Mazur’s theorem. If the submotive has potentially abelian 
$\ell$-adic realisation, we also verify the ordinariness conjecture by using Serre’s theory [Reference SerreSer98]. Finally, we provide some methods to deal with the parallel motivic weight 
$(3,\ldots ,3)$ in the Hilbert modular case.
2 Formulation of conjectures for $\text{IH}$
2.1 Polygons
Let 
$F$ be a number field with algebraic closure 
$F^{s}$, 
$\ell$ a prime number, 
$V$ a 
$\mathbb{Q}_{\ell }$-vector space of dimension 
$m<\infty$, and
$$\begin{eqnarray}\unicode[STIX]{x1D70C}:\operatorname{Gal}(F^{s}/F)\longrightarrow \operatorname{Aut}(V)\simeq \text{GL}_{m}(\mathbb{Q}_{\ell })\end{eqnarray}$$ a continuous representation that is unramified outside a finite set 
$S$ of maximal ideals of 
$\mathscr{O}_{F}$.
Definition 2.1.1. Assume that 
$\unicode[STIX]{x1D70C}$ is 
$\mathbb{Q}$-rational in the sense of Serre [Reference SerreSer98].
Then for each maximal ideal 
$\mathfrak{p}$ of 
$\mathscr{O}_{F}$ outside 
$S$ and with residue characteristic 
$p\neq \ell$, we define the Newton polygon 
$\text{NP}(\operatorname{Frob}_{\mathfrak{p}},\unicode[STIX]{x1D70C})=\text{NP}(\operatorname{Frob}_{\mathfrak{p}}\!|_{V})$ as the Newton polygon of the characteristic polynomial
$$\begin{eqnarray}\det (T-\operatorname{Frob}_{\mathfrak{p}}:V)\in \mathbb{Q}[T]\end{eqnarray}$$ with respect to the 
$p$-adic valuation 
$v_{\mathfrak{p}}$ on 
$\mathbb{Q}$ normalised by 
$v_{\mathfrak{p}}(\mathbb{N}\mathfrak{p})=1$.
Equivalently, choose an isomorphism 
$\overline{\mathbb{Q}}_{\ell }\simeq \overline{\mathbb{Q}}_{p}$ and let 
$x_{1},\ldots ,x_{m}\in \overline{\mathbb{Q}}_{\ell }$ be the eigenvalues of 
$\operatorname{Frob}_{\mathfrak{p}}$ on 
$V$. Then the multiset of slopes
$$\begin{eqnarray}\bigg\{\frac{v_{p}(x_{1})}{v_{p}(\mathbb{N}\mathfrak{p})},\ldots ,\frac{v_{p}(x_{m})}{v_{p}(\mathbb{N}\mathfrak{p})}\bigg\}\end{eqnarray}$$gives the Newton polygon. It is independent of the chosen isomorphism.
Definition 2.1.2. Assume that 
$\unicode[STIX]{x1D70C}$ is Hodge–Tate at every prime 
$\unicode[STIX]{x1D706}$ of 
$F$ lying over 
$(\ell )$, and that the set with multiplicities of the Hodge–Tate weights at 
$\unicode[STIX]{x1D706}$ is independent of 
$\unicode[STIX]{x1D706}|\ell$.
Then we define the Hodge–Tate polygon 
$\text{HTP}(\unicode[STIX]{x1D70C})=\text{HTP}(V)$ as the convex planar polygon starting from 
$(0,0)$ in which the slope 
$i$ appears as many times as the Hodge–Tate weight 
$i$ appears in 
$\unicode[STIX]{x1D70C}$.
There seem to be competing sign conventions for the Hodge–Tate weights. We take the ‘geometric’ one, so that 
$H^{1}$ of an elliptic curve has Hodge–Tate weights 
$\{0,1\}$.
2.2 Independence of Hodge–Tate weights
First, we show that the Hodge–Tate polygon we have defined coincides with the classical Hodge polygon for all André motives, thereby extending a theorem of Faltings [Reference FaltingsFal88, Reference FaltingsFal89]. For this we will crucially rely on the theory of motivated cycles and the resulting category of André motives, given in [Reference AndréAnd96].
Theorem 2.2.1. Let 
$M$ be an André motive over a finite extension field 
$K$ of 
$\mathbb{Q}_{p}$, and let 
$\unicode[STIX]{x1D70E}:K\longrightarrow \mathbb{C}$ be a complex embedding. Denote by 
$M_{p}$ its 
$p$-adic étale realisation, and by 
$M_{\unicode[STIX]{x1D70E}}$ its Betti realisation via 
$\unicode[STIX]{x1D70E}$. Then the set with multiplicities of the Hodge–Tate weights of 
$M_{p}$ coincides with that of the complex Hodge numbers of 
$M_{\unicode[STIX]{x1D70E}}$.
Proof. We may and will assume that 
$M$ is simple, and that there exist a projective smooth variety 
$Y$ of dimension 
$d$ over 
$K$, an integer 
$n$, and an André motivated cycle
$$\begin{eqnarray}\unicode[STIX]{x1D709}\in A_{\text{mot}}^{d}(Y\times _{K}Y)\end{eqnarray}$$ such that 
$\unicode[STIX]{x1D709}$ acts as the idempotent cutting out 
$M$ in 
$\mathfrak{h}^{n}(Y)$. Let 
$e_{p}$ (respectively, 
$e_{\unicode[STIX]{x1D70E}}$, 
$e_{\text{dR}}$) be the image of 
$\unicode[STIX]{x1D709}$ in the 
$p$-adic étale (respectively, 
$\unicode[STIX]{x1D70E}$-Betti, de Rham) realisation
$$\begin{eqnarray}e_{p}\in H^{2d}((Y\times Y)\otimes _{K}\overline{K},\mathbb{Q}_{p})(d),\quad e_{\unicode[STIX]{x1D70E}}\in H^{2d}(\unicode[STIX]{x1D70E}(Y\times Y),\mathbb{Q}(d)),\quad e_{\text{dR}}\in H_{\text{dR}}^{2d}(Y\times Y)(d).\end{eqnarray}$$We have the diagram
Here we suppressed 
$Y\times Y$ in the argument for all cohomology theories as well as the degree 
$2d$ and the Tate twist 
$(d)$. Undecorated arrows are extensions of scalars and Art denotes Artin’s comparison isomorphism.
Main point. The diagram is commutative. In particular, the image of 
$\unicode[STIX]{x1D709}$ in any group in the diagram is the same, no matter which path emanating from 
$A_{\text{mot}}^{d}(Y\times Y)$ is followed.
This follows from the definition of André motivated cycles, together with the fact that the comparison isomorphisms on display are isomorphisms between Weil cohomology theories (and as such compatible with pullback, pushforward, cup product, cycle class, and Poincaré duality, that are involved in the definition of André motivated cycles). See André [Reference AndréAnd96, §§2.3 and 2.4].
(In contrast, it is not clear whether the similar diagram would be commutative if we replace the apex 
$A_{\text{mot}}$ with the larger space of the absolute Hodge cycles.)
Now applying the idempotents obtained from 
$\unicode[STIX]{x1D709}$ to the similar diagram without apex,
we get the diagram
Now, on the one hand, the Hodge–Tate weights of 
$M_{p}$ can be read off from the filtration on
$$\begin{eqnarray}(M_{p}\otimes _{\mathbb{Q}_{p}}B_{\text{dR}})^{\operatorname{Gal}(\overline{K}/K)}\simeq M_{\text{dR}}\quad \text{(filtered isomorphism)}.\end{eqnarray}$$ On the other hand, the Hodge numbers of 
$M_{\unicode[STIX]{x1D70E}}$ can also be read off from the (algebraic) Hodge filtration on 
$M_{\text{dR}}$ in a similar manner.◻
Corollary 2.2.2. Let 
$X$ be any projective variety over any finite extension 
$K$ of 
$\mathbb{Q}_{p}$, and let 
$\unicode[STIX]{x1D70E}:K\longrightarrow \mathbb{C}$ be any complex embedding. Then for any integer 
$n$, the Hodge–Tate weights of 
$\text{IH}^{n}(X\otimes _{K}\overline{K},\mathbb{Q}_{p})$ coincide with the Hodge numbers of 
$\text{IH}^{n}(\unicode[STIX]{x1D70E}(X),\mathbb{Q})$.
Proof. Let 
$\unicode[STIX]{x1D70B}:Y\longrightarrow X$ be any resolution of singularities. We use the main theorem of de Cataldo and Migliorini [Reference de Cataldo and MigliorinideCM15], strengthened in 
$K$-rationality by Patrikis [Reference PatrikisPat16, §8], to deduce the existence of an André motivated cycle
$$\begin{eqnarray}\unicode[STIX]{x1D709}:=\unicode[STIX]{x1D709}_{n}\in A_{\text{mot}}^{d}(Y\times Y)\end{eqnarray}$$such that the Betti realisation
$$\begin{eqnarray}e_{\unicode[STIX]{x1D70E}}:=\text{cl}_{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D709})\in H^{2d}(\unicode[STIX]{x1D70E}(Y\times Y),\mathbb{Q}(d))\end{eqnarray}$$defines as a correspondence the idempotent for the direct summand
$$\begin{eqnarray}\text{IH}^{n}(\unicode[STIX]{x1D70E}(X),\mathbb{Q})\subseteq H^{n}(\unicode[STIX]{x1D70E}(Y),\mathbb{Q}),\end{eqnarray}$$ and similarly for the 
$p$-adic étale realisation
$$\begin{eqnarray}e_{p}:=\text{cl}_{\mathbb{Q}_{p}}(\unicode[STIX]{x1D709})\in H^{2d}((Y\times Y)\otimes _{K}\overline{K},\mathbb{Q}_{p}(d)).\end{eqnarray}$$ Using this, de Cataldo and Migliorini [Reference de Cataldo and MigliorinideCM15] and Patrikis [Reference PatrikisPat16] define the 
$K$-rational intersection de Rham cohomology of 
$X$,
$$\begin{eqnarray}\text{IH}_{\text{dR}}^{n}(X/K),\end{eqnarray}$$as the image of the idempotent
$$\begin{eqnarray}e_{\text{dR}}:=\text{cl}_{\text{dR}}(\unicode[STIX]{x1D709})\in H^{2d}(Y\times Y)(d)\end{eqnarray}$$ acting on 
$H_{\text{dR}}^{n}(Y)$. Clearly, there is a comparison isomorphism of 
$\text{IH}_{\text{dR}}^{n}(X/K)\otimes _{K}\mathbb{C}$ with the (transcendental) Hodge structure on the Betti realisation 
$\text{IH}^{n}(\unicode[STIX]{x1D70E}(X),\mathbb{Q})\otimes \mathbb{C}$. Moreover, this last Hodge structure coincides with the Hodge structure constructed by Morihiko Saito; see de Cataldo [Reference de CataldodeC12, Theorem 4.3.5].
Apply Theorem 2.2.1 to this situation. ◻
Corollary 2.2.3. Let 
$M$ be an André motive over a number field 
$K$, 
$\mathfrak{P}$ any maximal ideal of 
$\mathscr{O}_{K}$ of residue characteristic 
$p$, and 
$\unicode[STIX]{x1D70E}:K\longrightarrow \mathbb{C}$ any complex embedding. Then the Hodge–Tate weights of 
$M_{p}$ at 
$\mathfrak{P}$ coincide with the Hodge numbers of 
$M_{\unicode[STIX]{x1D70E}}$. In particular, the Hodge–Tate weights are independent of 
$\mathfrak{P}\in \text{MaxSpec}(\mathscr{O}_{K})$.
This applies, for example, to the André motives cut out by algebraic cycles from the cohomology of a projective smooth variety over 
$K$.
Corollary 2.2.4. Let 
$X$ be a projective variety defined over a number field 
$K$, 
$\mathfrak{P}$ any maximal ideal of 
$\mathscr{O}_{K}$ of residue characteristic 
$p$, and 
$\unicode[STIX]{x1D70E}:K\longrightarrow \mathbb{C}$ any complex embedding. Then for every integer 
$n$, the Hodge–Tate weights of 
$\text{IH}^{n}(X\otimes _{K}\overline{K},\mathbb{Q}_{p})$ at 
$\mathfrak{P}$ coincide with the Hodge numbers of 
$\text{IH}^{n}(\unicode[STIX]{x1D70E}(X),\mathbb{Q})$. In particular, the Hodge–Tate weights are independent of 
$\mathfrak{P}\in \text{MaxSpec}(\mathscr{O}_{K})$.
Remark 2.2.5. Strictly speaking, the results on the intersection cohomology can be proven by using the de Cataldo–Migliorini theorem [Reference de Cataldo and MigliorinideCM15] only (and not using the 
$K$-rational version [Reference PatrikisPat16]). To see this, note that the Hodge numbers and the Hodge–Tate weights are insensitive to the base change to a finite extension of 
$K$ (in both local and global cases), and the construction of [Reference de Cataldo and MigliorinideCM15] yields the necessary André motivated cycle over a finite extension of 
$K$.
In the case where 
$X=X^{\text{BB}}$ is the Baily–Borel compactification of a Shimura variety 
$X^{\circ }$ (we refer to Ash, Mumford, Rapoport and Tang [Reference Mumford, Rapoport, Ash and TaiMRAT75] and Pink [Reference PinkPin98] in general, and Brylinski and Labesse [Reference Brylinski and LabesseBL84] and Rapoport [Reference RapoportRap78] in the special case of Hilbert modular varieties), one further decomposes the intersection cohomology of 
$X$ into the Hecke isotypic components: the Hecke correspondences act on the intersection cohomology of 
$X$, and span a 
$\mathbb{Q}$-subalgebra 
$\mathscr{H}_{X,\mathbb{Q}}$ in the finite dimensional 
$\mathbb{Q}$-algebra 
$\operatorname{End}_{HS}(\text{IH}_{B}^{d}(X,\mathbb{Q}))$. By decomposing 
$\mathscr{H}_{X,\mathbb{Q}}$ into a product of 
$\mathbb{Q}$-algebras, we obtain the Hecke isotypic components.
Proposition 2.2.6. The Hecke isotypic components come from André motives over the reflex field 
$E$. As a consequence, Theorem 2.2.1 applies to these components.
Proof. This boils down to first finding an André (pure Nori) motive 
$\mathfrak{i}\mathfrak{h}(X)$ whose 
$\ell$-adic and Betti realisations give the 
$\ell$-adic and Betti intersection cohomology of 
$X$, and then lifting the action of the Hecke correspondences to one on 
$\mathfrak{i}\mathfrak{h}(X)$.
While the first step can be done as above in an ad hoc fashion, using a (non-canonical) resolution of singularities and using the theorems of de Cataldo, Migliorini and Patrikis, the second step is done most systematically (in our opinion) by using the theory of weight filtration. We learned the argument from Morel (cf. [Reference MorelMor08, §5]), which uses the more recent motivic constructions of Ivorra and Morel [Reference Ivorra and MorelIM19].
(Before giving the details, let us stress the main point and indicate where the innovations are. The intersection complex 
$\text{IC}$ (as a perverse sheaf in the derived category of constructible sheaves) was originally constructed as an iterated application of the two-step procedure: taking the direct image 
$Rj_{\ast }$ under open immersions 
$j$, and then truncating with respect to a topological stratification and a function called ‘perversity’; see the explicit formula in [Reference Beĭlinson, Bernstein and DeligneBBD82, Proposition 2.1.11].
One of the innovations in [Reference MorelMor08] was to realise 
$\text{IC}$ (for the middle perversity) over finite fields as the truncation with respect to the weight filtration; see [Reference MorelMor08, Theorem 3.1.4].
This renders the extension of the Hecke operators to 
$\text{IC}$ deceptively easy: one needs neither to worry about singularities in the boundary (which can be bad), to which one must pay heed if one uses the original (topological) definition, nor to rely on the toroidal compactifications, of which there is no canonical choice, and many are needed to extend the Hecke correspondences. This is why we adopt the idea.
In [Reference Ivorra and MorelIM19], Ivorra and Morel construct the four operations of Grothendieck (namely 
$f_{\mathscr{M}}^{\ast }$, 
$f_{\mathscr{M}}^{!}$, 
$f_{\ast }^{\mathscr{M}}$, 
$f_{!}^{\mathscr{M}}$ for morphisms 
$f$ between quasiprojective varieties) and the weight filtrations on the derived category of ‘perverse mixed motives’; this last abelian category is, moreover, shown to be equivalent to the Nori motives.
This allows one to formally apply the algorithm described in [Reference MorelMor08, §5], but this time applied in the motivic derived category of [Reference Ivorra and MorelIM19], rather than in the derived category of constructible sheaves as in [Reference MorelMor08]. Then the Betti and 
$\ell$-adic realisations of these constructions give rise to the Hecke operators constructed previously on the level of complexes of sheaves.)
Now let us turn to a more detailed argument, and indicate which constructions in [Reference Ivorra and MorelIM19] replace those in the parallel argument from [Reference MorelMor08, §5].
Let 
$j:X^{\circ }{\hookrightarrow}X=X^{\text{BB}}$ be the open immersion of the Shimura variety and 
$c_{1},c_{2}:Y^{\circ }\longrightarrow X^{\circ }$ be the two finite étale maps that give rise to a given Hecke correspondence. With 
$j^{\prime }:Y^{\circ }{\hookrightarrow}Y$ denoting the open immersion into the Baily–Borel compactification, the 
$c_{i}$ extend canonically to 
$\overline{c_{i}}:Y\longrightarrow X$. We start with the identity correspondence
$$\begin{eqnarray}u=1:c_{1}^{\ast }\mathbb{Q}_{X^{\circ }}\longrightarrow c_{2}^{!}\mathbb{Q}_{X^{\circ }}\end{eqnarray}$$ arising from the natural isomorphisms 
$c_{1}^{\ast }\mathbb{Q}_{X^{\circ }}\simeq \mathbb{Q}_{Y^{\circ }}$ and 
$c_{2}^{!}\mathbb{Q}_{X^{\circ }}\simeq \mathbb{Q}_{Y^{\circ }}$.
Here and below, the functors 
$f^{\ast }$ and 
$f^{!}$, etc., refer to the ones in [Reference Ivorra and MorelIM19, Theorem 5.1], where the notation 
$f_{\mathscr{M}}^{\ast }$, 
$f_{\mathscr{M}}^{!}$, etc., is used.
Just as in [Reference MorelMor08, §5.1], but using the motivic constructions of the four functors and the base change morphisms, stated in [Reference Ivorra and MorelIM19, Theorem 5.1], we take 
$Rj_{\ast }^{\prime }={j^{\prime }}_{\ast }^{\mathscr{M}}$ and use the base change morphisms
We then use the fact that the lowest weight filtration of 
$Rj_{\ast }\mathbb{Q}_{X^{\circ }}$ is canonically isomorphic to the intersection complex 
$j_{!\ast }(\mathbb{Q}_{X^{\circ }}[d])[-d]$. For this, it is enough to show that the (motivic) weight filtration has 
$\ell$-adic realisation equal to the (
$\ell$-adic) weight filtration. But this follows from the definitions and construction [Reference Ivorra and MorelIM19, Definitions 6.12, 6.13, and Proposition 6.16].
Then we proceed as in [Reference MorelMor08, Lemma 5.1.4] to obtain
$$\begin{eqnarray}\overline{u}:\overline{c_{1}}^{\ast }IC_{X}\longrightarrow \overline{c_{2}}^{!}IC_{X},\end{eqnarray}$$ lifting the cohomological correspondence in realisations. Again the point is that all the arrows in [Reference MorelMor08, Lemma 5.1.4] are constructed using (only) the functoriality of 
$Rj_{\ast }$, the base change morphisms, and the weight filtration. In our (motivic) context, we use the main theorem [Reference Ivorra and MorelIM19, Theorem 5.1] for the first two and the weight filtration constructed in [Reference Ivorra and MorelIM19, Proposition 6.16] for the last.◻
This applies in particular to the Hilbert modular varieties and the submotive 
$M(f)$ of 
$\mathfrak{i}\mathfrak{h}^{d}(X^{\text{BB}})$ cut out by any new cuspform 
$f$ of parallel weight 
$(2,\ldots ,2)$ and its conjugates, and Corollary 2.2.3 applies to it.
2.3 Conjectures
Now we can formulate the analogue of Katz’s conjecture.
Conjecture 2.4. Let 
$X$ be a projective variety over a number field 
$F$, and let 
$n$ be an integer.
Then there exists a finite set 
$S=S(X,n)$ of maximal ideals of 
$\mathscr{O}_{F}$ such that for every prime number 
$\ell$ and every maximal ideal 
$\mathfrak{p}$ of 
$\mathscr{O}_{F}$ outside 
$S$ and with residue characteristic 
$\neq \ell$, we have
$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}}\!|_{\text{IH}^{n}(X\otimes _{F}F^{s},\mathbb{Q}_{\ell })})\geqslant \text{HTP}(\text{IH}^{n}(X\otimes _{F}F^{s},\mathbb{Q}_{\ell })).\end{eqnarray}$$ In the case where 
$X$ is also smooth, this is known to be true, by theorems of Katz and Messing [Reference Katz and MessingKM74] (comparing the 
$\ell$-adic Frobenius at 
$\mathfrak{p}$ with the crystalline Frobenius), of Mazur [Reference MazurMaz73] (showing that the Newton polygon lies on or above the Hodge polygon for the crystalline cohomology), and of Faltings [Reference FaltingsFal88] (showing that the Hodge–Tate polygon is the same as the Hodge polygon).
We also formulate the analogue of the ‘ordinariness’ conjecture.
Conjecture 2.5. Let 
$X$ be a projective variety over a number field 
$F$, and let 
$n$ be an integer.
For every prime number 
$\ell$, there exists an infinite set of maximal ideals 
$\mathfrak{p}$ of 
$\mathscr{O}_{F}$ with residue characteristic not equal to 
$\ell$ such that
$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}}\!|_{\text{IH}^{n}(X\otimes _{F}F^{s},\mathbb{Q}_{\ell })})=\text{HTP}(\text{IH}^{n}(X\otimes _{F}F^{s},\mathbb{Q}_{\ell })).\end{eqnarray}$$ We note that the right-hand side of the conjectures is independent of 
$\unicode[STIX]{x1D706}$ or 
$\ell$ by Corollary 2.2.4, and that the left-hand side is independent of 
$\ell$ because the 
$\text{IH}^{n}(X,\mathbb{Q}_{\ell })$ form a strictly compatible system by Gabber [Reference FujiwaraFuj02] and by Katz and Laumon [Reference Katz and LaumonKL85, Theorem 3.1.2]. Therefore Conjectures 2.4 and 2.5 are independent of the auxiliary prime 
$\ell$.
In the case where 
$X$ is also smooth, Conjecture 2.5 is equivalent to Conjecture 1.1 recalled in § 1, since (1) the Newton polygons of the 
$\ell$-adic and crystalline Frobenius endomorphisms are the same by Katz and Messing [Reference Katz and MessingKM74], and (2) the Hodge–Tate polygon coincides with the Hodge polygon by Faltings [Reference FaltingsFal88].
3 Preparation
3.1 Notation
From this point on, 
$F\subseteq \overline{\mathbb{Q}}$ denotes a totally real number field of degree 
$d=[F:\mathbb{Q}]$ and discriminant 
$\text{disc}(F)$; 
$\widetilde{F}$ is the Galois closure of 
$F/\mathbb{Q}$, of degree 
$\widetilde{d}=[\widetilde{F}:\mathbb{Q}]$.
Let 
$f$ be a new normalised Hilbert eigencuspform of parallel weight 
$(2,\ldots ,2)$ of level 
$\mathfrak{n}\subseteq \mathscr{O}_{F}$. The Fourier coefficients of 
$f$ generate the number field
$$\begin{eqnarray}K_{f}:=\mathbb{Q}(\{{a_{\mathfrak{p}}\}}_{\mathfrak{p}}),\end{eqnarray}$$ where 
$\mathfrak{p}$ ranges over the primes of 
$\mathscr{O}_{F}$ not dividing 
$\mathfrak{n}$. It is either a totally real number field or a CM field, and we let 
$k_{f}:=[K_{f}:\mathbb{Q}]$.
We note that the ordinariness in this context is equivalent to the following simple condition: 
$\mathfrak{p}$ is an ordinary prime (for 
$f$) if and only if 
$a_{\mathfrak{p}}$ is non-zero and does not belong to any prime ideal 
${\wp}$ of 
$\mathscr{O}_{K_{f}}$ lying over 
$(p)=\mathfrak{p}\cap \mathbb{Z}$.
We fix once and for all a rational prime 
$\ell$ that splits completelyFootnote 2 in 
$K_{f}$. For every non-archimedean place 
$\unicode[STIX]{x1D706}$ of 
$K_{f}$ dividing 
$\ell$, we denote by
$$\begin{eqnarray}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}:\operatorname{Gal}(\overline{\mathbb{Q}}/F)\longrightarrow \text{GL}_{2}(K_{f,\unicode[STIX]{x1D706}})\end{eqnarray}$$ the associated semisimple, 
$K_{f}$-rational and integral Galois representation; see Deligne [Reference DeligneDel71], Ohta [Reference OhtaOht83], Carayol [Reference CarayolCar86], Wiles [Reference WilesWil88], Taylor [Reference TaylorTay89], Blasius and Rogawski [Reference Blasius and RogawskiBR93] and the references therein. The Tate twist of its determinant 
$\det (\unicode[STIX]{x1D70C})(1)$ is a character of finite order.
Let 
$G=G_{f,\unicode[STIX]{x1D706}}$ be the Zariski closure of the image of 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}$ in 
$\text{GL}_{2}$ over 
$K_{f,\unicode[STIX]{x1D706}}$. Since we assume 
$\unicode[STIX]{x1D70C}$ to be semisimple, the derived group of the connected component 
$(G^{\circ })^{\text{der}}=[G^{\circ },G^{\circ }]$ is a semisimple algebraic subgroup of 
$\text{SL}_{2}$, that is, either 
$\text{SL}_{2}$ or trivial. If the reductive group 
$G_{f,\unicode[STIX]{x1D706}}^{\circ }$ is a torus for some 
$\unicode[STIX]{x1D706}$, we say that 
$f$ is of CM type.Footnote 3
The product
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f,\ell }:=\mathop{\prod }_{\unicode[STIX]{x1D706}|\ell }\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}:\operatorname{Gal}(\overline{\mathbb{Q}}/F)\longrightarrow \mathop{\prod }_{\unicode[STIX]{x1D706}|\ell }\text{GL}_{2}(K_{f,\unicode[STIX]{x1D706}})=(\operatorname{Res}_{\mathbb{Q}}^{K_{f}}\text{GL}_{2})(\mathbb{Q}_{\ell })\end{eqnarray}$$ is 
$\mathbb{Q}$-rational and integral in the sense of Serre. We denote by 
$G_{f,\ell }$ the Zariski closure over 
$\mathbb{Q}_{\ell }$ of its image, and 
$G_{f,\ell }^{\circ }$ its connected component.
3.2 Frobenius field and Ribet’s argument
Following Ribet [Reference RibetRib76], for every finite extension 
$F^{\prime }$ of 
$F$, we consider the Frobenius field
$$\begin{eqnarray}\text{Tr}(\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}},F^{\prime }):=\mathbb{Q}(\{\text{Tr}\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}^{\prime }})\}_{\mathfrak{p}^{\prime }})\leqslant K_{f},\end{eqnarray}$$ where 
$\mathfrak{p}^{\prime }$ ranges over the primes of 
$\mathscr{O}_{F^{\prime }}$ coprime to 
$\text{disc}(F)\mathfrak{n}\cdot \ell$; it is independent of 
$\unicode[STIX]{x1D706}$, since the 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}$ form a strictly compatible system. Since 
$k_{f}=[K_{f}:\mathbb{Q}]<\infty$, there is the smallest Frobenius field of 
$f$:
$$\begin{eqnarray}K_{f}^{\circ }\leqslant K_{f}\quad \text{and}\quad k_{f}^{\circ }:=[K_{f}^{\circ }:\mathbb{Q}].\end{eqnarray}$$ It is totally real, since 
$\det (\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}})(1)$ has finite order and the eigenvalues of 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}^{\prime }})$ are Weil integers (see Lemma 4.1.3).
We thus have the following algebraic groups:
Here, by the 
$\mathbb{Q}$-algebraic group 
$(\operatorname{Res}_{\mathbb{Q}}^{K_{f}}\text{GL}_{2})^{\det \subseteq \mathbb{Q}^{\times }}$, we mean the following fibered product, which is often denoted by 
$G^{\ast }$ in the literature:
and similarly with 
$K_{f}$ replaced with 
$K_{f}^{\circ }$.
Proposition 3.2.1 (Ribet).
Suppose that 
$f$ is not of CM type. Then
$$\begin{eqnarray}G_{f,\ell }^{\circ }=((\operatorname{Res}_{\mathbb{ Q}}^{K_{f}^{\circ }}\text{GL}_{2})^{\det \subseteq \mathbb{Q}^{\times }})_{\mathbb{Q}_{\ell }}.\end{eqnarray}$$Proof. This amounts to showing that the (algebraic) Lie algebra 
$\mathfrak{g}$ of 
$G_{f,\ell }^{\circ }$ is equal to that of the right-hand side.
The containment 
$\subseteq$ follows from the fact that, if 
$F^{\prime }$ is any sufficiently large finite extension of 
$F$, then 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}^{\prime }})$ has trace and determinant in 
$K_{f}^{\circ }$ for any prime 
$\mathfrak{p}^{\prime }$ of 
$F^{\prime }$ coprime to 
$\text{disc}(F)\mathfrak{n}\ell$, so that if 
$\unicode[STIX]{x1D706}$ and 
$\unicode[STIX]{x1D706}^{\prime }$ are any two primes of 
$K_{f}$ that lie over the same prime of 
$K_{f}^{\circ }$ over 
$(\ell )$, then 
$G_{f,\ell }^{\circ }$ is contained in the partial diagonal of 
$(\operatorname{Res}_{\mathbb{Q}}^{K_{f}}\text{GL}_{2})_{\mathbb{Q}_{\ell }}$ where the 
$\unicode[STIX]{x1D706}$- and the 
$\unicode[STIX]{x1D706}^{\prime }$-components are equal.
To prove the containment 
$\supseteq$, we first note that since 
$f$ is not of CM type, 
$\mathfrak{g}$ surjects onto each factor 
$\mathfrak{g}\mathfrak{l}_{2,\unicode[STIX]{x1D706}^{\circ }}$, which contains 
$\mathfrak{s}\mathfrak{l}_{2,\unicode[STIX]{x1D706}^{\circ }}$. If 
$\unicode[STIX]{x1D706}_{1}^{\circ }$ and 
$\unicode[STIX]{x1D706}_{2}^{\circ }$ are distinct primes of 
$K_{f}^{\circ }$ lying over 
$\ell$, then the representations of 
$\mathfrak{g}$ in the two factors are non-isomorphic, since the representations of (germs of) 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ have different traces, and the image of 
$\mathfrak{g}$ in 
$\mathfrak{g}\mathfrak{l}_{2,\unicode[STIX]{x1D706}_{1}^{\circ }}\times \mathfrak{g}\mathfrak{l}_{2,\unicode[STIX]{x1D706}_{2}^{\circ }}$ contains 
$\mathfrak{s}\mathfrak{l}_{2}\times \mathfrak{s}\mathfrak{l}_{2}$.
Then by Goursat’s lemma (in the middle of the proof of Ribet [Reference RibetRib76, Theorem 4.4.10]) the image of 
$\mathfrak{g}$ contains 
$\prod _{\unicode[STIX]{x1D706}^{\circ }|\ell }\mathfrak{s}\mathfrak{l}_{2,\unicode[STIX]{x1D706}^{\circ }}$, where 
$\unicode[STIX]{x1D706}^{\circ }$ ranges over the primes of 
$K_{f}^{\circ }$ lying over 
$(\ell )$. Since the determinant on 
$G_{f,\unicode[STIX]{x1D706}^{\circ }}^{\circ }$ is a dominant map onto 
$\mathbf{G}_{m}$, we get the desired equality.◻
Definition 3.2.2. Let 
$F^{\circ }$ be the Galois extension of 
$F$ cut out by two representations with finite image:
$$\begin{eqnarray}\operatorname{Gal}(\overline{\mathbb{Q}}/F^{\circ })=\ker (\unicode[STIX]{x1D70C}_{f,\ell }:\operatorname{Gal}(\overline{\mathbb{Q}}/F)\longrightarrow G_{f,\ell }(\mathbb{Q}_{\ell })/G_{f,\ell }^{\circ }(\mathbb{Q}_{\ell }))\cap \ker (\det (\unicode[STIX]{x1D70C}_{f,\ell })(1)),\end{eqnarray}$$ and let 
$\widetilde{F^{\circ }}$ be the compositum 
$F^{\circ }\widetilde{F}$.
3.3 Variants of Sato–Tate equidistribution
Let 
$i_{1},\ldots ,i_{k_{f}^{\circ }}$ denote the complete set of embeddings of 
$K_{f}^{\circ }$ into 
$\mathbb{R}$. For each maximal ideal 
$\mathfrak{p}$ of 
$\mathscr{O}_{\widetilde{F^{\circ }}}$ coprime to 
$\text{disc}(F)\cdot \mathfrak{n}\cdot \ell$, we let
$$\begin{eqnarray}a_{\mathfrak{p}}=\text{Tr}\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}})\end{eqnarray}$$ and consider the set of vectors in 
$\mathbb{R}^{k_{f}^{\circ }}$,
$$\begin{eqnarray}A(f)=\bigg\{\biggl(\frac{i_{1}(a_{\mathfrak{p}})}{\sqrt{\mathbb{N}\mathfrak{ p}}},\ldots ,\frac{i_{k_{f}^{\circ }}(a_{\mathfrak{p}})}{\sqrt{\mathbb{N}\mathfrak{ p}}}\biggr)\bigg\}_{\mathfrak{p}}.\end{eqnarray}$$Definition 3.3.1. We say that 
$f$ satisfies (SST) if 
$A(f)$ is equidistributed in the 
$k_{f}^{\circ }$-fold product of the Sato–Tate (half-circle) measure on 
$[-2,2]$; and we say that 
$f$ satisfies (RST) if 
$A(f)$ is equidistributed in a measure 
$\unicode[STIX]{x1D711}(\mathbf{x})d\unicode[STIX]{x1D707}_{L}(\mathbf{x})$, where 
$\unicode[STIX]{x1D711}:[-2,2]^{k_{f}^{\circ }}\longrightarrow \mathbb{R}_{{\geqslant}0}$ is a continuous function and 
$d\unicode[STIX]{x1D707}_{L}$ is the Lebesgue measure.
For an integer 
$t\in [1,k_{f}^{\circ }]$, we say that 
$f$ satisfies (
$t$-ST
$^{\prime }$) if there exists a sequence 
$1\leqslant j_{1}<j_{2}<\cdots <j_{t}\leqslant k_{f}^{\circ }$ such that the projection 
$\text{pr}_{j_{1},\ldots ,j_{t}}(A(f))\subseteq [-2,2]^{t}$ is equidistributed in the 
$t$-fold product of the Sato–Tate measure on 
$[-2,2]$; we say that 
$f$ satisfies (
$t$-ST) if for all sequences 
$\mathbf{j}$ of length 
$t$, 
$\text{pr}_{\mathbf{j}}(A(f))$ is equidistributed in the 
$t$-fold product of the Sato–Tate measure.
We expect the strongest (SST) to be true; it fits into Serre’s general framework of Sato–Tate equidistribution [Reference SerreSer12, ch. 8], for almost all primes 
$\ell$ (depending on 
$f$).Footnote 4 Namely, the compact Lie group attached to 
$\unicode[STIX]{x1D70C}_{f,\ell }|_{\widetilde{F^{\circ }}}$ by Serre is the product of 
$k_{f}^{\circ }$ copies of 
$\text{SU}_{2}$ and the axioms 
$(A_{1})$ and 
$(A_{2})$ should hold.
When 
$t<k_{f}^{\circ }$, the mere conjunction of (RST) and (
$t$-ST) does not imply (SST).
Remark 3.3.2. The condition (SST) is stronger than the (usual) Sato–Tate equidistribution theorems available at the moment (see [Reference Harris, Shepherd-Barron and TaylorHST10, Reference Barnet-Lamb, Geraghty, Harris and TaylorBGHT11, Reference Barnet-Lamb, Gee and GeraghtyBGG11]).
In order to prove (SST) in the manner that the aforementioned results were obtained, one would need to control the 
$L$-functions not only of the symmetric powers,
$$\begin{eqnarray}\text{Sym}^{m_{j}}(i_{j}(f))\end{eqnarray}$$(through potential automorphy), but also of their tensor products,
$$\begin{eqnarray}\text{Sym}^{m_{1}}(i_{1}(f))\otimes \cdots \otimes \text{Sym}^{m_{k_{f}^{\circ }}}(i_{k_{f}^{\circ }}(f))\end{eqnarray}$$ for all tuples 
$(m_{1},\ldots ,m_{k_{f}^{\circ }})$.
The case of (
$t$-ST), for 
$t\leqslant 2$, looks accessible; see Harris [Reference HarrisHar09].
3.4 Multisets and Newton Polygons
Definition 3.4.6, the operations 
$\otimes$, 
$\oplus$ and the partial order will be used in Theorem 4.1.1.
We consider finite subsets with positive finite multiplicities, or simply multisets, of 
$\mathbb{Q}$. For example, 
$\{1/3,2/3\}$ (each with multiplicity 
$1$) and 
$\{1/2,1/2\}$ (with multiplicity 
$2$).
Definition 3.4.1. Let 
$S=\{s_{1},\ldots ,s_{m}\}$ and 
$T=\{t_{1},\ldots ,t_{n}\}$ be multisets. Define the sum
$$\begin{eqnarray}S\oplus T=\{s_{1},\ldots ,s_{m},t_{1},\ldots ,t_{n}\},\end{eqnarray}$$the product
$$\begin{eqnarray}S\otimes T=\{s_{i}+{t_{j}\}}_{1\leqslant i\leqslant m,\,1\leqslant j\leqslant n},\end{eqnarray}$$and the dual
$$\begin{eqnarray}S^{\vee }=\{-s_{1},\ldots ,-s_{m}\}.\end{eqnarray}$$ Also, for 
$k>0$, we write 
$S^{\oplus k}=S\oplus \cdots \oplus S$ and 
$S^{\otimes k}=S\otimes \cdots \otimes S$, repeated 
$k$ times.
The cardinality is denoted by 
$|S|$ or 
$\operatorname{rk}S$ (which is 
$m$ for the 
$S$ as above) and
$$\begin{eqnarray}\int S:=s_{1}+\cdots +s_{m}.\end{eqnarray}$$Proposition 3.4.2. Multisets form a commutative semiring with involution, in which the empty set is the additive neutral element and 
$\{0\}$ the multiplicative identity element.
The map 
$S\mapsto |S|$ is a semiring homomorphism into the natural numbers and
$$\begin{eqnarray}\int (S\oplus T)=\int S+\int T\quad \text{and}\quad \int (S\otimes T)=|T|\int S+|S|\int T.\end{eqnarray}$$ Given a multiset consisting of 
$a_{1}\leqslant \cdots \leqslant a_{n}$, we form its Newton polygon emanating from 
$(0,0)$ with the slopes 
$a_{1},\ldots ,a_{n}$ (in this order). Conversely, any finite Newton polygon emanating from the origin and with rational slopes uniquely determines a multiset of 
$\mathbb{Q}$.
From this point on, we will thus identify multisets with Newton polygons. This allows us to impose a partial order on the class of multisets:
$$\begin{eqnarray}S\leqslant T\quad \text{if and only if }|S|=|T|\text{and }\text{NP}(S)\leqslant \text{NP}(T),\end{eqnarray}$$ the last expression meaning that 
$\text{NP}(T)$ lies on or above 
$\text{NP}(S)$.
Proposition 3.4.3. Let 
$S\leqslant S^{\prime }$ and 
$T$ be three multisets. Then (1) 
$S\oplus T\leqslant S^{\prime }\oplus T$ and (2) 
$S\otimes T\leqslant S^{\prime }\otimes T$. If, in addition, 
$S$ and 
$S^{\prime }$ end at the same point, then (3) 
$S^{\vee }\leqslant {S^{\prime }}^{\vee }$.
Proof. (1) By induction on 
$|T|$, we are reduced to the case where 
$T$ consists of one element, say 
$T=\{t\}$. Twisting by 
$-t$ (i.e. taking 
$\otimes \{-t\}$) allows us to assume that 
$t=0$. Enumerate 
$S$ and 
$S^{\prime }$ in the order
$$\begin{eqnarray}s_{1}\leqslant s_{2}\leqslant \cdots \leqslant s_{m}\quad \text{and}\quad s_{1}^{\prime }\leqslant s_{2}^{\prime }\leqslant \cdots \leqslant s_{m}^{\prime },\end{eqnarray}$$ and let 
$a$ and 
$b$ be such that
$$\begin{eqnarray}s_{a}<0\leqslant s_{a+1}\quad \text{and}\quad s_{b}^{\prime }<0\leqslant s_{b+1}^{\prime };\end{eqnarray}$$ if all the 
$s_{i}$ are greater than or equal to 
$0$ (respectively, less than 
$0$), then we let 
$a:=0$ (respectively, 
$a:=m$), and similarly for 
$b$.
If we define 
$\unicode[STIX]{x1D6F4}_{S}(i):=s_{1}+\cdots +s_{i}$ for 
$i\in [0,m]$, the condition 
$S\leqslant S^{\prime }$ becomes
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}_{S}(i)\leqslant \unicode[STIX]{x1D6F4}_{S^{\prime }}(i)\quad \text{for all }i\in [0,m].\end{eqnarray}$$We need to prove
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}_{S\oplus \{0\}}(i)\leqslant \unicode[STIX]{x1D6F4}_{S^{\prime }\oplus \{0\}}(i)\quad \text{for all }i\in [0,m+1].\end{eqnarray}$$ (1a) Suppose that 
$a<b$. Then for 
$i\in [0,a]\cup [b+1,m+1]$, (3.4.3.1) is clearly satisfied. For 
$i\in [a+1,b]$, since 
$0$ is inserted into 
$S^{\prime }$ in 
$(b+1)$th place, we have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{S^{\prime }\oplus \{0\}}(i) & = & \displaystyle \unicode[STIX]{x1D6F4}_{S^{\prime }\oplus \{0\}}(b+1)-(s_{i+1}^{\prime }+\cdots +s_{b}^{\prime }+0)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6F4}_{S^{\prime }}(b)-(s_{i+1}^{\prime }+\cdots +s_{b}^{\prime })\geqslant \unicode[STIX]{x1D6F4}_{S^{\prime }}(b)\nonumber\end{eqnarray}$$ while, since 
$0$ is inserted into 
$S$ in 
$(a+1)$th place, we have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{S\oplus \{0\}}(i)=\unicode[STIX]{x1D6F4}_{S}(i-1)=\unicode[STIX]{x1D6F4}_{S}(b)-(s_{i}+\cdots +s_{b})\leqslant \unicode[STIX]{x1D6F4}_{S}(b), & & \displaystyle \nonumber\end{eqnarray}$$and we get (3.4.3.1).
(1b) Suppose that 
$a\geqslant b$. Then again for 
$i\in [0,b]\cup [a+1,m+1]$, (3.4.3.1) is trivially satisfied. For 
$i\in [b+1,a]$, we have this time:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{S^{\prime }\oplus \{0\}}(i) & = & \displaystyle \unicode[STIX]{x1D6F4}_{S^{\prime }}(i-1)=\unicode[STIX]{x1D6F4}_{S^{\prime }}(b)+(s_{b+1}^{\prime }+\cdots +s_{i-1}^{\prime })\geqslant \unicode[STIX]{x1D6F4}_{S^{\prime }}(b),\nonumber\\ \displaystyle \unicode[STIX]{x1D6F4}_{S\oplus \{0\}}(i) & = & \displaystyle \unicode[STIX]{x1D6F4}_{S}(i)=\unicode[STIX]{x1D6F4}_{S}(b)+(s_{b+1}+\cdots +s_{i})\leqslant \unicode[STIX]{x1D6F4}_{S^{\prime }}(b).\nonumber\end{eqnarray}$$This completes the proof of (1).
(2) By decomposing 
$T$ into singletons and using the distributive law, we deduce (2) from (1).
(3) The duals 
$S^{\vee }$ and 
${S^{\prime }}^{\vee }$ are enumerated:
$$\begin{eqnarray}-\!s_{m}\leqslant -s_{m-1}\leqslant \cdots \leqslant -s_{1}\quad \text{and}\quad -\!s_{m}^{\prime }\leqslant -s_{m-1}^{\prime }\leqslant \cdots \leqslant -s_{1}^{\prime }.\end{eqnarray}$$ The assumption that 
$S$ and 
$S^{\prime }$ end at the same point means that 
$\unicode[STIX]{x1D6F4}_{S}(m)=\unicode[STIX]{x1D6F4}_{S^{\prime }}(m)$. Thus
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}_{S^{\vee }}(i)=\unicode[STIX]{x1D6F4}_{S}(m-i)-\unicode[STIX]{x1D6F4}_{S}(m)\leqslant \unicode[STIX]{x1D6F4}_{S^{\prime }}(m-i)-\unicode[STIX]{x1D6F4}_{S^{\prime }}(m)=\unicode[STIX]{x1D6F4}_{{S^{\prime }}^{\vee }}(i)\end{eqnarray}$$ for all 
$i\in [1,m]$, and this completes the proof of the proposition.◻
Remark 3.4.4. In view of (3), one may want to consider the more restrictive partial order
$$\begin{eqnarray}S\leqslant ^{\prime }T\quad \text{if and only if }|S|=|T|,\int S=\int T\text{ and }\text{NP}(S)\leqslant \text{NP}(T),\end{eqnarray}$$ so as to make the involution 
$S\mapsto S^{\vee }$ order-preserving. Below, we use the partial order 
${\leqslant}$ only in the case where 
${\leqslant}^{\prime }$ also applies.
We are particularly interested in the following special cases.
Definition 3.4.5. By the partially ordered semiring of integral Newton polygons, we mean the subsemiring of multisets whose Newton polygons have integral breaking points.
The following polygons appear in the statement of Theorem 4.1.1.
Definition 3.4.6. Let 
$d\geqslant 1$, 
$k\geqslant 1$ and 
$i\in [0,k]$ be integers. We define the multiset (and the corresponding Newton polygon)
$$\begin{eqnarray}P(d;k,i):=(\{0,1\}^{\otimes d})^{\oplus (k-i)}\oplus (\{1/2,1/2\}^{\otimes d})^{\oplus i}.\end{eqnarray}$$ The Newton polygon of 
$P(d;k,i)$ has integral breaking points. By Proposition 3.4.3, we have
$$\begin{eqnarray}P(d;k,i)\leqslant P(d;k,j)\quad \text{if and only if }i\leqslant j.\end{eqnarray}$$3.5 Interaction of $F$ and $K$: slope and bisection
Let 
$G$ be a group acting on a finite set 
$X$.
Definition 3.5.1. By the length of maximal parts of 
$g\in G$ on 
$X$, which we denote by 
$\unicode[STIX]{x1D706}(g,X)$, we mean the largest of the cardinalities of the 
$g$-orbits in 
$X$. We define 
$\unicode[STIX]{x1D706}(G,X)$ as the supremum of 
$\unicode[STIX]{x1D706}(g,X)$, as 
$g$ ranges over 
$G$.
Definition 3.5.2. We say that an element 
$g\in G$bisects 
$X$ if 
$g$ has exactly two orbits in 
$X$ and the orbits have the same number of elements.
Let 
$F$ be a (ground) number field, 
$K$ a (coefficient) number field, and 
$F^{s}$ an algebraic closure of 
$F$. The Galois group 
$G:=\operatorname{Gal}(F^{s}/F)$ acts continuously on the discrete set
$$\begin{eqnarray}X:=\operatorname{Hom}(K,F^{s})\end{eqnarray}$$ of field embeddings of 
$K$ into 
$F^{s}$.
Definition 3.5.3. We define
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{F}(K):=\unicode[STIX]{x1D706}(\operatorname{Gal}(F^{s}/F),\operatorname{Hom}(K,F^{s})).\end{eqnarray}$$ When 
$F=\mathbb{Q}$, we drop 
$F$ from the notation and write 
$\unicode[STIX]{x1D706}(K)$.
In more concrete terms, when 
$F=\mathbb{Q}$, the Galois group of the normal closure 
$\widetilde{K}$ of 
$K/\mathbb{Q}$ determines 
$\unicode[STIX]{x1D706}(K)$. For example, if the group is the full symmetric group of degree 
$[K:\mathbb{Q}]$ or the cyclic group of 
$[K:\mathbb{Q}]$ elements, then 
$\unicode[STIX]{x1D706}(K)=[K:\mathbb{Q}]$. If the group is the alternating group, then 
$\unicode[STIX]{x1D706}(K)=[K:\mathbb{Q}]$ (respectively, 
$=[K:\mathbb{Q}]-1$) if 
$[K:\mathbb{Q}]$ is odd (respectively, even).
The notion of bisection is also determined by the Galois group; for example, the alternating group of even degree and the Klein 
$4$-group acting on itself by translation contain bisecting elements.
For general 
$F$, one needs to look at the action of the subgroup 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)\leqslant \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$.
Definition 3.5.4. Given two number fields 
$F$ and 
$K$, we define the slope of 
$K$ over 
$F$:
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{F}(K)=1-\frac{\unicode[STIX]{x1D706}_{F}(K)}{[K:\mathbb{Q}]}\in [0,1)\cap \mathbb{Q}.\end{eqnarray}$$ When 
$F=\mathbb{Q}$, we write 
$\unicode[STIX]{x1D70E}(K)=\unicode[STIX]{x1D70E}_{\mathbb{Q}}(K)$.
We call 
$\unicode[STIX]{x1D70E}$ the slope, in view of the following ‘semistability’ property, formally analogous to that of Harder and Narasimhan for vector bundles on curves, in the variable 
$K$.
Proposition 3.5.5. Let 
$K^{\prime }$ be a subfield of 
$K$ and let 
$n=[K:K^{\prime }]$. Then
$$\begin{eqnarray}n\cdot \unicode[STIX]{x1D706}(g,\operatorname{Hom}(K^{\prime },F^{s}))\geqslant \unicode[STIX]{x1D706}(g,\operatorname{Hom}(K,F^{s}))\end{eqnarray}$$ for all 
$g\in G=\operatorname{Gal}(F^{s}/F)$ and therefore
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{F}(K^{\prime })\leqslant \unicode[STIX]{x1D70E}_{F}(K).\end{eqnarray}$$Proof. Let 
$X=\operatorname{Hom}(K,F^{s})$ and 
$X^{\prime }:=\operatorname{Hom}(K^{\prime },F^{s})$. Then we have a surjective map of 
$G$-sets,
$$\begin{eqnarray}X\longrightarrow X^{\prime },\end{eqnarray}$$ obtained by restriction. Since 
$K/K^{\prime }$ is separable, each fiber has exactly 
$n$ elements.
The first inequality follows from inspecting the images of the 
$g$-orbits in 
$X$, and the second follows from the first by definition.◻
In the variable 
$F$, we trivially have
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{F}(K)\leqslant \unicode[STIX]{x1D70E}_{F^{\prime }}(K)\quad \text{if }F\subseteq F^{\prime }.\end{eqnarray}$$ The following proposition is useful in computing 
$\unicode[STIX]{x1D70E}$ and finding bisecting elements in practice.
Proposition 3.5.6. Let 
$F$ and 
$K$ be two number fields, with the respective normal closures 
$\widetilde{F}$ and 
$\widetilde{K}$ over 
$\mathbb{Q}$.
(1) If
$[K:\mathbb{Q}]$ is a prime number not dividing $[F:\mathbb{Q}]$, then $\unicode[STIX]{x1D70E}_{F}(K)=0$.(2) If
$\operatorname{Gal}(\widetilde{K}/\mathbb{Q})$ is the symmetric group of degree $[K:\mathbb{Q}]$ and if $[\widetilde{F}:\mathbb{Q}]$ is odd, then $\unicode[STIX]{x1D70E}_{\widetilde{F}}(K)=0$.(3) Suppose that
$\widetilde{K}$ is linearly disjoint from $\widetilde{F}$ over $\mathbb{Q}$ (which is the case, for example, if $F$ and $K$ have coprime discriminants). Then $\unicode[STIX]{x1D70E}_{F}(K)=\unicode[STIX]{x1D70E}_{\mathbb{Q}}(K)$, and $\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ possesses an element bisecting $\operatorname{Hom}(K,\overline{\mathbb{Q}})$ exactly when $\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$ does.
Proof. (1) Recall that 
$\operatorname{Gal}(\widetilde{K}/\mathbb{Q})$ acts transitively on 
$\operatorname{Hom}(K,\mathbb{Q})$, and therefore has order divisible by 
$p=[K:\mathbb{Q}]$. Since the image of 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ in 
$\operatorname{Gal}(\widetilde{K}/\mathbb{Q})$ (via 
$\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$) has index dividing 
$[F:\mathbb{Q}]$, the image also has order divisible by 
$p$. Therefore the image contains an element 
$g$ of exact order 
$p$, which has 
$\unicode[STIX]{x1D706}(g,\operatorname{Hom}(K,\mathbb{Q}))=p=[K:\mathbb{Q}]$.
(2) Use the fact that a symmetric group has no proper normal subgroup of odd index to deduce that the image of 
$\operatorname{Gal}(\overline{\mathbb{Q}}/\widetilde{F})$ in 
$\operatorname{Gal}(\widetilde{K}/\mathbb{Q})$ is the full symmetric group.
(3) By assumption, the natural map
$$\begin{eqnarray}(\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}):\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\longrightarrow \operatorname{Gal}(\widetilde{F}/\mathbb{Q})\times \operatorname{Gal}(\widetilde{K}/\mathbb{Q})\end{eqnarray}$$ is surjective and by definition 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)\supseteq \operatorname{Gal}(\overline{\mathbb{Q}}/\widetilde{F})=\ker (\unicode[STIX]{x1D719}_{1})$. Therefore 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ surjects onto 
$\operatorname{Gal}(\widetilde{K}/\mathbb{Q})$. The statements about the slope and bisecting elements follow from this.◻
3.6 Zariski density and Haar density (Serre)
We will use the following lemma in the proof of Theorem 4.1.1.
Lemma 3.6.1. Let 
$E$ be a finite extension of 
$\mathbb{Q}_{\ell }$, 
$G$ a connected algebraic group over 
$E$, 
$\unicode[STIX]{x1D6E4}\leqslant G(E)$ a compact and Zariski dense subgroup, and
$$\begin{eqnarray}\unicode[STIX]{x1D711}:G\longrightarrow \mathbb{A}_{E}^{1}\end{eqnarray}$$a regular morphism of algebraic varieties that is constant on the conjugacy classes.
Then for any finite subset 
$S$ of 
$E=\mathbb{A}^{1}(E)$ that does not contain 
$\unicode[STIX]{x1D711}(1_{G})$, the subset 
$\unicode[STIX]{x1D6E4}\cap \unicode[STIX]{x1D711}^{-1}(S)$ has Haar measure 
$0$ in 
$\unicode[STIX]{x1D6E4}$.
In particular, if 
$\unicode[STIX]{x1D6E4}$ is the image of a continuous representation 
$\unicode[STIX]{x1D70C}$ of 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ unramified outside a finite set of primes of the number field 
$F$, then the set of primes 
$\mathfrak{p}$ in 
$F$ such that 
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{p}}))\in S$ has (natural) density 
$0$.
Proof. This follows from Serre [Reference SerreSer12, Proposition 5.12] applied to 
$Z:=\unicode[STIX]{x1D711}^{-1}(S)$, which is a proper algebraic subset of 
$G$ by the assumptions and has Zariski density 
$0$ by definition.◻
4 Main theorems
4.1 Non-CM case
The notation and terminology in the following theorem are explained in the previous preparatory section. References to the precise subsections are provided as they arise.
Theorem 4.1.1. Let 
$f$ be a new normalised Hilbert eigencuspform of level 
$\mathfrak{n}\subseteq \mathscr{O}_{F}$ and parallel weight 
$(2,\ldots ,2)$, and suppose that it is not of CM type (§ 3.1).
Denote by 
$M(f)$ the André motive (see Proposition 2.2.6), whose realisations give the part of the intersection cohomology of the Hilbert modular variety corresponding to 
$\{\unicode[STIX]{x1D70E}(f)\}_{\unicode[STIX]{x1D70E}}$, where 
$\unicode[STIX]{x1D70E}$ ranges over all the embeddings of 
$K_{f}$ into 
$\overline{\mathbb{Q}}$.
(1) (Analogue of the Katz conjecture) For all rational primes
$p$ coprime to $\text{disc}(F)\cdot \mathfrak{n}\cdot \ell$, we have Moreover, if$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{p}\!|_{M(f)})\geqslant \text{HTP}(M(f)).\end{eqnarray}$$$p$ splits completely in $F$ (equivalently, in $\widetilde{F}$) and $p$ is unramified in $K_{f}$, then there exists an integer $k(p)\in [0,k_{f}]$ such that (Here$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{p}\!|_{M(f)})=P(d;k_{f},k(p)).\end{eqnarray}$$$k_{f}=[K_{f}:\mathbb{Q}]$ and we refer to Definition 3.4.6 for the right-hand side.)In the remaining parts, we only consider the primes splitting completely in
$F$ and unramified in $K_{f}$.(2) For a principally abundant set of primes
$p$, we have $$\begin{eqnarray}k(p)\leqslant \frac{k_{f}}{2}.\end{eqnarray}$$(3) If
$k_{f}^{\circ }=[K_{f}^{\circ }:\mathbb{Q}]\leqslant 2$ ($K_{f}^{\circ }$ is defined in § 3.2), then for a principally abundant set of primes $p$, we have $k(p)=0$, that is, the Newton and Hodge–Tate polygons coincide.(4) For an abundant set of primes
$p$, we have ($\unicode[STIX]{x1D70E}$ defined in § 3.5) $$\begin{eqnarray}k(p)\leqslant k_{f}\cdot \text{min}\{1/2,\unicode[STIX]{x1D70E}_{\widetilde{F}}(K_{f})\}.\end{eqnarray}$$
(4′) For an abundant set of primes
$p$, we have ($\widetilde{F^{\circ }}$ defined in § 3.2) $$\begin{eqnarray}k(p)\leqslant k_{f}\cdot \text{min}\{1/2,\unicode[STIX]{x1D70E}_{\widetilde{F^{\circ }}}(K_{f}^{\circ })\}.\end{eqnarray}$$
(5) If
$k_{f}^{\circ }$ is even, suppose that $f$ satisfies (RST) (respectively, ($t$-ST$^{\prime }$) for an integer $t\geqslant 1$), as defined in § 3.3. Then for a principally abundant set of primes $p$ (respectively, for an abundant set of primes $p$), we have in particular,$$\begin{eqnarray}k(p)\leqslant \frac{k_{f}}{k_{f}^{\circ }}\biggl\lfloor\frac{k_{f}^{\circ }-1}{2}\biggr\rfloor;\end{eqnarray}$$$k(p)<k_{f}/2$.(6) Suppose that
$f$ satisfies (RST) and that an element of $\operatorname{Gal}(\overline{\mathbb{Q}}/\widetilde{F^{\circ }})$ bisects $\operatorname{Hom}(K_{f}^{\circ },\overline{\mathbb{Q}})$ (§ 3.5). Then for an abundant set of primes $p$, we have $k(p)=0$, that is, the Newton and Hodge–Tate polygons coincide.
Proof. We have already fixed a rational prime 
$\ell$ that splits completely in 
$K_{f}$. Now for all rational primes 
$p\neq \ell$, we fix once and for all an isomorphism 
and pull back the 
$p$-adic valuation on the target to get a rank-
$1$ (discontinuous) valuation 
$v_{p}$ on 
$\overline{\mathbb{Q}}_{\ell }$, normalised by
$v_{p}(p)=1$.
To prove (1), we may pass to 
$\widetilde{F}$, and consider 
$\operatorname{Frob}_{\mathfrak{p}}$ for any prime 
$\mathfrak{p}$ lying over 
$p$, because doing so does not change the Newton polygon.
The key fact (from Brylinski and Labesse [Reference Brylinski and LabesseBL84]) that we use from the constructions (see Deligne [Reference DeligneDel71], Ohta [Reference OhtaOht83], Carayol [Reference CarayolCar86], Wiles [Reference WilesWil88], Taylor [Reference TaylorTay89] and Blasius and Rogawski [Reference Blasius and RogawskiBR93] and the references therein) of the Galois representations associated with the 
$\{\unicode[STIX]{x1D70E}(f)\}$ is the following: the 
$\ell$-adic étale realisation 
$M(f)_{\ell }$ of 
$M(f)$ is the direct sum of the tensor inductions (see Curtis and Reiner [Reference Curtis and ReinerCR87, §80C]):
This implies that for transversals (coset representatives) 
$g_{1},\ldots ,g_{d}\in \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$ of 
$\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$ modulo 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)$, we have that for any element 
$\unicode[STIX]{x1D6FE}$ in the finite-index normal subgroup 
$\operatorname{Gal}(\overline{\mathbb{Q}}/\widetilde{F})$ of 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F)$, the action of 
$\unicode[STIX]{x1D6FE}$ on 
$M(f)_{\ell }$ is given by
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}(f),\unicode[STIX]{x1D706}}(g_{1}\unicode[STIX]{x1D6FE}g_{1}^{-1})\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}(f),\unicode[STIX]{x1D706}}(g_{2}\unicode[STIX]{x1D6FE}g_{2}^{-1})\otimes \cdots \otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}(f),\unicode[STIX]{x1D706}}(g_{d}\unicode[STIX]{x1D6FE}g_{d}^{-1})).\end{eqnarray}$$ Let 
$K^{\prime }:=K_{f}(\operatorname{Frob}_{\mathfrak{p}})$ be the splitting field over 
$K_{f}$ of the polynomial
$$\begin{eqnarray}X^{2}-\text{Tr}(\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{ p}}))X+\det (\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{p}})),\end{eqnarray}$$ and let 
$R_{\mathfrak{p}}=\{\unicode[STIX]{x1D6FC}_{\mathfrak{p}},\unicode[STIX]{x1D6FD}_{\mathfrak{p}}\}\subset K^{\prime }$ be the roots. Each embedding 
$\unicode[STIX]{x1D70E}:K_{f}\longrightarrow \mathbb{Q}_{\ell }$ extends to (at most two) embeddings 
$\unicode[STIX]{x1D70E}^{\prime }:K^{\prime }\longrightarrow \overline{\mathbb{Q}}_{\ell }$, and the image 
$\unicode[STIX]{x1D70E}^{\prime }(R_{\mathfrak{p}})\subset \overline{\mathbb{Q}}_{\ell }$ is independent of the choice 
$\unicode[STIX]{x1D70E}^{\prime }$. Therefore we can unambiguously form the multiset of slopes:Footnote 5
$$\begin{eqnarray}S_{\mathfrak{p},\unicode[STIX]{x1D70E}}=\bigg\{\frac{v_{p}(\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FC}_{\mathfrak{p}}))}{v_{p}(\mathbb{N}\mathfrak{p})},\frac{v_{p}(\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FD}_{\mathfrak{p}}))}{v_{p}(\mathbb{N}\mathfrak{p})}\bigg\}.\end{eqnarray}$$ Since 
$\text{Tr}(\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{p}}))$ is an algebraic integer, its 
$p$-adic valuation is greater than or equal to 
$0$. Also, 
$\det (\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{p}}))$ is 
$\mathbb{N}\mathfrak{p}$ times a root of unity, so its 
$p$-adic valuation is equal to 
$v_{p}(\mathbb{N}\mathfrak{p})$. These two facts imply the inequalities on the 
$\unicode[STIX]{x1D70E}$-slopes of (4.1.1.3) for all 
$\unicode[STIX]{x1D70E}$:
$$\begin{eqnarray}\{0,1\}\leqslant S_{\mathfrak{p},\unicode[STIX]{x1D70E}}\leqslant \{1/2,1/2\}\end{eqnarray}$$ (see § 3.4 for the partial order by Newton polygon). Moreover, if 
$\mathbb{N}\mathfrak{p}=p$ (in particular, if 
$p$ splits completely in 
$F$) and 
$p$ is unramified in 
$K_{f}$, then one of the two inequalities must be an equality.
In view of the description of cohomology in terms of tensor induction (4.1.1.1) and (4.1.1.2), we have
$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}|_{M(f)}})=\bigoplus _{\unicode[STIX]{x1D70E}\in \operatorname{Hom}(K_{f},\mathbb{Q}_{\ell })}S_{\mathfrak{p},\unicode[STIX]{x1D70E}}^{\otimes d},\end{eqnarray}$$and since
$$\begin{eqnarray}\text{HTP}(M(f))=HP(M(f))=P(d;k_{f},0)=(\{0,1\}^{\otimes d})^{\oplus k_{f}},\end{eqnarray}$$we have proven (1).
Remark 4.1.2. We also get a bound for the denominators of the slopes: they are divisors of integers in the interval 
$[1,\widetilde{d}]$, or equal to 
$2$.
In order to proceed further, we first recall the following known fact (generalised Ramanujan–Peterson conjecture; see Taylor [Reference TaylorTay95b] and Blasius[Reference BlasiusBla06]),
Lemma 4.1.3. The roots 
$\unicode[STIX]{x1D6FC}_{\mathfrak{p}}$ and 
$\unicode[STIX]{x1D6FD}_{\mathfrak{p}}$ are 
$\mathbb{N}\mathfrak{p}$-Weil integers of weight 
$1$.
Proof of lemma.
If 
$d$ is odd or the automorphic representation 
$\unicode[STIX]{x1D70B}_{f}$ corresponding to 
$f$ is a discrete series representation at some finite prime, this follows from the essentially motivic nature of some of the constructions; see Blasius and Rogawski [Reference Blasius and RogawskiBR93], together with Deligne’s proof of the Weil conjectures [Reference DeligneDel74].
This can be proved in the general case, and only with the a priori non-motivic constructions of Wiles [Reference WilesWil88] and Taylor [Reference TaylorTay89]. Note that by the description (4.1.1.1), the algebraic integers 
$\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{d})$ and 
$\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FD}_{\mathfrak{p}}^{d})$, for any embedding 
$\unicode[STIX]{x1D70E}^{\prime }$ of 
$K^{\prime }$ into 
$\overline{\mathbb{Q}}_{\ell }$, are eigenvalues of 
$\operatorname{Frob}_{\mathfrak{p}}$ acting on the 
$\text{IH}^{d}$ of the Baily–Borel compactification 
$X^{\text{BB}}(\mathfrak{n})$ of the Hilbert modular variety.
Now this last variety admits a surjective, generically finite map from a projective smooth toroidal compactification over 
$\mathbb{Z}_{(p)}$ [Reference RapoportRap78].
By the decomposition theorem for perverse sheaves [Reference Beĭlinson, Bernstein and DeligneBBD82], the two algebraic integers therefore appear as eigenvalues of 
$\operatorname{Frob}_{\mathfrak{p}}$ in the 
$H^{d}$ of the projective smooth variety. Then by Deligne’s proof of the Weil conjectures, they have all the archimedean absolute values equal to 
$(\mathbb{N}\mathfrak{p})^{d/2}$. By taking the 
$d$th root, we get the lemma.◻
From this point on, we assume that 
$\mathfrak{p}$ is a prime of absolute degree 
$1$ over 
$(p)$ (in addition to being coprime to 
$\text{disc}(F)\cdot \mathfrak{n}\cdot \ell$). We also assume that 
$p$ is unramified in 
$K_{f}$.
(2) We now look more closely at
$$\begin{eqnarray}a_{\mathfrak{p}}:=\text{Tr}(\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}})).\end{eqnarray}$$ By the assumption that 
$f$ is not of CM type, the image of 
$\operatorname{Gal}(\mathbb{Q}/\widetilde{F})$ under 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}$ is Zariski dense in 
$\text{GL}_{2}$ over 
$K_{f,\unicode[STIX]{x1D706}}$. Since 
$\text{Tr}$ is a regular morphism of the algebraic variety 
$\text{GL}_{2}$ into 
$\mathbb{A}^{1}$ and takes value 
$2\neq 0$ at the identity element 
$I_{2}$, the set of primes 
$\mathfrak{p}$ of 
$\widetilde{F}$ such that 
$a_{\mathfrak{p}}=0$ has density zero by Lemma 3.6.1. We exclude them from this point on.
Let 
${\wp}_{1},\ldots ,{\wp}_{m}$ be the primes of 
$K_{f}$ lying over 
$(p)=\mathfrak{p}\cap \mathbb{Z}$, and write the ideal factorisation
$$\begin{eqnarray}a_{\mathfrak{p}}\cdot \mathscr{O}_{K_{f}}={\wp}_{1}^{e_{1}}\cdots {\wp}_{k}^{e_{m}}\cdot I,\end{eqnarray}$$ where 
$I$ is an integral ideal coprime to 
$p$, and we carry on with the argument preceding the lemma.
For each embedding 
$\unicode[STIX]{x1D70E}:K_{f}\longrightarrow \mathbb{Q}_{\ell }$, let 
${\wp}_{i(\unicode[STIX]{x1D70E})}$ be the inverse image in 
$\mathscr{O}_{K_{f}}$ of the maximal ideal of the integral closure 
$\overline{\mathbb{Z}_{p}}\subset \overline{\mathbb{Q}}_{p}$ of 
$\mathbb{Z}_{p}$ under the composite of 
$\unicode[STIX]{x1D70E}$ with the fixed 
$\overline{\mathbb{Q}}_{\ell }\simeq \overline{\mathbb{Q}}_{p}$:
Then 
$S_{\mathfrak{p},\unicode[STIX]{x1D70E}}$ is the Newton polygon of the polynomial (obtained by applying 
$\unicode[STIX]{x1D70E}$ to (4.1.1.3)) with respect to 
$v_{p}$ on 
$\mathbb{Q}_{\ell }$,
$$\begin{eqnarray}X^{2}-\unicode[STIX]{x1D70E}(a_{\mathfrak{ p}})X+\unicode[STIX]{x1D70E}(\det (\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{p}}))),\end{eqnarray}$$and as such is equal to
$$\begin{eqnarray}S_{\mathfrak{p},\unicode[STIX]{x1D70E}}=\left\{\begin{array}{@{}ll@{}}\{0,1\}\quad & \text{if }e_{i(\unicode[STIX]{x1D70E})}=0,\\ \{1/2,1/2\}\quad & \text{if }e_{i(\unicode[STIX]{x1D70E})}>0.\end{array}\right.\end{eqnarray}$$ Let 
$f_{1},\ldots ,f_{m}$ be the degrees of the residue class extensions:
$$\begin{eqnarray}f_{i}:=\dim _{\mathbb{F}_{p}}\mathscr{O}_{K_{f}}/{\wp}_{i}.\end{eqnarray}$$Then we have
$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}}\!|_{M(f)})=P(d;k_{f},k(p)),\end{eqnarray}$$ where 
$k(p)$ is the sum of those 
$f_{i}$ for which 
$e_{i}>0$.
Since 
$a_{\mathfrak{p}}\neq 0$, we may apply the product formula. By the lemma, we have
$$\begin{eqnarray}\mathop{\prod }_{v|\infty }\Vert a_{\mathfrak{p}}\Vert _{v}\leqslant (2\sqrt{p})^{k_{f}},\end{eqnarray}$$while by the factorisation (4.1.3.1),
$$\begin{eqnarray}\mathop{\prod }_{v|p}\Vert a_{\mathfrak{p}}\Vert _{v}=p^{-\!\mathop{\sum }_{i=1}^{m}e_{i}f_{i}}\end{eqnarray}$$and
$$\begin{eqnarray}\mathop{\prod }_{v\nmid p,\infty }\Vert a_{\mathfrak{p}}\Vert _{v}=\mathop{\prod }_{v\nmid p,\infty }\Vert I\Vert _{v}\leqslant 1.\end{eqnarray}$$Therefore
$$\begin{eqnarray}1=\mathop{\prod }_{v}\Vert a_{\mathfrak{p}}\Vert \leqslant 2^{k_{f}}p^{k_{f}/2-\mathop{\sum }_{i}e_{i}f_{i}},\end{eqnarray}$$ which implies, for all 
$p>2^{2k_{f}}$,
$$\begin{eqnarray}\frac{k_{f}}{2}\geqslant \mathop{\sum }_{i=1}^{m}e_{i}f_{i}\geqslant \mathop{\sum }_{i:e_{i}>0}f_{i}=k(p).\end{eqnarray}$$This proves (2).
For (3), we assume in addition that 
$p$ splits completely in 
$\widetilde{F^{\circ }}$, and choose a prime 
$\mathfrak{p}$ of 
$\widetilde{F^{\circ }}$ lying over 
$p$, so that by definition
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f,\ell }(\operatorname{Frob}_{\mathfrak{p}})\in G_{f,\ell }^{\circ }(\mathbb{Q}_{\ell })\quad \text{and}\quad a_{\mathfrak{p}}\in \mathscr{O}_{K_{f}^{\circ }}.\end{eqnarray}$$ If 
$k_{f}^{\circ }=1$, that is, if 
$K_{f}^{\circ }=\mathbb{Q}$, then 
$a_{\mathfrak{p}}\in \mathbb{Z}$ and 
$|a_{\mathfrak{p}}|_{\infty }<2\sqrt{p}$. As soon as 
$p\geqslant 5$, the only way 
$p|a_{\mathfrak{p}}$ is then 
$a_{\mathfrak{p}}=0$, which we have excluded above.
Suppose therefore that 
$k_{f}^{\circ }=2$, and consider the homomorphisms
and the regular map of algebraic varieties
$$\begin{eqnarray}\text{Tr}(\wedge ^{2}(\unicode[STIX]{x1D704})\otimes \det ^{-1}):((\operatorname{Res}_{\mathbb{ Q}}^{K_{f}^{\circ }}\text{GL}_{2})^{\det \subseteq \mathbb{Q}^{\times }})\otimes \mathbb{Q}_{\ell }\longrightarrow \mathbb{A}_{\mathbb{Q}_{\ell }}^{1},\end{eqnarray}$$ where 
$\wedge ^{2}(\unicode[STIX]{x1D704})$ takes values in 
$\text{GL}_{6}$ and 
$\det$ takes values in 
$\mathbf{G}_{m}$.
In order to prove (3), we find a set of primes 
$\mathfrak{p}$ of 
$\widetilde{F^{\circ }}$ of density equal to 
$1$ such that 
$a_{\mathfrak{p}}$ is not divisible by any prime of 
$K_{f}^{\circ }$ lying over 
$(p)$. If 
$p$ is inert in 
$K_{f}^{\circ }$, the bound (2) suffices, and we exclude the finitely many primes that are ramified in 
$K_{f}^{\circ }$, so we assume that 
$p$ splits:
$$\begin{eqnarray}p\cdot \mathscr{O}_{K_{f}^{\circ }}={\wp}_{1}{\wp}_{2}\quad \text{where }{\wp}_{1}\neq {\wp}_{2}\text{ are primes}.\end{eqnarray}$$ By (2), we may assume that at most one of the two primes can divide 
$a_{\mathfrak{p}}$, say 
$a_{\mathfrak{p}}\in {\wp}_{1}$ but 
$a_{\mathfrak{p}}\not \in {\wp}_{2}$. Let 
$\unicode[STIX]{x1D716}$ be the non-trivial field automorphism of 
$K_{f}^{\circ }$, let 
$\unicode[STIX]{x1D6FC}_{\mathfrak{p}}$ be a root of the polynomial 
$X^{2}-a_{\mathfrak{p}}X+p=0$, and let 
$\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{\prime }$ be a root of 
$X^{2}-\unicode[STIX]{x1D716}(a_{\mathfrak{p}})X+p=0.$
Then the four eigenvalues of 
$(\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D70C}^{\circ })(\operatorname{Frob}_{\mathfrak{p}})$ are 
$\{\unicode[STIX]{x1D6FC}_{\mathfrak{p}},p/\unicode[STIX]{x1D6FC}_{\mathfrak{p}},\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{\prime },p/\unicode[STIX]{x1D6FC}_{\mathfrak{p}}\}$, and the six eigenvalues of 
$(\wedge ^{2}\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D70C}^{\circ })(\operatorname{Frob}_{\mathfrak{p}})$ are 
$\{p,\unicode[STIX]{x1D6FC}_{\mathfrak{p}}\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{\prime },\unicode[STIX]{x1D6FC}_{\mathfrak{p}}(p/\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{\prime }),(p/\unicode[STIX]{x1D6FC}_{\mathfrak{p}})\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{\prime },(p/\unicode[STIX]{x1D6FC}_{\mathfrak{p}})(p/\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{\prime }),p\}$. Therefore the value of (4.1.3.2) at 
$\operatorname{Frob}_{\mathfrak{p}}$ is
$$\begin{eqnarray}\frac{1}{p}\biggl(2p+\biggl(\unicode[STIX]{x1D6FC}_{\mathfrak{p}}+\frac{p}{\unicode[STIX]{x1D6FC}_{\mathfrak{p}}}\biggr)\biggl(\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{\prime }+\frac{p}{\unicode[STIX]{x1D6FC}_{\mathfrak{p}}^{\prime }}\biggr)\biggr)=2+\frac{a_{\mathfrak{p}}\unicode[STIX]{x1D716}(a_{\mathfrak{p}})}{p}\in \mathbb{Z}.\end{eqnarray}$$Now by Lemma 4.1.3, which implies
$$\begin{eqnarray}|a_{\mathfrak{p}}|_{\infty },|\unicode[STIX]{x1D716}(a_{\mathfrak{p}})|_{\infty }\leqslant 2\sqrt{p},\end{eqnarray}$$ and by our assumption that 
$p$ is unramified in 
$K_{f}^{\circ }$, which implies that the inequalities are strict, we have
$$\begin{eqnarray}\text{Tr}(\wedge ^{2}(\unicode[STIX]{x1D704})\otimes \det ^{-1})(\operatorname{Frob}_{\mathfrak{ p}})\in [-1,5]\cap \mathbb{Z}.\end{eqnarray}$$ Therefore 
$a_{\mathfrak{p}}$ does not belong to any prime of 
$K_{f}^{\circ }$ lying over 
$(p)$, as soon as we avoid (4.1.3.4). But since
$$\begin{eqnarray}\text{Tr}(\wedge ^{2}(\unicode[STIX]{x1D704})\otimes \det ^{-1})(1)=6\end{eqnarray}$$ (here 
$1$ denotes the identity element in the group 
$G_{f,\ell }^{\circ }$), the set of 
$\mathfrak{p}$ for which (4.1.3.4) holds has density 
$0$ by Lemma 3.6.1. Now if 
$\mathfrak{p}$ avoids (4.1.3.4), then
$$\begin{eqnarray}a_{\mathfrak{p}}\mathscr{O}_{K_{f}}=(a_{\mathfrak{p}}\mathscr{O}_{K_{f}^{\circ }})\mathscr{O}_{K_{f}}\end{eqnarray}$$ is coprime to 
$(p)$, and we have 
$k(p)=0$. This completes the proof of (3).
For the sake of continuity in exposition, we treat the conditional (5) before the unconditional (4). By an argument similar to that for (2), but applied to the restriction 
$\unicode[STIX]{x1D70C}^{\circ }:\operatorname{Gal}(\overline{\mathbb{Q}}/\widetilde{F^{\circ }})\longrightarrow \text{GL}_{2}(K_{f,\unicode[STIX]{x1D706}^{\circ }}^{\circ })$ (where 
$\unicode[STIX]{x1D706}^{\circ }=\unicode[STIX]{x1D706}\cap K_{f}^{\circ }$), for a prime 
$\mathfrak{p}$ of density 
$1$ in 
$\widetilde{F^{\circ }}$, if we write
$$\begin{eqnarray}a_{\mathfrak{p}}\mathscr{O}_{K_{f}^{\circ }}={\wp}_{1}^{e_{1}}\cdots {\wp}_{m^{\prime }}^{e_{m^{\prime }}}I,\end{eqnarray}$$ where 
${\wp}_{1},\ldots ,{\wp}_{m^{\prime }}$ are the primes of 
$K_{f}^{\circ }$ lying over 
$p$ and 
$I$ is coprime to 
$p$, then we have
$$\begin{eqnarray}\mathop{\sum }_{i:e_{i}>0}\dim _{\mathbb{F}_{p}}(\mathscr{O}_{K_{f}^{\circ }}/{\wp}_{i})\leqslant \frac{k_{f}^{\circ }}{2},\end{eqnarray}$$and
$$\begin{eqnarray}k(p)=\frac{k_{f}}{k_{f}^{\circ }}\mathop{\sum }_{i:e_{i}>0}\dim _{\mathbb{F}_{p}}(\mathscr{O}_{K_{f}^{\circ }}/{\wp}_{i}).\end{eqnarray}$$ If 
$k_{f}^{\circ }$ is odd, then (4.1.3.5) trivially implies (5), so we assume that 
$k_{f}^{\circ }$ is even.
Now if the equality holds in (4.1.3.5), then we necessarily have 
$e_{i}=1$ whenever 
$e_{i}>0$, and by Lemma 4.1.3 and the product formula,
$$\begin{eqnarray}(2\sqrt{p})^{k_{f}^{\circ }}\geqslant \mathop{\prod }_{v|\infty }\Vert a_{\mathfrak{p}}\Vert _{v}=\biggl(\mathop{\prod }_{v|p}\Vert a_{\mathfrak{p}}\Vert _{v}\cdot \mathop{\prod }_{v\nmid p\infty }\Vert a_{\mathfrak{p}}\Vert _{v}\biggr)^{-1}\in p^{k_{f}^{\circ }/2}\mathbb{Z}.\end{eqnarray}$$ In other words, if 
$i_{1},\ldots ,i_{k_{f}^{\circ }}$ are the real embeddings of 
$K_{f}^{\circ }$, then we have
$$\begin{eqnarray}\mathop{\prod }_{j=1}^{k_{f}^{\circ }}\frac{i_{j}(a_{\mathfrak{p}})}{\sqrt{p}}\in \mathbb{Z}\cap [-2^{k_{f}^{\circ }},2^{k_{f}^{\circ }}].\end{eqnarray}$$ In 
$\mathbb{R}^{k_{f}^{\circ }}$, consider the nowhere dense real analytic subsets
$$\begin{eqnarray}B_{j}=\bigg\{(x_{1},\ldots ,x_{k_{f}^{\circ }}):\mathop{\prod }_{a=1}^{k_{f}^{\circ }}x_{a}=j\bigg\}\end{eqnarray}$$ for non-zero 
$j\in \mathbb{Z}\cap [-2^{k_{f}^{\circ }},2^{k_{f}^{\circ }}]$, 
$B_{0}=\{(0,\ldots ,0)\}$, and let 
$B$ be their union.
If 
$f$ satisfies (RST), then the set 
$A(f)$ in § 3.3 is equidistributed in 
$\unicode[STIX]{x1D711}(\mathbf{x})d\unicode[STIX]{x1D707}_{L}(\mathbf{x})$, where 
$\unicode[STIX]{x1D711}:[-2,2]^{k_{f}^{\circ }}\longrightarrow \mathbb{R}_{{\geqslant}0}$ is a continuous function and 
$d\unicode[STIX]{x1D707}_{L}$ is the Lebesgue measure. Therefore the set of primes 
$\mathfrak{p}$ of 
$\widetilde{F^{\circ }}$ such that
$$\begin{eqnarray}\biggl(\frac{i_{1}(a_{\mathfrak{p}})}{\sqrt{\mathbb{N}\mathfrak{ p}}},\ldots ,\frac{i_{k_{f}^{\circ }}(a_{\mathfrak{p}})}{\sqrt{\mathbb{N}\mathfrak{ p}}}\biggr)\in B\end{eqnarray}$$ has density 
$0$, since 
$\int _{B}\unicode[STIX]{x1D711}\,d\unicode[STIX]{x1D707}_{L}=0$.
If 
$f$ satisfies (
$t$-ST
$^{\prime }$), then there exists a sequence 
$1\leqslant j_{1}<\cdots <j_{t}\leqslant k_{f}^{\circ }$ such that 
$\text{pr}_{j_{1},\ldots ,j_{t}}(A(f))$ is equidistributed in the 
$t$-fold product of the Sato–Tate measure. Then the set
$$\begin{eqnarray}C=\bigg\{(x_{1},\ldots ,x_{k_{f}^{\circ }}):\mathop{\prod }_{a=1}^{t}|x_{j_{a}}|<2^{-(k_{f}^{\circ }-t)}\bigg\}\end{eqnarray}$$ is disjoint from 
$B_{j}$ for all non-zero 
$j\in \mathbb{Z}\cap [-2^{k_{f}^{\circ }},2^{k_{f}^{\circ }}]$. Since the set of 
$\mathfrak{p}$ such that 
$a_{\mathfrak{p}}=0$ has density 
$0$ as noted above, the lower natural density of the set of primes 
$\mathfrak{p}$ such that
$$\begin{eqnarray}\biggl(\frac{i_{1}(a_{\mathfrak{p}})}{\sqrt{\mathbb{N}\mathfrak{ p}}},\ldots ,\frac{i_{k_{f}^{\circ }}(a_{\mathfrak{p}})}{\sqrt{\mathbb{N}\mathfrak{ p}}}\biggr)\not \in B\end{eqnarray}$$is bounded from below by
$$\begin{eqnarray}c(k_{f}^{\circ },t):=\int _{|y_{1}|\cdots |y_{t}|<2^{t-k_{f}^{\circ }}}d\unicode[STIX]{x1D707}_{ST}(y_{1})\cdots \,d\unicode[STIX]{x1D707}_{ST}(y_{t})>0\quad \text{for }1\leqslant t<k_{f}^{\circ },\end{eqnarray}$$ where 
$d\unicode[STIX]{x1D707}_{ST}(y)=(1/2\unicode[STIX]{x1D70B})\sqrt{4-y^{2}}\,dy$ concentrated in 
$[-2,2]$.
(4) There is nothing to prove if 
$\unicode[STIX]{x1D70E}_{\widetilde{F}}(K_{f})\geqslant 1/2$, so we assume that
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}:=\unicode[STIX]{x1D706}_{\widetilde{F}}(K_{f})>k_{f}/2.\end{eqnarray}$$ We return to the primes 
$\mathfrak{p}$ of 
$\widetilde{F}$ of absolute degree 
$1$ over 
$\mathbb{Q}$. The conjugacy class of 
$\operatorname{Frob}_{\mathfrak{p}}$ in 
$\operatorname{Gal}(\overline{\mathbb{Q}}_{S}/\widetilde{F})$ maps into the conjugacy class of 
$\operatorname{Frob}_{p}$ in 
$\operatorname{Gal}(\overline{\mathbb{Q}}_{S}/\mathbb{Q})$. (Here 
$\overline{\mathbb{Q}}_{S}$ is the maximal subfield of 
$\overline{\mathbb{Q}}$ unramified outside 
$\text{disc}(F)\cdot \text{disc}(K_{f})\cdot \ell \cdot \mathbb{N}(\mathfrak{n})$.) The following diagram exhibits the interaction of 
$\widetilde{F}$ and 
$K_{f}$ (§ 3.5) and the Galois representation at hand:
Let 
$\unicode[STIX]{x1D6E4}$ be the image of 
$\operatorname{Gal}(\overline{\mathbb{Q}}_{S}/\widetilde{F})$ in 
$\operatorname{Aut}(\operatorname{Hom}(K_{f},\overline{\mathbb{Q}}))$, and let 
$H^{\sharp }\subseteq \unicode[STIX]{x1D6E4}$ be the non-empty subset of elements 
$h$ such that 
$\unicode[STIX]{x1D706}(h,\operatorname{Hom}(K_{f},\overline{\mathbb{Q}}))=\unicode[STIX]{x1D706}_{0}$; one sees easily that 
$H^{\sharp }$ is stable under conjugation by 
$\unicode[STIX]{x1D6E4}$. Then if 
$\operatorname{Frob}_{\mathfrak{p}}$ maps into 
$H^{\sharp }$, there exists a prime ideal 
${\wp}$ of 
$K_{f}$ lying over 
$(p)$ with
$$\begin{eqnarray}\dim _{\mathbb{F}_{p}}\mathscr{O}_{K_{f}}/{\wp}=\unicode[STIX]{x1D706}_{0}.\end{eqnarray}$$ Now the bound in (2) prevents 
${\wp}$ from occurring in the ideal factorisation of 
$a_{\mathfrak{p}}$ (4.1.3.1) with multiplicity greater than 
$0$. Therefore 
$k(p)$ is at most the sum of the degrees of the residue class field extensions at the other primes of 
$K_{f}$ lying over 
$(p)$, and
$$\begin{eqnarray}k(p)\leqslant k_{f}-\unicode[STIX]{x1D706}_{0}=k_{f}\cdot \unicode[STIX]{x1D70E}_{\widetilde{F}}(K_{f}).\end{eqnarray}$$ The density of such primes 
$\mathfrak{p}$ (i.e. not dividing 
$\text{disc}(F)\cdot \text{disc}(K_{f})\cdot \ell \cdot \mathbb{N}(\mathfrak{n})$, having 
$a_{\mathfrak{p}}\neq 0$, and whose 
$\operatorname{Frob}_{\mathfrak{p}}$ mapping into 
$H^{\sharp }$) in 
$\widetilde{F}$ is, by the Chebotarev density theorem, equal to 
$|H^{\sharp }|/|\unicode[STIX]{x1D6E4}|>0$, and we get (4).
The proof of (4
$^{\prime }$) is parallel to that of (4), except that we consider the degree-
$1$ primes of 
$\widetilde{F^{\circ }}$ and 
$a_{\mathfrak{p}}\in \mathscr{O}_{K_{f}^{\circ }}$, and we omit it.
(6) Consider a similar diagram (with 
$\widetilde{F}$ replaced with 
$\widetilde{F^{\circ }}$) to the one in (4), and let 
$\unicode[STIX]{x1D6E4}^{\circ }$ be the image of 
$\operatorname{Gal}(\overline{\mathbb{Q}}_{S}/\widetilde{F^{\circ }})$ in 
$\operatorname{Aut}(\operatorname{Hom}(K_{f}^{\circ },\overline{\mathbb{Q}}))$. This time, choose 
$H^{\sharp }$ to consist of those elements of 
$\unicode[STIX]{x1D6E4}^{\circ }$ that bisect 
$\operatorname{Hom}(K_{f}^{\circ },\overline{\mathbb{Q}})$. Again, 
$H^{\sharp }$ is stable under conjugation by 
$\unicode[STIX]{x1D6E4}^{\circ }$.
Then for any prime 
$\mathfrak{p}$ of 
$\widetilde{F^{\circ }}$ such that 
$\operatorname{Frob}_{\mathfrak{p}}$ maps into 
$H^{\sharp }$ and 
$p$ is unramified in 
$K_{f}^{\circ }$, there are exactly two primes of 
$K_{f}^{\circ }$ lying over 
$(p)$ with the same degree of residue class extension (namely, 
$k_{f}^{\circ }/2$). The density of such primes 
$\mathfrak{p}$ in 
$\widetilde{F^{\circ }}$ is 
$|H^{\sharp }|/|\unicode[STIX]{x1D6E4}^{\circ }|>0$ by the Chebotarev density theorem.
Now the bound in (5), which is in effect because we assume (RST), keeps either of the two primes from appearing in the ideal decomposition of 
$a_{\mathfrak{p}}\mathscr{O}_{K_{f}^{\circ }}$ with multiplicity greater than 
$0$, except for a set of primes 
$\mathfrak{p}$ with density 
$0$.◻
Remark 4.1.4. The constant 
$c(k,t)$ for 
$t=1$ (where 
$k=k_{f}^{\circ }$) can be expressed as
$$\begin{eqnarray}c(k,1)=\frac{2}{\unicode[STIX]{x1D70B}}\biggl(\frac{1}{2^{k}}\sqrt{1-\frac{1}{2^{2k}}}+\arcsin \biggl(\frac{1}{2^{k}}\biggr)\biggr),\quad \text{for }k\geqslant 2,\end{eqnarray}$$ and is asymptotically 
$1/(\unicode[STIX]{x1D70B}2^{k-2})$ as 
$k\rightarrow \infty$. Here are approximate values of 
$c(k,t)$ for 
$1\leqslant t\leqslant k\leqslant 6$:
4.2 CM case
Theorem 4.2.1. Let 
$f$ be a new normalised Hilbert eigencuspform of level 
$\mathfrak{n}\subseteq \mathscr{O}_{F}$ and parallel weight 
$(2,\ldots ,2)$. Suppose that 
$f$ is of CM type (§ 3.1).
Denote by 
$M(f)$ the André motive, whose realisations give the part of the intersection cohomology of the Hilbert modular variety corresponding to 
$\{\unicode[STIX]{x1D70E}(f)\}$, where 
$\unicode[STIX]{x1D70E}$ ranges over all the embeddings of 
$K_{f}$ into 
$\overline{\mathbb{Q}}$. Then:
(1) for all rational primes
$p$ coprime to $\text{disc}(F)\cdot \mathfrak{n}\cdot \ell$, we have $$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{p}\!|_{M(f)})\geqslant \text{HTP}(M(f));\end{eqnarray}$$(2) for a principally abundant set of primes
$p$, we have $$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{p}\!|_{M(f)})=\text{HTP}(M(f)).\end{eqnarray}$$
Proof. Let 
$\unicode[STIX]{x1D706}$ be a prime of 
$K_{f}$ lying over 
$(\ell )$ such that the connected component 
$G^{\circ }$ of the Zariski closure 
$G=G_{f,\unicode[STIX]{x1D706}}$ of the image of 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}$ is a torus. The argument employed in proving part (1) of Theorem 4.1.1 goes through without change: the non-CM condition was not used. This way we get the inequality (1) for primes 
$p$ coprime to 
$\text{disc}(F)\cdot \mathfrak{n}\cdot \ell$, and for those splitting completely in 
$F$ and unramified in 
$K_{f}$ in addition, an integer 
$k(p)\in [0,k_{f}]$ such that
$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{p}\!|_{M(f)})=P(d;k_{f},k(p)).\end{eqnarray}$$ Let 
$F^{\circ }$ be the Galois extension of 
$F$ cut out by the two representations with finite image,
$$\begin{eqnarray}\operatorname{Gal}(\overline{\mathbb{Q}}/F^{\circ })=\ker (\operatorname{Gal}(\overline{\mathbb{Q}}/F)\longrightarrow G(K_{f,\unicode[STIX]{x1D706}})/G^{\circ }(K_{f,\unicode[STIX]{x1D706}}))\cap \ker (\det (\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}})(1)),\end{eqnarray}$$ and let 
$\widetilde{F^{\circ }}$ be the compositum of 
$F^{\circ }$ and 
$\widetilde{F}$.
Since the restriction of 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}$ to 
$\widetilde{F^{\circ }}$ is then abelian and 
$K_{f}$-rational, by a theorem of Serre [Reference SerreSer98, ch. III, §3], augmented with a transcendence result of Waldschmidt [Reference WaldschmidtWal81] (see Henniart [Reference HenniartHen82]), this restriction is locally algebraic (and semisimple by assumption). Then by a theorem of Ribet [Reference RibetRib76, §1.6] (which extends that of Serre [Reference SerreSer98, § III.2.3]), there exist (i) a two-dimensional 
$K_{f}$-rational vector subspace 
$V_{0}$ of 
$K_{f,\unicode[STIX]{x1D706}}^{\oplus 2}$, (ii) a modulus 
$\mathfrak{m}$ of 
$\widetilde{F^{\circ }}$, and (iii) a rational representation
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{0}:S_{\mathfrak{m}}\otimes _{\mathbb{Q}}K_{f}\longrightarrow \text{GL}_{V_{0}}\end{eqnarray}$$ such that 
$\unicode[STIX]{x1D70C}|_{\widetilde{F^{\circ }}}$ is isomorphic to the 
$\unicode[STIX]{x1D706}$-adic representation associated with 
$\unicode[STIX]{x1D719}_{0}$.
The image of 
$\unicode[STIX]{x1D719}_{0}$ is a maximal algebraic torus of 
$\text{GL}_{V_{0}}$, since 
$\det \unicode[STIX]{x1D719}_{0}$ gives the Tate structure 
$\mathbb{Q}_{\ell }(-1)$ on 
$\operatorname{Gal}(\overline{\mathbb{Q}}/F^{\circ })$, and the cyclotomic character is not divisible by 
$2$ as the character of any number field.
Let 
$K^{\prime }$ be the splitting field over 
$K_{f}$ of this algebraic torus, so that 
$[K^{\prime }:K_{f}]\leqslant 2$ and 
$[G_{f,\unicode[STIX]{x1D706}}:G_{f,\unicode[STIX]{x1D706}}^{\circ }]\leqslant 2$. (It is worth clarifying that, unlike the 
$K^{\prime }$ introduced in the proof of Theorem 4.1.1 in a similar context, this 
$K^{\prime }$ depends only on 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}$ and is independent of 
$\mathfrak{p}$.)
For every prime 
$\mathfrak{p}$ of 
$\widetilde{F^{\circ }}$ of absolute degree 
$1$ and coprime to 
$\text{disc}(F)\cdot \mathfrak{n}\cdot \ell$, let 
$\{\unicode[STIX]{x1D6FC}_{\mathfrak{p}},\unicode[STIX]{x1D6FD}_{\mathfrak{p}}\}\subset K^{\prime }$ be the two eigenvalues of 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}})$. Since they are Weil 
$p$-integers by Lemma 4.1.3 and 
$\det (\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{p}}))=p$, we have
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\mathfrak{p}}=\frac{p}{\unicode[STIX]{x1D6FC}_{\mathfrak{p}}}=\overline{\unicode[STIX]{x1D6FC}_{\mathfrak{p}}},\end{eqnarray}$$ where the bar denotes the complex conjugation on 
$\mathbb{Q}(\unicode[STIX]{x1D6FC}_{\mathfrak{p}})=\mathbb{Q}(\unicode[STIX]{x1D6FD}_{\mathfrak{p}})$.
Now consider only those 
$\mathfrak{p}$ such that, in addition, 
$(p):=\mathfrak{p}\,\cap \,\mathbb{Z}$ splits completely in 
$K^{\prime }$, a fortiori also in 
$\mathbb{Q}(\unicode[STIX]{x1D6FC}_{\mathfrak{p}})$; the resulting set is clearly principally abundant. Then, since 
$(p)$ is unramified in 
$\mathbb{Q}(\unicode[STIX]{x1D6FC}_{\mathfrak{p}})$, 
$\unicode[STIX]{x1D6FC}_{\mathfrak{p}}$ cannot be totally real, and generates a CM field. Let 
$\{{\wp}_{1},\ldots ,{\wp}_{m},\overline{{\wp}_{1}},\ldots ,\overline{{\wp}_{m}}\}$ be the set of primes of 
$\mathbb{Q}(\unicode[STIX]{x1D6FC}_{\mathfrak{p}})$ lying over 
$(p)$, where 
$2m=[\mathbb{Q}(\unicode[STIX]{x1D6FC}_{\mathfrak{p}}):\mathbb{Q}]$. Equation (4.2.1.1) further shows that, perhaps after renaming the primes, we get
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{\mathfrak{p}}\cdot \mathscr{O}_{\mathbb{Q}(\unicode[STIX]{x1D6FC}_{\mathfrak{p}})}={\wp}_{1}\cdots {\wp}_{m}\quad \text{and}\quad \unicode[STIX]{x1D6FD}_{\mathfrak{p}}\cdot \mathscr{O}_{\mathbb{Q}(\unicode[STIX]{x1D6FC}_{\mathfrak{p}})}=\overline{{\wp}_{1}}\cdots \overline{{\wp}_{m}}.\end{eqnarray}$$It follows that
$$\begin{eqnarray}\text{Tr}(\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}}))=\unicode[STIX]{x1D6FC}_{\mathfrak{p}}+\unicode[STIX]{x1D6FD}_{\mathfrak{p}}\end{eqnarray}$$ does not belong to any prime ideal of 
$\mathscr{O}_{K^{\prime }}$ lying over 
$(p)$. Since 
$\text{Tr}(\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}}))\in \mathscr{O}_{K_{f}}$, it belongs to no prime of 
$\mathscr{O}_{K_{f}}$ lying over 
$(p)$ either. This proves that 
$k(p)=0$ and completes the proof of Theorem 4.2.1.◻
5 Examples
For the dimensions of and the Hecke orbits in the spaces of newforms, we rely on the information published in the ‘
$L$-functions and modular forms database’ (LMFDB; http://www.lmfdb.org/). We compute the slope 
$\unicode[STIX]{x1D70E}$ by using the polynomials given in the LMFDB generating 
$K_{f}$; sometimes the Galois group of 
$\widetilde{K_{f}}/\mathbb{Q}$ and the discriminant of 
$K_{f}$ are also given in the LMFDB, in which case we utilise the information also.
All the computations are for 
$\unicode[STIX]{x1D6E4}_{0}(\mathfrak{n})$ (trivial Nebentypus). Recall that we say two normalised eigencuspforms 
$f$ and 
$g$ with complex coefficients are conjugate (and that they belong to the same conjugacy class) if there is 
$\unicode[STIX]{x1D70E}\in \operatorname{Aut}(\mathbb{C})$ such that 
$f^{\unicode[STIX]{x1D70E}}=g$.
5.1 $F=\mathbb{Q}$
The number of new normalised eigencuspforms 
$f$ of weight 
$2$ and level 
$N\leqslant 300$ is
$$\begin{eqnarray}\mathop{\sum }_{N=1}^{300}\dim _{\mathbb{ C}}S_{2}^{\text{new}}(\unicode[STIX]{x1D6E4}_{0}(N),\mathbb{C})=2074.\end{eqnarray}$$ The degree of the field 
$K_{f}$ in this range takes the values
$$\begin{eqnarray}k_{f}=[K_{f}:\mathbb{Q}]\in \{1,2,3,4,5,6,7,8,9,10,11,12,14,16,17\}.\end{eqnarray}$$ For 
$2070$ of the 
$2074$ forms 
$f$, parts (3) and (4) of Theorem 4.1.1 and Theorem 4.2.1 show that 
$M(f)$ has an abundant set of ordinary primes. As to the four exceptions, there is one conjugacy class of four forms of level 
$275$ without CM, under the name 275.2.1.h in the LMFDB, such that
$$\begin{eqnarray}K_{f}=\mathbb{Q}(\sqrt{3},\sqrt{11}),\end{eqnarray}$$ which is Galois with the Klein 
$4$-group. There is a bisecting element, and 
$\unicode[STIX]{x1D70E}_{\mathbb{Q}}(K_{f})=1/2$.
If 
$K_{f}^{\circ }\neq K_{f}$, then part (2) of Theorem 4.1.1 provides a principally abundant set of ordinary primes. If 
$K_{f}^{\circ }=K_{f}$, part (5) and the univariate (i.e. 
$t=1$) Sato–Tate equidistribution (proven in [Reference Harris, Shepherd-Barron and TaylorHST10] and [Reference Barnet-Lamb, Geraghty, Harris and TaylorBGHT11]) gives an abundant set of primes 
$p$ (of lower density at least 
$0.0794$) such that 
$k(p)\in \{0,1\}$; if in addition 
$f$ satisfies (RST), then part (6) will imply the abundance of ordinary (
$k(p)=0$) primes.
5.2 $F=\mathbb{Q}(\sqrt{2})$
This quadratic field has discriminant 
$8$ and class number 
$1$.
The LMFDB lists 
$1047$ new normalised eigencuspforms 
$f$ of parallel weight 
$(2,2)$ of level 
$\mathfrak{n}$ with 
$\mathbb{N}(\mathfrak{n})\leqslant 350$, and the degree of 
$K_{f}$ takes the values
$$\begin{eqnarray}k_{f}\in \{1,2,3,4,5,6,7,8,9,11,13\}.\end{eqnarray}$$ For 
$1031$ of the 
$1047$, parts (3) and (4) of Theorems 4.1.1 and 4.2.1 show that 
$M(f)$ has an abundant set of ordinary primes. That leaves 
$16$ exceptions.
(a) For the eight forms
$f$ in the classes 161.2-c and 161.3-c, we have $K_{f}=\mathbb{Q}(\sqrt{3},\sqrt{11})$, which is Galois with the Klein $4$-group. As $K_{f}$ is linearly disjoint from $\widetilde{F}=F=\mathbb{Q}(\sqrt{2})$, by Proposition 3.5.6(3), $\unicode[STIX]{x1D70E}_{\widetilde{F}}(K_{f})=\unicode[STIX]{x1D70E}_{\mathbb{Q}}(K_{f})=1/2$ and there is an element of $\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ bisecting $\operatorname{Hom}(K_{f},\overline{\mathbb{Q}})$.(b) For the eight forms
$f$ in 329.2-c and 329.3-c, $[K_{f}:\mathbb{Q}]=4$, $\widetilde{K_{f}}/\mathbb{Q}$ has group $D_{8}$, the image of $\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ is a Klein subgroup, and $\unicode[STIX]{x1D70E}_{F}(K_{f})=1/2$.
In both cases, if 
$K_{f}^{\circ }\neq K_{f}$, then part (3) of Theorem 4.1.1 gives a principally abundant set of ordinary primes. If 
$K_{f}^{\circ }=K_{f}$, part (5) gives (unconditionally) an abundant set of primes 
$p$ such that 
$k(p)\in \{0,1\}$; if 
$f$ satisfies (RST) in addition, then part (6) will imply the abundance of ordinary primes.
5.3 $F=\mathbb{Q}(\cos (2\unicode[STIX]{x1D70B}/7))$
This is the largest totally real subfield of the cyclotomic field 
$\mathbb{Q}(e^{2\unicode[STIX]{x1D70B}i/7})$. It is Galois over 
$\mathbb{Q}$ with group 
$\mathbb{Z}/3$ and has discriminant 
$49$ and class number 
$1$.
The LMFDB lists 
$1075$ new normalised eigencuspforms 
$f$ of parallel weight 
$(2,2,2)$ and level 
$\mathfrak{n}$ with 
$\mathbb{N}(\mathfrak{n})\leqslant 800$, and the degree of 
$K_{f}$ takes the values
$$\begin{eqnarray}k_{f}\in \{1,2,3,4,5,6,7,8\}.\end{eqnarray}$$ For 
$1048$ of the 
$1075$, parts (3) and (4) of Theorems 4.1.1 and 4.2.1 show that 
$M(f)$ has an abundant set of ordinary primes. As to the 
$27$ exceptions, for 
$f$ in the classes 448.1-a, 547-1-c, 547.2-c, 547.3-c, 729.1-c, 729.1-d, 743.1-a, 743.2-a and 743.3-a, we have 
$F=K_{f}$ and 
$\unicode[STIX]{x1D70E}_{F}(K_{f})=2/3$.
For each of these 
$f$, if 
$K_{f}^{\circ }\neq K_{f}$, in which case 
$K_{f}^{\circ }=\mathbb{Q}$, then part (3) of Theorem 4.1.1 would give a principally abundant set of ordinary primes. If 
$K_{f}^{\circ }=K_{f}$, then the theorem only provides a principally abundant set of primes 
$p$ such that 
$k(p)\in \{0,1\}$.
5.4 $F=\mathbb{Q}(\cos (\unicode[STIX]{x1D70B}/8))$
This largest totally real subfield of 
$\mathbb{Q}(e^{2\unicode[STIX]{x1D70B}i/16})$ has discriminant 
$2048=2^{11}$ and class number 
$1$, and is Galois over 
$\mathbb{Q}$ with group 
$\mathbb{Z}/4$. The non-trivial proper subgroup of 
$\mathbb{Z}/4$ allows a richer array of examples in which Theorems 4.1.1 and 4.2.1 fall short.
The LMFDB lists 
$6185$ new normalised eigencuspforms 
$f$ of parallel weight 
$(2,2,2,2)$ and level 
$\mathfrak{n}$ with 
$\mathbb{N}(\mathfrak{n})\leqslant 607$, and the degree of 
$K_{f}$ takes the values
$$\begin{eqnarray}k_{f}\in \{1,2,\ldots ,12\}\cup \{14,15,16,17,18,19,20,22,24,25,26,27,28,30,33,39,42\}.\end{eqnarray}$$ For 
$6037$ of the 
$6185$, parts (3) and (4) of Theorems 4.1.1 and 4.2.1 show that 
$M(f)$ has an abundant set of ordinary primes. We are left with The 
$136$ confirmed exceptions and 
$12$ possible exceptions.
(a) For the
$24$ forms $f$ in the classes 392.1-f, 392.2-f, 544.1-$\ell$, 544.2-$\ell$, 544.3-$\ell$ and 544.4-$\ell$, $K_{f}$ is Galois over $\mathbb{Q}$ with the Klein $4$-group and linearly disjoint from $F$ over $\mathbb{Q}$. There is a bisecting element and $\unicode[STIX]{x1D70E}_{F}(K_{f})=\unicode[STIX]{x1D70E}_{\mathbb{Q}}(K_{f})=1/2$ (cf. exceptions in $F=\mathbb{Q}$ and (a) in $F=\mathbb{Q}(\sqrt{2})$).(b) For the
$20$ forms $f$ in the classes 81.1-c, 289.1-f, 289.4-f, 578.1-h and 578.4-h, $k_{f}=4$ and $\widetilde{K_{f}}$ is Galois over $\mathbb{Q}$ with group $D_{8}$, so $\unicode[STIX]{x1D70E}_{\mathbb{Q}}(K_{f})=0$. However, the image of $\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ is a Klein $4$-group, $\unicode[STIX]{x1D70E}_{F}(K_{f})=1/2$, and there is a bisecting element (cf. exceptions (b) in $F=\mathbb{Q}(\sqrt{2})$).(c) For the
$24$ forms $f$ in 289.7-k, 289.8-k, 289.9-k and 289.10-k, $K_{f}$ is Galois with group $\mathbb{Z}/6\mathbb{Z}$, and $\unicode[STIX]{x1D70E}_{\mathbb{Q}}(K_{f})=0$. However, the image of $\operatorname{Gal}(\overline{\mathbb{Q}}/F)$ is the subgroup $2\mathbb{Z}/6\mathbb{Z}$, $\unicode[STIX]{x1D70E}_{F}(K_{f})=1/2$, and there is a bisecting element.(d) For the
$68$ forms $f$ in $17$ classes (eight in level norm 289, one in 324 and eight in 578), we have $K_{f}=F$. Thus $\unicode[STIX]{x1D70E}_{F}(K_{f})=3/4$ and there is no bisecting element (cf. exceptions in $F=\mathbb{Q}(\cos (2\unicode[STIX]{x1D70B}/7))$).(e) For the
$12$ forms $f$ in 392.1-g and 392.2-g, $K_{f}$ has degree $6$ but is not cyclic over $\mathbb{Q}$ (hence qualitatively different from (c)). So far we have observed $\unicode[STIX]{x1D70E}_{\mathbb{Q}}(K_{f})=0$, $\unicode[STIX]{x1D70E}_{F}(K_{f})\leqslant 1/2$, and there is a bisecting element.
For the 
$f$ in (d), part (5) of Theorem 4.1.1 provides an abundant set of primes 
$p$ such that 
$k(p)\in \{0,1\}$ unconditionally.
In the remaining cases, we have 
$k(p)\leqslant k_{f}/2$ (respectively, 
$k(p)<k_{f}/2$) for a principally abundant (respectively, abundant) set of primes 
$p$ by part (2) (respectively, by part (5)), unconditionally. If 
$f$ satisfies (RST) in addition, then part (6) will provide an abundant set of ordinary (
$k(p)=0$) primes.
6 General motivic coefficients
6.1 Conjectures in a general setting
Let 
$X$ be a projective variety of dimension 
$d$ over a number field 
$F$, 
$j:U{\hookrightarrow}X$ the inclusion of a smooth dense open subset, and 
$\unicode[STIX]{x1D70B}:\mathscr{Y}\longrightarrow U$ a projective smooth scheme. For each integer 
$i$ and every prime number 
$\ell$, form the local system on 
$U$,
$$\begin{eqnarray}\mathscr{L}_{\ell }^{i}=R^{i}\unicode[STIX]{x1D70B}_{\ast }(\mathbb{Q}_{\ell }),\end{eqnarray}$$and the intermediate extension,
$$\begin{eqnarray}\overline{\mathscr{L}}_{\ell }^{i}=j_{!\ast }(\mathscr{L}_{\ell }^{i}[d])[-d].\end{eqnarray}$$Conjecture 6.2. Let the notation be as above, and let 
$k$ be any integer.
(a) There exists a pure Grothendieck homological motive
$\mathfrak{M}=\mathfrak{M}^{k,i}$ whose $\ell$-adic étale realisation $\mathfrak{M}_{\ell }$ is isomorphic to $H^{k}(X\otimes _{F}F^{s},\overline{\mathscr{L}}_{\ell }^{i})$ for every $\ell$.Footnote 6
(a’) There exists an André motive
$M=M^{k,i}$ such that $M_{\ell }\simeq H^{k}(X\otimes _{F}F^{s},\overline{\mathscr{L}}_{\ell }^{i})$ for every $\ell$.
For the following statements, we assume that (
$\text{a}^{\prime }$) is true.Footnote 7
Let 
$e$ be an idempotent endomorphism of 
$M$ in the category of André motives (with 
$\mathbb{Q}$-coefficients) and let 
$R$ be the direct summand of 
$M$ cut out by 
$e$, with the 
$\ell$-adic étale realisation 
$R_{\ell }$.
(b) The
$\ell$-adic Galois representations $R_{\ell }$ form a strictly compatible system.(c) There exists a finite set
$S=S(\unicode[STIX]{x1D70B},i,k,e)$ of primes of $F$ such that, for every prime $\ell$ and $\mathfrak{p}$ outside $S$ and not dividing $\ell$, we have $$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}},R_{\ell })\geqslant \text{HTP}(R_{\ell }).\end{eqnarray}$$(d) For infinitely many primes
$\mathfrak{p}$ of $F$ and every prime number $\ell$, we have $$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}},R_{\ell })=\text{HTP}(R_{\ell }).\end{eqnarray}$$
We note that, by Corollary 2.2.3, the Hodge–Tate polygon of 
$R_{\ell }$ at 
$\unicode[STIX]{x1D706}$ on the right-hand sides is independent of the 
$\ell$-adic place 
$\unicode[STIX]{x1D706}$ of 
$F$.
Proposition 6.2.1. Assume that part (a) of Conjecture 6.2 is true, and let 
$M$ be the André motive of 
$\mathfrak{M}$. Assume also that the idempotent 
$e$ is an algebraic cycle, and let 
$\mathfrak{R}$ be the Grothendieck motive cut out by 
$e$ from 
$\mathfrak{M}$. Then:
(1) parts (b) and (c) of the conjecture are also true for the André motive
$R$ of $\mathfrak{R}$;(2) if, in addition, there exists a finite extension
$F^{\prime }$ of $F$ such that $R_{\ell }$ restricts to an abelian Galois representation of $F^{\prime }$ for some (equivalently, every) prime $\ell$, then for a principally abundant set of primes $\mathfrak{p}$ of $F$, we have and, in particular, part (d) of the conjecture is also true for$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}},R_{\ell })=\text{HTP}(R_{\ell }),\end{eqnarray}$$$R$.
Proof. (1) The key point is that under the assumptions, we can use the crystalline realisation to compute the two polygons in part (c). Namely, for almost all 
$\mathfrak{p}$, we have the free 
$W(k(\mathfrak{p}))$-module 
$\mathfrak{R}_{\text{cris},\mathfrak{p}}$, equipped with the Hodge filtration and the crystalline Frobenius 
$\unicode[STIX]{x1D719}_{\text{cris},\mathfrak{p}}$ (induced from those on 
$\mathfrak{M}$).
Then, on the one hand, by Katz and Messing [Reference Katz and MessingKM74, Theorem 2], 
$\unicode[STIX]{x1D719}_{\text{cris},\mathfrak{p}}^{[k(\mathfrak{p}):\mathbb{F}_{p}]}$ has the same (multiset of) eigenvalues as the 
$\ell$-adic Frobenius 
$\operatorname{Frob}_{\mathfrak{p}}$ on 
$\mathfrak{R}_{\ell }$. Therefore they have the same Newton polygons. This also proves (b).
On the other hand, by Corollary 2.2.3, the Hodge–Tate polygon of 
$R_{\ell }=\mathfrak{R}_{\ell }$ also coincides with the Hodge polygon of 
$\mathfrak{R}_{\text{cris},\mathfrak{p}}$, which by definition is equal to the Hodge polygon of the de Rham realisation 
$\mathfrak{R}_{\text{dR}}$.
Now the statement (c) follows from Mazur’s theorem [Reference MazurMaz73] applied to 
$\mathfrak{R}_{\text{cris},\mathfrak{p}}$. In summary,
$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{\mathfrak{p}},R_{\ell })=\text{NP}(\unicode[STIX]{x1D719}_{\text{cris},\mathfrak{p}}|_{\mathfrak{R}_{\text{cris},\mathfrak{p}}})\geqslant HP(\mathfrak{R}_{\text{cris},\mathfrak{p}})=HP(\mathfrak{R}_{\text{dR}})=\text{HTP}(R_{\ell }).\end{eqnarray}$$ For (2), let 
$\widetilde{F^{\prime }}$ be the normal closure of 
$F^{\prime }$ over 
$\mathbb{Q}$ and replace 
$F$ with 
$\widetilde{F^{\prime }}$, so that 
$\unicode[STIX]{x1D70C}_{\ell }$ is abelian. Since 
$\unicode[STIX]{x1D70C}_{\ell }$ is 
$\mathbb{Q}$-rational and Hodge–Tate, by a theorem of Serre [Reference SerreSer98, § III.2.3], it is associated with a 
$\mathbb{Q}$-rational representation 
$\unicode[STIX]{x1D719}_{0}:S_{\mathfrak{m}}\longrightarrow \text{GL}_{V_{0}}$, where 
$V_{0}$ is a 
$\mathbb{Q}$-form of 
$R_{\ell }$ and 
$\mathfrak{m}$ is a modulus of 
$F$.
The restriction of 
$\unicode[STIX]{x1D70C}_{0}$ to 
$T_{\mathfrak{m}}\subseteq S_{\mathfrak{m}}$ can then be diagonalised: 
$\unicode[STIX]{x1D70C}_{0}|_{T_{\mathfrak{m}}}\otimes \overline{\mathbb{Q}}=\unicode[STIX]{x1D712}_{1}\oplus \cdots \oplus \unicode[STIX]{x1D712}_{N}$ and
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{i}=\mathop{\sum }_{[\unicode[STIX]{x1D70E}]}n_{\unicode[STIX]{x1D70E}}(i)[\unicode[STIX]{x1D70E}],\end{eqnarray}$$ where 
$[\unicode[STIX]{x1D70E}]$ ranges over the characters of 
$T_{\mathfrak{m}}$ arising from the embeddings 
$\unicode[STIX]{x1D70E}$ of 
$F$ into 
$\overline{\mathbb{Q}}$.
Since we already know part (b) of the conjecture, we can choose a rational prime 
$\ell$ that splits completely in 
$F$. Then we can identify the 
$\unicode[STIX]{x1D70E}$ with the embeddings of 
$F$ into 
$\mathbb{Q}_{\ell }$, once an embedding 
$\unicode[STIX]{x1D704}_{\ell }:\overline{\mathbb{Q}}\longrightarrow \overline{\mathbb{Q}}_{\ell }$ has been fixed. Under this identification, the multiset of the Hodge–Tate weights of 
$\unicode[STIX]{x1D70C}_{\ell }$ at any 
$\ell$-adic place 
$\unicode[STIX]{x1D706}:F\longrightarrow \overline{\mathbb{Q}}_{\ell }$ is 
$\{{n_{\unicode[STIX]{x1D70E}_{0,\unicode[STIX]{x1D706}}(i)}\}}_{i=1,\ldots ,N}$, where 
$\unicode[STIX]{x1D70E}_{0,\unicode[STIX]{x1D706}}$ is the (unique) embedding such that 
$\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D70E}_{0,\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}$, by [Reference SerreSer98, Proposition 2, § III.1.1].
On the other hand, let 
$\mathfrak{p}$ be any prime of 
$F$ lying over any rational prime 
$p\neq \ell$ that splits completely in 
$F$. We can also identify the embeddings 
$\unicode[STIX]{x1D70E}:F\longrightarrow \overline{\mathbb{Q}}$ with the embeddings into 
$\mathbb{Q}_{p}$, once we fix a 
$p$-adic place of 
$\unicode[STIX]{x1D704}_{p}:\overline{\mathbb{Q}}\longrightarrow \overline{\mathbb{Q}}_{p}$. Then the multiset of the 
$p$-adic valuations of 
$\unicode[STIX]{x1D70C}_{\ell }(\operatorname{Frob}_{\mathfrak{p}})$ is given by 
$\{{n_{\unicode[STIX]{x1D70E}_{1,\mathfrak{p}}(i)}\}}_{i=1,\ldots ,N}$, where 
$\unicode[STIX]{x1D704}_{p}\circ \unicode[STIX]{x1D70E}_{1,\mathfrak{p}}$ is the 
$p$-adic place 
$\mathfrak{p}$; see [Reference SerreSer98, Corollary 2, § II.3.4].
Since 
$\unicode[STIX]{x1D70C}_{0}$ is 
$\mathbb{Q}$-rational, the two multisets are independent of 
$\unicode[STIX]{x1D706}|\ell$ and 
$\mathfrak{p}|p$, respectively, and are equal to each other. This proves (2).◻
6.3 Hilbert modular forms of motivic weights
Let us specialise to the Baily–Borel compactification 
$X$ of the Hilbert modular variety 
$U$ defined over 
$\mathbb{Q}$ (of some level 
$\mathfrak{n}$) for the totally real field 
$F$. For 
$\mathscr{Y}$, we take the universal abelian scheme 
$\unicode[STIX]{x1D70B}:\mathscr{A}\longrightarrow U$ and the fibred product 
$\mathscr{A}\times _{U}\cdots \times _{U}\mathscr{A}$ over 
$U$.
Recall that a motivic weight 
$k=(k(\unicode[STIX]{x1D70F}))_{\unicode[STIX]{x1D70F}:F\longrightarrow \mathbb{R}}$ is a collection of integers 
$k(\unicode[STIX]{x1D70F})\geqslant 2$ of the same parity, for each real embedding 
$\unicode[STIX]{x1D70F}$ of 
$F$.
Proposition 6.3.1. Let 
$f$ be a new cuspform of any motivic weight 
$k\neq (2,\ldots ,2)$. Then:
Proof. The first part follows immediately from Proposition 6.2.1 and the motivic construction of Galois representations (see Blasius and Rogawski [Reference Blasius and RogawskiBR93] and the references therein). The second part follows from Proposition 6.2.1. ◻
In the case where 
$\mathscr{Y}=\mathscr{A}$ is the universal abelian scheme, the cohomology decomposes into the parts cut out by 
$f$ of parallel weight 
$(3,\ldots ,3)$.
Definition 6.3.2. Let 
$G$ be a group acting on a finite set 
$X$. For 
$g\in G$, we define 
$\unicode[STIX]{x1D706}^{\prime }(g,X)$ to be the smallest of the cardinalities of the 
$g$-orbits in 
$X$; we denote by 
$\unicode[STIX]{x1D706}^{\prime }(G,X)$ the supremum of 
$\unicode[STIX]{x1D706}^{\prime }(g,X)$ as 
$g$ ranges over 
$G$.
Given two number fields 
$F$ and 
$K$, we define
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{F}^{\prime }(K):=1-\frac{\unicode[STIX]{x1D706}^{\prime }(\operatorname{Gal}(\overline{\mathbb{Q}}/F),\operatorname{Hom}(K,\overline{\mathbb{Q}}))}{[K:\mathbb{Q}]}\in \mathbb{Q}\cap [0,1].\end{eqnarray}$$The proof of the following proposition is similar to that of Proposition 3.5.5, and is omitted.
Proposition 6.3.3. If 
$K^{\prime }$ is a subfield of 
$K$, then 
$\unicode[STIX]{x1D70E}_{F}^{\prime }(K^{\prime })\leqslant \unicode[STIX]{x1D70E}_{F}^{\prime }(K)$.
Definition 6.3.4. Let 
$d\geqslant 1$, 
$k\geqslant 1$ and 
$i\in [0,k]$ be integers. We define the multiset (and the corresponding Newton polygon)
$$\begin{eqnarray}P^{\prime }(d;k,i):=(\{0,2\}^{\otimes d})^{\oplus (k-i)}\oplus (\{1,1\}^{\otimes d})^{\oplus i}.\end{eqnarray}$$ This is the polygon obtained by vertically stretching 
$P(d;k,i)$ by a factor of 
$2$.
Proposition 6.3.5. Let 
$f$ be a new normalised Hilbert eigencuspform of level 
$\mathfrak{n}\subseteq \mathscr{O}_{F}$ and parallel weight 
$(3,\ldots ,3)$. Assume that 
$f$ is not of CM type, and denote by 
$\widetilde{F}$, 
$F^{\circ }$, 
$\widetilde{F^{\circ }}$, 
$K_{f}$ and 
$K_{f}^{\circ }$ the number fields defined in the manner of §§ 3.1 and 3.2; 
$\unicode[STIX]{x1D706}$ is a prime of 
$K_{f}$ lying over a rational prime 
$\ell$ splitting completely in 
$K_{f}$.
Denote by 
$M(f)$ the André motive (see Remark 2.2.6), whose realisations give the part of the intersection cohomology of the Hilbert modular variety corresponding to 
$\{\unicode[STIX]{x1D70E}(f)\}_{\unicode[STIX]{x1D70E}}$, where 
$\unicode[STIX]{x1D70E}$ ranges over all the embeddings of 
$K_{f}$ into 
$\overline{\mathbb{Q}}$.
(1) For all rational primes
$p$ that split completely in $F$ (equivalently, in $\widetilde{F}$) and are unramified in $K_{f}$, there exists an integer $k(p)\in [0,k_{f}]$ such that (Here$$\begin{eqnarray}\text{NP}(\operatorname{Frob}_{p}\!|_{M(f)})=P^{\prime }(d;k_{f},k(p)).\end{eqnarray}$$$k_{f}=[K_{f}:\mathbb{Q}]$ and we refer to Definition 3.4.6 for the right-hand side.)For the following parts, we only consider the primes splitting completely in
$F$ and unramified in $K_{f}$.(2) For a principally abundant set of primes
$p$, we have $k(p)\leqslant k_{f}-(k_{f}/k_{f}^{\circ })$.(3) For an abundant set of primes
$p$, we have $k(p)\leqslant k_{f}\cdot \min (\unicode[STIX]{x1D70E}_{\widetilde{F}}^{\prime }(K_{f}),\unicode[STIX]{x1D70E}_{\widetilde{F^{\circ }}}^{\prime }(K_{f}^{\circ }))$.
Proof. (1) The proof is similar to that of part (1) of Theorem 4.1.1. The only difference is that the linear (respectively, constant) coefficient of the polynomial (cf. (4.1.1.3))
$$\begin{eqnarray}X^{2}-\text{Tr}(\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{ p}}))X+\det (\unicode[STIX]{x1D70C}(\operatorname{Frob}_{\mathfrak{p}}))\end{eqnarray}$$ has 
$p$-adic valuation 
$=2$ (respectively, a non-negative integer or infinity) for those 
$p$ considered.
(2) We find a set of primes 
$\mathfrak{p}$ of 
$\widetilde{F^{\circ }}$ (respectively, of 
$\widetilde{F}$) of density equal to 
$1$ such that 
$a_{\mathfrak{p}}=\text{Tr}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D706}}(\operatorname{Frob}_{\mathfrak{p}}))$ is not divisible by at least one 
$p$-adic prime 
${\wp}$ of 
$\widetilde{F^{\circ }}$ (respectively, of 
$\widetilde{F}$), where 
$(p)=\mathfrak{p}\cap \mathbb{Z}$.
If 
$a_{\mathfrak{p}}$ is divisible by all the 
$p$-adic places, then it belongs to 
$p\cdot \mathscr{O}_{K_{f}^{\circ }}$ (respectively, to 
$p\cdot \mathscr{O}_{K_{f}}$). Since 
$M(f)$ has pure motivic weight 
$2$, for any archimedean place 
$v|\infty$, we have 
$|a_{\mathfrak{p}}|_{v}\leqslant 2p$, hence the algebraic integer 
$|a_{\mathfrak{p}}/p|_{v}\leqslant 2$, and we form the finite set
$$\begin{eqnarray}S=\{\unicode[STIX]{x1D6FC}^{2}:|\unicode[STIX]{x1D6FC}|_{v}\leqslant 2\text{ for all archimedean }v\text{ of }K_{f}^{\circ }\;(\text{respectively, }K_{f})\}.\end{eqnarray}$$ By the assumption that 
$f$ is not of CM type, the connected algebraic monodromy group 
$G_{f,\unicode[STIX]{x1D706}}^{\circ }$ is the full 
$\text{GL}_{2}$ over 
$(K_{f})_{\unicode[STIX]{x1D706}}$, and the regular map of algebraic varieties
$$\begin{eqnarray}\text{Tr}(\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}^{\circ }}^{\otimes 2}\otimes \det (\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}^{\circ }})^{-1}):\text{GL}_{2}\longrightarrow \mathbb{A}^{1}\end{eqnarray}$$ (respectively, with 
$\unicode[STIX]{x1D706}^{\circ }$ replaced with 
$\unicode[STIX]{x1D706}$) is non-constant, as 
$\unicode[STIX]{x1D70C}_{f,\unicode[STIX]{x1D706}^{\circ }}$ has Hodge–Tate weights both 
$0$ and 
$2$ at all 
$\ell$-adic places. Therefore the inverse image of 
$S\subseteq (K_{f}^{\circ })_{\unicode[STIX]{x1D706}}$ (respectively, 
$S\subseteq (K_{f})_{\unicode[STIX]{x1D706}}$) has Haar measure 
$0$. This proves the statement for density equal to 
$1$.
(3) With (2), we can now proceed with the Chebotarev-type argument, similar to the one in parts (4) and (4
$^{\prime }$) of Theorem 4.1.1. We omit the details.◻
Acknowledgements
The author has benefited from discussions with many mathematicians. He particularly thanks R. Taylor for his comments on the Sato–Tate equidistributions (known and conjectural) and his suggestion of using the uni- and bivariate distributions (which are known or accessible) in order to go beyond the Weil–Ramanujan–Peterson (‘square-root’) bound.
He also thanks J.-P. Serre for pointing out that our (SST) fits within his theoretical framework developed in [Reference SerreSer12]; M. Harris for his comments on the bivariate Sato–Tate conjecture; S. Morel and Y. André for discussions around André motives; L. Illusie and F. Orgogozo about constructibility theorems; R. Boltje for a discussion about tensor inductions; and N. Katz and B. Mazur for various suggestions.
Finally, he thanks the anonymous referees for their suggestions for improving the exposition.
