1. INTRODUCTION
Detailed information on the complex condition of dense plasmas is generally obtained by modern methods of X-ray spectroscopy (Renner et al., 2002). Thomson scattering of intense laser radiation (Kunze, 1968; Sheffield, 1975) in the optical range of the electromagnetic spectrum is being used since a long time for accurate measurements of density and temperature of low density plasmas as well as plasmas for inertial confinement fusion research (Glenzer et al., 1997). Recently an extension of this method to X-rays has been proposed (Landen et al., 2001) and applied to the characterization of solid-density and superdense plasmas (Glenzer et al., 2003; Gregori et al., 2003, 2004; Höll et al., 2004; Redmer et al., 2005). The scattering of electromagnetic waves by charged particles is therefore a tool for the diagnostics of low as well as high density plasmas providing a means for the simultaneous determination of various plasma parameters as e.g., temperature and density.
High-energy-density plasmas can be created by focusing intense beams of energetic heavy ions into solid targets. If the Bragg peak is behind the target, the energy deposition of the ions is very uniform over an extended volume (Hoffmann et al., 2005). When the beam diameter is larger than the target size, a dynamic confinement scheme allows to heat the target quasi-isochorically up to pulse durations of about 100 ns (Kozyreva et al., 2003; Lomonosov & Tahir, 2006). The target is thus transformed into a high energy density state in the so-called regime of warm dense matter (Lee et al., 2002). It is proposed to investigate this plasma with the method of spectrally resolved X-ray scattering with the PHELIX laser for the laser-plasma X-ray source (Neumayer et al., 2005), and to measure the intensity, spectral, and angular distribution of the scattered X-rays by the heated sample (Kozyreva et al., 2003; Riley & Rosmej, 2004; Hoffmann et al., 2005). Due to the small Thomson scattering cross section of 6.65 × 10−25 cm2 there is a need for an intense source of X-rays. The number of photons that are necessary for scattering experiments is more than 1015 photons in total (Landen et al., 2001; Riley & Rosmej, 2004). Simultaneously the spectral broadening Δλ/λ of the probe radiation must be smaller than

[eV] in order to resolve the Doppler broadening due to the scattering (Sheffield, 1975). A typical temperature of 2 eV in ion-beam produced plasmas corresponds to a broadening of Δλ/λ = 0.006. This requirement can be fulfilled by the thermally induced Heα line emission of medium-Z plasmas. The large number of photons and the high temperature that is needed, that the plasma mainly emits the Heα-line demands the use of a nanosecond high energy laser system, as e.g., the PHELIX laser, that will provide a laser pulse up to a kilojoule in a nanosecond. The sample will be heated by the SIS100 ion beam (Lomonosov & Tahir, 2006). When this intense laser is focused onto a medium-Z target, thermally induced Heα (1s2p1P1 − 1s2 1S0) line radiation in the keV range will be emitted. Together with the dielectronic satellites (1s2lnl′ − 1s22l), a narrow band of line radiation is formed. Therefore these X-rays can be used as a probe for warm dense matter.
The scattered radiation can be dispersed spectrally by a highly reflecting Bragg-crystal (e.g., a highly oriented pyrolytic graphite (HOPG) crystal) and can be detected with an X-ray CCD detector. The radiation of this source is narrowband, but not monochromatic. The underlying dielectronic satellites of Heα on the red side of this line lead to an asymmetric broadening in weak resolving spectrometers. This overlaps with the red-shifted scattered lines. Since the probe radiation is not monochromatic, the dielectronic satellites play an important role in the probe development for collective scattering measurements in dense plasmas (Urry et al., 2006). The scattering on the plasma electrons of the sample results in a red-shift due to Compton scattering. Additionally, there is a Doppler-shifted Thomson scatter feature that leads to a broadening of the Compton scattered line. There is no blue-shifted peak since the structure factors on either side of the central wavelength are related by S(−ω,k) ∝ S(ω,k)exp(−ħω/kBTe) (Gregori et al., 2003). Figure 1 shows a scatter profile of monoenergetic Cl-Heα radiation on heated hydrogen. The structure factor S(k,ω) is calculated in the random phase approximation following (Gregori et al., 2003). It was assumed that the monoenergetic Cl-Heα line with an energy of 2.789 keV (λ = 4.4447 Å) is scattered on an ion beam heated hydrogen sample with ne = 0.6 × 1023 cm−3 and various Te. The scattering angle is θ = 160°, this corresponds to a scattering factor of α = 0.26…0.5. The scattering factor is defined as α = 1/kλs with the wave vector k and the screening length λs. If α is >1, the scattering takes place in the collective scattering regime and if α < 1 in the non-collective regime. In case of ideal plasmas the screening length λs develops to the Debye length (Gregori et al., 2003). The sample plasmas considered here have strong coupling parameters Γ > 1, where Γ is the ratio of the potential and kinetic energy. Plasmas with Γ > 1 are known as strongly coupled or non-ideal. Therefore we have to use the parameter λs. The calculated spectrum was convoluted with a gaussian instrument response function with a full width at half maximum (FWHM) of 25 eV, that corresponds to a resolution of E/ΔE ≈ 100. This resolution is a typical value in current X-ray scattering experiments, e.g. (Glenzer et al., 2003). There the fitting to the measured X-ray scattered spectrum was done with a single wavelength as the probe. The energy shift of the Compton-downshifted peak is in the range of 10–30 eV, that is where the unshifted dielectronic satellites (e.g., the prominent jk-satellites 1s2p2 2D − 1s22p 2P) with an energy of 2.756 keV (λ = 4.4977 Å) are located. Thus both features overlap and can lead to misinterpretations of the spectrum!

Theoretical X-ray scattering spectrum. The image shows the dynamic structure factors S(k,ω) convoluted with a gaussian instrument response of 25 eV FWHM. The probe radiation was assumed to be Cl-Heα (E = 2.789 keV) that is scattered on an ion beam heated hydrogen sample with ne = 0.6 × 1023 cm−3 and various temperatures Te. The scattering angle is θ = 160° and therefore the scattering parameter α is between 0.26 and 0.5, that is less than 1. Thus the scattering is inelastic and the width of the red-shifted free electron component directly shows the temperature of the sample.
Since in real experiments there are large shot-to-shot fluctuations in the laser intensity and thus in the probe plasma parameters, it is necessary to measure the probe spectrum with a high spectral resolution simultaneously with the scatter measurement. As a first step, in this paper, we concentrate on the determination of the dielectronic satellites of the probe as they appear in the HOPG-spectrometer and were measured with another highly resolving spectrometer. We have used a focusing spectrometer with spatial resolution (FSSR) (Faenov et al., 1994; Rosmej et al., 2002a, 2002b; Skobelev et al., 1995) that observed the source plasma simultaneously with a HOPG-crystal spectrometer. With this set-up it was guaranteed that the spectrum was known with a high accuracy. We have developed a line calculation model that allows to calculate the probe spectrum as it would have been seen by the HOPG-spectrometer out of the measured spectrum of the highly resolving focusing spectrometer. After describing the experimental set-up in the next section, we explain the line calculation method in Section 3. In Section 4 the experimental results are presented. A comparison of the measured spectra and the line calculation model reveals the role of dielectronic satellites in general. The fitting of the line calculation model to the highly resolved spectrum and then calculating the weaker resolved HOPG-spectrum matches well with the experimental results. In Section 5 we show the importance of the probe spectrum for X-ray scattering experiments. The paper finalizes with a conclusion and outlook.
2. EXPERIMENTAL ARRANGEMENT
The experiments were done with the nanosecond high energy laser for heavy ion experiments nhelix at the Gesellschaft für Schwerionenforschung mbH (GSI). nhelix is a Nd:Glass laser system with a wavelength of λ = 1064 nm and a laser pulse duration of 14 ns FWHM. Details of the laser system can be found in Schaumann et al. (2005). The beam with an energy of 45 J was focused by a f/2 lens onto the target. The laser spot size on target was measured to be 200 μm which corresponds to an intensity of 1013 W/cm2. To prevent target debris from damaging the lens, the target was rotated by 45° with respect to the laser beam. The target consisted of polyvinyl chloride (PVC), a chlorine doped material. As mentioned before, the number of photons is critical in plasma scattering experiments and the spectrally dispersing element needs to be a highly reflective crystal. The material with the highest integral reflectivity is graphite (Renninger, 1954) and therefore we used a flat highly oriented pyrolytic graphite (HOPG) crystal (Moore, 1973) in a mosaic focusing configuration (Sánchez del Rìo et al., 1998). The peak reflectivity of HOPG is above 20%, much higher compared to mica (1%), or quartz (0.1%). With the help of the mosaic focusing and a near point like source, the spectral resolution of this spectrometer reached up to λ/Δλ ≈ 103.
This resolution is not enough to resolve all dielectronic satellites. Thus a focusing spectrometer with spatial resolution (FSSR) was used like in previous experiments with the nhelix laser (Rosmej et al., 2001a, 2001b, 2002a, 2002b, 2005). The spherically bent mica crystals (2d = 19.88 Å, bending radius R = 150 mm) allow a high spectral resolution up to λ/Δλ = 5000, and simultaneously a high spatial resolution up to Δz = 10 μm. This design combines the Bragg reflection of a crystal lattice with the optical reflection of a spherical mirror with a large aperture. The detector is placed on the Rowland circle. X-rays with the same wavelength coming out of the source are directed onto a point, as shown in Figure 2a. The image in the detector plane is independent of the source size. In the sagittal plane, perpendicular to the spectral dispersing (meridional) plane, a one-dimensional (1D) image of the source is formed. This is shown in Figure 2b. This scheme is called FSSR-1D (Skobelev et al., 1995) and does not need any slit or pinhole for the spatial resolution. Additionally, the mica crystals allow high reflection orders up to m ≈ 20. In the FSSR-1D scheme, the magnification M can be calculated directly from the wavelength:
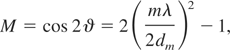
where ϑ is the Bragg angle, m is the reflection order, λ the wavelength, and dm the layer spacing of the crystal.

The FSSR-1D scheme. (a) shows the image formation in the meridional (spectral dispersing) plane, an extended source S is focused to a small size S′. (b) shows the image formation in the perpendicular plane. The image z is scaled to z′ = Mz following Eq. (1).
The line radiation of He-like chlorine was measured in fourth order with the FSSR (ϑ = 63°) and in first order with the HOPG-spectrometer (ϑ = 41.5°). The X-rays were detected by Kodak DEF-5 films (Kodak Molecular Imaging Systems, New Haven, CT). To prevent visible light from illuminating the films, the film boxes were covered with two layers of 1 μm polypropylene foil (C3H6) metalized with 0.1 μm Al from each side.
The spectra were scanned with a high-resolution drum-scanner (Dunvegan-Eurocore HI-SCAN) and were corrected for the scanner response with a calibrated gray scale from Kodak, for the film response (Henke et al., 1986), filter response, crystal reflectivity, and geometrical effects. The space resolved spectrum of the FSSR was averaged over the whole range in z-direction for allowing a comparison with the spectrum measured by the HOPG-spectrometer.
3. LINE IDENTIFICATION
The spectral emission is dominated by the resonance line w and its dielectronic satellites 1s2lnl′ → 1s2nl′. The notation of the 1s2l2l′-spectral lines follows the notation of Gabriel (1972). A detailed identification of the measured spectra was done with the development of a simple model for the dielectronic recombination (Q-spectrum) of helium-like ions, and inner shell excitation of lithium-like ions (K-spectrum). The present model is a specific case of the general description of satellite transitions (Rosmej, 2001). All transitions are modeled with an excitation followed by a spontaneous decay. This reduces the number of energy levels dramatically, because only the population densities of the ground states are important. A schematic energy level diagram is shown in Figure 3.

Schematic energy levels of He- and Li-like ions. a − v are dielectronic satellites with the notation of Gabriel (Gabriel, 1972), w is the resonance line 1s2p 1P1 → 1s2 1S0, y the intercombination line 1s2p 3P1 → 1s2 1S0, DC designates the dielectronic capture, Γ autoionisation and IS inner shell excitation.
This simple model allows the estimation of the electron temperature from the line ratio of the optically thin lines jk and the higher order dielectronic satellites 1s2l3l′ → 1s23l′. The necessary atomic data was calculated with the MZ-Code (Vainshtein & Safronova 1978, 1980) including all satellites up to 1s2l4l′.
If the collisional operator is set equal to zero, the general spectral distribution of satellite transitions (Rosmej, 2001) reduces to the Q-K-spectrum:
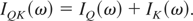
The spectral distribution of a Q-spectrum is given by
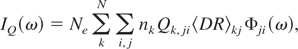
and the distribution of a K-spectrum by
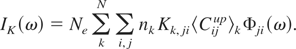
Here Ne is the electron density. The population density of the level where the dielectronic capture process (He-like ions) or the inner shell excitation (Li-like ions) starts is designated with nk. The first sum accounts for N possible excitations from the level k. The second sum describes all transitions j → i. The line profile Φji(ω) is modeled as a gaussian with a FWHM that is fitted to the measured spectra, representing the spectral resolution of the devices.
Qk,ji and Kk,ji are the intensity factors of dielectronic recombination and the branching ratio of a single satellite, respectively (Vainshtein & Safronova, 1978):
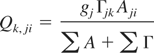
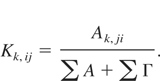
The statistical weights gj, autoionisation rate Γjk, and the rate for spontaneous decay Aji as well as Qk,ji and Kk,ji are calculated by the MZ-Code. In these equations the sum is over all radiative decays and autoionisation rates of the level j.
The rate coefficient 〈DR〉 of the dielectronic recombination (assuming a Maxwellian) is calculated in the following way (Gabriel, 1972):
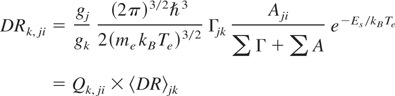
with
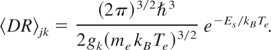
The capture energies Es for the 1s2l2l′-satellites are given in (Faenov & Loboda, 2006). For the higher order satellites they are approximated by
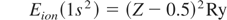
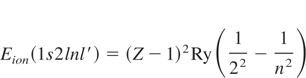
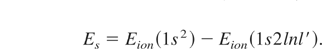
Z describes the atomic number, the value for Ry is Ry∞ hc = 13.6 eV.
The rate coefficient for inner shell excitation 〈Cijup〉 in (4) is calculated with the formula by van Regemorter (1962), but with a modified Gaunt-factor by Rosmej (Niemann et al., 2003):
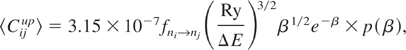
with β = ΔE/kBTe and
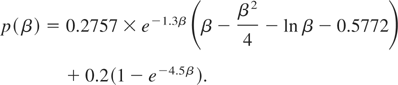
The oscillator strength fni→nj is determined from the spontaneous transition probability Aji
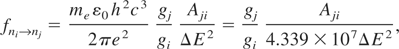
with Aji in s−1 and ΔE in eV.
The resonance line w (λ = 4.4447 Å, E = 2.789 keV) is calculated with (4) using Kk,ij = 1. The rate of collisional excitation of the intercombination line y (λ = 4.4682 Å, E = 2.775 keV) is determined by a Maxwellian average of the total collision strength Cij:
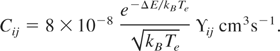
The value for ϒij is determined by averaging the values for Z = 16 and Z = 18 from Zhang and Sampson (1987). The value K = 1 for the resonance and intercombination lines accounts for their intensities in the corona limit and therefore neglects all density and cascading effects.
For the fitting to the measured data, the relative line ratios of the spectral lines are necessary, thus the ratio of the Q-spectrum (3) and K-spectrum (4). As the collisional operator (Rosmej, 2001) of the autoionising levels has been set to zero, density effects between the autoionising levels are not accounted for. The only parameters left are the electron temperature Te and the population densities nk. These population densities are the helium-like ground state 1s2 1S0 for the Q-spectrum, the lithium-like ground state 1s22s 1S1/2 and the first excited states 1s22p 2P3/2,1/2 for the K-spectrum. In the model the first excited states are regarded as one level n1s22p. The population density of the first excited states 1s22p is assumed to be in a Boltzmann relation to the ground state 1s22s 1S1/2 because of the high density in laser-produced plasmas. A fitting of the three parameters (Te, n1s2 and n1s22p) to the measured spectrum identifies the relative line ratios and the electron temperature Te. The population of these states as free parameters reflects the transient character of the ionization process. This means that the ion charge state distribution does not correspond to the temperature of free electrons in plasma and can be lower (ionizing plasma) or higher (recombining plasma) as in the equilibrium case.
The complete spectrum calculated with the line identification program including all dielectronic satellites of Heα up to 1s2l4l′ is shown in Figure 4. The resonance line w and the dielectronic 1s2l2l′-satellites are the dominant lines. The region marked with 1s2l3l′ does not overlap with the 2l′- or 4l′-satellites.

Detailed spectrum of the resonance line Heα and its satellites. This spectrum was calculated with the line identification program with the following parameters: Te = 300 eV, n1s2 = 0.7, n1s22p = 0.3, λ/Δλ = 2000. The notation of the spectral lines follows (Gabriel, 1972).
For low temperatures, the ratio of the dielectronic captured higher order satellites to the 1s2l2l′-satellites is exponentially decreasing with Te (Renner et al., 2001):
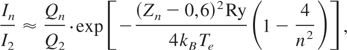
where Q determines the complete dielectronic satellite intensity factor. Assuming that the dominant mechanism is the dielectronic recombination, the line ratio of the 2l′ to 3l′ satellites depends only on temperature. Additionally, these lines are optically thin and do not suffer from photo absorption. Thus for the low temperatures reached in our experiments, the ratio of the 1s2l3l′ and j,k is larger than one and it can be used to deduce the temperature.
We like to point out that in the limit of low densities (ne < 1022 cm−3) this model represents an exact solution of the spectral distribution, since redistribution effects between autoionising levels can be neglected (Antsiferov et al., 1995).
4. RESULTS
A typical spectrum of both spectrometers is shown in Figure 5a. The upper image shows the spectrum of the FSSR with the wavelength scale from left to right. Perpendicular to the dispersion direction is the spatial resolution. From the imaging properties, the size of the hot plasma region where the Cl-Heα radiation originates is determined to be Δz = 200 μm, that is as small as the laser spot size.

Spectra of He-like chlorine. left: (i) shows the recorded spectrum of the FSSR with the wavelength scale from left to right. Perpendicular to this direction is the spatial resolution. (ii) shows the recorded spectrum of the HOPG-spectrometer in mosaic focusing mode without any spatial resolution. The wavelength increases from left to right. The spectral lines are a little bit blurred and inhomogeneous due to the mosaic spread of HOPG. right: The scanned spectra of both spectrometers in one graph overlaid. The He-like resonance line w, intercombination line y and the dielectronic satellites jk are resolved. Notation follows (Gabriel, 1972).
The lower image shows the spectrum of the HOPG-spectrometer. An effect of the mosaic spread of the crystal is that the lines itself do not have the same blackness over their length (Ohler et al., 1997). The influence of the mosaic blocks could be reduced by using the mosaic focusing properties. The resonance line w, intercombination line y, and the dielectronic satellites j and k are clearly visible. The right side of Figure 5 shows the scanned spectra of both spectrometers. Both spectra were placed in a way that the intercombination line y overlaps. Due to the lower resolution of the HOPG-spectrometer, the j and k satellites appear with different relative intensities compared to the lines measured with the FSSR. As will be shown below, the large intensity difference of the w-line is an effect of the resolution, too. For a more detailed identification, a synthetic spectrum with the model from the previous section was fitted to the spectrum measured by the FSSR. With this fitting procedure, the underlying dielectronic satellites could be identified. This is shown in Figure 6a. The parameters for the fitting were Te = 285 eV, n1s2 = 0.6, n1s22p = 0.4, and the fitted line width λ/Δλ = 2000. For this low temperature, there can be some higher order Be-like satellites 1s2sn2pm − 1s22sn2pm−1 (Rosmej, 1995) that overlap with the 1s2l2l′-satellites and may disturb the temperature approximation up to an error of 50% (Rosmej et al., 1997). Due to the lack of atomic data these lines could not be included. The region that is marked with “Blue-Sat.” can be from blue satellites that are in principle measurable (Rosmej & Abdallah, 1998).

(a) Line identification of the FSSR-spectrum of Figure 5. The theoretical spectrum was fitted to the measured one by using the line ratios of the 1s2lnl′- and jk-satellites. The parameters for the procedure were Te = 285 eV, n1s2 = 0.6, n1s22p = 0.4, and the fitted line width λ/Δλ = 2000. (b) Line identification of the HOPG-spectrum of Figure 5. The theoretical spectrum with the same parameters as in (a) was used, but the resolution was set to λ/Δλ = 950. Despite slight differences the spectrum is well reproduced. The intercombination line y is not well reproduced due to the simple modeling.
The separation of the j and k-satellites in Figure 5 allowed the derivation of the spectral resolution of the HOPG-spectrometer. This leads to a high spectral resolution of λ/Δλ = 950 for these crystals. We used the parameters for Te, n1s2 and n1s22p from the fitting to the spectrum of the FSSR (Fig. 6a) and the measured spectral resolution of the HOPG-spectrometer, to calculate a synthetic spectrum and compare it with the measured one, see Figure 6b. With this method the influence of the dielectronic satellites can be determined experimentally and therefore shot-to-shot variations in the experiments can be taken into account. This procedure shows that the difference in the relative intensities of the spectra of both spectrometers (Fig. 5) is a result only of the spectral resolution. It shows the influence of the higher order dielectronic satellites that lead to an asymmetric broadening on the red side of the resonance line w that is not resolved by the HOPG-spectrometer. The relative intensities of the dielectronic 1s2l2l′-satellites agree well with the calculated lines.
5. IMPLICATIONS FOR X-RAY SCATTERING EXPERIMENTS
In order to determine the influence of the non-monochromatic probe radiation on the shape of scattered lines, we have calculated synthetic scattering spectra in the RPA approximation following the theory of Gregori et al. (2003). We have assumed the dense plasma to be hydrogen with a temperature of Te = 2 eV and electron density of ne = 0.6 × 1023 cm−3. The scattering cross section is related to the dynamic structure factor according to
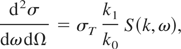
where σT is the Thomson cross section, k0(k1) are the initial (final) wave vectors of the probe radiation, and S(k,ω) can be written as
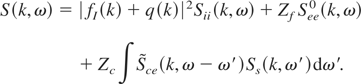
The first term accounts for electron density correlations that dynamically follow the ion motion. This includes core electrons that are represented by the ion form factor fI(k) and free as well as valence electrons that build a screening cloud around the ions, which is represented by q(k). Sii(k,ω) is the ion-ion density correlation function. In the model here, it is described as Sii(k,ω) = S(k)δ(ω). The second term accounts for scattering on free electrons and is the major part in current applications of X-ray scattering. Zf is the number of free and valence electrons of one plasma ion. The last term describes inelastic scattering on core electrons and can be neglected in the parameter range applied in this paper (Gregori et al., 2003). Since the most important part is the free electron structure factor See0(k,ω), its dependence on the scattering angle is shown in Figure 7.

Angular dependency of the free electron structure factor See0(k,ω) for Cl-Heα with E = 2.789 keV. The sample is assumed to be hydrogen with Te = 2 eV, ne = 0.6·1023 cm−3, and Zf = 0.5.
We have used the spectral line calculation from the previous chapter to produce a theoretical Cl-spectrum with a high temperature of 1 keV, as shown in Figure 8.

Theoretical spectrum at a temperature of 1 keV with a spectrometer response function of 2.8 eV FWHM.
The intercombination line y was multiplied by a stretching factor of 6, since our model underestimates the real height of this line. It was assumed that the spectrometer has a spectral resolution of 1000, so the lines were convolved with a 2.8 eV gaussian function. This spectrum was assumed to being scattered on a Te = 2 eV, ne = 0.6 × 1023 cm−3 hydrogen sample with Zf = 0.5. For the calculation of the scattered spectrum we have calculated a scattered spectrum for each line separately, multiplied each with its relative intensity compared to the maximum intensity, and finally added all scattered spectra. The various fractions of the spectral lines to the free electron dynamic structure factor See0(k,ω) are shown in Figure 9. The major parts are the resonance and intercombination lines that both add to a single feature. The dielectronic satellites lead to a further broadening on the red wing.

Contributions of the different spectral lines to the dynamic structure factor.
The complete scatter spectrum S(k,ω) is shown in Figure 10, for two different scattering angles. Figure 10a shows the scatter spectrum for θ = 160°, together with the spectrum of the static part Sii(k,ω), and the part of the free electron dynamic structure factor See(k,ω). The scattering parameter is α = 0.5, hence the scattering is in the non-collective regime. The spectrometer response function was assumed to be a 50 eV FWHM gaussian. The influence of the different spectral lines from the probe is not visible, but the Compton-downshifted feature See(k,ω) is still resolved. From the height and width of this feature the sample electron temperature, electron density, and degree of ionisation can be deduced. For a comparison, we have calculated a scattered spectrum with the same probe parameters, but with a single averaged line only with an energy of E = 2.783 keV. For a slightly larger spectrometer response function with 55 eV FWHM both spectra are identical. We conclude that for X-ray scattering experiments with α < 1 a weak resolving spectrometer is sufficient for the determination of the sample plasma parameters.

X-ray scattering spectra for two different angles. (a) shows the scattering for θ = 160°, α = 0.5, and a 50 eV FWHM gaussian spectrometer response function. The different spectral lines are not visible. The signal is asymmetrically broadenend on the left side, that is a result of the free electron feature See(k,ω). For comparison a scatter spectrum with a single line with E = 2.783 keV is shown. The spectrometer response was set to 55 eV FWHM for a complete overlapping. Although the spectra are nearly identical, this shows that for this scatter angle the dielectronic satellites are only negligible for a rather weak spectrometer resolution. (b) shows the scatter spectrum for θ = 50° and α = 1.26. The spectrometer response function was set to 2.8 eV. The high resolution is necessary to resolve the Compton-downshifted part See(k,ω). In this collective scatter regime the dielectronic satellites overlap with See(k,ω) and the determination of the sample plasma parameters gets difficult.
Figure 10b shows the scatter spectrum for θ = 50° and the same sample parameters. The scattering parameter is α = 1.26, hence the scattering is in the collective regime. The instrument resolution was set to ΔE = 2.8 eV, since the red-shift of See(k,ω) is small and must be resolved by the spectrometer. The resolution corresponds with our current HOPG-spectrometer spectral resolution of E/ΔE = 1000. The red-shifted feature See(k,ω) overlaps with the unshifted dielectronic satellites. It is clearly visible that it is necessary to observe the probe spectrum with a high spectral resolution simultaneously with the scatter experiment. Otherwise it would be extremely difficult to determine the part of the free electron dynamic structure factor and the probe plasma parameters.
6. CONCLUSIONS AND OUTLOOK
For scattering experiments it is necessary to know the spectrum of the source with a high resolution, since the Compton-downshifted part of probe radiation overlaps with the unshifted dielectronic satellites. After fitting a calculated spectrum to the measured one, the role of dielectronic satellites can be deduced directly. This allows to determine the broadening of the resonance line due to higher order dielectronic satellites experimentally. For scattering experiments with scattering parameter α < 1, it is sufficient to use a weaker spectral resolution and profit from the higher integral reflectivity. The individual spectral lines smear out and result in a “single line” with a wavelength λ′ that is the result of Heα and its higher order satellites.
It is shown that a laser-plasma produced spectrum is narrowband, but it is not monochromatic. Even for higher plasma temperatures, satellites, and the intercombination line will not vanish. This means that the spectrum cannot be more narrowband than the difference between w and y which is λy − λw = 0.0235 Å in the present case. The bandwidth is then at least Δλ/λ = 0.005 which is easily resolved by an X-ray spectrometer. As the relative intensity depends on temperature and density, this has to be taken directly into account to interpret the scattering data for plasma diagnostics. For experiments with α > 1 the scattered red-shifted feature overlaps with the unshifted dielectronic satellites. For a determination of the sample plasma parameters it is necessary to measure the probe spectrum with a high spectral resolution simultaneously. In summary we conclude that laser-plasma scattering experiments are always dealing with a non-monochromatic source, this complicates the interpretation of spectrally resolved scattering signals. Kα-radiation might be less effected by dielectronic satellite transitions and therefore be more monochromatic (Urry et al., 2006). However, at present, the conversion efficiency is rather low for practical applications (requesting kilojoule petawatt pulses).
ACKNOWLEDGMENT
The authors wish to thank R. Thiele, University of Rostock, for useful discussions and valuable suggestions with the calculation of the RPA integral.












