1. Introduction
Universality occurs when diverse systems exhibit similar scaling behavior on the approach to a critical phase transition. Critical phase transitions mark the point (the critical temperature) beyond which systems no longer undergo first-order phase transitions. It turns out that this similar scaling behavior can be very well described by power laws of the form ![]() , where t is proportional to the temperature deviation from the critical temperature and α is the critical exponent—a fixed number that leads to a characteristic curve on temperature-density plots.Footnote 1
, where t is proportional to the temperature deviation from the critical temperature and α is the critical exponent—a fixed number that leads to a characteristic curve on temperature-density plots.Footnote 1
Physical systems can be categorized into universality classes according to their behavior as they approach the critical point: members of the same class have identical critical behavior—the same set of critical exponents {α, β, …} for several power laws—while their behavior away from the critical point and microscopic organization may be radically different: fluids and magnets are in the same universality class despite otherwise having totally different chemical and physical properties. In fact, a paradigm example of universality is that the liquid-gas critical phase transition and the (uniaxial) ferromagnetic-paramagnetic critical phase transition share critical exponents (those of the three-dimensional Ising class). Both of these types of systems may be described by equivalent power laws as they transition from certain ordered states (liquid or ferromagnetic respectively) to critical states.
On the one hand, a great deal of experimental evidence is available that classifies many different physical systems into a few universality classes and finds the critical exponents to ever greater accuracy (see Sengers and Shanks Reference Sengers and Shanks2009). On the other, theoretical work is continually under way to refine and develop the theoretical models for each universality class (see Pelissetto and Vicari Reference Pelissetto and Vicari2002). Critical exponents derived both through computer modeling (Monte Carlo simulations) and field-theoretic derivations (using perturbation theory) closely match those discovered empirically.
This article has three aims: (i) to clarify the structure of the explanation of universality, (ii) to discuss the physics of the renormalization group (RG) explanations, and (iii) to examine the extent to which universality is thus explained.
In section 2 I outline a range of different explananda and distinguish the kinds of explanation that may satisfy each. This is important because some confusion in the philosophical debate over the explanation of universality has resulted from implicit appeal to different explanatory standards.
Section 3 details the physics of the real-space and field-theoretic approaches to the RG. I argue that the two approaches, which have different mathematical structures, offer distinct explanations. Paying attention to the physics further reveals that there are various technical lacunae in the RG explanation of universality, which have been neglected in the philosophical literature.
In section 4 I develop reasons for thinking that, despite various technical lacunae, the field-theoretic approach to the RG is sufficient to explain universality along the lines developed in section 2. There I also express doubts that a similar argument could be run in the context of the real-space approach.
In the physics literature it is standard practice to distinguish these two approaches; my aim here is to build on Mainwood’s (Reference Mainwood2006) insight that the distinction is also philosophically significant when assessing the RG explanation of universality. I, like Mainwood, endorse the field-theoretic explanation of universality while arguing that the real-space explanation is inadequate.Footnote 2 However, my reasons for believing this are somewhat distinct from his: Mainwood is worried by the fact that the real-space approach makes use of nonrenormalizable Hamiltonians, while I query the extent to which the physics can demonstrate that different systems indeed exhibit similar behavior (see sec. 4 for more details).
2. Structure of the Explanation of Universality
The discussants in the philosophical literature on the explanation of universality (e.g., Batterman Reference Batterman2000, Reference Batterman2017a; Butterfield and Bouatta Reference Butterfield and Bouatta2011; Callender and Menon Reference Callender, Menon and Batterman2013; Butterfield Reference Butterfield2014; Reutlinger Reference Reutlinger2014) seem to have different standards of explanation in mind. As such, in the table below, I set out what I take to be the various phenomena that need explaining (explananda marked ‘Q’ for explanatory question) and the explanations offered in response (explanantia marked ‘E’ for explanation). The table is organized into three rows: ‘Spec’ for specific explanations, ‘Com’ for common explanations, and ‘Abs’ for abstract explanations.
| Explananda (Q) | Explanantia (E) |
|---|---|
| SpecQ: System A has critical exponents {α} & system B has critical exponents {α} & … & system E has critical exponents {α}. | SpecE: {α} derived from Hamiltonian for system A & {α} derived from Hamiltonian for system B & … & {α} derived from Hamiltonian for system E. |
| ComQ: Systems A–E have certain behavior in common (or the differences between A–E are irrelevant to their behavior). | ComE: Identify common features shared by A–E and show that they are sufficient for common behavior (or demonstrate the irrelevance of heterogeneities). |
| AbsQ: There’s a generic commonality in behavior (or a generic irrelevance of certain details). | AbsE: The trajectories in the abstract space converge. |
SpecQ is a conjunction of seemingly independent facts about the critical exponents of different systems where each fact is offered a distinct explanation by SpecE. SpecQ is distinguished from ComQ to emphasize that ComQ requires a deeper explanation. The common behavior ought not to be explained by distinct explanations for each physical system; an explanation of the form of ComE is required that adduces a similarity in the systems and demonstrates its sufficiency for their common behavior.Footnote 3
Consider an analogy: a traveler visits a foreign country and goes from house to house observing the local customs. She observes an oddity in the locals’ behavior: in each family she visits, the youngest child sleeps in a bed angled such that his or her head is vertically lower than his or her feet. At each visit, she asks for an explanation of this phenomenon, and every family offers a different answer: “because he’s short and this way he’ll grow taller,” “because greater blood flow to her head will increase her intelligence,” “because it’s cooler and his head otherwise becomes hot,” “because that’s the only way to avoid the awakening smell of dinner,” and so on.
Our traveler will likely be dissatisfied with this range of distinct explanations—analogous to our dissatisfaction with SpecE. There is an unusual commonality, and she will seek a unified explanation along the lines of ComE.
A straightforward way to offer an explanation of universality follows ComE: one explains the common behavior by, first, isolating and pointing to an aspect of the descriptions that is shared by the different systems in the same class and, additionally, demonstrating that the common features lead to the observed common behavior. In sections 4.1 and 4.2 I respectively claim that the field-theoretic approach provides a common-type explanation while the real-space approach does not.
What about AbsE? Batterman appeals to an explanation along these lines: commonality is to be expected generically because of the convergence of flows in the abstract space. “It turns out that different physical Hamiltonians can flow to the same fixed point. Thus, their critical behaviors are characterized by the same critical exponents. This is the essence of the explanation for the universality of critical behavior” (Batterman Reference Batterman2000, 127). Of course, this explanation is insufficient if the converging trajectories are not linked to the systems that exhibit the commonality. Batterman claims that the link is due to the flow of ‘physical Hamiltonians’; as such, much of this article will explore how physical Hamiltonians may be defined in the context of critical phenomena. That is, I explore whether we can link the abstract convergent flows to the description of distinct systems that exhibit universality.
Without a link to the ComQ, AbsE remains a claim not grounded by reference to real physical systems. By analogy consider the claim ‘communities tend to share cultural practices’. The claim would be explanatorily insufficient if it could not, at least in principle, be demonstrated that this community shares cultural practices. Importantly, for both the analogy and the universality of critical phenomena, abstract-type claims may play an important explanatory role where the link to ComQ is available. I argue in this article that the physics is much less worked out than the literature seems to suggest. Nonetheless, we seem to have a framework available for an abstract-type explanation with the field-theoretic approach to the RG: in section 4.1 I show that there are sound theoretical arguments whereby the field-theoretic approach implies that convergent flows can be linked to trajectories in phase space that may represent the different physical systems that display common behavior.
Note that in the real-space RG context the formalism of convergent flows in a phase space can also be written down. There is, however, little reason to think that the distinct convergent trajectories represent the different physical systems of interest, although there are limited exceptions discussed in section 4.2. As such, I argue that the AbsE explanation fails for the real-space RG because it does not have the resources to imply ComQ. The real-space RG does, nonetheless, allow for the prediction of the critical exponents for certain (archetypal) systems in each universality class and can thus provide SpecE for some systems.
It may help to tie the difference in explanations provided by SpecE and ComE to a particular theory of explanation.Footnote 4 On the interventionist approach advocated by Woodward (Reference Woodward2003), explanations answer what-if-things-had-been-different ‘w-questions’. Answers to w-questions require us to describe the chain of dependencies that lead to the explananda and to demonstrate how the explananda would change given variation of various factors. SpecQ requires us to consider which features, if different, would prevent system A exhibiting behavior with critical exponent α …; ComQ, however, asks what changes would lead to the common behavior no longer being common. In other words, ComQ does not really care about precisely what happens to the individual systems; it prompts an explanation as to why they share features, which motivates us to locate a shared property and to demonstrate that sharing that property is sufficient for the common behavior in question. The claim that the sharing of behavior is merely coincidental is inconsistent with any nontrivial ComE but is compatible with an interesting SpecE.
There is a further issue that ought to be mentioned here—this pertains to the parenthetical statements in the table above. Batterman (Reference Batterman2000, 127) highlights the fact that the RG formalism allows one to demonstrate the irrelevance of aspects of our physical systems. What is important for Batterman is that the RG thus provides a robustness demonstration.Footnote 5 He claims that robustness with respect to microphysical perturbations implies that all systems that go to the critical point have a representation that is independent of microphysical details. This would thus establish that the distinguishing details are irrelevant and, by implication, that the common details are sufficient for common behavior. This robustness demonstration is rather like the AbsE explanation: in order for it to explain universality, we need an additional demonstration that the behavior of the different physical systems of interest is, in fact, described by the robust model. Throughout the rest of this article, I discuss the extent to which such arguments might succeed.
While other authors seem to ignore the conceptual links between irrelevance of details and universality, Batterman’s work is very important for its role in highlighting these connections. My contention in this article is that the field-theoretic RG is the proper context for gleaning such insights. The upshot of this section is that we have a framework for explaining universality: we may proceed either via ComE or via AbsE, provided that an appropriate link to ComQ is available.
The philosophy literature that refers to universality has a number of aims with respect to establishing theses about emergence, reduction, and explanation. My goal, here, is merely to clarify the nature of the RG explanation; thus, I will not presume to comment on such theses and interpretative issues, but I do hope that this article will shed light on future discussions. Although I assume that any theory of explanation adequate to explanations of universality will accept the distinctions elaborated above, I do not have space to provide a substantive analysis of the right theory of RG explanation. However, I should note that neither ComE nor AbsE requires that we use the RG mathematical framework, rather than some other means, for variously determining the relevance and irrelevance of different parts of the mathematical representation of the physical systems of interest; this observation may count against claims that RG explanations are sui generis.
3. The Physics
The following two sections involve some technical detail. Overall I claim that the two approaches to the RG provide different putative explanations of universality and that, as such, they ought to be distinguished.
For the real-space approach, I claim that critical exponents are derived based only on a representative model for each universality class. A model is not provided for each member of the same class, and it is not demonstrated that the details that distinguish each member of the same class are irrelevant to that system’s critical behavior. In addition, I argue that the mathematical model employed is insufficiently general to represent the common aspects of all members of the universality classes; thus, a common-type explanation is not available. Here, universality is not explained but assumed: no justification is given for the applicability of the models to the other members of each class. This conclusion is reached through consideration of the models and a sketch of the RG methods by which the critical exponents are derived for each such model. In section 4.2, I consider three responses to this assumed-not-explained objection; in all three cases I express doubts that the behavior of the broad range of systems that exhibit universality could be thus explained.
The field-theoretic RG makes use of a renormalizable Hamiltonian. I argue that this provides it with the tools to describe the commonalities in the various systems sufficient for their common behavior. The RG techniques then allow one to class all differences between systems so represented as irrelevant to the values of their critical exponents. As such, the field-theoretic RG provides a common-type explanation: common features are identified, and other features are demonstrated to be irrelevant. The standard account of this explanation implicitly depends on physics that has not been worked out; as such, it includes certain technical lacunae. These correspond to our in-practice inability to formulate Hamiltonians that represent the details that distinguish systems within the same universality class. Nonetheless, unlike in the real-space case, we have theoretical justification for the claim that such distinguishing details are irrelevant. In section 4.1 I further discuss the gaps in the physics and adduce reasons to consider the field-theoretic RG explanation adequate.
Overall the real-space RG provides a specific-type explanation for a few individual systems but does not achieve ComE. It looks like we can draw diagrams that provide AbsE as well, but the abstract picture of convergent trajectories fails to correspond to real physical systems in the same universality class. Conversely, the field-theoretic RG explains along the lines of ComE (where the common features are representation by the Landau-Ginzburg-Wilson Hamiltonian and the order parameter) and allows one to justify AbsE.
3.1. The Models
The critical behavior of the different universality classes can be derived from a range of simple model systems. I briefly describe the Ising model and its extension to the n-vector model, which defines a broad range of models classified according to their values for two variables. This model is crucial to understanding the real-space RG and is abstracted to provide the basis for the field-theoretic RG. Microphysical models are not defined for multiple members of the same universality class; rather, a representative model is used for each class.
Niss (Reference Niss2005) describes the early history of the Lenz-Ising model.Footnote 6 The Ising model was specifically designed to represent the physical characteristics of magnetic systems rather than the broader range of systems that display critical phenomena. According to the model, such systems are composed of an array of interacting micromagnets that have a discrete range of orientations. This latter assumption arose out of a combination of empirical data and considerations from early quantum mechanics.
In modern formulations, the Ising model consists of a D-dimensional cubic lattice with {ei} basis vectors with sites labeled ![]() . At each site there is a spin variable
. At each site there is a spin variable ![]() , although in extensions to this model the spin variable can take a greater range of values. A Hamiltonian is defined
, although in extensions to this model the spin variable can take a greater range of values. A Hamiltonian is defined
The coupling constant J takes a positive value and is assumed to be independent of all variables other than the system volume. The Ising model interaction is generally defined over nearest or next-nearest neighbors; thus, μ is a lattice vector that takes any vector to the relevant neighbor in the positive direction; B is an external magnetic field.
The Hamiltonian of a system corresponds to the energy of the system in a particular configuration; thus, we see (as is confirmed empirically) that the Ising Hamiltonian will take a lower value when the spins are aligned and a higher value when spins are disordered. The ferromagnetic-paramagnetic transition can be defined over this lattice as the transition from the spin configuration with all spins aligned to that where there is no general correlation between the spin directions. This transition will take place at the critical temperature (Tc). No analytic derivation of critical behavior for any three-dimensional model has been achieved.Footnote 7
Behaviors characteristic of systems approaching Tc are termed ‘critical phenomena’, and it is with respect to the power laws that describe such behavior that universality can be observed. Current mathematical procedures to describe such behavior involve the RG, described below. The n-vector model generalizes the Ising model to various universality classes. Stanley (Reference Stanley1999, S361) notes: “empirically, one finds that all systems in nature belong to one of a comparatively small number of such universality classes.”
The n-vector model includes spins that can take on a continuum of states:
Here, the spin ![]() is an n-dimensional unit vector. The two parameters that determine the universality class are the system dimensionality d (which will determine the set of nearest neighbors) and the spin dimensionality n. The standard, three-dimensional Ising model corresponds to
is an n-dimensional unit vector. The two parameters that determine the universality class are the system dimensionality d (which will determine the set of nearest neighbors) and the spin dimensionality n. The standard, three-dimensional Ising model corresponds to ![]() (3, 1), as it describes three-dimensional magnets that, in the ferromagnetic phase, will have spins either aligned or anti-aligned with a single axis.Footnote 8
(3, 1), as it describes three-dimensional magnets that, in the ferromagnetic phase, will have spins either aligned or anti-aligned with a single axis.Footnote 8
I now turn to a discussion of the RG derivation of critical exponents. A full exposition would require more space than we have here, but I sketch the procedure below.Footnote 9 RG transformations are constructed to preserve thermodynamical properties of the system of interest while increasing the mean size of correlations. Thus, for example, the RG transformations take a ferromagnetic system toward the critical point (where the order parameter fluctuates wildly).
3.2. Field-Theoretic and Real-Space Renormalization
The different RG approaches posit competing methods for deriving critical exponents:
Real-Space RG
Consider the Hamiltonian of a system on a lattice (e.g., in the Ising model). The higher energy interactions will probe the structure of the lattice, and, in order to consider the system probed at a larger length scale, we average over the higher energy contributions to the Hamiltonian. This can be done by increasing the effective lattice size and constructing a new Hamiltonian for a system on a larger lattice—referred to as ‘coarse-graining’ or ‘zooming out’. This may be thought of as a blocking procedure, whereby some group of particles is replaced by one particle that represents the group through an average or suchlike, as depicted in section 4.2.Footnote 10 On this model, the RG flow represents the changes in parameters that leave the form of the Hamiltonian and certain qualitative properties of the system unchanged (i.e., those that are derived from the partition function), while increasing the lattice size. Monte Carlo computer-based methods allow for the derivation of the critical exponents from the n-vector Hamiltonian (eq. [2]) via the real-space RG.
Field-Theoretic RG
The Hamiltonian (eq. [5]) considered in this case is more abstract (technically it is a functional of the order parameter [OP])—I outline one way of deriving it below. The calculation of this Hamiltonian for real systems involves integration over a range of scales and energies. The highest energy (smallest scale) cutoff (denoted Λ) corresponds to the impossibility of fluctuations on a scale smaller than the distance between the particles in the physical system. The RG transformation in this case involves decreasing the cutoff, thus increasing the minimum scale of fluctuations considered. This procedure is analogous to increasing the lattice size and will similarly generate a flow through parameter space designed to maintain the Hamiltonian form and qualitative properties of the system in question.
Both approaches to the RG can be formalized as follows. The RG transformation ![]() transforms a set of (coupling) parameters {K} to another set {K′} such that
transforms a set of (coupling) parameters {K} to another set {K′} such that ![]() . The set of parameters that corresponds to a fixed point is {K*}, defined such that
. The set of parameters that corresponds to a fixed point is {K*}, defined such that ![]() .Footnote 11 If we assume that
.Footnote 11 If we assume that ![]() is differentiable at the fixed point, this leads us to a version of the RG equations:
is differentiable at the fixed point, this leads us to a version of the RG equations:

There are now two more steps before we can define relevance and irrelevance. First, we define the eigenvalues of the matrix Tab as {λi} and its left eigenvectors as {ei}. Scaling variables (![]() ) are linear combinations of the deviations from the fixed points. By construction, these scaling variables will transform multiplicatively near the fixed point such that
) are linear combinations of the deviations from the fixed points. By construction, these scaling variables will transform multiplicatively near the fixed point such that ![]() . The second (trivial) step is to redefine the eigenvalues as
. The second (trivial) step is to redefine the eigenvalues as ![]() , where b is the renormalization rescaling factor and yi are known as the RG eigenvalues.
, where b is the renormalization rescaling factor and yi are known as the RG eigenvalues.
If ![]() , then ui is relevant; if
, then ui is relevant; if ![]() , ui is irrelevant; and if
, ui is irrelevant; and if ![]() , ui is marginally relevant. The relevant scaling variables will increase in magnitude after repeated RG transformations, while the irrelevant scaling variables will tend to zero after multiple iterations. (The behavior of the marginal scaling variables requires more analysis to determine.) Thus, given the Hamiltonian of one of our models, one can define an RG transformation that will allow one to (i) classify certain of the coupling parameters of the system in question as (ir)relevant to its behavior near the fixed point and (ii) extract the critical exponents from the scaling behavior near the fixed point. Up to this point the description is generic. Note that in the real-space approach the coupling parameters to the Ising-type Hamiltonians are marked as relevant or irrelevant, while in the field-theoretic approach it is the operators—functions of the order parameter—that are so labeled.
, ui is marginally relevant. The relevant scaling variables will increase in magnitude after repeated RG transformations, while the irrelevant scaling variables will tend to zero after multiple iterations. (The behavior of the marginal scaling variables requires more analysis to determine.) Thus, given the Hamiltonian of one of our models, one can define an RG transformation that will allow one to (i) classify certain of the coupling parameters of the system in question as (ir)relevant to its behavior near the fixed point and (ii) extract the critical exponents from the scaling behavior near the fixed point. Up to this point the description is generic. Note that in the real-space approach the coupling parameters to the Ising-type Hamiltonians are marked as relevant or irrelevant, while in the field-theoretic approach it is the operators—functions of the order parameter—that are so labeled.
The real-space RG depends on the application of a blocking transformation: a standard example is depicted in section 4.2, although almost any blocking transformation would do equally well. It is required that the Hamiltonian form is stable across these transformations. Since the Hamiltonians are not renormalizable this involves the application of a transformation and subsequent truncation of the Hamiltonian.Footnote 12
The field-theoretic RG approach derives the critical exponents using diagrammatic perturbation theory—I do not have space to elaborate this here. The Hamiltonian in this context is macroscopic and depends on the OP (ɸ) that, in the Ising model context, is proportional to a sum of the spins in a small region of volume δV at x: ![]() .Footnote 13 We require that
.Footnote 13 We require that ![]() , where a is the physical lattice spacing and l is the dominant statistical length (often the correlation length). One can approach the Hamiltonian’s construction from the Ising model as follows (see Klein, Gould, and Tobochnik Reference Klein, Gould and Tobochnik2012).Footnote 14
, where a is the physical lattice spacing and l is the dominant statistical length (often the correlation length). One can approach the Hamiltonian’s construction from the Ising model as follows (see Klein, Gould, and Tobochnik Reference Klein, Gould and Tobochnik2012).Footnote 14
Start with the Ising model (eq. [1]); then postulate a form for the Helmholtz free energy ![]() (ɸ) of a system in contact with a heat bath. The terms in equation (4) correspond (a) to the interaction of the coarse-grained Ising spins with an external magnetic field, (b) the interactions between the coarse-grained spins that depend only on the distance between blocks, and (c) an approximation of the entropy (using Stirling’s approximation):
(ɸ) of a system in contact with a heat bath. The terms in equation (4) correspond (a) to the interaction of the coarse-grained Ising spins with an external magnetic field, (b) the interactions between the coarse-grained spins that depend only on the distance between blocks, and (c) an approximation of the entropy (using Stirling’s approximation): ![]() .
.

After only a few steps, and a generalization to dimension d, one ends up with the Landau-Ginzburg-Wilson (LGW) Hamiltonian:

Note, however, that the LGW Hamiltonian is not the Ising model effective Hamiltonian. This latter object is more complicated; however, it is demonstrated in Binney et al. (Reference Binney1992, app. K)—and is plausible given its derivation—that equation (5) is a good approximation to a truncated form of the Ising Hamiltonian near the critical point.
The construction of equation (5) is quite different from equations (1) and (2). It builds on these models but abstracts from them. More details can be found in (e.g.) Fisher (Reference Fisher1974). There he demonstrates the field-theoretic methods that allow one to derive expressions for the critical exponents as functions of d and n. See equation (6) for the first few terms of the exponent α; this will give a value for various universality classes. This derivation depends on the functional integration of the LGW Hamiltonian over all functions ɸ(x).

Crucially, it can be shown that the addition of certain terms to the LGW Hamiltonian will lead to irrelevant contributions; these do not affect the values for critical exponents describing the approach to a given fixed point. In Binney et al. (Reference Binney1992, chap. 14), the criteria for relevance and irrelevance are derived. An operator Op is relevant if ![]() and irrelevant if
and irrelevant if ![]() , where d is the dimension of the system under investigation and p is a function of the exponent of ɸ.Footnote 15
, where d is the dimension of the system under investigation and p is a function of the exponent of ɸ.Footnote 15
This serves to establish that for the LGW Hamiltonian, for ![]() , any Op with
, any Op with ![]() will be irrelevant at the fixed point.Footnote 16 This is an important result for the discussion in the remainder of this article. Its generality depends on the justification for the applicability of the LGW Hamiltonian to various models. As we will see in what follows, this will depend in part on the OP assigned to each member of each universality class.
will be irrelevant at the fixed point.Footnote 16 This is an important result for the discussion in the remainder of this article. Its generality depends on the justification for the applicability of the LGW Hamiltonian to various models. As we will see in what follows, this will depend in part on the OP assigned to each member of each universality class.
The theory behind this result is relatively involved, but the idea is simple: the LGW Hamiltonian is renormalizable. This means that applying an RG transformation to the Hamiltonian will not add terms that cannot be absorbed into the parameters ζ, θ, η in equation (5). At the fixed point—which describes the location of the critical phase transition—renormalizable Hamiltonians are scale invariant: they are unaffected by RG transformations.Footnote 17 Thus, at the fixed point, the only elements that contribute to behavior are those in the renormalizable Hamiltonian; all irrelevant terms that may be added to that Hamiltonian will not contribute there. By contrast, the Hamiltonians employed in the real-space approach are not renormalizable, and the description of their behavior near the critical point relies on the imposition of scale invariance by truncating the Hamiltonian after each iteration of the RG transformation; as such, criteria for relevance and irrelevance of additions to those Hamiltonians cannot be specified in such generality.
The next section will explore the extent to which each RG approach can be considered to explain the universality of critical phenomena.
4. Universality Explained?
Universality is explained if we are able to show that each member of each universality class has features in common and to demonstrate that having those features is sufficient for the universal behavior—that is, an explanation along the lines of ComE (see sec. 2 for my taxonomy of explanations). Universality may be equally well explained by the convergence of flows in an abstract space, so long as we can draw a connection between such flows and the physical systems of interest. In this section, I build on the details of the physics given thus far. I argue that the field-theoretic explanation is adequate (sec. 4.1) but that the real-space explanation is inadequate both to common- and abstract-type explanations (sec. 4.2).
My claims here follow those of Mainwood (Reference Mainwood2006, 152–87), who argues that the real-space and field-theoretic approaches should be distinguished when assessing the RG explanation of universality. Mainwood shows that on the real-space approach one can only derive universality if one imposes the same RG transformations on each member of the same universality class and that the choice of such transformations for each model is, in some sense, up to us—this follows from the nonrenormalizability of the Hamiltonians used. Mainwood thus claims that the real-space approach fails to provide an adequate explanation.
I suggest that the real-space approach cannot explain universality for a more basic reason: it fails to represent the diverse range of systems that fall into the same class and thus does not demonstrate a flow of different systems into the same fixed point (I discuss this further in sec. 4.2).Footnote 18 Mainwood’s claims may bolster my own to the extent that even were the real-space RG to model each distinct system one would still have grounds for doubting the explanation of universality on offer.
In addition to my worries about the real-space RG, I argue that the standard characterization of the field-theoretic RG explanation of universality adverts to physics that is somewhat less developed than first appears. Below, I highlight these technical lacunae and demonstrate that they ought not to bother us excessively.
Where the explanation of universality is presented, it is commonly claimed (e.g., Kadanoff Reference Green and Batterman2013; Batterman Reference Batterman2017a) that we proceed by including the details of diverse physical systems in the mathematical representations and showing these to be irrelevant. Such arguments are often represented pictorially (see fig. 1) and described as follows: “The distinct sets of inflowing trajectories reflect their varying physical content of associated irrelevant variables and the corresponding nonuniversal rates of approach to the asymptotic power laws dictated by ![]() ” (Fisher Reference Fisher1998, 675). Multiple systems in the same universality class are represented at the critical point by the LGW Hamiltonian (eq. [5]). In order to represent the details that distinguish such systems, we would need to add irrelevant operators to that equation. This is not done for the specific systems that fall into the same universality class. In practice, it is not known how to model such systems, for the explicit formulation of effective Hamiltonians is a nontrivial task.Footnote 19 Thus, each distinct trajectory of figure 1 cannot be explicitly related to the real, physical systems whose behavior is captured. In principle one could also write down any microscopic Hamiltonian, but, as I argue in section 4.2, we cannot show that different systems thus represented will exhibit universal behavior. But, we can, with the field-theoretic approach, show that any system that satisfies certain symmetry and dimensionality conditions will exhibit universal behavior.
” (Fisher Reference Fisher1998, 675). Multiple systems in the same universality class are represented at the critical point by the LGW Hamiltonian (eq. [5]). In order to represent the details that distinguish such systems, we would need to add irrelevant operators to that equation. This is not done for the specific systems that fall into the same universality class. In practice, it is not known how to model such systems, for the explicit formulation of effective Hamiltonians is a nontrivial task.Footnote 19 Thus, each distinct trajectory of figure 1 cannot be explicitly related to the real, physical systems whose behavior is captured. In principle one could also write down any microscopic Hamiltonian, but, as I argue in section 4.2, we cannot show that different systems thus represented will exhibit universal behavior. But, we can, with the field-theoretic approach, show that any system that satisfies certain symmetry and dimensionality conditions will exhibit universal behavior.
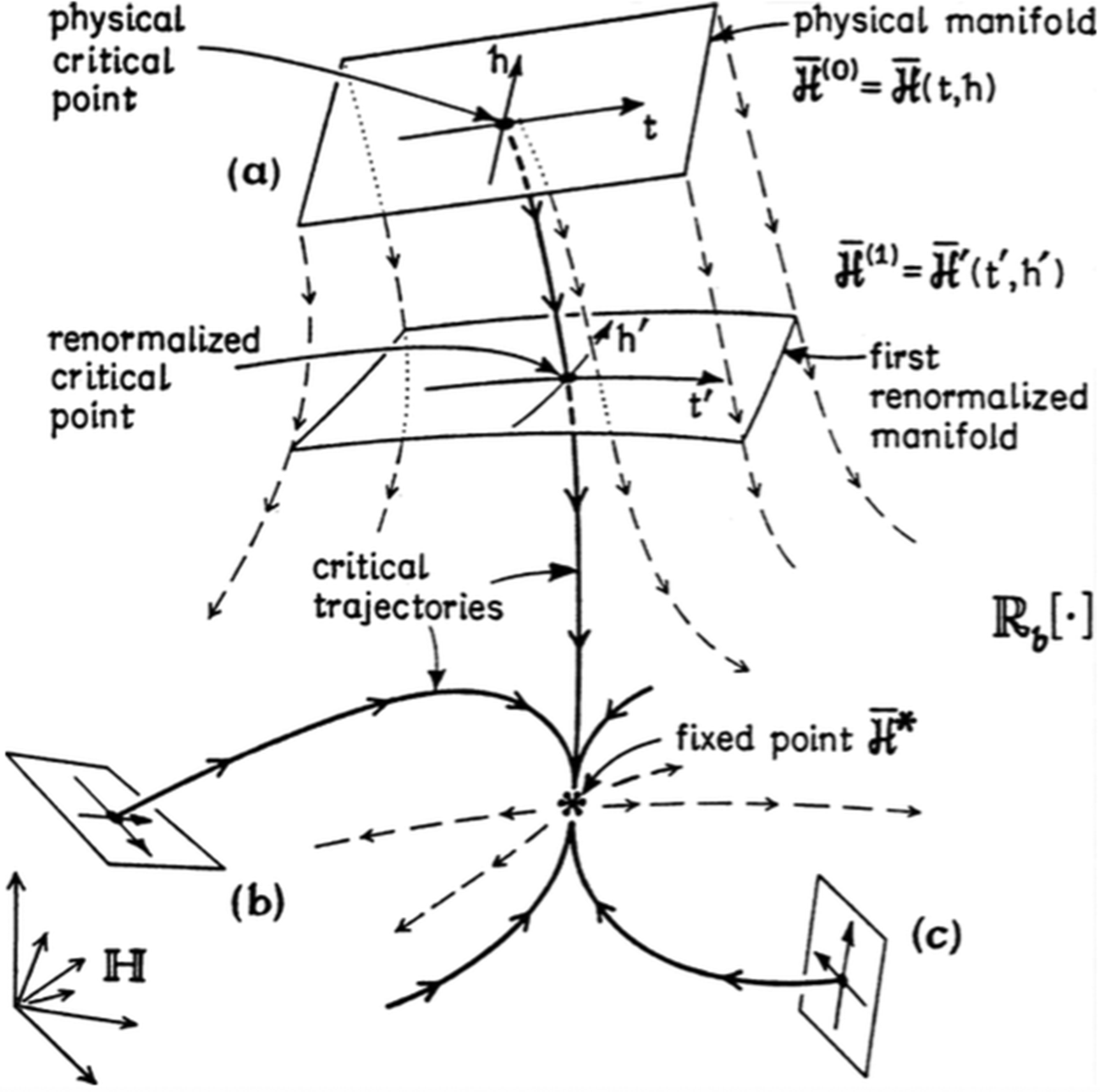
Figure 1. RG flow in the abstract space of Hamiltonians (or, more precisely, the space of couplings for a fixed Hamiltonian form). From Fisher (Reference Fisher1998); reproduced with permission of the American Physical Society via Copyright Clearance Center.
4.1. Field-Theoretic RG
We have sound theoretical reasons to think that the LGW Hamiltonian represents a wide range of physical systems. The physical analysis behind this claim is the renormalizability of the LGW Hamiltonian and the demonstration that certain classes of operators are irrelevant, as discussed above. Binney et al. (Reference Binney1992, 366) express this as follows: “to the accuracy of our calculation we have shown that any three-dimensional physical system whose Hamiltonian can be written as an even functional of a one-component scalar field should have the same critical behavior as the Landau-Ginzburg model.” Thus, we need to show, for each system of interest, that its order parameter (OP) can be written as a one-component scalar field. Paying close attention to the OP of each system will also ground the various assignations of systems to different universality classes. The OP accounts for the symmetry group (i.e., the n of the n-vector model) and the dimensionality. Defining the OP for a condensed matter system is not a straightforward process; it depends subtly on the kind of phase transition the systems undergoes and on which macroscopic features change at such a phase transition. Footnote 13 provides some examples of OPs.
The central operators of the LGW Hamiltonian together with the OPs represent the common aspects of the various systems in the same class at the critical point. Such systems are distinguished, at most, by operators that are, by RG arguments, irrelevant to the behavior at the critical point. Thus, the common aspects are sufficient for the systems’ exhibiting universal behavior, and we have a common-type explanation. Furthermore, this, in principle, justifies AbsE: the various systems are represented by Hamiltonians distinguished by irrelevant operators, and the flows of the distinct systems converge at the fixed point.
One might have the following worry: once the OP has been specified, common representation is assured for the different systems in the same class. As such, specification of the OP might be said to do all the explanatory work.
I do not think that this argument goes through. I claimed in section 2 that ComE explanations must identify common features and show that they are sufficient for common behavior.Footnote 20 The OP together with the LGW Hamiltonian represent the common features of the different systems, but the field-theoretic RG framework is required to demonstrate that such operators are sufficient for the universal behavior and that all other aspects of the descriptions are irrelevant at the critical point. Part of this explanation does lie in the matching of OPs to systems, but it also relies on the fact that all the nonrenormalizable operators, which otherwise represent the differences between systems’ behavior away from the critical point, are irrelevant at the critical point. This is nontrivial; in some contexts the irrelevance of certain details may be obvious, and thus may remain implicit, but where it is not obvious demonstrations of irrelevance play an important role in the explanation. It is also worth noting that, even were this point not granted, the OP does not play a role in the real-space approach, and, as such, it is only through the field-theoretic approach that we are able to identify the common features of universally behaving systems.
A further concern with this explanation rests on the observation that the OP and LGW Hamiltonian correspond to large-scale features of the systems of interest; thus, our explanation is not tied in detail to systems’ microscopic heterogeneities. So long as we have reason to believe that our model represents the different systems that exhibit universality, the explanation need not include all the details of each system; it has long been acknowledged that good explanations may abstract from underlying details (see, e.g., Woodward Reference Woodward2003).Footnote 21 We do have good reasons to link field-theoretic models to the physical systems of interest; chiefly, a microscopic justification of the choice of OP, discussion of irrelevant operators (continued below), and the empirical observation of approximate scale symmetry in physical systems at and near the critical point. Further justification akin to that provided by the derivation of the LGW Hamiltonian from the Ising model (see sec. 3.2) may provide a bottom-up account of critical phenomena, although this claim is subject to worries about the infinite idealizations invoked (see n. 11). I assume that unreduced explanations can be shown to be adequate before such questions of reduction are settled.
That we cannot, in practice, write down the irrelevant operators may be worrying. It may be thought that evidence is scant for the claim that such operators indeed represent the heterogeneities that distinguish physical systems away from the critical point.
I hope partially to alleviate such worries by briefly considering crossover theory.Footnote 22 The theoretical description of crossover tells us that in some cases we may derive a correspondence between certain operators and the details of physical systems. By showing that certain operators may represent the details that distinguish systems away from the critical point, this ought to bolster the analysis of the field-theoretic RG explanation presented just above.
Systems undergoing crossover display critical behavior characteristic of some universality class as they approach Tc, but under repeated iterations of the RG transformations (read: as the temperature moves closer to Tc) they deviate from that behavior and cross over to a different universality class. For example, a system near the Heisenberg fixed point may have an additional relevant operator; we might thus define a Heisenberg-type (![]() ) Hamiltonian including operators for isotropic and anisotropic couplings. It turns out that a system so described will cross over to Ising-type behavior; for further details, see Fisher (Reference Fisher1974) and Cardy (Reference Cardy1996).
) Hamiltonian including operators for isotropic and anisotropic couplings. It turns out that a system so described will cross over to Ising-type behavior; for further details, see Fisher (Reference Fisher1974) and Cardy (Reference Cardy1996).
Crossover theory is empirically successful, and such successes are predicated on deriving a relationship between operators and the details of physical systems. Although the operators for which such a correspondence can be shown are not irrelevant—these are relevant or marginally relevant operators—such correspondences help to establish that operators may play the required role in the field-theoretic RG explanation of universality.
For most instances of universality, we have yet to discover irrelevant operators that are physically interpreted as representing those features that distinguish multiple members of the same class. The phenomenon of crossover does suggest that such differences can be modeled. This in turn justifies the claim that the field-theoretic approach explains the universality of critical phenomena: it identifies shared features in our systems of interest (represented by the LGW Hamiltonian) sufficient to predict their display of the critical exponents. The expanded Hamiltonians with the irrelevant operators, together with the flow induced by the RG, may be depicted as in figure 1 and thus explain universality.
Is universality thus explained? I claimed above that one way to explain universality is by constructing a map between convergent flows and real physical systems (akin to AbsE). However, as noted above, no map can be explicitly constructed in this case since we do not know how to write down the irrelevant operators for the various systems of interest. Thus, an explanation of type AbsE with the necessary link to ComQ may be found only in principle; in practice ComE goes through.
4.2. Real-Space RG
The real-space RG may be understood by appeal to simple diagrams like that in figure 2. It is thus unfortunate that, as I argue in this section, the explanation provided by the real-space RG is inadequate.

Figure 2. Single application of the real-space RG where a block of spins is replaced by a single larger spin. From Fisher (Reference Fisher1998); reproduced with permission of the American Physical Society via Copyright Clearance Center.
The real-space approach allows for the derivation of critical exponents consistent with empirical observation for various models. Furthermore, we have an account of relevance and irrelevance and the claim that “in general, for fixed points describing second-order critical points, there are two relevant parameters: the temperature and the field conjugate to the order parameter (for the magnet it is the magnetic field)” (Cheung Reference Cheung2011, 51). Why is this explanation of universality not sufficient?
In section 2 I categorized a few options for how universality may be explained. I claimed that SpecE was insufficient but ComE or a supplemented AbsE could do the job. I think that neither latter option is live in the real-space case. This is because the mathematical model employed does not have the tools to represent systems other than the archetypal system for each universality class; the problem is that the Ising model is designed specifically for magnetic systems. In what follows, I explore a number of ways it might be adapted to represent other members of its class: Kadanoff’s proposal and the lattice-gas analogy. I conclude that none of these adaptations allows for a general RG explanation of universality: insofar as the correct critical exponents are predicted, this is done for individual systems and a common-type explanation is unavailable.
While the field-theoretic approach makes use of a Hamiltonian derived from the Ising model, the Hamiltonian used in that approach is renormalizable. As such, it includes a scale-invariant core at the critical point that represents a range of different systems. That is how ComE is achieved: by showing what is in common and the general demonstration that all possible distinguishing features are irrelevant.
The real-space approach does not make use of a renormalizable Hamiltonian, nor does it have a formalism that establishes generally that the Hamiltonians apply across a wide range of systems. Likewise, there seems to be little hope that a picture like that in figure 1 can be shown to correspond to distinct systems in the same universality class having convergent flows. The reason is that the real-space approach relies on Ising-type models, which do not represent the other systems in the same class—the lattice-gas analogy provides a possible counterargument, discussed below. To claim that Ising models in fact represent all the different systems would be to assume universality rather than to explain it. While one may be able to demonstrate that each system in the same universality class shares certain features (e.g., symmetry and dimensionality), the real-space approach does not provide the resources to demonstrate that such commonality leads to common behavior in general: we do not have an argument available on the real-space approach that common symmetry and dimensionality is sufficient for universality.Footnote 23 Thus, commonality sufficient for common behavior cannot be adduced for a common-type explanation, nor can an AbsE-ComQ link be established. It is only by recourse to the field-theoretic approach that a full explanation of universality is available. Three responses to these claims ought to be considered.
First, it could be noted that irrelevant couplings are discussed in the real-space context, and we know that only a few relevant couplings determine the critical exponents; thus, perhaps these relevant couplings provide the ComE explanation. But the model is still tied to the details of the system it was created to represent. Thus, the irrelevant couplings are those aspects of that system that will not affect its critical exponents. To show that some aspects of a given system are irrelevant to its behavior in a given context is quite different from showing that all systems with the same relevant properties (and with different properties otherwise) will display the behavior. The former, system-relative claim is established by the real-space RG, but the latter more general claim is not. The success of the field-theoretic RG explanation is due to the fact that we can categorize operators as relevant or irrelevant quite generally. In the real-space RG, potential couplings are only categorized for a given model.
Second, since the blocking transformation is tailored specifically to the behavior of systems at criticality, the transformation itself might represent the common features for ComE. The transformation is constructed so as to mirror the self-similarity of such systems, and its application to systems at criticality is thus justified. This would mean that the real-space RG explains universality by appeal to the fact that all these systems have some commonality (i.e., their self-similarity) that justifies the use of these techniques to derive their critical exponents.
The problem with this claim is that the real-space RG approach does not simply derive the exponents from the blocking transformations. In fact, such exponents are derived by applying the blocking transformation and then truncating the Hamiltonian so that it will retain its original form. As such, the original Hamiltonian significantly determines the application of the real-space RG and the exponents derived. It is thus not quite right to claim that self-similarity is a common feature sufficient for universality. Moreover, if one considers the phenomenon of crossover, it is clear that this depends specifically on the terms in the Hamiltonian of each system. I raise this here as evidence that the initial Hamiltonian is crucial to the real-space derivation and explanation. As such, the appeal to a common blocking RG transformation cannot provide a common-type explanation.
Third, for the remainder of this section I consider a pair of specific elaborations of the real-space RG approach that provide limited explanations of universality. The first demonstrates that critical exponents derived on the real-space approach do not depend on certain couplings in the Ising model. The second—the lattice-gas analogy—relates liquid gas to magnetic models. Neither, I argue, provides a general account of the range of classes and systems that behave universally. Such general accounts are currently unavailable.
Batterman (Reference Batterman2017b) highlights an argument found in Kadanoff (Reference Kadanoff and Green1971) to the effect that one can introduce a parameter λ into the free energy function for the Ising model, and it can be demonstrated that the critical exponents do not depend on the value of this parameter. In Kadanoff’s example this parameter corresponds to the ratio of the couplings for nearest-neighbor to next-nearest-neighbor models. As such, we may be assured of a particular kind of generality of the Ising model representation. The independence of the critical exponents from such parameters is, however, insufficient to establish the requisite generality for the real-space approach. If a similar argument were available for the variation between a liquid-gas system and a magnetic system, then this explanation would be far more convincing; such an argument has not yet been presented.
The lattice-gas analogy exemplifies a possible mapping that may provide reasons to view the Ising model as representing liquid-gas systems in addition to magnetic systems. If this succeeds it would justify a common-type explanation for the limited case at hand. However, it would not justify claims to an RG explanation of universality because the mapping is not one sourced in the relevance and irrelevance criteria of the RG. Rather, it would provide a distinct explanation of universality. Furthermore, it is not generalizable to other members of the various universality classes. In this respect the field-theoretic approach outdoes the real-space approach, even with the lattice-gas analogy.
The lattice-gas model is summarized as follows:
Consider the Hamiltonian
where ![]() , 1 depending if the site is empty or occupied, and μ is the chemical potential. If we define
, 1 depending if the site is empty or occupied, and μ is the chemical potential. If we define ![]() , we reobtain the Ising-model Hamiltonian with
, we reobtain the Ising-model Hamiltonian with ![]() , where q is the coordination number of the lattice. Thus, for
, where q is the coordination number of the lattice. Thus, for ![]() , there is an equivalent transition separating the gas phase for
, there is an equivalent transition separating the gas phase for ![]() from a liquid phase for
from a liquid phase for ![]() .
.
This mapping is clear enough but merely shifts the burden of justification. As Pelissetto and Vicari acknowledge, “The lattice gas is a crude approximation of a real fluid” (Reference Pelissetto and Vicari2002, 554). Their justification for this approximation is empirical: “Nonetheless, the universality of the behavior around a continuous phase-transition point implies that certain quantities, e.g., critical exponents … are identical in a real fluid and in a lattice gas, and hence in the Ising model” (554). The model is provided the following rationale in the context of its original presentation: “Theoretically speaking, by making the lattice constant smaller and smaller one could obtain successively better approximations to the partition function of the real gas” (Lee and Yang Reference Lee and Yang1952, 412). Although gases may often be modeled as continuum gases, this is itself an idealization that requires a physical justification. Furthermore, the problem with the application of the Ising model to a physical gas is not that the Ising model is discretized—we expect gases to contain finitely many particles. Rather one should be concerned that the molecules have more degrees of freedom available to them than the components of uniaxial magnets. This is not to suggest that idealized models are intrinsically problematic; rather, I am skeptical that this physical justification of the analogy is sufficient to explain universality.
If we were to accept this justification of the lattice-gas model, further questions would be raised, for magnets and liquid-gas systems do not display the same behavior away from the critical point. It is precisely because the systems behave so differently much of the time that universality is startling. Thus, even if the lattice-gas analogy gave a good account of liquid-gas systems at criticality, additional details are needed to explain the limited applicability away from criticality.
Do we have an explanation why these different systems undergo similar behavior near the critical point? It turns out, and this is surprising and interesting, that uniaxial magnets and fluids have some behavior that is approximately described by the same model, namely, the Ising model. But this result is a consequence of careful mapping between the systems; it was not an RG result. The RG was used for the derivation of the critical exponents from the models, not in the justification of the applicability of the models to various physical systems. The lattice-gas analogy provides an account of what is in common between systems with diverse microphysics by mapping the Ising model to a liquid-gas model. However, no generalized real-space RG explanation is available that tells us why all the members of the same class have identical behavior.
On the field-theoretic approach we were able to identify common features and demonstrate their sufficiency for common behavior—that is how ComE was achieved. On the real-space approach, insofar as we can derive the same critical exponents for different systems, we still have no characterization of their common features that would serve to demystify universality. I do not purport to rule out real-space explanations in principle: if the physics were sufficiently developed to allow real-space derivations for each member of each model, and one could use these to adduce common features, then universality would likely be explained. Alternatively, a Kadanoff-type approach might be extended for a more generalized account of universality. In section 2 I argued that SpecE and ComE explanations were to be distinguished: the real-space RG currently only provides SpecE for certain models but is insufficient for ComE.
On neither approach to the RG do we have a fully worked out bottom-up explanation of universality. Nonetheless, I claim that the field-theoretic approach is adequate just because we have a generalized account of universality on that approach, which provides conditions that, if satisfied, predict common behavior across a class of systems.
5. Conclusion
Batterman suggests the RG explanation of universality works by “first constructing an enormous abstract space each point of which might represent a real fluid, a possible fluid, a solid, etc. Next one induces on this space a transformation that has the effect, essentially, of eliminating degrees of freedom by some kind of averaging rule. … Those systems/models (points in the space) that flow to the same fixed point are in the same universality class—the universality class is delimited—and they will exhibit the same macro-behavior” (Reference Batterman2017a, 8–9). My aim in this article has been to spell out the physical details that underpin the quote above. In so doing I argued that the picture Batterman provides of the RG explanation is not workable on the real-space approach but that it is consistent with the field-theoretic approach. However, I claimed that, because of certain outstanding technical lacunae, the field-theoretic RG approach is better conceived as providing an explanation that adduces common aspects of the various systems that exhibit universality and demonstrates that such common aspects are sufficient for universal behavior.
The real-space approach starts with a model and derives the critical exponents on the basis of that model. It is difficult to see how this approach adequately explains the phenomenon that heterogeneous systems have identical critical behavior. The field-theoretic approach explains universality by positing an effective Hamiltonian and deriving the critical exponents from that. That this Hamiltonian is demonstrably general grounds the explanation of universality.




