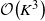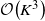1. Introduction
Restless bandits are a class of sequential resource allocation problems concerned with allocating one or more resources among several alternative processes where the evolution of the processes depends on the resources allocated to them. Such models arise in various applications, such as machine maintenance [Reference Glazebrook, Mitchell and Ansell18], congestion control [Reference Avrachenkov, Ayesta, Doncel and Jacko7], healthcare [Reference Deo11], finance [Reference Glazebrook, Hodge and Kirkbride15], channel scheduling [Reference Liu and Zhao21], smart grid [Reference Abad and Iyengar1], and others.
Restless bandits are a generalization of classical multi-armed bandits [Reference Gittins, Glazebrook and Weber13], where the processes remain frozen when resources are not allocated to them. Gittins [Reference Gittins14] showed that when a single resource is to be allocated among multiple processes, the optimal policy has a simple structure: compute an index for each process and allocate the resource to the process with the largest (or the lowest) index. In contrast, the general restless bandit problem is pspace-hard [Reference Papadimitriou and Tsitsiklis27]. Whittle [Reference Whittle32] showed that index-based policies are optimal for the Lagrangian relaxation of the restless bandit problem and argued that the corresponding index, now called the Whittle index, is a reasonable heuristic for restless bandit problems. Subsequently, it has been shown that the Whittle index heuristic is optimal under some conditions [Reference Lott and Teneketzis22, Reference Weber and Weiss31] and performs well in practice [Reference Ansell, Glazebrook, Niño-Mora and O’Keeffe5, Reference Glazebrook and Mitchell16, Reference Glazebrook, Ruiz-Hernandez and Kirkbride19].
The Whittle index heuristic is applicable if a technical condition known as indexability is satisfied. Sufficient conditions for indexability have been investigated under specific modeling assumptions: two-state restless bandits [Reference Avrachenkov, Ayesta, Doncel and Jacko7, Reference Liu and Zhao21]; monotone bandits [Reference Ansell, Glazebrook, Niño-Mora and O’Keeffe5, Reference Avrachenkov, Ayesta, Doncel and Jacko7, Reference Glazebrook, Hodge and Kirkbride15]; models with right-skip-free transitions [Reference Glazebrook, Mitchell and Ansell18, Reference Glazebrook, Ruiz-Hernandez and Kirkbride19]; models with monotone or convex cost/reward [Reference Ansell, Glazebrook, Niño-Mora and O’Keeffe5–Reference Ayesta, Erausquin and Jacko8, Reference Glazebrook, Ruiz-Hernandez and Kirkbride19, Reference Yu, Xu and Tong33]; models satisfying partial conservation laws [Reference Niño-Mora23, Reference Niño-Mora25]; and models arising in specific applications [Reference Archibald, Black and Glazebrook6, Reference Ayesta, Erausquin and Jacko8, Reference Glazebrook and Mitchell16, Reference Glazebrook, Mitchell and Ansell18, Reference Glazebrook, Ruiz-Hernandez and Kirkbride19].
Niño-Mora [Reference Niño-Mora25, Reference Niño-Mora26] proposed a generalization of the Whittle index called the marginal productivity index (MPI) for resource allocation problems where processes can be allocated fractional resources. In [Reference Niño-Mora25], he also proposed an algorithm called the adaptive greedy algorithm, to compute the MPI when the model satisfies a technical condition called partial conservation laws (PCL). For restless bandits which satisfy the PCL condition, the Whittle index can be computed using the adaptive greedy algorithm. However, for general restless bandits, there are no known efficient algorithms to exactly compute the Whittle index. It is possible to approximately compute the Whittle index by conducting a binary search over a penalty for the active action (or a subsidy for the passive action) [Reference Akbarzadeh and Mahajan2, Reference Qian, Zhang, Krishnamachari and Tambe29], but such a binary search is computationally expensive, because each step of the binary search requires solving a dynamic program.
In this paper, we revisit the restless bandit problem and present three contributions. Our first contribution is to provide general sufficient conditions for indexability which are based on an alternative characterization of the passive set. We also present easy-to-verify refinements of these sufficient conditions.
Our second contribution is to use a novel geometric interpretation of the Whittle index to show that a refinement of the adaptive greedy algorithm proposed by Niño-Mora [Reference Niño-Mora25] computes the Whittle index for all indexable restless bandits. We provide a computationally efficient implementation, which computes the Whittle indices of a restless bandit with K states in
![]() $\mathcal{O}\!\left(K^3\right)$
computations.
$\mathcal{O}\!\left(K^3\right)$
computations.
Our third contribution is to present three special cases: (i) restless bandits with optimal threshold-based policy, which were previously studied in [Reference Akbarzadeh and Mahajan3, Reference Ansell, Glazebrook, Niño-Mora and O’Keeffe5, Reference Avrachenkov, Ayesta, Doncel and Jacko7, Reference Glazebrook, Hodge and Kirkbride15, Reference Glazebrook, Kirkbride and Ouenniche17, Reference Wang, Ren, Mo and Shi30], (ii) stochastic monotone bandits which may be considered as a generalization of monotone bandits [Reference Ansell, Glazebrook, Niño-Mora and O’Keeffe5, Reference Avrachenkov, Ayesta, Doncel and Jacko7, Reference Glazebrook, Hodge and Kirkbride15], and (iii) restless bandits with controlled restarts, similar to [Reference Akbarzadeh and Mahajan3, Reference Wang, Ren, Mo and Shi30], which are a generalization of the restart models [Reference Glazebrook, Mitchell and Ansell18, Reference Glazebrook, Ruiz-Hernandez and Kirkbride19]. We show that these models are always indexable and the Whittle index can be computed in closed form.
Finally, we present a detailed numerical study comparing the performance of the Whittle index policy with that of the optimal and myopic policies. Our study shows that in general, the performance of Whittle index policy is comparable to that of the optimal policy and considerably better than that of the myopic policy.
Notation. Uppercase letters (X, Y, etc.) denote random variables, lowercase letters (x, y, etc.) denote their realization, and script letters (
![]() $\mathcal{X}$
,
$\mathcal{X}$
,
![]() ${\mathcal Y}$
, etc.) denote their state spaces. Subscripts denote time: so,
${\mathcal Y}$
, etc.) denote their state spaces. Subscripts denote time: so,
![]() $X_t$
denotes a system variable at time t and
$X_t$
denotes a system variable at time t and
![]() $X_{1:t}$
is shorthand for the system variables
$X_{1:t}$
is shorthand for the system variables
![]() $(X_1, \dots,X_t)$
.
$(X_1, \dots,X_t)$
.
![]() $\mathbb{P}({\cdot})$
denotes the probability of an event;
$\mathbb{P}({\cdot})$
denotes the probability of an event;
![]() $\mathbb{E}[{\cdot}]$
denotes the expectation of a random variable.
$\mathbb{E}[{\cdot}]$
denotes the expectation of a random variable.
![]() $\mathbb{Z}$
and
$\mathbb{Z}$
and
![]() $\mathbb{R}$
denote the sets of integers and real numbers. Given a matrix P,
$\mathbb{R}$
denote the sets of integers and real numbers. Given a matrix P,
![]() $P_{ij}$
denotes its (i,j)th element.
$P_{ij}$
denotes its (i,j)th element.
2. Restless bandits: problem formulation and solution concept
2.1. Restless bandit process
A discrete-time restless bandit process (RB) is a controlled Markov process
![]() $(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c, x_0)$
where
$(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c, x_0)$
where
![]() $\mathcal{X}$
denotes the state space, which is a finite or countable set;
$\mathcal{X}$
denotes the state space, which is a finite or countable set;
![]() $\{0, 1\}$
denotes the action space, where the action 0 is called the passive action and the action 1 is the active action; P(a),
$\{0, 1\}$
denotes the action space, where the action 0 is called the passive action and the action 1 is the active action; P(a),
![]() $a \in \{0, 1\}$
, denotes the transition matrix when the action a is chosen;
$a \in \{0, 1\}$
, denotes the transition matrix when the action a is chosen;
![]() $c\,:\, \mathcal{X} \times \{0, 1\} \to \mathbb{R}$
denotes the cost function; and
$c\,:\, \mathcal{X} \times \{0, 1\} \to \mathbb{R}$
denotes the cost function; and
![]() $x_0$
denotes the initial state. We use
$x_0$
denotes the initial state. We use
![]() $X_t$
and
$X_t$
and
![]() $A_t$
to denote the action of the process at time t. The process evolves in a controlled Markov manner; i.e., for any realization
$A_t$
to denote the action of the process at time t. The process evolves in a controlled Markov manner; i.e., for any realization
![]() $x_{0\,:\,t+1}$
of
$x_{0\,:\,t+1}$
of
![]() $X_{0\,:\,t+1}$
and
$X_{0\,:\,t+1}$
and
![]() $a_{0\,:\,t+1}$
of
$a_{0\,:\,t+1}$
of
![]() $A_{0\,:\,t+1}$
, we have
$A_{0\,:\,t+1}$
, we have
![]() $\mathbb{P}\big( {X}_{t+1} = {x}_{t+1} | {X}_{0\,:\,t} = {x}_{0\,:\,t}, {A}_{0\,:\,t} = {a}_{0\,:\,t}\big)=\mathbb{P} \big( X_{t+1} = x_{t+1} | X_{t} = x_{t}, A_{t} = a_t\big)$
, which we denote by
$\mathbb{P}\big( {X}_{t+1} = {x}_{t+1} | {X}_{0\,:\,t} = {x}_{0\,:\,t}, {A}_{0\,:\,t} = {a}_{0\,:\,t}\big)=\mathbb{P} \big( X_{t+1} = x_{t+1} | X_{t} = x_{t}, A_{t} = a_t\big)$
, which we denote by
![]() $P_{x_t x_{t+1}}(a_t)$
.
$P_{x_t x_{t+1}}(a_t)$
.
2.2. Restless multi-armed bandit problem
A restless multi-armed bandit is a collection of n independent RBs
![]() $\big(\mathcal{X}^i, \{0, 1\}, \{P^i(a)\}_{a \in \{0, 1\}}, c^i, x^i_0\big)$
,
$\big(\mathcal{X}^i, \{0, 1\}, \{P^i(a)\}_{a \in \{0, 1\}}, c^i, x^i_0\big)$
,
![]() $i \in {\mathcal N} \,:\!=\, \{1, \ldots, n\}$
. A decision-maker observes the state of all RBs, may choose to activate only
$i \in {\mathcal N} \,:\!=\, \{1, \ldots, n\}$
. A decision-maker observes the state of all RBs, may choose to activate only
![]() $m < n$
of them, and incurs a cost equal to the sum of the costs incurred by the individual RBs.
$m < n$
of them, and incurs a cost equal to the sum of the costs incurred by the individual RBs.
Let
![]() $\boldsymbol{\mathcal{X}} \,:\!=\, \prod_{i \in \mathcal N} \mathcal{X}^i$
and
$\boldsymbol{\mathcal{X}} \,:\!=\, \prod_{i \in \mathcal N} \mathcal{X}^i$
and
![]() $\boldsymbol{\mathcal A}(m) \,:\!=\, \bigl\{ \boldsymbol{a} = \big(a^1, \ldots, a^n\big) \in {\mathcal A}^{n} \,:\, \sum_{i \in {\mathcal N}} a^i = m\bigr\}$
denote the joint state space and the feasible action space, respectively. Let
$\boldsymbol{\mathcal A}(m) \,:\!=\, \bigl\{ \boldsymbol{a} = \big(a^1, \ldots, a^n\big) \in {\mathcal A}^{n} \,:\, \sum_{i \in {\mathcal N}} a^i = m\bigr\}$
denote the joint state space and the feasible action space, respectively. Let
![]() ${\boldsymbol{X}}_t \,:\!=\, \big(X^1_t, \dots X^n_t\big)$
and
${\boldsymbol{X}}_t \,:\!=\, \big(X^1_t, \dots X^n_t\big)$
and
![]() ${\boldsymbol{A}}_t = \big(A^1_t, \dots, A^n_t\big)$
denote the joint state and actions at time t. As the RBs evolve independently, for any realization
${\boldsymbol{A}}_t = \big(A^1_t, \dots, A^n_t\big)$
denote the joint state and actions at time t. As the RBs evolve independently, for any realization
![]() ${\boldsymbol{x}}_{0\,:\,t}$
of
${\boldsymbol{x}}_{0\,:\,t}$
of
![]() ${\boldsymbol{X}}_{0\,:\,t}$
and
${\boldsymbol{X}}_{0\,:\,t}$
and
![]() $\boldsymbol{a}_{0\,:\,t}$
of
$\boldsymbol{a}_{0\,:\,t}$
of
![]() ${\boldsymbol{A}}_{0\,:\,t}$
, we have
${\boldsymbol{A}}_{0\,:\,t}$
, we have
When the system is in the state
![]() ${\boldsymbol{x}}_t = \big(x^1_t, \ldots, x^n_t\big)$
and the decision-maker chooses action
${\boldsymbol{x}}_t = \big(x^1_t, \ldots, x^n_t\big)$
and the decision-maker chooses action
![]() $\boldsymbol{a}_t = \big(a^1_t, \ldots, a^n_t\big)$
, the system incurs a cost
$\boldsymbol{a}_t = \big(a^1_t, \ldots, a^n_t\big)$
, the system incurs a cost
![]() $\bar{c}({\boldsymbol{x}}_t, \boldsymbol{a}_t) \,:\!=\, \sum_{i \in {\mathcal N}} c^i\big(x^i_t, a^i_t\big)$
. The decision-maker chooses his actions using a time-homogeneous Markov policy
$\bar{c}({\boldsymbol{x}}_t, \boldsymbol{a}_t) \,:\!=\, \sum_{i \in {\mathcal N}} c^i\big(x^i_t, a^i_t\big)$
. The decision-maker chooses his actions using a time-homogeneous Markov policy
![]() ${\boldsymbol{g}}\,:\, \boldsymbol{\mathcal X} \to \boldsymbol{\mathcal A}(m)$
, i.e., chooses
${\boldsymbol{g}}\,:\, \boldsymbol{\mathcal X} \to \boldsymbol{\mathcal A}(m)$
, i.e., chooses
![]() ${\boldsymbol{A}}_t = {\boldsymbol{g}}({\boldsymbol{X}}_t)$
. The performance of any Markov policy
${\boldsymbol{A}}_t = {\boldsymbol{g}}({\boldsymbol{X}}_t)$
. The performance of any Markov policy
![]() ${\boldsymbol{g}}$
is given by
${\boldsymbol{g}}$
is given by
 \begin{equation*}J^{({\boldsymbol{g}})}({\boldsymbol{x}}_0) \,:\!=\, (1-\beta) \mathbb{E}\Biggl[ \sum_{t = 0}^{\infty}\beta^t \bar{c}({\boldsymbol{X}}_t, {\boldsymbol{g}}({\boldsymbol{X}}_t)) \bigg| {\boldsymbol{X}}_0 = {\boldsymbol{x}}_0\Biggr],\end{equation*}
\begin{equation*}J^{({\boldsymbol{g}})}({\boldsymbol{x}}_0) \,:\!=\, (1-\beta) \mathbb{E}\Biggl[ \sum_{t = 0}^{\infty}\beta^t \bar{c}({\boldsymbol{X}}_t, {\boldsymbol{g}}({\boldsymbol{X}}_t)) \bigg| {\boldsymbol{X}}_0 = {\boldsymbol{x}}_0\Biggr],\end{equation*}
where
![]() $\beta \in (0, 1)$
is the discount factor and
$\beta \in (0, 1)$
is the discount factor and
![]() ${\boldsymbol{x}}_0$
is the initial state of the system.
${\boldsymbol{x}}_0$
is the initial state of the system.
We are interested in the following optimization problem.
Problem 1. Given the discount factor
![]() $\beta \in (0,1)$
, the total number n of arms, the number m of active arms, RBs
$\beta \in (0,1)$
, the total number n of arms, the number m of active arms, RBs
![]() $\big(\mathcal{X}^i, \{0, 1\}, \{P^i(a)\}_{a \in \{0, 1\}}, c^i, x^i_0\big)$
,
$\big(\mathcal{X}^i, \{0, 1\}, \{P^i(a)\}_{a \in \{0, 1\}}, c^i, x^i_0\big)$
,
![]() $i \in {\mathcal N}$
, and the initial state
$i \in {\mathcal N}$
, and the initial state
![]() ${\boldsymbol{x}}_0 \in \boldsymbol{\mathcal X}$
, choose a Markov policy
${\boldsymbol{x}}_0 \in \boldsymbol{\mathcal X}$
, choose a Markov policy
![]() ${\boldsymbol{g}} \,:\, \boldsymbol{\mathcal X} \to \boldsymbol{\mathcal A}(m)$
that minimizes
${\boldsymbol{g}} \,:\, \boldsymbol{\mathcal X} \to \boldsymbol{\mathcal A}(m)$
that minimizes
![]() $J^{({\boldsymbol{g}})}({\boldsymbol{x}}_0)$
.
$J^{({\boldsymbol{g}})}({\boldsymbol{x}}_0)$
.
Problem 1 is a multi-stage stochastic control problem and one can obtain an optimal solution using dynamic programming. However, the dynamic programming solution is intractable for large n since the cardinality of the state space is
![]() $\prod_{i \in {\mathcal N}}|\mathcal{X}^i|$
, which grows exponentially with n. In the next section, we describe a heuristic known as the Whittle index to efficiently obtain a suboptimal solution of the problem.
$\prod_{i \in {\mathcal N}}|\mathcal{X}^i|$
, which grows exponentially with n. In the next section, we describe a heuristic known as the Whittle index to efficiently obtain a suboptimal solution of the problem.
2.3. Indexability and the Whittle index
Consider an RB
![]() $(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c, x_0)$
. For any
$(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c, x_0)$
. For any
![]() $\lambda \in \mathbb{R}$
, we consider a Markov decision process
$\lambda \in \mathbb{R}$
, we consider a Markov decision process
![]() $\{ \mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c_\lambda, x_0 \}$
, where
$\{ \mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c_\lambda, x_0 \}$
, where
The parameter
![]() $\lambda$
may be viewed as a penalty for taking the active action. The performance of any time-homogeneous policy
$\lambda$
may be viewed as a penalty for taking the active action. The performance of any time-homogeneous policy
![]() $g\,:\, \mathcal{X} \to \{0, 1\}$
is
$g\,:\, \mathcal{X} \to \{0, 1\}$
is
 \begin{equation}J^{(g)}_{\lambda}(x_0) \,:\!=\, (1-\beta) \mathbb{E}\Biggl[ \sum_{t = 0}^{\infty} \beta^t c_\lambda(X_t, g(X_t)) \bigg| X_0 = x_0 \Biggr].\end{equation}
\begin{equation}J^{(g)}_{\lambda}(x_0) \,:\!=\, (1-\beta) \mathbb{E}\Biggl[ \sum_{t = 0}^{\infty} \beta^t c_\lambda(X_t, g(X_t)) \bigg| X_0 = x_0 \Biggr].\end{equation}
Consider the following optimization problem.
Problem 2. Given the RB
![]() $\big(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c_\lambda, x_0\big)$
and the discount factor
$\big(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c_\lambda, x_0\big)$
and the discount factor
![]() $\beta \in (0,1)$
, choose a Markov policy
$\beta \in (0,1)$
, choose a Markov policy
![]() $g\,:\, \mathcal{X} \to \{0, 1\}$
to minimize
$g\,:\, \mathcal{X} \to \{0, 1\}$
to minimize
![]() $J_{\lambda}^{(g)}(x_0)$
.
$J_{\lambda}^{(g)}(x_0)$
.
Problem 2 is also a Markov decision process and one can obtain an optimal solution using dynamic programming. Let
![]() $V_\lambda\,:\, \mathcal{X} \to \mathbb{R}$
be the unique fixed point of the following:
$V_\lambda\,:\, \mathcal{X} \to \mathbb{R}$
be the unique fixed point of the following:
where
Let
![]() $g_\lambda(x)$
denote the minimizer of the right-hand side of
$g_\lambda(x)$
denote the minimizer of the right-hand side of
![]() $(3)$
, where we set
$(3)$
, where we set
![]() $g_\lambda(x) = 1$
if
$g_\lambda(x) = 1$
if
![]() $H_\lambda(x, 0) = H_\lambda(x, 1)$
. Then, from Markov decision theory [Reference Puterman28], we know that the time-homogeneous policy
$H_\lambda(x, 0) = H_\lambda(x, 1)$
. Then, from Markov decision theory [Reference Puterman28], we know that the time-homogeneous policy
![]() $g_\lambda$
is optimal for Problem 2.
$g_\lambda$
is optimal for Problem 2.
Define the passive set
![]() ${\Pi}_\lambda$
to be the set of states where the passive action is optimal, i.e.,
${\Pi}_\lambda$
to be the set of states where the passive action is optimal, i.e.,
Definition 1 (Indexability). An RB is indexable if
![]() ${\Pi}_\lambda$
is increasing in
${\Pi}_\lambda$
is increasing in
![]() $\lambda$
, i.e., for any
$\lambda$
, i.e., for any
![]() $\lambda^{\prime}, \lambda^{\prime\prime} \in \mathbb{R}$
,
$\lambda^{\prime}, \lambda^{\prime\prime} \in \mathbb{R}$
,
![]() $\lambda^{\prime} \leq \lambda^{\prime\prime}$
implies that
$\lambda^{\prime} \leq \lambda^{\prime\prime}$
implies that
![]() ${\Pi}_{\lambda^{\prime}} \subseteq {\Pi}_{\lambda^{\prime\prime}}$
.
${\Pi}_{\lambda^{\prime}} \subseteq {\Pi}_{\lambda^{\prime\prime}}$
.
Definition 2 (Whittle index). The Whittle index of state x of an indexable RB is the smallest value of
![]() $\lambda$
for which x is part of the passive set
$\lambda$
for which x is part of the passive set
![]() ${\Pi}_{\lambda}$
, i.e.,
${\Pi}_{\lambda}$
, i.e.,
![]() $ w(x) = \inf \left\{ \lambda \in \mathbb{R} \,:\, x \in {\Pi}_{\lambda} \right\}\!. $
$ w(x) = \inf \left\{ \lambda \in \mathbb{R} \,:\, x \in {\Pi}_{\lambda} \right\}\!. $
Alternatively, the Whittle index w(x) is a value of the penalty
![]() $\lambda$
for which the optimal policy is indifferent between taking the active and the passive action when the RB is in state x.
$\lambda$
for which the optimal policy is indifferent between taking the active and the passive action when the RB is in state x.
2.4. Whittle index heuristic
A restless multi-armed bandit problem is said to be indexable if all RBs are indexable. For indexable problems, the Whittle index heuristic is as follows: Compute the Whittle indices of all arms offline. Then, at each time, obtain the Whittle indices of the current state of all arms and play arms with the m largest Whittle indices.
As mentioned earlier, the Whittle index policy is a popular approach for restless bandits because (i) its complexity is linear in the number of alternatives and (ii) its performance is often close to optimal in practice [Reference Ansell, Glazebrook, Niño-Mora and O’Keeffe5, Reference Glazebrook and Mitchell16, Reference Glazebrook, Ruiz-Hernandez and Kirkbride19]. However, there are only a few general conditions to check indexability for general models.
2.5. Alternative characterizations of the passive set
We now present alternative characterizations of the passive set, which are important for the sufficient conditions for indexability that we provide later.
Let
![]() $\Sigma$
denote the family of all stopping times with respect to the natural filtration of
$\Sigma$
denote the family of all stopping times with respect to the natural filtration of
![]() $\{X_t\}_{t \ge 0}$
. For any state
$\{X_t\}_{t \ge 0}$
. For any state
![]() $x \in \mathcal{X}$
, penalty
$x \in \mathcal{X}$
, penalty
![]() $\lambda \in \mathbb{R}$
, and stopping time
$\lambda \in \mathbb{R}$
, and stopping time
![]() $\tau \in \Sigma$
, define
$\tau \in \Sigma$
, define
 \begin{align} M(x, \tau) &\,:\!=\, \mathbb{E}\bigl[ \beta^{\tau} | X_0 = x, \{ A_t = 0 \}_{t = 0}^{\tau-1} \bigr], \notag \\ L(x, \tau) &\,:\!=\, \mathbb{E}\Bigg[ \sum_{t = 0}^{\tau-1} \beta^{t} c(X_t, 0) + \beta^{\tau} c(X_{\tau}, 1) \Bigm| X_0 = x, \{ A_t = 0 \}_{t = 0}^{\tau-1} \Bigg], \notag \\ W_\lambda(x) &\,:\!=\, (1-\beta)\lambda + \beta \sum_{y \in \mathcal{X}} P_{xy}(1) V_\lambda(x).\end{align}
\begin{align} M(x, \tau) &\,:\!=\, \mathbb{E}\bigl[ \beta^{\tau} | X_0 = x, \{ A_t = 0 \}_{t = 0}^{\tau-1} \bigr], \notag \\ L(x, \tau) &\,:\!=\, \mathbb{E}\Bigg[ \sum_{t = 0}^{\tau-1} \beta^{t} c(X_t, 0) + \beta^{\tau} c(X_{\tau}, 1) \Bigm| X_0 = x, \{ A_t = 0 \}_{t = 0}^{\tau-1} \Bigg], \notag \\ W_\lambda(x) &\,:\!=\, (1-\beta)\lambda + \beta \sum_{y \in \mathcal{X}} P_{xy}(1) V_\lambda(x).\end{align}
Let
![]() $h_{\tau, \lambda}$
denote the (history-dependent) policy that takes the passive action up to time
$h_{\tau, \lambda}$
denote the (history-dependent) policy that takes the passive action up to time
![]() $\tau-1$
, takes the active action at time
$\tau-1$
, takes the active action at time
![]() $\tau$
, and then follows the optimal policy
$\tau$
, and then follows the optimal policy
![]() $g_\lambda$
(for Problem 2). We now present different characterizations of the passive set.
$g_\lambda$
(for Problem 2). We now present different characterizations of the passive set.
Proposition 1. The following characterizations of the passive set are equivalent:
-
 $\Pi^{(a)}_\lambda = \{x \in \mathcal{X} \,:\, g_\lambda(x) = 0 \}$
,
$\Pi^{(a)}_\lambda = \{x \in \mathcal{X} \,:\, g_\lambda(x) = 0 \}$
, -
 $\Pi^{(b)}_\lambda = \{x \in \mathcal{X} \,:\, H_\lambda(x, 0) < H_\lambda(x, 1) \}$
,
$\Pi^{(b)}_\lambda = \{x \in \mathcal{X} \,:\, H_\lambda(x, 0) < H_\lambda(x, 1) \}$
, -
 $\Pi^{(c)}_\lambda = \Big\{x \in \mathcal{X} \,:\, \exists \sigma \in \Sigma, \sigma \neq 0,\ {such\ that }\ J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) < J^{(h_0)}_{\lambda}(x) \Big\}$
,
$\Pi^{(c)}_\lambda = \Big\{x \in \mathcal{X} \,:\, \exists \sigma \in \Sigma, \sigma \neq 0,\ {such\ that }\ J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) < J^{(h_0)}_{\lambda}(x) \Big\}$
, -
 $\Pi^{(d)}_\lambda = \{x \in \mathcal{X} \,:\, \exists \sigma \in \Sigma, \sigma \neq 0, $
such that
$\Pi^{(d)}_\lambda = \{x \in \mathcal{X} \,:\, \exists \sigma \in \Sigma, \sigma \neq 0, $
such that
 $(1-\beta) \left( L(x, \sigma) - c(x, 1) \right) < W_\lambda(x) - \mathbb{E} [ \beta^{\sigma} W_\lambda(X_\sigma) | X_0 = x ] \}$
.
$(1-\beta) \left( L(x, \sigma) - c(x, 1) \right) < W_\lambda(x) - \mathbb{E} [ \beta^{\sigma} W_\lambda(X_\sigma) | X_0 = x ] \}$
.
See Appendix A for the proof.
3. Sufficient conditions for indexability
In this section, we identify sufficient conditions for an RB to be indexable.
3.1. Preliminary results
Consider an RB
![]() $(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c, x_0)$
. For any Markov policy
$(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}}, c, x_0)$
. For any Markov policy
![]() $g \,:\, \mathcal{X} \to \{0,1\}$
and
$g \,:\, \mathcal{X} \to \{0,1\}$
and
![]() $\lambda \in \mathbb{R}$
, we can write
$\lambda \in \mathbb{R}$
, we can write
where
 \begin{align*} D^{(g)}(x) &\,:\!=\, (1-\beta) \mathbb{E} \Bigg[ \sum_{t = 0}^{\infty} \beta^t c(X_t, g(X_t)) \bigg| X_0 = x \Bigg] \end{align*}
\begin{align*} D^{(g)}(x) &\,:\!=\, (1-\beta) \mathbb{E} \Bigg[ \sum_{t = 0}^{\infty} \beta^t c(X_t, g(X_t)) \bigg| X_0 = x \Bigg] \end{align*}
and
 \begin{align*} N^{(g)}(x) &\,:\!=\, (1-\beta) \mathbb{E} \Bigg[ \sum_{t = 0}^{\infty} \beta^t g(X_t) \bigg| X_0 = x \Bigg] \end{align*}
\begin{align*} N^{(g)}(x) &\,:\!=\, (1-\beta) \mathbb{E} \Bigg[ \sum_{t = 0}^{\infty} \beta^t g(X_t) \bigg| X_0 = x \Bigg] \end{align*}
are the expected discounted total cost and the expected number of activations under the policy g starting at the initial state x.
![]() $D^{(g)}({\cdot})$
and
$D^{(g)}({\cdot})$
and
![]() $N^{(g)}({\cdot})$
can be computed using policy evaluation formulas. In particular, define
$N^{(g)}({\cdot})$
can be computed using policy evaluation formulas. In particular, define
![]() $P^{(g)} \,:\, \mathcal{X} \times\mathcal{X} \to \mathbb{R}$
and
$P^{(g)} \,:\, \mathcal{X} \times\mathcal{X} \to \mathbb{R}$
and
![]() $c^{(g)} \,:\, \mathcal{X} \to \mathbb{R}$
as follows:
$c^{(g)} \,:\, \mathcal{X} \to \mathbb{R}$
as follows:
![]() $P^{(g)}_{xy} = P_{xy}(g(x)) \text{ and } c^{(g)}_\lambda(x) =c_\lambda(x, g(x)) = c^{(g)}(x, g(x)) + \lambda g(x)$
for any
$P^{(g)}_{xy} = P_{xy}(g(x)) \text{ and } c^{(g)}_\lambda(x) =c_\lambda(x, g(x)) = c^{(g)}(x, g(x)) + \lambda g(x)$
for any
![]() $x \in\mathcal{X}$
. We also view g as an element in
$x \in\mathcal{X}$
. We also view g as an element in
![]() $\{0,1\}^{|\mathcal{X}|}$
. Then, using the policy evaluation formula for infinite-horizon Markov decision processes [Reference Puterman28], we obtain
$\{0,1\}^{|\mathcal{X}|}$
. Then, using the policy evaluation formula for infinite-horizon Markov decision processes [Reference Puterman28], we obtain
We now provide a geometric interpretation of the value function
![]() $V_\lambda(x)$
as a function of
$V_\lambda(x)$
as a function of
![]() $\lambda$
. For any
$\lambda$
. For any
![]() $g \in {\mathcal G}$
, the plot of
$g \in {\mathcal G}$
, the plot of
![]() $J^{(g)}_\lambda(x) = D^{(g)}(x) + \lambda N^{(g)}(x)$
as a function of
$J^{(g)}_\lambda(x) = D^{(g)}(x) + \lambda N^{(g)}(x)$
as a function of
![]() $\lambda$
is a straight line with y-intercept
$\lambda$
is a straight line with y-intercept
![]() $D^{(g)}(x)$
and slope
$D^{(g)}(x)$
and slope
![]() $N^{(g)}(x)$
. By definition,
$N^{(g)}(x)$
. By definition,
![]() $ V_\lambda(x) = \inf_{g \in {\mathcal G}} J^{(g)}_\lambda(x). $
Thus,
$ V_\lambda(x) = \inf_{g \in {\mathcal G}} J^{(g)}_\lambda(x). $
Thus,
![]() $V_\lambda(x)$
is the lower concave envelope of the family of straight lines
$V_\lambda(x)$
is the lower concave envelope of the family of straight lines
![]() $\big\{J^{(g)}_\lambda(x)\big\}_{g \in {\mathcal G}}$
. (See Figure 1 for an illustration.) Thus, we have the following.
$\big\{J^{(g)}_\lambda(x)\big\}_{g \in {\mathcal G}}$
. (See Figure 1 for an illustration.) Thus, we have the following.

Figure 1. An illustration of the plot of
![]() $J^{({\cdot})}_\lambda(x)$
versus
$J^{({\cdot})}_\lambda(x)$
versus
![]() $\lambda$
for
$\lambda$
for
![]() $g \in {\mathcal G} \,:\!=\, \{h_1, h_2, h_3\}$
. Let
$g \in {\mathcal G} \,:\!=\, \{h_1, h_2, h_3\}$
. Let
![]() $\lambda^{ij}_c$
denote the
$\lambda^{ij}_c$
denote the
![]() $\lambda$
-value of the intersection of
$\lambda$
-value of the intersection of
![]() $J^{(h_i)}_\lambda(x)$
and
$J^{(h_i)}_\lambda(x)$
and
![]() $J^{(h_j)}_\lambda(x)$
. Note that in this plot, for all
$J^{(h_j)}_\lambda(x)$
. Note that in this plot, for all
![]() $\lambda \in \left( -\infty, \lambda^{12}_c \right]$
the policy
$\lambda \in \left( -\infty, \lambda^{12}_c \right]$
the policy
![]() $h_1$
is optimal; for all
$h_1$
is optimal; for all
![]() $\lambda \in \big[ \lambda^{12}_c, \lambda^{23}_c \big]$
the policy
$\lambda \in \big[ \lambda^{12}_c, \lambda^{23}_c \big]$
the policy
![]() $h_2$
is optimal; and for all
$h_2$
is optimal; and for all
![]() $\lambda \in \big[ \lambda^{23}_c, \infty\big)$
the policy
$\lambda \in \big[ \lambda^{23}_c, \infty\big)$
the policy
![]() $h_3$
is optimal. The lower concave envelope of
$h_3$
is optimal. The lower concave envelope of
![]() $J^{(h_i)}_\lambda(x)$
(shown as a thick line) is the value function
$J^{(h_i)}_\lambda(x)$
(shown as a thick line) is the value function
![]() $V_\lambda(x)$
, which is piecewise linear, concave, increasing, and continuous.
$V_\lambda(x)$
, which is piecewise linear, concave, increasing, and continuous.
Lemma 1. For any
![]() $x \in \mathcal{X}$
,
$x \in \mathcal{X}$
,
![]() $V_\lambda(x)$
is continuous, increasing, piecewise linear, and concave in
$V_\lambda(x)$
is continuous, increasing, piecewise linear, and concave in
![]() $\lambda$
. Furthermore, when
$\lambda$
. Furthermore, when
![]() ${\mathcal X}$
is finite,
${\mathcal X}$
is finite,
![]() $V_\lambda(x)$
is piecewise linear.
$V_\lambda(x)$
is piecewise linear.
Proof. For any Markov policy g,
![]() $N^{(g)}(x)$
is non-negative. Therefore,
$N^{(g)}(x)$
is non-negative. Therefore,
![]() $J^{(g)}_\lambda(x) = D^{(g)}(x) + \lambda N^{(g)}(x)$
is increasing and continuous in
$J^{(g)}_\lambda(x) = D^{(g)}(x) + \lambda N^{(g)}(x)$
is increasing and continuous in
![]() $\lambda$
. Since
$\lambda$
. Since
![]() $V_\lambda(x)$
is an infimization of a family of linear functions, it is concave (see Figure 1). In addition, as monotonicity and continuity are preserved under infimization, the value function is also increasing and continuous in
$V_\lambda(x)$
is an infimization of a family of linear functions, it is concave (see Figure 1). In addition, as monotonicity and continuity are preserved under infimization, the value function is also increasing and continuous in
![]() $\lambda$
. Finally, when
$\lambda$
. Finally, when
![]() ${\mathcal X}$
is finite, there are only finite number of pieces. Thus,
${\mathcal X}$
is finite, there are only finite number of pieces. Thus,
![]() $V_\lambda(x)$
is the minimum of finitely many linear functions, and hence piecewise linear.
$V_\lambda(x)$
is the minimum of finitely many linear functions, and hence piecewise linear.
Lemma 2. For any
![]() $\lambda^{\prime}, \lambda^{\prime\prime} \in \mathbb{R}$
,
$\lambda^{\prime}, \lambda^{\prime\prime} \in \mathbb{R}$
,
Consequently,
![]() $N^{(g_\lambda)}(x)$
is non-increasing in
$N^{(g_\lambda)}(x)$
is non-increasing in
![]() $\lambda$
.
$\lambda$
.
Proof. Recall that
![]() $V_\lambda(x) = J^{(g_\lambda)}_\lambda(x) \le J^{(g_{\lambda^{\prime}})}_\lambda(x)$
for any
$V_\lambda(x) = J^{(g_\lambda)}_\lambda(x) \le J^{(g_{\lambda^{\prime}})}_\lambda(x)$
for any
![]() $\lambda^{\prime} \neq \lambda$
. Thus,
$\lambda^{\prime} \neq \lambda$
. Thus,
 \begin{align} V_{\lambda^{\prime\prime}}(x) - V_{\lambda^{\prime}}(x) &= J^{(g_{\lambda^{\prime\prime}})}_{\lambda^{\prime\prime}}(x) - J^{(g_{\lambda^{\prime}})}_{\lambda^{\prime}}(x) \le J^{(g_{\lambda^{\prime}})}_{\lambda^{\prime\prime}}(x) - J^{(g_{\lambda^{\prime}})}_{\lambda^{\prime}}(x) \notag \\ &\stackrel{(a)}= (\lambda^{\prime\prime} - \lambda^{\prime})N^{(g_{\lambda^{\prime}})}(x), \end{align}
\begin{align} V_{\lambda^{\prime\prime}}(x) - V_{\lambda^{\prime}}(x) &= J^{(g_{\lambda^{\prime\prime}})}_{\lambda^{\prime\prime}}(x) - J^{(g_{\lambda^{\prime}})}_{\lambda^{\prime}}(x) \le J^{(g_{\lambda^{\prime}})}_{\lambda^{\prime\prime}}(x) - J^{(g_{\lambda^{\prime}})}_{\lambda^{\prime}}(x) \notag \\ &\stackrel{(a)}= (\lambda^{\prime\prime} - \lambda^{\prime})N^{(g_{\lambda^{\prime}})}(x), \end{align}
where (a) follows from (7). Similarly, we have
 \begin{align} V_{\lambda^{\prime\prime}}(x) - V_{\lambda^{\prime}}(x) &= J^{(g_{\lambda^{\prime\prime}})}_{\lambda^{\prime\prime}}(x) - J^{(g_{\lambda^{\prime}})}_{\lambda^{\prime}}(x) \ge J^{(g_{\lambda^{\prime\prime}})}_{\lambda^{\prime\prime}}(x) - J^{(g_{\lambda^{\prime\prime}})}_{\lambda^{\prime}}(x) \notag \\ &\stackrel{(a)}= (\lambda^{\prime\prime} - \lambda^{\prime})N^{(g_{\lambda^{\prime\prime}})}(x), \end{align}
\begin{align} V_{\lambda^{\prime\prime}}(x) - V_{\lambda^{\prime}}(x) &= J^{(g_{\lambda^{\prime\prime}})}_{\lambda^{\prime\prime}}(x) - J^{(g_{\lambda^{\prime}})}_{\lambda^{\prime}}(x) \ge J^{(g_{\lambda^{\prime\prime}})}_{\lambda^{\prime\prime}}(x) - J^{(g_{\lambda^{\prime\prime}})}_{\lambda^{\prime}}(x) \notag \\ &\stackrel{(a)}= (\lambda^{\prime\prime} - \lambda^{\prime})N^{(g_{\lambda^{\prime\prime}})}(x), \end{align}
where (a) follows from (7). The result follows from combining the above inequalities.
3.2. Sufficient conditions for indexability
Theorem 1. Define
![]() $\mathcal H = \{ (g,h) \,:\, g, h \,:\, \mathcal X \to \{0, 1\} \text{ such that for all } x \in \mathcal X, N^{(g)}(x) \ge N^{(h)}(x) \}$
. Each of the following is a sufficient condition for Whittle indexability:
$\mathcal H = \{ (g,h) \,:\, g, h \,:\, \mathcal X \to \{0, 1\} \text{ such that for all } x \in \mathcal X, N^{(g)}(x) \ge N^{(h)}(x) \}$
. Each of the following is a sufficient condition for Whittle indexability:
-
(a) For any
 $g,h \in \mathcal H$
, we have that for every
$g,h \in \mathcal H$
, we have that for every
 $x, z \in \mathcal{X}$
, (11)
$x, z \in \mathcal{X}$
, (11) \begin{equation} \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - \beta P_{zy}(1) \bigr]^+ N^{(h)}(y) \Bigr\} \le \frac{(1-\beta)^2}{\beta}. \end{equation}
\begin{equation} \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - \beta P_{zy}(1) \bigr]^+ N^{(h)}(y) \Bigr\} \le \frac{(1-\beta)^2}{\beta}. \end{equation}
-
(b) For any
 $g, h \in \mathcal H$
, we have that for every
$g, h \in \mathcal H$
, we have that for every
 $x \in \mathcal X$
, (12)
$x \in \mathcal X$
, (12) \begin{equation} \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - P_{xy}(0) \bigr]^+ N^{(h)}(y) \Bigr\} \le \frac{1-\beta}{\beta}. \end{equation}
\begin{equation} \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - P_{xy}(0) \bigr]^+ N^{(h)}(y) \Bigr\} \le \frac{1-\beta}{\beta}. \end{equation}
See Appendix B for the proof. The sufficient conditions of Theorem 1 can be difficult to verify. Simpler sufficient conditions are stated below.
Proposition 2. Each of the following is a sufficient condition for (11):
-
(a)
 $\max_{x, z \in \mathcal{X}} \sum_{y \in \mathcal{X}} \bigl[ \beta P_{z y}(1) - P_{x y}(1) \bigr]^{+} \leq (1 - \beta)^2/\beta$
.
$\max_{x, z \in \mathcal{X}} \sum_{y \in \mathcal{X}} \bigl[ \beta P_{z y}(1) - P_{x y}(1) \bigr]^{+} \leq (1 - \beta)^2/\beta$
. -
(b)
 $P_{xy}(1) = P_{zy}(1)$
, for any
$P_{xy}(1) = P_{zy}(1)$
, for any
 $x, y, z \in \mathcal{X}$
.
$x, y, z \in \mathcal{X}$
.
In addition, each of the following is a sufficient condition for (12):
-
(c)
 $\max_{x \in \mathcal{X}} \sum_{y \in \mathcal{X}} \left[ P_{xy}(0) - P_{xy}(1) \right]^{+} \leq (1 - \beta)/\beta$
.
$\max_{x \in \mathcal{X}} \sum_{y \in \mathcal{X}} \left[ P_{xy}(0) - P_{xy}(1) \right]^{+} \leq (1 - \beta)/\beta$
. -
(d)
 $\beta \le 0.5$
.
$\beta \le 0.5$
.
See Appendix C for the proof.
Some remarks
-
1. The sufficient conditions of Theorem 1 and of parts (a), (c), and (d) of Proposition 2 may be viewed as bounds on the discount factor
 $\beta$
for which an RB is indexable. Numerical experiments to explore such a property are presented in [Reference Niño-Mora25]. A qualitatively similar result was established in [Reference Niño-Mora23, Corollary 5], which showed that a restless bandit process is generalized-conservation-laws (GCL-) indexable for sufficiently small discount factors. GCL-indexability is a sub-class of PCL-indexability, which is a sub-class of Whittle indexability. Thus, Proposition 2 provides a quantitative characterization of the qualitative observation made in [Reference Bertsimas and Niño-Mora9] and generalizes it to a broader class of models.
$\beta$
for which an RB is indexable. Numerical experiments to explore such a property are presented in [Reference Niño-Mora25]. A qualitatively similar result was established in [Reference Niño-Mora23, Corollary 5], which showed that a restless bandit process is generalized-conservation-laws (GCL-) indexable for sufficiently small discount factors. GCL-indexability is a sub-class of PCL-indexability, which is a sub-class of Whittle indexability. Thus, Proposition 2 provides a quantitative characterization of the qualitative observation made in [Reference Bertsimas and Niño-Mora9] and generalizes it to a broader class of models. -
2. We refer to models that satisfy the sufficient condition of Proposition 2(b) as restless bandits with controlled restarts. Such models arise in various scheduling problems (e.g., machine maintenance, surveillance) where taking the active action resets the state according to a known probability distribution. Specific instances of such models are considered in [Reference Akbarzadeh and Mahajan3, Reference Wang, Ren, Mo and Shi30]. The special case when the active action resets to a specific (pristine) state are considered in [Reference Glazebrook, Mitchell and Ansell18, Reference Glazebrook, Ruiz-Hernandez and Kirkbride19].
-
3. A different class of restart models have been considered in [Reference Avrachenkov, Ayesta, Doncel and Jacko7, Reference Ayesta, Erausquin and Jacko8, Reference Jacko20], where the passive action resets the state of the arm. Note that such models do not satisfy Proposition 2(b), and additional modeling assumptions are required to establish indexability. See [Reference Avrachenkov, Ayesta, Doncel and Jacko7, Reference Ayesta, Erausquin and Jacko8, Reference Jacko20] for details.
4. An algorithm to compute the Whittle index
Given an indexable RB, a naive method to compute the Whittle index at state x is to do a binary search over the penalty
![]() $\lambda$
and find the critical penalty w(x) such that for
$\lambda$
and find the critical penalty w(x) such that for
![]() $\lambda \in ({-}\infty, w(x))$
,
$\lambda \in ({-}\infty, w(x))$
,
![]() $g_\lambda(x) = 0$
, and for
$g_\lambda(x) = 0$
, and for
![]() $\lambda \in [w(x), \infty)$
,
$\lambda \in [w(x), \infty)$
,
![]() $g_\lambda(x) = 1$
. Although such an approach has been used in the literature [Reference Akbarzadeh and Mahajan2, Reference Qian, Zhang, Krishnamachari and Tambe29], it is not efficient as it requires a separate binary search for each state. For a sub-class of restless bandits which satisfy an additional technical condition called partial conservation laws (PCL), Niño-Mora [Reference Niño-Mora24, Reference Niño-Mora25] presented an algorithm called the adaptive greedy algorithm to compute the Whittle index. In this section, we present an algorithm that may be viewed as a refinement of the adaptive greedy algorithm and show that it computes the Whittle index for all indexable RBs. The result of this section are restricted to the case of finite
$g_\lambda(x) = 1$
. Although such an approach has been used in the literature [Reference Akbarzadeh and Mahajan2, Reference Qian, Zhang, Krishnamachari and Tambe29], it is not efficient as it requires a separate binary search for each state. For a sub-class of restless bandits which satisfy an additional technical condition called partial conservation laws (PCL), Niño-Mora [Reference Niño-Mora24, Reference Niño-Mora25] presented an algorithm called the adaptive greedy algorithm to compute the Whittle index. In this section, we present an algorithm that may be viewed as a refinement of the adaptive greedy algorithm and show that it computes the Whittle index for all indexable RBs. The result of this section are restricted to the case of finite
![]() ${\mathcal X}$
.
${\mathcal X}$
.
Let K denote the number of states (i.e.,
![]() $K = |{\mathcal X}|$
), and let
$K = |{\mathcal X}|$
), and let
![]() $K_D (\leq K)$
denote the number of distinct Whittle indices. Let
$K_D (\leq K)$
denote the number of distinct Whittle indices. Let
![]() $\Lambda^* = \{\lambda_1, \dots, \lambda_{K_D}\}$
, where
$\Lambda^* = \{\lambda_1, \dots, \lambda_{K_D}\}$
, where
![]() $\lambda_1 < \lambda_2 < \dots < \lambda_{K_D}$
is the sorted list of distinct Whittle indices. Also, let
$\lambda_1 < \lambda_2 < \dots < \lambda_{K_D}$
is the sorted list of distinct Whittle indices. Also, let
![]() $\lambda_0 = -\infty$
. For any
$\lambda_0 = -\infty$
. For any
![]() $d \in \{0, \ldots, K_D\}$
, let
$d \in \{0, \ldots, K_D\}$
, let
![]() ${\mathcal P}_d \,:\!=\, \{x \in {\mathcal X}\,:\, w(x) \leq \lambda_d\}$
denote the set of states with Whittle index less than or equal to
${\mathcal P}_d \,:\!=\, \{x \in {\mathcal X}\,:\, w(x) \leq \lambda_d\}$
denote the set of states with Whittle index less than or equal to
![]() $\lambda_d$
. Note that
$\lambda_d$
. Note that
![]() ${\mathcal P}_0 = \emptyset$
and
${\mathcal P}_0 = \emptyset$
and
![]() ${\mathcal P}_{K_D} = {\mathcal X}$
. Let
${\mathcal P}_{K_D} = {\mathcal X}$
. Let
![]() $\Gamma_{d+1} = {\mathcal P}_{d+1}\backslash{\mathcal P}_d$
denote the set of states with Whittle index
$\Gamma_{d+1} = {\mathcal P}_{d+1}\backslash{\mathcal P}_d$
denote the set of states with Whittle index
![]() $\lambda_{d+1}$
.
$\lambda_{d+1}$
.
For any subset
![]() ${\mathcal S} \subseteq {\mathcal X}$
, define the policy
${\mathcal S} \subseteq {\mathcal X}$
, define the policy
![]() $\bar{g}^{(\mathcal S)}\,:\, {\mathcal X} \to \{0, 1\}$
as
$\bar{g}^{(\mathcal S)}\,:\, {\mathcal X} \to \{0, 1\}$
as
 \begin{equation} \bar{g}^{(\mathcal S)}(x) = \begin{cases} 0, \text{ if } x \in {\mathcal S}, \\[4pt] 1, \text{ if } x \in {\mathcal X}\backslash{\mathcal S}. \end{cases}\end{equation}
\begin{equation} \bar{g}^{(\mathcal S)}(x) = \begin{cases} 0, \text{ if } x \in {\mathcal S}, \\[4pt] 1, \text{ if } x \in {\mathcal X}\backslash{\mathcal S}. \end{cases}\end{equation}
Thus, the policy
![]() $\bar{g}^{(\mathcal S)}$
takes the passive action in the set
$\bar{g}^{(\mathcal S)}$
takes the passive action in the set
![]() ${\mathcal S}$
and the active action in the set
${\mathcal S}$
and the active action in the set
![]() ${\mathcal X}\backslash{\mathcal S}$
.
${\mathcal X}\backslash{\mathcal S}$
.
Now, for any
![]() $d \in \{0, \ldots, K_D-1\}$
and all states
$d \in \{0, \ldots, K_D-1\}$
and all states
![]() $y \in {\mathcal X}\backslash{\mathcal P}_{d}$
, define
$y \in {\mathcal X}\backslash{\mathcal P}_{d}$
, define
![]() $h_d = \bar{g}^{({\mathcal P}_d)}$
,
$h_d = \bar{g}^{({\mathcal P}_d)}$
,
![]() $h_{d,y} = \bar{g}^{({\mathcal P}_d \cup \{y\})}$
, and for all
$h_{d,y} = \bar{g}^{({\mathcal P}_d \cup \{y\})}$
, and for all
![]() $x \in \Lambda_{d, y}$
,
$x \in \Lambda_{d, y}$
,
Lemma 3. For an indexable RB with
![]() $d \in \{0, \ldots, K_D-1\}$
, we have the following:
$d \in \{0, \ldots, K_D-1\}$
, we have the following:
-
1. For all
 $y \in \Gamma_{d+1}$
, we have
$y \in \Gamma_{d+1}$
, we have
 $w(y) = \lambda_{d+1}$
.
$w(y) = \lambda_{d+1}$
. -
2. For all
 $y \in {\mathcal X}\backslash{\mathcal P}_d$
and
$y \in {\mathcal X}\backslash{\mathcal P}_d$
and
 $\lambda \in (\lambda_{d}, \lambda_{d+1}]$
, we have
$\lambda \in (\lambda_{d}, \lambda_{d+1}]$
, we have
 $J^{\left(h_{d,y}\right)}_\lambda(x) \geq J^{(h_d)}_\lambda(x)$
for all
$J^{\left(h_{d,y}\right)}_\lambda(x) \geq J^{(h_d)}_\lambda(x)$
for all
 $x \in {\mathcal X}$
, with equality if and only if
$x \in {\mathcal X}$
, with equality if and only if
 $y \in \Gamma_{d+1}$
and
$y \in \Gamma_{d+1}$
and
 $\lambda = \lambda_{d+1}$
.
$\lambda = \lambda_{d+1}$
.
Proof. See Appendix D.
Theorem 2. For an indexable RB, the following properties hold:
-
1. For any
 $y \in \Gamma_{d+1}$
, the set
$y \in \Gamma_{d+1}$
, the set
 $\Lambda_{d, y}$
is non-empty.
$\Lambda_{d, y}$
is non-empty. -
2. For any
 $x \in \Lambda_{d, y}$
,
$x \in \Lambda_{d, y}$
,
 $\mu_{d,y}(x) \geq \lambda_{d+1}$
, with equality if and only if
$\mu_{d,y}(x) \geq \lambda_{d+1}$
, with equality if and only if
 $y \in \Gamma_{d+1}$
.
$y \in \Gamma_{d+1}$
.
Proof. The proof of each part is as follows:
-
1. We prove the result by contradiction. Suppose that there exists a
 $y \in \Gamma_{d+1}$
such that
$y \in \Gamma_{d+1}$
such that
 $\Lambda_{d, y} = \emptyset$
, which means
$\Lambda_{d, y} = \emptyset$
, which means
 $N^{(h_d)}(x) = N^{\left({h}_{d, y}\right)}(x)$
for all
$N^{(h_d)}(x) = N^{\left({h}_{d, y}\right)}(x)$
for all
 $x \in {\mathcal X}$
. By Lemma 3, we have that Therefore, from (7) we infer
$x \in {\mathcal X}$
. By Lemma 3, we have that Therefore, from (7) we infer \begin{align*}J^{(h_d)}_{\lambda_{d+1}}(x) = J^{\left({h}_{d, y}\right)}_{\lambda_{d+1}}(x).\end{align*}
\begin{align*}J^{(h_d)}_{\lambda_{d+1}}(x) = J^{\left({h}_{d, y}\right)}_{\lambda_{d+1}}(x).\end{align*}
 $D^{(h_d)}(x) = D^{\left({h}_{d, y}\right)}(x)$
for all
$D^{(h_d)}(x) = D^{\left({h}_{d, y}\right)}(x)$
for all
 $x \in {\mathcal X}$
. Since both
$x \in {\mathcal X}$
. Since both
 $D^{(g)}(x)$
and
$D^{(g)}(x)$
and
 $N^{(g)}(x)$
do not depend on
$N^{(g)}(x)$
do not depend on
 $\lambda$
, (7) implies that for any
$\lambda$
, (7) implies that for any
 $\lambda$
and
$\lambda$
and
 $x \in \mathcal{X}$
, we have
$x \in \mathcal{X}$
, we have
 $J^{(h_d)}_{\lambda}(x) = J^{\left({h}_{d, y}\right)}_{\lambda}(x)$
. This implies that the policies
$J^{(h_d)}_{\lambda}(x) = J^{\left({h}_{d, y}\right)}_{\lambda}(x)$
. This implies that the policies
 $h_d$
and
$h_d$
and
 $h_{d,y}$
will be optimal for the same set of
$h_{d,y}$
will be optimal for the same set of
 $\lambda$
. Now, since the policy
$\lambda$
. Now, since the policy
 $h_d$
is optimal for all
$h_d$
is optimal for all
 $\lambda \in (\lambda_d, \lambda_{d+1}]$
(by definition), so is
$\lambda \in (\lambda_d, \lambda_{d+1}]$
(by definition), so is
 $h_{d,y}$
. Hence
$h_{d,y}$
. Hence
 $y \in \mathcal{P}_d$
. But we started by assuming that
$y \in \mathcal{P}_d$
. But we started by assuming that
 $y \not\in \mathcal{P}_d$
, so we have a contradiction.
$y \not\in \mathcal{P}_d$
, so we have a contradiction.
-
2. By Lemma 3, Part 2, for all
 $y \in {\mathcal X}\backslash{\mathcal P}_d$
,
$y \in {\mathcal X}\backslash{\mathcal P}_d$
,
 $\lambda \in (\lambda_{d}, \lambda_{d+1}]$
, and for all
$\lambda \in (\lambda_{d}, \lambda_{d+1}]$
, and for all
 $x \in \Lambda_{d, y}$
, we have
$x \in \Lambda_{d, y}$
, we have
 $J^{\left(h_{d,y}\right)}_\lambda(x) \geq J^{(h_d)}_\lambda(x)$
. Then, by (7), we infer Finally, we have
$J^{\left(h_{d,y}\right)}_\lambda(x) \geq J^{(h_d)}_\lambda(x)$
. Then, by (7), we infer Finally, we have \begin{align*}D^{\left(h_{d,y}\right)}(x) + \lambda N^{\left(h_{d,y}\right)}(x) \geq D^{(h_d)}(x) + \lambda N^{(h_d)}(x).\end{align*}
\begin{align*}D^{\left(h_{d,y}\right)}(x) + \lambda N^{\left(h_{d,y}\right)}(x) \geq D^{(h_d)}(x) + \lambda N^{(h_d)}(x).\end{align*}
 $\mu_{d,y}(x) \geq \lambda$
and thus
$\mu_{d,y}(x) \geq \lambda$
and thus
 $\mu_{d,y}(x) \geq \lambda_{d+1}$
for all
$\mu_{d,y}(x) \geq \lambda_{d+1}$
for all
 $x \in \Lambda_{d, y}$
. This proves the first part of the statement. To prove the second part, note that the policy
$x \in \Lambda_{d, y}$
. This proves the first part of the statement. To prove the second part, note that the policy
 $h_d$
is an optimal policy for
$h_d$
is an optimal policy for
 $\lambda \in (\lambda_d, \lambda_{d+1}]$
, and for any
$\lambda \in (\lambda_d, \lambda_{d+1}]$
, and for any
 $y \in \mathcal{P}_{d+1}$
, the policy
$y \in \mathcal{P}_{d+1}$
, the policy
 ${h}_{d, y}$
is an optimal policy for
${h}_{d, y}$
is an optimal policy for
 $\lambda \in (\lambda_{d+1}, \lambda_{d+2}]$
. From Lemma 1, we know that
$\lambda \in (\lambda_{d+1}, \lambda_{d+2}]$
. From Lemma 1, we know that
 $V_\lambda(x)$
is continuous in
$V_\lambda(x)$
is continuous in
 $\lambda$
for all
$\lambda$
for all
 $x \in \mathcal{X}$
. So, for all
$x \in \mathcal{X}$
. So, for all
 $x \in \mathcal{X}$
, Thus, for all
$x \in \mathcal{X}$
, Thus, for all \begin{align*} \lim_{\lambda \uparrow \lambda_{d+1}} J^{(h_d)}_\lambda(x) = \lim_{\lambda \uparrow \lambda_{d+1}} V_\lambda(x) = \lim_{\lambda \downarrow \lambda_{d+1}} V_\lambda(x) = \lim_{\lambda \downarrow \lambda_{d+1}} J^{\left(h_{d, y}\right)}_\lambda(x). \end{align*}
\begin{align*} \lim_{\lambda \uparrow \lambda_{d+1}} J^{(h_d)}_\lambda(x) = \lim_{\lambda \uparrow \lambda_{d+1}} V_\lambda(x) = \lim_{\lambda \downarrow \lambda_{d+1}} V_\lambda(x) = \lim_{\lambda \downarrow \lambda_{d+1}} J^{\left(h_{d, y}\right)}_\lambda(x). \end{align*}
 $x \in \mathcal{X}$
,
$x \in \mathcal{X}$
,
 $J^{(h_d)}_{\lambda_{d+1}}(x) = J^{\left({h}_{d, y}\right)}_{\lambda_{d+1}}(x)$
, and therefore, As a result,
$J^{(h_d)}_{\lambda_{d+1}}(x) = J^{\left({h}_{d, y}\right)}_{\lambda_{d+1}}(x)$
, and therefore, As a result, \begin{equation*} D^{(h_d)}(x) + \lambda_{d+1} N^{(h_d)}(x) = D^{\left({h}_{d, y}\right)}(x) + \lambda_{d+1} N^{\left(h_{d, y}\right)}(x). \end{equation*}
\begin{equation*} D^{(h_d)}(x) + \lambda_{d+1} N^{(h_d)}(x) = D^{\left({h}_{d, y}\right)}(x) + \lambda_{d+1} N^{\left(h_{d, y}\right)}(x). \end{equation*}
 $\lambda_{d+1} = \mu_{d,y}(x)$
for all
$\lambda_{d+1} = \mu_{d,y}(x)$
for all
 $x \in \Lambda_{d, y}$
.
$x \in \Lambda_{d, y}$
.
Theorem 2 suggests a method for identifying the Whittle index of any indexable RB by iteratively identifying the set
![]() ${\mathcal P}_d$
and the Whittle index
${\mathcal P}_d$
and the Whittle index
![]() $\lambda_d$
. By definition,
$\lambda_d$
. By definition,
![]() ${\mathcal P}_0 = \emptyset$
and
${\mathcal P}_0 = \emptyset$
and
![]() $\lambda_0 = -\infty$
. Now suppose
$\lambda_0 = -\infty$
. Now suppose
![]() ${\mathcal P}_0 \subset {\mathcal P}_1 \subset \ldots \subset {\mathcal P}_{d}$
and
${\mathcal P}_0 \subset {\mathcal P}_1 \subset \ldots \subset {\mathcal P}_{d}$
and
![]() $\lambda_0 < \lambda_1 < \ldots < \lambda_d$
have been identified. We will describe how to determine
$\lambda_0 < \lambda_1 < \ldots < \lambda_d$
have been identified. We will describe how to determine
![]() ${\mathcal P}_{d+1}$
and
${\mathcal P}_{d+1}$
and
![]() $\lambda_{d+1}$
:
$\lambda_{d+1}$
:
-
1. For
 $h_d = {\bar g}^{({\mathcal P}_d)}$
, compute
$h_d = {\bar g}^{({\mathcal P}_d)}$
, compute
 $N^{(h_d)}$
by solving (8).
$N^{(h_d)}$
by solving (8). -
2. For all
 $y \in {\mathcal X}\backslash{\mathcal P}_d$
, compute
$y \in {\mathcal X}\backslash{\mathcal P}_d$
, compute
 $N^{\left(h_{d, y}\right)}$
where
$N^{\left(h_{d, y}\right)}$
where
 $h_{d, y} = \bar{g}^{({\mathcal P} \cup \{y\})}$
by solving (8), and compute
$h_{d, y} = \bar{g}^{({\mathcal P} \cup \{y\})}$
by solving (8), and compute
 $\Lambda_{d, y}$
. Let
$\Lambda_{d, y}$
. Let
 $\mu^*_{d, y} = \min_{x \in \Lambda_{d, y}} \mu_{d, y}(x)$
, where
$\mu^*_{d, y} = \min_{x \in \Lambda_{d, y}} \mu_{d, y}(x)$
, where
 $\mu_{d,y}(x)$
is given by Theorem 2. Then
$\mu_{d,y}(x)$
is given by Theorem 2. Then
 $\lambda_{d+1} = \min_{y \in {\mathcal X}\backslash{\mathcal P}_d} \mu^*_{d, y}$
,
$\lambda_{d+1} = \min_{y \in {\mathcal X}\backslash{\mathcal P}_d} \mu^*_{d, y}$
,
 $\Gamma_{d+1} = \arg \min_{y \in {\mathcal X}\backslash{\mathcal P}_d} \mu^*_{d, y}$
, and we get
$\Gamma_{d+1} = \arg \min_{y \in {\mathcal X}\backslash{\mathcal P}_d} \mu^*_{d, y}$
, and we get
 ${\mathcal P}_{d+1} = {\mathcal P}_d \cup \Gamma_{d+1}$
(recall that argmin denotes the set of all minimizers) and
${\mathcal P}_{d+1} = {\mathcal P}_d \cup \Gamma_{d+1}$
(recall that argmin denotes the set of all minimizers) and
 $w(x) = \lambda_{d+1}$
for all
$w(x) = \lambda_{d+1}$
for all
 $x \in \Gamma_{d+1}$
.
$x \in \Gamma_{d+1}$
.
Iteratively proceeding in this way, we can compute the Whittle index for all states. The detailed algorithm is presented in Algorithm 1.

4.1. An efficient implementation using the Sherman–Morrison formula
We now present an efficient implementation of Algorithm 1 using the Sherman–Morrison inverse formula. Suppose
![]() $A \in \mathbb {R} ^{n\times n}$
is an invertible square matrix and
$A \in \mathbb {R} ^{n\times n}$
is an invertible square matrix and
![]() $u,v\in \mathbb {R} ^{n}$
are column vectors such that
$u,v\in \mathbb {R} ^{n}$
are column vectors such that
![]() $A + u v^{\textsf{T}}$
is invertible. Then the Sherman–Morrison inverse formula is
$A + u v^{\textsf{T}}$
is invertible. Then the Sherman–Morrison inverse formula is
Furthermore, given
![]() $b \in \mathbb{R}^n$
, if x is the solution of
$b \in \mathbb{R}^n$
, if x is the solution of
![]() $Ax = b$
and y is the solution
$Ax = b$
and y is the solution
![]() $Ay = u$
, then the solution of
$Ay = u$
, then the solution of
![]() $\big(A + u v^{\textsf{T}}\big) \tilde x = b$
is given by the following (see [Reference Egidi and Maponi12, Corollary 2]):
$\big(A + u v^{\textsf{T}}\big) \tilde x = b$
is given by the following (see [Reference Egidi and Maponi12, Corollary 2]):
Let
![]() $\Phi^{(g)} = \big(I - \beta P^{(g)}\big)^{-1}$
. Note that for any Markov policy g,
$\Phi^{(g)} = \big(I - \beta P^{(g)}\big)^{-1}$
. Note that for any Markov policy g,
![]() $\big(I - \beta P^{(g)}\big)$
is invertible, because
$\big(I - \beta P^{(g)}\big)$
is invertible, because
![]() $\beta P^{(g)}$
is a sub-stochastic matrix and has a spectral radius less than 1. Therefore, the conditions for using the Sherman–Morrison formula are satisfied. Hence, using (16), Equation (8) may be written (in matrix form) as
$\beta P^{(g)}$
is a sub-stochastic matrix and has a spectral radius less than 1. Therefore, the conditions for using the Sherman–Morrison formula are satisfied. Hence, using (16), Equation (8) may be written (in matrix form) as
Now, for any
![]() $d \in \{0, \ldots, K_D-1\}$
and a state
$d \in \{0, \ldots, K_D-1\}$
and a state
![]() $y \in {\mathcal X} \backslash {\mathcal P}_d$
, consider the policies
$y \in {\mathcal X} \backslash {\mathcal P}_d$
, consider the policies
![]() $h_d = \bar{g}^{({\mathcal P}_d)}$
and
$h_d = \bar{g}^{({\mathcal P}_d)}$
and
![]() $h_{d,y} = \bar{g}^{({\mathcal P}_{d,y})}$
. Let
$h_{d,y} = \bar{g}^{({\mathcal P}_{d,y})}$
. Let
![]() $e_y$
denote the unit vector with 1 in the yth location, and let
$e_y$
denote the unit vector with 1 in the yth location, and let
![]() $\rho_y$
be a vector given by
$\rho_y$
be a vector given by
![]() $ [\rho_y]_x = P_{yx}(1) - P_{yx}(0) $
, for all
$ [\rho_y]_x = P_{yx}(1) - P_{yx}(0) $
, for all
![]() $x \in {\mathcal X}$
. Then
$x \in {\mathcal X}$
. Then
![]() $P^{\left(h_{d,y}\right)} = P^{(h_d)} - e_y \rho^{\mathsf{T}}_y$
. Therefore,
$P^{\left(h_{d,y}\right)} = P^{(h_d)} - e_y \rho^{\mathsf{T}}_y$
. Therefore,
Let
![]() $\Phi^{\left(h_{d}\right)}_{\cdot y}$
denote the yth column of
$\Phi^{\left(h_{d}\right)}_{\cdot y}$
denote the yth column of
![]() $\Phi^{\left(h_{d}\right)}$
, i.e.,
$\Phi^{\left(h_{d}\right)}$
, i.e.,
![]() $\Phi^{\left(h_{d}\right)}_{\cdot y} = \Phi^{\left(h_{d}\right)} e_y$
. Then, by the Sherman–Morrison inverse formula ((15) and (16)), we have
$\Phi^{\left(h_{d}\right)}_{\cdot y} = \Phi^{\left(h_{d}\right)} e_y$
. Then, by the Sherman–Morrison inverse formula ((15) and (16)), we have
 \begin{align} \Phi^{\left(h_{d,y}\right)} = \Phi^{\left(h_{d}\right)} - \dfrac{\beta\Phi^{\left(h_{d}\right)} e_y \rho^{\mathsf{T}}_y \Phi^{\left(h_{d}\right)} }{1 + \beta \rho^{\mathsf{T}}_y \Phi^{\left(h_{d}\right)}_{\cdot y}}, \end{align}
\begin{align} \Phi^{\left(h_{d,y}\right)} = \Phi^{\left(h_{d}\right)} - \dfrac{\beta\Phi^{\left(h_{d}\right)} e_y \rho^{\mathsf{T}}_y \Phi^{\left(h_{d}\right)} }{1 + \beta \rho^{\mathsf{T}}_y \Phi^{\left(h_{d}\right)}_{\cdot y}}, \end{align}
 \begin{align} D^{\left(h_{d,y}\right)} = D^{\left(h_{d}\right)} - \dfrac{\beta\rho^{\mathsf{T}}_y D^{\left(h_{d}\right)} }{1 + \beta\rho^{\mathsf{T}}_y \Phi^{\left(h_{d}\right)}_{\cdot y}} \Phi^{\left(h_{d}\right)}_{\cdot y}, \quad N^{\left(h_{d,y}\right)} = N^{\left(h_{d}\right)} - \dfrac{\beta\rho^{\mathsf{T}}_y N^{\left(h_{d}\right)} }{1 + \beta\rho^{\mathsf{T}}_y \Phi^{\left(h_{d}\right)}_{\cdot y}} \Phi^{\left(h_{d}\right)}_{\cdot y}.\end{align}
\begin{align} D^{\left(h_{d,y}\right)} = D^{\left(h_{d}\right)} - \dfrac{\beta\rho^{\mathsf{T}}_y D^{\left(h_{d}\right)} }{1 + \beta\rho^{\mathsf{T}}_y \Phi^{\left(h_{d}\right)}_{\cdot y}} \Phi^{\left(h_{d}\right)}_{\cdot y}, \quad N^{\left(h_{d,y}\right)} = N^{\left(h_{d}\right)} - \dfrac{\beta\rho^{\mathsf{T}}_y N^{\left(h_{d}\right)} }{1 + \beta\rho^{\mathsf{T}}_y \Phi^{\left(h_{d}\right)}_{\cdot y}} \Phi^{\left(h_{d}\right)}_{\cdot y}.\end{align}
Thus, if
![]() $\Phi^{\left(h_{d}\right)}$
has been computed, then
$\Phi^{\left(h_{d}\right)}$
has been computed, then
![]() $\Phi^{\left(h_{d,y}\right)}$
can be computed in
$\Phi^{\left(h_{d,y}\right)}$
can be computed in
![]() $\mathcal{O}\big(K^2\big)$
computations. In addition, if
$\mathcal{O}\big(K^2\big)$
computations. In addition, if
![]() $\Phi^{\left(h_{d}\right)}$
,
$\Phi^{\left(h_{d}\right)}$
,
![]() $D^{\left(h_{d}\right)}$
, and
$D^{\left(h_{d}\right)}$
, and
![]() $N^{\left(h_{d}\right)}$
have been computed, then
$N^{\left(h_{d}\right)}$
have been computed, then
![]() $D^{\left(h_{d,y}\right)}$
and
$D^{\left(h_{d,y}\right)}$
and
![]() $N^{\left(h_{d,y}\right)}$
can be computed in
$N^{\left(h_{d,y}\right)}$
can be computed in
![]() $\mathcal{O}(K)$
computations.
$\mathcal{O}(K)$
computations.
So we can use (18) and (19) to implement Algorithm 1 in a more efficient manner. However, there is one additional step that needs to be handled, which we explain next.
As
![]() $h_{d+1} = \bar{g}^{\big({\mathcal P}_d \cup {\Gamma_{d+1}}\big)}$
, we get
$h_{d+1} = \bar{g}^{\big({\mathcal P}_d \cup {\Gamma_{d+1}}\big)}$
, we get
Thus,
![]() $I - \beta P^{\left(h_{d+1}\right)}$
is a rank-
$I - \beta P^{\left(h_{d+1}\right)}$
is a rank-
![]() $|\Gamma_{d+1}|$
update of
$|\Gamma_{d+1}|$
update of
![]() $I - \beta P^{\left(h_{d}\right)}$
. When
$I - \beta P^{\left(h_{d}\right)}$
. When
![]() $|\Gamma_{d+1}| > 1$
, we can either sequentially apply Equations (18) and (19) for all
$|\Gamma_{d+1}| > 1$
, we can either sequentially apply Equations (18) and (19) for all
![]() $y \in \Gamma_{d+1}$
or use the Woodbury formula to compute
$y \in \Gamma_{d+1}$
or use the Woodbury formula to compute
![]() $\Phi^{\left(h_{d+1}\right)}$
and compute
$\Phi^{\left(h_{d+1}\right)}$
and compute
![]() $D^{\left(h_{d+1}\right)}$
and
$D^{\left(h_{d+1}\right)}$
and
![]() $N^{\left(h_{d+1}\right)}$
using (17). The Woodbury formula is a generalization of the Sherman–Morrison formula. Suppose
$N^{\left(h_{d+1}\right)}$
using (17). The Woodbury formula is a generalization of the Sherman–Morrison formula. Suppose
![]() $A \in \mathbb{R}^{n\times n}$
is an invertible matrix and
$A \in \mathbb{R}^{n\times n}$
is an invertible matrix and
![]() $U, V \in \mathbb{R}^{n \times m}$
are such that
$U, V \in \mathbb{R}^{n \times m}$
are such that
![]() $A + U V^{\mathsf{T}}$
is invertible. Then the Woodbury formula is
$A + U V^{\mathsf{T}}$
is invertible. Then the Woodbury formula is
The complexity of sequentially applying the Sherman–Morrison formula is
![]() $\mathcal{O}\big(|\Gamma_{d+1}|K^2\big)$
to compute
$\mathcal{O}\big(|\Gamma_{d+1}|K^2\big)$
to compute
![]() $\Phi^{\left(h_{d+1}\right)}$
and
$\Phi^{\left(h_{d+1}\right)}$
and
![]() $\mathcal{O}\big(|\Gamma_{d+1}| K\big)$
to compute
$\mathcal{O}\big(|\Gamma_{d+1}| K\big)$
to compute
![]() $D^{\left(h_{d+1}\right)}$
and
$D^{\left(h_{d+1}\right)}$
and
![]() $N^{\left(h_{d+1}\right)}$
. The complexity of using the Woodbury formula is
$N^{\left(h_{d+1}\right)}$
. The complexity of using the Woodbury formula is
![]() $\mathcal{O}\big(|\Gamma_{d+1}|^{2.807} + K^2\big)$
to compute
$\mathcal{O}\big(|\Gamma_{d+1}|^{2.807} + K^2\big)$
to compute
![]() $\Phi^{\left(h_{d+1}\right)}$
and
$\Phi^{\left(h_{d+1}\right)}$
and
![]() $\mathcal{O}\big(K^2\big)$
to compute
$\mathcal{O}\big(K^2\big)$
to compute
![]() $D^{\left(h_{d+1}\right)}$
and
$D^{\left(h_{d+1}\right)}$
and
![]() $N^{\left(h_{d+1}\right)}$
.
$N^{\left(h_{d+1}\right)}$
.
We show the complete algorithm to efficiently compute the Whittle index in Algorithm 2, where we use sequential application of Sherman–Morrison formula to compute
![]() $\Phi^{\left(h_{d+1}\right)}$
,
$\Phi^{\left(h_{d+1}\right)}$
,
![]() $D^{\left(h_{d+1}\right)}$
, and
$D^{\left(h_{d+1}\right)}$
, and
![]() $N^{\left(h_{d+1}\right)}$
.
$N^{\left(h_{d+1}\right)}$
.

Some remarks
-
1. The idea of computing the index by iteratively sorting the states according to their index is commonly used in the algorithms to compute the Gittins index; for example, the largest-remaining-index algorithm, the state-elimination algorithm, the triangularization algorithm, and the fast-pivoting algorithm use variations of this idea. See [Reference Chakravorty and Mahajan10] for details.
-
2. The computational complexity of Algorithm 2 is
 $\mathcal{O}\!\left(K^3\right)$
, which can be characterized as follows. The algorithm starts with computing
$\mathcal{O}\!\left(K^3\right)$
, which can be characterized as follows. The algorithm starts with computing
 $\Phi^{(h_0)}$
, which requires
$\Phi^{(h_0)}$
, which requires
 $\mathcal{O}\big(K^{2.807}\big)$
computations (using Strassen’s algorithm), and
$\mathcal{O}\big(K^{2.807}\big)$
computations (using Strassen’s algorithm), and
 $D^{(h_0)}$
and
$D^{(h_0)}$
and
 $N^{(h_0)}$
, each of which requires
$N^{(h_0)}$
, each of which requires
 $\mathcal{O}\big(K^2\big)$
computations. Then, in the inner for loop, computing each of
$\mathcal{O}\big(K^2\big)$
computations. Then, in the inner for loop, computing each of
 $D^{\left(h_{d, y}\right)}$
,
$D^{\left(h_{d, y}\right)}$
,
 $N^{\left(h_{d, y}\right)}$
, and
$N^{\left(h_{d, y}\right)}$
, and
 $\mu^*_{d,y}$
requires
$\mu^*_{d,y}$
requires
 $\mathcal{O}(K)$
computations, and the inner loop is executed
$\mathcal{O}(K)$
computations, and the inner loop is executed
 $|{\mathcal X} \backslash {\mathcal P}_d|$
times. Afterwards, updating
$|{\mathcal X} \backslash {\mathcal P}_d|$
times. Afterwards, updating
 $\Phi^{\left(h_{d+1}\right)}$
,
$\Phi^{\left(h_{d+1}\right)}$
,
 $D^{\left(h_{d+1}\right)}$
, and
$D^{\left(h_{d+1}\right)}$
, and
 $N^{\left(h_{d+1}\right)}$
requires
$N^{\left(h_{d+1}\right)}$
requires
 $\mathcal{O}\big(|\Gamma_{d+1}|K^2\big)$
,
$\mathcal{O}\big(|\Gamma_{d+1}|K^2\big)$
,
 $\mathcal{O}(|\Gamma_{d+1}|K)$
, and
$\mathcal{O}(|\Gamma_{d+1}|K)$
, and
 $\mathcal{O}(|\Gamma_{d+1}|K)$
computations, respectively. Therefore, the computational complexity of the algorithm is where the first inequality uses the fact that
$\mathcal{O}(|\Gamma_{d+1}|K)$
computations, respectively. Therefore, the computational complexity of the algorithm is where the first inequality uses the fact that \begin{align*} & \mathcal{O}\big(K^{2.807}\big) + \mathcal{O}\big(K^2\big) + \sum_{d = 1}^{K_D} \big( \mathcal{O}(|{\mathcal X} \backslash {\mathcal P}_d| K) + \mathcal{O}\big(|\Gamma_{d+1}| K^2\big) + \mathcal{O}\big(2 |\Gamma_{d+1}| K\big) \big) \\ &\le \mathcal{O}\big(K^{2.807}\big) + \sum_{d = 1}^{K_D} \mathcal{O}\big(K^2\big) + \mathcal{O}\Biggl(\Biggl[ \sum_{d = 1}^{K_D} |\Gamma_{d+1}| \Biggr] K^2\Biggr) \\ &\le \mathcal{O}\big(K^{2.807}\big) + \mathcal{O}\!\left(K^3\right) + \mathcal{O}\!\left(K^3\right) \le \mathcal{O}\!\left(K^3\right), \end{align*}
\begin{align*} & \mathcal{O}\big(K^{2.807}\big) + \mathcal{O}\big(K^2\big) + \sum_{d = 1}^{K_D} \big( \mathcal{O}(|{\mathcal X} \backslash {\mathcal P}_d| K) + \mathcal{O}\big(|\Gamma_{d+1}| K^2\big) + \mathcal{O}\big(2 |\Gamma_{d+1}| K\big) \big) \\ &\le \mathcal{O}\big(K^{2.807}\big) + \sum_{d = 1}^{K_D} \mathcal{O}\big(K^2\big) + \mathcal{O}\Biggl(\Biggl[ \sum_{d = 1}^{K_D} |\Gamma_{d+1}| \Biggr] K^2\Biggr) \\ &\le \mathcal{O}\big(K^{2.807}\big) + \mathcal{O}\!\left(K^3\right) + \mathcal{O}\!\left(K^3\right) \le \mathcal{O}\!\left(K^3\right), \end{align*}
 $|\mathcal{X}\setminus\mathcal{P}_d| \le K$
and the second inequality uses the fact that
$|\mathcal{X}\setminus\mathcal{P}_d| \le K$
and the second inequality uses the fact that
 $\sum_{d=1}^{K_D}| \Gamma_{d+1}| = K$
.
$\sum_{d=1}^{K_D}| \Gamma_{d+1}| = K$
.
-
3. Note that Algorithm 2 computes the Whittle index exactly. In contrast, using binary search [Reference Akbarzadeh and Mahajan2] computes the Whittle index approximately. Let
 $C_{\max}$
and
$C_{\max}$
and
 $C_{\min}$
denote the upper and lower bound on the per-step cost. Then we know that for any state x,
$C_{\min}$
denote the upper and lower bound on the per-step cost. Then we know that for any state x,
 $w(x) \in [ C_{\min}, C_{\max} ]$
. Now, suppose we want to compute the Whittle index to an accuracy of
$w(x) \in [ C_{\min}, C_{\max} ]$
. Now, suppose we want to compute the Whittle index to an accuracy of
 $\delta$
. Then the interval
$\delta$
. Then the interval
 $[C_{\min}, C_{\max}]$
needs to be divided into
$[C_{\min}, C_{\max}]$
needs to be divided into
 $\log_2( (C_{\max} - C_{\min})/\delta)$
steps. For each step of the binary search, we need to solve the dynamic program (3). There are two main algorithms to solve dynamic programs [Reference Puterman28]: policy iteration, which gives an exact solution, and value iteration, which gives an approximate solution.
$\log_2( (C_{\max} - C_{\min})/\delta)$
steps. For each step of the binary search, we need to solve the dynamic program (3). There are two main algorithms to solve dynamic programs [Reference Puterman28]: policy iteration, which gives an exact solution, and value iteration, which gives an approximate solution.Each iteration of policy iteration has two steps: (i) policy evaluation, which is done by solving a linear system and has complexity
 $\mathcal{O}\!\left(K^3\right)$
, and (ii) policy improvement, which requires
$\mathcal{O}\!\left(K^3\right)$
, and (ii) policy improvement, which requires
 $\mathcal{O}\big(K^2\big)$
computations. Thus, the overall complexity of policy iteration is
$\mathcal{O}\big(K^2\big)$
computations. Thus, the overall complexity of policy iteration is
 $\mathcal{O}(N_{\text{PI}} K^3)$
, where
$\mathcal{O}(N_{\text{PI}} K^3)$
, where
 $N_{\text{PI}}$
is the number of iterations after which policy iteration converges.
$N_{\text{PI}}$
is the number of iterations after which policy iteration converges.Each iteration of value iteration requires
 $\mathcal{O}\big(K^2\big)$
computations. Let
$\mathcal{O}\big(K^2\big)$
computations. Let
 $N_{\text{VI}}$
denote the number of iterations for value iteration (typically, the iteration stops when a stopping criterion is met). Then the complexity of approximately solving the dynamic program is
$N_{\text{VI}}$
denote the number of iterations for value iteration (typically, the iteration stops when a stopping criterion is met). Then the complexity of approximately solving the dynamic program is
 $\mathcal{O}\big(N_{\text{VI}}K^2\big)$
.
$\mathcal{O}\big(N_{\text{VI}}K^2\big)$
.Note that the binary search needs to be repeated for each state. Thus, using binary search to compute the Whittle index to an accuracy of
 $\delta$
has a complexity of
$\delta$
has a complexity of
 $\mathcal{O}\big(\log_2\big( \big(C_{\max} - C_{\min}\big)/\delta\big) N_{\text{PI}} K^4\big)$
if the dynamic program at each step is solved exactly and has a complexity of
$\mathcal{O}\big(\log_2\big( \big(C_{\max} - C_{\min}\big)/\delta\big) N_{\text{PI}} K^4\big)$
if the dynamic program at each step is solved exactly and has a complexity of
 $\mathcal{O}\big(\log_2\big( \big(C_{\max} - C_{\min}\big)/\delta\big) N_{\text{VI}} K^3\big)$
if the dynamic program at each step is solved approximately.
$\mathcal{O}\big(\log_2\big( \big(C_{\max} - C_{\min}\big)/\delta\big) N_{\text{VI}} K^3\big)$
if the dynamic program at each step is solved approximately.
4.2. Discussion on PCL-indexability
As mentioned earlier, an algorithm very similar to Algorithm 1 was proposed in [Reference Niño-Mora25] for computing the Whittle index for RBs that satisfy a technical condition known as PCL-indexability. The analysis in [Reference Niño-Mora25] is done under the assumption that the system starts from a designated start state distribution
![]() $\pi_0$
. For any policy g, define
$\pi_0$
. For any policy g, define
![]() $\mathsf{N}^{(g)} = \sum_{x \in \mathcal{X}} N^{(g)}(x) \pi_0(x)$
, and define
$\mathsf{N}^{(g)} = \sum_{x \in \mathcal{X}} N^{(g)}(x) \pi_0(x)$
, and define
![]() $\mathsf{D}^{(g)} = \sum_{x \in \mathcal{X}} D^{(g)}(x) \pi_0(x)$
. Let
$\mathsf{D}^{(g)} = \sum_{x \in \mathcal{X}} D^{(g)}(x) \pi_0(x)$
. Let
![]() $x_1,\dots, x_K$
be a permutation of the state space such that the corresponding Whittle indices are non-decreasing:
$x_1,\dots, x_K$
be a permutation of the state space such that the corresponding Whittle indices are non-decreasing:
![]() $\lambda_1 \le \dots \le \lambda_K$
. For any
$\lambda_1 \le \dots \le \lambda_K$
. For any
![]() $k \in \{1, \dots, K\}$
, let
$k \in \{1, \dots, K\}$
, let
![]() $\bar{\mathcal{P}}_k$
denote the set
$\bar{\mathcal{P}}_k$
denote the set
![]() $\{ x_1, \dots, x_k \}$
.
$\{ x_1, \dots, x_k \}$
.
Now, for any
![]() $k \in \{1, \dots, K\}$
and all states
$k \in \{1, \dots, K\}$
and all states
![]() $y \in \mathcal{X}\setminus \bar{\mathcal{P}}_k$
, define
$y \in \mathcal{X}\setminus \bar{\mathcal{P}}_k$
, define
![]() $\bar h_k = \bar g^{\big(\bar{\mathcal{P}}_k\big)}$
,
$\bar h_k = \bar g^{\big(\bar{\mathcal{P}}_k\big)}$
,
![]() $\bar h_{k,y} = \bar g^{\big(\bar{\mathcal{P}}_k \cup\{y\}\big)}$
, and define
$\bar h_{k,y} = \bar g^{\big(\bar{\mathcal{P}}_k \cup\{y\}\big)}$
, and define
 \begin{equation} \bar \mu_{k,y} = \frac{ \mathsf{D}^{\big(\bar h_{k,y}\big)} - \mathsf{D}^{\big(\bar h_k\big)} } {\mathsf{N}^{\big(\bar h_k\big)} - \mathsf{N}^{\big(\bar h_{k,y}\big)}}.\end{equation}
\begin{equation} \bar \mu_{k,y} = \frac{ \mathsf{D}^{\big(\bar h_{k,y}\big)} - \mathsf{D}^{\big(\bar h_k\big)} } {\mathsf{N}^{\big(\bar h_k\big)} - \mathsf{N}^{\big(\bar h_{k,y}\big)}}.\end{equation}
In [Reference Niño-Mora25] an algorithm called the adaptive greedy algorithm is presented to iteratively identify the sets
![]() $\bar{\mathcal{P}}_k$
and compute the corresponding Whittle indices. This algorithm is shown in Algorithm 3.
$\bar{\mathcal{P}}_k$
and compute the corresponding Whittle indices. This algorithm is shown in Algorithm 3.

An RB is said to be PCL-indexable [Reference Niño-Mora25] if it satisfies the following conditions:
-
1. For any
 ${\mathcal S} \subseteq {\mathcal X}$
and
${\mathcal S} \subseteq {\mathcal X}$
and
 $y \in {\mathcal X}\backslash{\mathcal S}$
, we have
$y \in {\mathcal X}\backslash{\mathcal S}$
, we have
 $\mathsf{N}^{\big(\bar{g}^{({\mathcal S})}\big)} - \mathsf{N}^{\big(\bar{g}^{\left({\mathcal S} \cup \{y\}\right)}\big)} > 0$
.
$\mathsf{N}^{\big(\bar{g}^{({\mathcal S})}\big)} - \mathsf{N}^{\big(\bar{g}^{\left({\mathcal S} \cup \{y\}\right)}\big)} > 0$
. -
2. The sequence of index values produced by the adaptive greedy algorithm is monotonically non-decreasing.
Finally, the following result is established.
Theorem 3 (Theorem 1 of [Reference Niño-Mora25]). A PCL-indexable RB is indexable, and the adaptive greedy algorithm gives its Whittle indices.
The main differences between our result and that of [Reference Niño-Mora25] are as follows:
-
1. An implication of the first condition in the definition of PCL indexability is that the denominator in (21) is never zero. In contrast, we do not impose such a restriction and work with the non-empty subset of states for which the denominator in (14) is non-zero.
-
2. In Algorithm 3, the sets
 $\{ \bar{\mathcal P}_k \}_{k=1}^{K}$
are constructed by adding states one by one, even when
$\{ \bar{\mathcal P}_k \}_{k=1}^{K}$
are constructed by adding states one by one, even when
 $\bar \mu_{k,y}$
has multiple argmins. In contrast, in Algorithm 1, the sets
$\bar \mu_{k,y}$
has multiple argmins. In contrast, in Algorithm 1, the sets
 $\{ \mathcal{P}_d \}_{d=1}^{K_D}$
are constructed by adding all states which have the same Whittle index at once.
$\{ \mathcal{P}_d \}_{d=1}^{K_D}$
are constructed by adding all states which have the same Whittle index at once. -
3. In Algorithm 3, one has to check that the indices are generated in a non-decreasing order (which is the second condition of PCL-indexability). In contrast, in Algorithm 1, the indices are always generated in an increasing order, and therefore Condition 2 for PCL-indexability is always satisfied.
-
4. Finally, Theorem 3 only guarantees that Algorithm 3 computes the Whittle index for RBs which satisfy PCL-indexability. Moreover, the second condition for PCL-indexability can only be checked after running Algorithm 3. In contrast, Theorem 2 guarantees that Algorithm 1 computes the Whittle index for all indexable RBs.
We conclude this discussion by revisiting an example from [Reference Niño-Mora25] which is an indexable RB that is not PCL-indexable. For this example,
![]() $\mathcal{X} = \{1, 2, 3\}$
; the transition matrices are
$\mathcal{X} = \{1, 2, 3\}$
; the transition matrices are
 \begin{align*} P(0) = \left[\begin{matrix} 0.3629 & \quad 0.5028 & \quad 0.1343 \\[4pt] 0.0823 & \quad 0.7534 & \quad 0.1643 \\[4pt] 0.2460 & \quad 0.0294 & \quad 0.7246 \end{matrix}\right], \qquad P(1) = \left[\begin{matrix} 0.1719 & \quad 0.1749 & \quad 0.6532 \\[4pt] 0.0547 & \quad 0.9317 & \quad 0.0136 \\[4pt] 0.1547 & \quad 0.6271 & \quad 0.2182\end{matrix}\right]; \end{align*}
\begin{align*} P(0) = \left[\begin{matrix} 0.3629 & \quad 0.5028 & \quad 0.1343 \\[4pt] 0.0823 & \quad 0.7534 & \quad 0.1643 \\[4pt] 0.2460 & \quad 0.0294 & \quad 0.7246 \end{matrix}\right], \qquad P(1) = \left[\begin{matrix} 0.1719 & \quad 0.1749 & \quad 0.6532 \\[4pt] 0.0547 & \quad 0.9317 & \quad 0.0136 \\[4pt] 0.1547 & \quad 0.6271 & \quad 0.2182\end{matrix}\right]; \end{align*}
the per-step cost is
![]() $c(x,0) = 0$
for all
$c(x,0) = 0$
for all
![]() $x \in \mathcal{X}$
and
$x \in \mathcal{X}$
and
![]() $c(1, 1) = -0.44138$
,
$c(1, 1) = -0.44138$
,
![]() $c(2, 1) = -0.8033$
,
$c(2, 1) = -0.8033$
,
![]() $c(3, 1) = -0.14257$
; and
$c(3, 1) = -0.14257$
; and
![]() $\beta = 0.9$
. The corresponding Whittle indices are
$\beta = 0.9$
. The corresponding Whittle indices are
![]() $[0.18, 0.8, 0.57]$
.
$[0.18, 0.8, 0.57]$
.
This model is not PCL-indexable, since if
![]() $g = [1, 1, 0]$
and
$g = [1, 1, 0]$
and
![]() $h = [0, 1, 0]$
, then
$h = [0, 1, 0]$
, then
![]() $N^{(g)} = [5.66, 8.24, 4.23]$
and
$N^{(g)} = [5.66, 8.24, 4.23]$
and
![]() $N^{(h)} = [6.65, 8.59, 4.88]$
. Therefore, for any initial state distribution
$N^{(h)} = [6.65, 8.59, 4.88]$
. Therefore, for any initial state distribution
![]() $\pi_0$
,
$\pi_0$
,
![]() $\mathsf{N}^{(g)} < \mathsf{N}^{(h)}$
.
$\mathsf{N}^{(g)} < \mathsf{N}^{(h)}$
.
However, as the problem is indexable, we can still apply Algorithm 1 to compute Whittle indices without any limitations. The steps are as follows:
-
1. Initialize
 $d=0$
and have
$d=0$
and have
 ${\mathcal P}_0 = \emptyset$
. Thus
${\mathcal P}_0 = \emptyset$
. Thus
 ${\bar g}^{({\mathcal P}_0)} = [1, 1, 1]$
and we compute
${\bar g}^{({\mathcal P}_0)} = [1, 1, 1]$
and we compute
 $N^{\big({\bar g}^{({\mathcal P}_0)}\big)} = [10, 10, 10]$
and
$N^{\big({\bar g}^{({\mathcal P}_0)}\big)} = [10, 10, 10]$
and
 $D^{\big({\bar g}^{({\mathcal P}_0)}\big)} = [{-}6.43, -7.43, -6.51]$
.
$D^{\big({\bar g}^{({\mathcal P}_0)}\big)} = [{-}6.43, -7.43, -6.51]$
. -
2. There are three possibilities for
 $y \in \mathcal{X} \setminus \mathcal{P}_0 = \{1,2,3\}$
:
$y \in \mathcal{X} \setminus \mathcal{P}_0 = \{1,2,3\}$
:
-
For
 $y = 1$
,
$y = 1$
,
 $h_{0,1} = [0, 1, 1]$
. We compute
$h_{0,1} = [0, 1, 1]$
. We compute
 $N^{(h_{0,1})} = [7.88, 9.29, 9.13]$
and
$N^{(h_{0,1})} = [7.88, 9.29, 9.13]$
and
 $D^{(h_{0,1})} = $
$D^{(h_{0,1})} = $
 $[{-}6.05, -7.30, -6.35]$
. Therefore,
$[{-}6.05, -7.30, -6.35]$
. Therefore,
 $\Lambda_{0,1} = \big\{x \in \mathcal{X} \,:\, N^{(\bar g(\mathcal{P}_0)}(x) \neq N^{(h_{0,1})}(x) \big\} = \{1, 2, 3\}$
. Now for each
$\Lambda_{0,1} = \big\{x \in \mathcal{X} \,:\, N^{(\bar g(\mathcal{P}_0)}(x) \neq N^{(h_{0,1})}(x) \big\} = \{1, 2, 3\}$
. Now for each
 $x \in \Lambda_{0,1}$
, we compute
$x \in \Lambda_{0,1}$
, we compute
 $\mu_{0,1}(1) = \mu_{0,1}(2) = \mu_{0,1}(3) = 0.18$
. Therefore,
$\mu_{0,1}(1) = \mu_{0,1}(2) = \mu_{0,1}(3) = 0.18$
. Therefore,
 $\mu^*_{0,1} = 0.18$
.
$\mu^*_{0,1} = 0.18$
. -
For
 $y = 2$
,
$y = 2$
,
 $h_{0,2} = [1, 0, 1]$
. We compute
$h_{0,2} = [1, 0, 1]$
. We compute
 $N^{\left(h_{0,2}\right)} = [4.58, 2.93, 4.10]$
and
$N^{\left(h_{0,2}\right)} = [4.58, 2.93, 4.10]$
and
 $D^{\left(h_{0,2}\right)} = [{-}1.27, -0.7, -0.89]$
. Therefore,
$D^{\left(h_{0,2}\right)} = [{-}1.27, -0.7, -0.89]$
. Therefore,
 $\Lambda_{0,2} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_0)}}(x) \neq N^{\left(h_{0,2}\right)}(x) \Big\} = \{1, 2, 3\}$
. Now for each
$\Lambda_{0,2} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_0)}}(x) \neq N^{\left(h_{0,2}\right)}(x) \Big\} = \{1, 2, 3\}$
. Now for each
 $x \in \Lambda_{0,2}$
, we compute
$x \in \Lambda_{0,2}$
, we compute
 $\mu_{0,2}(1) = \mu_{0,2}(2) = \mu_{0,2}(3) = 0.95$
. Therefore,
$\mu_{0,2}(1) = \mu_{0,2}(2) = \mu_{0,2}(3) = 0.95$
. Therefore,
 $\mu^*_{0,2} = 0.95$
.
$\mu^*_{0,2} = 0.95$
. -
For
 $y = 3$
,
$y = 3$
,
 $h_{0,3} = [1, 1, 0]$
. We compute
$h_{0,3} = [1, 1, 0]$
. We compute
 $N^{(h_{0,3})} = [5.66, 8.24, 4.23]$
and
$N^{(h_{0,3})} = [5.66, 8.24, 4.23]$
and
 $D^{(h_{0,3})} = [{-}3.64, -6.30, -2.79]$
. Therefore,
$D^{(h_{0,3})} = [{-}3.64, -6.30, -2.79]$
. Therefore,
 $\Lambda_{0,3} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_0)}}(x) \neq N^{(h_{0,3})}(x) \Big\} = \{1, 2, 3\}$
. Now for each
$\Lambda_{0,3} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_0)}}(x) \neq N^{(h_{0,3})}(x) \Big\} = \{1, 2, 3\}$
. Now for each
 $x \in \Lambda_{0,3}$
, we compute
$x \in \Lambda_{0,3}$
, we compute
 $\mu_{0,3}(1) = \mu_{0,3}(2) = \mu_{0,3}(3) = 0.64$
. Therefore,
$\mu_{0,3}(1) = \mu_{0,3}(2) = \mu_{0,3}(3) = 0.64$
. Therefore,
 $\mu^*_{0,3} = 0.64$
.
$\mu^*_{0,3} = 0.64$
.
-
Now
 $\lambda_1 = \min \big\{ \mu^*_{0,1}, \mu^*_{0,2}, \mu^*_{0,3} \big\} = 0.18$
. Therefore,
$\lambda_1 = \min \big\{ \mu^*_{0,1}, \mu^*_{0,2}, \mu^*_{0,3} \big\} = 0.18$
. Therefore,
 ${\mathcal P}_1 = \{1\}$
,
${\mathcal P}_1 = \{1\}$
,
 $w(1) = 0.18$
,
$w(1) = 0.18$
,
 ${\bar g}^{({\mathcal P}_1)} = [0, 1, 1]$
. We have already computed
${\bar g}^{({\mathcal P}_1)} = [0, 1, 1]$
. We have already computed
 $N^{\big({\bar g}^{({\mathcal P}_1)}\big)} = [7.88, 9.29, 9.13]$
and
$N^{\big({\bar g}^{({\mathcal P}_1)}\big)} = [7.88, 9.29, 9.13]$
and
 $D^{\big({\bar g}^{({\mathcal P}_1)}\big)} = [{-}6.05, -7.30, -6.35]$
.
$D^{\big({\bar g}^{({\mathcal P}_1)}\big)} = [{-}6.05, -7.30, -6.35]$
.
-
3. There are two possibilities for
 $y \in \mathcal{X} \setminus \mathcal{P}_1 = \{2, 3\}$
:
$y \in \mathcal{X} \setminus \mathcal{P}_1 = \{2, 3\}$
:
-
For
 $y = 2$
,
$y = 2$
,
 $h_{1,2} = [0, 0, 1]$
. We compute
$h_{1,2} = [0, 0, 1]$
. We compute
 $N^{(h_{1,2})} = [1.48, 1.52, 2.57]$
and
$N^{(h_{1,2})} = [1.48, 1.52, 2.57]$
and
 $D^{(h_{1,2})} = [{-}0.21, -0.22, -0.37]$
. Therefore,
$D^{(h_{1,2})} = [{-}0.21, -0.22, -0.37]$
. Therefore,
 $\Lambda_{1,2} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_1)}}(x) \neq N^{(h_{1,2})}(x) \Big\} = \{1, 2, 3\}$
. Now for each
$\Lambda_{1,2} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_1)}}(x) \neq N^{(h_{1,2})}(x) \Big\} = \{1, 2, 3\}$
. Now for each
 $x \in \Lambda_{1,2}$
, we compute
$x \in \Lambda_{1,2}$
, we compute
 $\mu_{1,2}(1) = \mu_{1,2}(2) = \mu_{1,2}(3) = 0.91$
. Therefore,
$\mu_{1,2}(1) = \mu_{1,2}(2) = \mu_{1,2}(3) = 0.91$
. Therefore,
 $\mu^*_{1,2} = 0.91$
.
$\mu^*_{1,2} = 0.91$
. -
For
 $y = 3$
,
$y = 3$
,
 $h_{1,3} = [0, 1, 0]$
. We compute
$h_{1,3} = [0, 1, 0]$
. We compute
 $N^{(h_{1,3})} = [6.65, 8.59, 4.88]$
and
$N^{(h_{1,3})} = [6.65, 8.59, 4.88]$
and
 $D^{(h_{1,3})} = [{-}1.22, -0.66, -0.83]$
. Therefore,
$D^{(h_{1,3})} = [{-}1.22, -0.66, -0.83]$
. Therefore,
 $\Lambda_{1,3} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_1)}}(x) \neq N^{(h_{1,3})}(x) \Big\} = \{1, 2, 3\}$
. Now for each
$\Lambda_{1,3} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_1)}}(x) \neq N^{(h_{1,3})}(x) \Big\} = \{1, 2, 3\}$
. Now for each
 $x \in \Lambda_{1,3}$
, we compute
$x \in \Lambda_{1,3}$
, we compute
 $\mu_{1,3}(1) = \mu_{1,3}(2) = \mu_{1,3}(3) = 0.57$
. Therefore,
$\mu_{1,3}(1) = \mu_{1,3}(2) = \mu_{1,3}(3) = 0.57$
. Therefore,
 $\mu^*_{1,3} = 0.57$
.
$\mu^*_{1,3} = 0.57$
.
-
Now
 $\lambda_2 = \min \big\{ \mu^*_{1,2}, \mu^*_{1,3} \big\} = 0.57$
. Therefore,
$\lambda_2 = \min \big\{ \mu^*_{1,2}, \mu^*_{1,3} \big\} = 0.57$
. Therefore,
 ${\mathcal P}_2 = \{1, 3\}$
,
${\mathcal P}_2 = \{1, 3\}$
,
 $w(3) = 0.57$
,
$w(3) = 0.57$
,
 ${\bar g}^{({\mathcal P}_2)} = [0, 1, 0]$
. We have already computed
${\bar g}^{({\mathcal P}_2)} = [0, 1, 0]$
. We have already computed
 $N^{\big({\bar g}^{({\mathcal P}_2)}\big)} = [6.65, 8.59, 4.88]$
and
$N^{\big({\bar g}^{({\mathcal P}_2)}\big)} = [6.65, 8.59, 4.88]$
and
 $D^{\big({\bar g}^{({\mathcal P}_2)}\big)} = [{-}1.22, -0.66, -0.83]$
.
$D^{\big({\bar g}^{({\mathcal P}_2)}\big)} = [{-}1.22, -0.66, -0.83]$
.
-
4. There is only one possibility for
 $y \in \mathcal{X} \setminus \mathcal{P}_2 = \{2\}$
:
$y \in \mathcal{X} \setminus \mathcal{P}_2 = \{2\}$
:
-
For
 $y = 3$
,
$y = 3$
,
 $h_{3,2} = [0, 0, 0]$
,
$h_{3,2} = [0, 0, 0]$
,
 $N^{(h_{3,2})} = [0, 0, 0]$
, and
$N^{(h_{3,2})} = [0, 0, 0]$
, and
 $D^{(h_{3,2})} = [{-}0.21, -0.22, -0.37]$
. Therefore,
$D^{(h_{3,2})} = [{-}0.21, -0.22, -0.37]$
. Therefore,
 $\Lambda_{3,2} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_2)}}(x) \neq N^{(h_{3,2})}(x) \Big\} = \{1, 2, 3\}$
. Now for each
$\Lambda_{3,2} = \Big\{x \in \mathcal{X} \,:\, N^{(\bar g^{(\mathcal{P}_2)}}(x) \neq N^{(h_{3,2})}(x) \Big\} = \{1, 2, 3\}$
. Now for each
 $x \in \Lambda_{3,2}$
, we compute
$x \in \Lambda_{3,2}$
, we compute
 $\mu_{3,2}(1) = \mu_{3,2}(2) = \mu_{3,2}(3) = 0.8$
. Therefore,
$\mu_{3,2}(1) = \mu_{3,2}(2) = \mu_{3,2}(3) = 0.8$
. Therefore,
 $\mu^*_{3,2} = 0.8$
.
$\mu^*_{3,2} = 0.8$
.
-
Now
 $\mu^*_{3,2} = 0.57$
. Therefore,
$\mu^*_{3,2} = 0.57$
. Therefore,
 ${\mathcal P}_3 = \{1, 2, 3\}$
and
${\mathcal P}_3 = \{1, 2, 3\}$
and
 $w(2) = 0.8$
.
$w(2) = 0.8$
.
Finally, the Whittle indices are
![]() $[0.18, 0.8, 0.57]$
.
$[0.18, 0.8, 0.57]$
.
5. Some special cases
In this section, we refine the results developed in this paper to some special cases.
5.1. Restless bandits with optimal threshold-based policy
Consider an RB
![]() $\big(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}},c, x_0\big)$
where the state space
$\big(\mathcal{X}, \{0, 1\}, \{P(a)\}_{a \in \{0, 1\}},c, x_0\big)$
where the state space
![]() $\mathcal{X}$
is a totally ordered set, i.e.,
$\mathcal{X}$
is a totally ordered set, i.e.,
![]() ${\mathcal X} = \{1, \ldots, K\}$
. Let
${\mathcal X} = \{1, \ldots, K\}$
. Let
![]() $\mathcal{X}_0 = \{0, \dots, K\}$
; let
$\mathcal{X}_0 = \{0, \dots, K\}$
; let
![]() $\mathcal{X}_{\ge \ell}$
denote the set of states greater than or equal to the state
$\mathcal{X}_{\ge \ell}$
denote the set of states greater than or equal to the state
![]() $\ell$
, and let
$\ell$
, and let
![]() $\mathcal{X}_{\le \ell}$
denote the set of states less than or equal to the state
$\mathcal{X}_{\le \ell}$
denote the set of states less than or equal to the state
![]() $\ell$
. We suppose that the model satisfies the following assumption:
$\ell$
. We suppose that the model satisfies the following assumption:
-
(P) There exists a non-decreasing family of thresholds
 $\{\ell_\lambda\}_{\lambda \in \mathbb{R}}$
,
$\{\ell_\lambda\}_{\lambda \in \mathbb{R}}$
,
 $\ell_\lambda \in \mathcal{X}_0$
, such that the threshold policy
$\ell_\lambda \in \mathcal{X}_0$
, such that the threshold policy
 $g^{(\ell_\lambda)}$
is optimal for Problem 2 with activation cost
$g^{(\ell_\lambda)}$
is optimal for Problem 2 with activation cost
 $\lambda$
.
$\lambda$
.
Several models where (P) holds have been considered in the literature [Reference Akbarzadeh and Mahajan3, Reference Ansell, Glazebrook, Niño-Mora and O’Keeffe5, Reference Avrachenkov, Ayesta, Doncel and Jacko7, Reference Glazebrook, Hodge and Kirkbride15, Reference Glazebrook, Kirkbride and Ouenniche17, Reference Wang, Ren, Mo and Shi30]. A key implication of Property (P) is the following.
Lemma 4. Suppose an RB defined on a totally ordered state space satisfies Property (P). Then the RB is indexable and the Whittle index
![]() $w(\ell)$
is non-decreasing in
$w(\ell)$
is non-decreasing in
![]() $\ell \in {\mathcal X}$
.
$\ell \in {\mathcal X}$
.
Proof. Note that Property (P) implies that the passive set
![]() $\Pi_\lambda = \{ x \in \mathcal{X} \,:\, g_\lambda(x) = 0 \} = \mathcal{X}_{\le \ell_\lambda}$
, which is increasing in
$\Pi_\lambda = \{ x \in \mathcal{X} \,:\, g_\lambda(x) = 0 \} = \mathcal{X}_{\le \ell_\lambda}$
, which is increasing in
![]() $\lambda$
. Hence the RB is indexable. Moreover, for any state
$\lambda$
. Hence the RB is indexable. Moreover, for any state
![]() $\ell$
, the Whittle index
$\ell$
, the Whittle index
![]() $w(\ell)$
is the smallest value of
$w(\ell)$
is the smallest value of
![]() $\lambda$
such that
$\lambda$
such that
![]() $\ell_\lambda = \ell$
. Therefore, by Property (P),
$\ell_\lambda = \ell$
. Therefore, by Property (P),
![]() $w(\ell)$
is non-decreasing in
$w(\ell)$
is non-decreasing in
![]() $\ell$
.
$\ell$
.
As in Section 4, we assume that there are
![]() $K_D (\leq K)$
distinct Whittle indices given by
$K_D (\leq K)$
distinct Whittle indices given by
![]() $\Lambda^* = \{\lambda_1, \dots, \lambda_{K_D}\}$
, where
$\Lambda^* = \{\lambda_1, \dots, \lambda_{K_D}\}$
, where
![]() $\lambda_1 < \lambda_2 < \dots \lambda_{K_D}$
. We also let
$\lambda_1 < \lambda_2 < \dots \lambda_{K_D}$
. We also let
![]() $\lambda_0 = -\infty$
, and for any
$\lambda_0 = -\infty$
, and for any
![]() $d \in \{0, \dots, K_D\}$
, we let
$d \in \{0, \dots, K_D\}$
, we let
![]() $\mathcal{P}_d = \{ x \in \mathcal X \,:\, w(x) \le \lambda_d \}$
. As stated in the proof of Lemma 4, Property (P) implies that
$\mathcal{P}_d = \{ x \in \mathcal X \,:\, w(x) \le \lambda_d \}$
. As stated in the proof of Lemma 4, Property (P) implies that
![]() $\mathcal{P}_d = \mathcal{X}_{\le \ell_{\lambda_d}}$
. Therefore,
$\mathcal{P}_d = \mathcal{X}_{\le \ell_{\lambda_d}}$
. Therefore,
![]() $\Gamma_{d+1} = \big\{\ell_{\lambda_d} + 1, \dots, \ell_{\lambda_{d+1}}\big\}$
. Thus, Theorem 2 simplifies as follows.
$\Gamma_{d+1} = \big\{\ell_{\lambda_d} + 1, \dots, \ell_{\lambda_{d+1}}\big\}$
. Thus, Theorem 2 simplifies as follows.
Corollary 1. Suppose an RB defined on a totally ordered state space satisfies Property (P). Then the following properties hold:
-
1. For any
 $y \in \Gamma_{d+1}$
, the set
$y \in \Gamma_{d+1}$
, the set
 $\Lambda_{d, y}$
is non-empty.
$\Lambda_{d, y}$
is non-empty. -
2. For any
 $x \in \Lambda_{d, y}$
,
$x \in \Lambda_{d, y}$
,
 $\mu_{d,y}(x) \geq \lambda_{d+1}$
, with equality if and only if
$\mu_{d,y}(x) \geq \lambda_{d+1}$
, with equality if and only if
 $y \in \Gamma_{d+1}$
.
$y \in \Gamma_{d+1}$
.
Thus, based on Corollary 1, for models that satisfy Property (P), we can simplify Algorithm 2 as shown in Algorithm 4. Instead of computing
![]() $\mu^*_{d,y}$
for all
$\mu^*_{d,y}$
for all
![]() $y \in \mathcal{X} \setminus \mathcal{P}_d$
, we can compute it sequentially and break the loop when
$y \in \mathcal{X} \setminus \mathcal{P}_d$
, we can compute it sequentially and break the loop when
![]() $\mu^*_{d,y} \neq \lambda_{d+1}$
. Note that this simplification does not change the asymptotic complexity of the algorithm, which is still
$\mu^*_{d,y} \neq \lambda_{d+1}$
. Note that this simplification does not change the asymptotic complexity of the algorithm, which is still
![]() $\mathcal{O}\!\left(K^3\right)$
.
$\mathcal{O}\!\left(K^3\right)$
.

Remark 1. Note that if the model satisfies additional assumptions such that it is known up front that no two states have the same Whittle index, then we do not need the inner for loop (over y) in Algorithm 4, and can simply compute the Whittle index of the state
![]() $\ell$
as
$\ell$
as
 \begin{align*} w(\ell) = \min \frac{D^{\big(\bar g^{\left(\mathcal{X}_{\le \ell + 1}\right)}\big)}(x) - D^{\big(g^{\left(\mathcal{X}_{\le \ell }\right)}\big)}(x)} {N^{\big(\bar g^{\left(\mathcal{X}_{\le \ell}\right)}\big)}(x) - N^{\big(g^{\left(\mathcal{X}_{\le \ell + 1 }\right)}\big)}(x)}, \end{align*}
\begin{align*} w(\ell) = \min \frac{D^{\big(\bar g^{\left(\mathcal{X}_{\le \ell + 1}\right)}\big)}(x) - D^{\big(g^{\left(\mathcal{X}_{\le \ell }\right)}\big)}(x)} {N^{\big(\bar g^{\left(\mathcal{X}_{\le \ell}\right)}\big)}(x) - N^{\big(g^{\left(\mathcal{X}_{\le \ell + 1 }\right)}\big)}(x)}, \end{align*}
where the minimum is over all x such that the denominator is non-zero.
In the next section, we present a new model called stochastic monotone bandits, which may be considered as a generalization of monotone bandits [Reference Ansell, Glazebrook, Niño-Mora and O’Keeffe5, Reference Avrachenkov, Ayesta, Doncel and Jacko7, Reference Glazebrook, Hodge and Kirkbride15], and show that these models satisfy Property (P).
5.2. Stochastic monotone bandits
We first start with the definition of a submodular function. Given ordered sets
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
, a function
$\mathcal{Y}$
, a function
![]() $f\,:\, \mathcal{X} \times \mathcal{Y} \to \mathbb{R}$
is called submodular if for any
$f\,:\, \mathcal{X} \times \mathcal{Y} \to \mathbb{R}$
is called submodular if for any
![]() $x_1, x_2 \in \mathcal{X}$
and
$x_1, x_2 \in \mathcal{X}$
and
![]() $y_1, y_2 \in \mathcal{Y}$
such that
$y_1, y_2 \in \mathcal{Y}$
such that
![]() $x_2 \geq x_1$
and
$x_2 \geq x_1$
and
![]() $y_2 \geq y_1$
, we have
$y_2 \geq y_1$
, we have
![]() $f(x_1, y_2) - f(x_1, y_1) \geq f(x_2, y_2) - f(x_2, y_1)$
.
$f(x_1, y_2) - f(x_1, y_1) \geq f(x_2, y_2) - f(x_2, y_1)$
.
We say that the RB is stochastic monotone if it satisfies the following conditions:
-
(D1) For any
 $a \in \{0, 1\}$
, P(a) is stochastically monotone; i.e., for any
$a \in \{0, 1\}$
, P(a) is stochastically monotone; i.e., for any
 $x, y \in \mathcal{X}$
such that
$x, y \in \mathcal{X}$
such that
 $x < y$
, we have for any
$x < y$
, we have for any \begin{align*}\sum_{w \in \mathcal X_{\ge z}} P_{xw}(a) \leq \sum_{w \in \mathcal X_{\ge z}} P_{yw}(a)\end{align*}
\begin{align*}\sum_{w \in \mathcal X_{\ge z}} P_{xw}(a) \leq \sum_{w \in \mathcal X_{\ge z}} P_{yw}(a)\end{align*}
 $z \in \mathcal{X}$
.
$z \in \mathcal{X}$
.
-
(D2) For any
 $z \in \mathcal{X}$
,
$z \in \mathcal{X}$
,
 $S_{zx}(a) \,:\!=\, \sum_{w \in \mathcal X_{\ge z}} P_{xw}(a)$
is submodular in (x, a).
$S_{zx}(a) \,:\!=\, \sum_{w \in \mathcal X_{\ge z}} P_{xw}(a)$
is submodular in (x, a). -
(D3) For any
 $a \in \{ 0, 1 \}$
, c(x, a) is non-decreasing in x.
$a \in \{ 0, 1 \}$
, c(x, a) is non-decreasing in x. -
(D4) The cost c(x, a) is submodular in (x, a).
For ease of notation, for any
![]() $\ell \in \mathcal{X}_0$
, we let
$\ell \in \mathcal{X}_0$
, we let
![]() $g^{(\ell)} = \bar g^{(\mathcal X_{\le \ell})}$
denote a policy with threshold
$g^{(\ell)} = \bar g^{(\mathcal X_{\le \ell})}$
denote a policy with threshold
![]() $\ell$
(where
$\ell$
(where
![]() $\bar{g}^{(\mathcal S)}$
is as defined in (13)).
$\bar{g}^{(\mathcal S)}$
is as defined in (13)).
Lemma 5. A stochastic monotone RB satisfies the following properties:
-
1. For any
 $\lambda \in \mathbb{R}$
, there exists a threshold
$\lambda \in \mathbb{R}$
, there exists a threshold
 $\ell_\lambda \in \mathcal{X}^*$
such that the threshold policy
$\ell_\lambda \in \mathcal{X}^*$
such that the threshold policy
 $g^{(\ell_\lambda)}$
is optimal for Problem 2. If there are multiple such thresholds, we use
$g^{(\ell_\lambda)}$
is optimal for Problem 2. If there are multiple such thresholds, we use
 $\ell_\lambda$
to denote the largest threshold.
$\ell_\lambda$
to denote the largest threshold. -
2. If, for any
 $x \in \mathcal{X}$
,
$x \in \mathcal{X}$
,
 $N^{\big(g^{(\ell)}\big)}(x)$
is non-increasing in
$N^{\big(g^{(\ell)}\big)}(x)$
is non-increasing in
 $\ell$
, then
$\ell$
, then
 $\ell_\lambda$
is non-decreasing with
$\ell_\lambda$
is non-decreasing with
 $\lambda$
. Hence, the model satisfies Property (P) and is therefore indexable.
$\lambda$
. Hence, the model satisfies Property (P) and is therefore indexable.
Proof. For the first part, we note that Conditions (D1)–(D4) are the same as the properties of [Reference Puterman28, Theorem 4.7.4], which implies that there exists a threshold as stated.
For the second part, we first show that for any
![]() $\ell \in \mathcal{X}^*$
,
$\ell \in \mathcal{X}^*$
,
![]() $J^{\big(g^{(\ell)}\big)}_\lambda(x)$
is submodular in
$J^{\big(g^{(\ell)}\big)}_\lambda(x)$
is submodular in
![]() $(\ell,\lambda)$
for all
$(\ell,\lambda)$
for all
![]() $x \in \mathcal{X}$
. In particular, for any
$x \in \mathcal{X}$
. In particular, for any
![]() $k < \ell$
, we have
$k < \ell$
, we have
Now (D5) implies that the difference
![]() $J^{\big(g^{(\ell)}\big)}_\lambda(x) - J^{\big(g^{(k)}\big)}_\lambda(x)$
is non-increasing in
$J^{\big(g^{(\ell)}\big)}_\lambda(x) - J^{\big(g^{(k)}\big)}_\lambda(x)$
is non-increasing in
![]() $\lambda$
. Therefore,
$\lambda$
. Therefore,
![]() $J^{\big(g^{(\ell)}\big)}_\lambda(x)$
is submodular in
$J^{\big(g^{(\ell)}\big)}_\lambda(x)$
is submodular in
![]() $(\ell,\lambda)$
. Consequently, from [Reference Puterman28, Theorem 2.8.2],
$(\ell,\lambda)$
. Consequently, from [Reference Puterman28, Theorem 2.8.2],
is non-decreasing in
![]() $\lambda$
.
$\lambda$
.
5.3. Restless bandits with controlled restarts
Consider restless bandits with controlled restarts (i.e., models where
![]() $P_{xy}(1)$
does not depend on x). By Proposition 2(c), such models are indexable. In this section, we explain how to simplify the computation of the Whittle index for such models. For ease of notation, we use
$P_{xy}(1)$
does not depend on x). By Proposition 2(c), such models are indexable. In this section, we explain how to simplify the computation of the Whittle index for such models. For ease of notation, we use
![]() $P_{xy}$
to denote
$P_{xy}$
to denote
![]() $P_{xy}(0)$
and
$P_{xy}(0)$
and
![]() $Q_y$
to denote
$Q_y$
to denote
![]() $P_{xy}(1)$
.
$P_{xy}(1)$
.
Define
![]() $ \mathsf{D}^{(g)} = \sum_{x \in \mathcal{X}} Q_x D^{(g)}(x) \quad\text{and}\quad \mathsf{N}^{(g)} = \sum_{x \in \mathcal{X}} Q_x N^{(g)}(x).$
Now, following the discussion of Section 4, we can show that the result of Theorem 2 continues to hold when
$ \mathsf{D}^{(g)} = \sum_{x \in \mathcal{X}} Q_x D^{(g)}(x) \quad\text{and}\quad \mathsf{N}^{(g)} = \sum_{x \in \mathcal{X}} Q_x N^{(g)}(x).$
Now, following the discussion of Section 4, we can show that the result of Theorem 2 continues to hold when
![]() $\mu_{d,y}$
is replaced by
$\mu_{d,y}$
is replaced by
 \begin{align*} \hat{\mu}_{d,y} = \dfrac{\mathsf{D}^{(h_y)} - \mathsf{D}^{\big(\bar{g}^{({\mathcal P}_d)}\big)}} {\mathsf{N}^{\big(\bar{g}^{({\mathcal P}_d)}\big)} - \mathsf{N}^{(h_y)}}. \end{align*}
\begin{align*} \hat{\mu}_{d,y} = \dfrac{\mathsf{D}^{(h_y)} - \mathsf{D}^{\big(\bar{g}^{({\mathcal P}_d)}\big)}} {\mathsf{N}^{\big(\bar{g}^{({\mathcal P}_d)}\big)} - \mathsf{N}^{(h_y)}}. \end{align*}
Therefore, we can replace
![]() $\mu_{d,y}(x)$
in Algorithm 1 by
$\mu_{d,y}(x)$
in Algorithm 1 by
![]() $\hat{\mu}_{d,y}$
. Our key result for this section is that
$\hat{\mu}_{d,y}$
. Our key result for this section is that
![]() $\mathsf{D}^{(g)}$
and
$\mathsf{D}^{(g)}$
and
![]() $\mathsf{N}^{(g)}$
can be computed efficiently for models with controlled restarts.
$\mathsf{N}^{(g)}$
can be computed efficiently for models with controlled restarts.
For that matter, given any policy g, let
![]() $\tau_g$
denote the hitting time of the set
$\tau_g$
denote the hitting time of the set
![]() $\Pi^{(g)} = \{x \in \mathcal{X} \,:\, g(x) = 1 \}$
. Let
$\Pi^{(g)} = \{x \in \mathcal{X} \,:\, g(x) = 1 \}$
. Let
 \begin{align*} \mathsf{L}^{(g)} \,:\!=\, \mathbb{E}\Biggl[ \sum_{t=0}^{\tau_g} \beta^t c(X_t, g(X_t)) \Bigm| X_0 \sim Q \Biggr] \quad\text{and}\quad \mathsf{M}^{(g)} \,:\!=\, \mathbb{E}\Biggl[ \sum_{t=0}^{\tau_g} \beta^t \Bigm| X_0 \sim Q \Biggr]\end{align*}
\begin{align*} \mathsf{L}^{(g)} \,:\!=\, \mathbb{E}\Biggl[ \sum_{t=0}^{\tau_g} \beta^t c(X_t, g(X_t)) \Bigm| X_0 \sim Q \Biggr] \quad\text{and}\quad \mathsf{M}^{(g)} \,:\!=\, \mathbb{E}\Biggl[ \sum_{t=0}^{\tau_g} \beta^t \Bigm| X_0 \sim Q \Biggr]\end{align*}
denote the expected discounted cost and expected discounted time for hitting
![]() $\Pi^{(g)}$
starting with an initial state distribution of Q. Then, using ideas from renewal theory, we can show the following.
$\Pi^{(g)}$
starting with an initial state distribution of Q. Then, using ideas from renewal theory, we can show the following.
Theorem 4. For any policy g,
Proof. The proof follows from standard ideas in renewal theory. By the strong Markov property, we have
 \begin{align} \mathsf{D}^{(g)} &= \mathbb{E} \Bigg[ (1-\beta) \sum_{t = 0}^{\tau_g} \beta^{t} c(X_t, g(X_t)) + \beta^{\tau_g+1} \mathsf{D}^{(g)} \Bigm| X_0 \sim Q \Bigg] \nonumber \\ &= (1-\beta) \mathsf{L}^{(g)} + \mathbb{E}\big[ \beta^{\tau_g+1} | X_0 \sim Q \big] \mathsf{D}^{(g)}. \end{align}
\begin{align} \mathsf{D}^{(g)} &= \mathbb{E} \Bigg[ (1-\beta) \sum_{t = 0}^{\tau_g} \beta^{t} c(X_t, g(X_t)) + \beta^{\tau_g+1} \mathsf{D}^{(g)} \Bigm| X_0 \sim Q \Bigg] \nonumber \\ &= (1-\beta) \mathsf{L}^{(g)} + \mathbb{E}\big[ \beta^{\tau_g+1} | X_0 \sim Q \big] \mathsf{D}^{(g)}. \end{align}
Using the definition of
![]() $\mathsf{M}^{(g)}$
, we have
$\mathsf{M}^{(g)}$
, we have
![]() $\mathbb{E}\big[ \beta^{\tau_g+1} | X_0 \sim Q \big] = 1 - (1-\beta) \mathsf{M}^{(g)}$
. Substituting this in (22) and rearranging the terms we get
$\mathbb{E}\big[ \beta^{\tau_g+1} | X_0 \sim Q \big] = 1 - (1-\beta) \mathsf{M}^{(g)}$
. Substituting this in (22) and rearranging the terms we get
![]() $\mathsf{D}^{(g)} = \mathsf{L}^{(g)}/\mathsf{M}^{(g)}$
.
$\mathsf{D}^{(g)} = \mathsf{L}^{(g)}/\mathsf{M}^{(g)}$
.
For
![]() $\mathsf{N}^{(g)}$
, by the strong Markov property we have
$\mathsf{N}^{(g)}$
, by the strong Markov property we have
 \begin{align*} \mathsf{N}^{(g)} &= \mathbb{E}\Big[ (1-\beta) \beta^{\tau_g} + \beta^{\tau_g+1} \mathsf{N}^{(g)} \Bigm| X_0 \sim Q \Big] \nonumber \\ &= \mathbb{E}\big[ \beta^{\tau_g} | X_0 \sim Q \big] \big(1-\beta + \beta \mathsf{N}^{(g)}\big) = \dfrac{ 1-(1-\beta)\mathsf{M}^{(g)} }{\beta}\big(1-\beta + \beta \mathsf{N}^{(g)}\big).\end{align*}
\begin{align*} \mathsf{N}^{(g)} &= \mathbb{E}\Big[ (1-\beta) \beta^{\tau_g} + \beta^{\tau_g+1} \mathsf{N}^{(g)} \Bigm| X_0 \sim Q \Big] \nonumber \\ &= \mathbb{E}\big[ \beta^{\tau_g} | X_0 \sim Q \big] \big(1-\beta + \beta \mathsf{N}^{(g)}\big) = \dfrac{ 1-(1-\beta)\mathsf{M}^{(g)} }{\beta}\big(1-\beta + \beta \mathsf{N}^{(g)}\big).\end{align*}
Therefore, we get
![]() $\mathsf{N}^{(g)} = \bigl(1 - (1-\beta)\mathsf{M}^{(g)}\bigr) / \beta \mathsf{M}^{(g)}$
.
$\mathsf{N}^{(g)} = \bigl(1 - (1-\beta)\mathsf{M}^{(g)}\bigr) / \beta \mathsf{M}^{(g)}$
.
Given any policy g, we can efficiently compute
![]() $\mathsf{L}^{(g)}$
and
$\mathsf{L}^{(g)}$
and
![]() $\mathsf{M}^{(g)}$
using standard formulas for truncated Markov chains. For any vector v, let
$\mathsf{M}^{(g)}$
using standard formulas for truncated Markov chains. For any vector v, let
![]() $v^{(g)}$
denote the vector with components indexed by the set
$v^{(g)}$
denote the vector with components indexed by the set
![]() $\{ x \in \mathcal{X} \,:\, g(x) = 0 \}$
, and let
$\{ x \in \mathcal{X} \,:\, g(x) = 0 \}$
, and let
![]() $\tilde v^{(g)}$
denote the remaining components. For example, if
$\tilde v^{(g)}$
denote the remaining components. For example, if
![]() $\mathcal{X} = \{1, 2, 3, 4\}$
,
$\mathcal{X} = \{1, 2, 3, 4\}$
,
![]() $g = (1,0, 1, 0)$
, and
$g = (1,0, 1, 0)$
, and
![]() $v = [1, 2, 3, 4]$
, then
$v = [1, 2, 3, 4]$
, then
![]() $v^{(g)} = (2, 4)$
and
$v^{(g)} = (2, 4)$
and
![]() $\tilde v^{(g)}= (1,3)$
. Similarly, for any square matrix Z, let
$\tilde v^{(g)}= (1,3)$
. Similarly, for any square matrix Z, let
![]() $Z^{[g]}$
denote the square sub-matrix corresponding to the elements
$Z^{[g]}$
denote the square sub-matrix corresponding to the elements
![]() $\{ x \in \mathcal{X} \,:\, g(x) = 0\}$
, and let
$\{ x \in \mathcal{X} \,:\, g(x) = 0\}$
, and let
![]() $\tilde Z^{[g]}$
denote the sub-matrix with rows
$\tilde Z^{[g]}$
denote the sub-matrix with rows
![]() $\{x \in \mathcal{X}\,:\, g(x) = 0 \}$
and columns
$\{x \in \mathcal{X}\,:\, g(x) = 0 \}$
and columns
![]() $\{x \in \mathcal{X} \,:\, g(x) = 1 \}$
. For example, if
$\{x \in \mathcal{X} \,:\, g(x) = 1 \}$
. For example, if
![]() $g = [1, 0, 1, 0]$
and if
$g = [1, 0, 1, 0]$
and if
 \begin{align*}Z = \left[\begin{matrix} 1 & \quad 2 & \quad 3 & \quad 4 \\[3pt] 5 & \quad 6 & \quad 8 & \quad 8 \\[3pt] 9 & \quad 10 & \quad 11 & \quad 12 \\[3pt] 13 & \quad 14 & \quad 15 & \quad 16 \end{matrix}\right],\end{align*}
\begin{align*}Z = \left[\begin{matrix} 1 & \quad 2 & \quad 3 & \quad 4 \\[3pt] 5 & \quad 6 & \quad 8 & \quad 8 \\[3pt] 9 & \quad 10 & \quad 11 & \quad 12 \\[3pt] 13 & \quad 14 & \quad 15 & \quad 16 \end{matrix}\right],\end{align*}
then
 $Z^{[g]} = \left[\begin{matrix} 6 & \quad 8 \\[3pt] 14 & \quad 16 \end{matrix}\right]$
and
$Z^{[g]} = \left[\begin{matrix} 6 & \quad 8 \\[3pt] 14 & \quad 16 \end{matrix}\right]$
and
 $Z^{[g]} = \left[\begin{matrix} 5 & \quad 8 \\[3pt] 13 & \quad 15 \end{matrix}\right]$
. Then, from standard formulas for truncated Markov chains, we have the following.
$Z^{[g]} = \left[\begin{matrix} 5 & \quad 8 \\[3pt] 13 & \quad 15 \end{matrix}\right]$
. Then, from standard formulas for truncated Markov chains, we have the following.
Proposition 3. For any policy g, let
![]() $c_0$
and
$c_0$
and
![]() $c_1$
denote column vectors corresponding to
$c_1$
denote column vectors corresponding to
![]() $c(\cdot, 0)$
and
$c(\cdot, 0)$
and
![]() $c(\cdot, 1)$
. Then
$c(\cdot, 1)$
. Then
 \begin{align*} \mathsf L^{(g)} &= Q^{(g)} \big(I - \beta P^{[g]}\big)^{-1} \Big(c_0^{(g)} + \beta \tilde P^{[g]} \tilde c^{(g)}_1\Big) + \tilde Q^{(g)} \tilde c^{(g)}_1, \\ \mathsf M^{(g)} &= Q^{(g)} \big(I - \beta P^{[g]}\big)^{-1} \Big(\textbf{1}^{(g)} + \beta \tilde P^{[g]} \tilde{\textbf{1}}^{(g)}\Big) + \tilde Q^{(g)} \tilde {\textbf{1}}^{(g)}. \end{align*}
\begin{align*} \mathsf L^{(g)} &= Q^{(g)} \big(I - \beta P^{[g]}\big)^{-1} \Big(c_0^{(g)} + \beta \tilde P^{[g]} \tilde c^{(g)}_1\Big) + \tilde Q^{(g)} \tilde c^{(g)}_1, \\ \mathsf M^{(g)} &= Q^{(g)} \big(I - \beta P^{[g]}\big)^{-1} \Big(\textbf{1}^{(g)} + \beta \tilde P^{[g]} \tilde{\textbf{1}}^{(g)}\Big) + \tilde Q^{(g)} \tilde {\textbf{1}}^{(g)}. \end{align*}
This gives us an efficient method to compute
![]() $\mathsf{L}^{(g)}$
and
$\mathsf{L}^{(g)}$
and
![]() $\mathsf{M}^{(g)}$
, which can in turn be used to compute
$\mathsf{M}^{(g)}$
, which can in turn be used to compute
![]() $\mathsf{D}^{(g)}$
and
$\mathsf{D}^{(g)}$
and
![]() $\mathsf{N}^{(g)}$
and used in a modified version of Algorithm 1 as explained.
$\mathsf{N}^{(g)}$
and used in a modified version of Algorithm 1 as explained.
6. Numerical experiments
In this section, we evaluate how well the Whittle index policy (wip) performs compared to the optimal policy (opt) as well as to a baseline policy known as the myopic policy (myp) (shown in Algorithm 5). The code is available at [Reference Akbarzadeh and Mahajan4].

6.1. Experimental setup
In our experiments, we consider restart bandits with
![]() $P(1)= [\textbf{1},\textbf{0}, \dots, \textbf{0}]$
. There are two other components of the model: the transition matrix P(0) and the cost function c. We choose these components as follows.
$P(1)= [\textbf{1},\textbf{0}, \dots, \textbf{0}]$
. There are two other components of the model: the transition matrix P(0) and the cost function c. We choose these components as follows.
6.1.1. The choice of transition matrices
We have three setups for choosing P(0). The first setup is a family of four types of structured stochastic monotone matrices, which we denote by
![]() ${\mathcal P}_{\ell}(p)$
,
${\mathcal P}_{\ell}(p)$
,
![]() $\ell \in \{1, \ldots, 4\}$
, where
$\ell \in \{1, \ldots, 4\}$
, where
![]() $p \in [0,1]$
is a parameter of the model. The second setup is a randomly generated stochastic monotone matrix which we denote by
$p \in [0,1]$
is a parameter of the model. The second setup is a randomly generated stochastic monotone matrix which we denote by
![]() ${\mathcal R}(d)$
, where
${\mathcal R}(d)$
, where
![]() $d \in[0, 1]$
is a parameter of the model. In the third setup, we generate random stochastic matrices using the Lévy distribution. The details of these models are presented in the supplementary material.
$d \in[0, 1]$
is a parameter of the model. In the third setup, we generate random stochastic matrices using the Lévy distribution. The details of these models are presented in the supplementary material.
6.1.2. The choice of the cost function
For all our experiments we choose
![]() $c(x, 0) = (x-1)^2$
and
$c(x, 0) = (x-1)^2$
and
![]() $c(x, 1) =0.5(|\mathcal{X}|-1)^2$
.
$c(x, 1) =0.5(|\mathcal{X}|-1)^2$
.
6.2. Experimental details and results
We conduct different experiments to compare the performance of the Whittle index with the optimal policy and the myopic policy for different setups (described in Section 6.1) and for different choices of the size
![]() $|\mathcal{X}|$
of the state space, the number n of arms, and the number m of active arms. For all experiments we choose the discount factor
$|\mathcal{X}|$
of the state space, the number n of arms, and the number m of active arms. For all experiments we choose the discount factor
![]() $\beta = 0.95$
.
$\beta = 0.95$
.
We evaluate the performance of a policy via Monte Carlo simulations over S trajectories, where each trajectory is of length T. In all our experiments, we choose
![]() $S= 2500$
and
$S= 2500$
and
![]() $T = 250$
.
$T = 250$
.
Experiment 1.
Comparison of Whittle index with the optimal policy for structured models. The optimal policy is computed by solving the Markov decision process for Problem 1, which is feasible only for small values of
![]() $|\mathcal{X}|$
and n. We choose
$|\mathcal{X}|$
and n. We choose
![]() $|\mathcal{X}| = 5$
and
$|\mathcal{X}| = 5$
and
![]() $n = 5$
and compare the two policies for the model
$n = 5$
and compare the two policies for the model
![]() ${\mathcal P}_{\ell}({\cdot})$
,
${\mathcal P}_{\ell}({\cdot})$
,
![]() $\ell \in\{1, \ldots, 4\}$
and
$\ell \in\{1, \ldots, 4\}$
and
![]() $m \in \{1, 2\}$
.
$m \in \{1, 2\}$
.
For a given value of n and
![]() $\ell$
, we pick n equispaced points
$\ell$
, we pick n equispaced points
![]() $(p_1, \dots, p_n)$
in the interval
$(p_1, \dots, p_n)$
in the interval
![]() $[0.35, 1]$
and choose
$[0.35, 1]$
and choose
![]() $\mathcal{P}_{\ell}(p_i)$
as the transition matrix of arm i. We observed that
$\mathcal{P}_{\ell}(p_i)$
as the transition matrix of arm i. We observed that
![]() $$ \alpha_{\small\text{OPT}} = J({\small\text{OPT}})/J({\small\text{WIP}}) $$
, the relative (percentage) performance improvement of wip compared to opt, was in the range of 99.95%–100% for all parameters.
$$ \alpha_{\small\text{OPT}} = J({\small\text{OPT}})/J({\small\text{WIP}}) $$
, the relative (percentage) performance improvement of wip compared to opt, was in the range of 99.95%–100% for all parameters.
Experiment 2.
Comparison of Whittle index with the optimal policy for randomly sampled models. As before, we pick
![]() $|\mathcal{X}| = 5$
and
$|\mathcal{X}| = 5$
and
![]() $n = 5$
so that it is feasible to calculate the optimal policy. For each arm, we sample the transition matrix from
$n = 5$
so that it is feasible to calculate the optimal policy. For each arm, we sample the transition matrix from
![]() ${\mathcal R}(5/|\mathcal{X}|)$
and repeat the experiment 250 times. Histograms of
${\mathcal R}(5/|\mathcal{X}|)$
and repeat the experiment 250 times. Histograms of
![]() $\alpha_{\small\text{OPT}}$
over experiments for
$\alpha_{\small\text{OPT}}$
over experiments for
![]() $m \in \{1, 2\}$
appear in Figure 2, which shows that wip performs close to opt in all cases.
$m \in \{1, 2\}$
appear in Figure 2, which shows that wip performs close to opt in all cases.
Experiment 3.
Comparison of Whittle index with the myopic policy for structured models. We generate the structured models as in Experiment 1 but for
![]() $|\mathcal{X}| = 25$
,
$|\mathcal{X}| = 25$
,
![]() $n \in \{25, 50, 75\}$
, and
$n \in \{25, 50, 75\}$
, and
![]() $m \in \{1, 2, 5\}$
. In this case, let
$m \in \{1, 2, 5\}$
. In this case, let
![]() $\varepsilon_{\small\text{MYP}} = (J({\small\text{MYP}})-J({\small\text{WIP}}))/J({\small\text{MYP}})$
denote the relative improvement of wip compared to myp. The results of
$\varepsilon_{\small\text{MYP}} = (J({\small\text{MYP}})-J({\small\text{WIP}}))/J({\small\text{MYP}})$
denote the relative improvement of wip compared to myp. The results of
![]() $\varepsilon_{\small\text{MYP}}$
for different choices of the parameters are shown in Figure 3.
$\varepsilon_{\small\text{MYP}}$
for different choices of the parameters are shown in Figure 3.

Figure 2. Relative performance
![]() $\alpha_{\small\text{OPT}}$
of wip versus opt for Experiment 2.
$\alpha_{\small\text{OPT}}$
of wip versus opt for Experiment 2.

Figure 3. Relative improvement
![]() $\varepsilon_{\small\text{MYP}}$
of wip versus myp for Experiment 3.
$\varepsilon_{\small\text{MYP}}$
of wip versus myp for Experiment 3.
In Figure 3, we observe that wip performs considerably better than myp. In addition to that, the performance of wip is better with respect to myp when
![]() $\ell = 4$
, which is more complicated than models where
$\ell = 4$
, which is more complicated than models where
![]() $\ell \in \{1, 2, 3\}$
. However, increasing m does not necessarily contribute to better
$\ell \in \{1, 2, 3\}$
. However, increasing m does not necessarily contribute to better
![]() $\varepsilon_{\small\text{MYP}}$
, as overlap between the choices of the two policies may increase. Note that as
$\varepsilon_{\small\text{MYP}}$
, as overlap between the choices of the two policies may increase. Note that as
![]() ${\mathcal P}_4({\cdot})$
is very different from the rest of the models, the trend of bars in Figure 3d with respect to n varies differently from the rest of the models.
${\mathcal P}_4({\cdot})$
is very different from the rest of the models, the trend of bars in Figure 3d with respect to n varies differently from the rest of the models.
Experiment 4.
Comparison of Whittle index with the myopic policy for randomly sampled models. We generate 250 random models as described in Experiment 2 but for
![]() $|\mathcal{X}|= 25$
and larger values of n. For each case,
$|\mathcal{X}|= 25$
and larger values of n. For each case,
![]() $\varepsilon_{\small\text{MYP}}$
is computed. Histograms of
$\varepsilon_{\small\text{MYP}}$
is computed. Histograms of
![]() $\varepsilon_{\small\text{MYP}}$
for different choices of the parameters are shown in Figure 4.
$\varepsilon_{\small\text{MYP}}$
for different choices of the parameters are shown in Figure 4.

Figure 4. Relative improvement
![]() $\varepsilon_{\small\text{MYP}}$
of wip versus myp for Experiment 4.
$\varepsilon_{\small\text{MYP}}$
of wip versus myp for Experiment 4.
The results show that on average, wip performs considerably better than myp, and this improvement is guaranteed as the concentration of data for the sampled models is mostly on positive values of
![]() $\varepsilon_{\small\text{MYP}}$
.
$\varepsilon_{\small\text{MYP}}$
.
Experiment 5.
Comparison of Whittle index with the myopic policy for restart models. We generate 250 random stochastic matrices for P(0). Each row of the matrix is generate according to Section 1.3 of the supplementary material. We set
![]() $|\mathcal{X}| = 25$
,
$|\mathcal{X}| = 25$
,
![]() $n \in \{25, 50, 75\}$
, and
$n \in \{25, 50, 75\}$
, and
![]() $m \in \{1, 2\}$
. For each case,
$m \in \{1, 2\}$
. For each case,
![]() $\varepsilon_{\small\text{MYP}}$
is computed; histograms of
$\varepsilon_{\small\text{MYP}}$
is computed; histograms of
![]() $\varepsilon_{\small\text{MYP}}$
for different choices of the parameters are shown in Figure 5.
$\varepsilon_{\small\text{MYP}}$
for different choices of the parameters are shown in Figure 5.

Figure 5. Relative improvement
![]() $\varepsilon_{\small\text{MYP}}$
of wip versus myp for Experiment 5.
$\varepsilon_{\small\text{MYP}}$
of wip versus myp for Experiment 5.
7. Conclusion
We present two general sufficient conditions for restless bandit processes to be indexable. The first condition depends only on the transition matrix P(1), while the second condition depends on both P(0) and P(1). These sufficient conditions are based on alternative characterizations of the passive set, which might be useful in general as well. We also present refinements of these sufficient conditions that are simpler to verify. Two of these simpler conditions are worth highlighting: models where the active action resets the state according to a known distribution, and models where the discount factor is less than
![]() $0.5$
.
$0.5$
.
We then present a generalization of a previously proposed adaptive greedy algorithm, which was developed to compute the Whittle index for a sub-class of restless bandits known as PCL-indexable bandits. We show that the generalized adaptive greedy algorithm computes the Whittle index for all indexable bandits. We provide a computationally efficient implementation of our algorithm, which computes the Whittle indices of a restless bandit with K states in
![]() $\mathcal{O}\!\left(K^3\right)$
computations.
$\mathcal{O}\!\left(K^3\right)$
computations.
Finally, we show how to refine the results for two classes of restless bandits: stochastic monotone bandits and restless bandits with controlled restarts. We also present a detailed numerical study which shows that the Whittle index policy performs close to the optimal policy and is considerably better than a myopic policy.
Appendix A. Proof of Proposition 1
We first present a preliminary result.
Lemma 6. For
![]() $\tau = 0$
, the policy
$\tau = 0$
, the policy
![]() $h_0$
satisfies
$h_0$
satisfies
![]() $J^{(h_0)}_\lambda(x) = H_\lambda(x, 1) = (1-\beta)c(x, 1)+W_\lambda$
.
$J^{(h_0)}_\lambda(x) = H_\lambda(x, 1) = (1-\beta)c(x, 1)+W_\lambda$
.
Proof. Consider the stopping time
![]() $\tau = 0$
. The policy
$\tau = 0$
. The policy
![]() $h_0$
takes the active action at time 0 and follows the optimal policy afterwards. Thus, for any
$h_0$
takes the active action at time 0 and follows the optimal policy afterwards. Thus, for any
![]() $x \in \mathcal X$
,
$x \in \mathcal X$
,
By (4) and (6) we have
![]() $H_\lambda(x, 1) = (1-\beta)c(x, 1)+W_\lambda(x)$
.
$H_\lambda(x, 1) = (1-\beta)c(x, 1)+W_\lambda(x)$
.
We now proceed with the proof of Proposition 1. By definition,
![]() $\Pi^{(a)}_\lambda = \Pi_\lambda$
. We establish the equality of other characterizations:
$\Pi^{(a)}_\lambda = \Pi_\lambda$
. We establish the equality of other characterizations:
-
(i)
 $\Pi^{(a)}_\lambda = \Pi^{(b)}_\lambda$
. We have
$\Pi^{(a)}_\lambda = \Pi^{(b)}_\lambda$
. We have
 $ x \in \Pi_\lambda \overset{(a)}{\iff} g_\lambda(x) = 0 \overset{(b)}{\iff} H_\lambda(x, 0) < H_\lambda(x, 1), $
where (a) follows from (5) and (b) follows from the dynamic program (3).
$ x \in \Pi_\lambda \overset{(a)}{\iff} g_\lambda(x) = 0 \overset{(b)}{\iff} H_\lambda(x, 0) < H_\lambda(x, 1), $
where (a) follows from (5) and (b) follows from the dynamic program (3). -
(ii)
 $\Pi^{(b)}_\lambda \subseteq \Pi^{(c)}_\lambda$
. Let
$\Pi^{(b)}_\lambda \subseteq \Pi^{(c)}_\lambda$
. Let
 $\sigma$
denote the hitting time of
$\sigma$
denote the hitting time of
 $\mathcal{X} \setminus \Pi_\lambda$
. If we start in the state
$\mathcal{X} \setminus \Pi_\lambda$
. If we start in the state
 $x \in \Pi^{(b)}_\lambda = \Pi_\lambda$
, then the policy
$x \in \Pi^{(b)}_\lambda = \Pi_\lambda$
, then the policy
 $h_{\sigma, \lambda}$
is same as the optimal policy. Hence,
$h_{\sigma, \lambda}$
is same as the optimal policy. Hence,
 $J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) = H_\lambda(x, 0)$
. Thus, for any
$J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) = H_\lambda(x, 0)$
. Thus, for any
 $x \in \Pi^{(b)}_\lambda = \Pi_\lambda$
, where (a) follows from fact that
$x \in \Pi^{(b)}_\lambda = \Pi_\lambda$
, where (a) follows from fact that \begin{align*}J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) = H_\lambda(x, 0) \overset{(a)}{<} H_\lambda(x,1) \overset{(b)}{=} J^{(h_0)}_{\lambda}(x),\end{align*}
\begin{align*}J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) = H_\lambda(x, 0) \overset{(a)}{<} H_\lambda(x,1) \overset{(b)}{=} J^{(h_0)}_{\lambda}(x),\end{align*}
 $x \in \Pi^{(b)}_\lambda$
and (b) from Lemma 6.
$x \in \Pi^{(b)}_\lambda$
and (b) from Lemma 6.
-
(iii)
 $\Pi^{(c)}_\lambda \subseteq \Pi^{(b)}_\lambda$
. Let
$\Pi^{(c)}_\lambda \subseteq \Pi^{(b)}_\lambda$
. Let
 $x \in \Pi^{(c)}_\lambda$
, and let
$x \in \Pi^{(c)}_\lambda$
, and let
 $\sigma \in \Sigma$
denote a stopping time such that
$\sigma \in \Sigma$
denote a stopping time such that
 $J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) < J^{(h_0)}_{\lambda}(x)$
. Now, the optimal policy performs at least as well as the policy
$J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) < J^{(h_0)}_{\lambda}(x)$
. Now, the optimal policy performs at least as well as the policy
 $h_{\sigma, \lambda}$
. Therefore,
$h_{\sigma, \lambda}$
. Therefore,
 $V_\lambda(x) \leq J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x)$
. Combining this result with Lemma 6 we have
$V_\lambda(x) \leq J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x)$
. Combining this result with Lemma 6 we have
 $V_\lambda(x) < H_\lambda(x, 1)$
. Thus, we must have
$V_\lambda(x) < H_\lambda(x, 1)$
. Thus, we must have
 $V_\lambda(x) = H_\lambda(x, 0)$
, which results in
$V_\lambda(x) = H_\lambda(x, 0)$
, which results in
 $H_\lambda(x, 0) < H_\lambda(x, 1)$
, which implies
$H_\lambda(x, 0) < H_\lambda(x, 1)$
, which implies
 $x \in \Pi^{(b)}_\lambda$
.
$x \in \Pi^{(b)}_\lambda$
. -
(iv)
 $\Pi^{(c)}_\lambda = \Pi^{(d)}_\lambda$
. According to the definitions of
$\Pi^{(c)}_\lambda = \Pi^{(d)}_\lambda$
. According to the definitions of
 $L(x, \tau)$
and
$L(x, \tau)$
and
 $W_\lambda(x)$
we have (23)Thus,
$W_\lambda(x)$
we have (23)Thus, \begin{align} J^{(h_{\tau, \lambda})}_{\lambda}(x) = (1-\beta) L(x, \tau) + \mathbb{E} [ \beta^{\tau} W_\lambda(X_\tau) | X_0 = x ]. \end{align}
\begin{align} J^{(h_{\tau, \lambda})}_{\lambda}(x) = (1-\beta) L(x, \tau) + \mathbb{E} [ \beta^{\tau} W_\lambda(X_\tau) | X_0 = x ]. \end{align}
 $J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) < J^{(h_0)}_{\lambda}(x)$
if and only if (24)where we have used (23) for
$J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x) < J^{(h_0)}_{\lambda}(x)$
if and only if (24)where we have used (23) for \begin{align} (1-\beta) L(x, \sigma) + \mathbb{E} [ \beta^{\sigma} W_\lambda(X_\sigma) | X_0 = x ] < (1 - \beta) c(x, 1) + W_\lambda(x), \end{align}
\begin{align} (1-\beta) L(x, \sigma) + \mathbb{E} [ \beta^{\sigma} W_\lambda(X_\sigma) | X_0 = x ] < (1 - \beta) c(x, 1) + W_\lambda(x), \end{align}
 $J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x)$
and Lemma 6 for
$J^{\left(h_{\sigma, \lambda}\right)}_{\lambda}(x)$
and Lemma 6 for
 $J^{(h_0)}_{\lambda}(x)$
. Rearranging the terms of (24) we get the expression in
$J^{(h_0)}_{\lambda}(x)$
. Rearranging the terms of (24) we get the expression in
 $\Pi^{(d)}_\lambda$
. Hence,
$\Pi^{(d)}_\lambda$
. Hence,
 $\Pi^{(c)}_\lambda = \Pi^{(d)}_\lambda$
.
$\Pi^{(c)}_\lambda = \Pi^{(d)}_\lambda$
.
Appendix B. Proof of Theorem 1
B.1. Proof of Theorem 1(a)
We first present a preliminary result. Let
![]() $\Delta_\lambda \,:\!=\, \lambda^{\prime\prime} - \lambda^{\prime}$
.
$\Delta_\lambda \,:\!=\, \lambda^{\prime\prime} - \lambda^{\prime}$
.
Lemma 7. Under (11), for any
![]() $\lambda^{\prime\prime} > \lambda^{\prime}$
and
$\lambda^{\prime\prime} > \lambda^{\prime}$
and
![]() $\sigma \in \Sigma$
,
$\sigma \in \Sigma$
,
![]() $\sigma \neq 0$
, we have that for any
$\sigma \neq 0$
, we have that for any
![]() $x \in \mathcal X$
,
$x \in \mathcal X$
,
Proof. By (6), for any
![]() $x \in \mathcal{X}$
we have
$x \in \mathcal{X}$
we have
 \begin{align} &(W_{\lambda^{\prime\prime}}(x) - \mathbb{E} [ \beta^{\sigma} W_{\lambda^{\prime\prime}}(X_\sigma) | X_0 = x]) - (W_{\lambda^{\prime}}(x) - \mathbb{E} [ \beta^{\sigma} W_{\lambda^{\prime}}(X_\sigma) | X_0 = x])\nonumber\\ & = (1-\beta) \Delta_\lambda \bigl(1 - M(x, \sigma)\bigr) + \beta \mathbb{E}\Biggl[ \sum_{y \in \mathcal{X}} \bigl( P_{xy}(1) - \beta^\sigma P_{X_\sigma y}(1) \bigr) \bigl( V_{\lambda^{\prime\prime}}(y) - V_{\lambda^{\prime}}(y) \bigr) \biggm| X_0 = x \Biggr]. \end{align}
\begin{align} &(W_{\lambda^{\prime\prime}}(x) - \mathbb{E} [ \beta^{\sigma} W_{\lambda^{\prime\prime}}(X_\sigma) | X_0 = x]) - (W_{\lambda^{\prime}}(x) - \mathbb{E} [ \beta^{\sigma} W_{\lambda^{\prime}}(X_\sigma) | X_0 = x])\nonumber\\ & = (1-\beta) \Delta_\lambda \bigl(1 - M(x, \sigma)\bigr) + \beta \mathbb{E}\Biggl[ \sum_{y \in \mathcal{X}} \bigl( P_{xy}(1) - \beta^\sigma P_{X_\sigma y}(1) \bigr) \bigl( V_{\lambda^{\prime\prime}}(y) - V_{\lambda^{\prime}}(y) \bigr) \biggm| X_0 = x \Biggr]. \end{align}
Now, since
![]() $\sigma \ge 1$
,
$\sigma \ge 1$
,
![]() $M(x,\sigma) \le \beta$
, and
$M(x,\sigma) \le \beta$
, and
Now consider
 \begin{align} & \beta \mathbb{E}\Biggl[ \sum_{y \in \mathcal{X}} \bigl( P_{xy}(1) - \beta^\sigma P_{X_\sigma y}(1) \bigr) \bigl( V_{\lambda^{\prime\prime}}(y) - V_{\lambda^{\prime}}(y) \bigr) \biggm| X_0 = x \Biggr] \notag \\ & \stackrel{(a)}{\geq} \beta \mathbb{E}\Biggl[ \sum_{y \in \mathcal{X}} \bigl( P_{xy}(1) - \beta P_{X_\sigma y}(1) \bigr) \bigl( V_{\lambda^{\prime\prime}}(y) - V_{\lambda^{\prime}}(y) \bigr) \biggm| X_0 = x \Biggr] \notag \\ & \stackrel{(b)}{\geq} \beta \Delta_\lambda \mathbb{E} \Biggl[ \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ P_{xy}(1) - \beta P_{X_\sigma y}(1) \bigr]^{+} N^{(g_{\lambda^{\prime\prime}})}(y) \notag \\ & \qquad\qquad\qquad\quad + \bigl[ P_{xy}(1) - \beta P_{X_\sigma y}(1) \bigr]^{-} N^{(g_{\lambda^{\prime}})}(y) \Bigr\} \bigg| X_0 = x \Biggr] \notag \\ &\stackrel{(c)}\ge - \Delta_\lambda (1-\beta)^2, \end{align}
\begin{align} & \beta \mathbb{E}\Biggl[ \sum_{y \in \mathcal{X}} \bigl( P_{xy}(1) - \beta^\sigma P_{X_\sigma y}(1) \bigr) \bigl( V_{\lambda^{\prime\prime}}(y) - V_{\lambda^{\prime}}(y) \bigr) \biggm| X_0 = x \Biggr] \notag \\ & \stackrel{(a)}{\geq} \beta \mathbb{E}\Biggl[ \sum_{y \in \mathcal{X}} \bigl( P_{xy}(1) - \beta P_{X_\sigma y}(1) \bigr) \bigl( V_{\lambda^{\prime\prime}}(y) - V_{\lambda^{\prime}}(y) \bigr) \biggm| X_0 = x \Biggr] \notag \\ & \stackrel{(b)}{\geq} \beta \Delta_\lambda \mathbb{E} \Biggl[ \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ P_{xy}(1) - \beta P_{X_\sigma y}(1) \bigr]^{+} N^{(g_{\lambda^{\prime\prime}})}(y) \notag \\ & \qquad\qquad\qquad\quad + \bigl[ P_{xy}(1) - \beta P_{X_\sigma y}(1) \bigr]^{-} N^{(g_{\lambda^{\prime}})}(y) \Bigr\} \bigg| X_0 = x \Biggr] \notag \\ &\stackrel{(c)}\ge - \Delta_\lambda (1-\beta)^2, \end{align}
where (a) holds because
![]() $\sigma \geq 1$
, (b) holds by Lemma 2, and (c) follows from (11). Substituting (26) and (27) in (25), we get the result of the lemma.
$\sigma \geq 1$
, (b) holds by Lemma 2, and (c) follows from (11). Substituting (26) and (27) in (25), we get the result of the lemma.
We now proceed with the proof of Theorem 1(a). Consider
![]() $\lambda^{\prime} < \lambda^{\prime\prime}$
. Suppose
$\lambda^{\prime} < \lambda^{\prime\prime}$
. Suppose
![]() $x \in \Pi_{\lambda^{\prime}}$
. By Proposition 1(d), there exists a
$x \in \Pi_{\lambda^{\prime}}$
. By Proposition 1(d), there exists a
![]() $\sigma \neq 0$
such that
$\sigma \neq 0$
such that
![]() $(1-\beta) \left( L(x, \sigma) - c(x, 1) \right) < W_{\lambda^{\prime}}(x) - \mathbb{E}[ \beta^{\sigma} W_{\lambda^{\prime}}(X_\sigma) | X_0 = x ]. $
Combining this result with the result of Lemma 7, we infer
$(1-\beta) \left( L(x, \sigma) - c(x, 1) \right) < W_{\lambda^{\prime}}(x) - \mathbb{E}[ \beta^{\sigma} W_{\lambda^{\prime}}(X_\sigma) | X_0 = x ]. $
Combining this result with the result of Lemma 7, we infer
![]() $(1-\beta)\left( L(x, \sigma) - c(x, 1) \right) < W_{\lambda^{\prime\prime}}(x) - \mathbb{E} [\beta^{\sigma} W_{\lambda^{\prime\prime}}(X_\sigma) | X_0 = x ].$
Thus,
$(1-\beta)\left( L(x, \sigma) - c(x, 1) \right) < W_{\lambda^{\prime\prime}}(x) - \mathbb{E} [\beta^{\sigma} W_{\lambda^{\prime\prime}}(X_\sigma) | X_0 = x ].$
Thus,
![]() $x \in \Pi_{\lambda^{\prime\prime}}$
. Hence,
$x \in \Pi_{\lambda^{\prime\prime}}$
. Hence,
![]() $\Pi_{\lambda^{\prime}}\subseteq \Pi_{\lambda^{\prime\prime}}$
and the RB is indexable.
$\Pi_{\lambda^{\prime}}\subseteq \Pi_{\lambda^{\prime\prime}}$
and the RB is indexable.
B.2. Proof of Theorem 1.b
Consider
![]() $\lambda^{\prime} < \lambda^{\prime\prime}$
. An RB is indexable if
$\lambda^{\prime} < \lambda^{\prime\prime}$
. An RB is indexable if
![]() $\Pi_{\lambda^{\prime}}\subseteq \Pi_{\lambda^{\prime\prime}}$
, or equivalently, for any x such that
$\Pi_{\lambda^{\prime}}\subseteq \Pi_{\lambda^{\prime\prime}}$
, or equivalently, for any x such that
![]() $H_{\lambda^{\prime}}(x, 0) < H_{\lambda^{\prime}}(x, 1)$
, we have
$H_{\lambda^{\prime}}(x, 0) < H_{\lambda^{\prime}}(x, 1)$
, we have
![]() $H_{\lambda^{\prime\prime}}(x, 0) <H_{\lambda^{\prime\prime}}(x, 1)$
. A sufficient condition for this is to show that
$H_{\lambda^{\prime\prime}}(x, 0) <H_{\lambda^{\prime\prime}}(x, 1)$
. A sufficient condition for this is to show that
![]() $H_{\lambda^{\prime}}(x, 1) - H_{\lambda^{\prime}}(x, 0) \leq H_{\lambda^{\prime\prime}}(x, 1) -H_{\lambda^{\prime\prime}}(x, 0)$
, or equivalently, that
$H_{\lambda^{\prime}}(x, 1) - H_{\lambda^{\prime}}(x, 0) \leq H_{\lambda^{\prime\prime}}(x, 1) -H_{\lambda^{\prime\prime}}(x, 0)$
, or equivalently, that
![]() $H_{\lambda^{\prime\prime}}(x, 0) -H_{\lambda^{\prime}}(x, 0) \leq H_{\lambda^{\prime\prime}}(x, 1) - H_{\lambda^{\prime}}(x, 1)$
. We prove this inequality as follows.
$H_{\lambda^{\prime\prime}}(x, 0) -H_{\lambda^{\prime}}(x, 0) \leq H_{\lambda^{\prime\prime}}(x, 1) - H_{\lambda^{\prime}}(x, 1)$
. We prove this inequality as follows.
Let
![]() $\Delta_\lambda = \lambda^{\prime\prime} - \lambda^{\prime}$
. By (4), for any
$\Delta_\lambda = \lambda^{\prime\prime} - \lambda^{\prime}$
. By (4), for any
![]() $x \in \mathcal{X}$
we have
$x \in \mathcal{X}$
we have
 \begin{align*} & \left(H_{\lambda^{\prime\prime}}(x, 1) - H_{\lambda^{\prime}}(x, 1) \right) - \left(H_{\lambda^{\prime\prime}}(x, 0) - H_{\lambda^{\prime}}(x, 0) \right) \notag \\ & \quad = \Delta_\lambda(1-\beta) + \beta \sum_{y \in \mathcal{X}} (P_{xy}(1) - P_{xy}(0)) (V_{\lambda^{\prime\prime}}(y) - V_{\lambda^{\prime}}(y)) \notag \\ & \quad \stackrel{(a)}{\geq} \Delta_\lambda \Biggl( 1-\beta + \beta \sum_{y \in \mathcal{X}} \left[ P_{xy}(1) - P_{xy}(0) \right]^{+} N^{(g_{\lambda^{\prime\prime}})}(y) + \left[ P_{xy}(1) - P_{xy}(0) \right]^{-} N^{(g_{\lambda^{\prime}})}(y) \Biggr) \stackrel{(b)}{\geq} 0,\end{align*}
\begin{align*} & \left(H_{\lambda^{\prime\prime}}(x, 1) - H_{\lambda^{\prime}}(x, 1) \right) - \left(H_{\lambda^{\prime\prime}}(x, 0) - H_{\lambda^{\prime}}(x, 0) \right) \notag \\ & \quad = \Delta_\lambda(1-\beta) + \beta \sum_{y \in \mathcal{X}} (P_{xy}(1) - P_{xy}(0)) (V_{\lambda^{\prime\prime}}(y) - V_{\lambda^{\prime}}(y)) \notag \\ & \quad \stackrel{(a)}{\geq} \Delta_\lambda \Biggl( 1-\beta + \beta \sum_{y \in \mathcal{X}} \left[ P_{xy}(1) - P_{xy}(0) \right]^{+} N^{(g_{\lambda^{\prime\prime}})}(y) + \left[ P_{xy}(1) - P_{xy}(0) \right]^{-} N^{(g_{\lambda^{\prime}})}(y) \Biggr) \stackrel{(b)}{\geq} 0,\end{align*}
where (a) follows from Lemma 2 and (b) holds by (12). Therefore the RB is indexable.
Appendix C. Proof of Proposition 2
We prove the result of each part separately.
-
(a) This follows from observing that
where we are ignoring negative terms in (a) and using \begin{align*} & \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - \beta P_{zy}(1) \bigr]^+ N^{(h)}(y) \Bigr\} \\ & \quad\stackrel{(a)}\le \sum_{y \in \mathcal{X}} \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ N^{(g)}(y) \\ &\quad\stackrel{(b)}\le \sum_{y \in \mathcal{X}} \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ \le \max_{x,z \in \mathcal{X}} \sum_{y \in \mathcal{X}} \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+, \end{align*}
\begin{align*} & \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - \beta P_{zy}(1) \bigr]^+ N^{(h)}(y) \Bigr\} \\ & \quad\stackrel{(a)}\le \sum_{y \in \mathcal{X}} \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ N^{(g)}(y) \\ &\quad\stackrel{(b)}\le \sum_{y \in \mathcal{X}} \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ \le \max_{x,z \in \mathcal{X}} \sum_{y \in \mathcal{X}} \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+, \end{align*}
 $N^{(g)}(x) \le 1$
in (b).
$N^{(g)}(x) \le 1$
in (b).
-
(b) For any
 $x,y,z \in \mathcal{X}$
,
$x,y,z \in \mathcal{X}$
,
 $P_{xy}(1) - \beta P_{zy}(1) = (1-\beta) P_{xy}(1)$
. Thus,
$P_{xy}(1) - \beta P_{zy}(1) = (1-\beta) P_{xy}(1)$
. Thus,  \begin{align*} & \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - \beta P_{zy}(1) \bigr]^+ N^{(h)}(y) \Bigr\} \\ &\quad = - \sum_{y \in \mathcal{X}} (1-\beta) P_{xy}(1) N^{(h)}(y) \le 0 < \frac{(1-\beta)^2}{\beta}. \end{align*}
\begin{align*} & \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ \beta P_{zy}(1) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - \beta P_{zy}(1) \bigr]^+ N^{(h)}(y) \Bigr\} \\ &\quad = - \sum_{y \in \mathcal{X}} (1-\beta) P_{xy}(1) N^{(h)}(y) \le 0 < \frac{(1-\beta)^2}{\beta}. \end{align*}
-
(c) This follows from observing that
where we are ignoring negative terms in (a) and using \begin{align*} & \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - P_{xy}(0) \bigr]^+ N^{(h)}(y) \Bigr\} \\ &\quad\stackrel{(a)}\le \sum_{y \in \mathcal{X}} \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+ N^{(g)}(y) \\ &\quad\stackrel{(b)}\le \sum_{y \in \mathcal{X}} \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+ \le \max_{x\in \mathcal{X}} \sum_{y \in \mathcal{X}} \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+, \end{align*}
\begin{align*} & \sum_{y \in \mathcal{X}} \Bigl\{ \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+ N^{(g)}(y) - \bigl[ P_{xy}(1) - P_{xy}(0) \bigr]^+ N^{(h)}(y) \Bigr\} \\ &\quad\stackrel{(a)}\le \sum_{y \in \mathcal{X}} \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+ N^{(g)}(y) \\ &\quad\stackrel{(b)}\le \sum_{y \in \mathcal{X}} \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+ \le \max_{x\in \mathcal{X}} \sum_{y \in \mathcal{X}} \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+, \end{align*}
 $N^{(g)}(x) \le 1$
in (b).
$N^{(g)}(x) \le 1$
in (b).
-
(d) The fact that
 $\beta \le 0.5$
implies that which is the same as the sufficient condition (c) established above.
$\beta \le 0.5$
implies that which is the same as the sufficient condition (c) established above. \begin{align*} \dfrac{1-\beta}{\beta} \ge 1 \ge \max_{x \in \mathcal X} \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+, \end{align*}
\begin{align*} \dfrac{1-\beta}{\beta} \ge 1 \ge \max_{x \in \mathcal X} \bigl[ P_{xy}(0) - P_{xy}(1) \bigr]^+, \end{align*}
Appendix D. Proof of Lemma 3
The proof of each part is as follows:
-
1. Since the model is indexable and
 $y \in \Gamma_{d+1}$
,
$y \in \Gamma_{d+1}$
,
 $w(d) = \lambda_{d+1}$
. Therefore, the optimal policy is indifferent between choosing the active and the passive action at
$w(d) = \lambda_{d+1}$
. Therefore, the optimal policy is indifferent between choosing the active and the passive action at
 $\lambda = \lambda_{d+1}$
.
$\lambda = \lambda_{d+1}$
. -
2. By definition, for any
 $\lambda \in (\lambda_d, \lambda_{d+1}]$
,
$\lambda \in (\lambda_d, \lambda_{d+1}]$
,
 $h_d$
is an optimal policy. Therefore, we have
$h_d$
is an optimal policy. Therefore, we have
 $J^{\left({h}_{d, y}\right)}_\lambda(x) \geq J^{(h_d)}_\lambda(x)$
with
$J^{\left({h}_{d, y}\right)}_\lambda(x) \geq J^{(h_d)}_\lambda(x)$
with
 $y \in {\mathcal X}\backslash{\mathcal P}_d$
for all
$y \in {\mathcal X}\backslash{\mathcal P}_d$
for all
 $x \in {\mathcal X}$
, with equality if
$x \in {\mathcal X}$
, with equality if
 $y \in \Gamma_{d+1}$
and
$y \in \Gamma_{d+1}$
and
 $\lambda = \lambda_{d+1}$
.
$\lambda = \lambda_{d+1}$
.
Funding information
This research was funded in part by the Innovation for Defence Excellence and Security (IDEaS) Program of the Canadian Department of National Defence through grant CFPMN2-037, and the Fonds de Recherche du Quebec—Nature et Technologies (FRQNT).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.