INTRODUCTION
As Moschini (1999, p. 487) puts it “[a] critical implication of consumer-demand theory is that the expenditure function is concave in prices, which implies that the so-called Slutsky matrix is negative semidefinite. Yet this curvature property is often not maintained in empirical applications, and estimated demand functions frequently fail to satisfy the implications of a concave expenditure function.” For this reason, in the recent literature there is an attempt to treat the curvature property as a maintained hypothesis and built it into the models being estimated, very much like the homogeneity in prices and symmetry properties of neoclassical consumer theory.
In particular, Ryan and Wales (1998) suggest a relatively simple procedure for imposing local curvature conditions. Their procedure applies to those locally flexible demand systems for which, at the point of approximation, the n×n Slutsky matrix S can be written as
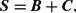
where B is an n×n symmetric matrix, containing the same number of independent elements as the Slutsky matrix, and C is an n×n matrix, whose elements are functions of the other parameters of the system. Curvature requires the Slutsky matrix to be negative semidefinite. Ryan and Wales (1998) draw on related work by Lau (1978) and Diewert and Wales (1987) and impose curvature by replacing S in (1) with −KK′, where K is an n×n lower triangular matrix, so that −KK′ is by construction a negative semidefinite matrix. Then solving explicitly for B in terms of K and C yields

meaning that the models can be reparameterized by estimating the parameters in K and C instead of the parameters in B and C. That is, we can replace the elements of B in the estimating equations by the elements of K and the other parameters of the model, thus ensuring that S is negative semidefinite at the point of approximation, which could be any data point.
Ryan and Wales (1998) applied their procedure to three locally flexible functional forms—the almost ideal demand system of Deaton and Muellbauer (1980), the normalized quadratic of Diewert and Wales (1988), and the linear translog. Moreover, Moschini (1999) suggested a possible reparameterization of the basic translog of Christensen, Jorgenson, and Lau (1975) to overcome some problems noted by Ryan and Wales (1998) and also imposed curvature conditions locally in the basic translog.
In this paper, we build on Ryan and Wales (1998) and Moschini (1999) and impose curvature conditions locally on the generalized Leontief model, introduced by Diewert (1974). In doing so, we exploit the Hessian matrix of second order derivatives of the reciprocal indirect utility function, unlike Ryan and Wales (1998) and Moschini (1999), who exploit the Slutsky matrix. The rest of the paper is organized as follows. Section 2 briefly discusses the generalized Leontief demand system, whereas Section 3 discusses our procedure for imposing local curvature conditions. The final section provides a brief conclusion.
THE GENERALIZED LEONTIEF MODEL
The generalized Leontief (GL) reciprocal indirect utility function, introduced by Diewert (1974), is
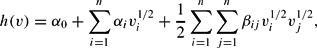
where B
is an n×n symmetric matrix of parameters and α0 and αi are other parameters, for a total of (n2+3n+2)/2 parameters.
Using Roy's identity the share equations of the GL demand system can be writtten as
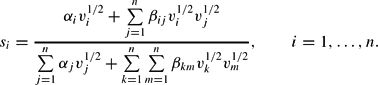
Because the share equations are homogenous of degree zero in the parameters, one can follow Barnett and Lee (1985) and impose the following normalization in estimation:
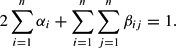
LOCAL CURVATURE FOR GL MODELS
Curvature of the reciprocal indirect utility function requires that the Hessian matrix is negative semidefinite. We can therefore impose local curvature (that is, at the reference point) by evaluating the Hessian terms of equation (2) at
∀i, as follows:
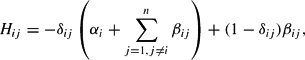
where δij=1 if i=j and 0 otherwise. By replacing H by −KK′, where K is an n×n lower triangular matrix and K′ its transpose, the above can be written as
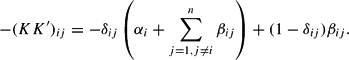
Solving for the αi and βij terms as a function of the (KK′)ij terms we can get the restrictions that ensure the negative semidefiniteness of the Hessian matrix (without destroying the flexibility properties of (2), as the number of free parameters remains the same). In particular, when i≠j (5) yields
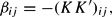
and for i=j it yields

Substituting βij from equation (6) in the above equation,
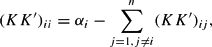
or
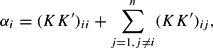
which after some rearrangement yields
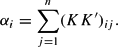
As an example, for the case of three goods, equation (6) and equation (7) imply the following six restrictions
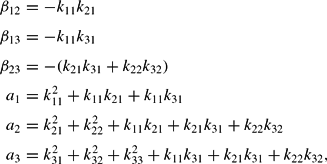
where the kij terms are the elements of the replacement matrix K.
CONCLUSION
We have illustrated a simple procedure for imposing curvature conditions locally in generalized Leontief models, building on earlier work in this area by Ryan and Wales (1998) and Moschini (1999). The procedure is rooted in the work by Lau (1978) and Diewert and Wales (1987), but, unlike the Ryan and Wales (1998) and Moschini (1999) procedures that exploit the Slutsky matrix, our procedure exploits the Hessian matrix of second-order derivatives of the reciprocal indirect utility function.
Serletis gratefully acknowledges financial support from the Social Sciences and Humanities Research Council of Canada.


