1. INTRODUCTION
Nowadays optical laser intensities exceeded the 1022 W/cm2 limit where radiation effects dominate the electron dynamics. In the field of laser–matter interaction a large number of non-linear response of atoms, molecules, and plasmas can be investigated both theoretically and experimentally. Such interesting high-field phenomena are high harmonic generations, or plasma-based laser-electron acceleration. These field intensities open the door to high-field quantum electrodynamics phenomena like vacuum-polarization effects of pair production (Di Piazza et al., Reference Di Piazza, Müller, Hatsagortsyan and Keitel2012). In most of the presented studies the dynamics of the participating electrons are investigated. Numerous surveys on laser-assisted electron collisions are available such as Ehlotzky et al. (Reference Ehlotzky, Jaron and Kaminski1998). However, there are only few nuclear photo-excitation investigations done where some low-lying first excited states of medium of heavy elements are populated with the help of X-ray free-electron laser pulses (Gunst et al., Reference Gunst, Litvinov, Keitel and Pálffy2014). Nuclear excitation by atomic electron re-scattering in a laser field was investigated by Kornev and Zon (Reference Kornev and Zon2007). Various additional concepts are under consideration for photo-nuclear reactions by laser-driven gamma beams (Habs et al., Reference Habs, Tajima, Schreiber, Barty, Fujiwara and Thirolf2009). Some applications of laser-induced nuclear physics can be found in the study of Ledingham (Reference Ledingham2005).
To our knowledge there are no publications available where laser-assisted proton nucleus collisions (or radiative proton–nucleus scattering) were investigated. This is the goal of our recent paper. We consider the global optical potential of Woods and Saxon (Reference Woods and Saxon1954) (WS) with the proper parameterization for moderate energy proton–12C collision (Abdul-Jalil & Jackson, Reference Abdul-Jalil and Jackson1979). The optical potential formalism has been a very successful method to study the single-particle spectra of nucleus in the last five decades. Detailed description and the validity of this formalism can be found in nuclear physics textbooks or in monographs like von Geramb (Reference von Geramb1979); Varner et al., (Reference Varner, Thompson, McAbee, Ludwig and Clegg1991); Hodgson (Reference Hodgson1994); Greiner and Maruhn (Reference Greiner and Maruhn1996).
The nuclear physics community recently managed to evaluate the closed analytic form of the Fourier transformed WS interaction (Hlophe et al., Reference Hlophe, Elster, Johnson, Upadhyay, Nunes, Arbanas, Eremenko, Escher and Thompson2013) which is a great success. Former time only an analytic series function was available to approximate the WS potentials (Pahlavani & Morad, Reference Pahlavani and Morad2010).
We incorporate these results into a first Born approximation scattering cross-section formula where the initial and final proton wave functions are Volkov waves and the induced photon emission and absorption processes are taken into account up to arbitrary orders (Bunkin & Fedorov, Reference Bunkin and Fedorov1965; Bunkin et al., Reference Bunkin, Kazakov and Fedorov1973; Faisal Reference Faisal1973; Reference Faisal1987; Kroll & Watson, Reference Kroll and Watson1973; Gontier & Rahman, Reference Gontier and Rahman1974; Bergou, Reference Bergou1980; Bergou & Varró, Reference Bergou and Varró1980). This kind of multi-photon description was very successful in the last four decades and helped to understand various optical and physical phenomena.
We hope that our description will open a new path in the field of photo-nuclear studies in the near future. For a better understanding we end our study with two physical examples where 49 MeV protons are scattered on 12C nuclei in various laser fields. At first we consider the field of a Ti:sapphire laser which has optical frequency with intensities even 1022 W/cm2. As a second case we present calculations for X-ray lasers which have much larger photon energy but much lower intensity available at the time.
2. THEORY
In the following, we summarize our applied non-relativistic quantum mechanical description. The laser field is handled in the classical way via the minimal coupling. The laser beam is taken to be linearly polarized and the dipole approximation is used. If the dimensionless intensity parameter (or the normalized vector potential) 
${a_0} = 8.55 \times {10^{ - 10}}\sqrt {I({\rm W}/{\rm c}{{\rm m}^2})} {\rm \lambda} ({\rm \mu m})$ of the laser field is smaller than unity the non-relativistic description in dipole approximation is valid. For 800 nm laser wavelength this means a critical intensity of I = 2.13 × 1018 W/cm2. In case of protons a 0 is replaced by a p = [(m p/m e)−1]a 0, where the proton to electron mass ratio is (m p/m e) = 1836. Accordingly, for 800 nm wavelength the critical intensity for protons is I crit = 3.91 × 1021 W/cm2.
Beyond the optical regime we investigate the scattering process in an X-ray laser field as well. Typical X-ray lasers can have photon energy in the range of 1–10 keV, pulse energy of 3 mJ and 1012–1013 photons/s photon number and the pulse duration is between 10 and 100 fs (the wavelength of a 10 keV X-ray photon is 18.2 nm). In the X-ray laser community, the photon number is the crucial parameter and not the intensity. However, the maximal achievable intensity can be calculated when the maximal focal spot is known. Focusing of X-ray laser pulses gives up numerous not trivial questions for experimentalist and still under development therefore we consider a maximal available intensity at 1016 W/cm2 for a 10 keV laser pulse in our last model, where the dimensionless intensity parameter a 0 = 1, 5 × 10−5. Note, that this is a small value compared to optical frequencies. The critical intensity for the 10 keV photon is a factor of 1836 times higher than for the 800 nm optical frequency.
Additionally, we consider moderate proton kinetic energy, not so much above the Coulomb barrier and neglect the interchange term between the proton projectile an the target carbon protons. This proton exchange effect could be included in the presented model with the help of Woods–Saxon potentials of non-local type (Barna et al., Reference Barna, Apagyi and Scheid2000) but not in the scope of the recent study.
To describe the non-relativistic scattering process of a proton on a nucleus in a spherically symmetric external field the following Schrödinger equation has to be solved,
$$\left[ {{1 \over {2m}}{{\left( {\hat{\bf p} - {e \over c}{\bf A}} \right)}^2} + U({\bf r})} \right]{\rm \Psi} = i\hbar {{{\rm \partial} {\rm \Psi} } \over {{\rm \partial} t}}, $$
where 
$\hat{\bf p}=- i\hbar {\rm {\rm \partial}} /{\rm \partial} {\bf r}$ is the momentum operator of the proton, and U(r) represents the scattering potential of the nucleon, 
$${\bf A}(t)={A_0}{\rm {\rm \epsilon} }\cos ({\rm \omega} t)$ is the vector potential of the external laser field with unit polarization vector ε. Figure 1 presents the scattering geometry for a better understanding. The pi and pf are the initial and final proton momenta, θ is the scattering angle of the proton, the laser is linearly polarized in the x–z plane, and the propagation of the laser field is parallel to the x-axis.
Fig. 1. The geometry of the scattering process. The 12C nucleus is in the center of the circle, pi and pf stand for the initial and final scattered proton momenta, θ is the proton scattering angle, laser pulse propagates parallel to the x-axis and linearly polarized in the x–z plane. The χ angle is needed for the laser-proton momentum transfer.
Without the external scattering potential U(r) the particular solution of (1) can be immediately written down as non-relativistic Volkov states φp(r, t) which exactly incorporate the interaction with the laser field,
$$\matrix{ {{{\rm \varphi} _{\rm p}}({\bf r},t) = } \hfill & {\displaystyle{1 \over {{{(2{\rm \pi} \hbar )}^{3/2}}}}{\rm exp}\left[ {\displaystyle{i \over \hbar }{\bf p} \cdot {\bf r} - \int_{{t_0}}^t dt^{\prime}\displaystyle{1 \over {2m}}{{\left( {{\bf p} - \displaystyle{e \over c}{\bf A}(t^{\prime})} \right)}^2}} \right].} \hfill \cr } $$Volkov states, which are modulated de Broglie waves, parameterized by momenta p and form an orthonormal and complete set,
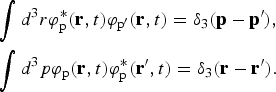$$\eqalign{& \int {d^3}r{\rm \varphi} _{\rm p}^{\rm \ast } ({\bf r},t){{\rm \varphi} _{{\rm p^{\prime}}}}({\bf r},t) = {{\rm \delta} _3}({\bf p} - {\bf p^{\prime}}), \cr & \int {d^3}p{{\rm \varphi} _{\rm p}}({\bf r},t){\rm \varphi} _{\rm p}^{\rm \ast } ({\bf r^{\prime}},t) = {{\rm \delta} _3}({\bf r} - {\bf r^{\prime}}).} $$To solve the original problem of Eq. (1) we write the exact wave function as a superposition of an incoming Volkov state and a correction term, which vanishes at the beginning of the interaction (in the remote past t 0→−∞). The correction term can also be expressed in terms of the Volkov states, since these form a complete set [see the equation of (3)],
$${\rm \Psi} ({\bf r},t) = {{\rm \varphi} _{{{\rm p}_{\rm i}}}}({\bf r},t) + \int {d^3}p{a_{\rm p}}(t){{\rm \varphi} _{\rm p}}({\bf r},t),\quad {a_{\rm p}}({t_0}) = 0. $$It is clear that the unknown expansion coefficients a p(t) describe the non-trivial transition symbolized as pi→p, from a Volkov state of momentum pi to another Volkov state with momentum p. If we take the projection of Ψ into some Volkov state φp(t), we get
$$\int {d^3}r{\rm \varphi} _{\rm p}^{\rm \ast } ({\bf r},t){\rm \Psi} ({\bf r},t) = {{\rm \delta} _3}({\bf p} - {{\bf p}_{\rm i}}) + {a_{\rm p}}(t). $$Bye inserting Ψ of Eq. (4) into the complete Schrödinger equation (1), we receive the following integro-differential equation for the coefficients a p(t):
$$\eqalign{i\hbar {{\dot a}_{{\rm p^{\prime}}}}(t) & =\int {d^3}r{\rm \varphi} _{{\rm p^{\prime}}}^{\rm \ast } ({\bf r},t^{\prime})U({\bf r}){{\rm \varphi} _{{{\rm p}_{\rm i}}}}({\bf r},t^{\prime}) \cr & \quad +\int {d^3}p{a_{\rm p}}(t)\int {d^3}r{\rm \varphi} _{{\rm p^{\prime}}}^{\ast} ({\bf r},t^{\prime})U({\bf r}){{\rm \varphi} _{\rm p}}({\bf r},t^{\prime}),} $$
where the scalar product was taken with 
${{\rm \varphi} _{{\rm p^{\prime}}}}(t)$ on both sides of the resulting equation and the orthogonality property of the Volkov sates was taken after all [see the first equation of (3)]. Owing to the initial condition a p(t 0) = 0, displayed already in Eq. (4) the formal solution of (6) can be written as
$$\eqalign{{a_{{\rm p^{\prime}}}}(t) & = - \displaystyle{i \over \hbar }\int_{{t_0}}^t dt^{\prime}\int {d^3}r{\rm \varphi} _{{\rm p^{\prime}}}^{\ast} ({\bf r},t^{\prime})U({\bf r}){{\rm \varphi} _{{{\rm p}_{\rm i}}}}({\bf r},t^{\prime}) \cr & \quad - \displaystyle{i \over \hbar }\int_{{t_0}}^tdt^{\prime}\int {d^3}p{a_{\rm p}}(t^{\prime})\int {d^3}r{\rm \varphi} _{{\rm p^{\prime}}}^{\ast} ({\bf r},t^{\prime})U({\bf r}){{\rm \varphi} _{\rm p}}({\bf r},t^{\prime}).} $$In the spirit of the iteration procedure used in scattering theory the (k+1)th iterate of a p(t) is expresses by the kth iterate on the right-hand side in (7) like
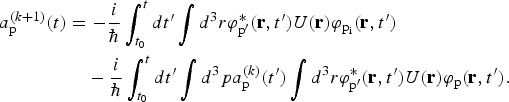$$\eqalign{a_{\rm p}^{(k+1)} (t)& = - \displaystyle{i \over \hbar }\int_{{t_0}}^t dt^{\prime}\int {d^3}r{\rm \varphi} _{{\rm p^{\prime}}}^{\ast} {\bf (r},t^{\prime})U({\bf r}){{\rm \varphi} _{{{\rm p}_{\rm i}}}}({\bf r},t^{\prime}) \cr & \quad - \displaystyle{i \over \hbar }\int_{{t_0}}^t dt^{\prime}\int {d^3}pa_{\rm p}^{(k)} (t^{\prime})\int {d^3}r{\rm \varphi} _{{\rm p^{\prime}}}^{\rm \ast } ({\bf r},t^{\prime})U({\bf r}){{\rm \varphi} _{\rm p}}({\bf r},t^{\prime}).} $$In the first Born approximation [where the transition amplitude is linear in the scattering potential U(r)], we receive the transition amplitude in the next form
$$\eqalign{T_{\rm fi} & = \mathop {\lim }\limits_{t \to \infty } \mathop {\lim }\limits_{{t_0} \to - \infty } a_{{{\rm p}_{\rm f}}}^{(1)} (t) \cr & =- \displaystyle{i \over \hbar }\int_{ - \infty }^\infty dt^{\prime}\int {d^3}r{\rm \varphi} _{{{\rm p}_{\rm f}}}^{\rm \ast } ({\bf r},t^{\prime})U({\bf r}){{\rm \varphi} _{{{\rm p}_{\rm i}}}}({\bf r},t^{\prime}).} $$By taking the explicit form of the Volkov states (2) with the vector potential A(t) = εA 0cos(ωt) we observe that the A 2 term drops out from the transition matrix element (9), and T fi becomes
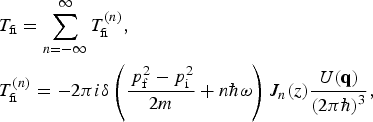$$\eqalign{&{T_{{\rm fi}}} = \sum\limits_{n =- \infty }^\infty T_{{\rm fi}}^{(n)}, \cr & T_{{\rm fi}}^{(n)} = - 2{\rm \pi} i{\rm \delta} \left( {\displaystyle{{\,p_{\rm f}^ 2 - p_{\rm i}^ 2 } \over {2m}} + n\hbar {\rm \omega} } \right){J_n}(z)\displaystyle{{U({\bf q})} \over {{{(2{\rm \pi} \hbar )}^3}}},} $$before the time integration was done, the exponential expression was expanded into a Fourier series with the help of the Jacobi–Anger formula (Abramowitz & Stegun, Reference Abramowitz and Stegun1972) which gave us the Bessel function
$${e^{iz\,{\rm sin}({\rm \omega} t)}} = \sum\limits_{n = - \infty }^\infty {J_n}(z)\,{e^{in{\rm \omega} t}}. $$ The U(q) is the Fourier transformed of the scattering potential with the momentum transfer of 
${\bf q} \equiv {{\bf p}_{\rm i}} - {{\bf p}_{\rm f}}$ where pi is the initial and pf is the final proton momenta. The absolute value is 
$q=\sqrt {\,p_{\rm i}^2 + p_{\rm f}^2 - 2{\,p_{\rm i}}{\,p_{\rm f}}{\rm cos}({{\rm \theta} _{{\,p_{\rm i}},{\,p_{\rm f}}}})} $. In our case, for 49 MeV energy protons absorbing optical photons the following approximation is valid q ≈ 2p i|sin(θ/2)|.
The Dirac delta describes photon absorptions (n<0) and emissions (n>0) with energy conservation.
J n(z) is the Bessel function with the argument of
$$z \equiv {{{m_{\rm e}}} \over {{m_{\rm p}}}}{a_0}(\hat{\bf q}{\rm \epsilon }){{2{\,p_i}} \over {\hbar {k_0}}}\vert {\rm sin}({\rm \theta} /2)\vert , $$
where m e and m p are the electron and proton masses, a 0 is the dimensionless intensity parameter (given above), 
$\hat{\bf q}$ and ε are the unit vectors of the momentum transfer and the laser polarization direction. It can be shown with geometrical means that for low-energy photons where (
${E_{{\rm ph}}}\lt {E_{{{\rm p}^+}}} $) the angle in the scalar product of 
$\hat{\bf q}{\rm \epsilon } \equiv {\rm cos}\,\chi $ is χ = π/2−θ/2 where θ is the scattering angle of the proton varying from 0 to π. See Figure 1.
From 
$({\,p_{\rm i}}/\hbar {k_0})=\sqrt {({m_{\rm p}}/{m_{\rm e}})} \sqrt {(2{m_{\rm e}}{c^2}{E_{\rm i}}/{\hbar ^2}{\rm \omega} _0^2 )} $ collecting the constants together the final formula for z reads
$$z = {{1.4166 \times {{10}^{ - 3}}} \over {\hbar {{\rm \omega} _0}}}\sqrt {{{{E_{\rm p}}} \over {1836}}} \sqrt I \times {\rm cos}(\rm \chi ) \times \vert {\rm sin}({\rm \theta} /2)\vert , $$where the laser energy ħω0 is measured in eV, the proton energy E p in MeV, and the laser intensity I in W/cm2 (note that this formula is valid for any kind of external laser field. For a 49 MeV proton projectile even the 10 keV X-ray laser has a negligible energy). The final differential cross-section formula for the laser associated collision with simultaneous nth-order photon absorption and emission processes is
$${{d{{\rm \sigma} ^{(n)}}} \over {d{\rm \Omega} }} = {{{\,p_{\rm f}}} \over {{\,p_{\rm i}}}}J_n^2 (z){{d{{\rm \sigma} _{\rm B}}} \over {d{\rm \Omega} }}. $$ The 
${d \sigma_B}/{d \Omega} = \lpar {m}/{2\pi \hbar^{2}} \rpar^2 \vert U({\bf{q}}) \vert^2 $ is the usual Born cross-section for the scattering on the potential U(r) alone (without the laser field). The expression Eq. (14) was calculated with different authors using different methods (Bunkin & Fedorov, Reference Bunkin and Fedorov1965; Bunkin et al., Reference Bunkin, Kazakov and Fedorov1973; Faisal, Reference Faisal1973; Reference Faisal1987; Kroll & Watson, Reference Kroll and Watson1973; Gontier & Rahman, Reference Gontier and Rahman1974; Bergou, Reference Bergou1980; Bergou & Varró, Reference Bergou and Varró1980).
In our case the scattering interaction U(r) is a central field U(r) which is the sum of the Coulomb potential of a uniform charged sphere (Rudchik et al., Reference Rudchik, Shyrma, Kemper, Rusek, Koshchy, Kliczewski, Novatsky, Ponkratenko, Piasecki, Romanyshyna, Stepanenko, Strojek, Sakuta, Budzanowski, Głowacka, Skwirczyńska, Siudak, Choiński and Szczurek2010) and a short range optical (Woods & Saxon, Reference Woods and Saxon1954) potential
$$U(r) = {V_{\rm c}}(r) + {V_{{\rm ws}}}(r) + i[W(r) + {W_{\rm s}}(r)] + {V_{{\rm ls}}}(r){\bf l} \cdot {\rm \sigma}, $$where the Coulomb term is
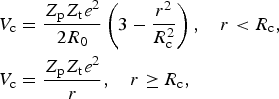$$\eqalign{{V_{\rm c}}& =\displaystyle{{{Z_{\rm p}}{Z_{\rm t}}{e^2}} \over {2{R_0}}}\left( {3 - \displaystyle{{{r^2}} \over {R_{\rm c}^2 }}} \right),\quad r\lt {R_{\rm c}}, \cr {V_{\rm c}} & =\displaystyle{{{Z_{\rm p}}{Z_{\rm t}}{e^2}} \over r},\quad r \geq {R_{\rm c}},} $$
where 
${R_{\rm c}}={r_0}A_{\rm t}^{1/3} $ is the target radius calculated from the mass number of the target with r 0 = 1.25 fm. Z p and Z t are the charge of the projectile and the target and e is the elementary charge. This kind of regularized Coulomb potential helps us to avoid singular cross-sections and routinely used in nuclear physics.
The short-range nuclear part is given via
$$\eqalign{{V_{{\rm ws}}}(r)& = - {V_{\rm r}}{\,f_{{\rm ws}}}(r,{R_0},{a_0}), \cr W(r) & = - {V_{\rm v}}{\,f_{{\rm ws}}}(r,{R_{\rm s}},{a_{\rm s}}), \cr {W_{\rm s}}(r)& = - {W_{\rm s}}( - 4{a_{\rm s}}){{\,f^{\prime}}_{{\rm ws}}}(r,{R_{\rm s}},{a_{\rm s}}), \cr {V_{{\rm ls}}}(r)& = - ({V_{{\rm so}}} + i{W_{{\rm so}}})( - 2){g_{{\rm ws}}}(r,{R_{{\rm so}}},{a_{{\rm so}}}), \cr {\,f_{{\rm ws}}}(r,R,a)& = {1 \over {1 + {\rm exp}\left( {\displaystyle{{r - R} \over a}} \right)}}, \cr {{\,f^{\prime}}_{{\rm ws}}}(r,R,a)& = {d \over {dr}}{\,f_{{\rm ws}}}(r,R,a), \cr {g_{{\rm ws}}}(r,R,a)& = {{\,f^{\prime}}_{{\hskip-4pt \rm ws}}}(r,R,a)/r.} $$ The constants V r, W v, V so, and Wso are the strength parameters, and a 0,s,so, R 0,s,so are the diffuseness and the radius parameters given for large number of nuclei. The f function is called the shape function of the interaction. As we will see at moderate collisions energies the complex terms become zero. In the last part of the present paper we will use the numerical parameters of Abdul-Jalil and Jackson (Reference Abdul-Jalil and Jackson1979) for proton–carbon collision. According to the work of Hlophe et al. (Reference Hlophe, Elster, Johnson, Upadhyay, Nunes, Arbanas, Eremenko, Escher and Thompson2013) the complete analytic form of the Fourier transform of the WS potential can be calculated via the following kind of complex integrals 
$V(q)=\int_0^{\infty} dz\left({(z\, exp(i{\rm \rho}_{\rm k}z))/(1+exp(z - {\rm \alpha}_{\rm k}))}\right)$, where ρk = qa k, αk = R k/a k and z = r/a k are dimensionless variables. The integrals can be evaluated by contour integration using the residuum theorem. For exhaustive details, see Hlophe et al. (Reference Hlophe, Elster, Johnson, Upadhyay, Nunes, Arbanas, Eremenko, Escher and Thompson2013). The Fourier transformed second term of Eq. (15) reads
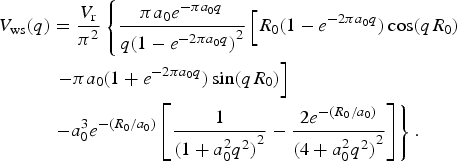$$\eqalign{V_{\rm ws}(q) & = {V_{\rm r} \over {\rm \pi ^2}} \left\{ {{\rm \pi} {a_0}e^{ - {\rm \pi} {a_0}q} \over {q{{(1 - {e^{ - 2{\rm \pi} {a_0}q}})}^2}}} \left[R_0(1 - e^{ - 2\pi {a_0}{q}})\,{\rm cos}(q{R_0}) \right. \right. \cr & \left. \left.-{{\rm \pi} {a_0}(1+{e^{ - 2{\rm \pi} {a_0}q}})\,{\rm sin}(q{R_0})} \right] \right. \cr & \left. - a_0^3 {e^{ - ({R_0}/{a_0})}}\left[ {\displaystyle{1 \over {{{(1+a_0^2 {q^2})}^2}}} - \displaystyle{{2{e^{ - ({R_0}/{a_0})}}} \over {{{(4 + a_0^2 {q^2})}^2}}}} \right] \right\}.} $$For the W(q) imaginary term, the same expression was derived with W v, a s, and R s instead of V r, a 0, and R 0. The surface term W s (r) [fourth term in Eq. (15)] gives the following formula in the momentum space:
$$\eqalign{{W_{\rm s}}(q) = & - 4{a_{\rm s}}{W_{\rm s} \over {\rm \pi ^2}} \left\{{{{\rm \pi} {a_{\rm s}}{e^{ - \pi {a_{\rm s}}q}}} \over {{(1 - {e^{ - 2{\rm \pi} {a_{\rm s}}q}})}^2}} \left[{({\rm \pi} {a_{\rm s}}(1+{e^{ - 2{\rm \pi} {a_{\rm s}}q}})}\right. \right. \cr & \left. \left. - {1 \over q}(1 - {e^{ - 2{\rm \pi} {a_{\rm s}}q}))}\,{\rm cos}(q{R_{\rm s}}) + {R_{\rm s}}(1 - {e^{ - 2{\rm \pi} {a_{\rm s}}q}})\,{\rm sin}(q{R_{\rm s}})\right] \right. \cr & \left.+ a_{\rm s}^2 {e^{ - ({R_{\rm s}}/{a_{\rm s}})}} \left[ {\displaystyle{1 \over {{{(1 + a_{\rm s}^ 2 {q^2})}^2}}} - \displaystyle{{4{e^{ - ({R_{\rm s}}/{a_{\rm s}})}}} \over {{{(4 + a_{\rm s}^2 {q^2})}^2}}}} \right] \right\}.} $$The last term in Eq. (15), the transformed spin–orbit coupling term leads to
$$\eqalign{& V_{\rm ls}(q) = - {a_{\rm so} \over {\rm \pi} ^2} (V_{\rm so} + i{W_{\rm so}}) \left\{{{2{\rm \pi} {e^{ - {\rm \pi} {a_{{\rm so}}}q}}} \over {1 - {e^{ - 2{\rm \pi} {a_{{\rm so}}}q}}}} {\rm sin}(q{R_{{\rm so}}})\right. \cr & \quad \left. + {e^{( - {R_{\rm so}}/{a_{\rm so}})}}\left( {{1 \over {1 + a_{\rm so}^2 {q^2}}} - {{2{e^{ - {R_{\rm so}}}}} \over {4+a_{\rm so}^2 {q^2}}}}\right)\right\}.} $$where the momentum transfer is defined as above q ≡ pi−pf. The low-energy transfer approximation formula q ≈ 2p i|sin(θ/2)| is valid.
The Fourier transform of the charged sphere Coulomb field is also far from being trivial
$$\eqalign{V_{\rm c}(q) & = \displaystyle{{Z_{\rm p}Z_{\rm t}e^2} \over {2^{(5/6)} \sqrt {\rm \pi} q^3}} \bigg(- 2 \!\cdot\! 3^{(1/3)}q{\rm \cos} [2^{(2/3)}3^{(1/3)}q] \cr & \quad +2^{(1/3)}(1+2 \!\cdot \!2^{(1/3)}3^{(2/3)}q^2){\rm \sin} [2^{(2/3)}3^{(1/3)}q] \bigg) \cr & \quad +3Z_{\rm p}Z_{\rm t}e^2 \sqrt {\displaystyle{2 \over {\rm \pi}}} \bigg( \displaystyle{{i{\rm \pi} \vert q\vert } \over {2q}} - {\rm Ci}[2^{(2/3)}3^{(1/3)}q]+\log (q). \cr & \quad - \log \vert q \vert - i{\rm Si}[2^{(2/3)}3^{(1/3)}q]\bigg),} $$where Ci and Si are the cosine and the sine integral functions, respectively; for details see Abramowitz and Stegun (Reference Abramowitz and Stegun1972).
3. RESULTS
We applied the outlined method to 49 MeV proton–12C scattering. Table 1 contains the parameters of the used Woods–Saxon potential.
Table 1. Parameters of the applied potential for proton–12C collision at E i = 49 MeV
Note that the complex part W v and the complex part of the spin–orbit term W so are zero at this energy.
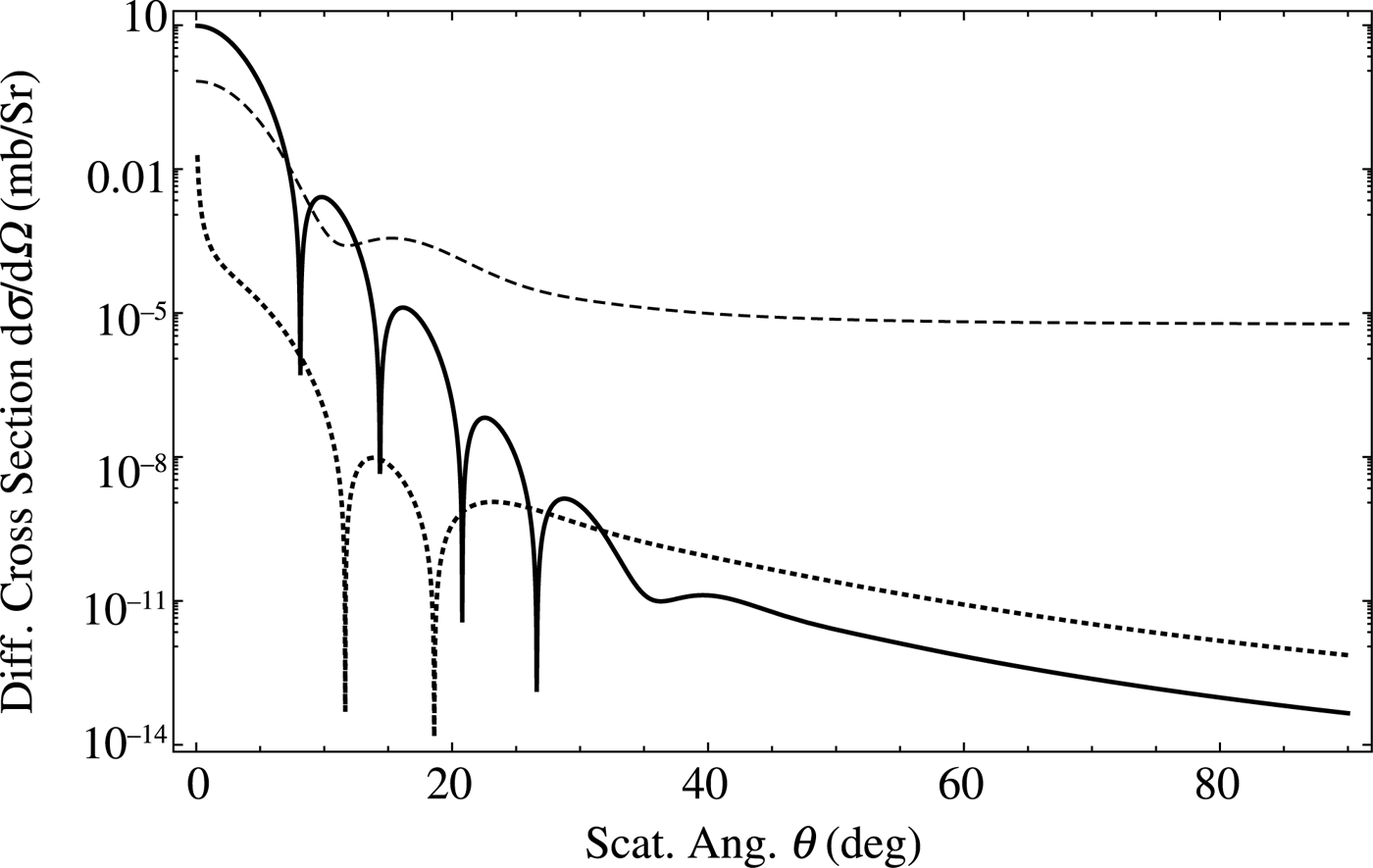
Figure 2 presents the angular differential cross-section in the first Born approximation of the various Woods–Saxon potential terms for 49 MeV elastic proton–12C scattering. The different lines represent the different terms Eqs. (18)–(20). The laboratory frame is used in the calculation. For a better transparency the contributions of the regularized Coulomb term is not presented. Our calculated total cross-section of the elastic scattering is 201 mbarn which is consistent with the data of Abdul-Jalil and Jackson (Reference Abdul-Jalil and Jackson1979).
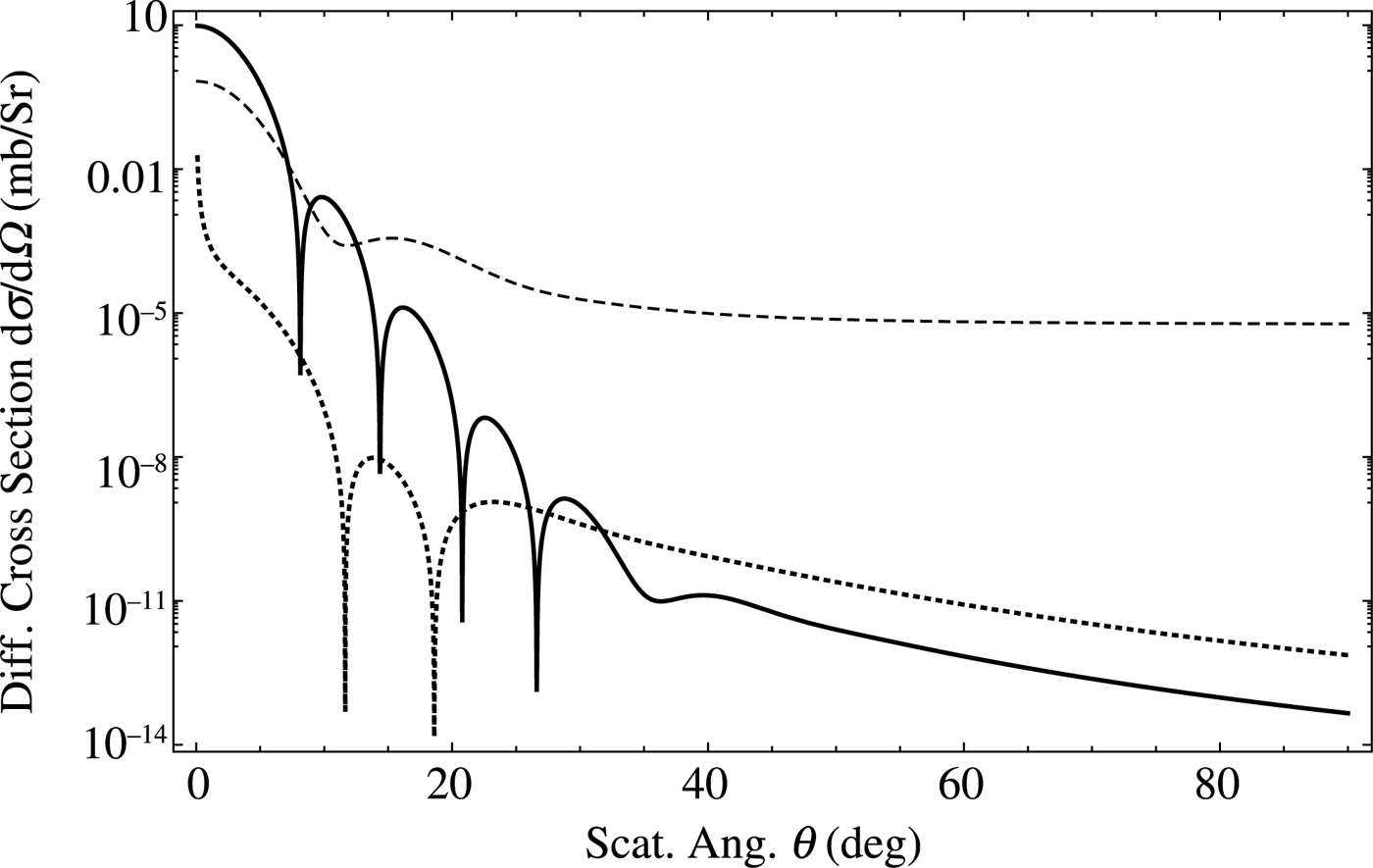
Fig. 2. The angular differential cross-sections in the first Born approximation of the various Woods–Saxon potentials terms for 49 MeV elastic proton–12C scattering. The solid, dashed, and dotted lines are the contributions of Eqs. (18, 19, 20), respectively. Note the different smoothness and different back scattering values of the different terms.
In our case, the laser photon energy is ħω0 = 1.56 eV, which means 800 nm wavelength and the proton energy is E p = 49 MeV. With these values the argument of the Bessel function Eq. (13) becomes the following:
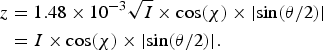$$\eqalign{z & = 1.48 \times {10^{ - 3}}\sqrt I \times {\rm cos}({\rm \chi} ) \times \vert {\rm sin}(\rm \theta /2)\vert \cr & = I \times {\rm cos}(\rm \chi ) \times \vert {\rm sin}({\rm \theta} /2)\vert .}$$Figure 3 shows the angular differential cross-section for n = 0, 1, 2 photon absorptions for I = 100 which means I = 4.56 × 1011 W/cm2 moderate intensity. Note that the cross-sections for single and double photon absorption are almost the same. The single-photon absorption total cross-section is 0.5 mbarn.
Fig. 3. The calculated angular differential cross-sections from Eq. (14) for I = 4.56 × 1011 W/cm2 laser field intensity (I = 100). The thick solid, thin long-dashed, and thin short-dashed lines are for n = 0,1,2 photon absorptions.
For large laser field intensities, which means large z arguments of the Bessel functions the following asymptotic expansion can be used for a fixed index (Abramowitz & Stegun, Reference Abramowitz and Stegun1972)
$${J_n}(z) = \sqrt {2/({\rm \pi} z)} \,{\rm cos}(z - n{\rm \pi} /2 - {\rm \pi} /4), $$
which means an approximate 
$1/\sqrt {{\rm sin}({\rm \theta} )\,{\rm cos}({\rm \theta} )} $ angle dependence which has a strong decay for large scattering angles. Note that even this function shows very rapid oscillations. Figure 4 shows the same kind of cross-sections for z = 10,000 (which means I = 4.56 × 1015 W/cm2 intensity) and for z = 6.61 × 106 (which means I = 2.0 × 1021 W/cm2 intensity), respectively. Only the n = 1 one photon absorption process is considered.
Fig. 4. Comparison of the calculated angular differential Born cross-sections to two laser-assisted cross-sections with a single-photon absorption at high photon intensities. The black thick line represents the Born cross-section, the black thin solid line is for I = 4.56 × 1015 W/cm2 intensity (I = 10,000). The dashed gray line is close to the relativistic threshold with I = 2.0 × 1021 W/cm2 laser field intensity (I = 6.61 × 106).
As a second physically relevant example we present the scattering cross-sections in the presence of an X-ray laser field. For the 10 keV laser field of 1016 W/cm2 intensity the I parameter in Eq. (22) has the values of 0.162. Figure 5 presents the cross-sections curves for n = 0, 1, 2. Note that the I parameter makes the Bessel functions very small at small angles.
Fig. 5. The calculated angular differential cross-sections for a 1016 W/cm2 intensity 10 keV X-ray laser beam. The thick solid, thin long-dashed, and thin short-dashed lines are for n = 0,1,2 photon absorptions, respectively.
4. SUMMARY
We presented a formalism which gives an analytic angular differential cross-section model for laser-assisted proton nucleon scattering on a Woods–Saxon optical potential where the nth-order photon absorption is taken into account simultaneously. We coupled the mathematical description of multi-photon processes to the well-established low-energy nuclear physics description. As an example the physically relevant proton–12Ca collision system was investigated at moderate 49 MeV proton energies. Two different kinds of laser fields are investigated. The first one is the optical Ti:sapphire system with wavelength of 800 nm with intensities in the range of 1011–1021 W/cm2. As a second system we took a 10 keV X-ray laser field with 1016 W/cm2 intensity. The calculated cross-sections are much lower than the elastic cross-sections in all cases. We hope that our study will give a strong impetus and couple the nuclear and laser physics community together to perform such experiments in the ELI or X-FEL facilities which will be available in a couple of years.
ACKNOWLEDGMENTS
We thank for Professor Gyula Bencze for useful discussions and comments. S. V. has been supported by the National Scientific Research Foundation OTKA, Grant No. K 104260. Partial support by the ELI-ALPS project is also acknowledged. The ELI-ALPS project (GOP-1.1.1-12/B-2012-0001) is supported by the European Union and co-financed by the European Regional Development Fund.
