Recent experimental and theoretical efforts to achieve inertial confinement fusion (ICF) have focused on the compression of the fuel in a 2.263 mm diameter fuel capsule, including a CH ablator, a thin Deuterium–Tritium (D–T) ice layer, and a D–T gas fill in the middle (Hurricane et al., Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Döppner, Hinkel, Berzak Hopkins, Kline, Le Pape, Ma, MacPhee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2014; Park et al., Reference Park, Hurricane, Callahan, Casey, Dewald, Dittrich, Döppner, Hinkel, Berzak Hopkins, Le Pape, Ma, Patel, Remington, Robey, Salmonson and Kline2014). The ablator layer was placed on the external surface to achieve a larger compression of the pellet. The outcome of these experiments was that most of the pellet broke into pieces due to Rayleigh–Taylor (RT) surface instabilities, which are common in surfaces under extreme dynamical pressure.

Already in the classical literature (Zel'dovich et al., Reference Zel'dovich and Raizer1969), mentioned that the way to avoid these instabilities is to make the compression and the detonation front a high-temperature radiation dominated front, which works to smooth out the RT instabilities propagating with the sound-speed, whereas the radiation is propagating with the speed of light.

From this well-known reason it must be obvious that the radiation dominated, high-temperature process must be described with relativistic fluid dynamics, wherein the pressure is not neglected compared with the energy density, and the propagation of radiative energy is described in a consistent way with all other dynamical processes.

Unfortunately the overwhelming majority of theoretical models that attempt to describe ICF experiments are: (i) non-relativistic, that is, neglecting pressure and (ii) radiation is assumed to have infinite speed in principle. (Of course such an “infinite speed” becomes an undefined speed, which depends on the space–time grid resolution and on the numerical method.)

In the present work, we concentrate on the “volume ignition” of the fuel by neglecting (for the 1st approximation) compression. We use a relativistic Rankine–Hugoniot description originally described by Taub (Reference Taub1948), which was then 39 years later corrected by Csernai (Reference Csernai1987), and used since then widely in the field of relativistic heavy-ion collisions (Csernai, Reference Csernai1994). Just as in the Rankine–Hugoniot non-relativistic description of shock waves the relativistic relations are also based on the energy–momentum tensor, T ^μν, and baryon charge current, N ^μ, conservation across a hyper-surface with a normal 4-vector Λ^ν, where the change of a quantity a across the hyper-surface is denoted by [a] = a ₂ − a ₁:

(1)$$[ {R^{\rm \mu} }] =[ {T^{{\rm \mu} {\rm \nu} }}{\Lambda _{\rm \nu} }] =0\comma \; \quad [ j] =[ {N^{\rm \mu} }{\Lambda _{\rm \mu} }] =0.$$

These conservation laws lead to the relativistic shock or detonation equations for the energy density, e, pressure, p, and generalized specific volume, X = (e + p)/n ²:

(2)$$\eqalign{& {\,j^2}={\Lambda ^{\rm \mu} }{\Lambda _{\rm \mu} }{\kern 1pt} [ p] /[ X] \comma \; \cr & [ p] \lpar {X_1}+{X_2}\rpar =[ \lpar e+p\rpar X] .} $$

This description treats detonations also across hyper-surfaces with time-like normal vectors (Λ^μΛ_μ = +1), and therefore has the name time-like detonation, which actually means simultaneous volume ignition.

For example, this description gives a correct, and rigorous description of the sudden and rapid hadronization of the Quark–Gluon Plasma (QGP) with the release of large latent heat of the QGP to hadronic matter phase transition (Csernai, Reference Csernai1987; Reference Csernai1994). Taub's description could be applied to “slow”, space-like fronts only.

This simplified model gives a quantitative estimate of the dynamics of volume ignition, which occurs in such a time-like detonation, thus completely avoiding the possibility of RT type of mechanical instability.

In the work of Csernai (Reference Csernai1987), the compression of the fuel in a sphere is neglected and the heating is described by isotropic radiation inwards from all sides, where Q is the heat radiated inwards in unit time per unit surface. The opacity of the target is assumed to be uniform inside the sphere, a fraction, C, of the radiated heat is absorbed in the fuel and it is assumed that the incoming energy is sufficient that it is absorbed by the fuel by the point when the incoming beam reached the surface of the fuel on the back side of the pellet and not before. Under these assumptions the temperature increases and reaches a critical (ignition) temperature at some space–time point, T(r, t) = T _c = 4πQC/C _v, where C _v is the specific heat.

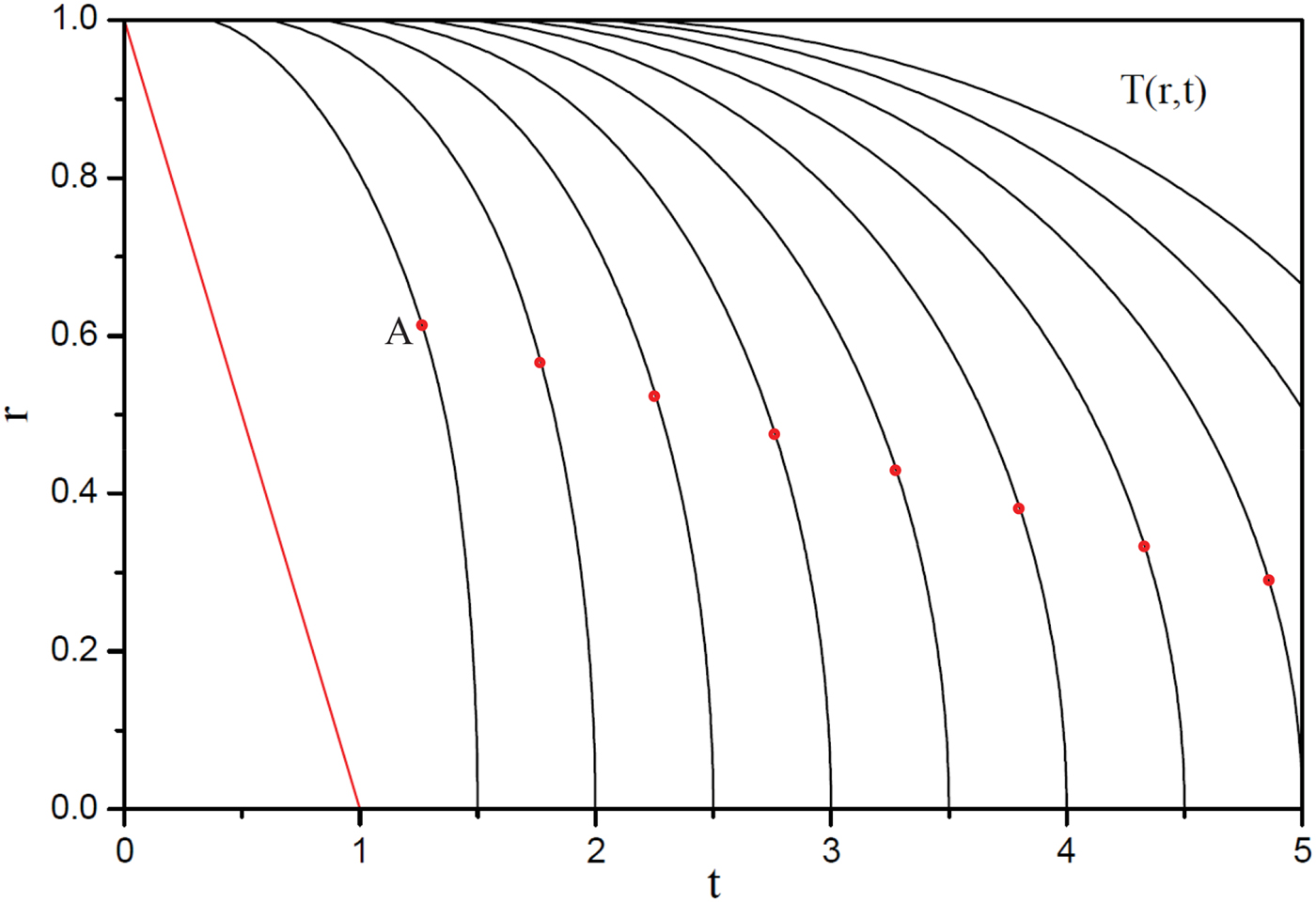
Under these assumptions an analytic solution is given by Csernai (Reference Csernai1987), providing the space–time points of a constant temperature hyper-surface, see Figure 1.

(3)$$T\lpar r\comma \; t\rpar \propto \left\{{\matrix{ {0\comma \; } & {t\lt 1 - r\comma \; } \cr {\displaystyle{t \over r}\left({\ln \displaystyle{t \over {1 - r}} - 1} \right)+\displaystyle{{1 - r} \over r}\comma \; } & {1 - r\lt t\lt 1+r\comma \; } \cr {\displaystyle{t \over r}\ln \displaystyle{{1+r} \over {1 - r}} - 2\comma \; } & {t\gt 1+r.} \cr } } \right.$$

The isotherm hyper-surface is such that in an external spherical layer the detonation starts from the outside with sub-luminous velocity propagating inwards. This “propagation” velocity increases, reaches c, the velocity of light, at a radius R _A (indicated by red dots on the T = const. contour lines, Fig. 1).

Fig. 1. Acceleration of the detonation fronts where the temperature, T, reaches T _c due to radiation from the outer surface at r = 1 inwards (to r = 0). The heating by radiation can lead to a smooth transition from space-like to time-like front at the red points A, where the front propagates with the speed of light. This is possible because the fluid does not move together with the front. The section of the detonation front outside the point A (r > r _A) is a space-like front, while the section within A (r < r _A) is time-like, which corresponds to volume ignition. The ten contour lines indicate the space–time points where T(r, t) = 1, 2,…,10T _c. If the radiation heating is so fast that ignition is reached at T(r, t) = T _c, then the internal domain of the front, up to r ≈ 0.6, is time-like or in this domain rapid volume ignition takes place. To achieve this the heat needed for ignition should be absorbed by the fuel within t _in = 1. If the irradiation is slower, so that ignition is reached only at T(r, t) = 10 T _c or later, then the domain of volume ignition is negligible, and the dominant space-like detonation is subject to mechanical RT instabilities. The world lines of the fluid particles are horizontal straight lines. The inward light cone is indicated with the red straight line starting from t = 0, r = 1 and reaching the center at t = 1. Here t is measured in units of R ₀/c, r in units of R ₀, and T in units of 2πCQ/C _V. Based on the work of Csernai (Reference Csernai1987).

Then the points of the detonation hyper-surface inside this radius are not in causal connection with each other and the ignition completes with a semi-simultaneous volume ignition. This process is not acausal, it is the consequence of the initial inward radiation, so that all points of the time-like detonation hyper-surface are within the light-cones of the energy emission at the initial external surface sphere of radios R ₀. The idea of volume ignition was presented earlier based on different arguments by Kasotakis et al. (Reference Kasotakis, Cicchitelli, Hora and Stening1989), with a short laser ignition pulse.

This model became relevant and applicable to the recently published ICF experiments performed at the National Ignition Facility (NIF). To achieve a rapid volume ignition the needed total ignition energy should be radiated inward in a time interval, t _in < 1 or t _in≪1 [in units of (R ₀/c)].

Of course the model is oversimplified. Even if we irradiate the fuel with light the radiation pressure is one third of the radiation energy density, p _R = e _R/3, and this presses the fuel before ignition. However, this lasts for a short enough time to avoid the build-up of a RT instability. The mechanical RT instability propagates with a speed much smaller than the speed of light, 10⁴–10⁵ times less in a solid, and about 10 times smaller at nuclear matter density.

The longer is t _in the greater probability we have for RT instability. If t _in > 3, then the RT instability can hardly be avoided, and the possible volume ignition domain size becomes negligible. Thus for an R ₀ = 3 mm pellet the ideal irradiation time for volume ignition would be t _in ≤ 10 ps (while for an R ₀ = 30 cm target it would be t _in = 1 ns).

At the NIF “High foot” pre-compression of the fuel capsule in fortunate configuration will not lead to RT instability. As presented by Hurricane et al. (Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Döppner, Hinkel, Berzak Hopkins, Kline, Le Pape, Ma, MacPhee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2014) this shorter, ~6 ns, “High foot” pre-compression led to a more isotropic polar view [Fig. 2b in Hurricane et al. (Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Döppner, Hinkel, Berzak Hopkins, Kline, Le Pape, Ma, MacPhee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2014)], giving rise to less RT instability as it is shown by Casey et al. (Reference Casey, Smalyuk, Raman, Peterson, Berzak Hopkins, Callahan, Clark, Dewald, Dittrich, Haan, Hinkel, Hoover, Hurricane, Kroll, Landen, Moore, Nikroo, Park, Remington, Robey, Rygg, Salmonson, Tommasini and Widmann2014), and higher total yield. As also mentioned in Atzeni et al. (Reference Atzeni, Ribeyre, Schurtz, Schmitt, Canaud, Betti and Perkins2014), the pre-compression stage should be concluded by an ignition spike of 10–30 ps. This is not very far from our suggestion of 10 ps or less to achieve volume ignition or a time-like detonation. In Atzeni et al. (Reference Atzeni, Ribeyre, Schurtz, Schmitt, Canaud, Betti and Perkins2014), this is not considered and only conventional shocks are discussed in the form of an imploding shock followed by a rebounding outgoing shock. These mechanical, pressure-driven processes are still subject to RT instability, whereas the somewhat shorter and more energetic irradiation can prevent the possibility of all mechanical instabilities.

Fig. 2. The shock and detonation adiabats in the pressure, p, generalized specific volume, X, plane, where the initial state is labeled by 1. The shock adiabat (I) goes through point 1, the detonation adiabat (II) represents the final state after the detonation with another Equation of State, which already contains the latent heat of the detonation process, and therefore it is at higher p and X than the shock adiabat. The lines starting from point 1 are the Rayleigh lines connecting the initial and final states. Their slope is determined by the current across the front, j. Mechanically stable final states are above the Chapman–Jouget point, O, while the section of the adiabat between points O and A are mechanically unstable, and the points between A and A′ were considered unphysical. Radiation dominated processes may stabilize final states in the section between O and A, and enable the existence of final states between A and A′ in time-like detonations or in simultaneous volume ignition. From the work of Csernai (Reference Csernai1987). For a more detailed discussion see the book by Csernai (Reference Csernai1994).

In the present ignition experiments, a compression stage precedes the ignition process (Hurricane et al., Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Döppner, Hinkel, Berzak Hopkins, Kline, Le Pape, Ma, MacPhee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2014; Park et al., Reference Park, Hurricane, Callahan, Casey, Dewald, Dittrich, Döppner, Hinkel, Berzak Hopkins, Le Pape, Ma, Patel, Remington, Robey, Salmonson and Kline2014). In the most successful experiments with an initial “High foot” shock of ~6 ns the capsule is heated up and compressed to a smaller size of a radius of about an order of magnitude smaller, making the target hotter and more dense. The hotter target became less opaque, and the target more compressed. Then the two final, more energetic shocks lasting for ~8 ns, resulted in a hot spot of ~37 µm radius, which is (partly) ignited and emitted almost the same energy that was invested to its compression and heating. The rapid ignition of an R ₀ = 300(100) µm target to ignition at a mostly time-like surface would need a short energetic pulse of t _in ≈ 1(0.3) ps, which is about 10³–10⁴ times less than it was done in the NIF experiment.

Nevertheless the radiation dominated implosion leads to increased stability in the space-like, mechanically unstable section of the detonation adiabat under the Chapman–Jouget point [point “O” in Figure 2, and see also the discussion in Chapter 5 of the textbook by Csernai (Reference Csernai1994)]. Thus, the shortening of the pulse of the last two shocks, without decreasing the total deposited energy, leads to radiation dominance and may increase the stability considerably compared with the relatively “slow” final compression and heating of ~8 ns.

Apart from the (i) short and energetic ignition pulse, the other critical condition is the (ii) sufficiently small opacity, such that the ignition pulse should be able to penetrate the whole target. Luckily the more energetic preheating pulses lead to a smaller target opacity and better thermal conductivity as shown by Hu et al. (Reference Hu, Collins, Boehly, Kress, Goncharov and Skupsky2014), so the appropriate tuning of the laser irradiation must be possible. The present pre-compression and heating with the starting “High foot” pulse led to higher temperature after the pre-compression, and this may be sufficient or adequate to achieve the optimal (low) opacity for the final short ignition pulse. The presented simple analytic model can be best applied to the stage of the process after the “High foot” pulse heated up the fluid sufficiently to achieve sufficiently small opacity.

Both these conditions may be more easily satisfied by heavy-ion beams, where the beam bunch length can be regulated by beam optics and could be adjusted, so that the length at the target becomes as short as 10 ps (or 3 mm) or less. The suggestions of Lalousis et al. (Reference Lalousis, Hora and Moustaizis2014) and Hora et al. (Reference Hora, Lalousis, Eliezer, Miley, Moustaizis and Mourou2014c) emphasize also fast ignition as this work; however, this is considered to happen in a well focused location with subsequent spreading the fusion flame through the whole (pre-compressed) target. The expansion of the target is counteracted by a strong magnetic field generated by a previous laser pulse. The primary aim is to generate mechanical compression as strong as possible. This is not the mechanism suggested here.

The detailed study of Fernandez et al. (Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014) has basically the same goal, although instead of the magnetic field the possibilities of using proton and ion beams are discussed. It is even discussed that to reach maximal acceleration and relativistic speeds in the implosion, the plasma should be made opaque to the extent that it “becomes sufficiently thick to isolate the rear target surface from the laser”.

The problem with these approaches is that this extreme compression leads to RT instabilities, which leads to a strong rebound of most of the target material. (In a collapse of a cold, ~20 Solar mass Supernova progenitor only up to a 2 Solar mass Neutron or Hybrid star remains compressed.) To describe these instabilities a very high resolution, 3 + 1 dimensional relativistic PICR code is necessary (Csernai et al., Reference Csernai, Strottman and Anderlik2012) with very small numerical viscosity. Using such a relativistic approach one can see that the explosive hadronization of QGP takes place in a large part of the QGP volume with an almost simultaneous detonation; see the works of Floerchinger and Wiedemann (Reference Floerchinger and Wiedemann2014) and Csernai et al. (Reference Csernai, Cheng, Horvát, Magas, Strottman and Zétényi2009). This is essentially the only secure way to prevent instabilities, and this requires a radiation dominated relativistic process, as shown also in Figure 1. To achieve this almost simultaneous ignition in a large part of the pre-heated target of ~100 µm, this target should not be further compressed, rather heated up by radiation, possibly simultaneously from all sides, so that radiation can reach also “the rear target surface”. Thus, in this aspect, the present suggestion is an alternative of the focused single point fast ignition discussed by Fernandez et al. (Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014), Lalousis et al., (Reference Lalousis, Hora and Moustaizis2014), and Hora et al. (Reference Hora, Lalousis, Eliezer, Miley, Moustaizis and Mourou2014c). On different grounds it was also found that picosecond pulses may lead to volume ignition. This in any case excludes the development of most instabilities as shown by Hora et al. (Reference Hora, Miley, Lalousus, Moustaizis, Clayton and Jonas2014a; Reference Hora, Lalousis and Moustaizis2014b) and Hora (Reference Hora2013).

The penetration length of heavy-ion beams can also be regulated by the well-chosen beam energy. This operation is well studied in connection with radiation therapy where the position of the absorption Bragg peak is tuned to the necessary depth in the body to reach the tumor. One could also study if in this case one can achieve a sufficiently short and energetic final pulse, so that the detonation becomes time-like in the majority of the compressed target. This may happen in the section of the detonation adiabat between points A and A′ in Figure 2.