2. REACTIONS FOLLOWING THE SELF-SIMILARITY MODEL AND VOLUME IGNITION

The first publications about laser fusion (Basov & Krokhin, 1963; Dawson, 1964; Hora, 1964) studied the fusion reactions from a spherical DT plasma if laser energy E_o is deposited there without discussing the details of the interaction mechanisms (see Section 4), and where the dynamics for the expansion, laser heating, and adiabatic cooling followed the self-similarity model (Fig. 1), known from earlier theory where the time dependence of the deposition of the laser energy was followed up (Hora & Miley, 1986; Schmalz, 1986; Hora, 1991: see Chapter 5). The fusion gain G as the ratio of the fusion energy per Energy E_o input into the reacting plasma, then calculated by simplifying this process to an instantaneous deposition of the laser energy into a DT (1:1 mixture) sphere of initial radius R_o or volume V_o of initial density n_o expressed as multiples of the solid state density n_s of DT was evaluated numerically and arrived for constant V_o in steep parabolas (Hora, 1991: Fig.13.3) which envelope corresponded to the highest optimized gains G. These envelopes followed the relation (Hora & Pfirsch, 1970)

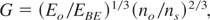
Self-similarity hydrodynamics of a spherical plasma of a uniform temperature T with an initial Gaussian density profile on the radius (|x|) and an initial linear profile of the velocity v. This linear velocity and Gaussian density profile is conserved in time changing only the maximum and the gradient at adiabatic change of the temperature.

where E_BE is the break-even energy for DT of 6.3 MJ defining the incorporated laser energy E_o for solid state density (n_o = n_s) where the gain G = 1. The numerical result is that the initial temperature at this optimum condition has to be

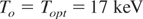
Expressing E_o by T_o and R_o using

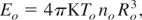
Eq. (1) results in

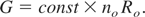
Which formula was published later by Kidder (1974) and Fraley et al. (1974)? While formula (4) was preferably used (mostly without indicating that this only refers to optimum temperature!), the formulation (2) immediately shows how compression of the plasma is of advantage. Compression to 1000 times the solid state needs one million times less laser energy for the same gain than at n_s.

The result of Eq. (2) was rather discouraging for laser fusion. The gains G were rather low even for very high laser energy E_o and very high compression (n_o /n_s above 1000). This was the main reason to look for another laser fusion mechanism, the spark ignition, as described in the following section. Nevertheless, the result (2) and its algebraically identical formulation (4) were based on very poor assumptions, and the situation changed drastically by the following basically nonlinear correction. The computations (Hora, 1964, 1971) were extended (Hora & Ray, 1978) by including:

For the re-heat, the binary interaction theories resulted in too long stopping lengths for the alphas compared with the collective interaction first derived by Gabor (1953) and reproduced (Ray & Hora, 1978) by quantum electrodynamics modification of the Fokker-Planck collisions. For the re-absorption of the bremsstrahlung after clarification that the conditions were outside of the restrictions of opacity, were based on the Kramer's spectra where the variation of temperature and density for each time step of the computation could be based on the uniformity within the plasma as known form the self-similarity properties of the plasma dynamics.

The resulting fusion gains depending on the input laser energy E_o for a set of initial densities given by n_o /n_s is shown as straight lines in Figure 2 (Hora, 1991, see Fig. 13.6). The lines are envelops of the before mentioned parabolas for constant initial volume drawn as dashed lines. These are nearly of the same values as calculated before without the generalizations (a) to (c) resulting in the gains below G = 8 of Eq. (2). The alpha reheat, however results in the fact that the parabolas are deformed for G > 8 with a steep rise as shown in the upper part of Figure 2. The action of the reheat could immediately be seen from the printout of the time dependence of the temperature of the plasma, Figure 3. If the optimized initial temperature of 1.07 keV corresponded to a point at the lower end of the steep rise, where temperature was nearly constant with a monotonic decrease resulting in the gain G of 0.77, not much higher than the case without re-heat. A little bit higher initial temperature (1.6 keV) showed an increase of the temperature first slowly growing above the 1.6 keV but then quickly reaching 170 keV from where on the fast adiabatic expansion was cooling the plasma. The gain jumped to the value G = 1900. If a further higher initial temperature of 2.7 keV was chosen, the rise of the temperature to 190 keV was faster, but the faster expansion and cooling did not permit as many reactions as before and the gain dropped to 1100. The change of the initial optimum temperature of 17 keV for G below 8 to the lower temperatures due to alpha re-heat can be seen in Figure 1 from the vertical dashed lines for given initial DT volume in the solid state before compression. Bending to the left for G above 8 indicates the ignition to the much lower initial temperature. The effect of the re-absorption of bremsstrahlung is strong for initial temperatures below 4.5 keV which cases are above the line LTI (low temperature ignition) (Hora et al., 1998).

Optimized core fusion gains G (full lines) for the three-dimensional self-similarity hydrodynamic volume compression (Stening et al., 1992) of simple burn (G < 8) (sometimes called quenching: Atzeni (1995) and volume ignition for G > 8 with low temperature ignition above LTE line. The measurements (see Hora et al., 1998) of Rochester (Soures et al., 1996) point A), Osaka (Takabe et al. (1988) point B), Livermore (point C) and Arzamas-16 (point D) agree with the isentropic volume burn model, while the earlier fast Pusher (point E) with strong entropy-producing shocks does not fit (Hora et al., 1998).

Calculated time dependence of the plasma temperature at volume burn (lowest curve) and volume ignition in which case the little higher energy input produces very high plasma temperatures and reaction gains due to alpha self heat and partial bremsstrahlung re-absorption (Hora & Ray, 1978).

This volume ignition was confirmed by several authors (Kirkpatrick & Wheeler, 1981; Basko, 1990; Lackner et al., 1994; Martinez-Val et al., 1994; Tahir & Hoffmann, 1994; Atzeni, 1995) where the results of Martinez-Val were especially significant showing for a special case of heavy ion beam fusion, how the volume ignition works with inclusion of reheat by neutrons apart from the alphas, and showing how the reheat is mostly going to the ions to a temperature near 200 keV, while the electron temperature goes only to 80 keV due to too short equipartition time and where the black-body background radiation goes to 8 keV only (Fig. 4).

General calculation of the time dependence of ion temperature, electron temperature and black-body radiation temperature at volume ignition with general hydrodynamic for a case of high gain heavy ion beam fusion (Martinez-Val et al., 1994) with the typical strong temperature increase as in Figure 3.

For fusion gains G below 8, there is no volume ignition but volume burn or sometimes called quenching (Atzeni, 1995) where the adiabatic self similarity compression is working with approximately Gaussian profiles of the density on the radius for each time step, a radically linear velocity profile with linear change of the gradient on time and a radically constant temperature at each time step as calculated from sophisticated details, Figure 4 (Martinez-Val et al., 1994) well showing nearly constant density in the DT fuel and constant temperature globally changing only on time as given by the adiabatic dynamics. It is remarkable (Hora et al., 1998, 2003) that the measurements with the highest fusion gains exactly followed theses shock-free properties of this volume burn as given at points A, B, C, and D in Figure 2, for the results at LLE Rochester, ILE Osaka, LLNL Livermore, and Arzamas-16, respectively. A fast pusher example (E in Fig. 1) with the usual high shock generation does not fit this volume burn model. These agreements in Figure 2 with the volume compression and in difference to the spark ignition were a splendid confirmation that this high gain laser fusion is on the way to volume ignition.

Before the volume ignition was discovered (Hora & Ray, 1978), the disappointingly low fusion gains of volume burn (quenching), Eq. (1) led to the concept of spark ignition where the laser driven compression of the fusion fuel is performed in such a special way—in strongest contrast to the natural adiabatic self similarity compression of volume ignition—such that the center of the compressed plasma has a high temperature and low density, while the surrounding plasma has a high density and a low temperature. The aim is that the central part (hot spot) is produced which will react as known from volume ignition, and this hot plasma will produce a fusion detonation wave at the outer low temperature high density plasma such that a high fusion gain will result. At highest compression, there is then a high temperature, low density core and low temperature high density outer plasma necessary to be produced.

The main problem is not only that the very exclusive special density and temperature profiles have to be produced, what is more critical is that that these profiles have to be equal all directions. If the exclusive profiles would be reached into on direction and would lead then to the fusion detonation wave but if the conditions would not have been reached into the other directions, nothing of the aimed symmetric hot-spot ignition will be possible. Nevertheless, this scheme reached very high gains, much above the gains of the fusion burn of Eq. (2). As was evaluated in details (Hora et al., 1998), the fusion gains at volume ignition are of similar high values as for spark ignition (perhaps up to a factor two lower), but the advantage of volume ignition is that the problems of Rayleigh–Taylor instabilities, of other parametric instabilities and conditions of symmetry are highly reduced. Lackner et al. (1994) called this kind of compression for volume ignition very “robust” compared to the scheme of spark ignition.

Volume ignition works like a diesel engine and there is—apart from the favor of the reabsorption of bremsstrahlung because of the very low temperature —a large amount of “additional driver energy” coming from its own produced alpha reheats. Detailed calculations (see He & Li, 1994; Martinez-Val et al., 1994), include additional self heat by neutrons and instead of assuming LTE they find that the ions are much hotter at maximum temperature, Figure 4, than the electrons and the background blackbody radiation. In this case (Martinez-Val et al., 1994), a pulse of 6 GeV bismuth heavy ions as driver of 1.6 MJ energy and 10 ns duration produces 120 MJ DT fusion energy. It should be mentioned that the neutron reheat—not included in the case of Figure 2—improved volume ignition (gains may increase up to a factor of two), while it was shown (Johzaki et al., 1996) that neutron reheat decreases the gain in spark ignition.

3. PROBLEMS OF LASER-PLASMA INTERACTION

The preceding chapters were devoted to the question of the fusion reaction after an appropriate deposition of laser energy was reached without discussing the laser-plasma interaction process though the examples of direct drive measurements in Figure 2 for highest fusion gains confirmed that the conditions for volume burn (or ignition) were automatically fulfilled. The difficulties for understanding the interaction process appeared from the early years of laser-plasma interaction studies (Hora, 1991). The interaction below laser powers of about 1 MW was fully classically. The laser heated the plasma to a few 10⁴ K, the ions emitted had energies of a few eV, the expansion of the plasma fully followed the classical magneto hydrodynamics, and the ion and electron emission currents were limited to current densities of a few mA/cm² as known from the limits of the Longmuir-Child space charge relation. Above this threshold of 1 MW laser power, the first nonlinear effects were seen by Linlor and Honig (see Hora, 1991) when the ion energies were suddenly in the keV (later measured above 100 MeV) range, the emitted ions were highly charged, were separated in groups with linear increase of their energy on the charge number Z, the ion and electron emission current densities were more than 10000 times higher than the space charge limit and more anomalies and nonlinearities were detected in due course. The explanation was the realization of a direct electrodynamics (collisionless non-thermal) interaction of the laser light with the plasma (Hora, 1969) where the first inclusion of dielectric (plasma) properties to the earlier known ponderomotive force was essential (Hora et al., 1967) which led to the general nonlinear force description (Hora, 1969a, 1985, 1991). The 1 MW power threshold could be seen from the first quantitative derivation of this threshold value for ponderomotive self-focusing (Hora, 1969a, 1969b) explaining the high explaining the keV ion energies and furthermore up to the MeV range due to the relativistic self-focusing (Hora, 1975). The nonlinear force was the essential reason for the parametric instabilities (known before in some way) as clarified by Chen et al. (1974).

Then followed an extremely long discussion of these parametric instabilities which reflectivity definitely could be detected from the 3/2 harmonics of the laser light emitted from the irradiated target. When laser beam smoothing was introduced (see Deng, Kato, Lehmberg, Obenschain etc. in Hora, 1991) with the motivation to eliminate the action of self-focusing filaments, suddenly it was observed, that these instabilities were reduced by a factor of 100 to 1000 (Giulietti et al., 1991; Wu et al., 2001). It was clarified (Hora & Aydin, 1999; Osman et al., 2004b) that these smoothing processes were not alone a question of suppression of fulmination but suppression of the 10 ps stochastic pulsating interaction. This pulsation was indicated in 1974 (Hora, 1991: Figs. 10.10) from the generation of laser-phase conform density rippling when after about one ps the laser light reflected at the critical density produced a partly standing wave pushing the plasma into the nodes by the nonlinear force. This change from mirror reflection with low reflectivity R form the whole plasma corona to the very high R phase reflection at the outermost corona was seen experimentally within the few ps resolution confirming the stochastic 10 ps pulsation (Maddever et al., 1990). This could be analyzed in all details (Hora & Aydin, 1992) and reproduced numerically. Calculating with a broad band laser beam, the phase reflection was avoided and low reflectivity R (less than 5%) was confirmed.

This result clarified that the earlier assumed need to work with shorter wave lengths that is, by using very expensive large KD*P crystals for producing the second or third harmonics was not necessary. In these measurement it was overlooked, that these were time integrated while the stochastic 10 to 20 ps pulsation mechanism as mentioned before was just a strong modification of this result. If one uses the just mentioned appropriate smoothing, the phase reflection can be avoided and the very low reflectivity will permit a strong coupling of the laser radiation into the plasma corona even for the read fundamental frequency.

Therefore, low cost appropriate smoothing permits the irradiation with the fundamental laser frequency without any energy loss from generating higher harmonics. How smoothing suppresses fulmination was shown from side-on pictures of the irradiated plasma corona (Labaune et al., 1992) but at the same time the pulsation with structures perpendicular to the laser beam were seen due to the stochastic pulsation, and how these pulsation process was suppressed by smoothing (Hora & Aydin, 1999; Osman et al., 2004b; Osman, 2004).

All these results for using appropriately smoothed red laser beam of high energy for direct drive

• without stochastic pulsation and subsequent very low reflectivity,
• with no fulmination, and
• with nearly no parametric instabilities

indeed clarify the position for long (above 100 ps) laser pulses only. The result for the longer pulses is relevant only for the conservative laser fusion scheme discussed in the following Section.

4. SINGLE-EVENT NANOSECOND LASER IFE

We describe now how the nanosecond laser pulses of MJ energy may lead to the fusion power station based on a single-event process. One important earlier result (Azechi et al., 1991) was the measurement of laser compression of a carbon polymer containing deuterium and tritium to 2000 times the solid-state density. The temperatures achieved, however, were disappointingly low, in the range of 300 eV only. As a consequence, Campbell et al. (2000) observed this all since 1985 and explained in his contribution to a celebration of Chiyoe Yamanaka that he had originally suggested additional heating should be done using short laser pulses in a two-step process. Campbell could develop a program to study this approach based on the newly discovered CPA technique of Mourou and Tajima (2002). This effort added new emphasis to the scheme of the fast ignitor (Tabak et al., 1994; Osman et al., 2004a; Wilks, 2005; Badziak et al., 2005; Schaumann et al., 2005; Hoffmann et al., 2005; Hora, 2005). Details about this are discussed further in the following Sections.

An alternative to the short pulse heating of the compressed plasma was revealed by following up the numerical results of the volume ignition, Figure 2. At this time, Atzeni (1995) discussed laser fusion schemes using laser pulses of some MJ energy in the ns range confirming the earlier results on volume ignition.

Coming back to the result of low temperatures at high compression (Atzeni, 1995), volume ignition can well provide a solution. If laser pulses of 5 MJ or more are available, volume ignition with compression to 3000 or 5000 times solid-state density results in optimum ignition temperatures as low as about 500 eV (Hora et al., 2003). These temperatures are, in fact, not much above the values already measured with energy laser pulses of about 100 times lower in energy. Detailed numerical evaluations confirm (Hora et al., 2003) that with few MJ laser pulses target conditions with natural self-similarity compression will arrive at a crossing point of parameters for high gain volume ignition. This approach avoids the need for additional short pulse laser input or sophisticated shaped density and temperature profiles as needed for spark ignition.

As we underlined in the preceding section, direct drive adiabatic self similarity compression has to use appropriate smoothing for suppression of stochastic pulsation, fulmination, and parametric instabilities for very low reflection using then the read fundamental light of the laser pulse without losses for frequency up-conversion.

Figure 5 shows the results for low temperature volume ignition with the ns laser pulses. These computations were done for non-degenerate plasmas. The upper part of Figure 5 is the range of electron degeneracy and need some corrections. The experiment (Azechi et al., 1991) with compression to 2000 n_s and 300 eV ion temperature was in the range of degeneracy where the Fermi energy of the electrons is above 1 keV. This case cannot immediately be compared with our computations for non-degenerate electrons of Figure 5 though these cases are rather close. For a one step ns laser fusion reaction we take laser pulse energy of 10 MJ and a hydrodynamic efficiency of 10% for 50:50 DT fuel. From Figure 5 we derive that the optimum temperature is 560 eV for the compression to 10000 n_s. The core gain G = 1300 based on the 1 MJ energy E_o in the reacting adiabatically compressed core is 560 eV. Therefore the total fusion gain per laser energy is G_tot = 130. Lightly higher gains of 140 are when using a 20 MJ laser pulse energy where the optimum temperature is 425 eV for the compression to ten thousand times the solid state density. These temperatures come very well down to the range of the earlier measured 300eV which indeed were achieved by compression to 2000 n_s with laser pulses of 20 kJ only (Azechi et al., 1991). The interesting cases to be evaluated numerically and compared with experiments for MJ laser pulses will for sure be somewhere between the numbers shown here. This only should confirm that a fusion reactor using the very conservative direct drive fusion with compression to few thousand times the solid state and with laser pulses in the few MJ range and gains of more than 100 from the very robust volume ignition can be considered as a possible solution.

Optimized core fusion gains G as in Figure 1 with the cross hatched area for Fermi degenerate electrons for evaluation of optimized volume ignition at temperatures in the 500 eV range.