Introduction
Argentine stem weevil (Listronotus bonariensis (Kuschel), Coleoptera: Curculionidae) was the most serious pest of Graminae in New Zealand's improved pasture for more than 100 years. When uncontrolled, this species was estimated to cause losses to the pastoral sector of NZ$78–251M annually (e.g. Prestidge et al., Reference Prestidge, Barker and Pottinger1991). The weevil has also been reported to cause sporadic problems elsewhere, usually in cereal crops. Gassen (Reference Gassen1984) identified L. bonariensis as being damaging to wheat in southern Brazil. Similarly in Argentina, it has been noted that the weevil larvae feed on wheat shoots and buds resulting in shoot mortality, reduction in shoot numbers and reduced yields (Anonymous, 1996). Listronotus bonariensis is also established in Australia, where it was first noted as a problem in sports turf (Hardy et al., Reference Hardy, Terauds, Rapley, Williams, Treson, Miller, Brieze-Stegeman and McQuillan1979).
The life history of L. bonariensis, as reflected in fig. 1, is well known and includes the occurrence of reproductive diapause and dispersive flights (e.g. Pottinger, Reference Pottinger1961; Goldson, Reference Goldson1981; Goldson et al., Reference Goldson, Proffitt and Baird1998a, Reference Goldson, Proffitt and Baird1999). In brief, the weevil is bivoltine, with first generation egg-laying commencing in late September following the cessation of weevil overwintering diapause. Eggs are laid in the sheaths of the grass tillers, and the resulting larvae develop through four larval instars, destroying 3–5 tillers in the process (Prestidge et al., Reference Prestidge, van der Zijpp and Badan1984). In addition, about 30% of the total larvae have also been found to develop in the pasture thatch (Goldson et al., Reference Goldson, Proffitt and Baird2001). Mature fourth instar/prepupal larvae cease feeding and move into the soil where they pupate in earthen cells. First generation adult eclosion begins in early December and peaks in early January. A second larval generation develops over the summer with second generation teneral adults appearing in early March with eclosion continuing well into the winter, ending in mid-June. This second generation of adults, along with some surviving first generation adults, overwinter in a state of reproductive diapause triggered by critical photoperiod. These weevils form the basis of the next season's spring reproductive population.

Fig. 1. Diagram showing the timing of, and estimated mortalities of L. bonariensis life stages used in this analysis. Shading of the life stages indicates relative abundance, with the darkest shading indicating peaks in abundance. Mortality rates are expressed as k-values where: k f,1 and k f,2=unrealized fecundity in the founding of the first and second generations per season respectively; k el,1 and k el,2=mortality of the egg and early instar larval stages in the first and second generations respectively; k pp,1 and k pp,2=mortality of the fourth (i.e. fourth instar/prepupal and pupal) stages in the first and second generations respectively; k ptm2=parasitism of second generation adults by M. hyperodae; and ko/w=overwintering mortality. The dashed line indicates that some of the late-emerging (February) first generation adults go directly into reproductive diapause and contribute to the overwintering adult generation (Goldson, Reference Goldson1981).
Resistance to weevil attack occurs when perennial ryegrass plants are infected with the endophyte Neotyphodium lolii (Latch Christensen and Samuels) (formerly Acremonium lolii) (Ascomycota Clavicipitaceae). Such infection deters oviposition and makes the tillers toxic to larvae (Prestidge et al., Reference Prestidge, Pottinger and Barker1982). The use of N. lolii has become an important component of New Zealand's pasture pest management (Easton, Reference Easton2007).
The severe economic impact of L. bonariensis led to the 1991 release of the South American thelykotous, koinobiont endoparasitoid wasp, Microctonus hyperodae Loan (Hymenoptera: Braconidae), as a control against L. bonariensis (Goldson et al., Reference Goldson, McNeill, Proffitt, Barker, Addison, Barratt and Ferguson1993). This wasp parasitises the adult weevils and almost immediately causes sterilisation; thereafter, the four larval instars develop within the still-live weevil. Host weevil mortality occurs at the time of fourth instar (prepupal) emergence. The parasitoid was found to establish rapidly throughout New Zealand, often resulting in peak host parasitism levels of as much as 80% (e.g. Goldson et al., Reference Goldson, Barker and Barratt1994).
Barker et al. (Reference Barker, Pottinger and Addison1989) have described L. bonariensis population dynamics prior to parasitoid release in comparatively warm and wet North Island Waikato dairy pastures (ca. 37.78°S, 175.35°E), which consist mainly of endophytic perennial ryegrass Lolium perenne L. plants (cultivar Grasslands Nui) and white clover Trifolium repens L. These workers showed that under such circumstances the weevil population regulatory processes primarily resulted from density dependent mortality of overwintering adult weevils, ovipositional competition for endophyte-free tiller resources and tiller resource competition between early-instars.
In contrast to the North Island Waikato region, while there have been some basic bionomic studies in dryland non-endophytic sheep pasture Lolium multiflorum×perenne L. (cultivar Grasslands Manawa) in Canterbury (Goldson et al., Reference Goldson, Proffitt and Baird1998a), there has been no comprehensive baseline population dynamics analysis studies of L. bonariensis. Consequently, to address this absence of information and as part of the overall biological control programme, weevil populations at Lincoln, Canterbury (ca. 43.64°S, 172.47°E) were monitored continuously over eight consecutive years. Such work is of significance because it was conducted in a dryland ecosystem, typical of where L. bonariensis can be particularly damaging (e.g. Goldson & Trought, Reference Goldson and Trought1980).
Based on the monitoring work, this contribution therefore uses historical data to investigate the regulation of the weevil pest populations prior to, and somewhat during, the establishment of the parasitoid in Canterbury dryland conditions. Thus, a significant goal of this study is to provide an L. bonariensis population dynamics baseline for any future work that aims to analyse the full effects of M. hyperodae on the weevil, now that equilibrium with the weevil host has been reached.
Materials and methods
Study site and sampling of weevil populations
Egg, larval and adult stages of L. bonariensis were sampled regularly from 26 November 1990 to 15 February 1999 at the AgResearch Farm at Lincoln. The paddock was first sown in autumn 1988 with a mixture of cv. Manawa ryegrass and white clover and was periodically renovated to maintain sward quality. This paddock was the site of the original M. hyperodae releases in the winter of 1991 (Goldson et al., Reference Goldson, McNeill, Proffitt, Barker, Addison, Barratt and Ferguson1993). Sampling of all stages of L. bonariensis occurred approximately fortnightly from spring to autumn and approximately monthly during the winter. The sampling techniques used are described in detail elsewhere (Goldson et al., Reference Goldson, Proffitt and Baird1998a); but, briefly, eggs were sampled by inspection of ryegrass tillers, larvae by heat extraction from ryegrass tillers and adults by flotation extraction from 450 mm×40 mm×80 mm deep turf pasture samples. The latter were taken from each of five designated blocks in the research paddock, and the number of turves taken per block varied from four to ten to maintain a standard error of the mean of ≤20% (Goldson et al., Reference Goldson, Proffitt and Baird1998a).
Life table preparation
Partial life tables (table 1) were constructed for the L. bonariensis populations monitored at Lincoln between late 1990 to early 1998. Figure 1 illustrates the phenology of the weevil population and defines the transitional mortality factors that were estimated in this analysis. The life tables were not entirely complete because two factors were not quantified. The first of these is the possibility of redistribution arising from trivial weevil flight (e.g. Goldson, Reference Goldson1981; Goldson et al., Reference Goldson, Proffitt and Baird1999). However, in established pasture, this effect is likely to be minor given that incoming weevils (from surrounding areas) were likely to have arrived in similar numbers to those leaving (Goldson, Reference Goldson1981; Goldson et al., Reference Goldson, Proffitt and Baird1999). Should any dispersive losses have occurred, they would have been included in the unrealised fecundity ‘mortality’ factor in the first and second summer generations (k f,1, k f,2), since flights can coincide with the times that overwintered (spring) and first summer generation adults are reproducing (fig. 1) (Goldson et al., Reference Goldson, Proffitt and Baird1999). The second factor is the contribution of M. hyperodae parasitism to unrealised fecundity of first generation adults, since parasitised weevils are not reproductive (Goldson et al., Reference Goldson, Proffitt and Baird1998a,b). It is notable, however, that, at least in the first phases of this study, parasitism levels were relatively low, as at that time the parasitoid populations were still building. Thus, taken across the whole study period, this influence would have been relatively minor (Goldson et al., Reference Goldson, Proffitt and Baird1998b). Nonetheless, these two factors need to be considered when interpreting the results.
Table 1. Stage-specific mortality rates for L. bonariensis populations at Lincoln (1990–1998).

Refer to figure 1 caption for stage mortality definitions.
The number of individuals entering the egg, prepupal and teneral adult stages were estimated using the graphical integration method of Southwood and Jepson (Southwood, Reference Southwood1978). For the egg and larval stages, the calculations were made using physiological time; where successive estimates of stage densities, obtained through sampling, were plotted against cumulative degree-days and the area under the resulting curve was divided by the mean duration (in degree-days) of the stage. The degree-day requirements and threshold temperatures for development used in these estimations were: 72.6 degree-days above 11.9°C for the egg stage to the prepupal stage and 33.6 degree-days above 12.2°C for the prepual stage to adult stage (Kalvelage, Reference Kalvelage1999). In this study, the term ‘prepupal’ was taken to include the fourth instar as it is this stage that exits the tillers pending pupation. Meteorological data were recorded by a weather station located approximately 500 m from the study site. Temperatures were assumed to vary sinusoidally through the 24-h day and the number of degree-days accumulated per day was calculated using the trapezium method (Barlow & Dixon, Reference Barlow and Dixon1980): degree-days per day=0.25((T max–T h)+(T min–T h)+2(T mean–T h)) where T max, T min and T mean are the maximum, minimum and mean daily temperatures, respectively, and T h is the threshold temperature for development for the stage.
Prepupae were chosen as the best estimate of larval density because they are relatively large and unlikely to be overlooked in tiller samples; they also have a relatively high survival rate and were unlikely to bias the estimates of stage recruitment. Also, their relatively long stage duration reduced the chances of them being missed between sampling dates. Prepupal densities were multiplied by 1.54 to correct for sampling bias arising from larval development in the thatch (Goldson et al., Reference Goldson, Proffitt and Baird2001).
The appearance of teneral adults was used to estimate recruitment to the adult stage; the teneral stage was assumed to last for approximately 14 days, based on laboratory observations (Pottinger, Reference Pottinger1961). Again, densities were estimated using the graphical integration method of Southwood and Jepson (Southwood, Reference Southwood1978).
Eight full seasons of data were available, but some data were omitted because of known sampling errors. In the 1991/92 season, no second generation eggs were detected from the tiller samples, yet larvae were subsequently found, indicating sampling deficiency rather than absence. To remedy this, the second generation egg density for this season was set to be the same as the maximum potential fecundity, which meant that unrealised fecundity was underestimated and egg to prepupal mortality was overestimated. However, assuming that the larval density estimates were accurate, total seasonal mortality would remain unaffected. It was, therefore, necessary that the estimates for second generation 1991/92 eggs and larvae be omitted. In the 1997/98 season, no estimates were made of adult density in early winter, with the last sample taken on 2 March 1998. Because recruitment of second generation adults continues after this time until early June (Goldson et al., Reference Goldson, Proffitt and Baird1998a), parasitism of second generation adults, overwintering mortality and, therefore, total seasonal mortality could not be estimated for 1997/98.
Key factor analysis
To compare the variation in mortality rates between stages and years, k-values were calculated as k=log (number entering stage)–log (number surviving to next stage), except where noted below. The unrealised fecundity k-values (k f,1 and k f,2) were estimated from the difference between the maximum potential fecundity of the weevil population present and the observed number of eggs laid. For the egg laying that founded the first generation, maximum potential fecundity was calculated by multiplying the peak number of overwintered fecund females by the species’ mean fecundity of 320 eggs (Malone, Reference Malone1987). For the egg laying that founded the second summer generation, maximum potential fecundity was calculated by dividing the number of teneral weevils by two (i.e. assuming a 50:50 sex ratio, (Goldson, Reference Goldson1979)) and multiplying this figure by mean female fecundity.
Overwintering mortality (k ow) was calculated as the logarithm of the (unparasitised) adult density in June minus the logarithm of the (unparasitised) adult density in late August/early September when the weevils come out of reproductive diapause.
Total seasonal mortality (K) was calculated as the sum of the individual stage k-values. The mortality contributing most to the total seasonal variation in mortality (i.e. the key factor) was assessed by visual comparison of the variation in k-values with K (Varley & Gradwell, Reference Varley and Gradwell1960) and by regression of the k-values on K (Podoler & Rogers, Reference Podoler and Rogers1975).
Manly key factor analysis
In addition to the Varley & Gradwell (Reference Varley and Gradwell1960) method and Podoler & Rogers’ (Reference Podoler and Rogers1975) method of key-factor analysis described above, the method of Manly (Reference Manly1977) was also used on the reduced data set (1991/92 and 1997/98 seasons excluded). This has the advantage that it takes into account the order in which the mortality factors operate, so that any damping of variation due to density dependence in earlier stages is accounted for in the analysis of the following stages. Unlike the earlier methods, which identify the life stage that mainly accounts for changes in total mortality, Manly's method identifies the most influential life stages causing population change and may recognise key factors which are unclear in other analyses (Manly, Reference Manly1977). The contribution of the variation in mortality in stage i to the variation in numbers entering the final stage n was estimated as:
where δ is the slope and var(ε) is the residual mean square estimated from the linear regression of stage k versus log (stage density). Ordinary least-squares regression was used except that the residual mean square was estimated as the mean square divided by the number of seasons–1 (S–1), rather than the usual S–2 (Manly, Reference Manly1990). Variation in the number of fecund females at the start of each season, A 0, was also included as a source of variation because the omission of the 1991/92 and 1997/98 seasons, and spring dispersal meant that the numbers at the start of each season were unrelated from one season to the next. The variance A 0 was calculated as above, except that var(ε) was replaced with the variance in fecund female density at the start of each season. The stage A i values were summed to give the variation in the numbers entering the final stage, var(R 9), which in this case was variation in the density of adults at the end of the winter diapause. The key factor is the stage whose weighted variation, A i, contributes most to the total variation, usually expressed as a percentage of var(R 9).
Considering that different factors play different roles in population dynamics, key factor analysis has some limitation in repeatedly determining the true key factor (if any) without fail (Royama, Reference Royama1996). However, by combining the results from the different key factor analytical methods described in this study, it is likely that the correct candidate factors were identified making such information useful for future investigation.
Density relationships
Density-dependent mortality factors were assessed by regressing estimated k-values against the logarithm of the stage densities (per m2) on which they acted; a positive slope is indicative of direct density dependence (Southwood, Reference Southwood1978). However, because log(N t) appears in both the x and y variables, such regressions can produce a spurious result due to sampling error (Southwood, Reference Southwood1978). Therefore, another test for density dependence, the functional regression (Smith, Reference Smith1973), was also used. This method calculates the functional relationship between the density of successive stages (log(N t+1) vs log(N t)), based on the assumption that the sampling errors in log(N t+1) and log(N t) will be similar. A functional regression coefficient (slope) that is significantly less than one suggests direct density dependence. The k-value regression tests were repeated using the ratio of the stage densities to tiller densities as log(N t/100 tillers) to investigate the effect of tiller availability on population regulation.
In addition, to ensure that the obtained density relationship is not attributed to a ‘spurious regression’, the Augmented Dickey-Fuller (ADF) test was conducted. Granger & Newbold (Reference Granger and Newbold1974) first introduced the notion of a ‘spurious regression’, which they argued produces statistically significant results between two non-stationary random-walk time series (i.e. two random time series plotted one against the other contain a trend). The ADF test assesses if each density is a non-stationary random-walk. The idea of a ‘spurious regression’ only becomes an issue if both densities in a regression are assessed as consisting of potentially non-stationary random-walk series.
Climate relationships
Relationships of k-values to six abiotic and resource variables were also tested. These were rainfall (mm), maximum and mean air temperatures (°C), minimum grass temperatures (°C) and number of ground frosts and average tiller density (tillers m−2). The tiller density and temperature variables affecting each life stage grouping were calculated as three-monthly means encompassing the month of peak abundance of the stage being tested and one month either side. Rainfall and frost were summed over the same periods. Stepwise linear regression was used to model each k-value against the logarithm of the early stage density on which it acts, as well as each of the six weather and resource variables.
Results
Key factors
Variation in the mortality of second summer generation fourth instar/prepupal larvae and pupae k pp,2 most closely followed variation in total mortality K (table 1, fig. 2). Regression of k-values on K confirmed k pp,2 as the key factor, as this gave a slope closest to unity, with a nearly significant 41% of the variation in R 9 explained by K (linear regression: k pp,2=−0.75+0.400 K, R 2=0.41, P=0.088). No secondary key factors were identified either visually or by regression although visually k f,1 could be interpreted as having an effect.

Fig. 2. k-factor analysis of Listronotus bonariensis at Lincoln, 1990–97. Refer to fig. 1 caption for stage mortality definitions.
Manly's (Reference Manly1977) key factor analysis also identified k pp,2 as the key factor, explaining 48% of the total variation in R 9 (table 2). The next largest contributor to total variation was second generation egg and early larval instar mortality k el,2. The importance of these two factors was confirmed by making them constant, which led to a 53% and 34% reduction, respectively, in the variation in R 9 (table 2). Variation in the number of fecund females at the start of each season did not contribute to the variation in the number of adults at the end of the season (table 2). The result from Podoler & Rogers’ (Reference Podoler and Rogers1975) method on the reduced dataset also identified k pp,2 as the key factor (table 3), although the second largest contributor in this method was first generation egg and early larval instar mortality k el,1 as opposed to k el,2.
Table 2. Summary of Manly's key factor analysis for L. bonariensis populations at Lincoln over six summer seasons (S=6). A i=variation in stage mortalities weighted by subsequent density dependence (equation 1) and var(R 9)=variation in the number of weevils entering the final stage.
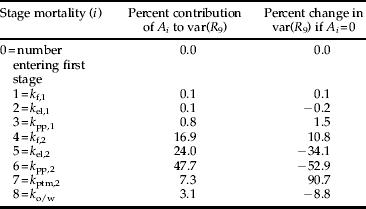
Table 3. Summary of Podoler & Rogers’ (Reference Podoler and Rogers1975) key factor analysis for L. bonariensis populations at Lincoln over six summer seasons (S=6).

Relationships with density and climate variables
Unrealised fecundity in first generation adults, k f,2, showed a positive relationship with density, indicating density dependence (linear regression: k f,2=−0.319+0.764 log(N t), R 2=0.49, df=5, P=0.048; fig. 3b); this relationship was improved by expressing density relative to tiller availability (linear regression: k f,2=0.887+0.809 log(N t/100 tillers), R 2=0.76, df=5, P=0.007). Using stepwise multiple regression, the influence of teneral weevil numbers and tiller density were found to be significant, with tiller density having a negative effect on unrealised fecundity whereas teneral density has a positive effect (k f,2=0.192–0.000136 tillers+0.843 log(N t), R 2=0.81, df=4, P=0.016). The functional regression test confirmed the direct density dependence in k f,2 (b=0.390, t=2.14, df=5, P=0.043), and the Manly key factor analysis suggested that this had the potential to regulate the population since removing the effect of this factor (by making it constant across seasons) led to an 11% increase in the variance of adult weevil density at the end of winter diapauses (table 2).

Fig. 3. Relationship of stage mortalities (expressed as k-values) with stage density. The data points circled in panel (c) are from 1990/91 and 1991/92 when the parasitoid M. hyperodae was not fully established. The k-value abbreviations are as in fig. 1 (×, 1st gen.; ●, 2nd gen.)
First generation prepupal stage (k pp,1) mortality was positively related to density (linear regression: k pp,1=−1.42+0.803 log(N t), R 2=0.50, df=6, P=0.031, fig. 3a; functional regression coefficient b=0.369, t=2.29, df=6, P=0.031), suggesting direct density dependence in this stage. The relationship was improved slightly by expressing density in relation to tillers (linear regression: k pp,1=−0.045+0.808 log(N t/100 tillers), R 2=0.55, df=6, P=0.021).
In the stepwise regression, however, tiller density was not significant, whereas larval density and maximum air temperature both showed positive influences on this mortality rate (k pp,1=−5.55+0.843 log(N t)+0.200 Max temp, R 2=0.83, df=5, P=0.005). Although k pp,1 was identified as being potentially density dependent using classical methods, the Manly key factor analysis suggested that this factor would have limited regulatory potential because if it was made constant there was little change in the variance of the number of weevils entering the final stage (table 2).
The Manly key factor analysis identified the factor with the greatest potential to regulate L. bonariensis populations as parasitism of second generation adults k ptm,2, since variation in adult density at the end of the season was predicted to increase by 90.7% if k ptm,2 was held constant (table 2). However, this result is very likely to be an artefact of the increasing levels of parasitism by M. hyperodae that occurred during the study. Figure 2c shows k ptm,2 values plotted against host density with the two lowest k-values (circled) occurring in the 1990/91 and 1991/92 seasons when the parasitoid was in its earliest establishment phases. These data increased the slope of the regression and led to an overestimation of the importance of k ptm,2 in modifying the variation in the earlier stages.
Mortality of first generation egg and early instar larvae k el,1 showed a negative relationship with minimum grass temperature (k el,1=2.89–0.611 Grass min temp, R 2=0.53, df=6, P=0.034), suggesting that cool spring conditions may hamper the survival of these early stages. Overwintering mortality showed no variation with density, and was constant at around 55% (k o/w≈0.35), except in the winter of 1995 when it was lower than usual (fig. 2d).
The results from the ADF tests indicated that none of the results presented above were attributed to a spurious regression.
Discussion
The results from this Canterbury dryland study indicate considerable divergence from the results gained from similar work in wetter and warmer Waikato dairy pastures (e.g. Barker et al., Reference Barker, Pottinger and Addison1989).
Key sources of mortality
In this study, second generation fourth instar mortality (k pp,2) (fig. 2, table 3) was identified as the key mortality factor. The reason for this mortality being so important for determining the densities of subsequent generations is not immediately apparent. However, these high mortality rates did coincide with the onset of autumnal conditions. The cooler weather could have arrested fourth instar/pupal development sufficiently for substantial mortality to have occurred during their resulting protracted developmental period. To this effect, it is notable that adult eclosion commences in early March and continues in low numbers until late June (Goldson et al., Reference Goldson, Proffitt and Baird1998a).
Although much smaller in terms of absolute mortality, the analysis suggested that another key contributor to total variation in mortality was second generation egg and early larval instar mortality k el,2 (table 2). This is consistent with the findings of Goldson (Reference Goldson1979, Reference Goldson1982), who found high mortality rates between the egg and larval stages relating to the need for the neonate first instars to burrow into the tillers before they desiccate. Once established, Goldson (Reference Goldson1979, Reference Goldson1982) found that larval mortality rates were thereafter low. It is, therefore, reasonable to assume that most of the mortality measured in this study occurred between the egg and first stage. In general, Goldson (Reference Goldson1982) found that this mortality was higher in the tougher tillers of L. perenne than L. multiflorum.
Density dependence
Unrealised fecundity
A major component of the unrealised fecundity observed in the overwintered populations (k f,1; fig. 1) was probably due to senescent overwintered female populations dying before laying their full egg complements. Similarly, unrealised fecundity observed in the first summer generation of weevils (k f,2) (fig. 3b) was probably largely caused by the onset of photoperiodically induced diapause in early March, again before they could lay their full complement of eggs (Goldson, Reference Goldson1981; Goldson et al., Reference Goldson, Proffitt and Baird1998a).
It is of interest that this loss of fecundity was density dependent. A significant positive relationship was found between density of the first summer generation weevil population and unrealised fecundity (k f,2) (fig. 3b). Likewise, a similar pattern was observed in the overwintered population between weevil density and unrealised fecundity (k f,1) (fig. 3b). Higher tiller densities tended to offset these unrealised fecundity effects.
It is possible that these field-recognisable density dependent effects were due to a spacing pheromone. In caged conditions, Goldson (Reference Goldson1981) found particularly strong evidence of ovipositional cessation and concomitant oocyte resorption. Barker et al. (Reference Barker, Pottinger and Addison1989), using potted ryegrass, also noted that L. bonariensis populations reduced per capita egg laying at high adult weevil densities. Similar experiments were conducted by Pilkington & Springett (Reference Pilkington and Springett1988), who suggested that the mechanism may be pheromonal. These workers noted that the proportion of weevil ovipositional holes plugged with frass increased with increasing weevil density and suggested that the pheromone was associated with the frass. Conversely, though, Barker et al. (Reference Barker, Pottinger and Addison1989) observed the opposite. Closer to the field environment, McNeill et al. (Reference McNeill, Baird and Goldson1998) used weevils confined in field plots and again found strong evidence for negative density dependent effects on egg-laying. That Prestidge et al. (Reference Prestidge, Barker and Pottinger1987) found a maximum of 3% multiple ovipositions per tiller and Barker et al. (Reference Barker, Pottinger and Addison1989) 6%, tends to support the Pilkington & Springett (Reference Pilkington and Springett1988) theory. Moreover, that tiller numbers were found to offset unrealised fecundity could well be the result of dilution of the effect of spacing pheromone, particularly if the effect is associated with the frequency of plugged (or unplugged) ovipositional holes.
Further work is required to clarify understanding of the changes in L. bonariensis oviposition behaviour and/or reproductive physiology as influenced by weevil density under field conditions. In terms of M. hyperodae biological control impact, interesting questions remain as to whether reduction in potential fecundity is in response to total adult weevils m−2 or just the unparasitised portion of the population. Should the latter apply, then potential population suppression through parasitoid-induced sterilisation and mortality of adult weevils could well be compensated for by increased reproductive effort by the unparasitised portion of the population. These questions are important subjects for future parasitoid impact analyses.
Egg to fourth instar mortality
The lack of any resource-based regulation of survival between the eggs to fourth instar stages in both generations (k el,1 and k el,2) in pasture with high densities of endophyte-free tillers (ca. 7000 m−2) (Goldson et al., Reference Goldson, Proffitt and Baird1998a) is to be expected. This is in marked contrast to Barker et al.’s Reference Barker, Pottinger and Addison(1989) Waikato study, which had far fewer endophyte-free tillers (<4000 m−2).
In their Canterbury survey, McNeill et al. (Reference McNeill, Proffitt, Barlow and Goldson2003) observed that even in Lolium perenne pasture with far lower numbers of endophyte-free tillers m−2 than in this study, they did not always exert population regulation. McNeill et al. (Reference McNeill, Proffitt, Barlow and Goldson2003) concluded that the effects of tiller resource limitation only became apparent when there were high weevil populations, reflecting some kind of non-linear density-dependent response. The Canterbury results, therefore, contrast with the Waikato finding of Barker et al. (Reference Barker, Pottinger and Addison1989) who found clear population regulation in varyingly endophytic dairy pasture with tiller densities of around ca. 4200 tillers m−2 (Barker et al., Reference Barker, Pottinger and Addison1984, Reference Barker, Prestidge and Pottinger1986).
In general, the results in this study and those of Barker et al. (Reference Barker, Pottinger and Addison1989) highlight the importance of pasture type and climate in L. bonariensis population regulation.
Density-dependent fourth instar mortality
First generation pre-pupal instar (k pp,1) (and pupal) mortality was positively related to density. This is difficult to explain as this mortality occurred at a time when pre-pupal fourth instar larvae had ceased to feed and emerge from the grass tillers before pupating in earthen cells. There is no evidence to suggest epizootics were the mechanism (Goldson, unpublished data). Moreover, although it was found that the relationship was improved slightly by expressing density in relation to tillers, it is most unlikely that resource limitation was an influence given that the cv. Manawa sheep pasture consisted of high densities of endophyte-free tillers (Goldson et al., Reference Goldson, Proffitt and Baird1998a). It is possible, however, that this density dependent effect was an artefact of the analytical method used. Although k pp,1 was identified as being potentially density dependent using Varley & Gradwell's (Reference Varley and Gradwell1960) method, the Manly key factor analysis suggested that this factor would have had limited regulatory potential (table 2). It is also significant that prepupal stage mortality was not related to density in the second generation (k pp,2) when larval densities were often higher and tiller densities were lower relative to those experienced by the first generation.
Overwintering mortality
Unlike populations from the Waikato (Barker et al., Reference Barker, Pottinger and Addison1989), L. bonariensis adults in Canterbury showed no evidence of any density dependent overwintering mortality. In fact, overwintering mortality was remarkably constant and relatively low at ca. 55%, compared to 85–96% measured in the Waikato (Barker & Pottinger, Reference Barker and Pottinger1982; Barker et al., Reference Barker, Pottinger and Addison1989). This tends to confirm the relative importance of disease between the two regions. The effect of these differences in overwintering mortality is apparent when considering the relative sizes of the subsequent first and second larval generations and the damage they cause. In Canterbury, at least in the absence of parasitism, first generation peaks were generally higher than the second (Goldson et al., Reference Goldson, Proffitt and Baird1998a), whereas in the Waikato the reverse was true with the second larval generation being the most damaging (Barker & Pottinger, Reference Barker and Pottinger1982).
Parasitoid effects
Although peripheral to the primary aim of this contribution, results suggest building impacts of parasitism on L. bonariensis population dynamics. This is consistent with the observation of Goldson et al. (Reference Goldson, Proffitt and Baird1998a), who found that the impact of parasitism considerably reduced the size of the first summer generation egg and larval peaks. The identification of the ecological factors determining M. hyperodae impacts on L. bonariensis would be informative for biological control theory and warrants further investigation.
Conclusion
This relatively long-term study has confirmed how important regional and plant cultivar differences can be in influencing the population dynamics of L. bonariensis. Canterbury pastures showed none of the resource-regulation of L. bonariensis populations identified in the Waikato.
A significant observation in this study is the inverse relationship between L. bonariensis adult populations and unrealised fecundity, possibly indicating a pheromonal spacing effect. This presents opportunity to advance theoretical insight into the interactions between parasitism and the mechanisms that lead to unrealised fecundity.
Acknowledgements
The authors thank their colleagues John Proffitt and Mark McNeill who collected and collated much of the data and freely shared their expertise. Thanks also to Dr Brian Manly of West Inc. for his advice on life table analysis.
The authors acknowledge the funding for this research via the New Zealand Foundation for Research, Science and Technology.








