Published online by Cambridge University Press: 09 February 2006
We propose a closed-form estimator for the linear GARCH(1,1) model.
The estimator has the advantage over the often used quasi-maximum
likelihood estimator (QMLE) that it can be easily implemented and does not
require the use of any numerical optimization procedures or the choice of
initial values of the conditional variance process. We derive the
asymptotic properties of the estimator, showing
T(κ−1)/κ-consistency for some κ
∈ (1,2) when the fourth moment exists and
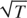 -asymptotic normality when the eighth moment exists. We
demonstrate that a finite number of Newton–Raphson iterations using
our estimator as starting point will yield asymptotically the same
distribution as the QMLE when the fourth moment exists. A simulation study
confirms our theoretical results.The first
author's research was supported by the Shoemaker Foundation. The
second author's research was supported by the Economic and Social
Science Research Council of the United Kingdom.
-asymptotic normality when the eighth moment exists. We
demonstrate that a finite number of Newton–Raphson iterations using
our estimator as starting point will yield asymptotically the same
distribution as the QMLE when the fourth moment exists. A simulation study
confirms our theoretical results.The first
author's research was supported by the Shoemaker Foundation. The
second author's research was supported by the Economic and Social
Science Research Council of the United Kingdom.
The estimation of the Bollerslev (1986) generalized autoregressive conditional heteroskedasticity (GARCH) model is often carried out using the quasi-maximum likelihood estimator (QMLE). The asymptotic properties of this estimator are by now well established (see Jeantheau, 1998; Lee and Hansen, 1994; Lumsdaine, 1996; Ling and McAleer, 2003), and its finite-sample properties have been examined through Monte Carlo studies (Fiorentini, Calzolari, and Panattoni, 1996; Lumsdaine, 1995). Recently, Giraitis and Robinson (2001) have proposed using the Whittle likelihood estimator, which exploits only the second-order properties of the series but does so in an optimal way. Unfortunately, the calculation of both these estimators requires the use of numerical optimization procedures because closed-form expressions are not available. Therefore, the resulting estimator depends on the implementation, with different optimization techniques leading to potentially different estimators. This has been demonstrated in the studies by Brooks, Burke, and Persand (2001) and McCullough and Renfro (1999) where different commercially available software packages were used to estimate GARCH models by quasi-maximum likelihood (QML). Both studies reported markedly different outputs across the various packages, reflecting the different initialization and algorithmic strategies employed.
We propose a simple estimator of the parameters in the GARCH(1,1) model based on the second-order properties of the series like Giraitis and Robinson (2001). We derive an autoregressive moving average (ARMA) representation of the squared GARCH process and use the implied autocovariance function to define closed-form estimators of the parameters of the GARCH model. This strategy has already been used in the literature on estimating standard ARMA models (see Tuan, 1979; Galbraith and Zinde-Walsh, 1994) and in ARFIMA models recently by Mayoral (2004). The ARMA representation of GARCH models was already noted by Bollerslev (1986), whereas Francq and Zakoïan (2000) and Gouriéroux and Jasiak (2001, p. 130) proposed to utilize this to obtain estimators of the parameters. However, the estimators of Francq and Zakoïan (2000) and Gouriéroux and Jasiak (2001) require numerical optimization. Baillie and Chung (2001) took a somewhat similar approach using a minimum distance estimator based on the autocorrelation function of the squared GARCH process; again, numerical optimization is required to obtain the actual estimator.
Our estimator can readily be implemented without using numerical optimization methods. Furthermore, the estimator does not require one to choose (arbitrary) initial values for the conditional variance process. In that sense, the proposed estimator is more robust compared to the aforementioned estimators. On the other hand, for the estimator to be consistent and asymptotically normally distributed, relatively strong assumptions about the moments of the GARCH process have to be made. Although consistency and asymptotic normality of the QMLE can be shown under virtually no moment restrictions of the GARCH process, we require fourth moments to obtain consistency and T(κ−1)/κ-convergence toward a so-called α-stable distribution with index κ ∈ (1,2), and eighth moments for

-asymptotic normality.
The

-asymptotic normality result when the eighth moment exists follows from standard central limit theorems because the asymptotic variance in this case is well defined. When the eighth moment does not exist, we are still able to show that a limiting distribution exists, but it does not have second moment, and the convergence rate is slowed down. The latter result is based on recent results by Mikosch and Stărică (2000). By combining our estimator with a finite-order Newton–Raphson (NR) procedure one can achieve

-asymptotic normality, and even full efficiency under Gaussianity of the rescaled errors, based on fourth moments.
We consider the GARCH(1,1) process given by


We assume that

, where

is the σ-field generated by {zt,zt−1,…}. We can write xt ≡ yt2 as

where εt = xt − σt2 is a martingale difference sequence with respect to

. From this expression, we see that xt is a (heteroskedastic) ARMA(1,1) process with parameters φ and θ. We shall throughout assume that φ < 1, implying that E [xt] < ∞ (cf. Bollerslev, 1988). We introduce the covariance function of the process

Assuming that {xt} is stationary with second moment, γ(·) is well defined. Using standard results, we then have that the autocorrelation function, ρ(k) = γ(k)/γ(0), solves the following set of Yule–Walker equations:


(cf. Harvey, 1993, Ch. 2, eqns. (4.13a) and (4.13b); these equations were also derived in Bollerslev, 1988, and He and Teräsvirta, 1999). We can express (4) as a quadratic equation in θ,

Observe that b is only well defined if φ ≠ ρ(1). It is easily checked that ρ(1) ≥ φ with equality if and only if φ2 = 1 or θ = 0. The first case is ruled out by our assumption that φ < 1, whereas in the following discussion we assume β > 0.1
If β = 0, ρ(1) = α, and we estimate α by the first-order sample correlation.

There is a second root that is reciprocal to the one stated here; however this has |θ| = β > 1, which is ruled out by φ < 1.2
This corresponds to the invertibility condition of the ARMA(1,1) model.

This last expression is utilized by Engle and Sheppard (2001) to profile out ω in their estimation procedure.
The expressions (4), (5), and (6) can now be used to obtain estimators of the parameters α, β, and ω. First, we can estimate φ by

, where

is the sample autocorrelation function of xt,

with


Substituting the estimator of φ into (5), we obtain an estimator of θ,

assuming that

. This leads to the following estimators of λ = (α,β,ω)[top ]:

In practice, this method may lead to

. To deal with this problem, the estimator can be Winsorized (censored) at zero and one or at ε and 1 − ε for small positive ε.
Note that

for any wj sequence with

so that a more general class of estimators can be defined based on this relationship. It can be expected that for a sufficiently general class of weights one can obtain the same efficiency as the Whittle estimator of Giraitis and Robinson (2001). We do not pursue this approach to achieving efficiency because a more standard approach is available; see the discussion that follows. Nevertheless, some smoothing of the ratio of autocorrelations based on (10) may be desirable in practice.
We derive the asymptotic properties of our estimator

under the following set of assumptions:
A.1. The error process {zt} is independent and identically distributed (i.i.d.) with marginal distribution given by a lower semicontinuous density with support

. It satisfies E [zt] = 0 and E [zt2] = 1.
A.2. The observed process {yt} is strictly stationary with E [(β + αzt2)2] < 1.
A.3. E [(β + αzt2)4] < 1.
Under (A.1), the moment condition in (A.2) is necessary and sufficient for the GARCH model to have a strictly stationary solution with a fourth moment. This solution will be β-mixing with geometrically decreasing mixing coefficients (cf. Meitz and Saikkonen, 2004, Thm. 1). We then assume that this is the one we have observed. Assumption (A.3) is a strengthening of (A.2) implying that also the eighth moment of yt exists.
In some of the results stated later, the i.i.d. assumption in (A.1) can be weakened to {zt} being a stationary martingale difference sequence; this is more realistic, allowing for dependence in the rescaled errors. In (A.2) we assume that we have observed the stationary version of the process. This is merely for technical convenience and can most likely be removed.
Under (A.1)–(A.2), we prove consistency of the estimator and derive its asymptotic distribution (toward which it converges with rate slower than T−1/2). If additionally (A.3) holds, the estimator is shown to be

-asymptotically normally distributed.
We first state a lemma that shows that the basic building blocks of our estimator are consistent and gives their asymptotic distribution. Under (A.2), E [yt4] < ∞, but the eighth moment does not necessarily exist. One can show for ARMA processes with homoskedastic errors that the sample autocorrelation function is asymptotically normally distributed with only a second moment of the errors. In our case however, the errors, εt, are heteroskedastic, and to obtain asymptotic normality the fourth moment, E [εt4] < ∞, seems to be needed; see, for example, Hannan and Heyde (1972) for results in both the homoskedastic and heteroskedastic cases. The fourth moment of εt translates into the eighth moment of yt.
The estimator

has a well-defined asymptotic distribution without requiring the eighth moment of the GARCH process to exist however, but the limit will not be Gaussian. This result has been established in Mikosch and Stărică (2000), see also Basrak, Davis, and Mikosch (2002) and Davis and Mikosch (1998). They show that

converges in distribution toward a so-called stable, regularly varying distribution with index κ ∈ (1,2); see Samorodnitsky and Taqqu (1994) and Resnick (1987) for an introduction. The index κ is shown to be the solution to E [(αzt2 + β)κ] = 1. The convergence takes place with rate TaT−1 where aT = T1/κl(T) and l(T) is a slowly varying function. The sequence aT satisfies TP(yt4 > aT) → 1, such that the index κ is a measure of the tail thickness.
LEMMA 1. Under (A.1)–(A.2), the estimators

in (7) and (8) satisfy

. Furthermore,

where

and

for some κ ∈ (1,2), where W(m) = (Zi − ρ(i)Z0)i=1,…,m and (Zi)i=0,…,m has a κ-stable distribution. If additionally (A.3) holds, then

where Vρ(m) is the m × m matrix given by

where Yt is an m × 1 vector with Yt,i = (yt2 − σ2)(yt+i2 − σ2), i = 1,…,m.
Mikosch and Stărică (2000) establish a weak convergence result without the fourth moment condition (A.2). But in this case, one does not have any consistency result because the law of large numbers does not hold. The preceding weak convergence result of

under (A.1)–(A.2) has the flaw that the limit distribution is not in explicit form, which makes it difficult in practice to carry out any inference.
The consistency results and the weak convergence results in (11) and (13) in the preceding lemma can be proved without the i.i.d. assumption on {zt} in (A.1) by using martingale limit theory. This can be done by utilizing the ARMA structure of {xt} and applying the results of Hannan and Heyde (1972). It is not clear whether the more general weak convergence result in (12) can be extended to a non-i.i.d. setting however.
Observe that our estimator of λ can be expressed in terms of

. A simple application of the continuous mapping theorem therefore yields the following result.
THEOREM 2. Under (A.1)–(A.2), the estimator

given in (9) is consistent,

, and

where W(2) and κ are as in Lemma 1 and the function D is given subsequently in equations (A.1)–(A.3). If additionally Assumption (A.3) holds, then


An estimator of the covariance matrix V in (16) can be obtained by first estimating Vσ2 and Vρ(2) using heteroskedasticity and autocorrelation consistent (HAC) variance estimators (see Robinson and Velasco, 1997) and then substituting

into ∂D(σ2,ρ(1),ρ(2))/∂(σ2,ρ(1),ρ(2)). One can alternatively use the analytic expressions of ρ(k) to obtain an estimator of Vσ2.
We here give a brief discussion of how one may improve on the efficiency of the closed-form estimator, in terms of both convergence rate and asymptotic variance. The basic idea is to perform a number of NR iterations using either the Whittle objective function or the Gaussian quasi-likelihood. Given closed-form estimates, one may wish to proceed to the QMLE or the Whittle estimator,3
Observe that the Whittle estimator proposed in Giraitis and Robinson (2001) in fact is the quasi-likelihood of the process {xt} assuming that it is Gaussian.

with the initial value being the closed-form estimator,

the criterion function.
4We here assume that

is invertible; Robinson (1988) discusses these issues in detail. Also, the step length is kept constant; it may however be a good idea in practice to use a line search in each iteration.

, one can show that

In general, the NR estimator will satisfy

where

is the actual M estimator (cf. Robinson, 1988, Thm. 2). Under regularity conditions, the M estimator will satisfy

where H = E [HT(λ0)] and Σ = E [ST(λ0)ST(λ0)[top ]] (see, e.g., Lee and Hansen, 1994, Thm. 2; Giraitis and Robinson, 2001, Thm. 1). Combining (18) and (19), we obtain the following result.
THEOREM 3. Assume that (19) holds together with (A.1)–(A.2). Then, with κ as in Lemma 1, for k ≥ 2 + [log(κ/2(κ − 1))/log(2)],

If additionally (A.3) is satisfied, the preceding result holds for k ≥ 1.
We now examine the quality of our estimator in finite sample through a Monte Carlo study. In particular, we are interested in its behavior when the fourth moment does not exist. We simulate the GARCH process given in (1)–(2) with zt ∼ i.i.d. N(0,1) for four different sets of parameter values. For each choice of parameter values, we simulated 5,000 data sets with T = 200, 400, 800, and 1,000 observations. For each data set, we obtained the QMLE using the Matlab GARCH Toolbox,
5The Matlab package uses a subspace trust region method based on the interior-reflective Newton method of Coleman and Li (1996).

, j = 1,2,3, and wj = 0, j > 3, and Winsorized at ε and 1 − ε with ε = 0.001. The GLS estimator reported here is based on two iterations. For the two first sets of parameter values, λ = (0.2, 0.15, 0.25)[top ] and λ = (0.2, 0.25, 0.35)[top ], both the fourth and eighth moments exist; for the third, λ = (0.2, 0.35, 0.45)[top ], only the fourth moment is well defined; and for the fourth, λ = (0.2, 0.10, 0.89)[top ], neither the fourth nor the eighth moment exists, but the second does.
The results in terms of bias, variance, and mean squared error (MSE) are reported in Tables 1, 2, 3, and 4 for the four different sets of parameters. For these results, we have discarded a small number of data sets (eight in total) where the Matlab GARCH Toolbox stalled and did not terminate the optimization procedure. We have also set the ARMA estimator equal to zero whenever it returned negative estimates.
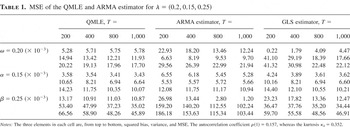
MSE of the QMLE and ARMA estimator for λ = (0.2, 0.15, 0.25)
MSE of the QMLE and ARMA estimator for λ = (0.2, 0.25, 0.35)

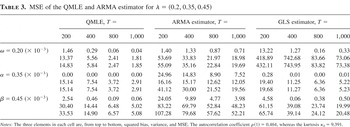
MSE of the QMLE and ARMA estimator for λ = (0.2, 0.35, 0.45)
MSE of the QMLE and ARMA estimator for λ = (0.2, 0.10, 0.89)

For the first set of parameters, the ARMA and GLS estimators are serious competitors to the QMLE. For small GARCH effects, the closed-form estimators seem to be a good alternative to the QMLE in terms of MSE. For the remaining three sets of parameters, the QMLE has significantly better performance compared to the two other estimators as expected. As α and/or β increases the variances of the ARMA and GLS estimators in general increase; this is consistent with the theory, which predicts that the convergence rate of the estimator deteriorates as α + β increases. However, contrary to the theory, it seems as if the ARMA estimator of α and β remains consistent even if the fourth moment is not well defined; the performance of the closed-form estimator of ω is very poor, though. The GLS estimator based on two iterations yields a large improvement in the precision relative to the initial ARMA estimator, except for the estimation of ω. The improvement might have been even more pronounced if we had done further iterations.
The procedure easily extends to the case where there is a mean process, say, yt = β[top ]xt + σt zt for some covariates xt, by applying the preceding process to the residuals from some preliminary fitting of the mean. Some aspects of the procedure extend to various multivariate cases and to GARCH(p,q). Specifically, in the multivariate case the relationships (3) and (6) continue to be useful and can be used as in Engle and Sheppard (2001) to reduce the dimensionality of the optimization space.
One may also consider other GARCH models that can be represented as an ARMA-like process. For example, suppose that the conditional variance is given as σt2 = ω + βσt−12 + αyt−121(yt−12 > 0) + δyt−121(yt−12 ≤ 0). Then for xt ≡ yt2 we have xt = ω + φxt−1 + ut, where ut is a martingale difference sequence with respect to

and φ = β + αm2+ + δm2−, where m2+ = E [zt21(zt > 0)] and m2− = E [zt21(zt ≤ 0)]. Furthermore, σ2 = ω/(1 − φ) so that we can identify ω and φ as before from the variance and the second-order covariance. To proceed further one needs to make strong assumptions about the distribution of zt, for example, symmetry about zero, in which case φ = β + (α + δ)/2.
Our estimator also allows for a simple t-test for no GARCH effect because the asymptotic distribution derived earlier does not require α,β > 0 in contrast to the QMLE, where the Taylor expansion used requires this.
Proof of Lemma 1. The consistency part is a simple application of the law of large numbers for stationary and ergodic processes because E [xt] < ∞ and E [xt xt+k] < ∞ under (A.1)–(A.2). The weak convergence result in (12) follows from Mikosch and Stărică (2000, Sec. 5).
The convergence results in (11) and (13) are proved using a standard central limit theorem for Markov chains that are strongly mixing with geometric rate (cf. Meyn and Tweedie, 1993, Thm. 17.0.1). It is easily seen that

for any s,t ≥ 0 and k > 0. Thus, the asymptotic covariance between

is zero. █
Proof of Theorem 2. We have that

, where D = (Dα,Dβ,Dω)[top ] is given by



with

and F(ρ(1),ρ(2)) = ρ(2)/ρ(1). It is easily seen that D is a continuously differentiable mapping of σ2, ρ(1), and ρ(2). The convergence result in (14) now follows from the continuous mapping theorem together with the fact that

is

-consistent whereas

converge at a slower rate. The convergence result stated in (15) follows from the standard result for differentiable transformations of asymptotically normally distributed variables. █

MSE of the QMLE and ARMA estimator for λ = (0.2, 0.15, 0.25)

MSE of the QMLE and ARMA estimator for λ = (0.2, 0.25, 0.35)

MSE of the QMLE and ARMA estimator for λ = (0.2, 0.35, 0.45)

MSE of the QMLE and ARMA estimator for λ = (0.2, 0.10, 0.89)