1. Introduction
Open access to natural resources, like water, fisheries, pastures and forests, is widespread in developing economies and often characterized by excessive exploitation of the resource (see, for instance, Baland and Platteau, Reference Baland and Platteau1996). Motivated by fiscal and environmental concerns, governments seek to restrict access to these resources. This is typically done by privatizing, that is by defining and enforcing exclusive property rights. Privatization does not necessarily imply individual property rights and, in the recent past, a competing trend has been to allocate to local communities the exclusive right to manage local natural resources like forest, fish and wildlife. The idea is that local communities are in a better position to monitor local resources and, hence, enforce property rights than the central government (Ostrom, Reference Ostrom1990).
From an efficiency point of view, privatization may be desirable. It is well known that open access leads to a ‘tragedy of the commons’, characterized by economic losses and environmental degradation. With well-defined property rights, profit maximizing behavior leads to the conservation of the resource and thereby improves economic efficiency. However, this comes at a distributive cost since, by excluding traditional users from their access to the resource, privatization necessarily hurts them. Samuelson (Reference Samuelson1974) and Weitzman (Reference Weitzman1974) demonstrate that, in the absence of redistribution, workers are always better off under an inefficient open access regime than under private property. This is because privatization restricts access to the resource, and thereby reduces the demand for labor and, hence, labor incomes. In the words of Weitzman (Reference Weitzman1974: 234) … there may be a good reason for propertyless variable factor units to be against efficiency improving moves toward marginalism like the introduction of property rights or tolls unless they get a specific kickback in one form or another. One type of ‘kickback’ is ownership shares: it is clear that if given adequate property rights, traditional users may indeed benefit from privatization (see, e.g., Roemer and Sylvestre, Reference Roemer and Sylvestre1993).
In this paper we demonstrate that, in the context of renewable resources, privatization necessarily increases employment in the long run, which is positive for labor. This effect is based on the conservation efforts by the private owner, which lead to a larger future stock of the resource. Conservation implies a short-term reduction but a long-term increase in labor demand. This increase may be large enough for privatization to be Pareto-improving: traditional users may gain from being excluded from access to the resource, even when they do not receive any direct compensation for this exclusion. These gains are larger the larger is the initial stock of the resource or its growth rate.
With the exception of Hartwick (Reference Hartwick1980), the literature has largely ignored the dynamic impact of privatization in the case of renewable resources, and has thereby overlooked its long-run conservation properties. Hartwick (Reference Hartwick1980) focused exclusively on the dynamic externality and showed that open access was associated with less conservation and lower long-run stocks of the resource than private property. He did not, however, investigate the employment and income implications of the different property regimes, which are the focus of the present paper.Footnote 1 Other contributions, keeping with the traditional, static approach of the open access resources, have extended Weitzman's framework. For instance, de Meza and Gould (Reference de Meza and Gould1985) show that when the commons consist of different resources, privatization can increase employment on some of them, even though total employment must fall. In another paper, de Meza and Gould (Reference de Meza and Gould1987) demonstrate that, if multiple inputs are simultaneously used on the commons, the welfare of traditional users may go up. For example, a well-managed pasture may increase the value of the cattle so much that cattle owners benefit from the privatization of the commons, even though they lost their free access to it. In a similar vein, Brito et al. (Reference Brito, Intriligator and Sheshinski1997) investigate the case where labor supplied to the resource is not uniformly productive, and show that, under some conditions, labor returns may again rise. Finally, Baland and Francois (Reference Baland and Francois2005) show that open access may protect poor people against adverse income shocks, a property which may be hard to replicate with a privatized resource in the presence of information problems.
To illustrate the potential benefits of restricted access, consider the case of the island of Hispaniola (Diamond, Reference Diamond2005). The two countries that share this island, Haiti and the Dominican Republic, have experienced radical differences in both economic and ecological performance. Despite the geographical and historical similarity between the two countries, per capita income is five times higher in the Dominican Republic than in Haiti. Ecologically, there are also sharp differences, with 28 per cent of the Dominican Republic being forested, compared to only 1 per cent in Haiti. The remaining forests of Haiti are also continuously being threatened by the demand for charcoal.
In Haiti, weak formal institutions and short-sighted policies have led to a de facto open access to the forests, resulting in a tragedy of the commons. Deforestation has caused severe soil erosion and is seen as the primary cause of the decline in agricultural productivity in the country. Given the importance of agriculture as a source of employment, this environmental disaster has important economic consequences for large parts of the Haitian population.Footnote 2 In contrast, the Dominican Republic has for a long time had a top-down approach to environmental management, launched under the Trujillo era (1930–61). Trujillo took control over the forests and was personally involved in the forest industry. In the process, he expanded national parks and enforced forest protection, curbing wasteful practices of indiscriminate logging and burning, and prohibiting people from free access to forests. In the long run, this policy contributed to higher income levels in the population and a sounder ecology.
Relatedly, the recent wave of devolution policies directly promoting community management of local resources is often perceived as directly benefitting traditional users by giving them well-defined ownership rights while improving the management of the resource. In practice, however, improved conservation does not always translate into direct benefits for the traditional users of the resource. Thus, in an overview of community management practices in Africa, Roe et al., (Reference Roe, Nelson and Sandbrook2009) describe frequent instances of elite capture. For instance, in a process of decentralization in Mali, the newly established regional fishing councils became dominated by local fishing chiefs who monopolized decisions about the management of the resource and the distribution of the rents. Similarly, in Kenya, the Group Ranch structure of land and resource management has been captured by local elites who rewarded themselves by appropriating land and revenues, thereby effectively converting communal property to individual property. Our argument is that, even when communal resource management initiatives are captured by local elites, these policies can still generate long-term benefits to the poorer parts of the population.
The paper is organized as follows. Section 2 presents the model, starting with the equilibrium under open access and then moving on to the privatized arrangement. Section 3 contains the analysis, comparing labor income under the two property regimes. Section 4 discusses the robustness of our results. Section 5 concludes.
2. The model
We consider an economy composed of two sectors: a resource extracting sector and another sector. The production technology in the resource sector is such that, in period t, the value of the marginal productivity of labor is equal to 1 if the number of workers l t does not exceed the existing stock of the resource R t. Otherwise, the marginal productivity of labor falls to zero and the resource is exhausted.
There are two periods. The amount of the resource which has not been harvested in period 1 grows at a given rate g, so that the available stock of resource in period 2, R 2, is given by:
$$R_{2}=\max \lsqb 0\comma \; \lpar 1+g\rpar \lpar R_{1}-l_{1}\rpar \rsqb \comma \;$$where R 2 is equal to zero if l 1 ≥ R 1.
Total labor endowment in the economy is normalized to 1. When not employed in the resource sector, workers find employment in the other sector, where they earn a wage rate given by:
$$w_{t}=f\lpar 1-l_{t}\rpar =w\lpar l_{t}\rpar \comma \;$$With w ′ > 0.Footnote 3 For the sake of simplicity, we assume that w(0) = 0. We also assume that, if all workers are employed in the resource sector, the wage rate in the alternative sector is greater than one: w(1) > 1. This implies that, in equilibrium, the resource sector does not absorb all workers in the economy. In this way, we abstract from corner solutions in the labor market, while still keeping open possible corner solutions in the extraction of resources (i.e., the possibility of full depletion in the short run).
The starting point of our analysis is the tragedy of the commons associated with open access. Now, for the tragedy of the commons to apply, two assumptions must hold. First, depletion of the resource in the first period must be inefficient. This implies that second-period income must be sufficiently important. Letting δ > 0 denote the discount factor, this condition can be written as δ(1 + g) > 1. Second, the resource must be depleted in the second period. Otherwise there would be no scarcity, and hence no reason for conservation. This implies that the resource cannot provide productive employment for all workers over the two periods: 
$R_{1}\lt 1+{1\over 1+g}.$ Under these two assumptions, the economy we consider here is one where the resource is not overly abundant and where the future is sufficiently important to make conservation desirable for society.
We first analyze resource allocation and labor income prevailing under open access to the resource before turning to the situation under private property.
2.1. Open access
Under open access, income from the resource is shared equally among the workers in that sector. There are two possible cases, depending on whether the resource is fully depleted in the first period (the ‘scarcity case’) or not (the ‘abundance case’).
In the case of scarcity (which we refer to by the subscript a), w(R 1) < 1. As long as l 1 < R 1, the marginal productivity of labor in the resource sector exceeds returns to labor in the alternative occupation. As a result, the equilibrium number of resource sector workers under open access, l O1a, is greater than R 1. The first-period labor market equilibrium is then given by:
$${R_{1}\over {l_{1a}^{O}}}=w\lpar l_{1a}^{O}\rpar \comma \;$$where l O1a represents the equilibrium level of employment in the resource sector and w(l O1a) the associated wage under open access. The resource is fully exhausted in the first period and all workers are employed in the alternative sector in period 2. The present value of total labor income over the two periods is given by:
$$I_{a}^{O}=w\lpar l_{1a}^{O}\rpar +\delta w\lpar 0\rpar ={R_{1}\over{l_{1a}^{O}}}.$$The abundance case (referred to by the subscript b) is characterized by w(R 1) ≥ 1. In this case, the resource is not depleted during the first period. The amount of resources available for period 2 is given by R 2 = (R 1 − l 1bO)(1 + g) and the period 2 interior labor market equilibrium can be written:
$${R_{2}\over{l_{2b}^{O}}}=w\lpar l_{2b}^{O}\rpar .$$The present value of total labor income in this scenario, indicated by subscript b, is given by:
$$I_{b}^{O}=1+\delta w\lpar l_{2b}^{O}\rpar =1+ \delta {R_{2}\over {l_{2b}^{O}}}.$$Figure 1 illustrates the first-period labor market equilibrium under open access, with two different levels of initial resource wealth, R 1a and R 1b. Since w(R 1a) < 1, the situation with R 1a is a case of relative scarcity, resulting in equilibrium resource sector employment l 1aO and wages w a. Since l 1aO > R 1a, the resource is completely depleted in period 1. In contrast, with R 1b there is relative abundance, since w(R 1b) > 1. Resource sector employment is now given by l 1bO with corresponding wages given by w b =1. Since l 1bO < R 1b, the resource is not completely depleted.
Figure 1. First-period open access labor market equilibrium.
There are two different sources of inefficiency under open access. Weitzman (Reference Weitzman1974) and Samuelson (Reference Samuelson1974) focused on the static inefficiency. This inefficiency is due to employment sharing in the resource sector which involves crowding externalities, and is captured here by the fact that the marginal productivity of some workers in an interior equilibrium is equal to zero. Our model however highlights another, dynamic, externality: traditional users do not internalize the impact of their harvesting decisions on the future stock of the resource. As a result, open access leads to the overexploitation of the resource in the first period and destroys long-term employment opportunities in that sector. Both the static and the dynamic externality lead to the overexploitation of the resource. This fact is most obvious under scarcity, where the resource is fully depleted in period 1.
2.2. Private ownership
Under private ownership, resource owners decide on the number of workers to hire in period 1, l 1, and period 2, l 2, so as to maximize profits. To simplify the exposition, we refer here to a situation where exclusive property rights over the resource have been given to a single owner over the two periods. The owner behaves competitively on the labor and the product markets. In particular, we do not consider here the possibility of monopsony on the labor market, an issue to which we shall return in section 4. In the absence of market power, the aggregate extraction and employment paths do not depend on the number of private owners of the resource.
The present value of profits is given by:
$$\pi =\lpar 1-w_{1}\rpar l_{1}+\delta \lpar 1-w_{2}\rpar l_{2}\comma \;$$where l 2 = (1 + g)(R 1 − l 1), which expresses the fact that the dynamic externality is explicitly taken into account by the resource owner. Maximizing profits with respect to l 1, while taking w 1 and w 2 as given, yields the following first-order condition for an interior solution:
$$1-w_{1}=\delta \lpar 1+g\rpar \lpar 1-w_{2}\rpar .$$As wages depend on resource employment by equation (2), (8) implicitly defines an equilibrium employment and extraction profile over time. Let l 1P and l 2P = (1 + g)(R 1 − l 1p) be the equilibrium levels of employment in the privatized resource sector in the first and second periods, respectively. Equation (8) can be written as follows:
$$1-w\lpar l_{1}^{P}\rpar =\delta \lpar 1+g\rpar \lpar 1-w\lpar \lpar 1+g\rpar \lpar R_{1}-l_{1}^{P}\rpar \rpar .$$Note that both l 1P and l 2P are increasing in R 1: a larger initial resource stock implies more employment and hence higher wages in both periods. The present value of total labor income with an interior equilibrium is given by:
$$I^{P}=w\lpar l_{1}^{P}\rpar +\delta w\lpar \lpar 1+g\rpar \lpar R_{1}-l_{1}^{P}\rpar \rpar \comma \;$$where the first and the second term on the RHS of the equation represent labor incomes in the first and the second period, respectively.
It is also possible that, if the biological growth rate of the resource is sufficiently high, private owners will choose full preservation of the resource in period 1. This defines a corner solution where the optimal level of first-period employment in the resource sector, denoted by l 1P, is equal to zero, and the second-period employment is given by l 2P = (1 + g) R 1. In this case, we can rewrite equation (8) as follows:
$$1-w\lpar 0\rpar \leq \delta \lpar 1+g\rpar \lpar 1-w\lpar \lpar 1+g\rpar R_{1}\rpar \rpar .$$
When holding with equality, the above expression defines a threshold level of initial resources, 
$\overline{R}_{1}=\overline{R}\lpar g\comma \; \delta\rpar $, such that for all levels of 
$R_{1}\leq \overline{R}_{1}$, profit maximization involves full preservation of the resource in period 1. The sign of 
$\bar{R}_{g}^{\prime}$ cannot be determined a priori, as a rise in g increases both the amount of resources in the second period, but also the cost of harvesting these resources.
3. Open access vs. private property
We first present the consequences of privatization for the level of employment and the wage rates.Footnote 4 We find that:
Proposition 1
The first-period wages are strictly lower under private ownership than under open access.
Proof: When the resource is scarce, w(R 1) < 1, there is full depletion of the resource under open access. In contrast, private owners will necessarily conserve part of the resource for the second period. This implies that first-period resource sector employment is higher under open access than under private ownership, and given w ′(l) > 0, that the first-period wages are lower under private ownership. In the case of abundance, i.e., w(R 1) ≥ 1, the resource is not fully depleted under open access. In this case, the first-period wage under open access is given by unity, w(l 1bO) = 1. From (9) we observe that for δ > 0, then w(l 1P) < 1, so that first-period wages under private ownership are also lower than under open access.
This observation is in accordance with the classic result by Weitzman (Reference Weitzman1974): unless adequately compensated, traditional users lose from privatization. The key insight from the present paper, however, relates to the dynamic benefits of privatization:
Proposition 2
The second-period wages are strictly higher under private ownership than under open access.
Proof: This follows immediately from Proposition 1: in the scarcity scenario, the resource is fully exhausted in the first period under open access, leading to no resource sector employment and hence a zero wage in period 2, while profit maximizing owners always preserve some resource for the future, thereby generating a demand for resource sector employment and positive wages. In the abundance scenario, there is necessarily more preservation under private ownership than under open access, so that second-period resource employment and therefore wages are higher under private ownership.
As an example, consider g = 0 and δ = 1. Under private property, cost minimization yields a balanced extraction path over time: 
$l_{1}^{P}=l_{2}^{P}={1\over 2}R_{1}$. A positive growth rate further increases conservation, implying 
$l_{2}^{P}\gt l_{1}^{P}.$ This is in sharp contrast the situation prevailing under open access, where employment on the resource is necessarily larger during the first period.
These two propositions illustrate the major trade-off regarding labor incomes when privatization is considered. As shown by Weitzman (Reference Weitzman1974), privatization of an open access resource reduces employment and income in the first period, by eliminating overcrowding on the resource. However, privatization also preserves the resource for future exploitation, which increases income and employment in the second period. The net effect is in general indeterminate, and depends on the initial stock of the resource and its growth rate.
To make more precise statements when comparing labor incomes across the two property regimes, we need an additional assumption about the wage function. This is due to the fact that, depending on the shape of the wage function, a (small) reduction in period 1 employment may have a relatively small or a large effect on wages in period 2.Footnote 5 For simplicity, we assume that the function w(l t) is linear: w(l t) = al t. This assumption makes it more likely for open access to generate higher present value labor income than a strictly concave wage function. Under this assumption, when the growth rate or the initial stock of the resource is low, labor incomes are larger under open access. The income, sharing properties of open access dominate in this case. By contrast, if the growth rate or the initial stock are high enough, labor incomes are larger under private property because of the resource preservation impact of privatization. We have:
Proposition 3
For a given value of g, there always exists 
$R_{1}^{\ast}\lpar g\rpar >0$, with 
$R_{1}^{\ast}\prime \lt 0$, such that 
$I^{P}\gtreqless I^{O}$ iff 
$R_{1}\gtreqless R_{1}^{\ast}$. Conversely, for any given level of the resource 
$0 \lt R_{1} \lt {1\over a}$, there always exists 
$g^{\ast}\lpar R_{1}\rpar \gt 0$, with 
$g^{\ast}\prime \lt 0$, such that 
$I^{P}\gtreqless I^{O}$ iff 
$g\gtreqless g^{\ast}$. If 
$R_{1}\geq {1\over a}$, I P > I O for all values of g.
Proof: See Appendix B.
Figure 2 provides a graphical illustration of Proposition 3. The resource growth rate is measured on the horizontal axis, and the initial resource stock on the vertical axis. The level ρ1 denotes the threshold level of initial resources below which privatization leads to full conservation in period 1, and above which there is resource extraction in both periods. ρ2 and ρ3 show the threshold level of initial resources at which I O = I P, in the former case when privatization is associated with an interior solution (i.e., l 1P,l 2P > 0) and in the latter case when privatization is associated with a corner solution (i.e., l 1P = 0,l 2P > 0). The letter ‘P’ and the letter ‘O’ indicate the areas where labor incomes are higher under private ownership and open access, respectively.Footnote 6
Figure 2. Private ownership vs open access.
Even when denied any ownership rights on the resource, traditional users prefer privatization if g or R 1 is sufficiently large, that is, when the potential of resource preservation for future employment creation is important. Moreover, the range of initial endowments for which private ownership Pareto-dominates open access increases with g. Conversely, when R 1 and g are small, privatization lowers the incomes of the traditional users, unless they are also given a large enough share of the property rights.
An increase in a shifts the ρ2 and ρ3 curves downward, making private ownership even more attractive for traditional users: when wages are more responsive to employment in the resource sector, the increase in employment caused by privatization leads to larger rises in their incomes.
4. Discussion
Privatization of a natural resource often consists of transferring property rights to a single owner, typically a semi-private or a state company. Where the resource is concentrated, this may involve a dominant position on the local labor market, which affects employment negatively. It is therefore important to discuss the consequences of privatization when the private owner exercises some market power on the labor market. To simplify the discussion, we again assume that w t = al t, and let a = 1. Moreover, we also assume that g = 1, and examine the cases of a monopsony and of a duopsony.
Under a monopsony, the employer internalizes the fact that the wage rate varies with the demand for labor. Using the fact that, in equilibrium, l 2 = (1 + g) (a(R − l 1)), the profit function of the monopsonist, indicated by superscript m, can be written as:
$$\pi^{m}=\lpar 1-al_{1}\rpar l_{1}+\delta \lpar 1-\lpar 1+g\rpar \lpar a\lpar R-l_{1}\rpar \rpar \rpar \lpar R_{1}-l_{1}\rpar .$$Maximizing with respect to l 1, and using a = 1, and g = 1, we find that the optimal level of period 1 employment (l 1Pm) is:
$$l_{1}^{Pm}={4R\delta +1-\delta \over 2\lpar 1+2\delta\rpar }.$$We consider now a duopsony between two identical firms a and b, indicated by superscript d. The objective function of firm i = A, B is given by:
$$\pi_{i}^{d}=\lpar 1-a\lpar l_{1}\rpar \rpar l_{1i}+\delta \lpar 1-a\lpar 1+g\rpar \lpar \lpar R_{1}-l_{1}\rpar \rpar \rpar \lpar R_{1}-l_{1i}\rpar \comma \;$$where R i is the resource endowment of firm i, with R 1 = R 1A + R 1B, and where l 1i is period 1 employment by firm i, with l 1 = l 1A + l 1B. Using the same steps as above, total period 1 resource sector employment in the symmetric Nash equilibrium is given by:
$$l_{1}^{Pd}={12R\delta +2\lpar 1-\delta\rpar \over 3\lpar 1+2\delta\rpar }.$$Finally, using equation (9) and under the same assumptions, employment under perfect competition is given by:
$$l_{1}^{P}={{4R_{1}\delta +1- 2\delta}\over{1+4\delta}}>0.$$Figure 3 illustrates how the level of employment in the resource sector in period 1 and, hence, the time profile of resource extraction, depends on market power, in the (R 1, δ) space. The condition that conservation is efficient implies that l 1P <R 1. The curve μ3 shows the combinations of R 1 and δ where l 1P = R 1.Footnote 7 To the left of μ3, l 1P = R 1, and we therefore ignore that part of the picture, corresponding to the area denoted by (i). To the right of the μ4-curve there is full conservation under perfect competition, implying that l 1P = 0.
Figure 3. Monopsony power and resource extraction.
The curve μ1 represents the combinations of R 1 and δ where first-period employment is identical under perfect competition and monopsony, i.e., l 1P = l 1Pm. To the left of μ1, l 1P > l 1Pm, meaning that there is more conservation under monopsonistic ownership than under atomistic ownership. Intuitively, areas (iv) and (v) are characterized by relatively high discount rates (low δ), and atomistic owners extract a relatively large share of the resource in period 1. This drives up the extraction costs today, leaving future extraction costs relatively low. The monopsonistic owner internalizes this effect on wages and chooses a more balanced extraction profile by reducing employment in the first period. By contrast, to the right of μ1 (areas (ii) and (iii)), discount rates are lower, and perfect competition involves a substantial amount of conservation, which drives up wages in period 2. The monopsonist then chooses to extract more of the resource today so as to keep labor costs lower in the future. In this case, therefore, l 1P < l 1Pm.
The curve μ2 represents the combinations of R 1 and δ where first-period employment is identical under perfect competition and duopsony, i.e., l 1P = l 1Pd. To the left of μ2, l 1P > l 1Pd, implying that conservation is higher under duopsony while the opposite holds to the right of μ2. The mechanisms at work are the same as those discussed when comparing perfect competition and monopsony.
We have only considered an open access situation, in the sense that traditional users simply equate the current income they derive from the resource (i.e., their average productivity) to the opportunity cost of labor. As has been documented by Ostrom (Reference Ostrom1990) and Baland and Platteau (Reference Baland and Platteau1996), traditional communities are often able to implement a number of rules to preserve the resource, typically by restricting access to their members or imposing better management practices. In these circumstances, ‘common property’ involves a more efficient pattern of use than open access, resulting in larger incomes for the traditional users. The case for privatization is then less clear as the set of circumstances under which privatization raises their incomes is much more restricted. Also, we have assumed that privatization involves secure property rights in the future. In many circumstances, however, future rights to the resource are not perfectly guaranteed, which prompts current owners to overexploit the resource. This again reduces the case for privatization.Footnote 8
Finally, we have considered in this paper a two-period model. This choice was made for simplicity, and in the appendix we provide an infinite horizon version of the model, in which corresponding results can be derived. Interestingly, private owners always preserve some of the resource and thereby provide positive employment in all periods. It follows that, for any initial resource stock, there always exists a positive discount rate below which private property Pareto-dominates common property.
5. Concluding remarks
Privatization typically restricts access to resources that have traditionally been freely available to local communities. While there are strong efficiency arguments in favor of restricting access and enforcing clearly defined property rights, changes in property regimes may have negative distributional implications. In particular, it has been shown in a static framework that, without adequate compensation, employment and labor incomes from the resource necessarily fall.
In the present paper, we focus on renewable resources and investigate the distributive impact of privatization in a dynamic perspective. We demonstrate that, since private owners preserve the resource, employment rises in the long run but falls in the short run. When the initial stock of the resource or its growth rate are large enough, the long-run effect dominates, which leads to an increase in total employment and labor incomes. In these circumstances, privatization not only leads to efficiency gains, but also benefits the traditional users of the resource. The arguments in favor of privatization are less relevant if it implies the creation of a monopsony on the local labor market, if future property rights are uncertain, if discount rates are high or if traditional communities already enforce sustainable practices in the use of the resource.
Appendix A: An infinite horizon extension
In an infinite horizon framework, profit maximization implies:
$$1-w_{t}=\delta \lpar 1+g\rpar \lpar 1-w_{t+1}\rpar$$where δ represents the discount factor and t the time period. As in the two-period model, the technology in the alternative occupation is such that w t = al t. For the sake of notation, we also assume that a = 1, so that equation (A.1) can be rewritten as:
$$1-l_{t}^{P}=\delta \lpar 1+g\rpar \lpar 1-l_{t+1}^{P}\rpar$$which can be expressed as:
$$l_{t+1}^{P}=1+b^{t}\lpar l_{1}^{P}-1\rpar$$
where 
$b={1\over \delta \lpar 1+g\rpar }.$
In this appendix, we shall focus on the case where 
$R_{1}\leq {1+g \over g}$. The extension to large endowments in the resource follow easily at the cost of notational complexity. The biological process of growth of the resource stock, R t, is such that:
$$R_{t+1}=\lpar 1+g\rpar \lpar R_{t}-l_{t}\rpar .$$Combining the two last equations, we obtain:
$$1-R_{t}+{R_{t+1}\over {1+g}}=\delta \lpar 1+g\rpar \left(1-R_{t+1}+{R_{t+2}\over{1+g}}\right)$$or:
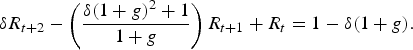$$\delta R_{t+2}-\left({\delta \lpar 1+g\rpar ^{2}+1\over{1+g}}\right)R_{t+1}+R_{t}=1-\delta \lpar 1+g\rpar .$$The solution to this differential equation is given by:
$$R_{t}={C_{1}\over \delta^{t}\lpar 1+g\rpar ^{t}}+C_{2}\lpar 1+g\rpar ^{t}+{1+g \over g}\comma \;$$
where C 1 and C 2 are constants. By the transversality condition, 
${lim}_{t\rightarrow \infty} \delta^{t}\lambda^{t}R_{t}=0$, where 
$\lambda_{t}={\lambda_{0}\over \delta^{t}\lpar 1+g\rpar ^{t}}\comma \; $ is the shadow price derived from the analogous Lagrangean problem (with λ0 > 0). It follows that C 1 = 0 and 
$C_{2}= R_{1}-{1+g \over g}.$ Hence,
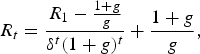$$R_{t}={R_{1}-{1+g \over g}\over \delta^{t}\lpar 1+g\rpar ^{t}}+{1+g \over g}\comma \;$$or, using equation (A.3):
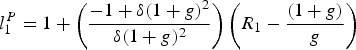$$l_{1}^{P}=1+\left({-1+\delta \lpar 1+g\rpar ^{2}\over {\delta \lpar 1+g\rpar ^{2}}}\right)\left(R_{1}-{\lpar 1+g\rpar \over g}\right)$$which describes the optimal extraction path in the first period.
The present value of labor income in the privatized regime is equal to:
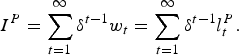$$I^{P}=\sum_{t=1}^{\infty}\delta^{t-1}w_{t}=\sum_{t=1}^{\infty}\delta^{t-1}l_{t}^{P}.$$Using equations (A.3) and (A.5) and rearranging terms, we obtain:
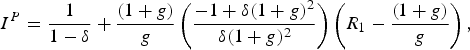$$I^{P}={1\over {1-\delta}}+{\lpar 1+g\rpar \over g}\left({-1+\delta \lpar 1+g\rpar ^{2}\over {\delta \lpar 1+g\rpar ^{2}}}\right)\left(R_{1}-{\lpar 1+g\rpar \over{g}}\right)\comma \;$$while the present value of labor income under the commons is equal to
$$I^{O}=\sqrt{R_{1}}.$$The impact of privatization on labor income can then directly be obtained by comparing I P and I O given in the last two expressions. Again, one can easily see that I P > I O if R 1 is close to one, the growth rate of the resource is large or the discount factor is close to one (i.e., if the discount rate is sufficiently low).
Appendix B: Proof of Proposition 3
First, consider the interior solution under private property. With w(l t) = al t and for simplicity assuming δ = 1, total labor income is given by:
$$I^{P}=al_{1}^{P}+a\lpar 1+g\rpar \lpar R_{1}-l_{1}^{P}\rpar$$where
$$l_{1}^{P}={{aR_{1}\lpar g+1\rpar ^{2}-g}\over{a\lpar \lpar g+1\rpar ^{2}+1\rpar }}.$$The point at which l 1P is exactly equal to zero defines the function ρ1(g) such that, for all R 1 < ρ1(g), profit maximisation involves a corner solution. Setting l 1P = 0 in equation (A.10), we obtain:
$$\rho_{1}\lpar g\rpar ={g\over a\lpar g+1\rpar ^{2}}.$$ρ1(g) is maximized at g = 1, with ρ1(1) = 1/4a.
We first consider values of R 1 : R 1 > 1/4a, so that profit maximization always involves positive levels of employment in both periods, with income defined by equation (A.9). Under open access, total income is given by:
$$I^{O}=al^{O}=\sqrt{aR_{1}}.$$Setting I P = I O and using equations (A.12) and (A.9), we obtain, after some algebraic manipulations,
$$\rho_{2}\lpar g\rpar ={{8g+4g^{2}-2g^{3}-g^{4}+4+\lpar 2\lpar 1+g\rpar +g^{2}\rpar \sqrt{8g-8g^{3}-3g^{4}+4}}\over{2a\lpar g+2\rpar ^{2}\lpar g+1\rpar ^{2}}}$$such that I P < I O for R < ρ2(g), corresponding to area (i) in figure 2, and I P > I O for R 1 > ρ2(g), corresponding to area (ii) in the figure. The function ρ2(g) is strictly decreasing in g, with ρ2(0) = 1/a and ρ2(1) = 1/4a.
We now consider R 1 < 1/4a, for which corner solutions under private property are possible. Using the critical level of resource ρ1(g) defined in equation (A.11), we know that, for R 1 ≤ ρ1(g), l 1P = 0 and I P = a(1 + g) R 1. Consider first the values of g: g < 1 and R 1 ≤ ρ1(g), corresponding to area (iii) in figure 2. Comparing income levels under the two property regimes, we obtain:
$$I^{P}\geq I^{O}\ {\rm if}\ a\lpar 1+g\rpar R_{1}\geq \sqrt{aR_{1}}\Longleftrightarrow R_{1}\geq {1\over a\lpar 1+g\rpar ^{2}}.$$
Since g < 1 and 
$R_{1}\leq {{g}\over{a\lpar g+1\rpar ^{2}}}$, the latter condition is never satisfied, and I P < I O. For the values of R 1: 1/4a > R 1 > ρ1(g), an interior solution prevails under private property. However, as ρ2(g) > 1/4a for these values of g, I P < I O, see area (iv) in figure 2.
We now turn to the values of g:g ≥ 1. For R 1 ≤ ρ1(g), the corner solution prevails, and
$$I^{P}=I^{O}\Longleftrightarrow R_{1}={1\over a\lpar 1+g\rpar ^{2}}.$$
Note first that the level R 1 defined in the latter expression is lower than ρ1(g) for all values of g ≥ 1. The expression in equation (A.13) defines a function ρ3(g), such that, for all R 1 < ρ3(g), I P < I O, corresponding to area (v) in figure 2. For ρ3(g) < R 1≤ ρ1(g), I P > I O, see area (vi). Moreover, for R 1 > ρ1(g), the interior solution prevails, and it is easy to check that I P > I O. The function ρ3(g) is strictly decreasing, with ρ3(1) = 1/4a, and 
$lim_{g\rightarrow \infty}\rho_{3}\lpar g\rpar =0$.
Given that ρ3(1) = ρ2(1), we have therefore defined for all the values of g a function R(g), with R(g) = ρ2(g) for g < 1 and R(g) = ρ3(g) for g ≥ 1, which is continuous and strictly decreasing, and such that 
$I^{P}\gtrless I^{O}\Longleftrightarrow R_{1}\gtrless R\lpar g\rpar $. Proposition 3 follows.
Appendix C
This appendix provides the formal results behind the discussion of market power in section 4. Since conservation is efficient, competitive owners do not deplete the resource in period 1, and l 1P < R 1. Given a = 1 and g = 1, l 1P = R 1 can be expressed as:
$$R_{1}=1-\delta \lpar 1+g\rpar \equiv \mu_{3}\lpar \delta\rpar .$$We focus on the case of μ > μ3, which also defines a threshold level of δ as a function of R 1. Note that complete conservation under perfect competition, i.e., l 1P = 0, implies the following:
$$R_{1}^{\ast}={1\over 2\lpar 1-\delta\rpar }\equiv \mu_{4}\lpar \delta\rpar .$$ For 
$R_{1}\leq R_{1}^{\ast}$, there is complete conservation. The critical level of R 1, as a function of δ, for which first-period employment is identical under perfect competition and monopsony, is found by setting l 1P = l 1Pm:
$$R_{1}^{\prime}={3\delta +4\delta^{2}-1 \over 4\delta}\equiv \mu_{1}\lpar \delta\rpar .$$Similarly, comparing perfect competition to duopsony, we find that l 1P = l 1Pd requires:
$$R_{1}^{''}={1-6\delta -4\delta^{2}\over{24\delta^{2}}}=\mu_{2}\lpar \delta\rpar .$$
