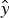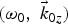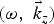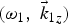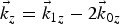Introduction
Surface plasma wave (SPW) is an electromagnetic wave that exists at the boundary between two media for example, metal–free space interface, its amplitude falls off exponentially in a direction perpendicular to the surface (Raether, Reference Raether1988). The excitation of SPWs over smooth metal surfaces by lasers is not possible due to k-vector mismatch as the SPW wave number is greater than the component of the laser wave vector along the interface. Numerous techniques were utilized to increase the momentum of the light for the excitation of SPWs.
In recent years, extensive research has been done towards the excitation of SPW both experimentally and theoretically. With low laser powers, SPWs can be excited by attenuated total reflection configuration or by creating density ripple on the metal surface (Kretschmann & Reather, Reference Kretschmann and Reather1968). With high powers lasers, the excitation of a SPW occurs at the interface of vacuum over-dense plasma which can be created during the interaction of an intense laser pulse with a solid metal target (Brodin & Lundberg, Reference Brodin and Lundberg1991; Parashar et al., Reference Parashar, Pandey and Tripathi1998; Macchi et al., Reference Macchi, Battaglini, Cornolti, Lisseikina, Pegoraro, Ruhl and Vshivkov2002). The interaction of high power lasers with solid density targets leads to nonlinear phenomena having vast applications in high harmonic generation, ion acceleration, laser ablation of materials, and so on (Bulanov et al., Reference Bulanov, Naumova and Pegoraro1994; Lee & Cho, Reference Lee and Cho1999; Macchi et al., Reference Macchi, Battaglini, Cornolti, Lisseikina, Pegoraro, Ruhl and Vshivkov2002; Baeva et al., Reference Baeva, Gordienko and Pukhov2006).
In view of the various applications, it would be interesting to consider wave-wave interactions involving SPWs. Yasumoto (Reference Yasumoto1981) analyzed theoretically the decay instability of a high-frequency SPW and a low-frequency ion acoustic surface wave due to an intense electromagnetic plane wave incident perpendicularly on an unmagnetized semi-infinite plasma from a vacuum. He also investigated the parametric decay instability of two high frequency SPWs in semi-infinite plasma (Yasumoto & Noguchi Verma, Reference Yasumoto and Noguchi Verma1982). The growth rate for the instability and the threshold amplitude of the incident wave are determined. The threshold amplitude of the order of 8.56 × 102 Vm−1 is obtained for an incident angle of the plane wave (θ) = 40°. The process of two surface plasmon decay (TSWD) is similar to two-plasmon decay (TPD) in laser-produced plasma, though the former is primarily a surface phenomenon whereas the latter is a volume phenomenon. Macchi et al. (Reference Macchi, Cornolti, Pegoraro, Lisseikina, Ruhl and Vshivkov2001) observed a new electron parametric instability involving the decay of one-dimensional (1D) electrostatic oscillation of frequency 2ω into two surface waves each of ω frequency using particle-in-cell simulations (PIC). Later he discussed an analytical model involving the parametric excitation of electromagnetic surface waves in the interaction of an ultrashort, intense laser pulse with overdense plasma. The growth rate of the process is maximum for normal incidence of the laser (Macchi et al., Reference Macchi, Battaglini, Cornolti, Lisseikina, Pegoraro, Ruhl and Vshivkov2002). Singh & Tripathi (Reference Singh and Tripathi2007) the explored the possibility of resonant SPW excitation by beating two laser beams, obliquely incident on a metal surface. The two lasers exert the ponderomotive force on free electrons at the beta frequency, producing a nonlinear current that resonantly derives the SPW. Kumar & Tripathi (Reference Kumar and Tripathi2007) studied the resonant plasma oscillations at the second harmonic by obliquely incident high power laser on a vacuum plasma interface. The plasma oscillations parametrically excite a pair of counter-propagating SPWs. Recently, Goel et al. (Reference Goel, Chauhan, Varshney, Singh and Sajal2015) theoretically studied the stimulated Compton scattering of a SPW, excited on the metal–vacuum interface by a high-frequency laser. The parametric decay of the SPW into another surface wave can be realized via quasi-static plasma wave in metals. The growth rate of the Compton process increases with the pump wave frequency, the width of the metal layer, laser amplitude and its spot size.
The motivation of the paper is to study the effect of the static magnetic field on the parametric excitation of two SPW by high-intensity laser over the surface of dense plasma, created by laser irradiation of a metallic target. The magnetic field is parallel to the surface and perpendicular to the SPW propagation. The transmitted field of the laser inside the metal acts as a pump wave of frequency (ω0, k 0z) and exerts the ponderomotive force on the metal electrons resulting in resonantly driven plasma oscillations at the second harmonic when 2ω0 = ωp (where ωp is the plasma frequency). The ponderomotive force displaces the electrons creating the self-consistent electrostatic potential. The potential couples with the oscillatory velocity due to one SPW and gives rise to a nonlinear density perturbation to drive other SPW. Growth rate equation is obtained on the basis of parametric coupling of a pump wave and two SPWs. This paper has been organized into four sections where introduction is presented as the first section. In the section Parametric growth of the SPW, the parametric coupling of a pump wave and two SPWs in the presence of external magnetic field is presented. A discussion of results and conclusions are given in the third and fourth section, respectively.
Parametric growth of the SPWs
Consider the metal–free space interface at x = 0 with half-space x > 0 is the free space and x < 0 is the plasma of equilibrium electron density n 0. The external constant magnetic field 
$(\vec B_{\rm s})$ is applied in 
$\hat y$-direction that is, a magnetic field is parallel to the surface and perpendicular to the SPW propagation. A high power laser is obliquely incident on the interface from the free space at an angle of incidence θ as shown Figure 1. The field of the incident laser is
$$\vec E_{\rm I} = A_{\rm I}\cos {\rm \theta} \left( {\hat z + \displaystyle{{k_{0z}} \over {k_{0x}}}\hat x} \right)e^{ - i({\rm \omega} _0t - k_{0z}z + k_{0x}x)}$$where k 0x = ω0/c cos θ and k 0z = ω0/c sin θ. The reflected laser from the plasma surface is
$$\vec E_R = A_{\rm I}\cos {\rm \theta} \left( {\hat z - \displaystyle{{k_{0z}} \over {k_{0x}}}\hat x} \right)e^{ - i({\rm \omega} _0t - k_{0z}z - k_{0x}x)}$$
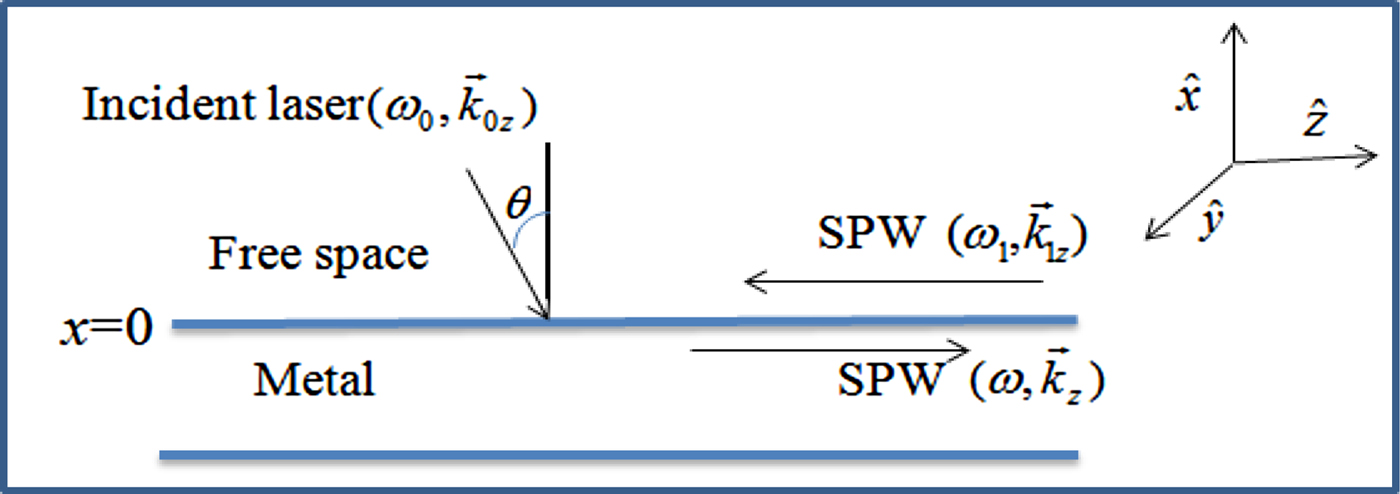
Fig. 1. Schematic of parametric excitation of SPW at the metal–free space interface.
The transmitted field inside the metal is
$$\vec E_T = \displaystyle{{2A_I\cos {\rm \theta} \left( {\hat z - {\rm \zeta} _0\hat x} \right)} \over {1 + (k_{0x}/k_{0z})( - {\rm \varepsilon} _{0xx}{\rm \zeta} _0 + {\rm \varepsilon} _{0xz})}}e^{{\rm \alpha} _0x}e^{ - i({\rm \omega} _0t - k_{0z}z)}$$ Where ζ 0 = (ik 0zε0xx − α0ε0xz/α0ε0xx + ik 0zε0xz), 
${\rm \varepsilon} _{0xx} = {\rm \varepsilon} _{\rm L} (1 - {\rm \omega} _{\rm p}^2 / ({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 ))$, 
${\rm \alpha} _0^2 = k_{0z}^2 - {{({\rm \omega} _0^2} / {c^2)}}{\rm \varepsilon} _{v0}$, 
${\rm \varepsilon} _{0xz} = i{\rm \omega} _{\rm c}{\rm \omega} _{\rm p}^2 {\rm \varepsilon} _{\rm L} / {\rm \omega} _0 (({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )$, and 
${\rm \varepsilon} _{v0} = {\rm \varepsilon} _{0xx} + {\rm \varepsilon} _{0xz}^2 /{\rm \varepsilon} _{0xx}$. εL is the lattice permittivity. 
${\rm \varepsilon} _{\rm p} = \sqrt {n_0e^2/m{\rm \varepsilon} _0} $ and ωc = eB s/m are the plasma and cyclotron frequency respectively. − e and m are the charge and effective mass of electron.
Under the influence of the transmitted laser field, plasma electrons oscillate in the presence of a static magnetic field. The oscillatory velocity of electrons is given by
$${\rm \nu} _{0x} = \displaystyle{e \over m}\displaystyle{{(i{\rm \omega} _0{\rm \zeta} _0 + {\rm \omega} _{\rm c})} \over {({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}E_{Tz}$$
$${\rm \nu} _{0z} = \displaystyle{e \over m}\displaystyle{{( - i{\rm \omega} _0 + {\rm \zeta} _0{\rm \omega} _{\rm c})} \over {({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}E_{Tz}$$The laser exerts ponderomotive force on the electrons at frequency ω0, given by
$$\vec F_{\rm p} = - \displaystyle{m \over 2}[\vec v_0.\nabla \vec v_0] - \displaystyle{e \over 2}[\vec v_0 \times \vec B]$$
where 
$\vec B = i\vec k_0 \times \vec E_{\rm T}/i{\rm \omega} _0$ is the magnetic field of pump wave inside the overdense plasma. On substituting the values from Eqs. (4) and (5) into Eq. (6), we obtained
$$\eqalign{& F_{{\rm p}x} = \displaystyle{{ - e} \over 2}\displaystyle{{E_{Tz}} \over {({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}\displaystyle{{\left( { - i{\rm \omega} _0{\rm \varepsilon} _{0xz} + {\rm \omega} _{\rm c}{\rm \varepsilon} _{0xx}} \right)} \over {\left( {{\rm \alpha} _0{\rm \varepsilon} _{0xx} + ik_{0z}{\rm \varepsilon} _{0xz}} \right)}}\nabla ^2{\rm \nu} _{ox} \cr & \qquad \ - \displaystyle{e \over {2i{\rm \omega} _0}}\displaystyle{{\left( {{\rm \varepsilon} _{0xx}E_{Tz}} \right)} \over {\left( {{\rm \alpha} _0{\rm \varepsilon} _{0xx} + ik_{0z}{\rm \varepsilon} _{0xz}} \right)}}\nabla ^2{\rm \nu} _{oz}} $$
$$\eqalign{ F_{{\rm p}z} & = \displaystyle{{ - e} \over 2}\displaystyle{{E_{Tz}} \over {({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}\displaystyle{{\left( { - i{\rm \omega} _0{\rm \varepsilon} _{0xz} + {\rm \omega} _c{\rm \varepsilon} _{0xx}} \right)} \over {\left( {{\rm \alpha} _0{\rm \varepsilon} _{0xx} + ik_{0z}{\rm \varepsilon} _{0xz}} \right)}}\nabla ^2{\rm \nu} _{oz} \cr & \qquad + \displaystyle{{e^2} \over {2i{\rm \omega} _0}}\displaystyle{{({\rm \varepsilon} _{0xx}E_{Tz})} \over {({\rm \alpha} _0{\rm \varepsilon} _{0xx} + ik_{0z}{\rm \varepsilon} _{0xz})}}\nabla ^2{\rm \nu} _{ox}} $$
Here, F px and F pz are the x and z components of ponderomotive force and 
$\nabla = i(k_{0z}\hat z - i{\rm \alpha} _0\hat x)$. The ponderomotive force displaces the electrons creating the space charge potential 
$(E_{2{\rm \omega} _0} = - \nabla _{2{\rm \omega} _0}{\rm \phi} _{2{\rm \omega} _0})$ where 
$\nabla _{2{\rm \omega} _0} = 2i(k_{0z}\hat z - i{\rm \alpha} _0\hat x)$. On solving equation of motion and continuity equation, we obtain the density perturbation 
$(n_{2{\rm \omega} _0})$ due to ponderomotive force and space charge potential as follows
$$\eqalign{& n_{2{\rm \omega} _0} = \displaystyle{{ - {\rm \chi} _e} \over {4{\rm \pi} e}}\nabla _{2{\rm \omega} _0}^2 {\rm \phi} _{2{\rm \omega} _0} + \displaystyle{{n_0} \over {4m{\rm \omega} _0({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}} \cr & \left[ {2{\rm \omega} _0({\rm \alpha} _0F_{{\rm p}x} + ik_{0z}F_{{\rm p}z}) + 2i{\rm \omega} _{\rm c}({\rm \alpha} _0F_{{\rm p}z} - ik_{0z}F_{{\rm p}x})} \right] = n_{2{\rm \omega} _0}^{\rm L} + n_{2{\rm \omega} _0}^{{\rm NL}}} $$
where 
$n_{2{\rm \omega} _0}^{\rm L} $ and 
$n_{2{\rm \omega} _0}^{{\rm NL}} $ are the linear and nonlinear part of the electron density perturbation. 
${\rm \chi} _{\rm e} = - {\rm \omega} _{\rm p}^2 /4({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )$ is the electron susceptibility. Using Eq. (9) in Poisson's equation 
$\nabla ^2{\rm \phi} = 4{\rm \pi} n_{2{\rm \omega} _0}e$, we get
$${\rm \phi} _{2{\rm \omega} _0} = \displaystyle{{4{\rm \pi} en_{2{\rm \omega} _0}^{{\rm NL}}} \over {4({\rm \alpha} _0^2 - k_{0z}^2 ){\rm \varepsilon}}} $$where ε = 1 + χ e. Using Eq. (10) in Eq. (9), we get
$$n_{2{\rm \omega} _0} = \left( {1 - \displaystyle{{{\rm \chi} _e} \over {\rm \varepsilon}}} \right)n_{2{\rm \omega} _0}^{{\rm NL}} $$The density perturbation couples with plasma oscillations and excites the two counter propagating SPWs of frequency ω and ω1, in the plasma. The wave equation governing electric fields of two SPWs can be written as
$$\nabla ^2\vec E_{\rm \omega} - \nabla (\nabla. \vec E_{\rm \omega} ) = \displaystyle{{4{\rm \pi}} \over {c^2}}\displaystyle{{\partial \vec J_{\rm \omega} ^{\hskip1.5pt NL}} \over {\partial t}} + \displaystyle{{\tilde {\rm \varepsilon}} \over {c^2}}\displaystyle{{\partial ^2{\vec E}_{\rm \omega}} \over {\partial t^2}}$$
$$\nabla ^2\vec E_{{\rm \omega} _1} - \nabla (\nabla. \vec E_{{\rm \omega} _1}) = \displaystyle{{4{\rm \pi}} \over {c^2}}\displaystyle{{\partial \vec J_{{\rm \omega} _1}^{\hskip1.8pt {\rm NL}}} \over {\partial t}} + \displaystyle{{{\tilde {\rm \varepsilon}} _1} \over {c^2}}\displaystyle{{\partial ^2{\vec E}_{{\rm \omega} _1}} \over {\partial t^2}}$$In the absence of nonlinear coupling, Eqs. (12) and (13) yield the field structure of the SPWs as
$$E_{{\rm \omega} z} = a{\rm \psi} (x,z)$$
where 
${\rm \psi} (x,z) = \left\{ \matrix{e^{ - {{\rm \alpha}} ^{\prime}x}e^{ - i({\rm \omega} t - k_zz)}\quad {\rm for}\;x \gt 0 \cr \hskip-6.2pt e^{{\rm \alpha} x}e^{ - i({\rm \omega} t - k_zz)}\quad {\rm for}\;x \lt 0 } \right.$ and
$$E_{{\rm \omega} _1z} = a_1{\rm \psi} _1(x,z)$$where
$${\rm \psi} _1(x,z) = \left\{ \matrix{e^{ - {{{\rm \alpha}} ^{\prime}}_1x}e^{ - i({\rm \omega} _1t - k_{1z}z)}\quad {\rm for}\;x \gt 0 \cr \hskip1pt e^{{\rm \alpha} _1x}e^{ - i({\rm \omega} _1t - k_{1z}z)}\qquad \!\!\!{\rm for}\;x \lt 0 } \right.$$
where 
${{\rm \alpha}} ^{\prime 2}= k_z^2 - {\rm \omega} ^2/c^2$, 
${\rm \alpha} ^2 = k_z^2 - {\rm \omega} ^2{\rm \varepsilon} _v/c^2$, 
${{\rm \alpha}} ^{\prime 2}_1 = k_z^2 - {\rm \omega} _1^2 /c^2$, and 
${\rm \alpha} _1^2 = k_z^2 - {\rm \omega} _1^2 {\rm \varepsilon} _{v1}/c^2$. The dispersion relation of these SPWs is given by
$${\rm \alpha} + {{\rm \alpha}} ^{\prime}{\rm \varepsilon} _v + ik_z\displaystyle{{{\rm \varepsilon} _{xz}} \over {{\rm \varepsilon} _{xx}}} = 0\;{\rm and}\;{\rm \alpha} _1 + {{\rm \alpha}} ^{\prime}_1{\rm \varepsilon} _{v1} + ik_{1z}\displaystyle{{{\rm \varepsilon} _{1xz}} \over {{\rm \varepsilon} _{1xx}}} = 0$$
where 
${\rm \varepsilon} _v = {\rm \varepsilon} _{xx} + ({\rm \varepsilon} _{xz}^2 /{\rm \varepsilon} _{xx})$ and 
${\rm \varepsilon} _{v1} = {\rm \varepsilon} _{1xx} + ({\rm \varepsilon} _{1xz}^2 /{\rm \varepsilon} _{1xx})$ The phase matching conditions for the parametric decay are k z = k 1z − 2k 0z and ω = ω1 − 2ω0. On replacing 
$\nabla = (\partial \hat x/\partial x) + (\partial \hat z/\partial z)$ in Eqs. (12) and (13) and simplification yields the following set of equations.
$$\eqalign{& \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{xx}\left[ {\displaystyle{{\partial ^2E_z} \over {\partial x^2}} - \left( {k_z^2 - \displaystyle{{{\rm \omega} ^2} \over {c^2}}\left( {{\rm \varepsilon} _{xx} + \displaystyle{{{\rm \varepsilon} _{xz}^2} \over {{\rm \varepsilon} _{xx}}}} \right)} \right)E_z} \right] \cr & \qquad \ \, = \displaystyle{{4{\rm \pi} i{\rm \omega}} \over {c^2}}\left[ {J_{{\rm \omega} z}^{{\rm NL}} \left( {k_z^2 - \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{xx}} \right) - J_{{\rm \omega} x}^{{\rm NL}} \left( {ik_z - \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{xz}} \right)} \right]}$$
$$\eqalign{& \displaystyle{{{\rm \omega} _1^2} \over {c^2}}{\rm \varepsilon} _{1xx}\left[ {\displaystyle{{\partial ^2E_{1z}} \over {\partial x^2}} - \left( {k_{1z}^2 - \displaystyle{{{\rm \omega} _1^2} \over {c^2}}\left( {{\rm \varepsilon} _{1xx} + \displaystyle{{{\rm \varepsilon} _{1xz}^2} \over {{\rm \varepsilon} _{1xx}}}} \right)} \right)E_{1z}} \right] \cr & \qquad\quad \! = \displaystyle{{4{\rm \pi} i{\rm \omega} _1} \over {c^2}}\left[ {J_{{\rm \omega} _1z}^{{\rm NL}} \left( {k_{1z}^2 - \displaystyle{{{\rm \omega} _1^2} \over {c^2}}{\rm \varepsilon} _{1xx}} \right) - J_{{\rm \omega} _1x}^{{\rm NL}} \left( {ik_{1z} - \displaystyle{{{\rm \omega} _1^2} \over {c^2}}{\rm \varepsilon} _{1xz}} \right)} \right]} $$ The coupling of SPWs with plasma oscillations excites non-linear current densities 
$\vec J_{\rm \omega} ^{\,\,{\rm NL}} = - {{en_{2{\rm \omega} _0}^* v_{{\rm \omega} _1}} / 2}$ and 
$\vec J_{{\rm \omega} _1}^{\,\,{\rm NL}} = - {{en_{2{\rm \omega} _0}^* v_{\rm \omega}} / 2}$ at a frequency ω and ω1 respectively. 
$\tilde {\rm \varepsilon} = 1$ and 
$\tilde {\rm \varepsilon} _1 = 1$ for free space and in the metal are the dielectric tensors due to the presence of the external magnetic field, given by
$$\tilde {\rm \varepsilon} = \left( {\matrix{ {{\rm \varepsilon} _{\rm L}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2 ({\rm \omega} + i{\rm \nu} )} \over {{\rm \omega} ({({\rm \omega} + i{\rm \nu} )}^2 - {\rm \omega} _{\rm c}^2 )}}} \right)} & 0 & {\displaystyle{{ - i{\rm \omega} _{\rm c}} \over {\rm \omega}} \displaystyle{{{\rm \varepsilon} _{\rm L}{\rm \omega} _{\rm p}^2} \over {({({\rm \omega} + i{\rm \nu} )}^2 - {\rm \omega} _{\rm c}^2 )}}} \cr 0 & {{\rm \varepsilon} _{\rm L}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} ({\rm \omega} + {\rm \nu} i)}}} \right)} & 0 \cr {\displaystyle{{i{\rm \omega} _{\rm c}} \over {\rm \omega}} \displaystyle{{{\rm \varepsilon} _{\rm L}{\rm \omega} _{\rm p}^2} \over {({({\rm \omega} + i{\rm \nu} )}^2 - {\rm \omega} _{\rm c}^2 )}}} & 0 & {{\rm \varepsilon} _{\rm L}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2 ({\rm \omega} + i{\rm \nu} )} \over {{\rm \omega} ({({\rm \omega} + i{\rm \nu} )}^2 - {\rm \omega} _{\rm c}^2 )}}} \right)} \cr}} \right)$$and
$$\tilde {\rm \varepsilon} _1 = \left( {\matrix{ {{\rm \varepsilon} _{\rm L}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2 ({\rm \omega} _1 + i{\rm \nu} )} \over {{\rm \omega} _1({({\rm \omega} _1 + i{\rm \nu} )}^2 - {\rm \omega} _{\rm c}^2 )}}} \right)} & 0 & {\displaystyle{{ - i{\rm \omega} _{\rm c}} \over {{\rm \omega} _1}}\displaystyle{{{\rm \varepsilon} _{\rm L}{\rm \omega} _{\rm p}^2} \over {({({\rm \omega} _1 + i{\rm \nu} )}^2 - {\rm \omega} _{\rm c}^2 )}}} \cr 0 & {{\rm \varepsilon} _L\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _1({\rm \omega} _1 + {\rm \nu} i)}}} \right)} & 0 \cr {\displaystyle{{i{\rm \omega} _c} \over {{\rm \omega} _1}}\displaystyle{{{\rm \varepsilon} _{\rm L}{\rm \omega} _{\rm p}^2} \over {({({\rm \omega} _1 + i{\rm \nu} )}^2 - {\rm \omega} _{\rm c}^2 )}}} & 0 & {{\rm \varepsilon} _{\rm L}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2 ({\rm \omega} + i{\rm \nu} )} \over {{\rm \omega} _1({({\rm \omega} _1 + i{\rm \nu} )}^2 - {\rm \omega} _{\rm c}^2 )}}} \right)} \cr}} \right)$$The SPWs impart oscillatory velocities to the electrons. The x and z components of the velocity at frequency ω and ω1 are given by
$$v_x = \displaystyle{e \over m}\displaystyle{{( - i{\rm \omega} E_x + {\rm \omega} _{\rm c}E_z)} \over {({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 )}}\; \;{\rm and}\;v_z = \displaystyle{{ - e} \over m}\displaystyle{{({\rm \omega} _{\rm c}E_x + i{\rm \omega} E_z)} \over {({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 )}}$$
$$v_{1x} = \displaystyle{e \over m}\displaystyle{{( - i{\rm \omega} _1E_{1x} + {\rm \omega} _{\rm c}E_{1z})} \over {({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}}\;{\rm and}\;v_{1z} = \displaystyle{{ - e} \over m}\displaystyle{{({\rm \omega} _{\rm c}E_{1x} + i{\rm \omega} _1E_{1z})} \over {({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 )}}$$where
$$E_{1x} = \displaystyle{{ - ik_{1z}{\rm \varepsilon} _{1xx} + {\rm \alpha} _1{\rm \varepsilon} _{1xz}} \over {ik_{1z}{\rm \varepsilon} _{1xz} + {\rm \alpha} _1{\rm \varepsilon} _{1xx}}}E_{1z} = {\rm \zeta} _1E_{1z}$$
$$E_x = \displaystyle{{ - ik_z{\rm \varepsilon} _{xx} + {\rm \alpha} {\rm \varepsilon} _{xz}} \over {ik_z{\rm \varepsilon} _{xz} + {\rm \alpha} {\rm \varepsilon} _{xx}}}E_z = {\rm \zeta} E_z$$ Substituting the values from Eqs. (14) and (15) and the corresponding nonlinear current at frequency ω and ω1 in Eqs. (16) and (17), respectively. On multiplying the resultant equations by ψ* and 
${\rm \psi} _1^* $ respectively and integrating them from − ∞ to ∞ yields
$$\eqalign{& a\left[ {\left( {{\rm \alpha} ^2 - k_z^2 + \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _v} \right)\displaystyle{1 \over {2{\rm \alpha}}} + \left( {{\rm \alpha} ^{\cdot 2} - k_z^2 + \displaystyle{{{\rm \omega} ^2} \over {c^2}}} \right)\displaystyle{1 \over {2{{\rm \alpha}} ^{\prime}}}} \right] \cr & = \displaystyle{{n_{2{\rm \omega} _0}^{^\ast} a_1e^2} \over {4m}}\displaystyle{{4{\rm \pi} i} \over {{\rm \omega} ({\rm \omega} _1^2 - {\rm \omega} _{\rm c}^2 ){\rm \varepsilon} _{xx}}}\displaystyle{1 \over {(2{\rm \alpha} _0 + {\rm \alpha} _1 + {\rm \alpha} )}} \cr & \times \left[ {\left( {k_z^2 - \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{xx}} \right)({\rm \omega} _{\rm c}{\rm \zeta} _1 + i{\rm \omega} _1) + \left( {ik_z{\rm \alpha} - \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{xz}} \right)( - i{\rm \omega} _1{\rm \zeta} _1 + {\rm \omega} _{\rm c})} \right]} $$
$$\eqalign{& a_1\left[ {\left( {{\rm \alpha} _1^2 - k_{1z}^2 + \displaystyle{{{\rm \omega} _1^2} \over {c^2}}{\rm \varepsilon} _{v1}} \right)\displaystyle{1 \over {2{\rm \alpha} _1}} + \left( {{\rm \alpha} _1^{\cdot 2} - k_{1z}^2 + \displaystyle{{{\rm \omega} _1^2} \over {c^2}}} \right)\displaystyle{1 \over {2{{{\rm \alpha}} ^{\prime}}_1}}} \right] \cr & = \displaystyle{{n_{2{\rm \omega} _0}^{^\ast} ae^2} \over {4m}}\displaystyle{{4{\rm \pi} i} \over {{\rm \omega} _1({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 ){\rm \varepsilon} _{1xx}}}\displaystyle{1 \over {(2{\rm \alpha} _0 + {\rm \alpha} _1 + {\rm \alpha} )}} \times \cr & \left[ {\left( {k_{1z}^2 - \displaystyle{{{\rm \omega} _1^2} \over {c^2}}{\rm \varepsilon} _{1xx}} \right)\left( {{\rm \omega} _{\rm c}{\rm \zeta} + i{\rm \omega}} \right) + \left( {ik_{1z}{\rm \alpha} _1 - \displaystyle{{{\rm \omega} _1^2} \over {c^2}}{\rm \varepsilon} _{1xz}} \right)\left( { - i{\rm \omega} {\rm \zeta} + {\rm \omega} _{\rm c}} \right)} \right]} $$where
$$\eqalign{& n_{2{\rm \omega} _0}^{^\ast} = \displaystyle{{n_0} \over {4m{\rm \omega} _0({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}} \cr & \left[ {2{\rm \omega} _0({\rm \alpha} _0F_{{\rm p}x}^{^\ast} - ik_{0z}F_{{\rm p}z}^{^\ast} ) - 2i{\rm \omega} _{\rm c}({\rm \alpha} _0F_{{\rm p}z}^{^\ast} + ik_{0z}F_{{\rm p}x}^{^\ast} )} \right]\left( {1 - \displaystyle{{{\rm \chi} _e} \over {\rm \varepsilon}}} \right)} $$
$F_{{\rm p}x}^* $ and 
$F_{{\rm p}z}^* $ are the complex conjugate of the x and z components of ponderomotive force. In the absence of nonlinear coupling (i.e., with zero RHS of Eqs. (16) and (17)), these equations give eigen functions (14) and (15) and frequencies of two surface plasma waves as ω ≅ ωr and ω1 ≅ ω1r respectively. These frequencies are modified in the presence of nonlinear coupling [i.e., v ω ≠ 0 and 
$v_{{\rm \omega} _1} \ne 0$] and are given by ω = ωr + iγ and ω1 = ω1r + iγ, where γ is the growth rate of the two surface wave decay obtained under the influence of external magnetic field numerical values of the growth rate can be calculated by solving Eqs. (18) and (19) for different values of normalized cyclotron frequency (ωc/ωp), incident laser angle (θ), and amplitude (a 0 = eA I/mω pc). The other parameters are ωp = 2ω0, a 0 = 0.05, and ν/ωp = 0.01. The normalized frequency (ω/ωp) and normalized growth rate (γ/ωp) of SPW is plotted as a function of laser incidence angle (θ) for different values of ωc/ωp in Figures 2 and 3, respectively. The frequency of the SPW (ωc/ωp) increases with θ and ωc/ωp and saturates at its higher values. At ωp = 2ω0, the frequency of other SPW can be calculated using the phase matching conditions ω = ω1 − 2ω0. The growth rate (γ/ωp) of the process reduces to half on increasing ωc/ωp = 0.004 to ωc/ωp = 0.02. At fixed ωc/ωp, the maximum growth rate is obtained around θ = 40°. In Figures 4(a) and 4(b), the transmitted field of incident laser and ponderomotive force are plotted with ωc/ωp. Figure 5 shows the normalized growth rate (γ/ωp) for different values of laser amplitude (a 0). Growth rate increases with the amplitude of the incident laser.
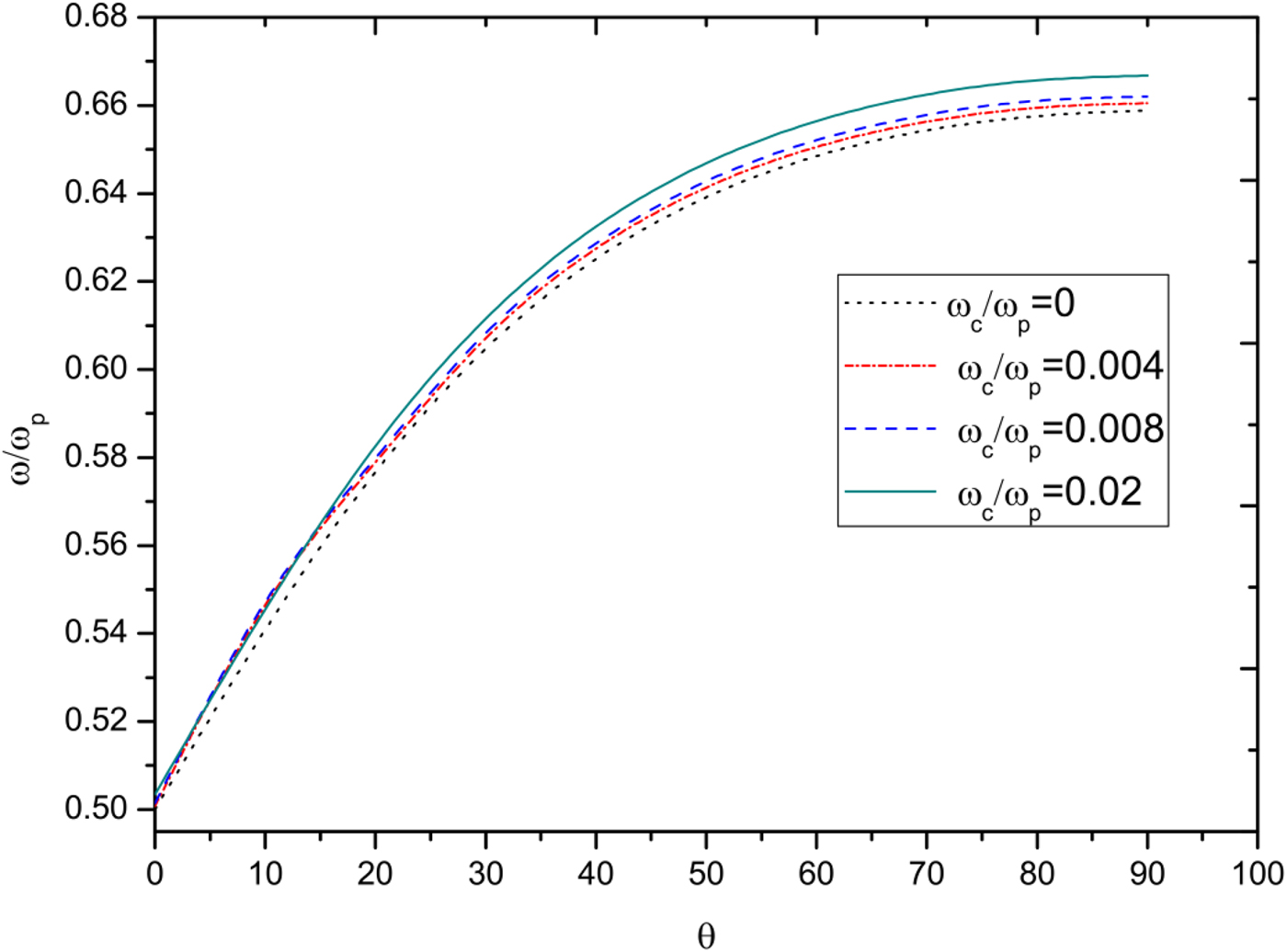
Fig. 2. Variation of the normalized frequency of surface plasma wave (ω/ωp) with the angle of incidence of the laser pulse at (ω0/ωp) = 0.5.
Fig. 3. The plot of normalized growth rate (γ/ωp) with the angle of incidence of the laser pulse on varying normalized cyclotron frequency (ωc/ωp) for (ω0/ωp) = 0.5.
Fig. 4. (a) Variation of laser transmitted field in the metal and (b) ponderomotive force on the metal electrons as a function of the incidence angle of laser for different values of the normalized magnetic field.
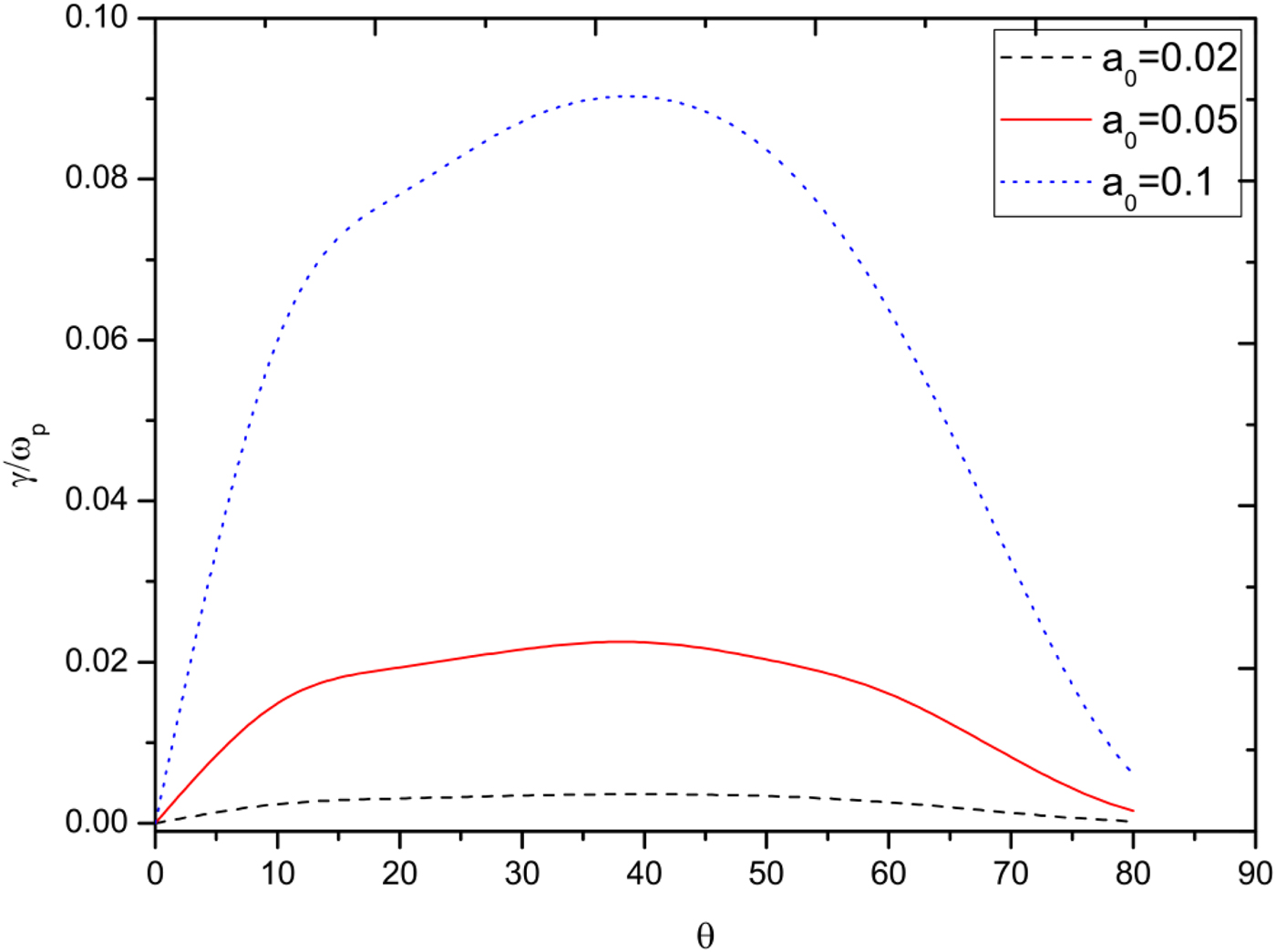
Fig. 5. The plot of normalized growth rate (γ/ωp) with the angle of incidence of the laser pulse on varying the normalized amplitude of the laser pulse.
Discussion
In the present work, effects of static magnetic field (ωc = eB s/m, where B s is the external magnetic field) are examined on the parametric excitation of a pair of SPW over the metal surface by a laser. The equation of motion of the metal electrons is solved along with continuity equation to study the effect of the externally applied magnetic field. The applied magnetic field induces changes in the dispersion relation of the SPWs and a complex mathematical expression for the growth rate of the SPW is obtained which reduces to the expression obtained by Kumar & Tripathi (Reference Kumar and Tripathi2007) in the absence of magnetic field (ωc/ωp = 0). Macchi et al. (Reference Macchi, Battaglini, Cornolti, Lisseikina, Pegoraro, Ruhl and Vshivkov2002) studied the process of SPW excitation using 2D particle in cell simulation and postulated that growth rate is maximum for normal incidence of the laser on the metal surface. Kumar & Tripathi (Reference Kumar and Tripathi2007) theoretically verified the results. However, in the presence of the external magnetic field, the growth rate increases with the angle of incidence reaches a maximum value at θ = 40° and starts decreasing afterwards as observed in Figure 3. The transmitted field of the laser [Eq. (3)] is modified due to the applied magnetic field and not maximum for normal incidence of the laser as observed in Figure 4(a). It decreases with further increase in magnetic field. Also, the ponderomotive force experienced by the metal electrons decreases with the magnetic field as shown in Figure 4(b). The growth rate decreases with the applied magnetic field due to the decrease in transmitted field of the laser in metal and ponderomotive force with the applied magnetic field. It is clear from Eqs. (18) and (19), that growth rate is directly proportional to the amplitude of the laser and increases significantly with the laser amplitude as observed in Figure 5. The parametrically excited SPW may be useful for heating of plasma ions. In relativistic case (laser intensity I ≥ 1019 W/cm2) the plasma electrons become highly energetic and their mass modify by Lorentz factor. In this situation, the resonance condition W p = 2W 0, may be change due to relativistic effect.
In mild relativistic case, electron mass is modified by relativistic mass, and it affects the resonance condition as well as the growth rate of the SPW. While in strong relativistic case, SPW excitation process becomes more complicated due to other effects like hole boring, particle acceleration etc, during ultra-high laser interaction with mater.
In the present analysis, we have considered very high magnetic, that is, like a few tens or Tesla. Hosokai et al. (Reference Hosokai, Kinoshita, Zhidkov, Maekawa, Yamazaki and Uesaka2006), observed the effect of external static magnetic in on electron bean generation in their setup. Although they have applied less than 1 T, now a days one can get the pulsed magnetic field up to 70 T (Lagutin et al., Reference Lagutin, Rosseel, Herlach, Vanacken and Bruynseraede2003). Nalini et al. (Reference Nalini, Kaushic and Gupta2010), also proposed a scheme through which they generated hundreds of Tesla in inertial magnets. The strength of external magnetic field can also be optimized with laser intensity. At low laser intensity, the optimum values of the magnetic field are very high; however, it decreases with high laser intensity. If such a strong magnetic field is not available at a laboratory, then the experiment can be carried out at high laser intensity, but in that case, the relativistic effect should also be considered.
Conclusions
In this work, we discussed two surface wave decay of the high power laser obliquely incident at the metal–free space interface in the presence of an external magnetic field. The decay is possible due to plasma density perturbations at the second harmonic when ωp = 2ω0. The growth rate of the process increases with the angle of incidence of laser upto a particular value and decreases at higher angles. With the increase in magnetic field strength, growth rate decreases from ≃0.022ωp to ≃ 0.013ωp. Thus, the applied magnetic field can be optimized for efficient growth of the SPW.
