Problem-solving in math is a crucial exercise whereby children may learn to adopt effective approaches to manage challenges in their learning and daily life. Attempts to identify sources of influence on students’ learning ability have identified self-regulated learning (SRL) and executive functions as being related to math learning and future school achievement (McClelland et al., Reference McClelland, Cameron, Duncan, Bowles, Acock, Miao and Pratt2014; Schmitt et al., Reference Schmitt, Geldhof, Purpura, Duncan and McClelland2017). In fact, the complexity and the dynamics of problem-solving in math may involve various phases and different intellectual processes, such as, accessing pre-stored information and applying problem-solving strategies (Swanson, Reference Swanson2016). Therefore, WM (which is a domain-general cognitive process, Aragón et al., Reference Aragón, Navarro, Aguilar, Cerda and García-Sedeño2016) and SRL are determining for good performance in this type of multiphase exercise. As a complex and multicomponent construct, SRL operates across several dimensions of human functioning, such as social-emotional, cognitive, behavioral and motivational (Zimmerman, Reference Zimmerman2013).
In the current study we will include WM as an antecedent of SRL to explain academic performance in math. Therefore, in this research we conceptualize WM and SRL as different constructs that influence academic performance (Nyroos et al., Reference Otto2015). SRL appears in the literature as an individual’s response to different task performance and is often described as being associated with the executive functions of WM (Knouse et al., Reference Knouse, Feldman and Blevins2014). In contexts of academic performance, SRL plays an important role in reducing tension through higher task-focusing due to the emotional regulation, emotion-focusing and cognitive-appraisal processes linked to SRL (Schutz et al., Reference Schutz, Distefano, Benson and Davis2004).
Conceptually, WM appears as a distinct construct from SRL since it refers to a purely cognitive concept comprising several executive functions with updating, shifting, and inhibition potentially operating in a different way to explain performance in planning (Miyake & Friedman, Reference Miyake and Friedman2012) and other SRL processes. In addition, WM may be defined as the capacity to direct attentional focus and processing capacity toward relevant goals and inhibit those that are distractive (Barrett et al., Reference Barrett, Tugade and Engle2004). WM has also been defined as the capacity to simultaneously sustain information and process additional work (Baddeley et al., Reference Baddeley, Hitch, Allen, Logie, Camos and Cowan2021).
Moreover, SRL skills and math knowledge seem to be correlated (DeFlorio et al., Reference DeFlorio, Klein, Starkey, Swank, Taylor, Halliday, Beliakoff and Mulcahy2019), therefore, we postulate that SRL may play a determining role in explaining the relationship between WM and problem-solving accuracy in math. In fact, in line with previous calls to consider the need to differentiate aspects of SRL processes (Bridgett et al., Reference Bridgett, Oddi, Laake, Murdock and Bachmann2013), the current study aims to fill this gap in the literature by providing a deeper understanding the role of SRL and its different processes in the relationship between WM and problem-solving accuracy in math in primary school children.
WM and Problem-Solving Accuracy in Math
Certain competencies, such as literacy and arithmetic proficiency may mediate the relationship between WM and performance in problem-solving in math (Swanson & Fung, Reference Swanson and Fung2016). In fact, the literature has highlighted that all WM components play an important role in predicting problem-solving accuracy (Clements & Sarama, Reference Clements, Sarama, Fritz, Haase and Räsänen2019), however, basic academic skills (i.e., in reading and in math) may complement the effects of WM on children’s mathematical problem-solving (Zheng et al., Reference Zheng, Swanson and Marcoulides2011). For instance, unique predictors of problem-solving can include language comprehension, attention, mathematics vocabulary, and mathematics computation (Lin, Reference Lin2020). WM seems to predict performance in problem-solving in math less when children’s knowledge regarding the processes that guide problem-solving in math is introduced in this relationship (Muñez et al., Reference Muñez, Lee, Bull, Khng, Cheam and Rahim2022). In view of these findings, the literature has suggested that more research is needed to understand the role of WM in predicting performance in problem-solving in math when other competencies are considered. Accordingly, Zheng et al. (Reference Zheng, Swanson and Marcoulides2011) found that reading skills and math calculation proficiency mediated the relationship between the central executive component and the phonological loop and problem-solving accuracy in math. In addition, when other competencies were introduced as mediators (i.e., reading, calculation and fluid intelligence), the storage facet of WM had a significant direct effect on problem-solving accuracy in math, as opposed to the executive system, which did not. Moreover, Fung and Swanson (Reference Fung and Swanson2017) found that reading skills, calculation proficiency and domain-specific knowledge mediated the relationship between the executive component of WM and children’s problem-solving accuracy in math.
As mentioned, WM is responsible for the storage capacity and simultaneous processing of information (Baddeley, Reference Baddeley2012). WM has multiple facets (von Bastian & Oberauer, Reference von Bastian and Oberauer2013) associated to coordination, simultaneous storage and transformation of information, and supervision. Coordination refers to the capacity to build new relations between isolated stimuli and to coordinate the relationship between them to obtain a meaningful and coherent structure. A typical task requires the capacity to coordinate parts (e.g., a geometric pattern, noun phrases, etc.) with the aim of integrating these parts into one complex structure (e.g., a mental image, sentence comprehension, etc.). Supervision is associated to the capacity to monitor continuous operations and actions, as well as to activate (i.e., select) relevant information and to inhibit distracting stimuli. Participants must switch between two competing categories that appear randomly in a sequence and have to maximize the need to inhibit distractive or competitive categories and to activate the intended category or information. Finally, simultaneous storage and transformation consists of the capacity to retain new information that is briefly presented over a period of time in which the information is no longer accessible, while developing cognitive transformations on the storage information or other new-presented elements. Experimentally, participants must retain verbal or spatial stimuli and then make decisions through a transformational process (von Bastian & Oberauer, Reference von Bastian and Oberauer2013). Decisions consist of recalling digits (after random presentation) in the ascending or descending order or eventually letters in the order of the alphabet.
The developmental changes involved in WM abilities are often interpreted as better memory span. Generally, memory span develops from 4 to 8 years of age and gradually increases until approximately 12 years of age (Gathercole, Reference Gathercole1999). The literature has proposed that WM determines problem-solving by directing attention to relevant information, managing several cognitive resources, and constraining irrelevant information (Clements & Sarama, Reference Clements, Sarama, Fritz, Haase and Räsänen2019; Fuchs et al., Reference Fuchs, Fuchs, Seethaler and Barnes2020). For example, a study conducted with a group of children with difficulties in mathematics revealed that the WM ability to inhibit irrelevant information was lower in the group where children had more difficulties in math processing tasks (Passolunghi & Siegel, Reference Passolunghi and Siegel2004). Other studies have suggested that the inhibitory control mechanisms are associated with better academic achievement and adaptive functioning in terms of learning capacity, capacity to work hard and positive and appropriate behavior at school (Clements & Sarama, Reference Clements, Sarama, Fritz, Haase and Räsänen2019; Vuontela et al., Reference Vuontela, Carlson, Troberg, Fontell, Simola, Saarinen and Aronen2013).
Considering that certain aspects of the WM executive functioning in the relationship with SRL processes may overlap (Bridgett et al., Reference Bridgett, Oddi, Laake, Murdock and Bachmann2013), for research purposes, we will opt to include only one of the mentioned facets (von Bastian & Oberauer, Reference von Bastian and Oberauer2013). Therefore, in the current study, we will only adopt tasks requiring mainly storage and transformation (i.e., reading and computation span) because they are good predictors for reading (Swanson & Fung, Reference Swanson and Fung2016), math performance (Campos et al., Reference Campos, Almeida, Ferreira, Martinez and Ramalho2013), and other decision-making processes (Offergeld et al., Reference Offergeld, Martinez and Ferreira2020). Moreover, previous experimental, psychometric and neuropsychological studies have emphasized that memory visuospatial and verbal-numeric memory domains are independent subsystems (Ferreira et al., Reference Ferreira, Almeida and Prieto2011; Thalmann & Oberauer, Reference Thalmann and Oberauer2017). Several studies have provided evidence of the relation between working memory and mathematics performance (Berkowitz et al., Reference Berkowitz, Edelsbrunner and Stern2022; Silverman & Ashkenazi, Reference Silverman and Ashkenazi2022). In fact, the relationship between WM and math achievement has been well established and several other studies using SEM have already provided evidence of this relationship in different mathematical contexts (e.g., Aragón et al., Reference Aragón, Navarro, Aguilar, Cerda and García-Sedeño2016). However, this research is significant because of the SRL role in solving problems with a methodological approach which is sufficient to contrast the established hypotheses. In order to control this particular effect, in the current study, we will consider two tasks with the same content: Verbal-numeric. In line with these previous studies, we propose our first hypothesis:
H 1: Children with high WM performance will also get higher accuracy scores in mathematic.
SRL and Problem-Solving in Math
Competencies to solve problems in math can be developed through discovery, incentive and practice (Polya, 1965/Reference Polya1981). The phases that have been considered to solve problems include understanding the problem, planning how to solve it, carrying out the plan and reviewing the process (Polya, 1965/Reference Polya1981) - a SRL process which may lead to better problem-solving accuracy in math. Self-regulation entails the reciprocal influence of the environment on the person, which is mediated through behavior (Bandura, Reference Bandura2001). Accordingly, in educational contexts, SRL is the level of active metacognitive, motivational and behavioral participation students have in their own learning process (Zimmerman, Reference Zimmerman2013).
This study focuses on the social cognitive approach of SRL, which considers this process as the reciprocal influence of the environment on the person, which is intermediated through behavior (Zimmerman, Reference Zimmerman2013). Moreover, there are distinct phases through which problem-solving in math may be guided, namely, understanding the problem, elaborating a plan to solve the problem, executing the plan and analyzing the results (Polya, Reference Polya2004). Solving math problems involves both verbal comprehension and fluid reasoning abilities. Hence, this type of activity in particular, provides opportunities for students to improve their fluency by requiring skills such as estimating, collecting, and interpreting data, using mathematical language, selecting the appropriate unit of measurement, and recalling factual knowledge and concepts quickly. In accordance, as in problem-solving in math, SRL also includes various phases with similar processes which are cyclical and influence each other mutually (da Silva et al., Reference da Silva, Simão and Sá2004; Zimmerman, Reference Zimmerman2013). Firstly, it includes a forethought phase which involves task analysis and self-motivational beliefs, where students can set goals, plan their use of strategies, value tasks and direct performance with the aid of self-efficacy beliefs and outcome expectancies (Zimmerman, Reference Zimmerman, Boekaerts, Pintrich and Zeidner2000).
SRL also includes a performance phase, which entails self-control, where students can use self-instruction techniques, use imagery and task strategies, structure their learning environment, seek help and focus their attention on the task (Zimmerman, Reference Zimmerman2013). Lastly, it includes a self-reflection phase, which encloses self-judgments, where students self-evaluate the effectiveness of their learning performance and attribute causality regarding the outcomes (da Silva et al., Reference da Silva, Simão and Sá2004; Zimmerman, Reference Zimmerman2013). The self-reflection phase also involves different self-reactions, such as self-satisfaction and adaptive/defensive inferences about how the learning process was conducted (i.e., the need to maintain or change a certain strategy) to proceed to the next learning challenge. Accordingly, in this study, we propose to examine SRL as a four-phase process which guides children in problem-solving in math.
Research has provided evidence of the positive effects of SRL in problem-solving in math (Otto, Reference Otto2007). For instance, in a five-week intervention study conducted with fourth-grade students, Otto (Reference Otto2007) found significant positive effects of SRL strategies on mathematical problem-solving. Perels et al. (Reference Perels, Dignath and Schmitz2009) investigated whether training 6th grade students on how to regulate their learning could influence their academic performance in math. The authors found that there were significant interactions between time and group for most of the SRL variables in favor of the group that had training. Specifically, this study demonstrated that training in how to regulate one’s learning could support math achievement. Thus, we hypothesize that:
H2: If children’s SRL is high, then they will attain better problem-solving accuracy in math.
The Mediating Role of SRL in the Relationship between WM and Problem-Solving Accuracy in Math
Previous studies revealed that WM capacity and SRL are intrinsically correlated, showing that WM moderates the impact of automatic and controlled dispositions in human behavior (Hofmann et al., Reference Hofmann, Schmeichel and Baddeley2012). In fact, there is also evidence that individual differences toward WM capacity may explain different self-regulatory behavior in the ability to control cognitive processes in high-demanding attentional tasks (Barrett et al., Reference Barrett, Tugade and Engle2004). Research has found that WM influences the means through which knowledge is activated (Conway & Engle, Reference Conway and Engle1994) and therefore, children’s capacity to identify the appropriate operations and algorithms, as well as numerical and irrelevant information come into play when solving math problems (Swanson, Reference Swanson2004). That is, the psychological processes that underlie WM can contribute to problem-solving accuracy in math (Swanson et al., Reference Swanson, Arizmendi and Li2021). A study conducted by Muñez et al. (Reference Muñez, Lee, Bull, Khng, Cheam and Rahim2022) showed that WM training alone did not improve WM capacity and, as a consequence, did not contribute to mathematical performance. What this study showed was that students only improved their skills in numerical activities when participants not only develop their WM capacities, but also had numeracy training through an adaptive computerized game-based task. Despite not being discussed by the authors, we concur that the numeracy training may have also helped the students to develop their SRL skills and thus, be more effective with numerical skills.
Despite the notorious implications on the relationship between WM capacity and performance (Swanson & Alloway, Reference Swanson, Alloway, Harris, Graham, Urdan, McCormick, Sinatra and Sweller2012; Vuontela et al., Reference Vuontela, Carlson, Troberg, Fontell, Simola, Saarinen and Aronen2013), these findings open new avenues for research into the path between WM capacity and different approaches to self-regulatory behavior. Individuals with high capability for temporary storage tend to control their cognitive behavior (Hofmann et al., Reference Hofmann, Schmeichel and Baddeley2012), however there is a lack of understanding regarding how children can translate high cognitive performance into academic achievement through the role of more controlled dispositions attributed to SRL. In view of the findings with respect to the effect of other competencies on the relationship between WM and problem-solving accuracy in math, we propose that:
H 3: If children’s SRL is high, then it will mediate the relationship between WM capacity and problem-solving accuracy in math.
According to the literature, the forethought process of being able to understand the problem and strategic planning, can help provide the necessary resources for students to make decisions to solve problems when the resolution process is not clear (Das et al., Reference Das, Naglieri and Kirby1994). In fact, the self-regulatory phases are carried out by the cognitive process of planning (Kroesbergen et al., Reference Kroesbergen, van Luit, Naglieri, Taddei and Franchi2010). Considering the Planning, Attention, Simultaneous and Successive (PASS) theory of intelligence, the cognitive process of planning determines attention, simultaneous and successive processes involved in learning (Das et al., Reference Das, Naglieri and Kirby1994). Moreover, planning is fundamental for learning as it guides students in establishing task objectives, in adopting strategies to reach those objectives and in regulating the learning process (Das et al., Reference Das, Naglieri and Kirby1994; McCormack & Atance, Reference McCormack and Atance2011). In a recent study, Mayoral-Rodríguez et al. (Reference Mayoral-Rodríguez, Timoneda-Gallart and Pérez-Álvarez2018) found that planning skills determined high school students’ performance in math and problem-solving. In fact, if students were familiar with the objectives of the task, their planning process would be influenced by the experience of establishing or changing plans to reach goals. This enabled students to develop their own effective learning strategies. In view of these findings and considering da Silva et al.’s model of SRL (2004), we propose that:
H 4: The planning phase will be a greater indicator of students’ SRL in problem-solving in math if its factor weight scores are higher than other SRL phases.
Method
Participants and Context
A total sample of 269 primary school students (M age = 8.84, SD = 0.81, 58% boys) was used in this study. There were 87 3rd grade students (4 classes) and 182 4th grade students (8 classes total). The sampling strategy was based on the needs appointed by the Lisbon’s City Hall. Children’s participation in this investigation also depended on their own volunteerism, teachers’ permission, the schools’ boards of directors, as well as parental consent.
The children who participated in this study lived in areas with schools belonging to the Portuguese Priority Intervention Educational Territories Program (PIETP). The PIETP program is an initiative for schools located in economically and socially disadvantaged areas, where low-income families live. The schools belonging to the PIETP program include educational projects to promote quality education, better students learning and results, as well as reduced drop-out rates and retention.
Instruments
Reading Span Task
This task comprises 12 sentences which were presented sequentially and remained on the screen for 4 seconds, followed by a 4 second inter-stimulus-interval, and then the next sentence. Children had to assess the sentence as being either true or false during a 4 second interval by writing the answer on an answering sheet (coded 1 for incorrect answers and 2 for correct answers). Moreover, they had to remember the last word of each sentence. After the sentences were presented, children were asked to write down the last words in their order of presentation. The time limit on the presentation of the sentences was established to decrease individual differences in strategy, as previous research has suggested (Engle et al., Reference Engle, Cantor and Carullo1992). The sentences were composed according to three criteria supported by the literature (Cowan, Reference Cowan2015). Firstly, the sentences had to be short (i.e., between four and seven words) and simple in terms of syntax to lessen linguistic difficulties, which may not be associated with WM. Secondly, sentences had to be trivial in terms of content to reduce knowledge demands. Thirdly, the last word had to be a well-known noun with three syllables or less. In joining sentences into lists for the test items, we tried to minimize semantic associations between the sentences, namely, their last words (Figure 1). This task revealed good reliability with a Cronbach’s alpha = .85.
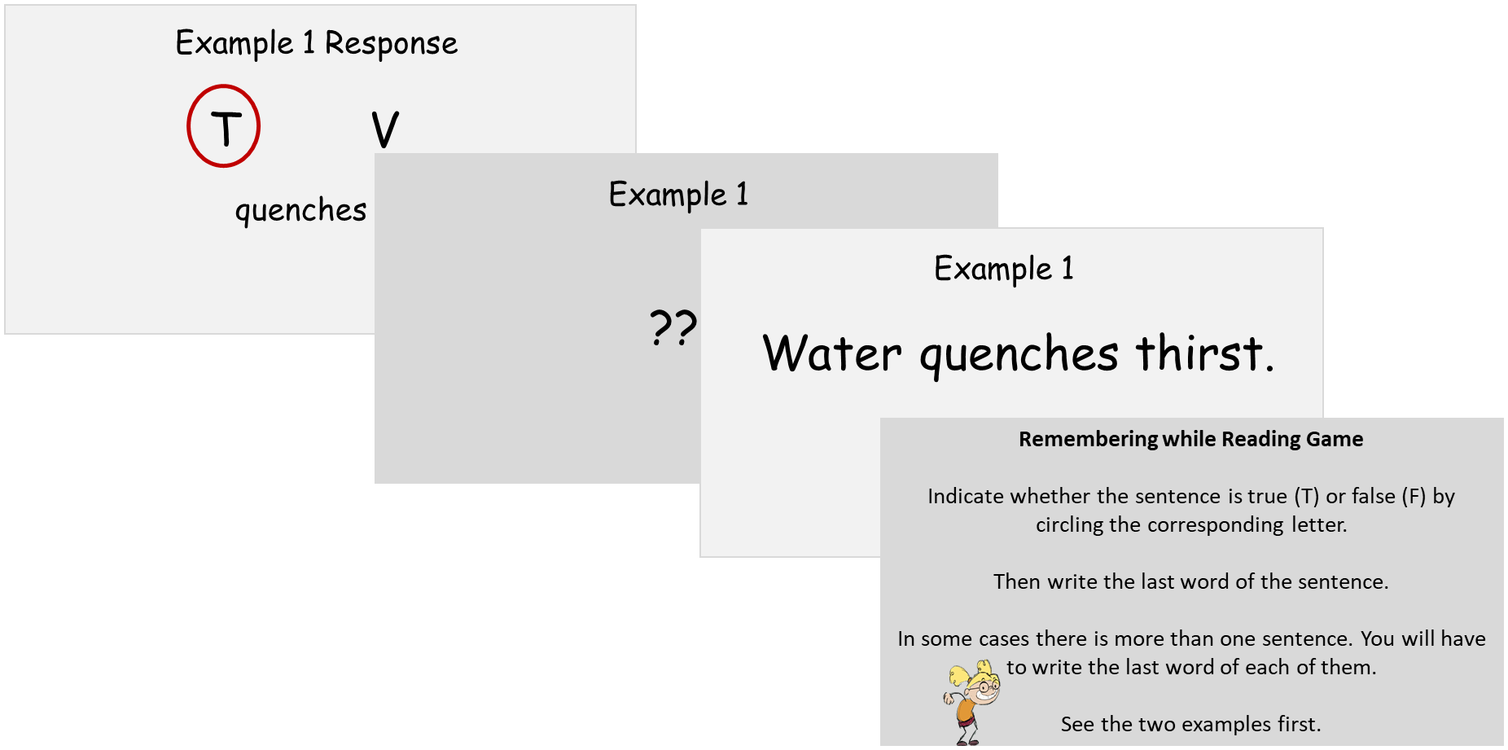
Figure 1. Reading Span Task Example
Computation Span Task
This task was similar to the reading span task, but with numerical content. Children had to verify simple equations, as opposed to sentences. The equations comprised one addition or subtraction, and only one- and two-digit numbers were involved. The answer to each equation to be remembered from a list had to be repeated in the correct order after the list presentation had finished. The results were always one-digit numbers (Figure 2). The presentation time for this task was the same as for the reading span task. Responses were written into empty slots on the answer sheet (coded 1 for incorrect answers and 2 for correct answers). This task revealed a good reliability with a Cronbach’s alfa = .85.

Figure 2. Computation Span Task Example
As in previous studies (Turner & Engle, Reference Turner and Engle1989), two demonstration examples and 3 practice trials were presented for each task. There were 12 items for each list length, which were presented in ascending order of length. List length ranged from 1 to 5 for reading span, and from 1 to 8 for computation span. Scoring was done based on right and wrong answer as previously noted.
The Learning Environment “Festarola”
The learning environment involves the digital game “Festarola”, which is meant to be played in 3 different sessions and was designed for young children aged 8 to 10, to train mathematics and problem-solving skills. Specifically, the children’s learning goal in Festarola was to organize a birthday party (Figure 3) considering their guests’ interests when choosing a theme, what they would need for the party, and the time they had to shop for items they needed, without overspending their budget. The gameplay had the same methodological characteristics of the adaptive computerized game-based recently published by Muñez et al. (Reference Muñez, Lee, Bull, Khng, Cheam and Rahim2022), and integrates different phases of problem-solving to raise awareness of the processes involved in children. It was also designed to promote SRL, since the children must register written responses regarding the choices they make in the different phases of SRL. We opted for a game-based learning environment to promote better and more meaningful learning experiences for students, as previous research has indicated (Taub et al., Reference Taub, Mudrick, Azevedo, Millar, Rowe and Lester2017).
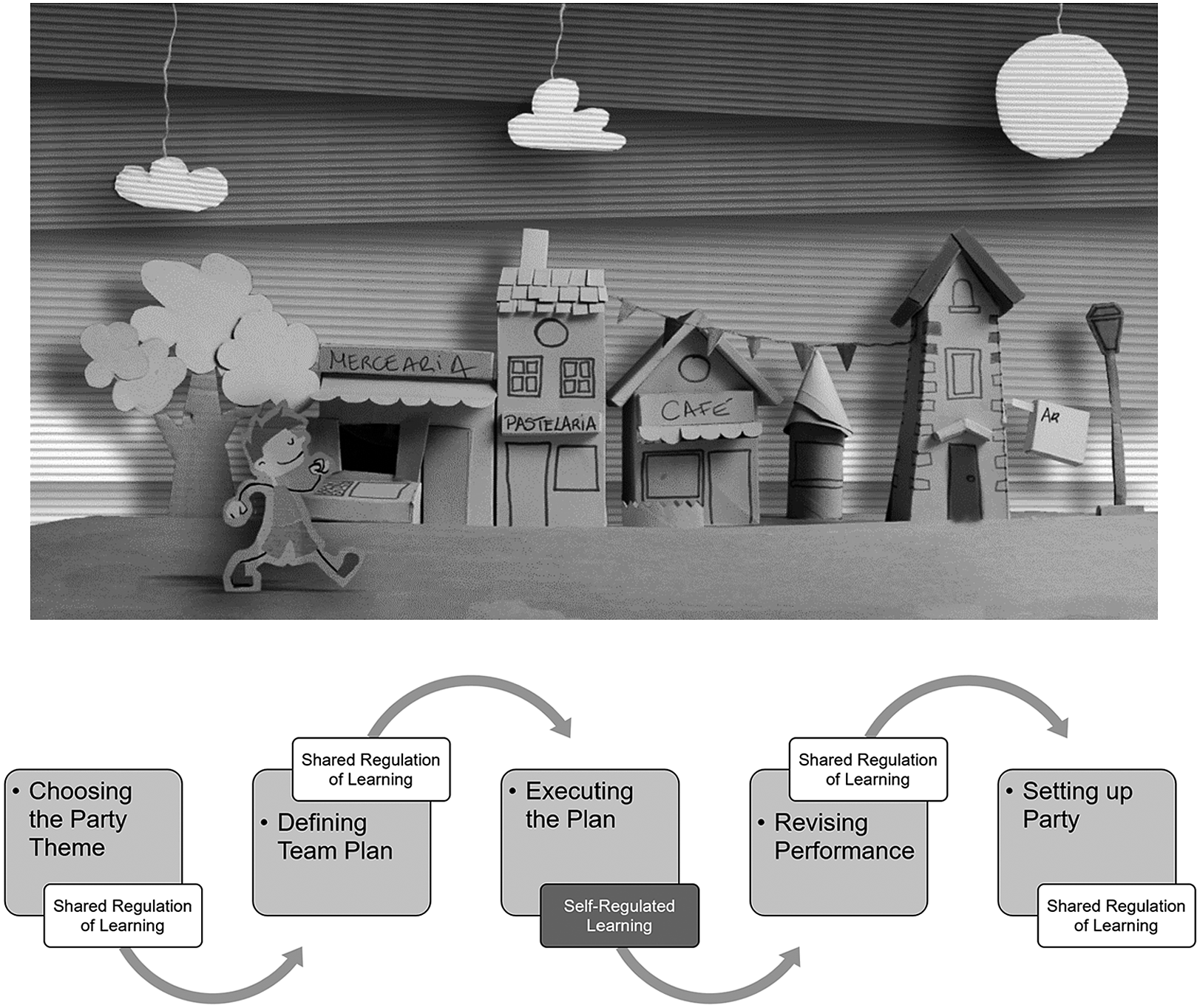
Figure 3. Festarola Cardboard Mockup and Activities
Festarola’s five activities in order of execution. Most are performed in groups and focus on shared regulation of learning, except for executing the plan which is performed individually and focuses on self-regulated learning.
At the beginning, each player is asked to choose a character and give it a name. This character serves as the player’s avatar during the game. Once all players are happy with their avatars, they must choose a name for their team. The main idea of this step is to reinforce their individual participation as members of a team and to establish the team itself. Moreover, the team’s name is used to support, save and resume mechanisms as well. After initializing the game, which starts after players define their team’s name, they have the option to resume a previously saved game. Saving is automatically performed after each activity.
The game includes two additional characters to guide players in the activities and to prompt them to reflect on their decisions. At the beginning of each session, a character presents a description of the activity, whereas another character asks players to justify their actions and decisions during the activity or at the end. For example, players should justify the theme they chose, the way the group divided the tasks and budget in the plan, the reasons for their shopping options in town, and why they returned items (or not) during the revision activity. These justifications are written in a text box and are in most cases the team’s responsibility; therefore a discussion among the group of children is expected.
Each participant is part a team, which is made up of two to four players. The team needs to perform tasks in a sequence that highlights different processes of problem-solving, including: Understanding the problem, identifying options to solve the problem, designing a possible solution, executing the solution (done individually) and, reflecting on the results and dealing with potential consequences. The overall goal is to comply with the established plan and please the guests of the party.
The game is designed to promote face to face discussions and to be used in classes at school. The first and third sessions are played collaboratively at the same computer. In the second session, players are invited to move to different computers (individual work) to execute the plan they agreed upon with the other members of the group in the first session. See the Appendix file for a more detailed description of the game, players’ actions, the coding answer scheme, the intraclass correlations of inter-rater agreement and reliability scores.
Performance score for players and analysis. The game score that is shown to players includes three different components, namely, the success of the party (which compares the theme of the objects with the preferences of the party participants), the budget spent (which is based on the number of items returned due to overspending) and the time taken while shopping for items. For this study, game achievement was evaluated by the number of items students returned, as this indicated students were not able to execute the task individually according to the plan they had agreed to and overspent money, thus, not respecting their budget. The budget score was computed based on the number of items returned in the revision of the execution phase. The rationale behind this scoring mechanism was the fact that the main reason for returning items was overspending beyond the limits of the budget. The less items returned, the higher the score (i.e., 1 to 5).
Problem in Mathematics Task: Processes and Calculations
Participants were asked to solve a traditional math problem individually (Simão et al., Reference Simão, da Silva, Marques, Ferreira and Paulino2015) and explain how they solved it. This problem was based on the problems given by the national exams provided by the Portuguese government. According to Ministry of Education and Science Guidelines, students must design and apply strategies to solve problems with non-negative rational numbers, in different contexts, as well as understand statistical information represented in different ways, and assess the plausibility of the results (Ministério da Educação e Ciência, 2013). The mathematics problem was elaborated by primary school teachers in order to be according to the current school curriculum for these grades. This procedure ensured that the semantic structure, data format, algorithm involved, and level of difficulty were all appropriate for the competencies required of students during these school years. Students were expected to articulate and discuss mathematical concepts, techniques, and reasoning using mathematics language from the different topics studied. They must also read and interpret data presented in tables, graphs, and diagrams, as well as analyze information that collects data of various types — discrete, qualitative, and quantitative—and summarize and represent the information gathered.
Essentially, participants were asked to explain: (a) What they had to do (problem understanding, planning and solving); (b) how they arrived at the problem solution (implementation of the plan); (c) how they knew if the answer was correct (results´ analysis and reflection).
Such questions follow the SRL process of problem-solving. The purpose of this activity was to understand how students solved the problem by considering the SRL phases. The math problem revealed a reasonable reliability of Cronbach’s alpha = .71. Primary school teachers coded and categorized students’ responses into various categories in accordance with each question and instructions of the problem to solve.
Questions 1 and 2 were coded as follows. 1 – No answer; 2 – Made an effort but provided the wrong answer; 3 – Half of the answer was correct (“The shepherd who has the most sheep is Filipe”; “João, Bento and Tino OR Zeca, Agostinho and Rogério.”, respectively); 4 – The full answer was given correctly (“The shepherd who has the most sheep is Filipe and he has 60 sheep.”; “João, Bento and Tino each have 30 sheep and/or Zeca, Agostinho and Rogério each have 40 sheep.”, respectively).
Questions 3, 4 and 5 were coded as follows. 1 – No answer; 2 – Made an effort but provided the wrong answer; 3 – Provided the correct answer (“There are 320 sheep total.”; “The average number of sheep per flock is 40.”; “Bento will make 375 euros.”, respectively).
Question 6 was coded as follows. 1 – No answer; 2 – Mentioned that they did not know how to explain how they solved the problem; 3 – Gave a description of what they did without referring specific strategies; 4 - Gave a description of what they did and mentioned what SRL strategies they used to reach their goal.
Question 7 was coded as follows. 1 – No answer regarding a distractor element included in the problem; 2 – Mentioned the distractor factor in the problem.
Procedures
Authorization for this study to be conducted and data to be gathered was granted by Lisbon´s City Hall, the schools’ boards of directors, the teachers, the parents and the students themselves. The schools’ boards of directors were contacted personally, and teachers sent out written consent forms to parents through the students. All of the instruments in this study were pilot tested with a class of 20 students. All participants were informed that they could quit the intervention program at any time.
The students performed the WM tasks prior to the game sessions with the aid of a computer and a hand-written worksheet where they placed their answers individually. Students also solved a traditional math problem on paper.
The intervention program (see Table 1) intended to promote SRL strategies which facilitated problem-solving in 3rd and 4th grade primary school children. Accordingly, the students’ role was essential in setting goals and in designing plans to execute the tasks proposed by teachers. Considering SRL strategies enable students to take a more active role in problem-solving, this project proposed to provide a better understanding of the processes involved in SRL in these primary school children. Therefore, the intervention program aimed to: (a) Stimulate and develop problem-solving strategies, based on SRL processes; (b) increase declarative and procedural knowledge about problem-solving strategies; (c) foster students’ knowledge of SRL strategies through various learning scenarios (i.e., digital game scenarios); (d) facilitate students’ compliance to solving problems by using computerized activities; and (e) promote students’ motivation to solve math problems.
Table 1. Sessions and Activities of the Intervention Program

The intervention included two workshops with teachers (one at the beginning and other at the end of the program) and eight sessions with each class of students in the 3rd and 4th grades (12 classes total). Each intervention session lasted approximately 60 minutes, for a total of 96 sessions. The intervention included different autonomous classroom activities for students and teachers. As so, it focused on the development of methodologies to teach problem-solving in math with the use of SRL strategies. Hence, different learning and teaching tools were developed to promote learning strategies that stimulated autonomy skills in problem-solving in math. Throughout the sessions, the different phases of SRL and problem-solving were worked on. Thus, specific sessions were developed to understand and train appropriate strategies for interpreting and understanding the problem, planning, implementing and monitoring the plan and revising. The game “Festarola” allowed participants to collaborate and observe how others approach problem-solving. Students monitored and regulated their own and each other’s thinking while observing how they operated mathematically and made group and individual decisions to express conclusions.
Furthermore, the project’s various tasks and instruments were designed to resemble a classroom environment in which learning and assessment take place in both individual and group formats. The game portrays the collaborative and individual dynamics of classroom activities, and the individual performance in a math problem reflects students’ competencies, including those developed in group tasks. Such transferability of learning, with regard to contexts and formats, has been suggested by several authors (Hadwin et al., Reference Hofmann, Schmeichel and Baddeley2017; Shukor et al., Reference Shukor, Abu and Ahmad2015).
Self-regulation, co-regulation, and socially shared regulation appear to co-occur during online tasks (Shukor et al., Reference Shukor, Abu and Ahmad2015). This is most likely because performance requires group observation and assessing task response accuracy, which cannot be achieved solely through self- and co-regulation. Individuals self-regulate by monitoring their own comprehension, and then they co-regulate by monitoring the comprehension of others. When an individual notices a group’s error, shared regulation occurs. Once they have socially regulated the new information, individuals engage in self-regulation (Shukor et al., Reference Shukor, Abu and Ahmad2015). Accordingly, research has suggested that other individuals’ perspectives can be applied to build and shape individual knowledge, which may be reflected in students’ learning.
Data Analysis
Structural equation modeling (SEM), specifically path analysis, was computed using the AMOS 23.0 software package (IBM, SPSS, Amos, 26). Firstly, we calculated Little’s MCAR test (Missing Completely at Random) with IBM, SPSS, 26, to examine whether missing data were randomly distributed (Little, Reference Little1988), providing a non-significant result (χ2 = 45.49; df = 36; p > .05) and therefore suggesting that the missing data was randomly distributed. The response rate was 93.7% (N = 269). We used the Expectation-Maximization data imputation technique to estimate the missing values. We checked for data normality with the Shapiro-Wilk test, which revealed that our data deviated from normal distribution. Therefore, we used the asymptotically distribution free method, which does not depend on the normal distribution of data. We also checked for multicollinearity in the data and none was present. All predictor variables (direct and indirect affects individually) and control variables age and gender (Patterson et al., Reference Patterson, Rowett, Hale, Grant, Roberts, Cousans and Martin2016) were tested for problem-solving accuracy in math, as suggested in the literature (Preacher & Hayes, Reference Preacher and Hayes2008). An alternative model was tested to examine whether WM could have only an indirect effect through SRL. This particular model presented a worse fit, χ2(19) = 2.62, CFI = .91, TLI =.86, IFI = .91, RMSEA = .08, 90% CI [.05, .11], p < .01, than the chosen model, which is shown in the results section. Moreover, we tested a model in which the variables ran in the opposite direction (where SRL mediated the relationship between performance and WM, where WM was predicted). The opposite model did not provide significant mediation effects.
Results
Table 2 shows the descriptive statistics of the measured variables. The chosen causal model presented a good fit (Byrne, Reference Byrne2013) to the data with the independent variable of WM (with computation span as a greater indicator of the construct than reading span: Factor weight scores respectively = .40 and .26), the dependent variables of performance in a traditional paper problem to solve in math and the results of the game, as well as the mediating variable of SRL, χ2(17) = 11.20, CFI = 1.00, TLI = 1.00, IFI = 1.00, RMSEA = .00, 90%CI [.00, .03], p > .05; SRMR .03, with factor score weights of .17 for understanding the problem, .28 for strategic planning, .20 for execution and .12 for self-reflection/self-evaluation. Bootstrapping confidence intervals were used and the p-values were calculated, according to Shrout and Bolger (Reference Shrout and Bolger2002) and Preacher and Hayes’ (Reference Preacher and Hayes2008) recommendations to test the significance of the indirect effects. The model proposes that the variance between WM and performance in problem-solving in math is explained by SRL.
Table 2. Means, Standard Deviations and Correlations of the Measured Variables
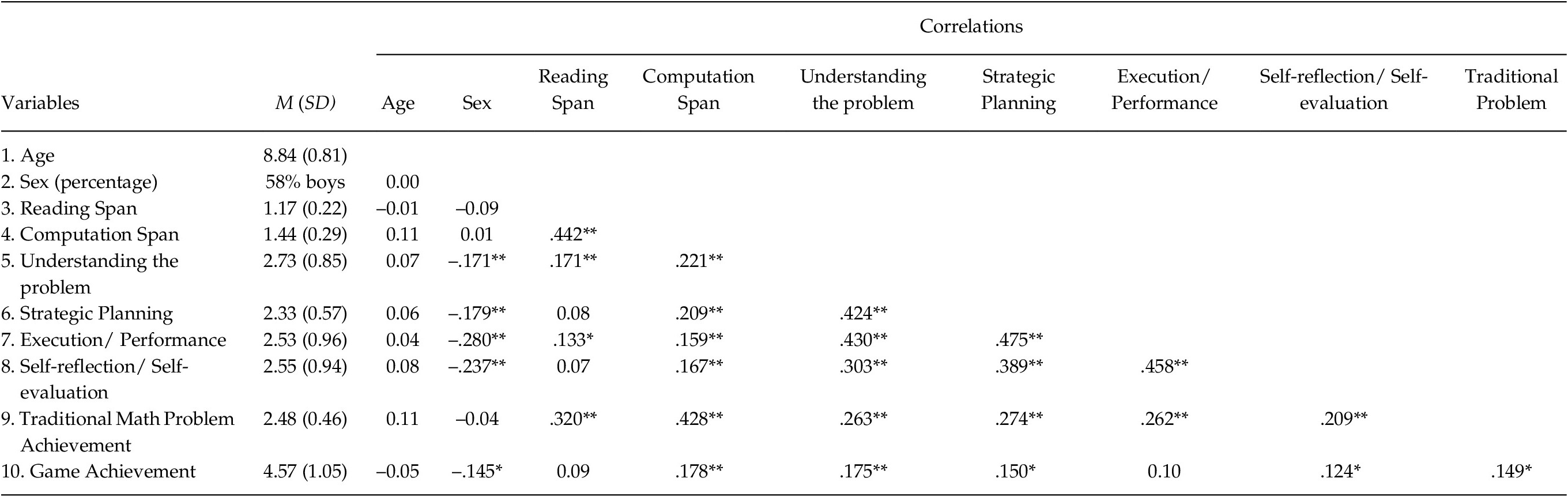
Note. * Correlation is significant at the 0.05 level (2-tailed). ** Correlation is significant at the 0.01 level (2-tailed).
All trajectories were positive and statistically significant. The total, direct and indirect effects of WM on the dependent variables (problem-solving accuracy/achievement in the traditional math problem and in the game) may be seen in Table 3. These results support the first two hypotheses of this study. Children with high WM performance showed higher accuracy scores in mathematic (Hypothesis 1). Also, those who were more self-regulated in their learning attained better accuracy (Hypothesis 2).
Table 3. Standardized Total, Direct and Indirect Effects of the Proposed Model

Note. * p < .05. ** p < .01.
The indirect effect of WM (mediated by SRL) was lower on performance in problem-solving than the direct effect. This result supports the third hypothesis of this study, namely, that children’s SRL process mediated the relationship between WM capacity and problem-solving accuracy in math, such that the effect of WM capacity had a lower effect on problem-solving accuracy in math through SRL. Moreover, the planning phase was in fact, a greater indicator of students’ SRL in math problem-solving, thus, supporting the fourth hypothesis of this study (factor weight score = .28).
All of the effects were statistically significant according to the Bootstrap sampling method (p < .01). Figure 4 shows our statistical model. Moreover, in the proposed model, we used an effect size converterFootnote 1 and the results suggested that the effect size of WM was .87 on SRL and 1.50 on traditional problem-solving, which are large and .50 on game results, which is considered medium (Cohen, Reference Cohen1988).
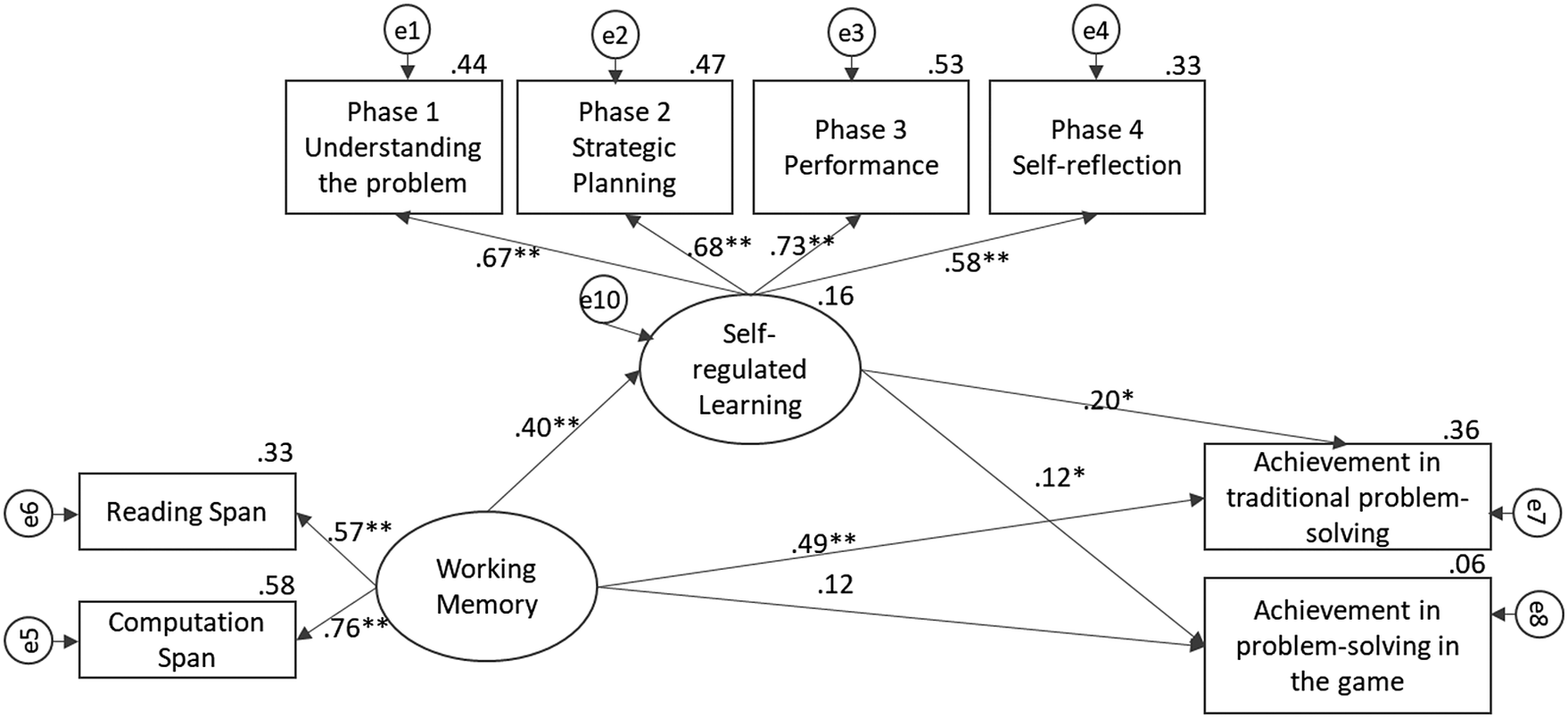
Figure 4. Statistical Model Showing the Standardized Regression Weights and Squared Multiple Correlations of the Mediation Model
Note. *= p < .01. ** p < .001.
Discussion
This study aimed to understand the role of SRL and its different phases in the relationship between WM and accuracy in problem-solving in math in primary school children. In line with previous research (Campos et al., Reference Campos, Almeida, Ferreira, Martinez and Ramalho2013; Swanson, Reference Swanson2016; Swanson et al., Reference Swanson, Arizmendi and Li2021), findings revealed that WM predicted children’s problem-solving accuracy in math, such that those with higher capability for temporary storage attained better accuracy. Both computation and reading span tasks were part of our WM construct in predicting problem-solving accuracy. A possible interpretation is that these WM dimensions both contributed to predicting performance in the game and children’s performance in a traditional problem because the tasks entailed numeracy and verbal skills to interpret the problem (e.g., Conway et al., Reference Conway, Kane, Bunting, Hambrick, Wilhelm and Engle2005). Furthermore, because children were using a ludic resource, such as the “Festarola” which inevitably implies emotional factors, another possible interpretation is that any of the students’ potential math anxiety could have not interfered, since this emotional aspect has been known to hinder better performance in problem-solving (Passolunghi et al., Reference Passolunghi, Cargnelutti and Pellizzoni2019). Moreover, our results revealed that computation span was a greater indicator of the construct than reading span. It would be likely that computation span would have a greater weight in the prediction since the final scores of both the game performance and the traditional problem required numerical processing. This interpretation is in accordance with previous findings that revealed that the predictive usefulness of different dimensions of WM relied on the type of tasks that were being performed (Perlow & Jattuso, Reference Perlow and Jattuso2018). Specifically, with regards to previous findings, a strategy development task depended more on linguistic abilities than numerical reasoning (Perlow & Jattuso, Reference Perlow and Jattuso2018).
In fact, the educational literature is relatively consistent in the relationship between executive functions and math skills (Bull et al., Reference Bull, Espy, Wiebe, Sheffield and Nelson2011). Although the math skills tested in previous studies included math grades provided from schools or simple problem-solving exercises, the current study advances in terms of the ecological and external validity by considering two WM tasks tapping the phonological loop structure requiring mainly storage and transformation (Ferreira et al., Reference Ferreira, Almeida and Prieto2011). Furthermore, it included not only a traditional math problem on paper (Campos et al., Reference Campos, Almeida, Ferreira, Martinez and Ramalho2013), but also the performance in the digital game, which is associated with high levels of enjoyment and WM capacity (Núñez Castellar et al., Reference Núñez Castellar, All, de Marez and van Looy2015).
Moreover, we also found that SRL predicted children’s problem-solving accuracy in math, such that those who were more self-regulated in their learning attained better accuracy (Otto, Reference Otto2007). This relationship may be attributed to the students’ capacity to set goals, plan their use of strategies, focus their attention on the tasks, their ability to self-record their own learning activities and the capacity to self-evaluate their learning performance (Zimmerman, Reference Zimmerman2013). Hence, this study adds to the literature by including measures taping the different phases of SRL considering Zimmerman’s model (Reference Zimmerman2013). Therefore, in a 21st century pedagogical environment surrounded by technology, this study validates the Zimmerman’s (Reference Zimmerman2013) SRL model with the inclusion of a digital game platform. This technology may be used as a tool to evaluate and monitor students’ level of SRL considering each phase of the model.
In addition, we found that children’s SRL process mediated the relationship between WM capacity and problem-solving accuracy in math, such that the effect of WM capacity had a lower effect through SRL on problem-solving accuracy in math. In fact, evidence has been provided regarding the issue that literacy and arithmetic proficiency mediate the relationship between WM and math performance (Swanson & Fung, Reference Swanson and Fung2016). Despite the important role of executive functions in math, the literature emphasizes that reading skills, calculation proficiency (Fung & Swanson, Reference Fung and Swanson2017; Zheng et al., Reference Zheng, Swanson and Marcoulides2011) and domain-specific knowledge (Fung & Swanson, Reference Fung and Swanson2017) can contribute to explain children’s problem-solving performance in math (Lin, Reference Lin2020). Therefore, since there is a positive relation between reading or math performance and self-regulation processes (Day & Connor, Reference Day and Connor2017), we can provide strong theoretical support to understand the mediating role of SRL to explain the path between WM capacity and performance in math problem-solving. Some literature has referred that planning (one of the phases of SRL) and WM are commonly used to label cognitive executive functions (Packwood et al., Reference Packwood, Hodgetts and Tremblay2011). Therefore, the current study sheds some light on the delimitation of both constructs: WM and SRL. This study provides an interesting contribution to the literature by showing that the WM simultaneous storage and transformation facet of the von Bastian and Oberauer (Reference von Bastian and Oberauer2013) model indirectly explained math achievement through the way students performed the different phases of the Zimmerman’s (Reference Zimmerman2013) SRL model. Based on these findings, we suggest that future studies should also test the other facets of the WM model (i.e., coordination, and supervision), as well as their indirect relationship with academic achievement through repeated measures methodologies considering the different phases of the Zimmerman’s (Reference Zimmerman2013) SRL phases.
Lastly, our results indicated that the planning phase was a greater indicator of students’ SRL in math problem-solving with greater factor weight scores. This evidence reinforces the importance of the PASS theory of intelligence (Das et al., Reference Das, Naglieri and Kirby1994) to explain the relationship between WM performance and math performance. In line with our findings, previous studies suggested that the PASS theory has been relevant to explain the role of the cognitive process of planning, specifically, to understand how students develop their metacognitive strategies (Mayoral-Rodríguez et al., Reference Mayoral-Rodríguez, Timoneda-Gallart and Pérez-Álvarez2018). Therefore, our study provides a significant contribution to understand the role of SRL and WM in explaining math performance. Accordingly, we highlight the importance of metacognitive strategies and the capacity to plan their use of strategies (Zimmerman, Reference Zimmerman, Boekaerts, Pintrich and Zeidner2000) to explain the link between WM capacity and math problem-solving.
In sum, the current research provides at least three contributions to the literature, specifically in the fields of cognitive and educational psychology. Firstly, with these findings, we provided a comprehensive theoretical framework that explains the important role of SRL in explaining the relationship between verbal and non-verbal WM tasks and math performance considering different math tasks. Secondly, our study is an important attempt to integrate problem-solving phases (Polya, 1965/Reference Polya1981) and the SRL phases (Zimmerman, Reference Zimmerman2013) and explain performance in problem-solving accuracy in math. Thirdly, we provided a model that explains which phases are more relevant in explaining the indirect path between WM capacity and math performance. Therefore, our study reinforces the relevance of the PASS theory of intelligence (Das et al., Reference Das, Naglieri and Kirby1994) to understand the SRL phases, and specifically the planning phase that provided a greater contribution in the indirect relationship between WM capacity and math performance.
Despite its contributions, this study is not without limitations. Firstly, the cross-sectional design of the present study does not allow for causal conclusions. Moreover, since the effects of this intervention were not controlled (i.e., all children participated due to the requirements from the Lisbon’s City Hall), we cannot provide specific information regarding the degree to which problem-solving and its relation with WM were due to training and thus, generalize our results. Nonetheless, the current study provides important insights and resources for future studies to use with different samples and sampling strategies (i.e., populations of children without treatment). Moreover, we studied data from students from one country only. Therefore, it would be interesting for future research to investigate cross-cultural differences in this area. Also, we did not consider any individual cases for analysis purposes. Considering we focused mainly on storage and transformation WM tasks, future studies could consider other cognitive functions in the relationship with the SRL phases in problem-solving in math. Specifically, future studies might include other WM facets (von Bastian & Oberauer, Reference von Bastian and Oberauer2013) associated to the primary functions of coordination, and supervision. Since cognitive abilities may be dependent on individual differences (Zheng et al., Reference Zheng, Swanson and Marcoulides2011), we suggest that future studies investigate the role of different components of WM on the different dimensions of SRL in performance in problem-solving in math. There is evidence that improving math performance may actually lead to improvements in executive functions and vice versa (Clements et al., Reference Clements, Sarama and Germeroth2016). A future study may consider within-subjects longitudinal analysis where the dynamics of SRL can be measured with more accuracy.
Future research may analyze the developmental trajectories of these skills (McClelland et al., Reference McClelland, Cameron, Duncan, Bowles, Acock, Miao and Pratt2014). Also, since our sample consisted of 3rd and 4th graders, it would be interesting to understand how these findings fit the findings of younger and older children, considering developmental trajectories of SRL and WM in solving math problems.
Despite the limitations, the current study constitutes an important methodological advance with the inclusion of a digital game and task measures of math performance. Additionally, the study includes two measures of WM capacity that cover the executive functioning complexity in terms of the phonological loop (von Bastian & Oberauer, Reference von Bastian and Oberauer2013).
Our results provide important insights as to how guiding students in the regulation of learning can have positive implications in terms of problem-solving accuracy in math in contemporary learning environments. Thus, providing students with instruments and meaningful environments, where they can engage individually and collaboratively in tasks using technology, can help them become more reflective and strategic in managing their learning process. Our findings highlighted the role of the SRL phase of planning to explain the indirect path between WM capacity and problem-solving accuracy in math.
Since previous studies reported positive effects of planning on math performance (Mayoral-Rodríguez et al., Reference Mayoral-Rodríguez, Timoneda-Gallart and Pérez-Álvarez2018), we propose the need to develop training platforms or gamified interventions to develop students’ capacity to develop planning. Since the Portuguese Ministry of Education and Science Guidelines propose that students must design and apply strategies to solve problems with non-negative rational numbers, in different contexts, understand statistical information represented in different ways, and assess the plausibility of the results (Ministério da Educação e Ciência, 2013), we believe that the learning environment (serious game “Festarola”) we presented in this study includes all of the required features that enable students to follow all the aforementioned guidelines and accomplish their respective goals. Specifically, teachers used technology, such as our proposed learning environment and reinforced SRL as an important process to achieve those goals, with a special emphasis on the planning phase. Moreover, by using such resources, teachers in this study were able to work on their students’ cognitive and affective abilities, which are considered relevant in problem-solving (Passolunghi et al., Reference Passolunghi, Cargnelutti and Pellizzoni2019) - as the “Festarola” fosters the development of both areas.
The opportunities that come with the technological advancements enable students to learn in a meaningful and authentic manner and to register the learning process (Taub et al., Reference Taub, Mudrick, Azevedo, Millar, Rowe and Lester2017). Researchers and educational professionals should consider these advancements and be prepared to deal with new learning and teaching challenges and guidelines to maximize the possibilities that enable the learning/teaching processes.
Appendix
Detailed Description of the Game, Players’ Actions, the Coding Answer Scheme and Reliability
The problem presented in «A Festarola» was created according to the Portuguese Ministry of Education and Science guidelines for this level of education, concerning complexity, difficulty, and themes. Mathematical tasks and operations were developed in collaboration with a group of teachers teaching 3rd and 4th grades. This means that students must read and evaluate statements; mobilize knowledge of facts, concepts, and relationships; select and apply previously studied and trained rules and procedures properly; review, the recommended method as needed; and analyze the final outcomes. Aside from these skills, the game “A Festarola” addresses two curricular domains from the third and fourth years, namely time (time, addition and subtraction) and money (addition and subtraction of amounts of money).
The game was developed to be a tool to be used by teachers and researchers. For this reason, it records all actions performed in the activities and all texts written by the students, to allow future analysis. Additionally, different scenarios may be presented in the game by configuring a set of features. The set of interests of the group of participants can change, thus, altering the difficulty of the overall challenge. For example, if most participants share common interests, it is easy to reach a good solution regarding the theme of the party; however, in case of conflicting interests, it will be more difficult to reach a decision. Teachers and researchers can also define a budget limit and time limit to complete tasks. By doing this, teachers can define different levels of pressure and flexibility of the tasks, which enables more exploration and correction if the time limit is greater. Lastly, the items’ prices in the shops can be changed as well. This may change the nature and difficulty of the math calculations needed in the game. For example, if the prices are all whole small numbers (e.g., a one digit number), it will be easier for the players to estimate the overall costs of buying items rather than if the numbers in the prices are greater (e.g., two digit numbers) or include decimals.
Students should choose a theme, and establish the team plan (interpreting the problem and strategic planning – collaborative work). Each student is responsible for choosing the products they will acquire for the party. Then, students go shopping individually (session two – individual task) on different computers and lastly, revise what was done individually - execution phase (session three – collaborative task).
The game is divided into three sessions. The first session provides information and sets the game’s objectives. This session includes the interpretation and planning phases of self-regulated problem-solving. This session is discussed in group and students are asked to interpret the information that is being given to them and what is being asked of them (e.g., “What information do you have and what do you have to do?”). Each student may write a response on the computer. For Phase 1 “understanding the problem”, we coded as 1 for no answers. We coded irrelevant information to solve the problem as 2 (e.g., "My birthday is on the same day as my colleagues’”; “A lot of things”); we coded as 3 specific information (e.g., number of guests; time-out; money; theme) or what was requested of them (e.g., “We were asked to organize a party successfully”); and lastly, we coded as 4 specific information with what was requested of students (e.g., “We have to organize a party that will have 8 guests, we have 100 euros to spend and we have a time limit. We have to try to make our party a success.”). In order to verify the inter-rater reliability, we computed an Intraclass Correlation (ICC), which gave us good values for the ICC (2, 2) = .99, according to the literature (McGraw & Wong, Reference McGraw and Wong1996). Essentially, 99% of the variance in the mean of two raters was true score variance.
The first session also includes choosing the theme of the party and defining a plan for the team, which consists of a list of things to buy, rent or hire. Defining the plan includes assigning individual responsibilities. Different shopping lists are defined (one per team member) and part of the overall budget is assigned to each player. At the end, players need to agree on which list each one is responsible for. At the end of this session, students are asked why they chose to proceed the way they did individually. Each student may write a response on the computer. Students’ responses were coded as follows: 1 = no response; 2 = irrelevant information to solve the problem (e.g., “because it’s interesting”); 3 = explanation as to why students planned the way they did, including the suitability of the theme to the guests’ interests (e.g., “we divided the budget evenly so we could all have time to go shopping”; “because the most guests liked this theme.”). We verified the inter-rater reliability by computing an intraclass correlation, which gave us good values for the ICC (2, 2) = 1.00, according to the literature (McGraw & Wong, Reference McGraw and Wong1996). Specifically, 100% of the variance in the mean of two raters was true score variance.
The second session of the game is performed individually. Each player goes shopping at the town shops according to the items on their list and the assigned budget. However, this activity does not impose strong restrictions. That is, players can buy different things and go over budget. Actions in town take time, hence there is a limited number of actions that players can perform in this phase. At the end of this session, each student is asked why he/she bought what they did individually. Students’ responses are coded as follows: 1 = no response; 2 = irrelevant information (e.g., “because they are cute”); 3 = information provided mentions the game’s overall objective of organizing a party (e.g., “we bought things for the party”); 4 = information provided mentions the team’s specific plan to organize the party, which is also part of the game’s objective (i.e., “I respected the budget I planned with my colleagues.”). We computed an intraclass correlation to verify the inter-rater reliability, which gave us good values for the ICC (2, 2) = .95, according to the literature (McGraw & Wong, Reference McGraw and Wong1996). Accordingly, 95% of the variance in the mean of two raters was true score variance.
The third session is played in group again to confirm the items players’ bought. During this phase, they have the opportunity to check the initial plan and revise their shopping options by returning items. Each student can return items in their cart. These decisions are made together and once agreement is reached, the game advances to the set-up of the party. In this activity, the players distribute the items in the room where the party will take place. Once they finish, the party begins and the final score is presented. Then, students are asked to reflect on their score and explain why they received that score individually and in group. Students’ responses are coded as follows: 1 = no response; 2 = irrelevant information (e.g., “because it was like this”; 3 = general self-evaluation without mentioning the criteria they had to follow in the game, such as, time, money, guests and theme) (e.g., “we did well”); 4 = specific self-evaluation mentioning one or more criteria they had to follow in the game (e.g., we did well because we bought only what we had planned to.”). We computed an intraclass correlation to verify the inter-rater reliability concerning players’ responses, which gave us good values for the ICC (2, 2) = .99, according to the literature (McGraw & Wong, Reference McGraw and Wong1996). Accordingly, 99% of the variance in the mean of two raters was true score variance. These self-regulated problem-solving phases revealed a reasonable reliability with a Cronbach’s alpha = .71.









