Academic performance in mathematics is a growing concern within the educational community, especially if the results obtained by Spanish students in mathematical proficiency tests, such as the Programme for International Student Assessment (PISA) test (Cordero-Ferrera, Cebada, & Pedraja-Chaparro, Reference Cordero-Ferrera, Cebada and Pedraja-Chaparro2013; Organization for Economic Co-operation and Development, OECD, 2012) or the TIMSS (Trends in International Mathematics and Science Study) conducted by the International Association for the Evaluation of Educational Achievement (IEA, 2011) are taken into account. In both cases, Spanish students have achieved stable results over the last few years, which have been lower than expected and lower than those observed in the other countries evaluated. Specifically, in the PISA test of 2011, which included 65 countries, Spanish students scored 484 points (10 below the OECD mean, OECD, 2012) and, in the test carried out in 2015, Spain was one of the 72 participating countries, obtaining 486 points (4 below the OECD average, OECD, 2016). Furthemore, in the TIMSS test in which 4183 Spanish students enrolled in 4th year of primary school took part, obtaining 482 points were obtained. This score was below the average of the 63 participating countries and below the 522 points of average score in OECD.
Given this situation, it is relevant to analyze what aspects determine success in learning. Some authors have pointed out the importance of promoting the self-regulation of the learning process and the possibilities offered by new technologies. In this line, this article aims to analyze whether the intervention with a hypermedia tool in fifth and sixth grade of primary mathematics generates benefits on the improvement of students’ knowledge and their perceived use of self-regulated strategies.
Self-regulated learning process
A key factor in academic success within the area of mathematics is self-regulated learning ability (Cheng, Liang, & Tsai, Reference Cheng, Liang and Tsai2013; Du Toit, 2012; Önemli & Yöndem, Reference Önemli and Yöndem2012). Self-regulated learning is understood as an active process in which students set the goals that guide their learning by trying to monitor, regulate and control their cognition, metacognition, motivation and behavior with the intention of achieving them (González-Pienda, Fernández, Bernardo, & Núñez, Reference González-Pienda, Fernández, Bernardo and Núñez2014; You & Kang, Reference You and Kang2014; Zimmerman, Reference Zimmerman2008). Thus, self-regulated learning includes three dimensions, cognition, metacognition and motivation.
With respect to metacognition, Pintrich describes it as a higher order ability that allows directing and regulating cognitive, affective and motivational processes to achieve a specific goal (Ifenthaler, Reference Ifenthaler2012). It implies two main components: knowledge and skill (Lucangeli & Cabriele, 2006). Metacognitive knowledge refers to information about learning strategies and how, when and why to use them. The metacognitive abilities imply the application or use of this knowledge and, therefore, the regulation of our cognitive activity and the process of learning (planning, executing and assessment during the performance of the tasks; Pennequin Sorel, Nanty, & Fontaine, 2010; Zimmerman, Reference Zimmerman2008). The distinction between knowledge and metacognitive skills lies mainly in the fact that, even when students are aware of the different strategies, they do not always implement them effectively (Bransford, Brown, & Cocking, Reference Bransford, Brown and Cocking2000). In this sense, authors such as Pennequin et al. (Reference Pennequin, Sorel, Nanty and Fontaine2010) have pointed out that the acquisition and development of knowledge would precede its use and, therefore, would precede metacognitive skills. While knowledge begins to develop at the age of 6, its correct application does not seem to reach maturity until 11–12 years of age (Veenman, Wilhelm, & Beishuizen, Reference Veenman, Wilhelm and Beishuizen2004).
The development of knowledge and metacognitive skills is relevant given its relationship with successful learning in areas such as mathematics. However, students are not always good regulators of their own learning (Dignath, Buettner, & Langfeldt, Reference Dignath, Buettner and Langfeldt2008; Lehmann, Hähnlein, & Ifenthaler, Reference Lehmann, Hähnlein and Ifenthaler2014; Pacheco, García, & Díez, Reference Pacheco, García and Díez2009).
Involvement of new technologies in learning
The difficulties in the teaching learning process of students are even more noticeable when deploying their metacognitive and self-regulatory skills when learning takes place in open, technological and virtual environments such as hypermedia applications (Azevedo & Jacobson, Reference Azevedo and Jacobson2008). These hypermedia applications are understood as adaptive learning systems usually based on an online program that provides a personalized learning environment (Özyurt, Özyurt, Baki, Güven, & Karal, Reference Özyurt, Özyurt, Baki, Güven and Karal2012). Despite the fact that students are very familiar with this type of tools, they do not show this same habituation regarding its use for educational purposes (Núñez et al., Reference Núñez, Cerezo, Bernardo, Rosario, Valle, Fernández and Suárez2011). In this sense, self-regulation is influenced both by the learning situation and the individual characteristics of the student, as well as by the characteristics of the task (Valle et al., Reference Valle, Rodríguez, Cabanach, Núñez, González-Pienda and Rosário2009). With respect to the characteristics of the task, computer learning environments add certain difficulties for students in essential disciplines such as mathematics or social sciences, for example, as they are more demanding regarding the application of self-regulatory processes (Azevedo, Reference Azevedo2005; Graesser, McNamara, & VanLehn, Reference Graesser, McNamara and VanLehn2005). In addition, authors such as Samruayruen, Enriquez, Natakuatoong, and Samruayruen (Reference Samruayruen, Enriquez, Natakuatoong and Samruayruen2013) or Tsai, (2010) point out that those less self-regulated students are less successful in technological or IT learning environments. This fact warrants the need for technological tools such as hypermedia applications to guide the learning process by encouraging self-regulation, in addition to promoting the acquisition of content and skills.
Therefore, the question to be asked is whether the use of technology can be used to improve student self-regulation during the learning process, highlighting the essential role of this process (self-regulation) in student interaction with the computer (Panaoura, Reference Panaoura2012; Steffens, Reference Steffens2001). In this line, Azevedo (Reference Azevedo2005) developed a metacognitive tool called MetaTutor to highlight the role of the metacognitive and self-regulatory processes used by Secondary Education students during learning. Their results have indicated that learning a science subject through a hypermedia tool provides the necessary scaffolding for the regulation of learning. The explanation of the effectiveness of this type of scaffolding has centered on the changes in student’s mental models, gains in the declarative knowledge of the pretest at the posttest and the process data regarding the self-regulatory behavior (Azevedo, Reference Azevedo2005). In relation to the improvement of self-regulation in mathematics through new technologies, Harskamp and Suhre’s (2006, 2007) studies should be noted. These authors (2007) developed a computer program aimed at problem solving and analyzed its effectiveness both in the execution of these activities and in their planning and review or assessment. The results of its application on 198 students aged between 15 and 17 years of age (initially classified on the basis of their performance using five mathematical problems) indicated that students had learned to effectively analyze problems and to reach a correct solution approach. However, the benefits were greater in the case of more expert solvers (whose performance in pretest mathematical problems had been higher). Nevertheless, in their previous work, Harskamp and Suhre (Reference Harskamp and Suhre2006) observed that both expert students and those with less ability benefited equally, showing greater effectiveness in their analysis and verification abilities of problem solving.
In this line, Núñez et al. (Reference Núñez, Cerezo, Bernardo, Rosario, Valle, Fernández and Suárez2011) carried out a study with the objective of comparing the effectiveness of an intervention program in virtual format to train self-regulatory strategies among university students. They used a quasi-experimental design, with an experimental group (n = 167) and a control group (n = 206) and pre and posttest measurements. Among the variables of this study, there were the declarative knowledge of self-regulatory learning strategies and the use of the planning-execution-assessment self-regulated learning macro-strategy (Zimmerman, Reference Zimmerman2008). Planning relates to the processes that precede the accomplishment of the task, the foresight; Execution refers to the processes that occur during the execution of the task; and Assessment covers those processes that occur after learning in order to assess performance. The obtained data showed that the students who participated in the training program improved significantly in their domain of declarative knowledge and in the general use of learning strategies, in addition to showing significant improvements in academic performance.
These investigations, such as Núñez et al.’s (2011) or Harskamp and Suhre’s (2006, 2007), were carried out on university and compulsory secondary education students, respectively. In addition, in the case of Harskamp and Suhre’s (2006, 2007) studies, the classification of the sample was carried out through the student’s performance of five mathematical problems and the assessment of their abilities of planning and assessment through the students’ comments on their problem-solving process. Harskamp and Suhre’s (2006, 2007) studies did not assess the execution phase of self-regulation.
In the present line of research, two objectives were set out for this paper. First, to analyze the effectiveness of a hypermedia tool aimed at the mathematical contents of fifth and sixth grade of Primary Education (Hipatia; Cueli, González-Castro, Krawec, Núñez, & González-Pienda, Reference Cueli, González-Castro, Krawec, Núñez and González-Pienda2016) on improving the knowledge and perceived use of self-regulatory strategies in low-, medium-, and high-performing students. The starting hypothesis was that, taking into account the relationship between performance and self-regulated learning (Samruayruen et al., Reference Samruayruen, Enriquez, Natakuatoong and Samruayruen2013; Tsai, Reference Tsai2010) and Harskamp and Suhre’s (2007) results, the treatment group with better academic performance would be those who would present a greater increase in knowledge and perceived use of the planning-execution-assessment strategy after the intervention.
Secondly, the other objective was to analyze the effect of the intervention based on the perceived knowledge of the self-regulation strategies (low, medium and high), in order to determine whether those who present a greater perceived knowledge, manifest using more planning-execution-assessment strategies. In this case, the hypothesis was that students with higher perceived knowledge would also indicate a greater use of the self-regulatory strategy given that, as pointed out by Pennequin et al. (Reference Pennequin, Sorel, Nanty and Fontaine2010) and Veenman et al. (Reference Veenman, Wilhelm and Beishuizen2004), the development of knowledge precedes the ability and, therefore, its use or initiation.
Method
Participants
A total of 624 students took part in this study, 298 girls and 326 boys, between the ages of 10 and 13 years (M = 10.98, SD = 0.718) enrolled in 5th (46%) and 6th (54%) of Primary Education (PE). The sample was obtained through an intentional procedure, following a convenience sampling (Casal & Mateu, 2000). The participants were assigned to one of two experimental conditions: a treatment group (TG n = 391; they received treatment with the Hipatia hypermedia application) and a comparative group (CG n = 233; they followed the usual learning methodology in mathematics).
The analyzes showed statistically significant differences between the TG and the CG as a function of the year course χ2(1) = 4.006, p = .045; and the age F(1, 622) = 11.492, p = .001, η2 = .018, although with a small effect size. Given the equivalence between course and age, the latter was taken as a covariate in later analyzes. There were no statistically significant differences between the two groups according to sex χ2(1) = 1.256, p = .262.
To reach the first objective, participants were classified into three groups based on their academic performance in mathematics (on a scale of 0 to 10) in the second school evaluation period: Low performance (participants with a score between 0 and 5), mid performance (participants with a score between 6 and 8) and high performance (participants with a score of 9 or 10). One hundred and sixty-nine students with low performance (84 girls and 85 boys; 64 in 5th PE and 105 in 6th PE), 129 with a medium performance (65 girls and 64 boys; 56 in 5th PE and 73 in 6th PE), and 79 with a high performance (37 girls and 42 boys, 32 in 5th PE and 47 in 6th PE) were included in the TG. In the CG, 78 students with low performance (30 girls and 48 boys, 32 in 5th PE and 46 in 6th PE), 76 with a medium performance (29 girls and 47 boys, 33 in the 5th PE and 43 in 6th PE) and 46 with high performance (29 girls and 17 boys, 23 in 5th PE and 23 in 6th PE) were included.
Afterwards, in order to fullfill the second objective, the students were classified based on their perceived knowledge of self-regulation strategies (CEA in Spanish, or KSS in English) in three groups: low, medium and high knowledge. The TG consisted of 126 students with low CEA (55 girls, 71 boys, 57 in 5th year, 69 in 6th year), 88 students with medium CEA (45 girls, 43 boys, 40 in 5th, 48 in 6th year) and 177 students with a high performance (93 girls, 84 boys, 69 in 5th PE and 108 in 6th year PE). In the CG, 71 students with low CEA (27 girls, 44 boys, 41 in 5th and 30 in 6th year PE), 44 students with medium CEA (23 girls, 21 boys, 26 in 5th and 18 in 6th year PE) and 118 students with high performance (55 girls, 63 boys, 54 in 5th year and 64 in 6th year PE) were included.
Instruments
In order to achieve the above objective, measures of academic performance and self-regulation were taken. Academic performance in mathematics was recorded prior to the intervention with the hypermedia tool (students’ final grades for the second assessment period). In the Spanish Education System, the academic course consists of at least three assessment periods that indicate the academic performance and acquisition of contents achieved by the students through a rating scale ranging from 0 to 10. For the present study, the scores obtained for the 2nd assessment period were considered.
Self-regulation was assessed through two questionnaires, the Knowledge of Self-Regulatory Strategies Questionnaire (“Cuestionario de Conocimiento de Estrategias de Autorregulación”, CEA, Rosário et al., 2007) and the Self-Regulation Processes Inventory (“Inventario de Procesos de Autorregulación”, IPAA), (González-Pienda et al., Reference González-Pienda, Fernández-Cueli, García, Suárez, Fernández, Tuero-Herrero and Da Silva2012; Rosário et al., Reference Rosário, González-Pienda, Pinto, Ferreira, Lourenço and Paiva2010).
The Knowledge of Self-Regulatory Strategies Questionnaire (Rosário et al., Reference Rosário, Mourao, Núñez, González-Pienda, Solano and Valle2007) assesses the student’s perception of self-regulatory strategies. Thus, it allows us to specify to what extent the student reports knowing the strategies, resources and decisions that imply self-regulated learning. It consists of ten closed-ended questions with three response options, two false and one true (see Appendix 1.). The maximum direct score in this test is ten and the minimum is zero. Once the test was performed, the number of correct answers yielded the direct score. The studied variable was the knowledge of self-regulatory strategies. The questionnaire has shown good reliability indexes with a Cronbach’s alpha of .89 (García, Rodríguez, González-Castro, Álvarez-García, & González-Pienda, Reference García, Rodríguez, González-Castro, Álvarez-García and González-Pienda2016; Núñez et al., Reference Núñez, Cerezo, Bernardo, Rosario, Valle, Fernández and Suárez2011), and of .55 when administered to the present sample.
The Self-Regulatory Processes Inventory (IPAA) (Rosário et al., Reference Rosário, González-Pienda, Pinto, Ferreira, Lourenço and Paiva2010) assesses the student’s perception of the application of self-regulation strategies that he/she performs during the three phases of the process (planning, execution and assessment). The IPAA consists of twelve items with a Likert-style response format of five alternatives: 1 (never), 2 (rarely), 3 (sometimes), 4 (many times) and 5 (always) (see Appendix 2). In this case, the items were adapted to the self-regulatory processes in the area of mathematics. The IPAA items are representative of the three phases of Zimmerman’s (2002, 2008) model of self-regulatory learning, that is, planning, execution and assessment. This questionnaire was applied since the goal of the hypermedia tool is to guide the student to perform these three phases during his/her work in mathematics. To assess this process, the student was asked to respond taking into account his/her work and study in the subject of mathematics. The variables to be taken into account with the completion of the questionnaire were the planning, execution and assessment. The score was obtained from the mean of the student’s answers in the set of items that assessed each one of these three dimensions. That is, the mean score was calculated for those items that assess planning, another mean score was calculated for those items that assess execution and another for those that evaluate assessment. The maximum score in each variable was five and the minimum was one. Cronbach’s alpha was .80 for the planning factor, .85 for the execution factor, and .87 for the assessment factor (García et al., Reference García, Rodríguez, González-Castro, Álvarez-García and González-Pienda2016; Rosário et al., Reference Rosário, González-Pienda, Pinto, Ferreira, Lourenço and Paiva2010). For the present sample, the reliability index was .747.
Intervention Program
According to Mayer (Reference Mayer2004), the process that leads to meaningful learning depends on both, how the student processes the information and on the material presented. Thus, the promotion of learning depends on both, the improvement in the students’ processing of information and on how the materials are presented (Valle et al., Reference Valle, Rodríguez, Cabanach, Núñez, González-Pienda and Rosário2009). Therefore, in the present study, an intervention program was applied, namely a hypermedia application called Hipatia (Cueli et al., Reference Cueli, González-Castro, Krawec, Núñez and González-Pienda2016), originally developed at the University of Minho Footnote 1 . The development of Hipatia was carried out through a multidisciplinary team of psychologists, mathematics and computer science teachers. The theoretical concepts and activities included in this hypermedia application were supervised by experts in the field (mathematics teachers) in both, the Portuguese and Spanish versions.
Hipatia, given its nature and theoretical foundation, is aimed at improving or enhancing students’ self-regulatory skills and the acquisition of specific mathematical skills. The design of the tool was established on a web page that both students and teachers could easily access from their personal computer (at home or at school) or from a digital whiteboard. In this space, the tool offered different contents (geometric places, angles, polygons, areas, etc.) adapted to the competences of 5th and 6th year of Primary Education. All of these topics followed the same learning routine. They were divided into 10 sections, which had different activities that included theoretical concepts, practical exercises and solving mathematical problems. To perform these activities, the program used several tools, with the three main ones being the pencil, the pen and the rubber or eraser (in addition to the calculator, compass, tools to draw parallel lines, perpendicular lines,…). The pencil allows students to write and carry out operations, while the pen allows them to point or highlight data. Students use these tools to carry out the requested activities, to calculate in order to solve a problem, to schematize and/or to search for problem-solving strategies.
The theoretical basis of Hipatia is based on Zimmerman’s model (2002, 2008) of self-regulation, on the basis of which self-regulated students direct their learning through the implementation of a series of strategies, activating and modifying their cognitive, metacognitive and behavioral processes, before, during and after learning takes place and following the phases of planning, execution and assessment of the process. The hypermedia tool guides this process through specific instructions that favor each of the self-regulatory phases. A detailed description of the tool in relation to the self-regulatory model is given in Cueli et al.’s (2016) study.
In Hipatia, the topics are exposed based on the following dynamics: first, a concept is presented through an example (activating prior knowledge), afterwards, the content is developed simply and the degree of difficulty is progressively increased, encouraging the student to focus on main ideas and concepts (trying to strengthen the planning phase). This fact is especially relevant considering that mathematical skills develop in a hierarchical and integrating manner, hence the importance of the contents being sequenced in a suitable way according to the degree of difficulty and the necessary prior knowledge (Kikas, Peets, Palu, & Afanasjev, Reference Kikas, Peets, Palu and Afanasjev2009; Olkun, Altun, & Deryakulu, Reference Olkun, Altun and Deryakulu2009).
Once the knowledge has been acquired, it is put into practice through different guided activities in which students are given clues as to how resolve a problem after they have commited an error (thus enhancing the execution phase). In the execution of these activities, students and teachers have the possibility to change the numerical data of the problems, thus multiplying the number of activities that the student can perform to consolidate learning. This process of execution is permanently guided by instructions, “clues” and reminders of the theoretical information necessary for the correct resolution, as according to Swanson (Reference Swanson1999) and Kroesbergen and van Luit (2003), the two teaching practices in Mathematics with the best results are direct instruction and cognitive strategies of self-regulation and control.
Finally, all the topics have a final section that summarizes the main ideas and poses some questions with alternative response options. This is to promote the process of self-assessment and monitoring of learning (assessment), which is key considering that the greater the amount of revision performed, the higher the academic performance (Valle et al., Reference Valle, Rodríguez, Cabanach, Núñez, González-Pienda and Rosário2009). Lastly, unlike usual teaching, in Hipatia it is the student himself/herself who sets the pace of learning by having control over the sequence in which a concept is progressively extended or new ideas are presented. By enabling autonomous and permanent learning, these self-regulatory competences allow students to increase their performance and academic success, to control and regulate aspects of their cognition, motivation and behavior, to select and structure learning environments mediating between contextual and personal characteristics and to set goals and monitor their compliance (Núñez et al., 2006; Valle et al., Reference Valle, Rodríguez, Cabanach, Núñez, González-Pienda and Rosário2009).
Although Hipatia contains different subjects from the 5th and 6th year Primary Education curriculum, the present study only applied the Geometric Places topic, which included different concepts (circumference, circle, circular crown, line segment bisector, angle bisector, equidistant points of a line, and geometric places in the space). All the students started the intervention working on the same content.
Procedure
After obtaining the authorization on behalf of the schools and the consent of the students’ parents and/or guardians, the pre-test information was recorded during a class session (approximately 50 minutes). Student participation was voluntary, and the confidenciality of their data was ensured at all times. After the pre-test assessment, the tool was applied with the TG. This application was carried out by the teacher in charge of the mathematics subject in each center. All the teachers received the same training in the usage of Hipatia and in the work sequence to be followed for the selected topic. Once a week, a professional attended each of the schools in order to control the application process and ensure the established guidelines for the intervention with the tool were being followed. To do this, the professional complied with a protocol in which he/she confirmed whether the teacher had followed these five steps: (1) presentation of the content to the students through an example; (2) each student works individually on the computer; (3) monitoring is carried out by teachers on an individual basis; (4) the corresponding activity is carried out on the computer; (5) the session is shared and summarized. Contact with the schools was carried out on a weekly basis by telephone in order to control the intervention process.
At the same time, the teaching staff of the CG taught the same topic (geometric places) following the usual methodology, which is based on the presentation of concepts by the teacher following the contents of the reference book. The classes were expositive, with all groups following the same division and organization of the contents that do not differ between the comparative group and the TG (both worked on the same subject and contents). In addition, all the students from the comparative group performed the practical activities listed in the reference book.
After the intervention, the posttest assessment was performed on both groups. The two assessment moments were carried out through a web platform that could be accessed by each student with his/her username and password and the indicated assessment instruments could be completed.
Finally, the mathematics scores obtained in the second assessment period were collected, which were provided by the schools through anonymous assessment reports.
Data analyses
Given the objectives of this study, in addition to the descriptive statistics study, univariate analysis of covariance (ANCOVAs) and Student’s t-tests were carried out. Initially, the differences between the TG and the CG were analyzed for variables such as age and sex. The differences were significant according to age, which was treated as a covariate. Differences in pretest measurements were analyzed and, where significant, were included as covariates in the posttest analysis.
First, the effectiveness of the hypermedia tool on perceived knowledge and the perceived use of the planning-execution-assessment strategy was analyzed. Four ANCOVAs with the experimental condition (TG and CG) and academic performance (low, medium and high) as fixed factors were carried out. The dependent variable was, in each case, the CEA score and the IPAA variables, planning, execution and assessment. Moreover, the Student t-statistic for related samples was calculated to analyze the pretest-posttest linear evolution of the three performance groups in the CEA variables, planning, execution and assessment. Secondly, the effectiveness was analyzed based on the perceived knowledge of self-regulatory strategies. Three ANCOVAs were performed using perceived knowledge (low, medium and high) and experimental condition (TG and CG) as fixed factors. The IPAA scores (planning, execution and assessment) were included as a dependent variable. Furthermore, the Student’s t-statistic was calculated for the three groups of perceived knowledge. Finally, the effect of the interaction between performance and perceived knowledge in the TG was calculated. Planning, execution and assessment were included as dependent variables. These statistical analyses were performed using the SPSS 19.0 (IBM, Chicago, IL) statistical software.
Results
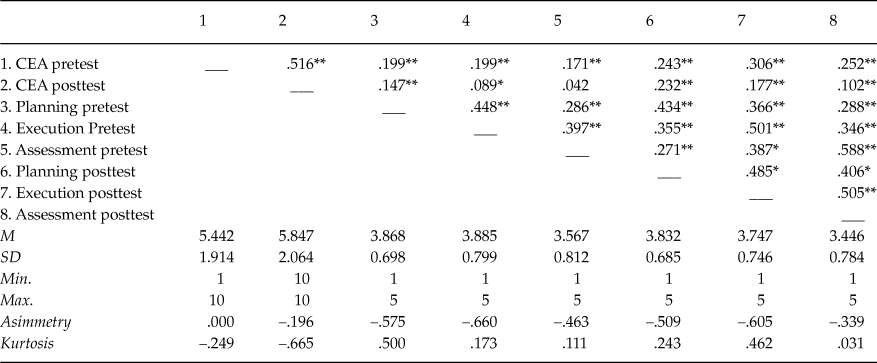
Table 1 shows the descriptive statistics (mean and standard deviation) as well as the asymmetry and kurtosis data of the variables included in the study (prestest and posttest), along with the correlations between them. Following Finney and DiStefano’s (2006) criteria, which establishes scores between 2 and –2 in asymmetry and 7 and – 7 in kurtosis, it was concluded that all variables showed a normal distribution.
Table 1. Correlations between the Planning, Execution and Assessment Variables in the Prestest and the Posttest. Means, Standard Deviations, Minimums, Maximums, Asimmetry and Kurtosis
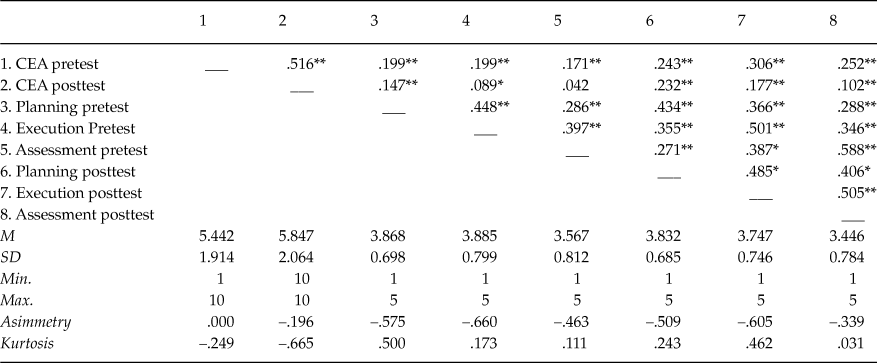
Note: **The correlation is significant at a level of .001. *The correlation is significant at a level of .05.
Differences based on academic performance and experimental condition
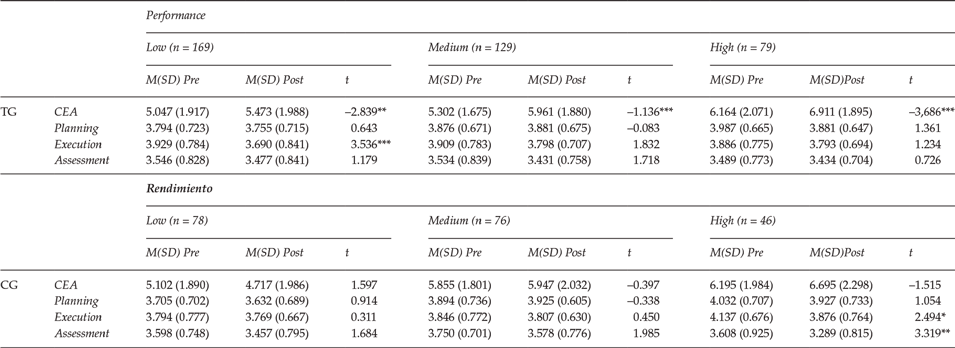
The ANCOVA of the pretest measures showed no statistically significant differences for the interaction between performance x condition (CEA p = .332; planning p = .623; execution p = .074; assessment p = .493). Significant differences were obtained independently for performance CEA F(2, 571), = 13.30, p ≤ .001 η p 2 = .045 and planning F(2, 571), p = .004, η p 2 = .019, but not for the experimental condition. Means and standard deviations are shown in Table 2.
Table 2. Means, standard deviations and Student’s t-test results for students with low, medium, and high performance in the knowledge of self-regulatory strategies, planning, execution and assessment variables

Note: M = mean; SD = Standard Deviation; TG = Treatment Group; CG = Comparative Group; t = Student’s t -test; CEA = Perceived knowledge of self-regulated strategies.
* =p < .05; **=p < .01; ***=p < .001.
The ANCOVAs of the posttest measures showed that the performance x condition interaction was not significant for CEA (p = .314), planning (p = .571), execution (p = .891), or assessment (p = .241). As covariates, the CEA and planning were significant (p ≤ .001; for both cases).
If only the performance was taken into account, the differences were significant in the case of CEA F(2, 569) = 17.048, p ≤ .001, η p 2 = .057 and of planning F(2, 569) = 3.199, p = .042, η p 2 = .011; but not in the case of execution (p = .472) or assessment (p = .292). In the CEA, post hoc analyzes revealed differences between the low-medium, low-high and medium-high performance groups (p ≤ .001; for all three cases). In planning, post hoc analyzes indicated statistically significant differences between the low-medium groups (p = .020).
Taking into account only the experimental condition, the differences were significant for CEA F(2, 569) = 7.057, p = .008, η p 2 = .012; but not for planning (p = .897), execution (p = .443), or assessment (p = .827). The direction of the differences can be seen in Table 2.
Finally, with the linear contrast through the Student’s t test, the evolution from the prestest to the posttest was analyzed (Table 2). The results showed that in the case of CEA, the TG with low, medium and high performance improved statistically significantly from pretest to posttest. Regarding the perceived use of the strategy, the differences were statistically significant in the TG with low performance for execution. In the CG, the differences were statistically significant in the perceived use of execution and assessment, where scores were reduced in the posttest.
Differences based on the perceived knowledge of self-regulatory strategies and the experimental condition
Initially, the ANCOVAs with the pretest measures indicated that the interaction between perceived knowledge and experimental condition was not statistically significant (planning p = .301; execution p = .772; assessment p = .162). Independently, knowledge was found to be significant for the three variables (planning F(2, 568) = 10.015, p ≤ .001, η p 2 = .034; execution F(2, 568) = 13.365, p ≤ .001, η p 2 = .045; assessment F(2, 568) = 10.717, p ≤ .001, η p 2 = .036), but not the condition.
The ANCOVAs for the posttest, with perceived knowledge x experimental condition as intersubject variable, were not statistically significant for planning (p = .237), execution (p = .257), or assessment (p = .316). The covariates were significant (p ≤ .001, in all cases).
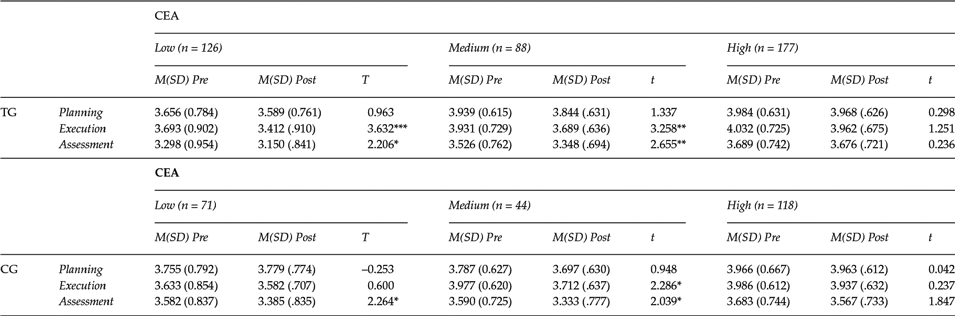
If only the perceived knowledge was taken into account, the differences were found to be significant for the three variables, planning F (2, 616) = 5.137, p = .006, η p 2 = .0316, execution F (2, 616) = 14.420, p ≤ .001, η p 2 = .045 and assessment F(2, 616) = 8.720, p ≤ .001, η p 2 = .028. The direction of these differences can be seen in Table 3. The post hoc results showed differences for planning between groups of low-high perceived knowledge (p ≤ .001), for execution between low-medium (p = .022), low-high (p ≤ .001) and medium-high (p = .003); and for assessment between low-high (p ≤ .001) and medium-high (p = .002).
Table 3. Means, standard deviations and Student’s t-test results for students with low, medium, and high knowledge of self-regulatory strategies, planning, execution and assessment variables
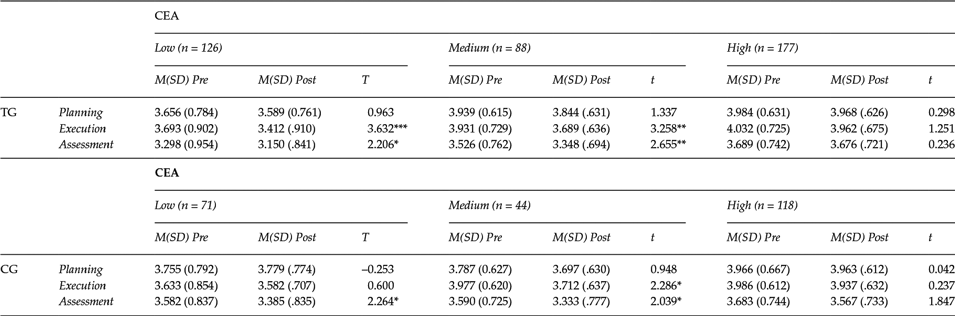
Note: M = mean; SD = Standard Deviation; TG = Treatment Group; CG = Comparative Group; t = Student’s t-test; CEA = Perceived knowledge of self-regulated strategies.
* =p < .05; **=p < .01; ***=p < .001.
Only taking into account the experimental condition, the ANCOVA results were not statistically significant for planning (p = .723), execution (p = .244), or assessment (p = .575)
Finally, for the pretest-posttest evolution, Student t-tests were performed in all three groups (low, medium and high CEA) (Table 3). The analysis showed that in the TG, the differences were statistically significant for the execution and assessment in the low and medium CEA groups. In CG, differences were statistically significant in execution (in the medium CEA group) and assessment (in the low and medium CEA group).
Differences based on perceived knowledge and academic performance
Finally, three ANCOVAs were carried out for the TG with the objective of specifying the posttest differences according to the interaction between perceived knowledge and performance (fixed factors) on the IPA variables. Only age was considered as covariate since the pretest measures were not significant (planning p = .091, execution p =.637, assessment p = .862). The posttest differences did not yield any significance (planning p = .081, execution p =.550, nor assessment p = .837). Only taking perceived knowledge into account, significant differences were found for planning F(2, 367) = 8.181, p ≤ .001, η p 2 = .043, execution F(2, 367) = 15.415, p ≤ .001, η p 2 = .077 and assessment F(2, 367 = 14.541, p ≤ .001, η p 2 = .073. Post hoc analyzes revealed differences in planning between the low-medium (p = .026) and low- high (p ≤ .001); in execution for low-medium (p = .031), low-high (p ≤ .001) and medium-high (p = .022); and in assessment for low-high (p ≤ .001) and medium-high (p = .004). In the case of performance as fixed factor, the differences were not statistically significant either (planning p = .262, execution p =.560 or assessment p = .390).
Discussion
Two objectives were initially set out in this paper. Firstly, to analyze the differential effect of the intervention with a hypermedia tool as a function of academic performance of mathematics students (measured through the scores in the subject before the intervention) on the perceived knowledge of self-regulatory strategies and the perceived use of the planning-execution-assessment strategy. Secondly, to analyze the differential effect in terms of the perceived knowledge of self-regulatory strategies on the perceived use of the planning-execution-assessment strategy.
Regarding the first objective, the differences in the interaction between the experimental condition and performance were not statistically significant for the CEA, planning, execution or assessment. From the analyses of the evolution of the prestest to the posttest, it was observed that students in the TG with low, medium and high performance, showed after the intervention higher levels in the knowledge of the self-regulatory strategies in a statistically significant way. This was not the case in the planning, execution and assessment variables where, similarly to Harskamp and Suhre’s (2006) results, both students with high performance and those with lower performance benefited equally, with no significant differences between them. Although the differences were not statistically significant, their direction indicates that, in the three self-regulatory phases, the students who were part of the TG had lower means in the posttest compared to the pretest. This may be related to the increase in the knowledge of self-regulatory strategies, which leads students to be aware of the absence of such process in their behavior during learning. In other words, after treatment, students are aware of adequate self-regulatory strategies and can recognize the absence of such strategies in their learning, a situation that does not occur in students in the comparative group in which there is no such increase in their general knowledge of self-regulatory strategies. As authors like Valle et al. (Reference Valle, Rodríguez, Cabanach, Núñez, González-Pienda and Rosário2009) pose, students should not only understand and know what strategies to use but also how and when to use them.
Regarding the second objective, the differences in the interaction between condition and perceived knowledge were not statistically significant for any of the three dependent variables (planning, execution and assessment). The analysis of the pretest-posttest differences in the use of the strategy based on the perceived knowledge reflected a certain decrease in the use of the planning-execution-assessment strategy in the post-test, which was statistically significant in students with low and medium knowledge of TG. The reason for this finding may be related to the proposals of authors such as Annevirta and Vauras (Reference Annevirta and Vauras2006), who have pointed out that an extensive metacognitive knowledge, self-regulatory in this case, does not necessarily guarantee the application of this knowledge to practice. In addition, the interaction between knowledge and performance for the treatment group was not significant but, when knowledge was analyzed independently, significant differences were found, as opposed to the performance. This reveals a greater weight of perceived knowledge versus performance in explaining the differences in students’ use of the planning, execution and assessment strategy.
The increase in the knowledge of self-regulatory strategies is very relevant considering that this knowledge precedes the application of metacognitive abilities (Flavell, Reference Flavell1979), which are developed following a process of maturation that occurs between the ages between 11 and 12 years (Veenman et al., Reference Veenman, Wilhelm and Beishuizen2004). The participants in this study were aged between 10 and 13 years, so the results could be related to a lack of maturation that would mean that students do not yet have the necessary skills to use the self-regulatory strategy. In any case, this finding highlights the need to work on increasing the knowledge of strategies, especially because an improvement at this level may allow the student to adjust his/her perceptions to reality. Moreover, an increased knowledge can benefit the subsequent acquisition of abilities. In any case, although this stimulation of students’ self-regulation abilities is necessary, their internalization and correct application entail a longer process that will allow them to be able to carry out self-regulatory learning in the future, provided they have received a specific training for that end. Similarly to Núñez et al.’s (2011) study, after an intervention on university students, not only the knowledge of self-regulatory strategies increases but also the use of these strategies.
Finally, some disadvantages of this study, such as the short duration of the intervention and the small sample size in the CG with high academic performance or in the CG with a medium perceived knowledge of strategies, should be highlighted. Moreover, another limitation to be noted is the absence of process measures and repeated measures of student execution during the work with the hypermedia tool. In this case, only the use or the lack of use of the strategy has been analyzed and not the effectiveness of its use, which, would be yielded from the analysis of the process followed by the student. In addition, the absence of continuous and subsequent assessments has not allowed a longitudinal analysis. This type of analysis would allow us to deepen in the progress achieved during the intervention or, in any case, the benefits after its completion over time. The inclusion of these variables would be useful in contrasting the information provided by the students, especially since some studies have shown a low correspondence between the actual performance in the execution of children and adolescents and the difficulties observed in several areas of daily life (Lezak, Howieson Bigler, & Tranel 2012).
Taking into account the limitations exposed, the possibility of taking into account the relationship between the information provided by the student about his/her self-regulatory process and the recording of his/her actual performance during the learning situation is posed as a future line of research. Furthemore, it would be pertinent to analyze the differences between the actual execution and the one informed by the student according to age groups, in order to establish when the perception is more adjusted to the reality of the execution.
Appendix 1
CUESTIONARIO DE ESTRATEGIAS DE AUTORREGULACIÓN (CEA) SELF_REGULATED STRATEGIES QUESTIONNAIRE
Please answer the questionnaire by choosing the option (only one) you consider is the most correct.
Before starting any task (an exam, work, …), it is important to: (A) Think about the goals and objectives, and make a plan to achieve them; (B) Wait for the teacher to say what needs to be done; (C) Do the task as diligently as possible, without wasting time and avoiding excuses.
In personal study, a fundamental aspect is the organization and management of time, which implies: (A) To prepare schedules to organize the time in the days before the exams; (B) To prepare personal schedules that include time for daily study, preparation of exams, for essays, for leisure …; (C) To be flexible when performing tasks, leaving time to play, relax, and talk with friends.
To avoid procastination (leaving study assignments for another time), it is best to: (A) Promise yourself awards or treats if you complete the task on time; (B) Divide the task into small steps and allot a certain amount of time for each one; (C) Try to motivate yourself by doing other things (go for a walk, talk with friends, use the computer, …) and then get on with the task.
In order to take notes that help you when studying and preparing for exams, it is important to: (A) Try to write down everything the teacher says; (B) Copy the exercises of the best student in the class; (C) To write down the most important aspects that the teacher points out in class and afterwards complete them at home with the help of the textbook.
Highlighting is a study strategy whose main function is: (A) To indicate those contents that will have to be studied later; (B) To select the most important information, after reading and understanding the text; (C) To decorate the notes in order to make them more colourful and motivating when it comes to studying them.
The objective of abstracts and conceptual maps is: (A) To organize and elaborate the information in a personal way, ordering it according to its level of importance; (B) To reduce information in order to facilitate studying; (C) To write the information so as to memorize it.
To study a text, it is important to memorize comprehensively, which implies: (A) Re-writing the contents in order to learn them; (B) Relating the new information to the knowledge you already have; (C) Repeating the new contents again and again until you know them off by heart.
When preparing for exams, you should: (A) Study the day before the exam to ensure you remember it; (B) Prepare cheats for data and dates that are useless to learn from memory; (C) Take into account the type of exam you are going to sit, as the way you study should be adapted to it.
In personal study, the search for help when dealing with a difficulty is considered: (A) as a constructive and very important way of solving problems when you are stuck; (B) A useful strategy to avoid potential failure; (C) A way of “giving up”.
After sitting an exam, you should: (A) Do nothing, because the important work has already been done, you should just wait for the score; (B) Analyze what you have done and the results, in order to draw conclusions and be able to improve; (C) assess the results you obtained in comparison to you classmates’ scores.
Appendix 2
INVENTARIO DE PROCESOS DE AUTORREGULACIÓN DEL APRENDIZAJE SELF-REGULATED LEARNING PROCESSES INVENTORY (IPAA)
Now, we are going to show you 9 things you can do “more or less” when you study Mathematics. Below each one, we have given you an example so that you can understand them better.
Mark the (1) box when you NEVER do the task you have been described, or box (2) if you RARELY do it, box (3) if you SOMETIMES do it, box (4) if you ALMOST ALWAYS do it or box (5) if you ALWAYS do it.