Deductive reasoning is at the core of the human mind, without it many intellectual disciplines, such as maths, law, physics or logic, to name but a few could not be possible. Also, much of our diary inferences are based on deductive arguments, such as “if you study hard you can get the grant and it is the case that you are studying hard”; in this instance, people do not find it difficult to infer that “you can get the grant” is a valid conclusion. However, the content and logical structure of arguments could affect our deductive inferences. Many studies have showed that the content of problems (or their semantics) affects the inferences that people build or evaluate on conditionals problems (Evans, Newstead, & Byrne, Reference Evans1993). Another factor that affects the inferences that people make is the logical structure of the problem, which could generate a directional effect in problems with one or multiple premises. The logical structure is related to the order of the terms in the premise while directional effect involves the fact that people find it easier to make or to process inferences in one direction rather than in the other. For instance, it has been shown that in the conditional rule if A, then B, participants make more forward inferences (from A to B) than backward inferences (from B to A), whereas for the conditional form A only if B, participants make more backward inferences than forward inferences (Evans, Reference Evans1977, Reference Evans1993; Evans & Beck, Reference Evans and Beck1981). Other studies have shown that the amount of time that reasoners take to endorse backward or forward inferences varies according to different conditional forms (Grosset & Barrouillet, Reference Grosset and Barrouillet2003; Santamaría & Espino, Reference Santamaría and Espino2002). The logical structure in problems with two premises depends on the figure of the problem. As in the case of syllogisms, four different types of figures can be distinguished in double conditionals:

In each figure, there are three different terms (A, B, C). The term that is repeated in both premises (B) is called the middle-term and the other two terms (A, C) are called the end-terms. As well as in one-premise problems, directional effect has been found in conditionals with two premises (e.g., Espino & Hernández, Reference Espino and Hernández2009; Oberauer, Hörnig, Weidenfeld, & Wilhelm, Reference Oberauer, Hörnig, Weidenfeld and Wilhelm2005). For instance, Oberauer et al. (Reference Oberauer, Hörnig, Weidenfeld and Wilhelm2005) have found that when the conditional took the shape of figure 4, participants took less time to process forward inferences (from A to C) than backward inferences (from C to A); but when the conditional corresponded to figure 1, it took them less time to process backward inferences. Directional effect in conditionals is a very controversial topic. Different hypotheses have been offered to explain the directionality effect in simple and double premises: one hypothesis claims that the directional effect is due to the order of the terms in the working memory (FIFO hypothesis) during the integration of the premises. Another hypothesis claims that the directional effect stems from the fact that people prefer to make inferences from the term that plays the role of relatum to the term that plays the role of object (semantic hypothesis).

The FIFO hypothesis (Johnson-Laird, Reference Johnson-Laird1984) provides an explanation of the directional effects based on two assumptions. First, the account claims that in order to construct an integrated model of the two premises, people attempt to bring middle terms together. Second, it suggests that the way to state a conclusion is based on the “first in, first out” principle (FIFO; Broadbent, Reference Broadbent1958): the first piece of information entering the integrated model of the premises will be the first element in the conclusion. On simple conditionals, such as “If A then B”, only the second assumption is considered. In this case, a forward directional effect (from A to B) is predicted for any conditional and bi-conditional due to the fact that the first information entering the working memory is the first term (A). For double conditionals, such as “If A then B and if B then C”, the FIFO hypothesis predicts different directional effects depending on the figure. When the two middle terms (B) of the premises occur in sequence (for example, if A then B and If B then C), the FIFO hypothesis claims that the two premises can be easily combined to form an integrated model. In this case (figure 4: A-B/B-C), the first term in the integrated model is “A” and consequently, by the FIFO principle, the most frequent conclusion will be in the forward direction (from A to C). However, when the middle terms are not in sequence, additional operations will be necessary in order to bring them together. According to Johnson-Laird (Reference Johnson-Laird1984), when the middle terms are not in sequence (such as in figure 1: B-A/C-B), people could use two different procedures to build the integrated mental model of the premises. First, the order of the terms within the first premise (B-A) and the second premise (C-B) could be switched round (A-B / B-C). The second strategy to build the integrated model consists in reversing (renewing) the order of the two models of the two premises. The way to proceed is to construct a model of the second premise and then to add the information from the first premise (C-B-A). Once the terms of the premises are in sequence, reasoners will select the conclusion, and the FIFO principle will determine the direction. However, “it is not clear what mechanism might lead reasoners to choose one or the other strategy. However, this selection may well be influenced by superficial factors” (Espino & Santamaría, Reference Espino and Santamaría2013, p. 318).

In figure 2 (A-B/ C-B) and figure 3 (B-A / B-C), there are two ways to obtain the integrated model; in the first case, the integrated model can be “A-B-C” and, in the second case, it can be “C-B-A”. For example, in figure 2, one procedure starts with the second strategy (C-B), after which the first strategy needs to be applied (B-A) to obtain the integrated model (C-B-A). In that case, according to the FIFO hypothesis, people should make more C-A than A-C conclusions. However, the second way to obtain the integrated model is by using only the first strategy in the second premise (B-C). In this case, according to the FIFO principle, participants should make more A-C than C-A conclusions. Given that either procedure could be used to obtain the integrated model in figure 2 and 3, the FIFO hypothesis does not predict any differences as far as the direction of the inferences (A-C versus C-A) is concerned. In brief, the main claim of the FIFO hypothesis is that the directional effect depends on the figure: there should be a directional effect in figures 1 and 4, but not in figures 2 and 3. Contrary to this claim, we will show that the directional effect does not necessarily depend on the figure, but on the semantic role of the end term, as the semantic hypothesis has suggested.

Our main goal in this paper is to explain the ways in which the directional effect works in double conditionals with different directionality according to the semantic hypothesis (Oberauer & Wilhelm, Reference Oberauer and Wilhelm2000; Oberauer et al., Reference Oberauer, Hörnig, Weidenfeld and Wilhelm2005). This hypothesis introduced different factors to explain how the figure of problems affects premise integration and interferes during the inference stage. As far as premise integration is concerned, three factors were suggested in order to explain the directional effect: the inherent directionality, the “relatum = given” and the “given-new” principles. The first factor claims most connectives used in a deductive reasoning task have an inherent directionality. Based on the works of Logan (Reference Logan1995) and Gernsbacher (Reference Gernsbacher1991), the authors claim that the meaning of a statement “is in part represented as a set of cognitive procedures for building a representation of the situation described by a statement. These procedures start with establishing the referent of one term as a reference object that serves as the foundation of a new structure, and then proceed to add a representation of the other term as a target object in the required relation to the reference object” (Oberauer & Wilhelm, Reference Oberauer and Wilhelm2000, p. 1703). These authors claimed that this procedure establishes an inherent directionality in the resulting representation, “such that reasoning processes tend to start with the reference object and proceed to the target object, rather than the reverse” (Oberauer & Wilhelm, Reference Oberauer and Wilhelm2000, p. 1703). Also, they claim that some conditionals have an inherent directionality while in other conditionals and biconditionals the directionality is indeterminate. In the conditional “if A, then B”, the term “A” is the reference object or relatum, while the term “B” is the target object, and consequently this conditional has a directionality from A to the term B (A → B). On the reverse conditional “A, if B”, the term “B” is the reference object or relatum, while the term “A” is the target object, consequently this conditional has a directionality from B to the term A (A ← B). However, the conditional “A only if B” and the biconditional “if and only if A, B” have an indeterminate inherent directionality. Oberauer and Wilhelm (Reference Oberauer and Wilhelm2000) claim that the “process of interpreting “p only if q” starts with a direction from p to q (the first step), but in many cases it ends with the opposite direction (second step). This can lead to different predictions for directionality effects, depending on the task context” (p. 1706). For instance, for the conditional “A only if B”, while Oberauer & Wilhelm (2000, experiment 3) found a forward directional effect in a verification task, Evans (Reference Evans, Newstead and Byrne1993) found a backward directional effect in an inference task. These authors have tried to explain these diverging results as a consequence of using different tasks. The verification task prompts participants to engage in the first step while the inference task plus the negative minor premise “not-B” prompt people to engage in the second step. Oberauer and Wilhelm (Reference Oberauer and Wilhelm2000) suggest that the preferences for backward inferences from “only if” premises noted by Evans (Reference Evans1993) result from the direction of the second step of the procedure. They claim that “once a premise like “p only if q” is given together with the minor premise “not-q”, the standard two-step procedure of interpreting the conditional statements leads directly to the MT conclusion that p must be false” (Oberauer & Wilhelm, Reference Oberauer and Wilhelm2000, p. 1009). However, the authors were right when they concluded that their explanation “must remain speculative until more direct evidence is available” (Oberauer & Wilhelm, Reference Oberauer and Wilhelm2000, p. 1712). As far as the biconditional is concerned, these authors claimed that sentences of the form “if and only if p, then q” are decomposed into two standard conditionals. “The first variant can be phrased as “if p then q”, and “if not-p then not-q”. This results in strong directionality from p to the q term. The second variant is “if p then q, and if q then p”, if interpreted in this way, the directionality cancel each other” (Oberauer & Wilhelm, Reference Oberauer and Wilhelm2000, p. 1706). The indeterminate inherent directionality of conditionals and biconditional makes it very difficult to predict a directional effect in simple and double conditionals when “A only if B”, “if and only if A, B and “only if A, B” (with no inherent directionality predicted by the semantic hypothesis) are used. Contrary to Oberauer and Wilhelm (Reference Oberauer and Wilhelm2000), we suggest that people usually take the term that follows “if” as relatum, then in the premises “B only if A” or “B if and only if A”, people usually takes “A” as relatum.

The “relatum = given” and the “given-new” principles allow us to understand how people integrate one premise into the other. The “relatum = given” principle claims that “the second premise is integrated more easily with the first premise if the relatum of the second premise has already been given by the first premise” (Oberauer et al., Reference Oberauer, Hörnig, Weidenfeld and Wilhelm2005, p. 1226). In the problem “if A then B / if B then C” (also the problem “if B then A / if B then C”), the second premise is easier to integrate into the first premise because the relatum (B) in the second premise has been given in the first premise. However, in the following problems “if B then A /if C, then B” (and also in “if A then B / If C then B”) the second premise is more difficult to integrate into the first premise, because the relatum of the second premise (C) has not been given in the first premise. The “given-new” principle claims that “premise integration is easier when the term already given in the first premise (i.e., the middle term occurring in both premises) is mentioned first in the second premise” (Oberauer et al., Reference Oberauer, Hörnig, Weidenfeld and Wilhelm2005, p. 1228). For example, in the problem “if B then A / if B then C” (and also in “if A then B / if B then C”), the second premise is easier to integrate into the first premise because the former starts with the middle term (B). However, in the problem “if A then B / if C then B” (and also in “if B then A/ if C then B”), it is harder to integrate the second premise into the first because the former does not start with the middle term. Then the integration processes will be easier in the problems “if A then B/ if B then C” and “if B then A / if B then C” than in the problems “if A then B / if C then B” and “if B then A/ if C then B”, since in the first two problems the relatum = given and given-new principles are satisfied, while in the last two neither principle is satisfied. Oberauer et al. (Reference Oberauer, Hörnig, Weidenfeld and Wilhelm2005) also claimed that the difficulty of integrating different figures depends on the inherent directionality of the premises involved. With forward directionality, figure 4 (A-B / B-C) and figure 3 (B-A / B-C) will be more easily integrated than figure 2 (A-B / C-B) and figure 1 (B-A / C-B). However, with backward directionality, figures 1 and 2 will be more easily integrated than figures 4 and 3.

In order to explain the directional effect in double conditionals, Oberauer and Wilhelm (Reference Oberauer and Wilhelm2000) and Oberauer et al. (Reference Oberauer, Hörnig, Weidenfeld and Wilhelm2005) have also provided two other factors. The first factor is the inherent directionality of the relation between the target object and the relatum, “which is preserved in the integrated mental model if and only if it is needed to preserve a semantic asymmetry” (Oberauer et al., Reference Oberauer, Hörnig, Weidenfeld and Wilhelm2005, p. 1244). The second factor is the recency effect of working memory (Espino, Santamaría, & García-Madruga, Reference Espino, Santamaría and García-Madruga2000) that generates an advantage for the C-A directionality regardless of the relation. The semantic view predicts a forward directional effect for the problem “if A then B /if B then C”, due to the fact that the directionality of the resulting integrated model of both premises (A → B → C) goes from A (the relatum) to C (target object). On the other hand, the semantic view predicts a backward directional effect in the problem “A if B / B if C” due to the fact that the directionality of the integrated mental model of the premises (A ← B ← C) goes from C (relatum) to A (target object). The actual version of the semantic hypothesis cannot explain the directional effect on conditionals with different directionality, such as “B only if A, and only if B, C”. In this paper we present a new extension of the semantic hypothesis that could explain directional effect during the integration step of the premises.

Our main assumption is that people start to build the integrated model from the premise in which the end-term plays the role of relatum (the end-term in the if-clause). Then, they add the middle-term that is in the then-clause. Second, they add the other premise in which the middle-term is in the if-clause (the middle-term plays the role of relatum). Then, they add the end-term that is in the then-clause. This assumption is based on the idea that the easiest way to integrate one premise into the other premises successfully happens to be when only one end-term plays the role of relatum, because this end-term will be the hypothetical background space for the rest of terms (middle-terms and end-term). For example, in the problem “If A, then B / if B then C”, the end-term “A” in the if-clause is the hypothetical background space for the middle-term “B” in the then-clause (first premise), the middle-term “B” in the if-clause is the hypothetical background space for the end-term “C” in the then-clause (second premise) and by the transitivity rule (if A bears some relation to B and B bear the same relation to C, then A bears it to C), the end-term “A” should be the hypothetical background space for the end-term “C”.

Let us consider the following example “A, if B / if C then B”; people should start to build the integrated model from the end-term that plays the role of relatum, which is in the second premise (“C”); then, the middle-term (“B”) is added. Next, they search for the other middle-term that plays the role of relatum, which is in the first premise (“B”) and it is added to the representation; then, they add the other end-term (“A”). Finally, they can apply the transitivity rule to find the relation between C and A. We claim that during the inference stage, people prefer to build (or to accept) a conclusion from the end-term that has played the role of relatum in the premises, rather than from the other end-term. Then, we predict that people should accept or build more frequently backward than forward inferences in the above-mentioned problem, because the end-term “C” that has played the role of relatum is in the second premise.

We suggest that when both end-terms (“A” and “C”) play the role of relatum (“if A then B / only if C, B”) or when neither of them does (A, if B / only if B, C), participants should find it much more difficult to integrate the models of the two premises, and this could lead to a suppression of the directional effect. The suppression effect could be due to the fact that participants could build an integrated model either from the end-term in the first premise or from the end-term in the second premise. The first option leads to an integrated model with forward directionality, while the second option leads to an integrated model with backward directionality; then, one directionality cancel the other. In brief, we make the following two sets of predictions in relation to the inference stage:

1. a) If only one end-term plays the role of relatum, then there will be a directional effect. If the end-term playing the role of relatum is in the first premise, the directional effect will be forward. If the end-term that plays the role of relatum is in second premise, the directional effect will be backward.

2. b) If both end-terms or neither of them play the role of relatum, a suppression effect for directionality is predicted.

On the other hand, if we want to check our hypothesis we need not only forward and backward conditionals but different types of forward (for example “if A then B”, “only if A, B”) and backward conditionals (for example, “A if B”, “A only if B”). For example, if we want to check that there will be a forward directional effect in figure 4 problem, when only the first term of the premise plays the role of relatum, we could use the following problem “if A then B / if B then C”; but if we want to check that there will not be any directional effect in figure 4 when both end-terms play the role of relatum, we need to introduce a backward conditional “if A then B / B only if C”.

The task of making inferences from connectives in which the end-terms play different roles poses a challenge to current theories of directional effect, such as the FIFO hypothesis (Johnson-Laird, Reference Johnson-Laird1984).

Method

Design

A 2x2x2x2 within-participant design was used. The first variable was the type of figure (figure 2 vs. figure 3); the second variable was the locus of the end-term that plays the role of relatum in the premises (first premise vs. second premise). The end-term that follows if is the end-term that plays the role of relatum. Third variable was the direction of the categorical premise (forward vs. backward): the forward categorical premises were MP and DA and the backward categorical premises were AC and MT. The fourth variable was the polarity of the categorical premise (affirmative vs. negative): the affirmative categorical premises were MP and AC and the negative categorical premises were DA and MT. The dependent variable was the percentage of forward (from A to C) and backward (from C to A) responses.

Participants

The 46 participants who took part in the experiment were undergraduate students at the Universidad of La Laguna, Tenerife, Spain. None of them had formal training in logic.

Materials and Procedure

Participants were tested in groups of 15 subjects. Each of them received a booklet containing the task instructions and the complete set of conditional premises. During the initial instruction phase, the task was explained to them by an experimenter. Then they were allowed as much time as they required to complete the booklet. In this experiment, participants were asked to draw conclusions from sets of three premises. The first two premises were conditional statements, whereas the third premise was the categorical premise that affirmed or negated one of the two end-terms. Participants were then asked to select one conclusion from the three offered. They had to make four inferences (MP, AC, DA, MT), depending on the nature of the connective used. Below we show an example of a problem of the MP inference that was used in the experiment:

On the table there is a star if there is a triangle

On the table if there is a star, then there is a circle

There is a triangle

And participants had to choose one of three options:

There is a circle

There is not a circle

Maybe there is a circle or maybe there is no circle

They received problems in which only one end-term played the role of relatum. Sixteen problems were given, each with one of the following formats:

They received eight problems in which the end-term played the role of relatum (A) in the first premise (problems 1 and 4) and eight problems in which the end-term played the role of relatum (C) in the second premise (problems 2 and 3).

Results and discussion

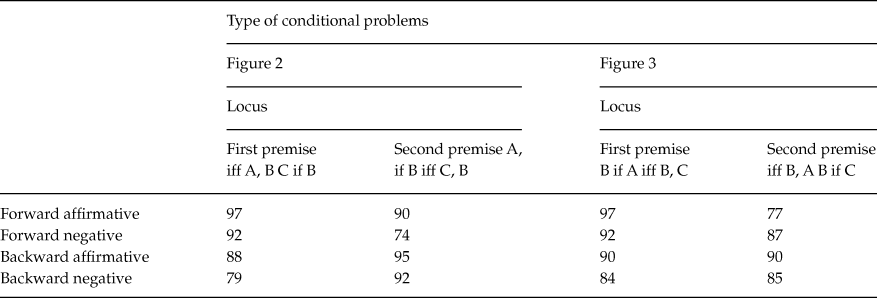
Table 1 shows the percentages of endorsement of the inferences as a function of the figure type, the locus of the end-term that is the relatum, the directionality and the polarity of the inference. We performed a 2 (figure type: figure 2 vs. figure 3), x 2 (locus: the end-term that is the relatum was in the first premise or in the second premise) x 2 (directionality of the categorical premise: forward or backward) x 2 (polarity of the categorical premise: affirmative or negative) analysis of variance with repeated measures. In this and the next analysis, the Greenhouse–Geisser correction against the violation of sphericity assumption was used. This analysis revealed a double interaction between locus and directionality, F(1, 45) = 9.47, Mse = .28, p < .005, ηp ² = .17, in the sense that participants made more forward than backward inferences in those problems in which the end-term that played the role of relatum was in the first premise (91% vs. 81%; t (45) = 2.73 p < .01) while they made more backward than forward inferences in those problems in which the end-term that played the role of relatum was in the second premise (92% vs. 79% t (45) = 2.84 p < .01). Main effect for polarity was reliable, F(1, 45) = 8.77, Mse = .18, p < .005, ηp ² = .16, in the sense that participants made more affirmative than negative inferences (91% vs. 81%). Main effect for other variables, double interactions, triple interactions and quadruple interaction was not found (in any case p > .05).

Table 1. Percentages of endorsement of the inferences as a function of their figure (figure 2 and figure 3), locus of end-term that plays the role of relatum (first premise versus second premise), direction of the categorical premise (forward versus backward) and polarity of the categorical premise (affirmative versus negative)

These results confirmed our predictions. As anticipated, there was an interaction between the locus of the end term that played the role of relatum and the directionality of the inference: when the end-term that played the role of relatum was in the first premise, there was a forward directional effect; but when the end-term that played the role of relatum was in the second premise, there was a backward directional effect.

Method

Participants, design, procedure, and materials

The participants were a new set of 38 undergraduates at the Universidad de La Laguna. The design and procedure were the same as in the previous experiment. However the conditional (“if, then”) was replaced by the biconditional (“if and only if”). Participants received problems in which only one end-term played the role of relatum. Sixteen problems were given, each with one of the following formats:

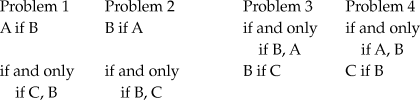
They received eight problems in which the end-term played the role of relatum (A) in the first premise (problems 2 and 4) and eight problems in which the end-term played the role of relatum (C) in the second premise (problems 1 and 3).

Results and discussion

Table 2 shows the percentages of endorsement of the inferences as a function of the figure type, the locus of the end-term that is the relatum, the directionality and the polarity of the inference. We performed a 2 (figure type: figure 2 vs. figure 3), x 2 (locus: the end-term that it is the relatum was in the first premise or in the second premise) x 2 (directionality of the categorical premise: forward or backward) x 2 (polarity of the categorical premise: affirmative or negative) analysis of variance with repeated measures. This analysis revealed a double interaction between locus and directionality, F(1, 38) = 8.23, Mse = .14, p < .01, ηp ² = .18, in the sense that participants made more forward than backward inferences in those problems in which the end-term that played the role of relatum was in the first premise (95% vs. 86%; t(38) = 12.06, p < .05), while they made more backward than forward inferences in those problems in which the end-term that played the role of relatum was in the second premise (90% vs. 82% t(38) = 2.21, p < .04). Main effect for other variables, double interactions, triple interactions and quadruple interaction was not found (in any case p > .05).

Table 2. Percentages of endorsement of the inferences as a function of their figure (figure 2 and figure 3), locus of end-term that plays the role of relatum (first premise versus second premise), direction of the categorical premise (forward versus backward) and polarity of the categorical premise (affirmative versus negative)

Again, these results confirmed our predictions. As we anticipated, there was an interaction between the locus of the end term that played the role of relatum and the directionality of the inference: when the end-term that played the role of relatum was in the first premise, there was a forward directional effect; but when the end-term that played the role of relatum was in the second premise, there was a backward directional effect.

Results and discussion

Table 3 shows the percentages of endorsement of the inferences as a function of the problem type, the directionality and the polarity of the inference. We performed a 3 (type of problem: one end-term played the role of relatum, two-end terms played the role of relatum and neither end-term played the role of relatum) x 2 (directionality of the categorical premise: forward or backward) x 2 (polarity of the categorical premise: affirmative or negative) analysis of variance with repeated measures. This analysis revealed a double interaction between type of problem and directionality, F(2, 68) = 3.73, Mse = .18, p < .03, ηp ² = .10, in the sense that participants made more backward than forward inferences in those problems in which the end-term that played the role of relatum was in the second premise (90% vs. 76%; t(34) = 2.14, p< .04) while there was no directional effect for those problems in which both end-terms played the role of relatum (74% vs. 63%; t(34) = 1.39, p = .17) or when both middle-terms (or neither of the end-terms) played the role of relatum (66% vs. 71% t(34) = .78, p = .44). A main effect for polarity, F(1, 34) = 13.52, Mse = .22, p < .001, ηp ² = .29, was found, in the sense that participants made more affirmative than negative inferences (80% vs. 63%). Main effect for other variables, double interactions, triple interactions and quadruple interaction was not found (in any case p > .05).

Table 3. Percentages of endorsement of the inferences as a function of problem types (two end-terms play the role of relatum, none end-term plays the role of relatum and one end-term plays the role of relatum), direction of the categorical premise (forward versus backward) and polarity of the categorical premise (affirmative versus negative)

Again, these results confirmed our predictions. As we anticipated, there was an interaction between the type of problems and the directionality of the inference: there was a backward directional effect in those problems in which the end-term that played the role of relatum was in the second premise, but there was no directional effect in those problems in which the end-term that played the role of relatum was in both premises or in neither premise.