II. Rawls’s Well-Ordered Society Model

Throughout his work, Rawls used the idea of a well-ordered society as an account of a realistic utopia. The basic structure of this idealized society is regulated by principles of justice, this fact is publicly known, and its citizens all have an effective sense of justice so as to comply with the directives of the basic structure, which they regard as just.^{Footnote 14} This sense of justice drives people to impose the rules of their society on themselves, and their compliance renders a WOS stable for the right reasons. Further, a WOS contains stabilizing forces, such that “when infractions occur, [these] should exist that prevent further violations and tend to restore the arrangement.”^{Footnote 15} A WOS must be able “to generate its own support” rather than have it imposed from without.^{Footnote 16}

The final model of a well-ordered society, then, is understood as a representation of three social facts, the first of which I will update based on Rawls’s embrace of reasonable pluralism about justice.^{Footnote 17} A well-ordered society must satisfy these three conditions:

1. (1) Everyone accepts, and knows that everyone else accepts, some member of a limited set of reasonable political conceptions of justice, which establish shared points of view from which citizens’ claims on society can be adjudicated.^{Footnote 18}

2. (2) Its basic structure — that is, its main political and social institutions and how they fit together as one system of cooperation — is publicly acknowledged, or with good reason believed, to satisfy these principles (or some mix of them).

3. (3) Its citizens have a normally effective sense of justice, and so generally comply with society’s basic institutions, which they regard as just (if not fully just).

While this description is fairly rich, we need to say much more to explain the sense in which a WOS is in equilibrium. First, for Rawls, a stable society is in equilibrium on a conception of justice, not primarily on institutions.^{Footnote 19} But institutional rules must also be self-stabilizing because they institutionalize a conception of justice. Since I want to allow for conceptions of justice to vary, as Rawls ultimately did, I will not presume that a WOS is in equilibrium on a conception of justice; but I will assume it is in equilibrium on the rules that lead officials and citizens to issue behavioral directives to others. These rules must be issued by social structures or organizations that citizens can, on reflection, see as institutionalizing their (presumably reasonable) conceptions of justice.

A WOS is a kind of Nash equilibrium, which is suggested by Rawls’s claim that in a WOS, compliance with justice is each person’s “best reply . . . to the corresponding demands of the others.”^{Footnote 20} Rawls also says that equilibrium is reached when each person’s “plan of life” is his “best reply to the similar plans of his associates.”^{Footnote 21} The idea, then, appears to be that no one can improve her position unilaterally through defecting from compliance with justice. But this is too strong, since a society-wide equilibrium does not require perfect compliance. Instead, a society’s basic rules must be “more or less regularly complied with” and “when infractions occur” stabilizing forces should tend to restore conditions of cooperation.^{Footnote 22} Finally, Rawls says that in a WOS “inevitable deviations from justice are effectively corrected or held within tolerable bounds by forces within the system.”^{Footnote 23} So deviations from justice are inevitable, and only need to be held within tolerable bounds. Rawls allows individual behavior to rationally deviate in at least a few cases.

The WOS also requires assurance if it is to be in equilibrium. For reasonable citizens only have sufficient practical reason to act justly if they are assured that others will generally do likewise. Fortunately, Rawls has a lot to say about assurance, which he understands in terms of “publicity.” For Rawls, and other Rawlsians, a WOS is by definition “regulated by an effective public conception of justice,” which means that citizens must be able to determine for themselves whether their institutions comply with justice, and determine that others can do likewise from their own perspectives.^{Footnote 24} Publicity has three levels, but we need only focus on the first, which is realized when “citizens accept and know that others likewise accept those principles [of justice], and this knowledge is in turn publicly recognized,” the institutions of the basic structure of society are just (as defined by those principles),” and everyone sees that these institutions are just. So equilibrium also requires assurance.

That said, Rawls has little to say about how a WOS generates assurance. In response, Paul Weithman has argued that we should interpret Rawls as arguing that the use of public reasons serves as an assurance mechanism. Public reasons are those derived from shared public values — they are the reasons endorsed by the public based on their conception of justice.^{Footnote 25} By using public reasons in political discussion on matters of basic justice and constitutional essentials, citizens publicly signal their allegiance to just institutions.

We have reason to be concerned about Rawls’s WOS model. First, there is good reason to worry about whether public reasons can provide adequate assurance. John Thrasher and I have argued that they cannot. Even reasonable agents can face conditions of communicative drift, noise, and cheap talk that undermine the capacity of deliberation based on public reasons to provide adequate assurance.^{Footnote 26} Rawls also does not entertain the possibility of emergent destabilizing elements in his model. In particular, he does not acknowledge the possibility that different institutional demands may counteract one another. My model suggests that the degree of disorder within a WOS depends upon the character of reasonable agents, in particular the extent to which agents can preserve stability by caring relatively little about the behavior of other players vis-à-vis their natural inclination to engage in reasonable behavior. Rawls also does not specify how a WOS can stabilize itself given the threat of external shocks, such as limits on resources or the entry of uncooperative agents into the system. This suggests we need to describe the conditions under which a WOS can and must resist invasion.

Fortunately, we can build a subtler model to show how elements of a WOS are logically consistent in a way that yields an attractive and feasible ideal. An ABM will reveal dimensions and degrees of political stability that Rawlsian WOS models cannot. That is, the ABM allows us to distinguish types of stability and to treat the factors that generate stability as continuum notions, rather than as binary.

III. A Simplified WOS Model

Enough Rawls. I now want to take the essential elements of his approach and simplify them enough that they are subject to modeling. I will understand a WOS as follows: (i) its citizens are generally good-willed and care about engaging in reciprocal, cooperative behavior, (ii) they regard the norms that govern their fundamental institutions as mostly just and legitimate, and so comply with the directives of those institutions and the demands of others to follow them. Finally, (iii) they believe that other members of society regard their situation similarly, despite their diverse personal points of view; that is, they have a high degree of assurance.

I employ the idea of an n-person Nash equilibrium, where agents play strategies in pairs, and generate a stable, high degree of cooperation as an emergent property of the system. A WOS is therefore best understood as a macro-level equilibrium. Only mass defection needs to be self-correcting. Macro-level stability is a function of local compliance, but it does not require individual compliance in every case. The dominant mixed-strategy of agents is to adopt a high probability of compliance with rules and directives established by just institutions, such that across the history of their interactions with others, agents cannot improve their position by adopting a non-cooperative strategy.^{Footnote 27}

I forgo appeals to common knowledge. Instead, each agent merely makes reliable judgments about the level of compliance within her environment. My ABM instructs each agent to observe the fraction of cooperative plays in the system at any one time, and partly base her choice in her next encounter on that observation. Agents do not know what other players know.

When agents cooperate, I assume they comply with norms of justice, or regular social practices, enforced by social demands, ostracism, and blame, and in some cases, the law.^{Footnote 28} They are norms of justice because infractions of the norms are seen not only as wrong or immoral but unjust. Importantly, these norms need not be part of a unified conception of justice. Instead, agents must merely see following them as a matter of justice and be subject to disapprobation when the norms are violated. In general, given the importance of assurance and the idea of social trust discussed below, I understand cooperative behavior as trustworthy behavior, where persons comply with expectations set by social norms within that society. This means that they will forgo pursuing gains from defection not merely because they are in public, but because they are independently motivated to cooperate.

We can understand defection, following David Rose, as a kind of opportunism.^{Footnote 29} Rose defines opportunism as “acting to promote one’s welfare by taking advantage of a trust extended by an individual, group, or society as a whole.”^{Footnote 30} This trust is based on the expectation that everyone complies with the norms of justice present in that society. A critical feature of opportunism is that it does not always cause perceptible harm, or even any harm at all. If a society is sufficiently large, small acts of opportunism are not in themselves sources of harm. For example, suppose John downloads an episode of Game of Thrones without an HBO subscription; it does no perceptible harm, but it is opportunistic. However, with sufficient opportunism, some parties will be harmed. This is partly because a society’s social trust in future cooperative behavior will tend to decrease in response to opportunism, reducing the efficacy of many social institutions.^{Footnote 31} So when agents interact within just institutions, defection involves breaking the mutually agreed upon terms of implicit and explicit agreements that are not unjust.

I will understand defection in terms of first-degree opportunism, which involves taking advantage of the imperfect enforceability of contracts by reneging on contracts.^{Footnote 32} I focus on first-degree opportunism because it is relatively simple and detectable.

IV. A Simple Agent-Based Model of a Well-Ordered Society

I begin introducing my ABM based on elements in the previous section. In the simple WOS model, all the agents are of a single type that I call “reasonable,” following Rawlsian terminology.^{Footnote 33} But to avoid normatively thick and loaded conceptions of reasonableness, let us say that all reasonable agents are committed to reciprocity when they will cooperate with other agents so long as they believe others will do likewise. We can therefore model reasonable agents as conditional cooperators, who cooperate given the expectation that others will do the same. This means that the main difficulty faced by a society of reasonable people is assuring one another that they will respond cooperatively to cooperative behavior.

I understand cooperation, defection, and associated game-theoretic concepts maximally capaciously. Appealing to game theory does not require representing agents as merely instrumentally rational, for instance. There is no reason that game-theoretic modeling cannot model persons as having utility functions that include rich moral commitments and cooperative dispositions. I understand the idea of “utility” with similar capaciousness as representing whatever agents regard as choiceworthy. In sum, the tools of game theory do not require a homo economicus conception of the individual and make no significant individualist methodological assumptions.^{Footnote 34} Or so I assume henceforth.

A reasonable agent’s decision-making heuristic is a simple propensity to cooperate. The agent calculates her propensity based on two factors: the intrinsic utility she derives from cooperating successfully and her observation of the percentage of cooperative agents in the system. The first factor is the agent’s intrinsic propensity to cooperate, which is her general liking of cooperation, or how much the agent would cooperate if she were indifferent to how others treat her. The second factor involves the agent calculating the ratio between the agents who cooperated in their last interaction to the total number of agents in the system, yielding some ratio between 0 and 1.^{Footnote 35} An agent’s social sensitivity is understood as the relative weighting of the observed ratio of cooperation and an agent’s intrinsic propensity. When an agent’s observation is combined with her intrinsic propensity according to the weighting specified by its social sensitivity, this determines its effective propensity or the probability with which she will cooperate in a given interaction.

Social sensitivity can be set at any value between 0 and 1, such that sensitivity functions as a weighting relative to an agent’s intrinsic propensity, which is set as an input by the modeler. Suppose that an agent’s intrinsic propensity to cooperate is 90 percent (.90). If social sensitivity is set at .5, and the agent observes only 60 percent (.6) of agents cooperating, then she calculates her effective propensity like so:

In this case, then, we have .5(.6) + (1-.5)(.90) or .75. This means that the next time the agent plays a game with another agent her effective propensity to cooperate is 75 percent. She rolls a four-sided die with three directives to cooperate and one directive to defect, and follows the directive rolled. Notice that the agent begins with a very high propensity to cooperate in the absence of information about cooperation in the system. If we set social sensitivity to 0, the agent will cooperate 90 percent of the time, since she entirely discounts her information about what others are doing. Once social sensitivity is positive, however, the agent adjusts her propensity to cooperate based on her observation.

In this way, social sensitivity is an assurance parameter because the agent’s estimation of the ratio of cooperative agents to defecting agents can be understood as a kind of assurance that others will behave cooperatively. I believe that social sensitivity allows the model to capture the essence of reasonable Rawlsian agents and a thin notion of publicity. Unlike Rawlsian agents, however, reasonable agents make finer-grained judgments about the likelihood of cooperation and they will defect in proportion to their observation of defection.

Our final piece of the simple WOS model is the output variable — social trust. Social trust is calculated by taking the average of the effective propensities of all agents at a single time. Social trust, therefore, represents the degree to which the system as a whole is prepared to cooperate with others. This technical definition of social trust, then, bears some resemblance to more common usages of the term.^{Footnote 36}

Reasonable agents also have a general desire to engage with other reasonable agents rather than unreasonable agents. In the model, an agent calculates the average position of cooperative agents and turns toward it after playing a game. She also turns away from the average position of those who defected (regardless of their hardwired strategy). She does not also move toward cooperators or away from defectors. Since she only turns, she takes a somewhat random walk tilted toward recently cooperative populations and away from recently somewhat less cooperative populations. Reasonable agents recalculate this location after each play.

In the simple model with only reasonable agents, this form of correlation has a significant effect, leading players to congregate in a central hub. The reason for this is intriguing. With a simple turn toward cooperators, and 90 degree range of movement left or right, reasonable agents will start to encounter one another more often; but the more often they interact, the more often they turn toward one another, which leads them to cooperate more often, increasingly centralizing the cooperators. The formation of the cooperative hub is an emergent feature of a very simple dynamic: after each play, face those who have just cooperated, and take a somewhat random walk.

The important point here is that reasonable agents have the ability to correlate their behavior by congregating so as to play many games with one another. In this way, I draw on the idea of “network reciprocity” in game theory, where previous cooperation leads agents to interact with one another more often, forming a pro-social network.^{Footnote 37} The dynamic that drives network reciprocity in the WOS model is rudimentary. Agents do not learn the agent-strategies of other players, so they do not distinguish between agent types. Nor do they record the effective propensities of other agents at any one time. Instead, all they know is each player’s present play, or its last play, if it is not partnered with another agent when the observation occurs. So there is no complex reputation effect. Each player merely has a drive to face players who have cooperated and face away from those who have defected.

Even if all reasonable agents are naturally disposed to cooperate in every interaction with others, they will cooperate less if they do not realize that others are similarly disposed. Cooperation among reasonable agents can quickly break down if the agents lack assurance. Consequently, we should not model a WOS by assuming that all reasonable persons always cooperate with one another.^{Footnote 38} This critical alteration to Rawls’s model helps us to more accurately represent the dilemmas faced by cooperative agents in a well-ordered society.^{Footnote 39}

Reasonable agents should have two further features, both of which I omit for presentation purposes. First, agents do not make observational errors, whereas the most accurate modeling assumptions would allow for mistakes. Further, reasonable agents are prepared to defect when the cost of complying with a rule is too great, even if others are prepared to cooperate. Even a reasonable agent should defect if she expects cooperation will kill her! I have omitted this “cost caveat” from the model because my aim is to model a well-ordered society operating under favorable conditions, such that cooperation should almost always prove beneficial, if less beneficial than getting away with defection.

We can understand the simple WOS ABM as describing citizen-agents interacting in a legal environment that applies payoffs to agents based on cooperative or uncooperative behavior, such that cooperative behavior is rewarded and uncooperative behavior is punished. Importantly, however, reasonable agents in the simple model do not care about their payoffs, and so focus exclusively on reciprocity. I will only partly relax this assumption in the more complex model, and only for what I will call merely rational agents, not reasonable agents.

V. Results of the Simple WOS ABM

In the simple WOS ABM, each iteration of the model — a “tick” in Netlogo modeling software technology — brings reasonable agents closer to a system-wide cooperative equilibrium whose social trust is equal to the average intrinsic propensity of agents to cooperate. In other words, given that all agents are reasonable, the fact that these agents are socially sensitive to what other reasonable agents are doing does not discourage them from cooperation in the long run. Second, the agents quickly cluster into a tight network, with only some agents moving around outside of the core cluster. The clustering effect is robust across the number of agents in the system and reasonable agents’ intrinsic propensity to cooperate.

The significant feature of the model is that social sensitivity has a substantial short-term effect on the range of social trust found across each run (which I define as 500 ticks). While the average equilibrium level is set early in each run, typically in the first 100 ticks, the variability of short-run social trust increases as the social sensitivity of the agents increases. Compare the average level of social trust in a game where fifty agents each have an intrinsic propensity of .9. In the first display of Figure 1, social sensitivity is set to .3 and in the second display to .9:

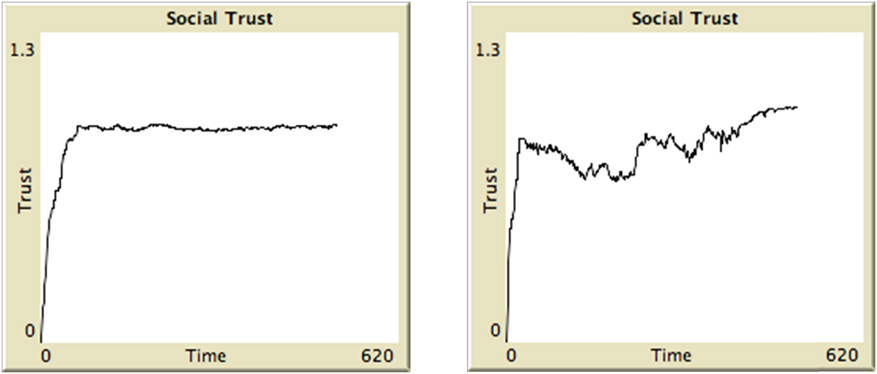
Figure 1. Social Sensitivity and Trust Variability – Steady and Shaky

Recall that a system’s level of social trust is the average of the effective propensities of all agents at a time; the graphs show the variation of social trust over time. Figure 1 only represents social trust during one run of the model. While the system is nondeterministic, such that different runs yield different curves, Figure 1 nonetheless represents general system behavior at the two levels of social sensitivity.

The model shows that the more agents care about what other agents are doing, the more social trust will vary in the short run. However, the average level of social trust will remain constant over the long run. Average social trust is determined by the intrinsic propensities of the agent set by the modeler, such that the higher the intrinsic propensity, the higher average level of social trust.^{Footnote 40} The variance of social trust, however, is a function of social sensitivity. As social sensitivity increases, the volatility of the system increases, though this has almost no effect on the average level of social trust, as demonstrated in Figure 1.

Consider now the two societies represented in Figure 1. Steady (at left) and Shaky (at right) have the same high average level of social trust. In this sense, then, both are stable for the right reasons. But in Steady, the variation in social trust across time is quite small (as it is at .3 social sensitivity), whereas in Shaky, the variation in social trust is quite large (at .9 social sensitivity). Which society is better, given Rawlsian aspirations? I believe Steady should come out ahead, as I argue below. It not only has the capacity to stabilize its constituent norms by maintaining a high level of social trust and cooperation, but exhibits low variance in that capacity.

In this way, the ABM allows us to distinguish two types of stability: durability and balance. Durability is defined as a system’s average level of social trust over time. A durable system is one with high average social trust among agents. It may initially seem strange to describe an average level of anything as a form of stability. Stability as a concept seems to denote variability in a level of some feature of a complex system, not the level itself.^{Footnote 41} But remember what sort of level we’re talking about — it is a level of social trust, which is a degree of cooperation with the constitutive moral and legal rules in a WOS. Justified moral and legal rules are maintained by cooperation, which involves stabilizing them. Stabilization requires a lot of cooperation, then, and mass defection leads these rules, which are a kind of social norm, to collapse. To illustrate, imagine a social system with an invariant, but low level of cooperation. That society is unstable in the sense that its justified rules are fragile equilibria if they are equilibria at all, given the high concentration of defection. To understand durability as a kind of stability, then, we must remember that cooperation in a WOS maintains justified moral and legal rules, such that large amounts of defection lead to unstable rules or norms.

We can understand durability as a kind of first-order stability, the capacity of a system to stabilize its constituent norms. Balance refers to the variability of social trust over some time period. That is, balance is a kind of second-order stability, or the stability of a measure of stability. Thus, durability and balance are different answers to the question, “Stability of what?” Durability measures the stability of a society’s constituent social norms by measuring its degree of social trust. Balance measures the stability of a society’s level of social trust.^{Footnote 42}

We can distinguish forms of balance in two ways: first, by the length of the relevant time series over which variability is measured, say over 100 or 500 ticks, and second, by distinguishing between frequency measurement and amplitude measurement. Consider the two series in Figure 2, each of which has an average of 100 units and covers the same length of time.

Figure 2. Frequency and Amplitude

The two series have the same amplitude but different frequencies, and there is a good argument that Series B is more stable than Series A, as it transitions more slowly through more fine-grained states. For our purposes, I restrict balance to short-run frequency. A social system is balanced when, like Steady, it has a low variability in social trust over the short run. If the system resembles Shaky, we can call it volatile.

I argue that a WOS should be understood as both balanced and durable. Durability enables the system to maintain a high level of social trust, which is obviously critical. The case for balance is less obvious, but still strong. Low variance is a social good because high variance systems contain highly undesirable periods, and most people will prefer steady, reliable expectations even if it means fewer high points. This is likely true simply in virtue of human risk aversion. Big highs aren’t worth big lows. Second, Shaky might yield negative social consequences based on the fact that some agents will recognize the volatility and act less cooperatively as a result. That is, variability in social trust in the short run may reduce the level of social trust in the long run. The simple model lacks a complex learning algorithm required to test this claim, but we could program reasonable agents to periodically measure the maximum and minimum level of social trust over a lengthy period of time, and then adjust their effective propensities up or down based on the size of the range. As complexity increases, generating the logical consequences of the model becomes a much more computationally demanding task; so I do not present that model here. But the point should be clear enough. We not only care about having a high average level of social trust, but that it not vary too much.

An unbalanced system also varies randomly, such that it is impossible to predict the system’s capacity to stabilize its constituent norms at any one time. This creates challenges for actors who wish to alter and improve their legal order, since predicting the effect of a legal change depends upon the predictor’s understanding of how the new law will be received by those subject to it. A balanced order will be predictable: either people will be relatively more likely to comply with the new law, or relatively less likely, but laws can be based on a high degree of certitude about a society’s level of social trust. An unbalanced order makes these predictions much harder, and at the limit, impossible.

A third problem with an unbalanced order derives from the fact that a highly variable level of social trust will increase transaction costs between agents at the local level. Agents cannot form expectations about how likely others are to cooperate or defect. And this makes engaging in any social activity risky, since at least agents in a low-trust society will know not to stick their necks out. This will likely lead to a less cooperative and trusting social order over the long run, given that fewer people will be likely to take the risks necessary to create a productive, high-trust order.

The potential upside of an unbalanced order is that it is harder to take advantage of cooperative agents. Since balance is a function of social sensitivity, agents in an unbalanced order will take the behavior of others into account more than they would in a balanced order. This means that they will generally be more responsive to non-cooperative behavior from other agents. That said, the complex ABM discussed below suggests that an unbalanced order is less immune from invasion by merely rational agents than otherwise. Increases in social sensitivity depress immunity somewhat. So we have at least some evidence that the purported downside balance fails to materialize in the model.

An unbalanced order may also seem to realize the good of having a dynamic and disruptive order, which will be more effective at discovering new ways for persons to coordinate and cooperate. However, while I think discovery is an important part of a WOS that has been almost entirely ignored in Rawlsian models, discovery orientation is compatible with balance. Balance obtains when the level of compliance with norms is low; if these norms permit and encourage social experimentation, then balance promotes discovery rather than discouraging it.^{Footnote 43}

We can already start to see the challenges the ABM poses to traditional political liberal approaches to stability. First, public reason liberals, including me, have not distinguished between durability and balance, much less between forms of balance. Reaching durability and balance may require different social mechanisms, a fact which threatens the case for appealing to a single dynamic to establish stability. The model also uncovers an ambiguity in the idea of a reasonable person, particularly in specifying the extent to which reasonable people should cooperate with others based on their intrinsic character traits or their observations of how others behave. Thus, we must decide how much reasonable people care about the actions of others.

To ensure that we understand the results of the model, let’s take an informal tour through the experience of a single agent in an environment with some similarity to the one in my model. Call her Reba. Reba is good-willed in general, and eagerly cooperates when she sees others doing likewise. Much like us, Reba underestimates the extent to which others affect her evaluations, thinking that her intrinsic propensity to cooperate drives her behavior. But in reality, her behavior is determined much more by social expectations than stable features of her character. Let’s assume other agents are similarly spirited. For this reason, we assign each agent in that system a 90 percent intrinsic propensity to cooperate with .9 social sensitivity — they care nine times as much about what they experience with others than drawing on their own character. That is a lot, I grant, but it will prove illuminating.

Now imagine that Reba has moved to a new neighborhood; she has heard good things about it, but she knows no one there. She is optimistic that other people will be as good-willed as she is. So long as others are kind to her, Reba thinks, she will be kind in return. Next imagine that once Reba has moved into a neighborhood, she begins to interact with her neighbors on a regular basis. Let’s understand her interactions commercially: she is engaged in economic exchanges with others, say through yard sales, maintaining a neighborhood watch, keeping the neighborhood park clean, contributing to the yearly block party, and so on.

Most of Reba’s neighbors are kind. They almost always offer fair prices at yard sales, participate in the neighborhood watch, and throw away trash at the park. They even bring food to the block party every year. But other neighbors are not as kind: John sometimes shirks; he is tempted to opportunism. So John charges too much at yard sales, or offers too little for valuable items; he sometimes participates in the neighborhood watch, but he gets lazy on Mondays, and this led to a successful burglary last month. John picks up trash when others are around, but he occasionally litters in their absence. And he sometimes forgets to bring anything to the block party. Reba notices that her other neighbors start to shirk a bit more after observing John’s behavior, and she resents investing so heavily in the good of the neighborhood. Her resentment leads her to reduce her participation. When others observe Reba, community pillar, contributing less, they draw back as well. And this lowers the level of social trust in the neighborhood.

But Reba doesn’t give up. Buoyed by her mostly positive interactions with others, she tends to spend more time at their homes, focuses more on their yard sales, and doesn’t go to John’s anymore, and so on. John sees this behavior, feels guilty, and starts to clean up his act a bit. The result of all these actions is a neighborhood with a high level of social trust but with some variability. When John starts to shirk, Reba withdraws, which reduces shirking and maintains social trust. In our terms, the neighborhood is durable, but less than fully balanced. The average level of social trust is high, such that beneficial social norms can stabilize and generate desirably high levels of compliance. However, Reba and other neighbors care a great deal about what others are doing, and so generate periods of variable neighborly spirit.

Notice also that neighborhood stability is based on the moral motivations associated with being a good neighbor, and how those motives interact with a desire for personal gain. This is clear from John and Reba’s behavior. The neighborhood, then, is not merely durable, but durable for the right reasons. While it lacks some balance, it is still largely balanced for the right reasons. Similarly, if Reba and other neighbors begin to care less about what others are doing, and commit themselves to contributing simply because it is the right thing to do, the neighborhood will remain durable for the right reasons, and become more balanced for the right reasons. Consequently, Reba and John’s neighborhood becomes more well-ordered.

VI. Relaxing Compliance

I would now like to model a well-ordered society that relaxes the assumption that agents fully comply with its rules. While reasonable agents may decide not to cooperate only if they lack assurance, some agents are now allowed to defect even if they have assurance. I relax the compliance assumption for two reasons. First, relaxing compliance allows us to isolate dynamics that allow a less well-ordered society to develop into a more well-ordered society, which is a critical part of nonideal theory understood as the theory of transition from present circumstances to the ideal.^{Footnote 44} Second, relaxing compliance allows us to identify a third attractive conception of stability — immunity. Immunity in general specifies the degree to which a WOS can recover from external shocks. Immunity resembles durability in this way because both are forms of first-order stability, though they differ in what they measure. Durability measures social trust, whereas immunity measures the survival rates of reasonable agents in competition with rational agents.

Critically, there are as many conceptions of immunity as there are kinds of external shocks to a social system. A society might be immune because it can repel an invasion of defectors. Alternatively, a society might be immune from unexpected events like an economic supply shock on the grounds that it can quickly recover from a change in economic circumstances. In this essay, I will focus exclusively on immunity against the invasion of small numbers of defectors who can enter at variable rates depending upon how well defectors in the system perform vis-à-vis reasonable agents.

I call the second WOS model a complex, real well-ordered society model to connote both that the model represents a wide range of social phenomena and that it is a better representation of our real social challenges. The most important addition to the simple WOS model is the second type of agent that simply acts to maximize her utility in each play. I call these “merely rational” agents, or “rational” agents for short.^{Footnote 45} Their expected utility is determined by the game they believe they are playing with other agents. To demonstrate the robustness of political stability despite the presence of agents willing to defect, merely rational players are given prisoner’s dilemma payoffs, such that their dominant strategy is defection.

Notice, then, that I have relaxed the compliance assumption by adding merely rational agents, and not by altering the strategies of reasonable agents. This assumption employs simpler decision-making algorithms, and so simplifies the model. It also allows us to effectively isolate the damage that merely rational players can wreak on political stability. We will see that they hit durability hard.

To properly flesh out the model, we must recall the mechanism by which information about cooperation and defection is transmitted. In the real WOS, reasonable agents do not distinguish between themselves and rational agents. All they know is which agents are presently cooperating or defecting, or who cooperated or defected in their last play with an agent. All they do with this information is face the general direction of agents who cooperated and turn away from those who have defected. The emergent effect is that reasonable agents cluster with one another and flee rational agents. This creates what is, in effect, a form of network reciprocity, where reasonable agents play games with reasonable players more often than with rational players, though they do so without recognizing this fact. In other versions of the complex model, I have given reasonable agents more information, such as the effective propensities of each agent. In that case, reasonable agents are much more effective at building cooperative networks, but I wanted to see if the same effect would hold under conditions of extremely limited information. And, in fact, it does hold.

Rational agents also face agents who have cooperated, but they do not also turn away from defectors. This difference is vital. Reasonable agents can effectively run from defecting agents and toward one another, and since rational agents always or nearly always defect, over time reasonable agents evade rational agents, even though they cannot act based on identifying a rational agent as a rational agent. What justifies this differential treatment? The main justification is that rational agents are not as enthusiastic about cooperating in comparison to reasonable agents. They want to interact with reasonable agents, but they do not dislike one another. In contrast, reasonable agents dislike and flee merely rational agents because they recognize that they, the reasonable agents, are subject to exploitation. Merely rational agents like cooperating, but they will defect in order to benefit; reasonable agents like cooperating so much that they prefer not to defect even when it benefits them. So reasonable agents are driven into cooperative interactions with one another, despite having very little information about how each other will behave. Note that the rational agents use the same information that reasonable agents do, no more and no less, but they are less desperate to escape defectors since they have no intrinsic liking of cooperation. Again, an important, emergent result of these different motivations is that reasonable agents find one another quickly, such that they can increase the frequency of the games they play with one another, allowing them to accumulate more resources. This is because in doing so they can outscore the merely rational players through a simple higher frequency of interactions. Even if they sometimes interact with rational players and lose, the reasonable agents do better over time on the whole. We will see that the capacity to build networks will have important effects on the entry-exit dynamic introduced below by helping reasonable agents signal for new agents to enter the system at a rate faster than rational agents, which enables reasonable agents to resist invasion.

I think my assumption is backed up by some recent work in social evolutionary theory, which shows that cooperative agents can out-compete uncooperative agents by correlating their behavior. The property assigned to cooperative agents is similar to the notion of network reciprocity, which again involves cooperative agents finding ways to interact primarily with other cooperative agents.^{Footnote 46} Defector agents have a generally harder time forming cooperative relations because they are uncooperative in general, and network reciprocity requires consistent cooperation if it is to form and grow.

VII. Results of the Real WOS ABM

The introduction of merely rational players into the environment has significant negative effects. Suppose we have fifty reasonable agents and five merely rational agents. So long as the merely rational players play Prisoner’s Dilemmas, under a broad range of payoffs, they will depress durability. Intrinsic propensities and durability are tightly correlated in the simple WOS model, as an intrinsic propensity of .9 will always yield a long-run average social trust level of .9. The introduction of rational agents drags durability down from that level. Further, as intrinsic propensity increases, the degree of durability depression increases, from around 11.2 percent when reasonable agents have an intrinsic propensity of .7 to 16 percent when reasonable agents have an intrinsic propensity of 1. The reason for this increasing degree of durability depression is that merely rational agents can more easily exploit players with very high intrinsic propensities to cooperate, as reasonable agents’ love of cooperation will make them vulnerable to defection more and more often.

Durability is dramatically depressed as social sensitivity increases, especially at an intrinsic propensity of 1, as represented in Figure 3.^{Footnote 47} At a social sensitivity level of .2, durability is only depressed 2 percent by the presence of a few rational agents. But depression increases to 12 percent at a social sensitivity of .6 and a whopping 49 percent at a social sensitivity of .9.^{Footnote 48} The reason for the increased depression is that, as social sensitivity increases, an agent’s intrinsic propensity to cooperate counts for less and less in determining agent choices, from 80 percent at a social sensitivity of .2 to 10 percent at a social sensitivity of .9. So the dynamics of observation and correlation take over at high social sensitivities, such that hard-wired rational agents can dramatically disrupt the system.^{Footnote 49}

Figure 3. Fall in Durability as Social Sensitivity Increases

Let’s now extend our walkthrough to the real WOS model. Assume that John and Reba’s neighborhood has achieved durability and balance. The neighborhood is nearly well-ordered. Then Sarah moves in. Sarah is a pure opportunist. She doesn’t care about her neighbors at all, or what they think of her. She will engage in cooperative activities when she thinks it will benefit her and perhaps her family, but otherwise not. And in cases where she can drain social resources without consequence, she will. Sarah is the person who doesn’t bring food to the block party, but drinks all the beer. She is the person whose house is safe but who never bothers to look out for dangers to the community. Sarah doesn’t even recycle! If Sarah is caught engaging in uncooperative behavior, she will comply to divert attention away from her behavior, say by bringing food to the block party the next year, or bothering to peak out her windows when she knows her neighbors will see her. She picks up some trash here and there and charges below market prices at her yard sales. Since she’s being watched, Sarah doesn’t steal. Not for a while, at least.

John, Reba, and the other neighbors are generally able to determine that Sarah or someone else is a drain on the community. Recognizing that someone is deliberately violating social norms leads to somewhat more noncompliance by John and Reba. John thinks that, with everyone so mad at the shirker, people won’t notice if he shirks a bit. And perhaps Reba gets so angry at the shirkers that she reciprocates with non-cooperative behavior. As a result, neighborhood trust falls, more defection ensues, and attempts to reestablish order are punctuated and brief, and only occasionally successful.

VIII. Entry and Exit

I now introduce the final major feature of the model — entry and exit. The real WOS model has a carrying capacity parameter that sets how many agents the system can hold. Once carrying capacity is reached, an exit algorithm kicks in by removing agents at random at a rate sufficient to keep the total number of agents under the carrying capacity. Further, all agents can “reproduce” up to the carrying capacity, which I represent as introducing a new agent into the system with the same agent-strategy as the “parent” agent-strategy—either reasonable or merely rational.^{Footnote 50}

In the real WOS ABM, entry is cued by the “profit” margins that one agent strategy gains over the other. If the profit margin is 0, then whenever one agent-strategy’s score exceeds the others’ score, that strategy receives a new agent. If the margin is set at .02, then if one agent-strategy ever achieves a 2 percent higher average score at any time, another agent hard-wired to play that strategy will enter. The reasonable agents receive payoffs, just as rational agents do, even though they do not make decisions based on payoffs but rather merely on their expectation of reciprocal cooperation. So when I index entry rates to relative payoffs, I am appealing to payoff information for both rational agents and reasonable agents that reasonable agents do not consult. I find this is a helpful simplifying assumption for distinguishing conceptions of stability.

I should say a bit about the scoring system. All agents receive set payoffs depending upon the combination of plays by the agent and its partner, ranked in line with the formal structure of the Prisoner’s dilemma, where the payoffs are ranked as follows for the agent whose strategy is represented by the first variable: DC > CC > DD > CD. The agent gets the most when she defects and the other cooperates, less when both cooperate, still less when both defect, and even less when she cooperates and the other defects. The system then stockpiles the payoffs received in each game. An agent-strategy’s score is the sum of the stockpiles of each agent playing that strategy.

When the exit and entry algorithms are combined, one agent strategy can quickly replace another. If one strategy has a higher score than the other strategy more often than the reverse, it will reproduce faster. Since the exit algorithm removes agents from the environment at random, it will tend to remove more agents with the losing strategy than agents with the winning strategy. Entry and exit algorithms, then, create a new kind of equilibrium condition that is similar to an evolutionarily stable strategy in evolutionary game theory — one that can resist invasion by alternative strategies in a particular environment when the new strategy is relatively rare.^{Footnote 51}

The primary upshot of the complex well-ordered society model is identifying our conception of immunity, which is realized when reasonable agents can repel invasion by rational agents. So a society has significant immunity when the majority population of reasonable agents resists replacement by rational agents. A society is perfectly immune when it not only resists invasion by rational players but also actively out-reproduces them, replacing them up to the full carrying capacity of the environment. If, for instance, we start with 10 rational agents and 90 reasonable agents, with a carrying capacity of 200, then a society has full immunity when it always reaches equilibrium at 200 reasonable agents and 0 rational agents at some point in the not too distant future. It has a high, but not perfect degree of immunity when its equilibrium state is, say, composed of 90 percent reasonable agents and 10 percent rational agents.

To be clear, immunity does not increase during a model’s run, and can only be attributed to a system once the carrying capacity has been reached and the competition between agent-strategies begins. So the immunity of a system is a property described by its final equilibrium state. The society is immune if and only if its end state retains a much larger number of reasonable agents than rational agents; and it is fully immune if it can repel a sizeable number of rational agents entirely. So a WOS is fully immune when reasonable players resist replacement under a very robust range of conditions.

Raising immunity is a difficult social achievement, due to merely rational agents who believe they face PD payoffs with all other agents. Because of the randomness in the model, rational agents can sometimes achieve a higher average score long enough to significantly increase their proportion of the population. In a few cases, rational players take over. But there are more cases where reasonable agents repel rational agents long enough for the rational agents to die out. Once reasonable agents are victorious, a real WOS is logically indistinguishable from a simple WOS with an entry-exit dynamic. The simple reason is that all the rational agents have left, and the carrying capacity of the society has been reached, so reasonable agents are only interacting with one another.^{Footnote 52}

The significant result is that the real WOS has a dynamic that creates a transitional path to a fully well-ordered society — a simple WOS with an entry-exit dynamic. This means that we can connect nonideal theory and ideal theory. For Rawls, a WOS is populated exclusively by reasonable agents; Rawls classifies problems with noncompliant, unreasonable agents as nonideal theory.^{Footnote 53} A social order with sufficient immunity can resist invasion by a large number of noncompliant agents, which means that it can transition from a nonideal, or less-than-well-ordered society, to the ideal of a well-ordered society.^{Footnote 54} The WOS model developed here, then, can play an important role both in understanding how a nonideal order can transition into a WOS.

Another nice feature of the entry-exit dynamic is that it allows us to represent a number of social factors that influence political stability. Recall that Rawls only allows agents to enter his model by birth and exit by death.^{Footnote 55} But with a sufficiently high entry and exit rate, we can model a relaxation of this requirement. For instance, the real WOS ABM can potentially account for emigration and immigration effects on stability, along with generational shifts. Alternatively, we can use the entry and exit of rational and reasonable agents to represent strategy changes among people in a society. Specifically, we can represent this event by removing a reasonable agent from the system and replacing it with a rational agent.

IX. Results of the Entry-Exit Dynamic in a Real WOS ABM

The full real WOS model illuminates the notion of immunity based on two simplifying assumptions. First, rational players always defect, since they simply maximize expected utility in each game they play. They respond to no incentive to become more cooperative. Second, players only know what other agents are presently doing or how they played in their very last play. They do not know player reputations, or each agent’s strategy-type.

In light of these simplifying assumptions, what factors cause immunity? One obvious factor is the ratio of reasonable to rational players in the model’s starting conditions. With many rational agents in the system from the outset, reasonable players seldom replace rational players, and rarely do so entirely. This is not a problem for the model, since it is fair to assume that most people are not pure defectors, but instead are conditional cooperators who care about reciprocity and fairness. The question is whether a few bad apples can spoil the bunch. A second factor is that reasonable agents can flee rational agents, and so form tight networks of reciprocal benefit. Reasonable agents play many games together, increasing their average scores faster than merely rational agents who deliberately gravitate toward those cooperative hubs. With a higher average score, reasonable agents enter more quickly than rational agents, and usually replace them.

Readers can explore the parameters and results of the model through the outboard appendix. But we can see from Figure 4 how much the entry-exit dynamic matters. Here I stick to an intrinsic propensity of 1 and graph durability as a function of social sensitivity (excluding a social sensitivity of 1, since this makes intrinsic propensity irrelevant in agent calculations, and social sensitivities of 0 and .1, which are too low).

Figure 4. Durability with rational agents and the entry-exit dynamic

Figure 5. Balance variation due to the entry-exit dynamic.

Introducing five merely rational agents into the simple WOS significantly decreases durability, and more so as social sensitivity increases. But with the entry-exit dynamic, the depression of durability is considerably reduced. As the agents become more socially sensitive, they are much better at resisting invasion by rational agents vis-à-vis their counterparts in the system without the entry-exit dynamic; the slope of falling durability is much lower. Over the course of a thousand runs of the model, to 500 ticks, the introduction of the entry-exit dynamic increases the durability of the system by 30 percent, with a 20 percent reduction in durability from the simple WOS model with only reasonable agents. Introducing merely rational agents still depresses durability, but its effects are limited.

The entry-exit dynamic has a remarkable effect on balance. If we compare complex WOS models, one with an entry-exit dynamic, and the other a closed system, we generate sharply divergent results. Without the entry-exit dynamic, the standard deviation of the system is quite low, rising from 0 at a social sensitivity of .2 to .1 at a social sensitivity of 1.0. The system with the entry-exit dynamic is far more volatile.

The introduction of the entry-exit dynamic generates a very fat tailed curve, where all levels of social sensitivity generate a standard deviation between .25 and .35, rather than 0 and .11. What this suggests is that the full WOS model has low balance and that restricting entry and exit conditions could increase balance. But notice that, just like the simple WOS model, a social system can have a high degree of durability despite depressed balance.

Survival is more complicated. At an intrinsic propensity of 1, agents prefer to cooperate all of the time, but they discount this liking the more socially sensitive they become. Without the entry-exit dynamic, survival is irrelevant, since the number of rational and reasonable agents does not change. But with the entry-exit dynamic, destruction is a live option. Consider Figure 6, which represents the average degree of survival of 1000 runs at each tenth of social sensitivity (excluding 0, .1, and 1).

Figure 6. Survival Rates

Here we can see that survival is by no means assured in the full WOS model. However, the large majority of the time (74 percent–84 percent of the time) reasonable agents take over the system. And many of these runs, were they allowed to exceed 500 ticks, would yield a higher level of survival. Once the reasonable agents get to a sufficient size, they can resist invasion permanently, and so will ultimately survive rational agents. So Figure 6 understates the degree of immunity in the system.

Immunity, balance, and durability bear interesting and sometimes unexpected relationships to each other. A system with low immunity will be destroyed, such that balance and durability will disappear. So immunity is a precondition for balance and durability. However, once a society has a sufficient degree of immunity, increases in balance and durability have little further effect on immunity. We have already seen that durability and balance come apart as well. The version of the complex model in Figure 6 represents a society with an intrinsic propensity to cooperate of 1. If we focus on versions of the system with a social sensitivity of .5, we find a durability of 86 percent, balance at .296, and immunity of 79 percent. The model also shows that systems with high degrees of balance (low standard deviations) can also have high durability and immunity.

Let’s bring these types of stability into concrete terms via our walkthrough. We can represent the ideas of entry and exit by movement in and out of Reba and John’s neighborhood. Suppose that Sarah is a successful defector — a career opportunist — and so frustrates Reba that Reba decides to move across town. Or perhaps Sarah convinces her like-minded friends that Reba’s community is ripe for the taking. In both cases, Sarah and her friends will become a larger portion of the population relative to Reba’s group of cooperators. Alternatively, Reba and John’s strategy of avoiding interactions with Sarah’s defector cohort might so deprive her of the relevant community goods that she moves to another neighborhood where she can take better advantage of others. Sarah will still pursue interactions with John and Reba, but they are busy building one another up through cooperation, and so only interact with defectors periodically.

Such an order will possess a high degree of immunity, due to Reba’s and John’s ability to resist the invasion of Sarah and her pack of opportunists. John and Reba gradually, and perhaps without realizing it, build a cooperative neighborhood together, ignoring Sarah’s occasional incursions. In doing so, John and Reba establish a neighborhood with a high degree of long-run social trust. However, to represent low balance, we should allow that John and Reba are observant and care a great deal about what others are doing. Thus, the prospect of Sarah and her pack invading, and their occasional appearance can cause social trust to break down quickly, but also with the ability to return to high levels of social trust in the future.

X. A Well-Ordered Society: Durable, Balanced, and Immune

My results are tentative because my model has a number of drawbacks. First, the agents in the WOS are extremely cognitively limited. They cannot track different agent strategies, they make extremely coarse-grained observations of cooperation, rational agents always defect, reasonable agents don’t pay attention to their payoffs, players cannot change agent-strategies, and reasonable agents flee non-cooperators more effectively than rational agents. But simple models have virtues. The modest assumptions of the ABM, and ABM modeling in general, allow us to enhance our understanding of political stability by illuminating distinct social processes that can be stable or unstable.

The ABM has three implications beyond showing that a well-ordered society must be durable, balanced, and immune for the right reasons. First, even setting immunity aside, distinguishing durability and balance reveals that we may not be able to establish stability via a single social mechanism. Consequently, the arguments made on behalf of various assurance mechanisms in a WOS are threatened. For example, some political liberals have argued that complying with the requirements of public reason can help citizens of a well-ordered society assure one another that they are committed to one or a small set of political conceptions of justice. The point of assurance is to generate a political order that is stable for the right reasons. But if the ideal of political stability is deeply ambiguous, it is no longer clear what standard assurance mechanisms accomplish.

Second, the ABM identifies three new lines of research within the public reason project: (i) identifying different assurance mechanisms for different types of stability, (ii) determining how socially sensitive reasonable persons must be, or the extent to which we should allow their social sensitivity to vary, and (iii) uncovering varied transitional paths from a society that is not well-ordered to one that is. On this final point, we can see from the model that a real WOS can transition into a simple WOS so long as cooperative agents can form cooperative networks that allow them to systematically out-produce and replace rational agents.^{Footnote 56} Immunity connects ideal and nonideal theory by helping us understand how a nonideal order can transition into a WOS.

Finally, I believe the ABM allows us to develop a more sophisticated public reason liberal approach to constitutional choice. This essay is part of a broader project that attempts to specify how contractarian parties can choose a constitutional arrangement for themselves. I have developed a generic model with three stages, the last of which concerns political stability and is specified by the model developed here. Within public reason liberalism, constitutional arrangements must be stable for the right reasons, so whichever rules are chosen must be subjected to a stability test. This essay specifies that test. A constitutional rule is publicly justified only when it generates an adequate degree of durability, balance, and immunity. The last factor, immunity, will prove especially important if we believe that constitutional rules should be selected under nonideal conditions, such that constitutional rules will contain provisions for discouraging defection. Thus, the model developed here can specify the choice of constitutional rules in both ideal and nonideal circumstances.