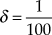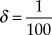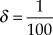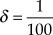I. Introduction
John Nash in the 1950s developed the bargaining problem, a game-theoretic framework for analyzing problems where the interests of different parties are imperfectly aligned and some must make concessions to others in order for them all to arrive at a resolution.Footnote 1 Soon after Nash’s seminal work, Richard Braithwaite argued that the bargaining problem can serve as a tool for analyzing problems of fair division, and defended a specific egalitarian solution as the fair resolution of a 2-agent division problem.Footnote 2 Over the years since Nash’s and Braithwaite’s foundational contributions, the bargaining problem has generated immense bodies of theoretical and experimental research and has become important in philosophy for analyzing problems of distributive justice. Yet in certain respects this problem remains quite recalcitrant. The various solution concepts proposed for the bargaining problem all fall short of satisfying the desiderata in a small set of desirable structural properties. Even in especially ideal settings for rational choice game theorists, where the agents engaged in a bargaining problem are assumed to have common knowledge of their rationality, their preference structures, and a fixed procedure for bargaining, there is no such procedure that yields a determinate outcome in any but the simplest cases where only two claimants vie for shares of an infinitely divisible good. And bargaining experiments have yielded results “all over the map” according to the various experimental designs.
Broadly speaking, game theory has two traditions, one based upon rational choice and the epistemic conditions ideally rational agents need in order to “solve” their game, and another based upon what limitedly rational agents can infer from their environment and from repeated experience to help them settle into outcomes that become their “solutions.” According to the rational choice tradition, the solution of a bargaining problem is an outcome that satisfies certain structural properties or that rational bargainers would select as a consequence of their common knowledge of the structure of this problem and their rationality. This tradition has produced important results, but falls far short of producing a theory that can predict what rational bargainers will do in all instances of the bargaining problem. According to the more empirical tradition, the solutions to bargaining problems are conventions that stem from focal point effects and inductive learning. In this essay I adopt the conventionalist perspective. Below I argue that agents who can learn through repeated interactions can indeed learn to follow a variety of convention equilibria of bargaining problems, and that they can come to regard certain solutions of the bargaining problem as focal given what they learn.
The remainder of this essay is structured as follows: In Section II, I review the basics of Nash’s bargaining problem and the closely related demand game. I argue here that agents engaged in a bargaining problem will not follow a principle of fair division as a consequence of the logic of rational choice. In Section III I discuss the limitations of the standard a priori approaches to analyzing the bargaining problem. None of the solution concepts of the axiomatic approach that requires a solution to satisfy a set of specific structural properties satisfies all of what might be regarded the “core” desired properties. And the strategic bargaining approach that explicitly models the process of exchanging offers yields determinate results only for a very limited class of problems and assumes far more common knowledge than is ever likely to obtain in actual bargaining situations. In Section IV I consider more empirical approaches to analyzing the bargaining problem that incorporate learning and focal points. I show by example that agents who engage in a bargaining problem repeatedly and who update their beliefs about each other according to a simple model of inductive learning can reach a variety of equilibria that characterize conventions, and that the equilibria of the egalitarian and equal division solutions can have a certain attracting power of this learning process that can make these equilibria focal for these agents. In the concluding section I discuss some general implications one can draw from the conventionalist analysis of the bargaining problems examined here. One important conclusion is that this analysis lends some empirical support to the Aristotelian principle of distributive justice, since this principle is equivalent to the egalitarian solution for an appropriate scaling of the agents’ payoffs. I also discuss some possible areas for future research and some related literature.
II. Fair Division Problems
Aristotle claims that everyone agrees upon a proportionality principle of distributive justice, according to which the ratios of the values of shares received and of the recipients’ worth are equal. According to this principle, equals according to the criteria of worth are to receive equally valuable shares.
[A]ll men think justice to be a sort of equality; . . . For they say that what is just is just for someone and that it should be equal for equals. But there still remains a question: equality or inequality of what? Here is a difficulty which calls for philosophical speculation.Footnote 3
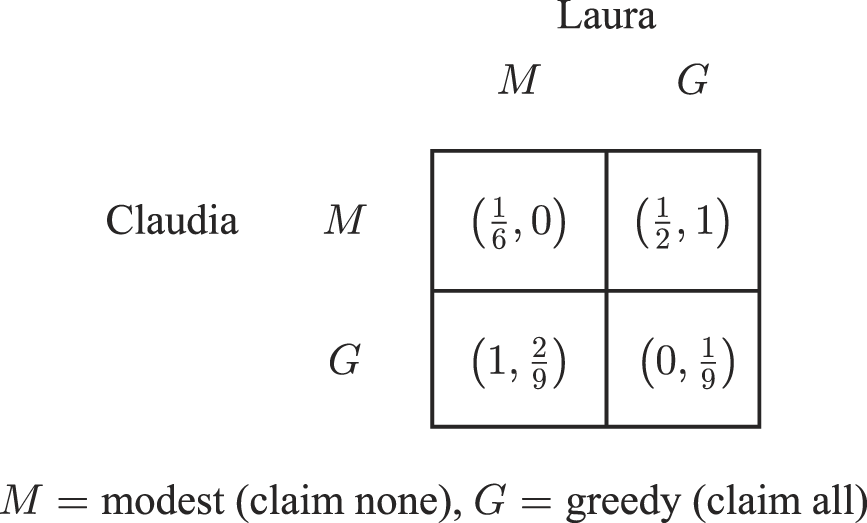
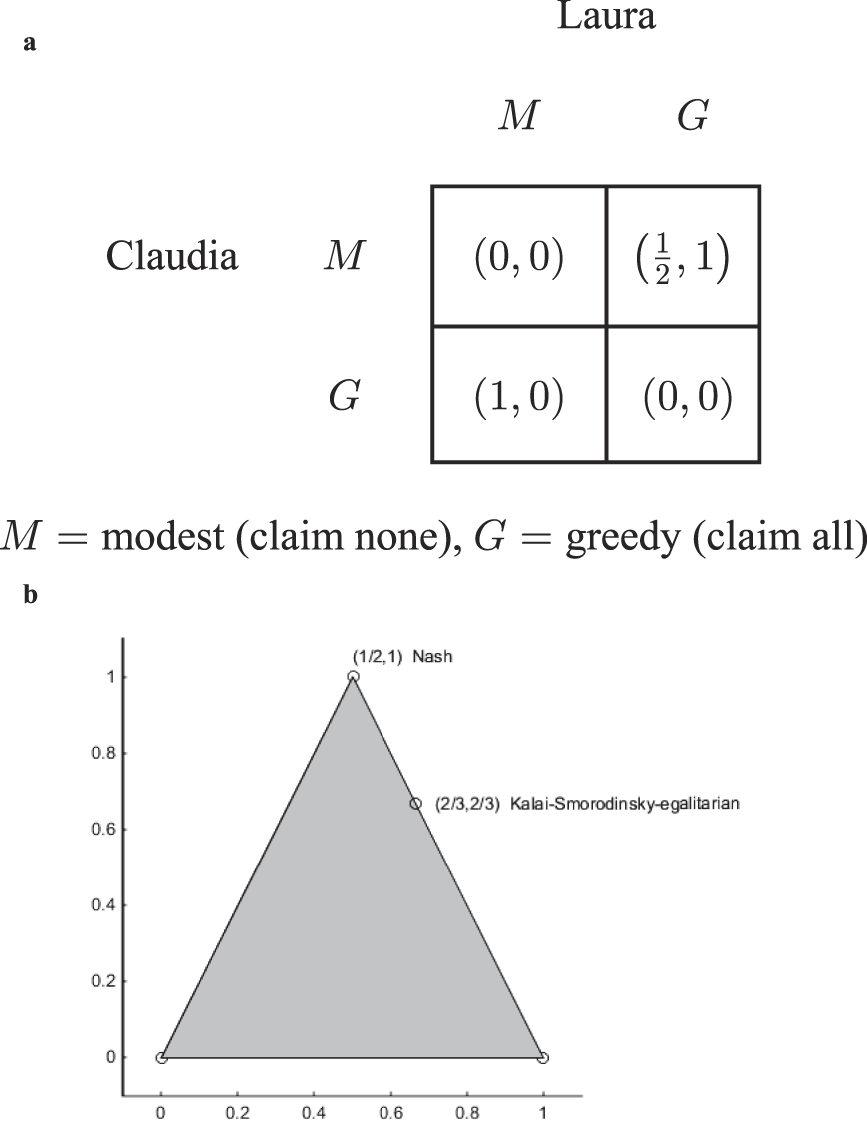
In fact, the formal proportionality principle Aristotle thinks is universally accepted is itself a matter for philosophical speculation. This principle is not a consequence of the orthodox logic of rational choice, according to which a rational agent consistently chooses options that are best in the sense of maximizing expected utility or payoff. One of the simplest of resource division problems is the Chocolate Cake problem, where hungry claimants each claim a share of a cake, and then each receives the share she has claimed if her claim is compatible with those of all the other claimants. In this way there is enough cake to supply each her own claim and otherwise each receives nothing because the cake spoils while they spat over having made incompatible claims. When the claimants are assigned payoffs reflecting their preferences for cake, their problem becomes a demand game. When there are two claimants and the payoff each receives is exactly equal to the fraction defining her received share of cake, the 2×2 Figure 1 game is a basis for defining the payoff structure of this demand game.
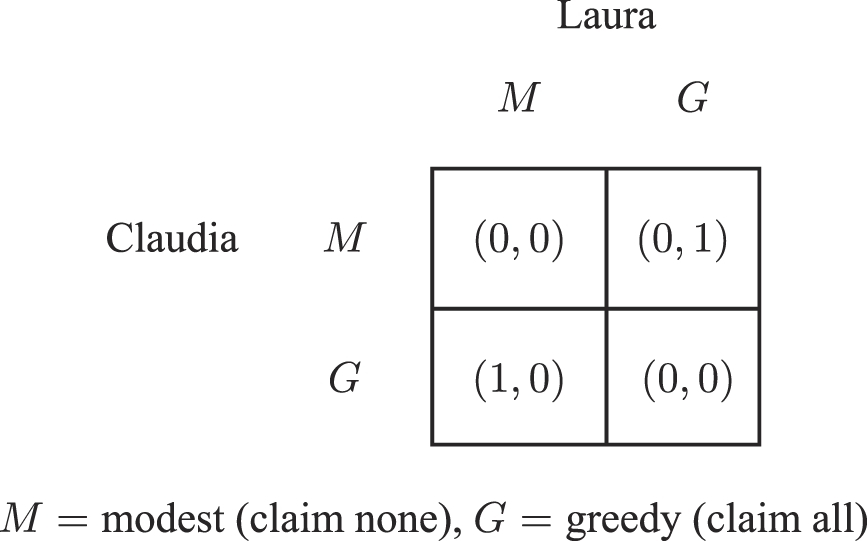
Figure 1. Chocolate Cake Basis Game
In a basis game such as this game, each claimant can be modest (M) and claim none of the resource (M) or greedy (G) and claim all of the resource.Footnote 4 In the Chocolate Cake Basis Game, , (G, M) and (G, G) are Nash equilibria, that is, each agent’s part of each of these outcomes is a best response in terms of expected payoff given that the other follows this outcome. For both the claimants Claudia and Laura, G is the weakly dominant strategy, that is, whatever strategy the other chooses, each always does at least as well and sometimes better by choosing G rather than M. So apparently if Laura and Claudia both choose rationally they end up following the (G, G) equilibrium where neither gets any chocolate cake with the payoff vector (0, 0).
Suppose Claudia’s and Laura’s strategy sets are enriched so that each can claim any desired fraction of the resource. If Claudia and Laura issue compatible respective claims ![]() ${x_1},{x_2} \in \left( {0,1} \right)$, then Claudia’s payoff is x 1 > 0 and Laura’s payoff is x 2 > 0, so both fare better than they fare at (G,G).Footnote 5 How much should each claim? Each claimant’s best strategy in this demand game now depends upon the strategy the other chooses. If
${x_1},{x_2} \in \left( {0,1} \right)$, then Claudia’s payoff is x 1 > 0 and Laura’s payoff is x 2 > 0, so both fare better than they fare at (G,G).Footnote 5 How much should each claim? Each claimant’s best strategy in this demand game now depends upon the strategy the other chooses. If ![]() ${x_1} + {x_2} < 1$, than Claudia can gain a greater payoff by increasing her own claim, and Laura can do likewise. If
${x_1} + {x_2} < 1$, than Claudia can gain a greater payoff by increasing her own claim, and Laura can do likewise. If ![]() ${x_1} + {x_2} > 1$, then their claims are not compatible. In this case, Claudia can increase her own expected payoff by lowering her claim so as to be compatible with x 2, and Laura can increase her own expected payoff similarly. But if
${x_1} + {x_2} > 1$, then their claims are not compatible. In this case, Claudia can increase her own expected payoff by lowering her claim so as to be compatible with x 2, and Laura can increase her own expected payoff similarly. But if ![]() ${x_1} + {x_2} = 1$, then their claims are in Nash equilibrium. In this case, if Laura were to deviate unilaterally from the claim pair
${x_1} + {x_2} = 1$, then their claims are in Nash equilibrium. In this case, if Laura were to deviate unilaterally from the claim pair ![]() $\left( {{x_1},{x_2}} \right)$ by claiming less, she would get less than her original claim x 2, and if she were to deviate by claiming more, then she would get nothing. Similarly, Claudia would get strictly less than her original claim x 1 were she to unilaterally deviate. When
$\left( {{x_1},{x_2}} \right)$ by claiming less, she would get less than her original claim x 2, and if she were to deviate by claiming more, then she would get nothing. Similarly, Claudia would get strictly less than her original claim x 1 were she to unilaterally deviate. When ![]() ${x_1} + {x_2} = 1$,
${x_1} + {x_2} = 1$, ![]() $\left( {{x_1},{x_2}} \right)$ is a strict Nash equilibrium, that is, each claim is a unique best response to the other. For this demand game, such a strict Nash equilibrium
$\left( {{x_1},{x_2}} \right)$ is a strict Nash equilibrium, that is, each claim is a unique best response to the other. For this demand game, such a strict Nash equilibrium ![]() $\left( {{x_1},{x_2}} \right)$ is also Pareto optimal, that is, there are no other outcomes in this game where both fare at least as well and at least one fares better in terms of expected payoff. For any claim
$\left( {{x_1},{x_2}} \right)$ is also Pareto optimal, that is, there are no other outcomes in this game where both fare at least as well and at least one fares better in terms of expected payoff. For any claim ![]() $x \in \left( {0,1} \right)$ Claudia might make, if Laura responds by claiming
$x \in \left( {0,1} \right)$ Claudia might make, if Laura responds by claiming ![]() $1 - x$, then the claim pair
$1 - x$, then the claim pair ![]() $\left( {x,1 - x} \right)$ characterizes a strict Nash equilibrium. So when
$\left( {x,1 - x} \right)$ characterizes a strict Nash equilibrium. So when ![]() ${x_1} + {x_2} = 1$, the claim pair
${x_1} + {x_2} = 1$, the claim pair ![]() $\left( {{x_1},{x_2}} \right)$ is then one of many distinct strict equilibria of this game, that is,
$\left( {{x_1},{x_2}} \right)$ is then one of many distinct strict equilibria of this game, that is, ![]() $\left( {{x_1},{x_2}} \right)$ characterizes a convention of this demand game that is equivalent to Claudia and Laura following (G, M) for x 1 of the time and
$\left( {{x_1},{x_2}} \right)$ characterizes a convention of this demand game that is equivalent to Claudia and Laura following (G, M) for x 1 of the time and ![]() $\left( {M,G} \right)$ for the remaining x 2 of the time.Footnote 6 The perfect symmetry of the payoff structure of this game reflects an important background assumption, namely, that neither Claudia nor Laura is more deserving than the other of this chocolate cake. In this situation they are equals with respect to the relevant criteria of worth. If Aristotle is right, then all would agree that Laura and Claudia should receive equal shares of chocolate cake. But Claudia and Laura might not accept this conclusion so blithely. A rational agent placed in a division problem like the Chocolate Cake Demand game might make one of any number of different claims, depending on how cautious or aggressive she might be and how cautious or aggressive she expects her counterpart claimants to be. The convention of the
$\left( {M,G} \right)$ for the remaining x 2 of the time.Footnote 6 The perfect symmetry of the payoff structure of this game reflects an important background assumption, namely, that neither Claudia nor Laura is more deserving than the other of this chocolate cake. In this situation they are equals with respect to the relevant criteria of worth. If Aristotle is right, then all would agree that Laura and Claudia should receive equal shares of chocolate cake. But Claudia and Laura might not accept this conclusion so blithely. A rational agent placed in a division problem like the Chocolate Cake Demand game might make one of any number of different claims, depending on how cautious or aggressive she might be and how cautious or aggressive she expects her counterpart claimants to be. The convention of the ![]() $\left( {{1 \over 2},{1 \over 2}} \right)$ equilibrium where each claims half is only one of a whole continuum of conventions available to Claudia and Laura. Even if both do follow strategies according to orthodox standards of rational choice, equal division of the cake does not follow from this fact, not even if this fact is common knowledge between them.Footnote 7
$\left( {{1 \over 2},{1 \over 2}} \right)$ equilibrium where each claims half is only one of a whole continuum of conventions available to Claudia and Laura. Even if both do follow strategies according to orthodox standards of rational choice, equal division of the cake does not follow from this fact, not even if this fact is common knowledge between them.Footnote 7
Because the above Chocolate Cake problem has a perfectly symmetric payoff structure reflecting the claimants’ equal worth with respect to shares of the cake, it is at least clear that according to the Aristotelian principle in this problem each claimant’s fair share should be half of the cake. For a division problem with payoff asymmetries, what counts as a fair share might not be at all obvious. Figure 2 summarizes a game equivalent to the game Braithwaite used as a basis for generating the demand game he used to illustrate his approach to solving a 2-agent resource division problem. The Braithwaite Basis Game is a conflictual coordination game, since Claudia and Laura have available to them a plurality of strict Nash equilibria, namely (G, M) and (M, G), and their preferences over these equilibria differ. In the corresponding demand game, Laura and Claudia can coordinate on a strict convention equilibrium equivalent to their following (G, M) for ![]() $x \in \left[ {0,1} \right]$ of the time and (M, G) the remaining
$x \in \left[ {0,1} \right]$ of the time and (M, G) the remaining ![]() $1 - x$ of the time only when at least one of them gives in to the preferences of the other to at least some extent. If both carry out threats to be greedy, the resulting
$1 - x$ of the time only when at least one of them gives in to the preferences of the other to at least some extent. If both carry out threats to be greedy, the resulting ![]() $\left( {G,G} \right)$ outcome is the worst possible for Claudia, but not for Laura. So Laura has a threat advantage. Laura and Claudia might agree with Braithwaite that the solution they ultimately follow in their demand game should be fair.Footnote 8 But given the asymmetries in this game, Claudia and Laura might have some difficulty identifying an outcome they would regard as a fair solution.
$\left( {G,G} \right)$ outcome is the worst possible for Claudia, but not for Laura. So Laura has a threat advantage. Laura and Claudia might agree with Braithwaite that the solution they ultimately follow in their demand game should be fair.Footnote 8 But given the asymmetries in this game, Claudia and Laura might have some difficulty identifying an outcome they would regard as a fair solution.
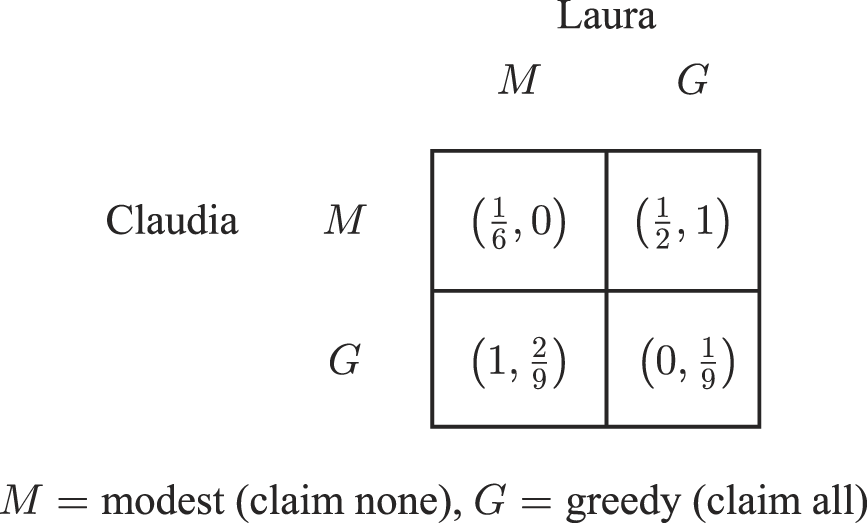
Figure 2. Braithwaite Basis Game
The simple symmetric and asymmetric demand games presented here illustrate the basic structure of a bargaining problem as formulated by John Nash. Nash characterized a given bargaining problem as a feasible set that is the set of all the payoff vectors the agents involved might achieve by taking some agreed upon joint action together with a baseline or nonagreement point that specifies the payoffs agents end up with should they fail to agree upon any joint action. In many cases where the bargaining problem is also a problem of dividing some fixed quantity of a good, the feasible set is defined simply as the set of payoff vectors determined by compatible claims.Footnote 9 I will use this definition of the feasible set in all of the fair division bargaining problems discussed in this essay. Figure 3 depicts the feasible sets of the Chocolate Cake and the Braithwaite Demand Games according to this definition.
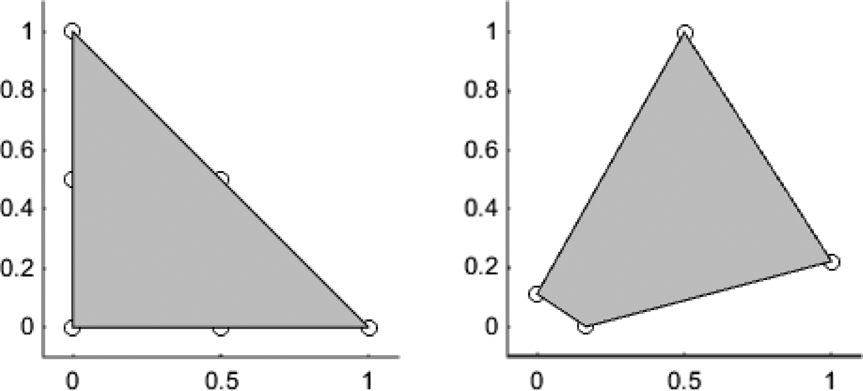
Figure 3. Feasible Sets of Chocolate Cake and Braithwaite Demand Games
In his own discussion of fair division problems, Nash proceeded from the premises that each agent’s payoff is nondecreasing in the amount of good she receives and that the nonagreement point is the outcome where each claimant claims all of the good at stake, so that no agent receives any. In Chocolate Cake and the Braithwaite Games, this second premise implies that ![]() $\left( {G,G} \right)$ defines the nonagreement point. The feasible set payoffs of Chocolate Cake and the Braithwaite Game reflect the first premise, since each agent in fact fares better than she fares at the nonagreement point if she receives a positive share of the good. In each of the Figure 3 sets, the part of the boundary joining the ideal points for each of the two agents characterizes the Pareto frontier, the set of all the Pareto optimal outcomes. A bargaining problem is nontrivial if its Pareto frontier consists of more than a single point.Footnote 10 In both the Chocolate Cake and the Braithwaite Games, the Pareto frontier is the set of payoff vectors defined by the alternation schemes
$\left( {G,G} \right)$ defines the nonagreement point. The feasible set payoffs of Chocolate Cake and the Braithwaite Game reflect the first premise, since each agent in fact fares better than she fares at the nonagreement point if she receives a positive share of the good. In each of the Figure 3 sets, the part of the boundary joining the ideal points for each of the two agents characterizes the Pareto frontier, the set of all the Pareto optimal outcomes. A bargaining problem is nontrivial if its Pareto frontier consists of more than a single point.Footnote 10 In both the Chocolate Cake and the Braithwaite Games, the Pareto frontier is the set of payoff vectors defined by the alternation schemes ![]() $x \cdot \left( {G,M} \right) + \left( {1 - x} \right) \cdot \left( {M,G} \right)$,
$x \cdot \left( {G,M} \right) + \left( {1 - x} \right) \cdot \left( {M,G} \right)$, ![]() $x \in \left[ {0,1} \right]$, that characterize the conventions where the claimants follow Claudia’s ideal outcome x of the time and Laura’s ideal outcome
$x \in \left[ {0,1} \right]$, that characterize the conventions where the claimants follow Claudia’s ideal outcome x of the time and Laura’s ideal outcome ![]() $1 - x$ of the time.
$1 - x$ of the time.
III. Rational Choice Approaches
Nash argued that in principle one can analyze any bargaining problem either axiomatically by considering which allocations satisfy certain formal desiderata, or from the perspective of agents who settle upon an allocation via some strategic bargaining process. Nash regarded these two approaches as complementary.Footnote 11 According to Nash’s own proposed axiomatic solution, if at a set ![]() $x = \left( {{x_1},...,{x_n}} \right)$ of claims that can but need not be compatible each Agent i’s payoff is
$x = \left( {{x_1},...,{x_n}} \right)$ of claims that can but need not be compatible each Agent i’s payoff is ![]() ${u_i}\left( x \right)$ and
${u_i}\left( x \right)$ and ![]() $\left( {{u_{01}},...,{u_{0n}}} \right)$ is the payoff vector of the nonagreement point so that Agent i receives
$\left( {{u_{01}},...,{u_{0n}}} \right)$ is the payoff vector of the nonagreement point so that Agent i receives ![]() ${u_{0i}}$ at this point, then the good is divided so as to maximize the Nash product
${u_{0i}}$ at this point, then the good is divided so as to maximize the Nash product ![]() $\left( {{u_1}\left( x \right) - {u_{01}}} \right) \cdot \cdot \cdot \left( {{u_n}\left( x \right) - {u_{0n}}} \right)$. In the Chocolate Cake Demand Game, the Nash product is
$\left( {{u_1}\left( x \right) - {u_{01}}} \right) \cdot \cdot \cdot \left( {{u_n}\left( x \right) - {u_{0n}}} \right)$. In the Chocolate Cake Demand Game, the Nash product is ![]() $x \cdot \left( {1 - x} \right)$, which is maximized at
$x \cdot \left( {1 - x} \right)$, which is maximized at ![]() $x = {1 \over 2}$, so that at the Nash solution Claudia and Laura follow (G, M) for
$x = {1 \over 2}$, so that at the Nash solution Claudia and Laura follow (G, M) for ![]() ${1 \over 2}$ the time and (M, G) the remaining
${1 \over 2}$ the time and (M, G) the remaining ![]() ${1 \over 2}$ of the time. In the Braithwaite Demand Game, at the Nash solution Claudia and Laura follow (G, M) for
${1 \over 2}$ of the time. In the Braithwaite Demand Game, at the Nash solution Claudia and Laura follow (G, M) for ![]() ${1 \over {14}}$ of the time and
${1 \over {14}}$ of the time and ![]() $\left( {M,G} \right)$ for
$\left( {M,G} \right)$ for ![]() ${{13} \over {14}}$ of the time.Footnote 12
${{13} \over {14}}$ of the time.Footnote 12
Game theorists and philosophers have challenged Nash’s analysis of the bargaining problem on several fronts and have proposed a variety of competing axiomatic solution concepts for this problem. Axiomatic bargaining theory is today a research area in its own right, and whole families of alternative solutions to bargaining problems have been developed and continue to be debated.Footnote 13 Two other axiomatic solution concepts, both first introduced by Howard Raiffa, rival Nash’s solution in importance.Footnote 14 Raiffa, and Braithwaite after him, concurred with Nash that the outcome where each agent claims all of the good at stake defines the nonagreement point. According to one of Raiffa’s solutions, one first scales payoffs so that each Agent i’s most desired and least desired outcomes have respective payoffs 1 and 0, and then picks the point on the Pareto frontier yielding the agents equal gains from their individual nonagreement point payoffs according to this payoff scale. In the Braithwaite Demand Game, this egalitarian solution has Claudia and Laura follow (G, M) for ![]() ${7 \over {23}}$ of the time and (M, G) for
${7 \over {23}}$ of the time and (M, G) for ![]() ${{16} \over {23}}$ of the time. Braithwaite, who took inspiration from Nash’s analysis of bargaining but who also thought Nash’s solution of Braithwaite’s Demand Game problem is plainly too lopsided in Laura’s favor, defended a variation of Raiffa’s egalitarian solution as the basis for a fair division in this problem.Footnote 15 Another of Raiffa’s solutions selects a point on the Pareto frontier at which the ratio of each Agent i’s received payoff less her nonagreement point payoff to her ideal payoff where she gets all the resource less her nonagreement point payoff is the same for all the agents. Some years after Raiffa’s work, Ehud Kalai and Meir Smorodinsky axiomatized this solution.Footnote 16 In the Braithwaite Demand Game, at this Kalai-Smorodinsky solution the two agents follow (G, M) for
${{16} \over {23}}$ of the time. Braithwaite, who took inspiration from Nash’s analysis of bargaining but who also thought Nash’s solution of Braithwaite’s Demand Game problem is plainly too lopsided in Laura’s favor, defended a variation of Raiffa’s egalitarian solution as the basis for a fair division in this problem.Footnote 15 Another of Raiffa’s solutions selects a point on the Pareto frontier at which the ratio of each Agent i’s received payoff less her nonagreement point payoff to her ideal payoff where she gets all the resource less her nonagreement point payoff is the same for all the agents. Some years after Raiffa’s work, Ehud Kalai and Meir Smorodinsky axiomatized this solution.Footnote 16 In the Braithwaite Demand Game, at this Kalai-Smorodinsky solution the two agents follow (G, M) for ![]() ${4 \over {11}}$ of the time and (M, G) for
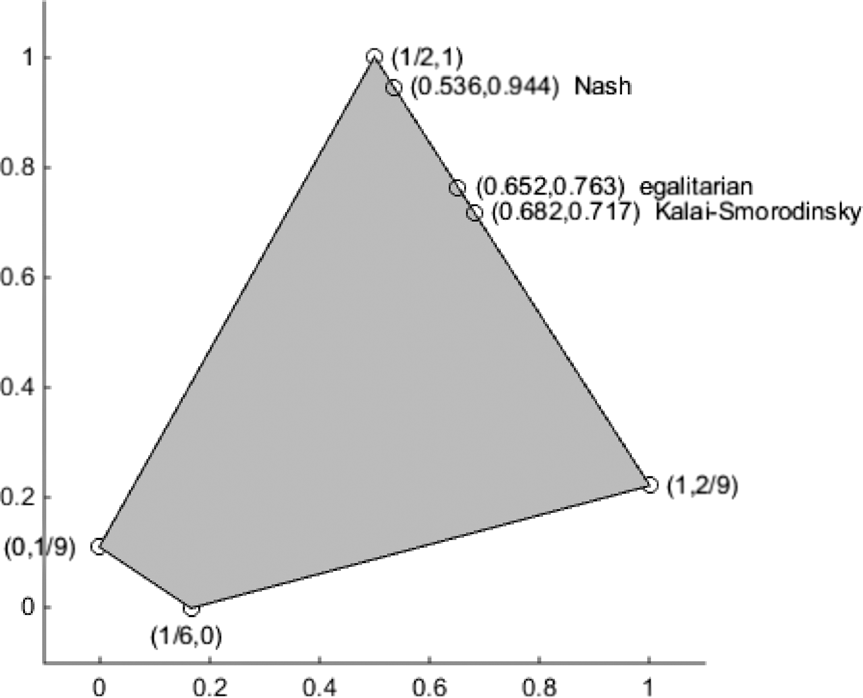
${4 \over {11}}$ of the time and (M, G) for ![]() ${7 \over {11}}$ of the time. In Morals by Agreement, David Gauthier defended a minimax relative concession solution for the n-agent bargaining problem that is the Kalai-Smorodinsky solution in the 2-agent case.Footnote 17 While Raiffa, and Kalai and Smorodinsky refrained from declaring that the Kalai-Smorodinsky solution is generally superior to others, when Gauthier published Morals by Agreement he maintained that minimax relative concession solves the bargaining problem.Footnote 18 The Nash, egalitarian, and Kalai-Smorodinsky solutions of the Braithwaite Demand Game are depicted in Figure 4.
${7 \over {11}}$ of the time. In Morals by Agreement, David Gauthier defended a minimax relative concession solution for the n-agent bargaining problem that is the Kalai-Smorodinsky solution in the 2-agent case.Footnote 17 While Raiffa, and Kalai and Smorodinsky refrained from declaring that the Kalai-Smorodinsky solution is generally superior to others, when Gauthier published Morals by Agreement he maintained that minimax relative concession solves the bargaining problem.Footnote 18 The Nash, egalitarian, and Kalai-Smorodinsky solutions of the Braithwaite Demand Game are depicted in Figure 4.

Figure 4. Axiomatic Solutions of the Braithwaite Demand Game
Braithwaite and Gauthier may have thought that the axiomatic approach can produce the fair solution to any given division problem, even if they defended different solutions. But is any axiomatic solution fully satisfactory? Each of the various axiomatic solution concepts that game theorists have proposed fails to satisfy some property central to motivating some of the competing solution concepts. For example, the shares of the egalitarian solution can vary according to one’s choice of payoff scales, and Nash and Kalai and Smorodinsky require their solution concepts to satisfy scale invariance.Footnote 19 On the other hand, if the feasible set is expanded with new payoff vectors that increase the possible gain of exactly one Agent i, then it is possible that the Nash solution of the expanded bargaining problem actually leaves Agent i worse-off than at the Nash solution of the original problem. The Kalai-Smorodinsky and egalitarian solutions satisfy monotonicity properties that guarantee that an Agent i does not lose as the result of the feasible set being enlarged with payoff vectors more favorable to Agent i herself. And the Kalai-Smorodinsky solution is not stable when it is reapplied across subgroups. If the Kalai-Smorodinsky solution is applied first to all of the good, and all the claimants are assigned their shares accordingly, and then if this concept is reapplied to the fraction of the good originally assigned to some proper subset of the claimants, the reapplication could leave some in this subset worse-off than they were according to the original application. The Nash and the egalitarian solutions satisfy reapplication stability properties that forestall this defect of the Kalai-Smorodinsky solution. Plainly, the Nash, Kalai-Smorodinsky and egalitarian solutions all have drawbacks that accompany their virtues. In fact, any solution concept that requires a Pareto optimal division and equal division when the feasible set is perfectly symmetric is unstable with respect either to expansion of the feasible set in any agent’s favor, reapplication across subgroups, or rescaling of payoffs.Footnote 20
Game theorists have made some important steps toward completing the Nash program of relating the axiomatic and strategic bargaining approaches Nash proposed, but the strategic bargaining approach in its present state is of limited value for predicting the outcomes ideally rational and knowledgeable agents would follow in bargaining problems. Some of the central results of the alternating offers models of bargaining first proposed in the 1970s and 1980s by Ingolf Stähl and Ariel Rubinstein show that a pair of rational agents who are to exchange successive proposals for allocation of an infinitely divisible good will converge upon a unique solution given common knowledge of their rationality, their payoffs, the bargaining procedure and how much each discounts her payoff for the share she ultimately receives over the time periods they can submit new proposals.Footnote 21 As the length of these time periods approaches zero, this solution for the Rubinstein model maximizes the weighted Nash product ![]() ${\left( {{u_1}\left( x \right) - {u_{01}}} \right)^{{\alpha _1}}} \cdot {\left( {{u_2}\left( x \right) - {u_{02}}} \right)^{{\alpha _2}}}$ for
${\left( {{u_1}\left( x \right) - {u_{01}}} \right)^{{\alpha _1}}} \cdot {\left( {{u_2}\left( x \right) - {u_{02}}} \right)^{{\alpha _2}}}$ for ![]() ${\alpha _1},{\alpha _2} \ge 0$. In this product
${\alpha _1},{\alpha _2} \ge 0$. In this product ![]() ${\alpha _i}$ reflects Agent i’s bargaining power and is defined as an increasing function of Agent i’s discount factor, so that a more patient agent has greater bargaining power. And for the special case where
${\alpha _i}$ reflects Agent i’s bargaining power and is defined as an increasing function of Agent i’s discount factor, so that a more patient agent has greater bargaining power. And for the special case where ![]() ${\alpha _1} = {\alpha _2} = 1$, this product is the ordinary Nash product. This result is conceptually remarkable, since it shows how the outcome of an axiomatic solution could emerge from agents’ individual strategic moves in certain special circumstances. But even assuming the underlying common knowledge of payoffs and discount factors that seldom, if ever, exists among agents in actual bargaining situations, alternating offers models like the Rubinstein model give determinate solutions only for the 2-agent case where the good is infinitely divisible. In a bargaining problem with three or more agents, given sufficiently large discount factors, the corresponding alternating offers models can converge on such a large set of distinct equilibria that these models do not even serve to narrow down the set of equilibrium outcomes the bargaining agents might reach in any interesting way.Footnote 22 And even in the 2-agent case, if the good is divisible only up to finitely many increments, like a sum of money, then two agents who otherwise satisfy the assumptions of the Rubinstein model might settle into practically any outcome better for both than the nonagreement point.Footnote 23
${\alpha _1} = {\alpha _2} = 1$, this product is the ordinary Nash product. This result is conceptually remarkable, since it shows how the outcome of an axiomatic solution could emerge from agents’ individual strategic moves in certain special circumstances. But even assuming the underlying common knowledge of payoffs and discount factors that seldom, if ever, exists among agents in actual bargaining situations, alternating offers models like the Rubinstein model give determinate solutions only for the 2-agent case where the good is infinitely divisible. In a bargaining problem with three or more agents, given sufficiently large discount factors, the corresponding alternating offers models can converge on such a large set of distinct equilibria that these models do not even serve to narrow down the set of equilibrium outcomes the bargaining agents might reach in any interesting way.Footnote 22 And even in the 2-agent case, if the good is divisible only up to finitely many increments, like a sum of money, then two agents who otherwise satisfy the assumptions of the Rubinstein model might settle into practically any outcome better for both than the nonagreement point.Footnote 23
In sum, each of the two rational choice approaches Nash proposed for analyzing the bargaining problem yields a negative moral along with its positive conclusions. The axiomatic approach shows that every bargaining problem has a unique solution satisfying several of a set of intuitively appealing properties, but no axiomatic solution concept satisfies all these properties. One who follows Braithwaite and Gauthier’s lead and defends a certain axiomatic solution as the fair solution of division problems will have to “pick her poison” and decide which sort of solution instability to accept. The strategic bargaining approach shows that for a 2-agent bargaining problem where the good is infinitely divisible, a highly stylized model of the process of bargaining between rational agents will reach a solution that coincides with an axiomatic solution. But for bargaining problems outside this narrow class, this approach yields no determinate results.
IV. Focal Points and Inductive Learning
A quite different approach emphasizes learning and focal points. Some of the early pioneers of game theory, including R. Duncan Luce, Howard Raiffa, and Nash himself argued that agents who engage in a game repeatedly could gradually converge to equilibria as the result of what they learn through these repeated engagements.Footnote 24 In The Strategy of Conflict, Thomas Schelling argued that agents who engage in coordination problems, including bargaining problems, can coordinate their actions on equilibrium outcomes far more often than random chance would predict by inferring how to act in accord with clues from the context of their interaction that they all recognize.
Finding the key, or rather finding a key—any key that is mutually recognized as the key becomes the key—may depend on imagination more than on logic; it may depend on analogy, precedent, accidental arrangement, symmetry, aesthetic or geometric configuration, casuistic reasoning, and who the parties are and what they know about each other.Footnote 25
Remarkably, these inductive learning and focal point approaches to equilibrium selection in games are foreshadowed in David Hume’s analysis of convention.Footnote 26 Focal point explanations of efficient allocations in bargaining problems are illustrated in many examples in ordinary life and in the laboratory. In unstructured bargaining experiments, where the details of the bargaining process are left to the subjects themselves, subjects try to follow certain divisions they regard as focal.Footnote 27
What makes a focal point focal? Schelling, and Hume before him, frankly acknowledge that the agents engaged in a coordination problem tend to employ different sets of contextual clues in different situations, and that such agents might in the end settle upon some outcome for reasons that seem frivolous to an outsider and perhaps even to themselves.Footnote 28 The bargaining problem as Nash formulates it might seem especially open-ended with respect to focal points given the huge number of strategy profiles, and accompanying payoff vectors, defined by various claim combinations available to the agents in any nontrivial bargaining problem. In principle, any outcome of a bargaining problem could be focal simply because the bargaining agents can distinguish this outcome from all of the others. But as already noted, empirical evidence confirms that in many bargaining problems the agents involved do use focal points to coordinate on efficient divisions. What could explain the origins of the focal point effect? This effect can stem from learning. Game theorists have traditionally treated the learning and the focal point approaches to equilibrium selection separately. In fact, these two approaches are better viewed as interdependent. Any focal point effect in a coordination situation depends crucially upon what the agents trying to concert their actions know about each other. Trial and error learning can serve as one source of this knowledge. In bargaining problems, agents can learn to follow certain types of equilibria more often than others even when they have no contextual information other than their own individual payoffs, and the results of the learning process can lead them to regard certain solutions as focal.
In the remainder of this section I will explore how a focal point effect could emerge from learning by applying a simple model of inductive learning to some specific bargaining problems. The specific learning model is known among game theorists as weighted fictitious play, and is a variation on Rudolf Carnap’s system of inductive logic where an agent forms her subjective conjecture over the likelihoods of events in a given event set as a probability distribution that is a mixture of her initial probability distribution over these events and the observed frequencies of each of these events over time.Footnote 29 In game theory the interpretation of a fictitious play process is that in a game repeated over time periods, at each period each agent engaged in the game updates her conjecture over her counterparts’ strategy profiles according to the frequency of past observed profiles and then follows a best response given her updated conjecture. The epistemic assumptions of this model are far less demanding than those of rational choice models of equilibrium selection such as the alternating offers models of bargaining. In particular, no common knowledge of agent specific parameters like discount factors is required. Agents need only know their own payoffs in the game and the strategies their counterparts have followed in the past in order to update their beliefs according to this form of inductive learning. And while weighted fictitious play is surely an oversimplified model of inductive learning, this model fits the findings of laboratory experiments on simple coordination games fairly well.Footnote 30 The mathematical definition of this model is summarized in the Appendix.
I begin with the Chocolate Cake problem. For this problem and the asymmetric bargaining problems discussed below, I will apply weighted fictitious play to a demand game that approximates with claim precision ![]() $\delta = {1 \over {100}}$ the corresponding demand game where each agent can claim any fraction of the good. In the approximating demand game each agent may claim any fraction
$\delta = {1 \over {100}}$ the corresponding demand game where each agent can claim any fraction of the good. In the approximating demand game each agent may claim any fraction ![]() ${m \over {100}}$ of the good where
${m \over {100}}$ of the good where ![]() $m \in \left\{ {0,1,...,100} \right\}$. Any rest point of the weighted fictitious play process is a Nash equilibrium, and a strict Nash equilibrium is an attracting point of this process in the sense that different sequences of updated conjectures will converge to the conjectures that define this equilibrium.Footnote 31 So each claim pair
$m \in \left\{ {0,1,...,100} \right\}$. Any rest point of the weighted fictitious play process is a Nash equilibrium, and a strict Nash equilibrium is an attracting point of this process in the sense that different sequences of updated conjectures will converge to the conjectures that define this equilibrium.Footnote 31 So each claim pair ![]() $\left( {{m \over {100}},{{100 - m} \over {100}}} \right)$ where
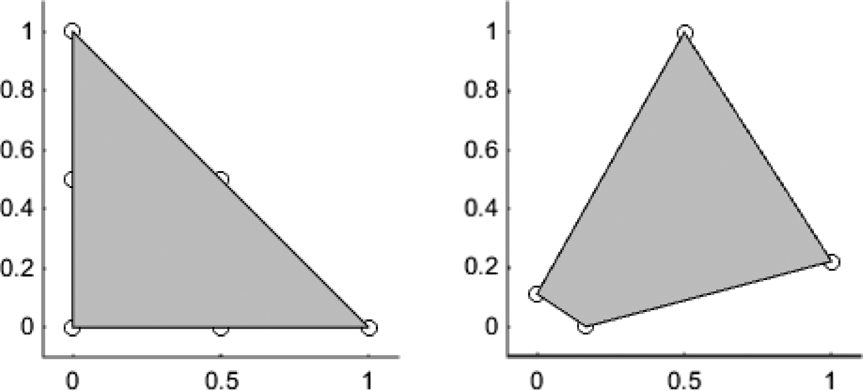
$\left( {{m \over {100}},{{100 - m} \over {100}}} \right)$ where ![]() $m \in \left\{ {1,...,99} \right\}$ that characterizes a convention of the Chocolate Cake Demand Game is an attractor of this learning process. But the different convention equilibria need not all have the same attracting power. The basin of attraction for weighted fictitious play of a strict Nash equilibrium is the set of possible initial conjectures according to this learning process, and the size of this basin is the fraction of the simplex of all possible conjectures defined by the conjectures of this basin. Figure 5 summarizes the relative sizes of the basins of attraction of the weighted fictitious play dynamic applied to this Chocolate Cake Demand Game.
$m \in \left\{ {1,...,99} \right\}$ that characterizes a convention of the Chocolate Cake Demand Game is an attractor of this learning process. But the different convention equilibria need not all have the same attracting power. The basin of attraction for weighted fictitious play of a strict Nash equilibrium is the set of possible initial conjectures according to this learning process, and the size of this basin is the fraction of the simplex of all possible conjectures defined by the conjectures of this basin. Figure 5 summarizes the relative sizes of the basins of attraction of the weighted fictitious play dynamic applied to this Chocolate Cake Demand Game.
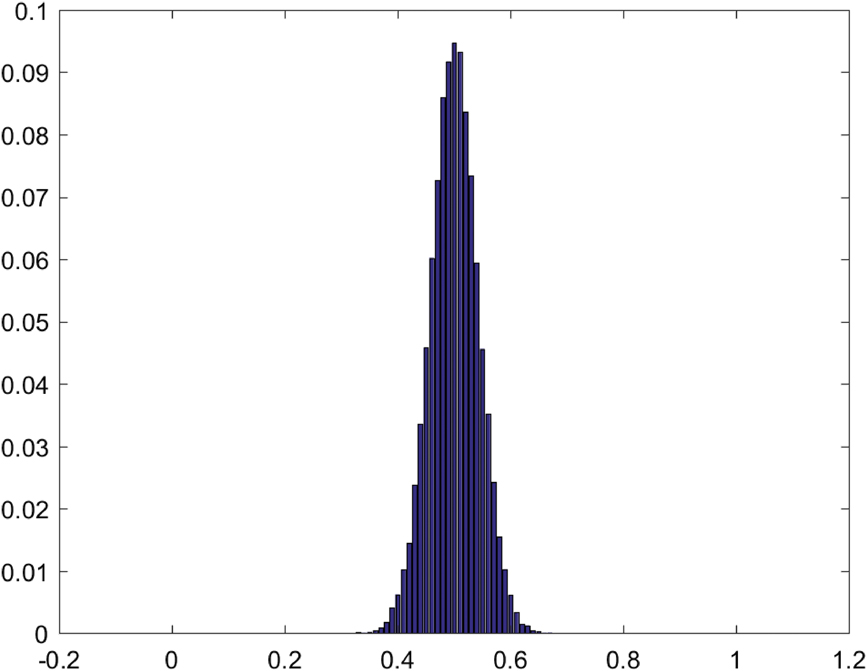
Figure 5. Relative Sizes of Basins of Attraction of Chocolate Cake Demand Game with Claim Precision ![]() $\delta = {1 \over {100}}$
$\delta = {1 \over {100}}$
As one would expect, the limits of the orbits starting from initial points chosen at random in the belief simplex are distributed across the set of convention equilibria. But the equilibrium ![]() $\left( {{{50} \over {100}},{{50} \over {100}}} \right) = \left( {{1 \over 2},{1 \over 2}} \right)$ has the largest basin of attraction, and the distribution of orbit limits is centered around this convention equilibrium. This indicates that inductive learners who engage repeatedly in a structurally symmetric bargaining problem like the Chocolate Cake problem might settle into a variety of division conventions, and that they will have some tendency to converge on the equal division convention. This dovetails with everyday experience, where parties in a completely symmetric division problem might regard equal division as salient and follow the equal division equilibrium most of the time, but perhaps not always.
$\left( {{{50} \over {100}},{{50} \over {100}}} \right) = \left( {{1 \over 2},{1 \over 2}} \right)$ has the largest basin of attraction, and the distribution of orbit limits is centered around this convention equilibrium. This indicates that inductive learners who engage repeatedly in a structurally symmetric bargaining problem like the Chocolate Cake problem might settle into a variety of division conventions, and that they will have some tendency to converge on the equal division convention. This dovetails with everyday experience, where parties in a completely symmetric division problem might regard equal division as salient and follow the equal division equilibrium most of the time, but perhaps not always.
In the Chocolate Cake bargaining problem, the Nash, Kalai-Smorodinsky, and egalitarian solutions all coincide at the ![]() $\left( {{1 \over 2},{1 \over 2}} \right)$ point of equal division. Do inductive learners tend to converge on equilibria at or near any of these axiomatic solutions in an asymmetric bargaining problem? I next consider three such asymmetric problems. In Morals by Agreement, David Gauthier presents a simple example to illustrate how the Nash and the Kalai-Smorodinsky solutions can differ.Footnote 32 Figure 6 summarizes the underlying Gauthier Basis Game and the feasible set that characterizes the corresponding demand game. In the Gauthier Demand Game, Laura’s payoffs are the same as in the Chocolate Cake Demand Game, but Claudia’s payoff at (M, G) where she concedes all of the good to Laura is
$\left( {{1 \over 2},{1 \over 2}} \right)$ point of equal division. Do inductive learners tend to converge on equilibria at or near any of these axiomatic solutions in an asymmetric bargaining problem? I next consider three such asymmetric problems. In Morals by Agreement, David Gauthier presents a simple example to illustrate how the Nash and the Kalai-Smorodinsky solutions can differ.Footnote 32 Figure 6 summarizes the underlying Gauthier Basis Game and the feasible set that characterizes the corresponding demand game. In the Gauthier Demand Game, Laura’s payoffs are the same as in the Chocolate Cake Demand Game, but Claudia’s payoff at (M, G) where she concedes all of the good to Laura is ![]() ${1 \over 2}$ and Claudia receives an addition of
${1 \over 2}$ and Claudia receives an addition of ![]() ${1 \over 2}x$ to her
${1 \over 2}x$ to her ![]() $\left( {M,G} \right)$ payoff for any positive share x of the good she receives. In the Gauthier Basis Game, G is Laura’s weakly dominant strategy, whereas either M or G can be Claudia’s best response given her conjecture regarding Laura. The Kalai-Smorodinsky and egalitarian solutions of the Gauthier Demand Game coincide at
$\left( {M,G} \right)$ payoff for any positive share x of the good she receives. In the Gauthier Basis Game, G is Laura’s weakly dominant strategy, whereas either M or G can be Claudia’s best response given her conjecture regarding Laura. The Kalai-Smorodinsky and egalitarian solutions of the Gauthier Demand Game coincide at ![]() $\left( {{2 \over 3},{2 \over 3}} \right)$, and at this point Claudia’s share is
$\left( {{2 \over 3},{2 \over 3}} \right)$, and at this point Claudia’s share is ![]() ${1 \over 3}$ and Laura’s share is
${1 \over 3}$ and Laura’s share is ![]() ${2 \over 3}$.Footnote 33 The Nash solution is
${2 \over 3}$.Footnote 33 The Nash solution is ![]() $\left( {{1 \over 2},1} \right)$, and the corresponding Nash equilibrium is (M, G) where Laura receives all of the good while Claudia receives none. The asymmetry in their preferences over the other’s ideal point gives Laura a perfect threat advantage according to Nash’s theory, even though
$\left( {{1 \over 2},1} \right)$, and the corresponding Nash equilibrium is (M, G) where Laura receives all of the good while Claudia receives none. The asymmetry in their preferences over the other’s ideal point gives Laura a perfect threat advantage according to Nash’s theory, even though ![]() $\left( {G,G} \right)$ is the worst possible outcome for both. The Nash solution might strike one as plainly unfair, and it certainly seems to strike Gauthier this way. The Kalai-Smorodinsky-egalitarian solution may appear more equitable since this solution awards Claudia a positive share yet still respects Laura’s evident advantage to some extent. Figure 7 summarizes the relative sizes of the basins of attraction of weighted fictitious play applied to the Gauthier Demand Game with
$\left( {G,G} \right)$ is the worst possible outcome for both. The Nash solution might strike one as plainly unfair, and it certainly seems to strike Gauthier this way. The Kalai-Smorodinsky-egalitarian solution may appear more equitable since this solution awards Claudia a positive share yet still respects Laura’s evident advantage to some extent. Figure 7 summarizes the relative sizes of the basins of attraction of weighted fictitious play applied to the Gauthier Demand Game with ![]() $\delta = {1 \over {100}}$ claim precision. As was the case with the Chocolate Cake Demand Game, in the Gauthier Demand Game the weighted fictitious play process converges on a whole distribution of convention equilibria. But in this game, the orbits tend to converge on equilibria near the Kalai-Smorodinsky-egalitarian solution, and the modal attractors are particularly close to this solution. The Nash solution has a negligible basin of attraction. The Kalai-Smorodinsky-egalitarian solution looks like the “winner” over the Nash solution for the Gauthier Demand Game.
$\delta = {1 \over {100}}$ claim precision. As was the case with the Chocolate Cake Demand Game, in the Gauthier Demand Game the weighted fictitious play process converges on a whole distribution of convention equilibria. But in this game, the orbits tend to converge on equilibria near the Kalai-Smorodinsky-egalitarian solution, and the modal attractors are particularly close to this solution. The Nash solution has a negligible basin of attraction. The Kalai-Smorodinsky-egalitarian solution looks like the “winner” over the Nash solution for the Gauthier Demand Game.
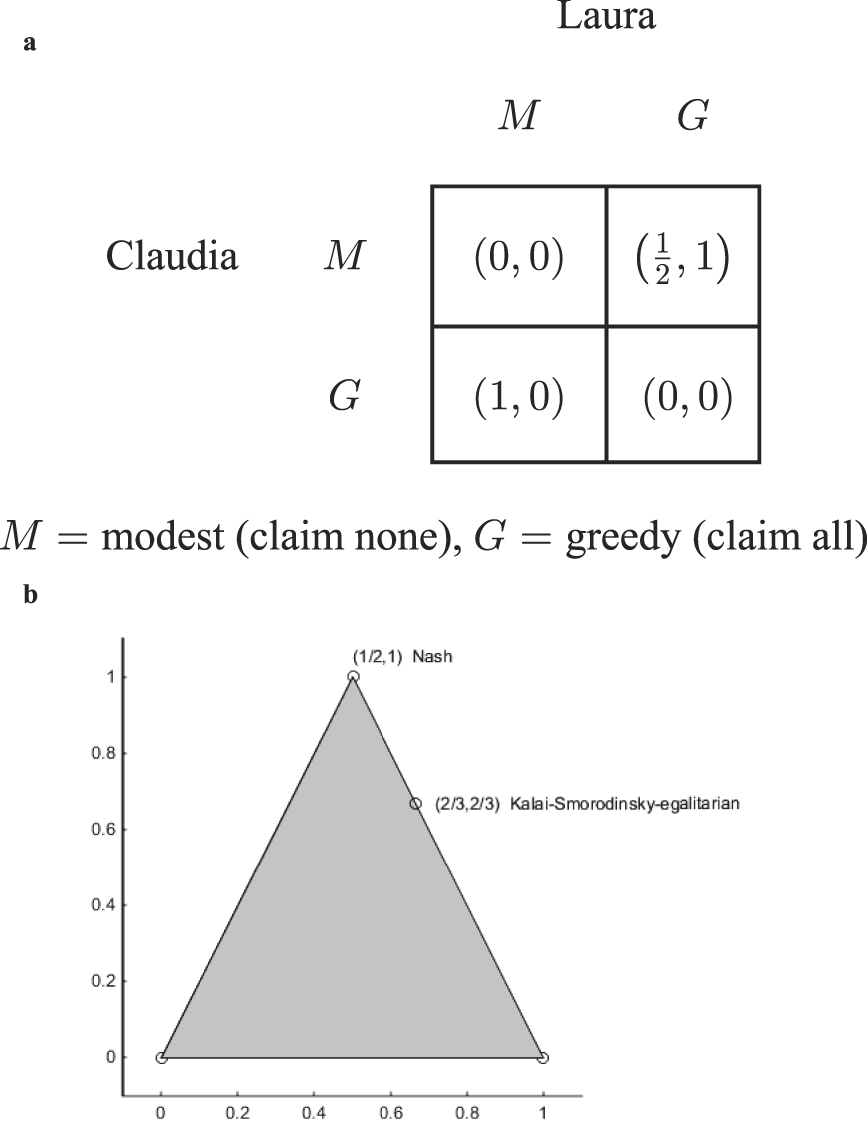
Figure 6. a. Gauthier Basis Game; b. Feasible Set of Gauthier Demand Game
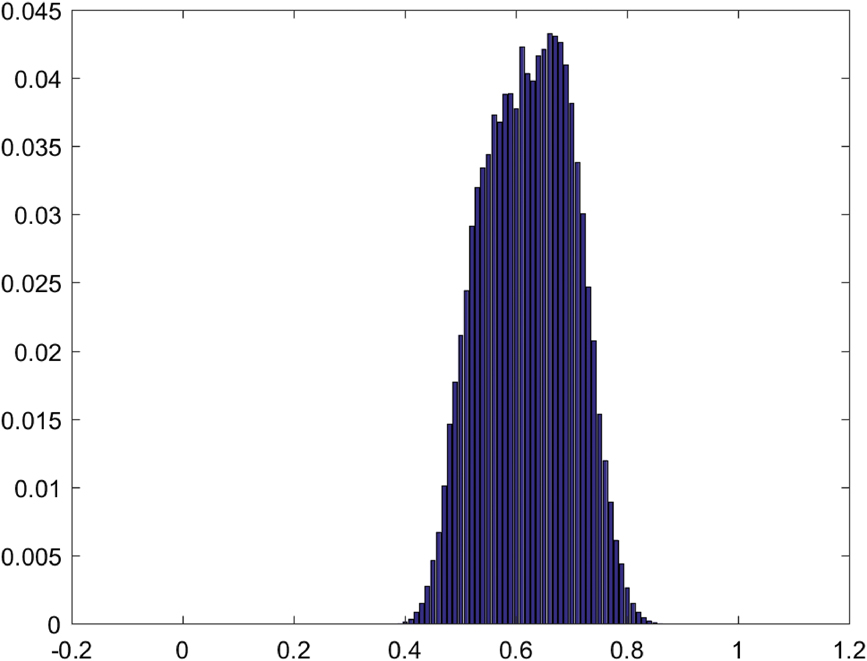
Figure 7. Relative Sizes of Basins of Attraction of Gauthier Demand Game with Claim Precision ![]() $\delta = {1 \over {100}}$
$\delta = {1 \over {100}}$
The next example is based on a conflictual coordination basis game where Claudia’s and Laura’s respective ideal points (G, M) and (M, G) are both strict Nash equilibria. Figure 8 depicts the payoff structure of a 2×2 False Mirror Basis Game together with the feasible set of the corresponding demand game.Footnote 34 False Mirror gets its name because the geometric symmetries of the feasible set might give one the immediate impression that the solution of this bargaining problem should be ![]() $\left( {{{13} \over {16}},{{13} \over {16}}} \right)$ where each receives
$\left( {{{13} \over {16}},{{13} \over {16}}} \right)$ where each receives ![]() ${1 \over 2}$ of the good. But the False Mirror Basis Game is asymmetric in its nonequilibrium outcomes, and has a relevant asymmetry at its nonagreement point. Laura has a greater tolerance than Claudia for suffering the consequences of arriving at the nonagreement point
${1 \over 2}$ of the good. But the False Mirror Basis Game is asymmetric in its nonequilibrium outcomes, and has a relevant asymmetry at its nonagreement point. Laura has a greater tolerance than Claudia for suffering the consequences of arriving at the nonagreement point ![]() $\left( {G,G} \right)$ and consequently has the threat advantage. In this bargaining problem the Kalai-Smorodinsky solution is
$\left( {G,G} \right)$ and consequently has the threat advantage. In this bargaining problem the Kalai-Smorodinsky solution is ![]() $\left( {{{10} \over {13}},{{89} \over {104}}} \right)$ at which Claudia receives
$\left( {{{10} \over {13}},{{89} \over {104}}} \right)$ at which Claudia receives ![]() ${5 \over {13}}$ and Laura receives
${5 \over {13}}$ and Laura receives ![]() ${8 \over {13}}$ of the good. The Nash and the egalitarian solutions coincide at
${8 \over {13}}$ of the good. The Nash and the egalitarian solutions coincide at ![]() $\left( {{5 \over 8},1} \right)$ where the agents follow (M, G), Laura’s ideal outcome. Figure 9 summarizes the relative sizes of the basins of attraction of weighted fictitious play applied to the False Mirror Demand Game with
$\left( {{5 \over 8},1} \right)$ where the agents follow (M, G), Laura’s ideal outcome. Figure 9 summarizes the relative sizes of the basins of attraction of weighted fictitious play applied to the False Mirror Demand Game with ![]() $\delta = {1 \over {100}}$ claim precision. The Nash-egalitarian solution is the modal attracting equilibrium, and the entire distribution of orbit limits is skewed towards this solution.
$\delta = {1 \over {100}}$ claim precision. The Nash-egalitarian solution is the modal attracting equilibrium, and the entire distribution of orbit limits is skewed towards this solution.

Figure 8. a. False Mirror Basis Game; b. Feasible Set of False Mirror Demand Game
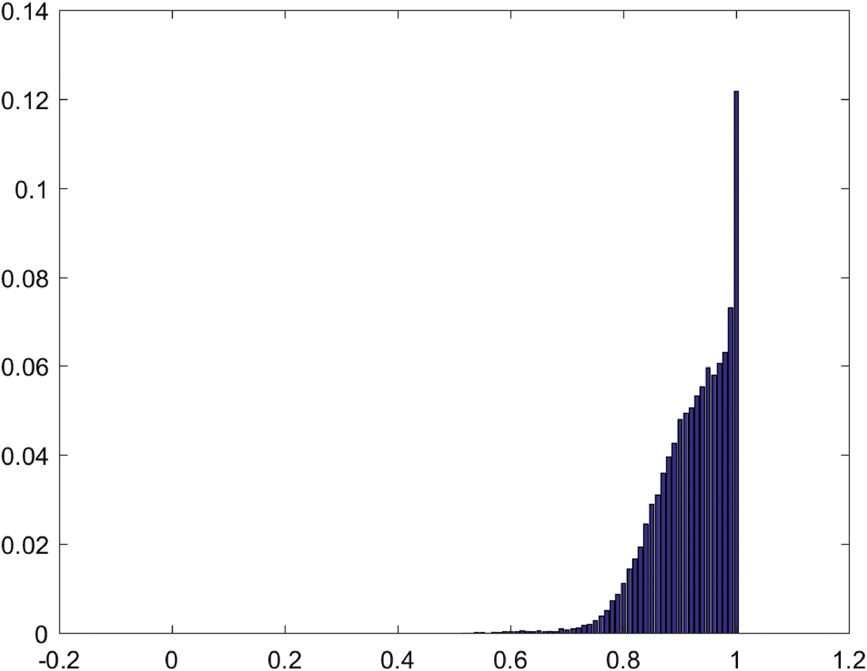
Figure 9. Relative Sizes of Basins of Attraction of False Mirror Demand Game with Claim Precision ![]() $\delta = {1 \over {100}}$
$\delta = {1 \over {100}}$
The final example I will examine is Braithwaite’s bargaining problem. In this bargaining problem the Nash, Kalai-Smorodinsky, and egalitarian solutions are mutually distinct. Figure 10 summarizes the relative sizes of the basins of attraction of weighted fictitious play applied to the Braithwaite Demand Game with claim precision ![]() $\delta = {1 \over {100}}$. Once more the egalitarian solution has a certain attracting power for this form of inductive learning. For this game the distribution of the orbits of the weighted fictitious play process is centered quite near the equilibrium of the egalitarian solution. The equilibrium nearest the Nash solution has a negligible basin of attraction. The equilibria closest to the Kalai-Smorodinsky and to the egalitarian solutions have nonnegligible basins of attraction, but the basins of the latter equilibria are larger than those of the former, reflecting the stronger attracting power of the egalitarian solution. Interestingly, here the distribution of basin sizes shows a slight bimodality, with the smaller peak skewed towards the equilibrium of equal division that disregards Claudia’s and Laura’s payoffs. This indicates that the equal division has some small independent attracting power of its own, though far less than that of the egalitarian solution.
$\delta = {1 \over {100}}$. Once more the egalitarian solution has a certain attracting power for this form of inductive learning. For this game the distribution of the orbits of the weighted fictitious play process is centered quite near the equilibrium of the egalitarian solution. The equilibrium nearest the Nash solution has a negligible basin of attraction. The equilibria closest to the Kalai-Smorodinsky and to the egalitarian solutions have nonnegligible basins of attraction, but the basins of the latter equilibria are larger than those of the former, reflecting the stronger attracting power of the egalitarian solution. Interestingly, here the distribution of basin sizes shows a slight bimodality, with the smaller peak skewed towards the equilibrium of equal division that disregards Claudia’s and Laura’s payoffs. This indicates that the equal division has some small independent attracting power of its own, though far less than that of the egalitarian solution.

Figure 10. Relative Sizes of Basins of Attraction of Braithwaite Demand Game with Claim Precision ![]() $\delta = {1 \over {100}}$
$\delta = {1 \over {100}}$
V. Conclusion
What do these computer experiments of specific bargaining problems reveal? The above examples illustrate a general conclusion that is not at all surprising, namely, that inductive learning can generate a variety of different conventions for the same bargaining problem. At the same time, these examples also show that not all bargaining conventions must be equally likely to emerge. I conjecture that they illustrate how two general rules for dividing a good, namely one rule that assigns claimants equal shares and another that aims to assign claimants equal benefits, could come to regulate some of the division problems that occur in communities and how the equilibria they define even come to be regarded as focal points of division processes. I conjecture further that when these rules yield different results the equal benefits rule tends to prevail, other things being equal. In each of these examples, where payoffs are scaled so that the claimants’ ideal point payoffs are equal, the simple process that mimics inductive learning converges to a variety of equilibria whose distribution is concentrated at or near the equilibrium of the egalitarian solution. So this analysis lends some empirical support to Braithwaite’s conclusion via his own a priori analysis that the fair solution to a 2-agent bargaining problem is the egalitarian solution.Footnote 35 To be sure, I must not claim too much from only this handful of examples. Inductive learning models should be applied to many other more complex bargaining problems, including problems having more than two claimants and problems with more complex payoff structures. The examples of this section suggest the need for a larger research program on inductive learning models of bargaining that would complement the existing bodies of research on analytical models and field and laboratory experiments on bargaining. But they at least illustrate how parties in a situation like Hobbes’ State of Nature, where there are no antecedent obligations to restrain one’s conduct, can learn how to follow certain principles of fair division. In this context, “playing fair” can be the product of inductive learning.
Another and surely more controversial conclusion one can draw from the above analysis is that it lends support for admitting interpersonal utility comparisons into the analysis of fair division problems. Inductive learning can tend to make the egalitarian solution focal for the community of inductive learners. As Raiffa recognized when he first introduced the egalitarian solution, this solution concept presupposes that the utilities of the agents can be measured against each other according to some common scale, so that it makes sense to refer to points where all benefit equally with respect to the nonagreement point. For this axiomatic solution, the “poison” one must pick is to incorporate interpersonal utility comparisons. Many follow Nash in doubting that one can compare utilities across individuals in a meaningful way. Others, like John Harsanyi, argue that interpersonal utility comparisons are unavoidable in any reasonable theories of morality and justice, and that rather than evade the issue philosophers and social scientists must strive to develop rigorous logical foundations for interpersonal utility comparisons.Footnote 36 Skeptics continue to ask, “But how?”, although I believe significant progress has been achieved in recent years.Footnote 37 Luce and Raiffa took a more mitigated stance in the 1950s, and I think their position continues to have merit. They acknowledge that interpersonal utility comparisons have yet to be put on a scientific footing, but also point out that in many actual bargaining situations the bargainers themselves make informal references to interpersonal utility comparisons, and that mathematical abstractions of such situations should reflect such comparisons.Footnote 38 When he introduced the egalitarian solution, Raiffa did this by converting the payoffs of each agent to a 0-1 scale. One way to interpret the grounds for this particular conversion is to assume that in the corresponding bargaining problem, each agent would receive the same positive benefit at her ideal point where she receives all of the good at stake that the other would receive at his ideal point. The above examples show that when the agents’ payoffs are scaled this way, the egalitarian solution has a certain “pull” in the learning process.
The above analysis also suggests a focal point explanation of the wide acceptance of the Aristotelian proportionality principle. If one grants that interpersonal utility comparisons make sense in some contexts, then one can establish an equivalence between the egalitarian solution of the bargaining problem and Aristotle’s principle. To apply the proportionality principle, claimants need to agree upon how to ascertain the value of a quantity of the good at stake and upon the relevant criteria of worth.Footnote 39 If they can agree then the claimants have a common standard for measuring their gains relative to their worth, but as Aristotle observes more than once claimants tend to disagree over the criteria of worth.Footnote 40 Suppose that Laura and Claudia have resolved these problems and agree how to measure both the value of a share of the good at stake and their relative worth. If Claudia and Laura conform their respective claims x 1 and x 2 to Aristotle’s principle, then these claims must satisfy
or equivalently
where ![]() $V\left( {{x_i}} \right)$ is the value of a share x i of the good and
$V\left( {{x_i}} \right)$ is the value of a share x i of the good and ![]() ${w_1} > 0$
${w_1} > 0$ ![]() ${w_2} > 0$ are the respective measures of Claudia’s and Laura’s relative worth with respect to this good.Footnote 41 If Claudia’s and Laura’s payoffs are calibrated to equal their weighted gains so that
${w_2} > 0$ are the respective measures of Claudia’s and Laura’s relative worth with respect to this good.Footnote 41 If Claudia’s and Laura’s payoffs are calibrated to equal their weighted gains so that ![]() ${u_1}\left( {{x_1}} \right) - {u_{01}} = w_1^{ - 1}V\left( {{x_1}} \right)$ and
${u_1}\left( {{x_1}} \right) - {u_{01}} = w_1^{ - 1}V\left( {{x_1}} \right)$ and ![]() ${u_2}\left( {{x_2}} \right) - {u_{02}} = w_2^{ - 1}V\left( {{x_2}} \right)$, then the egalitarian solution of the corresponding demand game is the value of
${u_2}\left( {{x_2}} \right) - {u_{02}} = w_2^{ - 1}V\left( {{x_2}} \right)$, then the egalitarian solution of the corresponding demand game is the value of ![]() $x \in \left[ {0,1} \right]$ that solves
$x \in \left[ {0,1} \right]$ that solves
which is the Aristotelian proportionate solution of their division problem.Footnote 42 For example, in the Chocolate Cake problem where Claudia and Laura are assumed to be equally worthy with respect to shares of the cake, the Aristotelian solution becomes the solution to ![]() ${u_1}\left( {{x_1}} \right) = {x_1} = {u_2}\left( {{x_2}} \right) = {x_2}$, namely,
${u_1}\left( {{x_1}} \right) = {x_1} = {u_2}\left( {{x_2}} \right) = {x_2}$, namely, ![]() ${x_1} = {x_2} = {1 \over 2}$ . If asked just why everyone accepts the formal proportionality principle for dividing a good justly, Aristotle can take a helping hand from Hume and respond that this principle defines a focal convention of the equivalent bargaining problem.
${x_1} = {x_2} = {1 \over 2}$ . If asked just why everyone accepts the formal proportionality principle for dividing a good justly, Aristotle can take a helping hand from Hume and respond that this principle defines a focal convention of the equivalent bargaining problem.
The findings presented in this essay complement those of some previous studies. In some major experimental studies, investigators have created focal point effects in bargaining problems by giving subjects certain information the subjects come to associate with payoffs.Footnote 43 I have used the examples of this essay to argue that inductive learning can generate focal point effects in bargaining problems even when the agents are not assumed to have any information other than their own individual payoffs. Some authors have applied the replicator dynamic that is a staple of evolutionary game theory to bargaining problems like the Chocolate Cake problem that are completely symmetric or where the asymmetries are such that the Nash and egalitarian solutions coincide. The results of these studies are broadly consistent with those presented here, in that they show that for these games strategies that characterize the egalitarian solution can emerge and persist as the result of the evolutionary forces of this dynamic.Footnote 44 However, the authors of these replicator dynamic studies do not examine games where the Nash and egalitarian solutions differ, and they make no attempt to test the attracting power of the egalitarian solution directly as I have done here.Footnote 45 Others have applied an adaptive learning dynamic to bargaining problems and have shown that the most stable points of this dynamic can be either the weighted Nash, the Kalai-Smorodinsky or the simple equal division solution, depending upon the agents’ payoffs in the corresponding demand game.Footnote 46 The adaptive learning dynamic is of limited practical value because in most realistic settings it is likely to require far more time to reach its most persistent limit than the expected lifespan of the community of adaptive learners.Footnote 47 Indeed, this dynamic may not even be practically testable in the laboratory or in the field. As the above examples illustrate, the weighted fictitious play inductive learning process discussed in this essay tends to converge over a relatively short time frame. As noted above, weighted fictitious play has also been tested empirically and been found to model the learning process in coordination games fairly well. This dynamic is also easy to apply to bargaining games having sufficient asymmetries in payoff structure to make the Nash, egalitarian and Kalai-Smorodinsky solutions mutually distinct. This was illustrated with the simulations of learning in the demand game of Braithwaite’s bargaining problem, which despite its relatively long history in game theory has not been previously tested with either computer or human subject experiments to ascertain the attracting power of its many equilibria.
Appendix
The weighted fictitious play process is defined for agents who engage in a 2-agent game repeatedly over time periods as follows: At each period ![]() $t \ge 0$, row Agent 1 follows a pure strategy
$t \ge 0$, row Agent 1 follows a pure strategy ![]() ${s_1}\left( t \right)$ that is a best response given her current conjecture
${s_1}\left( t \right)$ that is a best response given her current conjecture ![]() $\mu _1^t\left( \cdot \right)$, a subjective probability distribution over the pure strategies the counterpart column Agent 2 can follow. At each period
$\mu _1^t\left( \cdot \right)$, a subjective probability distribution over the pure strategies the counterpart column Agent 2 can follow. At each period ![]() $t > 0$, Agent 1 updates her conjecture according to the recursive rule
$t > 0$, Agent 1 updates her conjecture according to the recursive rule
where: (i) ![]() $\mu _i^0\left( {{s_{ - i}}} \right) = {1_{{s_{ - i}}}}\left( 0 \right)$ is Agent i’s prior probability that Agent 2 follows strategy S 2i, (ii) for
$\mu _i^0\left( {{s_{ - i}}} \right) = {1_{{s_{ - i}}}}\left( 0 \right)$ is Agent i’s prior probability that Agent 2 follows strategy S 2i, (ii) for ![]() $t > 0$,
$t > 0$, ![]() ${1_{{s_{2i}}}}\left( t \right)$ is the indicator function for S 2i at t, that is,
${1_{{s_{2i}}}}\left( t \right)$ is the indicator function for S 2i at t, that is,
and (iii) ![]() ${\theta _i} \in \left( {0,1} \right)$ is Agent i’s weighting factor by which Agent i discounts the past. Agent 2 updates his conjectures over Agent 1’s pure strategy options similarly, mutatis mutandis.
${\theta _i} \in \left( {0,1} \right)$ is Agent i’s weighting factor by which Agent i discounts the past. Agent 2 updates his conjectures over Agent 1’s pure strategy options similarly, mutatis mutandis.
For each demand game discussed in Section III, the claim precision was ![]() $\delta = {1 \over {100}}$, so that each agent could claim any whole number percentage of the good. Agent 1 in the role of Claudia and Agent 2 in the role of Laura each could follow one of 101 pure strategies
$\delta = {1 \over {100}}$, so that each agent could claim any whole number percentage of the good. Agent 1 in the role of Claudia and Agent 2 in the role of Laura each could follow one of 101 pure strategies ![]() ${s_0},{s_1},...,{s_{100}}$ where each follows S m by claiming
${s_0},{s_1},...,{s_{100}}$ where each follows S m by claiming ![]() $m \cdot \delta$,
$m \cdot \delta$, ![]() $m \in \left\{ {0,1,...,100} \right\}$. The resulting game had
$m \in \left\{ {0,1,...,100} \right\}$. The resulting game had ![]() ${101^2} = 10,201$ pure strategy profiles of the form
${101^2} = 10,201$ pure strategy profiles of the form ![]() $\left( {{s_m},{s_l}} \right)$ and 101 Nash equilibria in pure strategies of the form
$\left( {{s_m},{s_l}} \right)$ and 101 Nash equilibria in pure strategies of the form ![]() $\left( {{s_m},{s_{100 - m}}} \right)$ where
$\left( {{s_m},{s_{100 - m}}} \right)$ where ![]() $m,l \in \left\{ {0,1,...,100} \right\}$. The 99 of these equilibria where
$m,l \in \left\{ {0,1,...,100} \right\}$. The 99 of these equilibria where ![]() $m \in \left\{ {1,...,99} \right\}$ correspond to conventions where Claudia and Laura each receive a positive share of the good. The remaining two equilibria
$m \in \left\{ {1,...,99} \right\}$ correspond to conventions where Claudia and Laura each receive a positive share of the good. The remaining two equilibria ![]() $\left( {{s_{100}},{s_0}} \right)$ and
$\left( {{s_{100}},{s_0}} \right)$ and ![]() $\left( {{s_0},{s_{100}}} \right)$ respectively characterize the Nash equilibria (G, M) and (M, G) of the basis game.
$\left( {{s_0},{s_{100}}} \right)$ respectively characterize the Nash equilibria (G, M) and (M, G) of the basis game.
To explore the properties of weighted fictitious play applied to these 2-agent demand games, for each of these games I simulated 100,000 orbits of 100 time periods each for the weighted fictitious play processes and where each orbit was set to begin at a prior probability distribution that was a point chosen randomly in the belief simplex.Footnote 48 For every game examined the majority of the orbits converged to an equilibrium over 100 or fewer periods, confirming that weighted fictitious play learners tend to reach a limit point of learning relatively quickly. For each orbit, each Agent i’s weighing factor was set at ![]() ${\theta _i} = \bar{\theta } + \sigma$ where
${\theta _i} = \bar{\theta } + \sigma$ where ![]() $\bar{\theta } = 0.375$ and
$\bar{\theta } = 0.375$ and ![]() $\sigma$ was sampled from a normal distribution with mean 0 and standard deviation 0.125. These weighting factors were selected so as to vary across orbits in a manner consistent with known experimental results of weighted fictitious play applied to coordination games.Footnote 49
$\sigma$ was sampled from a normal distribution with mean 0 and standard deviation 0.125. These weighting factors were selected so as to vary across orbits in a manner consistent with known experimental results of weighted fictitious play applied to coordination games.Footnote 49