The elaboration and solution of quadratic equations in Song dynasty China is one of the most important subjects in the historical study of mathematics in China. Algebra in China is often exemplified by the procedure of the Celestial Source (tian yuan shu 天元術).Footnote 1 The earliest description of this procedure appears in two treatises authored by the thirteenth-century mathematician, Li Ye 李冶 (1192-1279). One of them, the Ceyuan haijing 測圓海鏡 (1248), has attracted the attention of historiansFootnote 2 for its sophistication in presenting the procedure, but the second, the Yigu yanduan 益古演段 (1259), has often been neglected because its presentation of the procedure seems too simple (Pollet Reference Pollet2014). The Yigu yanduan presents the procedure alongside its geometrical counterpart, the Section of Pieces [of Areas] (tiao duan 條段).Footnote 3 The two procedures are used to set up quadratic equations. Historians interested in the Section of Pieces [of Areas] have concluded that it anticipates the procedure of the Celestial Source, and they agree on the geometrical origin of the algebraic procedure (Lam Lay-yong Reference Lam Lay-Yong1984, 264); (Mei Rongzhao Reference Mei1966, 143); (Kong Guoping Reference Kong1999, 173; 197); (Horiuchi, Reference Horiuchi2000, 253); (Xu Yibao Reference Xu1990). Although this assertion still holds, the Yigu yanduan is more complex than commonly acknowledged.
A similarly-named procedure appears in a treatise written by another mathematician, Yang Hui 楊輝 (second half of the thirteenth century). The second chapter of the Yang Hui suanfa 楊輝算法 (1275), titled Tianmu bilei chengchu jiefa 田畝比類乘除捷法 presents a procedure called yan duan 演段. Although it is a similar procedure, the two treatises emphasise different ways of elaboration, as if there were several stages of elaboration. The stage illustrated in the Yang Hui suanfa seem a precursor to those in the Yigu yanduan. But the Yigu yanduan also contains an another version of the procedure of the Section of Pieces [of Areas], named the Old Procedure (jiushu舊術). This version of the procedure seems to predate the one in the Yang Hui suanfa. This raises the question as to whether these versions are pictures of different steps of elaboration. Or are they several layers of composition that reflect a specific moment in a work dealing with algorithms and geometrical representations?
The main objective of this paper is to tease apart these different approaches and thereby to illuminate the development of the procedures. Several studies have examined the Yang Hui suanfa and the Yigu yanduan, but none so far has compared the two treatises. In addition, there is limited critical engagement with the Old Procedure presented by Li Ye (with the exception of Xu Yibao Reference Xu1990). A comparative study of the Yigu yanduan and the Yang Hui suanfa allows us to see lines of filiation in the elaboration of the procedure and its related mathematical objects. In this process, the importance of indeterminate, negative coefficients and equality are crucial to appreciate the algebraic approach that the methods present. Again, to date there has been no study on negative coefficients and the difficulty of their geometrical representation. On this point, modern mathematical transcriptions of equation and geometrical figures are problematic as negative areas are simply impossible concepts.
The methodology used in this study depends on philology and on mathematical transcription. The transcription into modern mathematical notation does not completely describe a procedure. The way historians transcribe equation into symbolic algebra differently points out the diversity of understanding of mathematical objects in Song dynasty era. For several decades, historians of ancient mathematics have been turning away from translating text into symbolic algebra because of the resulting anachronisms. Mathematical transcription fails to explain the practices and logical processes of historical subjects who did not use that method. Three mathematical objects in particular, indeterminates, negative terms, and equality, have so far not been considered in studies of the treatises, although they inhere to quadratic equations. The methodology used here relies on systematic and literal translations. This does not mean that symbolical algebra cannot be useful as a heuristic tool. In the present study, I confront symbolic modern notation to literal translation. Lexicography and geometrical representation of negative coefficients bear witness to the evolution of the procedure to set up quadratic equation.
The drawing of diagrams, manual execution of algorithm and written discourse are interdependent. The present analysis focuses on three dimensions: first, on the correct understanding of the characters duan 段 (segment, pieces), yi 益 (augmented) and xu 虛 (empty); second, on the relationship between textual elements (mathematical discourse and diagram) and calculating surface, conceptualization and choice of terms; third, on the problem of correct translation of ancient Chinese text into modern symbolic algebra. This analysis presents connections between several procedures (yanduan, tiaoduan, jiushu) and confirms the origin of Celestial Source algebra in geometry. It aims to detail the type of connection between Celestial Source polynomial equations and geometry as practiced with diagrams. The mathematical activity developed in the Chinese treatises reveals meanders of a work on what modern language would call “negative coefficient.” The comparison of Li Ye and Yang Hui’s works shows diversity and changes in the conceptualization of mathematical objects. There is no continuous and progressive elaboration, but a work of exploration. Li Ye and Yang Hui both explored previous works and rewrote objects in their own terms revealing developmental changes between what was in the material they read and what they applied in terms of mathematical procedures.
The first section of this article describes the source materials and their known contextual elements as well as a primary and partial interpretation of the relations among sources, thus providing a preliminary overview of the history of the procedure by Section of Pieces [of Areas]. The second section describes the content of the materials and representation of equations. It enumerates the links between the algorithmic equation of the procedure of Celestial Source and its counterpart in the procedure of Section of Pieces [of Areas]. In both texts, the concepts of equation differ considerably from modern notions. This raises the question of transcription into mathematical language. Section 3 investigates how historians dealt with this question of transcription. Transcribing negative coefficients is especially problematic because the transcription of equations depends on an interpretation of Chinese characters signifying negativity. With literal translation and analysis of practice with diagrams, it is possible to interpret those Chinese characters differently and this allows us to unveil new steps in the history of work with equations. I apply the same method to three samples from different sources in sections 4 and 5. This reveals that Song dynasty authors did not read diagrams the same way, as previously surmised. Comparing practices of diagram shows a more complex history of geometrical and algebraic procedures. This article thus shows that there was a shift in practice of drawing diagrams in early Song dynasty.
I. The Sources and context of Yang Hui and Li Ye’s Yanduan: Liu Yi and Jiang Zhou
Both mathematicians, Li Ye and Yang Hui, refer to earlier sources for the Section of Pieces [of Areas]. Li Ye presents his motivation for writing the treatise in his preface: inspired by a book titled Yiguji 益古集 (Collection Augmenting the Ancient [knowledge]).Footnote 4 He compared its contents to the works of two famous commentators Liu Hui 劉徽 (third century) and Li Chunfeng 李淳風 (seventh century), who clarified the Han dynasty classic, the Jiu zhang suan shu 九章算術 (Nine Chapters on Mathematical Procedures). Li Ye found the Yiguji obscure and incomplete and therefore decided to revise it and add diagrams.Footnote 5 The revised text, though, was not differentiated from the original.
The Yigu yanduan presents itself as a list of 64 problems solved first by the procedure of the Celestial Source and then by the Section of Pieces [of Areas]. Twenty-three problems are also solved by a third procedure, called the Old Procedure. It is generally accepted that these 23 solutions came from the Yiguji, as implied by its name (Lam Lay-yong Reference Lam1984, 241); (Mei Rongzhao Reference Mei1966, 140); (Kong Guoping Reference Kong1999, 174); (Ho Peng Yoke Reference Peng Yoke and Gillispie1973, 319). The preface written by the editor of the Yigu yanduan in 1282 states that the Yiguji contained 70 problems, but the preface of the Yigu yanduan in the eighteenth-century re-edition in the imperial encyclopaedia, the Siku quanshu 四庫全書 (Complete Library of Four Treasuries) argues that the number was smaller, probably 64 problems. Because no edition of the Yiguji is extant, the relationship between the 23 problems solved by the Old Procedure and the 64 total problems has never been elucidated.
Neither are the names of the author or the date of compilation known with certainty. According to Mei Rongzhao (Reference Mei1966, 139), the Yiguji can probably be attributed to Jiang Zhou 蔣周 from Ping Yang 平陽 in the province of Shanxi 山西. Mei Rongzhao relies on two references to a book, the title of which begins with the two characters Yigu 益古. In the preface to Si yuan yu jian 四元玉鑑 (The Precious Mirror of Four Sources) by Zhu Shijie 朱世杰, Zu Yi 祖頤 (1303) lists the works to which later readers are indebted for the knowledge of the procedure of the Celestial Source. The first book on the list, Yigu by Jiang Zhou, is mentioned as elaborating the procedure of the Celestial Source.Footnote 6 At the end of the sixteenth century, the Ming mathematician Cheng Dawei 程大位, compiled a list of mathematical texts produced between 1078 and 1224. Among them, a book titled Yigu Suanfa 益古算法 (Computing Method Augmenting the Ancient [Knowledge]) may be the Yiguji. Xu Yibao found another citation of the same person from the Song dynasty (1990, 67). Chapter fourteen of Zhizhai shu lu jieti 直齋書錄解題 (Commented library catalogue of the Zhizhai Studio, 1244) by Chen Zhensun 陳振孫 mentions the Yingyong suanfa 應用算法 (Computing Method for Application) written before 1080 by Jiang Shunyuan 蔣舜元 from Ping Yang. Xu Yibao argues that Jiang Zhou and Jiang Shunyuan are two different names for the same person.
Yang Hui presents extracts of an older, lost work titled Yigu genyuan 議古根源 (Discussion on the Origin of Ancient Methods)Footnote 7 written by Liu Yi 劉益. According to Yang Hui, the Yigu genyuan contained one hundred problems.Footnote 8 Yang Hui repeated twenty-one problems, fourteen of which contain a solution called yan duan 演段. Liu Yi lived in Zhongshan 中山 in the province of Hebei 河北 during the late tenth or early eleventh century (Te Gusi Reference Te1990, 56). On the strength of a comparison of the problems of the Yang Hui suanfa and those of the Yigu yanduan, Xu Yibao (Reference Xu1990, 72) concludes that the Yiguji was probably composed in the middle of the eleventh century and was based on the Yigu genyuan. These observations extend the procedure of the Section of Pieces [of Areas] back to the eleventh century.
The procedure of the Celestial Source, also used by Li Ye, is not used in the extant books by Yang Hui. Among the authors of mathematical texts written in Chinese, only Yang Hui and Li Ye recorded diagrams and substantial evidence of the procedure of the Section of Pieces [of Areas].Footnote 9 It is difficult to deduce the origins of the procedure of the Section of Pieces [of Areas] or how widely it was used in the Song Dynasty. Li Ye, Jiang Zhou and Liu Yi were all natives of northern areas overlapping with the modern provinces of Hebei 河北 and Shanxi 山西, but Yang Hui hailed from Zhejiang 浙江 in southern China. Liu Yi and Jiang Zhou lived near Bianjing 汴京 the capital of the Northern Song Dynasty (960-1127). After the Song Dynasty lost control of northern China to the Jin Dynasty, the capital moved to Linan 臨安 (now Hangzhou in Zhejiang Province) in 1127. Li Ye remained in the north after the conquests of the Jin and Yuan dynasties and lived as a recluse in the Fenglong Mountains. The political conflicts of that time suggest that Yang Hui and Li Ye may never have met. No information elucidates a network of mathematicians of that time or their libraries. If the works of Liu Yi formed part of the imperial library, their transfer from the old capital to the new one could explain how Liu Yi’s mathematics reached Yang Hui. However, several studies (Zürcher Reference Zürcher2007) show that distance is less an obstacle to the probability of transmission than natural obstacles or the facility of trade routes. Bianjing is separated from Linan by only 875km of central plains, across the Huai and Yellow river, and one or two minor mountains. Daniel P. Morgan (Reference Morgan2015) shows the existence of a connected elaborated network of personal, professional, educational, and family ties extending across institutional, geographic and war-torn political divides in early imperial China, by example of the mathematical astronomy from the Cao-Wei 曹魏 court (220-265). This shows that as texts circulated, they evolved as well as did the knowledge they propagated. There was probably such a network in the Song dynasty as well, but its reconstruction is still pending.
From these preliminary observations, it is tempting to draw a first genealogy among procedures as shown in Figure 1. The new reading of geometrical diagrams and their related algorithmic procedure proposed here will show that the relation of filiation among procedures is rather more complex. As a result, the chronology of both content and transmission of these foundational texts must be revised. The next section describes textual materials and the equations contained wherein.

Fig. 1. Preliminary Genealogy of Procedures.
II. Description of texts on the procedure of Section of Pieces [of Areas]
The unifying characteristic of the Sections of Pieces [of Areas] is the fact that the terms of an algorithmic equation are derived from a geometrical figure divided into various sections, named duan 段. The term duan appears in two expressions yan duan 演段 and tiao duan 條段.Footnote 10 In the Yigu yanduan, the expression yan duan appears only in the title, while tiao duan appears in the problems.Footnote 11 In the Yang Hui suanfa, the expression tiao duan does not occur, but the expression yan duan appears in the titles of problems 46 to 53 and 62 to 64.Footnote 12 The fact that yan duan appears only in the title (Yigu yanduan) but Li Ye prefers tiao duan in the discourse suggests synonymy between the two expressions.
In the Yigu yanduan, each of the 64 problems starts with a statement of a problem and its answers illustrated by a first diagram. Then, two procedures establish the algorithmic equationFootnote 13 successively: the procedure of the Celestial Source followed by the procedure of the Section of Pieces [of Areas]. A diagram accompanies the second one. The first paragraph of the second procedure repeats the sentence yi tiao duan qiu zhi 依條段求之 ‘one looks for this (i.e. the unknown) according to [the procedure of] the Section of Pieces [of Areas]’and briefly lists the operations that generate the three terms of the algorithmic equation, named according to their positions on a counting surface. The majority of the problems in the Yigu yanduan, the Section of Pieces [of Areas], occupies two small paragraphs containing a diagram (fig. 2).

Fig. 2. Yigu yanduan, problem 18, republished in 1798 in Zhibuzu zhai congshu by Li Rui.
The procedure of the Celestial Source in the Yigu yanduan contains many representations of polynomials and quadratic equations. They are presented on three rows as horizontal and vertical lines, which symbolise numbers represented by counting rods on a counting surface.Footnote 14 For example, figure 3 denotes 3780 + 228x + 1x2 = 0.

Fig. 3. Example of the notation of the equation 3780 + 228x + 1x² = 0.
Each row indicates a term of consecutive degree. The upper row contains the constant term; the middle row, the coefficient of the first-order indeterminate (x); and the lower row, the coefficient of the second order indeterminate (x²). The translation of counting rods tabulation into an equation in symbolical algebra implies that we can transform the setting into an equality. However, nowhere does the Chinese text read “equal to zero.” Instead, the text presents this as an algorithm on procedure (shu 術). The Section of Pieces [of Areas] reveals how the algorithmic dimension is related to its geometrical counterpart and the use of a counting surface.
The Section of Pieces [of Areas] does not use such a representation, but nonetheless mentions rows. The first row contains the constant term and is named the shi 實 “dividend.” The second row contains the first-order indeterminate term named cong 從 “adjunct."Footnote 15 The last row contains the second-order indeterminate term named chang fa 常法 “constant divisor” (or sometimes yu 隅 “corner”). These words are abstract, technical names for the terms, but also the names of positions on a counting surface on which counting rods are manipulated.Footnote 16 What I refer to as “terms” are the entries on different rows of a counting surface. No expression signifies the indeterminate or the equality.
This particular setting for polynomials and equations finds its origin in the algorithm of root extraction, which in turn finds its own root in the one of the divisions. Several studies have already deeply investigated the relation between these operations.Footnote 17 The procedure of root extraction demonstrates a remarkable similarity with the procedures for division, where the operation mechanically brings back the extraction of the root to a division. This general technique to extract the square root of a number is not only used as an algorithm; it also provides the basis for the development of a further procedure in solving quadratic equations. This is the reason why the terms shi is translated as “dividend” and fa as “divisor.” The commentary by Liu Hui 劉徽 (225-295) to the classic Jiu zhang suan shu 九章算術 (Nine Chapters on the Mathematical Procedures) contains a description of the extraction of square root using geometry whose features are reminiscent of the Section of Pieces [of Areas].Footnote 18 The concept of the square root extraction was based on geometrical considerations, where geometrical concepts were correlated to their arithmetization on the counting support (Lam Lay yong Reference Lam1977); (Martzloff Reference Martzloff1987, 222-223); (Chemla and Guo Reference Chemla and Shuchun2004, 912-3). That is the reason why geometrical vocabulary names entries on the counting surface.
For example, consider the sentence in problem 8:
依條段求之和步幂內減十六之見積為實. 六之和步為從. 三步常法.
One looks for this according to the Section of Pieces [of Areas]. From the square of the bu (步) of the sum (和步), one subtracts sixteen times the real area (見積) to make the dividend. Six times the bu of the sum makes the adjunct. Three bu is the constant divisor.Footnote 19
The “bu of the sum” and the “real area” are quantities known from the statement of the problem. The “bu of the sum” denotes the sum of a perimeter and a circumference, and the “real area” is the area of a square reduced by the area of a circle. Both are constants measured in units of bu. In modern mathematical notation, the first sentence would read a² − 16A, where a is the “bu of the sum” and A the “real area.”Footnote 20 The second sentence corresponds to 6ax, and the final sentence would be represented as 3x². The equation would be a² − 16A = 6ax + 3x², which relates two coefficients of the equation to the known values of the “bu of the sum” and the “real area” with a directly stated third term. The sentence, however, also relates which row of the counting surface the quantities occupy (dividend, adjunct or constant divisor). In fact, in this procedure, geometrical diagrams have replaced tabular representations. This replacement, together with an understanding of the manipulation of counting rods on the counting surface given in the texts, enables insights into the changing conceptualisation of these equations. As stated above, it is not clear how the data given in the statement of the problem are transformed into an equation. This is where an understanding of the diagram and the manipulations on the counting surface becomes important.
After the statement of the question and the answer, the problem presents a diagram containing captions, accompanied by a paragraph titled yi 義 “meaning.” The “meaning” links the diagram to the preceding list of operations.Footnote 21 The “meaning” contains the operations to be performed on the counting surface, and advice on how to proceed with different pieces of the diagram, or on how to draw it. This discourse is not narrative: it neither describes nor explains the successive steps of the algorithm. Only a few sentences give “hints” to some particular steps of the algorithm. Li Ye mentions only those details he deems necessary, but the algorithm is never entirely described. The “meaning” comments on the function of the diagram rather than describing or enumerating a complete list of operations. The diagram is therefore central to the “meaning,” and it informs something not enunciated by the “meaning.” The reader must complement the “meaning” with the diagram.
The Yang Hui suanfa, like the Yigu yanduan, starts problems with a statement and its answer. No diagram illustrates this part. Then, a sentence titled shu 術 “procedure” tells the reader how to compute the coefficients, in vocabulary (shi 實, cong 從, yu 隅) similar to the Yigu yanduan.Footnote 22 This sentence is followed by a paragraph titled yan duan. This paragraph functions like the yi in the Yigu yanduan. It refers to a diagram and its caption.Footnote 23 The rest of the problem begins with the title cao 草 “working"Footnote 24 and solves the quadratic equation. This solution is accompanied by a diagram in problems 46 and 47 (fig. 4).

Fig. 4. Yang Hui suanfa, republished in Guo Shuchun Reference Guo1993.
In the Yigu yanduan, the procedure lists the steps to set up an equation, but the solution is never given. It is assumed that the readers know how to find the roots themselves. In the Yang Hui suanfa, all the problems of the second chapter focus on the solution and the various procedures to extract the roots. Both authors distinguish two phases of solving a problem, the creation of the equation and the extraction of its roots. Li Ye focused on the former; Yang Hui emphasized the latter. This diversity of focus is due to two factors: the authors’ differing practices of drawing diagrams and, in correlation, the manipulation of rods on a counting surface. From the differing focus, distinct concepts of equation emerged. One of the resulting problems is the transcription of equation into modern terms. This is the object of the next section.
III. The question of transcribing equations
How may the equations in the procedure of the Section of Pieces [of Areas] be understood? How may an equation be rendered into modern notation when equality, indeterminates, and the sign of a number are unwritten? The Yigu yanduan does not explain how negative and positive quantities were differentiated. There are no traces of a symbolic notation. The characters fu 負 “negative” and zheng 正 “positive,” usually name negative or positive quantities. But in the present case, they appear only in the text concerning the Section of Pieces [of Areas].Footnote 25 Importantly, these characters fu and zheng only appear in a commentary on problem 14 by Li Ye, but not in the procedure itself.Footnote 26 On the other hand, terms xu 虛 “empty” and yi 益 “augmented” were associated in some translations with the expression transcribed as negative quantities in modern mathematical terms. Are these characters synonyms for fu, “negative”? To determine that, one needs to consider the semantic range of the characters in questions as well as their transcription into modern notation. This transcription depends on one’s knowledge of the sign used for a given term.
Lam Lay-yong (1983, 260) notes that for an equation of the form ax² + bx = c, “if any of the terms a or b are negative, then the term xu or yi is prefixed.” Kong Guoping (1989, 98-100; 1999, 178; 183) also interprets yi 益 and xu 虛 as synonyms of fu 負 ‘negative.’ Martzloff (Reference Martzloff1987, 222) translates the character yi as “negative” in his explanation of Qin Jiushao’s extraction of square roots.Footnote 27 Indeed, with this reading, the first sentence of the procedure of the Sections of Pieces [of Areas] echoes modern mathematical terms to establish an equation between a constant term and a polynomial composed of two terms in x and x². In this way, the terms yi 益 and xu 虛 would coincide with the idea of negative coefficients.Footnote 28 The way in which modern readers interpret the characters and the mathematical concepts with which they are correlated directs the transcription of the equation into modern mathematical terms.
If one were to adopt the reading of yi and xu as “negative,” resulting interpretations ought to conform to the different transcriptions found in secondary literature. Historians do not always transcribe the same equation in the same way: the signs and the equation can be interpreted differently. Since the equation is never stated directly in the Yigu yanduan, the same expression can be transcribed as ax² + bx − c = 0; ax² + bx = c; or bx = c − ax². In the first case, the constant term is negative. In the second, there are no negative quantities, and in the third, the second-order indeterminate term is expected to be negative. An examination of how historians have read the equations of the Sections of Pieces [of Areas] will lead on to the question of how Li Ye writes about what has later been identified as negative terms and equality.
Mei Rongzhao (Reference Mei1966, 140) does not discuss the meaning of xu or how negative quantities are recorded, because he presents only examples that contain positive quantities. The only reference to negative terms appears in his description of equations, in the form of ax² + bx = c, where c > 0, b ≥ 0 and a > 0 or a < 0. Xu Yibao (Reference Xu1990, 69) also presents the equations as a comparison between a constant term and the indeterminate expressions. For example, in the portion of problem 5, which literally reads “From forty-eight pieces of area of the field, one subtracts three pieces of the square of the bu that does not attain to make the dividend. Six times the difference makes the adjunct. One is the empty corner,"Footnote 29 which is presented as ![]() $ - {x^2} + 6 \times 168x = 48 \times 13.2 \times 240 - 3 \times {168^2}$. Xu Yibao does not mention the presence of xu or yi. Similarly, Kong Guoping (Reference Kong1987) transcribes the equations as equivalences between a constant and a, the indeterminate terms. The equation from problem 8, which reads “from the square of the bu of the sum, one subtracts sixteen times the real area to make the dividend. Six times the bu of the sum makes the adjunct. Three bu is the constant divisor” is represented as
$ - {x^2} + 6 \times 168x = 48 \times 13.2 \times 240 - 3 \times {168^2}$. Xu Yibao does not mention the presence of xu or yi. Similarly, Kong Guoping (Reference Kong1987) transcribes the equations as equivalences between a constant and a, the indeterminate terms. The equation from problem 8, which reads “from the square of the bu of the sum, one subtracts sixteen times the real area to make the dividend. Six times the bu of the sum makes the adjunct. Three bu is the constant divisor” is represented as ![]() $3{x^2} + 6 \times 300x = {300^2} - 16 \times 3300$.Footnote 30 Like Mei Rongzhao (Reference Mei1966), Kong Guoping renders the equations as expressions of ax² + bx = c, where c > 0, b ≥ 0 and a ≠0.
$3{x^2} + 6 \times 300x = {300^2} - 16 \times 3300$.Footnote 30 Like Mei Rongzhao (Reference Mei1966), Kong Guoping renders the equations as expressions of ax² + bx = c, where c > 0, b ≥ 0 and a ≠0.
Guo Xihan (Reference Guo1996) transcribes the equations of the Yang Hui suanfa in the same way as Xu Yibao and Kong Guoping. For instance, his “problem 9” (problem 46 in Lam Lay-yong) is transcribed as 60x − x²= 846, where −x² is named yi yu 益隅 by Yang Hui. Guo Xihan comments that the “yi yu represents the second coefficient as equal to −1."Footnote 31 Neither the meaning nor the geometrical representation of yi or fu is discussed. Lam Lay-yong (Reference Lam1977) cautiously translates the Yang Hui suanfa by separating the terms yi and fu. In the translation, Lam Lay-yong adopts the Wade–Giles transliterations i yü or fu yü (yi yu and fu yu in pinyin) as loanwords and notes “Yang Hui’s ingenious handling of negative terms” (1977, 259). In the commentary and discussion, Lam proposes translating yi yu as “adding the areas formed by the yü,” but she concedes that “the word fu is prefixed to the names of the terms … in order to distinguish negative from positive coefficients” (1977, 265). Lam Lay-yong concluded that Yang Hui was familiar with negative terms (1977, 261). This reading results in the aforementioned problem 46 (problem 9 in Guo Xihan) being rendered as −x² + 60x = 864.
In a description of two examples quoted by Yang Hui from the Yigu genyuan, however, Horiuchi (Reference Horiuchi2000, 246; 249) translates the term yi, which can also prefix yu, as “added,” which results in the “added corner” (‘coin ajouté’) or “corner to be added” (‘coin à ajouter’) as indicative of a positive quantity added to the dividend in the algorithm of resolution for the equation. Consequently, the equality in the equation changes in modern notation, that is, c + ax² = bx. Horiuchi furthermore notes that the equality suggested by the diagram is rather of the type c = bx + ax². For problem 20 (problem 62 in Lam Lay-yong), Horiuchi reads “12sx = (4A− 12s²) + x²,” that is, an equation of the adjunct divisor (12sx) and the dividend (4A − 12s²) to which a corner (x²) is added. However, Horiuchi interprets the accompanying diagram as (4A−12s²) = 12sx − x², but does not explain these two different expressions in detail. The discussion suggests that different readings of the equation are permitted, and that the translation of yi 益 as “negative” is debatable. This reading calls into question the association of yi 益 with xu 虛. Horiuchi does not explain the character xu for the simple reason that it never appears in the extant part of the Yigu genyuan. Only yiyu 益隅 “added corner”; fuyu 負隅 “negative corner”; fu cong 負從 “negative adjunct,” and zhengyu正隅 “positive corner” appear in reference to positions on the tabular setting in the Yang Hui suanfa. Apparently, only Li Ye uses the character xu in such situations.
The diagrams accompanying the Section of Pieces [of Areas] are essential to understanding the signs and equality. In order to consider negative terms, the practitioner must conceive and represent a negative geometrical area. With regard to the conceptualisation of a ‘negative’ piece of field, a study of problems 18 of Yigu yanduan and 46 of Yang Hui suanfa offers illuminating examples. Problem 18 illustrates the use of xu, and problem 46 clarifies the use of yi. On the strength of these examples, the character xu 虛 may be effectively translated as “empty” and yi 益 as “augmented.” The next two sections propose a literal translation and reading of diagrams.
IV. Elaboration of negative coefficients by means of geometry: Two examples
For these problems, the Chinese text appears first with modern punctuation followed by a literal translation. Then follows a mathematical explanation. This section presents partial translations of the problems. The Appendices provide the remaining parts of the problem.
1. Xu “empty” in the Section of Pieces [of Areas] in problem 18 from the Yigu yanduan
[18.1]Footnote 32 第十八問. 今有圓田一段, 內有方池, 水占 之外計地三百四十七步.只云外圓周內方周共得二百八步. 問內外周各多少. 荅曰:外圓周一百八步. 內方周一百步.
[18.1] Problem eighteen.
Let us suppose there is one piece of a circular field, inside of which there is a square pond. Outside the [area] occupied by water, one counts three hundred forty-seven bu of land. It is only said that the circumference of the outer circle and the perimeter of the inside square [added] together yields two hundred eight bu.
One asks: How much are the outer circumference and the inside perimeter?
The answer: The circumference of the outer circle is one hundred eight bu and the perimeter of the inside square is one hundred bu.
[18.10] 依條段求之. 以十二之積步, 減和步冪為實. 八之和步為虛從. 四常法.
[18.10] One looks for this [i.e. the unknown] according to the Section of Pieces [of Areas]. [From] the square of the bu of the sum, one subtracts twelve times the bu of the area to make the dividend (shi 實). Eight times the bu of the mutual sum makes the empty adjunct (xu cong 虛從). Four is the constant divisor (chang fa 常法).
[18.11] 義曰: 十二段圓田內有十二个方池. 於方周冪內, 補了十二池. 外猶欠四个. 故以四為隅法.
[18.11] The meaning: Inside the twelve pieces of the circular field, there are twelve square ponds. Inside the square of the perimeter of the square, once the twelve ponds are compensated, outside, in what remains, it lacks four [ponds]. Therefore, with four, one makes the corner divisor.
[18.12] 此式元係虛從. 今却為虛隅, 命之故以四為虛常法.
[18.12] The plate (shi 式) originally empties the adjunct (xu cong 虛從). Now, on the contrary, the corner is emptied (xu yu 虛隅). That is why I recommend (ming 命) that four makes the empty constant divisor (xu chang fa 虛常法).
[18.13] 舊術曰: 相和步自乘. 於頭位. 以十二之積步. 減頭位餘八, 而一為實. 相和步為從. 法廉. 常置半步. 減從.
[18.13] The Old Procedure: self-multiply the bu of the mutual sum; place them in the top position. [Multiply] the bu of the area by twelve; subtract them from what is in the top position. Divide the remainder by eight to make the dividend. The bu of the mutual sum makes the adjunct. There is a divisor and an edge. The constant [divisor] is half a bu. Subtract the adjunct.
The following section provides a mathematical explanation aiming to describe what the text instructs the reader to do. The statement of the problem in [18.1] in modern terms is the following: Let a be the sum of the circumference and the perimeter, 208 bu (translated as “the bu of the sum” or “the bu of the mutual sum”); let A be the area of the circular field (C) minus the area of the square pond (S), 347 bu (“the bu of the area”); and let x be the side of the pond (fig. 6).
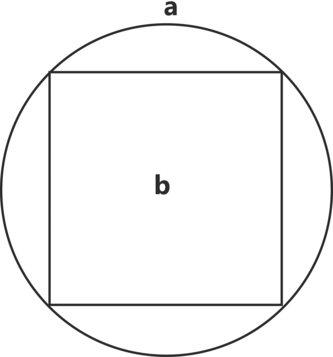
Fig. 5. a. 圓田 “circular field.” b. 二十五步 “twenty five bu.”
Diagrams are reproduced from Zhibuzu zhai congshu, 1798, with Geogebra program.

Fig. 6. a. 此外圓周冪也該十二圓田積 “This is the square of the circumference of the outer circle; it produces twelve areas of the circular field.” c. 1. 連下十六池面為四之和步從 “Below are sixteen ponds; the side of the square makes four times the bu of the mutual sum. That is the adjunct.” c. 2. 連右十六池面為四之和步從 “On the right are sixteen ponds; the side of the square makes four times the bu of the mutual sum. That is the adjunct.” j1-4: 減 “Subtract.”

Fig. 7. Illustration of statement of problem 18 section [18.1].
This procedure requires a developed explanation to understand the meaning of the paragraphs [18.10] to [18.12] above. The first sentence of the Section of Pieces [of Areas] [18.10] lists the operations that generate the coefficients. I use a symbolic transcription of the statement of the problem, A and a, to tabulate the coefficients. This table (Table 1), however, represents a modern creation that is not in the text. In this way [18.10], which reads “[From] the square of the bu of the sum, one subtracts twelve times the bu of the area to make the dividend (shi 實). Eight times the bu of the mutual sum makes the empty adjunct (xu cong 虛從). Four is the constant divisor (chang fa 常法),” is reported by the following elements in Table 1:
Table 1. Data of problem 18 section [18.10]

Reading xu cong 虛從 as “negative adjunct” implies that the two other terms are positive. If we read the equality as made between a constant term and its indeterminate expression, this results in a transcription of the equation as a² − 12A = −8ax + 4x². This equation differs from the one presented in the procedure of the Celestial Source for the same problem (see Appendix C). If the two procedures are considered equivalent, the transcription should read either a² − 12A − 8ax + 4x² = 0, like in the procedure of the Celestial Source, or a² − 12A = 8ax − 4x². Xu Yibao (Reference Xu1990, 66) transcribes the equation as 4x² − 8 × 208x = 12 × 347 − 208², but does not compare this transcription to the one obtained by the procedure of the Celestial Source. The diagram and the “meaning” [18.11] accompanying it suggest a better interpretation, based on the correlation of sentences with an analysis of the diagram (fig. 6).
First, the practitioner constructs a figure with known data: a and A, the circumference of the field plus the perimeter of the pond and the area of the square field minus the area of the circular pond, respectively. With these two quantities, it is possible to represent a square of side a from which a square of 12A is removed (fig. 8). The result is the “dividend” (shi) or constant term of the equation. Next, the same area is expressed in terms of indeterminate quantities. The remaining dark area of [figure 8] is composed of two “adjunct” rectangles of width 4x and length a.

Fig. 8. Illustration of problem 18 step 1.
These two rectangles are superimposed on a square corresponding to 16x² (fig. 9) thus represents 8ax + 16x².

Fig. 9. Illustration of problem 18 step 2.
As in previous problems of the Yigu yanduan, from 2 onwards, the superimposed area is displayed as a square external to the main figure (fig. 10) (see Pollet Reference Pollet2012).

Fig. 10. Illustration of problem 18 step 3.
This extra square is removed. Fig. 11 represents 8ax – 16x².

Fig. 11. Illustration of problem 18 step 4.
However, following this process, too much area is removed. Li Ye states that “inside the twelve pieces of the circular field, there are twelve square ponds.” In order to produce the correct area, 12 squares of side x must be “compensated,” that is, added back to the original square and placed on the right side at the bottom. [Figure 12] represents 8ax – 16x² + 12x². Li Ye writes that “inside the square of the perimeter of the square, once the twelve ponds were compensated, outside, in what remains, it lacks four [ponds],” namely, 8ax – 4x². This area is equal to a² − 12A, as presented in fig. 8.

Fig. 12. Illustration of problem 18 step 5.
The diagram can be interpreted as a superposition of areas, which shows that a known area is equivalent to an indeterminate expression. Therefore, the diagram permits two readings: one interprets the diagram as a constant, the other as an unknown. The diagram relates these two readings through the quadratic equation. This double reading of the superimposed areas reveals the two halves of the equality. The total area corresponds to the constant term, and the drawing is equivalent to the writing that this value is equal to the square portions representing the terms in x and x². The diagram embodies an accumulation of pieces representing the terms of the equation. As this example indicates, the accumulation is conceptualised as jie 疊 “piled”Footnote 33 and xu 虛 “emptied” areas. By following the procedure, the rectangles representing the “adjunct” coefficient were literally “emptied” in fig. 10 and fig. 11, while in the modern notation of the equation, 8ax remains positive.
The procedure above suggests the equation a² − 12A = 8ax − 4x². The “dividend” (a² − 12A) is therefore positive, as is the “adjunct” (8ax), but the “corner” or “constant divisor” (− 4x²) is negative. The procedure in the diagram literally “emptied the adjunct” rectangles; that is, it removed the extra area made by the superimposition of adjunct rectangles. This representation is why xu is translated as “empty” or “to empty.” Thus, the modern concept of “negative” is distinct from the word “empty.” The word xu denotes the removal of an area, as opposed to other areas, which are “full.” On the other hand, the “corner” was filled. These details demonstrate the caution needed when transcribing equations into modern symbolic language: here, xu does not name a sign but a relation between signs.
In [18.12] Li Ye adds a recommendation that may be understood in this context. “The plate originally empties the adjunct. Now, on the contrary, the corner is emptied. That is why I recommend that four makes the empty constant divisor.”Footnote 34 In the procedure above, the adjunct was ‘emptied’. After that, the lost area was restored by adding twelve squares of side x. In a short sentence, Li Ye recommended emptying the corner instead of the adjunct rectangle. Instead of displaying the extra square area in fig. 10, removing it, and adding 12 squares in compensation, Li Ye recommends directly performing the transformations on the 16 squares of side x (bottom right in fig. 9).
From these 16 squares, 4 squares are removed. Instead of 8ax + 16x² − 12x², the recommendation of Li Ye directly generates 8ax – 4x². In other words, the steps fig. 10 and fig. 11 are skipped.
Thus, the extra squares of the adjunct need not be removed and the lost area need not be compensated, because the “corner” (隅) was “emptied” (虛). In this way, Li Ye improves the computational economy of the procedure.
Concerning this example, there are two conclusions. Firstly, the term xu refers to the transformation of areas into diagrams, and extends to include the entries on the counting surface corresponding to these areas. This term only applies to coefficients of indeterminate terms and not to the dividend, which is always positive. An area can be xu while its coefficient remains positive. Eventually, xu was generalized to name an expression of the area in terms of the indeterminate in the procedure of the Celestial Source, as opposed to its expression in terms of the constant.Footnote 35 Secondly, in addition to the two geometrical procedures, the Section of Pieces [of Areas] and the Old Procedure of the Yigu Yuanduan, a third type of procedure survives in a commentary on the Section of Pieces [of Areas]: that the yuan 元 “original” is to be distinguished from the ming 命 “recommended” by Li Ye. Therefore, there is more than one way to read the procedure in the Yigu yanduan. Before this point can be addressed, the Old Procedure must be analyzed, and this procedure depends on an understanding of the yi yu 益隅 in the Yang Hui suanfa. A translation and mathematical description of problem 46 of Yang Hui suanfa will illustrate the meanings of these terms.
2. Yi “augmented” in Problem 46 of the Yang Hui suanfa
The translation and transcription follow the format of problem 18 of the Yigu yanduan.
[46.1] 真田積八百六十四步, 只云長闊共六十步. 卻先求闊步得几何. 答曰: 二十四步.
[46.1] The area of a rectangular field is eight-hundred-sixty-four bu. It is said only that the length and the breadth together are sixty bu. Look first for the bu of the breadth.
The answer: twenty-four bu.
[46.2] 益隅術曰: 置積為實, 共步為 從方, 以一為益隅, 開平方除之.
[46 2] The method of the augmented corner: the area is placed to make the dividend. The bu of the sum makes the adjunct square, one makes the augmented corner. Open the square by dividing.
[46.3] 演段曰: 一積止有一長. 若以長 闊共步為從方,正少一闊, 所以用一位益隅, 入一段闊方, 以應從方除數. …
[46.3] The Development of Pieces [of Areas]: one area has only one length. If the bu of the sum of the length and breadth makes the adjunct square, [the area] is short of one breadth. Therefore, one [square] is used to make the augmented corner, adding one piece of the square of the breadth. …
Like the Yigu yanduan, the description of the statement of problem [46.1] and tabulation [Table 2] in [46.2] can be summarized in the following manner:
Table 2. Data of problem 46 section [46.2]

[46.1] Let A be the area of the rectangle, L the length, a the sum of the length and breadth, and x the breadth.
In [46.3], A is ‘the area placed to make the dividend’. ‘The bu of the sum’, a, ‘makes the adjunct square’. ‘The augmented corner’ is one.
Subsequently, the practitioner constructs a diagram with the known data. Because A is known, a rectangle with area equal to A is drawn. Now, a superimposed rectangle of length a, the sum of breadth and width must be drawn and the two rectangles must fit together. However, the segment a is too long to fit with the length of A. Thus the area A lacks something, which Yang Hui describes as “one area has only one length. If the bu of the sum of the length and breadth makes the adjunct square, [the area] is short of one breadth.” Now, if a rectangle of length a and breadth x is compared to A, there is an extra square of side x inside the adjunct rectangle, ax. Therefore, in fig. 15, “one [square] is used to make the augmented corner, adding one piece of the square of the breadth.” In this way, a corner (yu 隅) augments (yi 益) the area of A. The diagram is thus read as A + x² = ax.
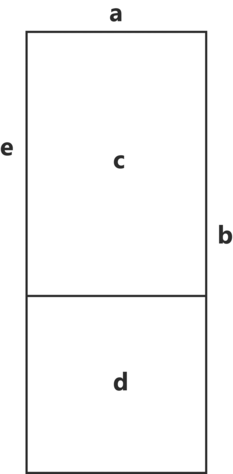
Fig. 13. a. 闊二十步 “Breadth: Twenty-Four.” b. 一長一闊共六十步為從方 “Sum of One Length and One Breadth Sixty bu as Adjunct Square.” c. 本積八百六十四步 “Original Area: Eight-Hundred-Sixty-Four bu.” d. 益闊方積五百七十六 “Augmented Area of the Square of the Breadth: Five-Hundred-Seventy-Six.” e. 長三十六 “Length: Thirty-Six.”

Fig. 14. Illustration of statement of problem 46 section [46.1].

Fig. 15. Illustration of problem 46 section [46.3].
Yi and xu can both be explained geometrically, but they do not have the same origin. Therefore, I translate yi and xu differently. The former is an added figure and the latter is an emptied figure. An analysis of the texts shows that a negative coefficient cannot be directly expressed. The transformations implied by the text, however, read as if the authors may be considering negative coefficients, and that they consider them differently. The concept of negative coefficients is not clear and the expression of equality is equally ambiguous. There are different ways to read the two layers of the diagrams. In the Yigu yanduan, the diagram is always read as a known area, re-expressed in terms of unknowns, and is transcribed ax + bx² = c [See table 4]. In the Yang Hui suanfa, a diagram can be read in different ways and transcribed as either ax + bx² = c or c + ax² = bx, depending on the problem [See table 5]. Yang Hui does not use the diagrams as systematically as Li Ye.
These two examples illustrate another important difference between the two treatises. In the Yigu yanduan, the number of adjunct rectangles is always even, but no more than one adjunct rectangle appears in the Yang Hui suanfa. A consideration of the Old Procedure in the Yigu yanduan explains this phenomenon. Here I present an attempt of reconstitution of the Old Procedure.
V. Diagrams of the old procedure
Twenty-three problems of the Yigu yanduan refer to the Old Procedure.Footnote 36 This procedure is stated in one sentence, like the sentence inaugurating the procedure of the Section of Pieces [of Areas], which also describes the computation of the coefficients of the equation. Like the Sections of Pieces [of Areas], this passage describes a manipulation performed on the counting surface. The top position, where the ‘dividend’ is constructed, is mentioned in many of the problems,Footnote 37 and some coefficients are moved ‘backwards’ (problems 9, 10), ‘to the left’ (problem 44), or shifted to the lower rank (problem 45).
This procedure is also geometrical and involves drawing a diagram, like in the Section of Pieces [of Areas]. Nonetheless, problem 22 is the only case with a surviving diagram.Footnote 38 A few comments by Li Ye help clarify some of the terms in the equations by means of geometry and sometimes clearly indicate that drawing the diagram constitutes part of the solution.
The Old Procedure and the new one are different. The Old Procedure is always simple. This mathematical procedure favors only what is easy and simple. The reason why it is replaced by a new procedure is because the Section of Pieces [of Areas] is difficult to draw with the Old Procedure. [This new procedure] is like [the old one] and complements it.Footnote 39
In contrast to the Section of Pieces [of Areas] described in examples before, there are no characters xu 虛, yi 益, fu 負 or zheng 正. Nowhere in the discourse of the Old Procedure are there any expressions for indeterminate terms, equality or signs.
The Old Procedure is usually stated in a single paragraph. For example, the Old Procedure of problem 18 is stated in [18.13]. The example of problem 18 discussed above presents a case of the division of coefficients by a common factor, where the coefficients of the equation stated in the procedure of the Section of Pieces [of Areas] have been divided by 8.
The given values may be tabulated in Table 3.
Table 3. Data of problem 18 section [18.13]

From [18.13] and what is known about the Section of Pieces [of Areas], I propose a tentative reconstruction of the Old Procedure. First, a figure is constructed with the known values for a and A, as in previous cases in fig. 8. Secondly, the same area is expressed in terms of the indeterminate fig. 9. Each of the two rectangles of fig. 9 are composed of four bands of width x and length a. Thus, a total of eight bands can be assembled like a long ribbon of length 8a (fig. 16). This ribbon is divided by 8. Fig. 16 represents the result (ax) of the division of the adjunct rectangle. Fig. 17 includes four squaresof side x. In the previous procedure, the term 4x2 had to be removed. For the same reason, here, ![]() ${{4{x^2}} \over 8}$ must be removed. Fig. 18 represents ax – 1/2x². This rectangle is equal to a² − 12A divided by eight. Therefore, the equation becomes
${{4{x^2}} \over 8}$ must be removed. Fig. 18 represents ax – 1/2x². This rectangle is equal to a² − 12A divided by eight. Therefore, the equation becomes ![]() ${{{a^2} - 12A} \over 8} = ax - {1 \over 2}{x^2}$.
${{{a^2} - 12A} \over 8} = ax - {1 \over 2}{x^2}$.

Fig. 16. Illustration of problem 18 Old Procedure step 1.

Fig. 17. Illustration of problem 18 Old Procedure step 2.

Fig. 18. Illustration of problem 18 Old Procedure step 3.
Here, the multiple adjunct rectangles are reduced to one. Indeed, in twelve of the cases of the Old Procedure, there is no more than a single “adjunct”; that is, either x = 0 or the “adjunct” is transcribed as ax in Table 4.Footnote 40 The same pattern is observed in problem 46 of the Yang Hui suanfa translated above and other problems in the Yang Hui suanfa share the same pattern.Footnote 41
The patterns of the Old Procedure of the Yigu yanduan and the Yang Hui suanfa resemble each other. The Yang Hui suanfa, like the Old Procedure of problem 18 of the Yigu yanduan, reduces the ‘adjunct’ rectangles to a single rectangle. Table 5 collects the equations of the Yang Hui suanfa (see Appendix B), for which there is either no adjunct (x = 0) or a single adjunct (ax).Footnote 42 In the cases presented in the Section of Pieces [of Areas] for the Yigu yanduan (i.e. the “original” or “recommended” procedures of problem 18), the adjunct is always represented by an even number of rectangles. These rectangles are either multiple, superimposed areas or appended side-by-side. Therefore, it is clear that the procedure as presented by Li Ye had evolved. In the Old Procedure, the reduction to a single ‘adjunct’ rectangle results from the division of the coefficients by a common factor. In the new procedures there is no division in the text itself, but the diagram presents multiple adjunct rectangles.
The change of procedure clearly affected the drawing of the diagram. In the Old Procedure of problem 18, several diagrams of different shapes were necessary, while the Section of Pieces [of Areas] used only one diagram for the same problem. This detail might explain why Li Ye differentiated between the two procedures in problem 15 quoted above. Indeed, in problem 18 and other similar cases, the Old Procedure was simpler because the “adjunct” coefficient was reduced to a single piece in the diagram and to smaller quantities on the counting surface. On the other hand, the diagrams were more complex because they required several drawings. The new procedures of the Section of Pieces [of Areas] employed more complex and larger quantities for “adjunct” rectangles on the counting support, but the drawing remained simple. A single diagram is sufficient to illustrate the whole procedure. Everything else is matter of mental visualization.
Conclusion
The vocabulary used by Li Ye in the commentary differs from that of the discourse of the procedure. Li Ye wrote about fu and zheng coefficients, while the Section of Pieces [of Areas] discusses xu and yi. Moreover, there is no specific vocabulary for signs in the Old Procedure. It is, however, possible to discern several layers of composition within the procedure. The ancient authors of the tenth to eleventh centuries, Liu Yi and Jiang Zhou, dealt with negative numbers in relation to “empty” and “augmented” areas. By Liu Yi’s time, distinct expressions referred to negative and positive quantities. However, because equations were based on the construction of diagrams, and there are no negative areas, the geometric elaboration of negative coefficients presented a problem. On the counting surface, the positive and negative quantities were treated independently. The algorithmic equation represents a perceived correspondence between tabular exposition and diagrammatic representation. However, the distinctive elements were not clearly stated in the third procedure, the Old Procedure: negative coefficients, equalities and unknowns are all absent from the discourse. The evolution of computational practices with diagrams, especially the geometric representation of a mathematical object called cong 從 “adjunct” which was filled or emptied, ensured that the negative quantities became associated with negative coefficients.Footnote 43 When Li Ye and Yang Hui collated these sources and composed their texts, they already had different ideas about these concepts.
At the time of Li Ye and Yang Hui, negative coefficients are clearly constructed, and quadratic equations are free from geometrical concepts. As a matter of fact, the geometrical approach disappears completely after the thirteenth century. In their treatises, Li Ye and Yang Hui present several vignettes in the work of algorithmic equations with negative coefficients. The various aspects of the procedure described here demonstrate that there were several forms of conception of equations by negative coefficients. The treatises at the center of this study do, in fact, testify to meandering mutations in the construction of mathematical concepts and their reception by later readers. The relation among these procedures may be developmental, but the chronological order remains uncertain. There was no pre-ordained form in the stages leading to a maturation of quadratic equations. Chemla (Reference Chemla, Chemla and Keller2017) and Zhu Yiwen (Reference Yiwen2016) have argued that differences in procedures, particularly as concerns root extraction, are indicative of different coexisting mathematical cultures. It could be a way to justify the disparity of mathematical practices at play here.
The comparison of the procedures in the two treatises displays variations of mathematical concepts. Such a comparison also shows that procedures named the same in several texts can disguise various practices. Hence it is important to distinguish the elaboration of mathematical concepts (in this case, from the eleventh century) from their transmission and reinterpretation (from the thirteenth century). The procedure attributed to Liu Yi by Yang Hui presents different mathematical objects compared to the Old Procedure presented by Li Ye in the Yigu yanduan. The Old Procedure presents a specific pattern of a single adjunct in a diagram. The various types of procedure show a change in the use of the diagrams, from complex drawings to simpler compositions with more direct readings of the figures. The diagram disappeared first from the root extraction, and subsequently from the construction of the equation. The pattern of diagrams of a single adjunct appears in other problems of the Yang Hui suanfa, but had totally disappeared from the Section of Pieces [of Areas] of the Yigu yanduan. This leads us to think that the Old Procedure may be older than the procedure preserved in the Yang Hui suanfa, and that the procedure of the Yang Hui suanfa is anterior to the Section of Pieces [of Areas]. As a consequence, this study also leads to a reconsideration of some chronological elements elucidated in the introduction and opens up new questions. Li Ye added a “recommendation” instead of changing the “original” procedure of problem 18 presented here. The vocabulary used in his commentary differs from that of mathematical discourse. Taken together, these facts indicate that there are several layers of composition to the Yigu yanduan, which means that more than the twenty-three Old Procedures remaining in Jiang Zhou’s Yiguji were preserved in the Yigu yanduan. Nonetheless, the origin of the Old Procedure remains vague: was it a reconstruction by Li Ye or an ancient artefact already preserved in the Yiguji? In other words, this analysis raises a philological problem pertaining to the question of textual transmission and the nature of Li Ye’s authorship.
Acknowledgments
This work was supported by a grant from the Taiwan Ministry of Research and Technology. Thanks are due to the members of the Academy of Sciences in Beijing for their courtesies and insights in Beijing in 2010. Furthermore, a debt of gratitude is owed to Horng Wannsheng, Karine Chemla, and Alexei Volkov for their advice. All remaining mistakes are mine. Chinese terms are transcribed in Hanyu Pinyin and written with traditional characters.
Charlotte-V. Pollet is associate professor in National Chiao-Tung University (Taiwan). She received her dual Ph.D from Paris 7 University and National Taiwan Normal University in 2011. Her research interests concern the transmission and elaboration of mathematical objects and procedures in Asia. She relies on philological technics to investigate pre-modern mathematical texts written in Chinese or Sanskrit and their historiography.
APPENDIX
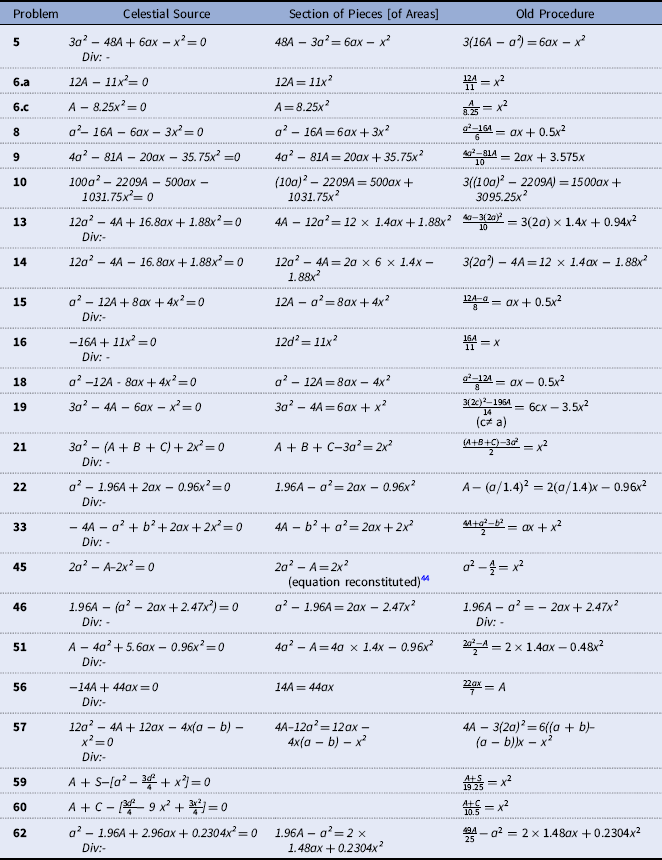
A. [Table 4]: Table of equations of problems solved by the three procedures in the Yigu yanduan
All equations are expressed according to the data given in the statement of the problem and named here by capital or lower case letters.
A: capital letters express areas given in the statement of the problem.
a: lower case letters express the distances given in the statement of the problem.
Div:-: Dividend is negative. In all other cases, the dividend is positive.
B. [Table 5] Equations of problems titled yan duan in Yang Hui suanfa

C. Complements to Problem 18 of Yigu yanduan

Fig. 19. Problem 18 of Yigu yuanduan, text and translation of the Celestial Source procedure. 1.

Fig. 20. Problem 18 of Yigu yuanduan, text and translation of the Celestial Source procedure. 2
Mathematical description:
The Procedure of the Celestial Source:
[18.2] Perimeter of the square = 4x
[18.3] Circumference = a − 4x = 208 − 4x
[18.4] Square of the circumference = (a − 4x)² = a² − 8ax + 4x² = 43264 − 1664x + 16x² = 12C
[18.5] 12S = 12x²
[18.6] Because 12C − 12S = 12A, 12C − 12S = a² − 8ax + 4x² − 12x² = 43264 − 1664x + 16x² − 12x² = 43264 − 1664x + 4x²
[18.7] 12A = 4164 bu
[18.8] The equation: a² − 12A − 8ax + 4x² = 0. With the values of the coefficients: 39100 − 1664x + 4x² = 0
[18.9] The side of the square: x = 25
The perimeter: 4x = 100. The circumference: a − 4x = 208 − 100 = 108


























