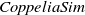1. Introduction
Unmanned aerial vehicles (UAVs) play an important role in the fields of aerospace, agriculture, and delivery due to their high maneuverability, flexible deployment, multi-aircraft cooperation, and easy to carry object for long-distance flight and dexterous manipulation [Reference Jiao, Chou, Rong and Dong1]–[Reference Wu, Zeng and Zhang4]. In these fields, the flight operation of UAV equipped with manipulator has attracted more and more attention [Reference Jiao, Wang, Chu, Dong, Rong and Chou5].
Kim et al. [Reference Kim, Lee, Jung and Cho6] designed a foldable arm that was carried to a UAV to perform a variety of tasks in a confined space. Lee and Jung [Reference Lee and Jung7] designed a shooting and rapidly retracting manipulator that could be carried on the UAV, which can bring a
![]() $30\,\textrm{g}$
mass located at
$30\,\textrm{g}$
mass located at
![]() $0.8\,\textrm{m}$
away within
$0.8\,\textrm{m}$
away within
![]() $600\,\textrm{ms}$
. However, most of the UAVs are operated by remote controller, which results in weak human–machine interaction because the operator cannot feel the operation status of the UAV, thus making the operation of the UAV less effective. Friendly interactive control can improve the operation performance of UAV [Reference Liang, Cao and Wang8], so many researchers have been exploring UAV control methods, such as visual gesture control [Reference Perera, Law and Chahl9, Reference Liu and Sziranyi10], data glove control [Reference Han11, Reference Fang, Sun, Liu and Guo12], and brain wave control [Reference Shi, Wang and Zhang13]. Among these control methods, data glove can provide better feelings for operators, because it makes the control of UAV more intuitive and can accurately recognize dynamic gestures in complex environment with less computation [Reference Kumar, Verma and Prasad14, Reference Luzhnica, Simon, Lex and Pammer15]. Also, data glove-based methods cannot be affected by the occlusion problem, which is a critical issue in optic tracking-based systems. Furthermore, data gloves are widely used in many fields, such as robot arm control [Reference Fang, Sun, Liu and Guo12], sign language recognition [Reference Dong, Fang, Li, Sun and Liu16], and UAV control [Reference Mezzinolu and Karakse17]. For example, ref. [Reference Muezzinoglu and Karakose18] presents an intelligent human–UAV interaction approach in real time based on machine learning using wearable gloves; it used data gloves in the Multi-Mode UAV Human-Computer Interaction System.
$600\,\textrm{ms}$
. However, most of the UAVs are operated by remote controller, which results in weak human–machine interaction because the operator cannot feel the operation status of the UAV, thus making the operation of the UAV less effective. Friendly interactive control can improve the operation performance of UAV [Reference Liang, Cao and Wang8], so many researchers have been exploring UAV control methods, such as visual gesture control [Reference Perera, Law and Chahl9, Reference Liu and Sziranyi10], data glove control [Reference Han11, Reference Fang, Sun, Liu and Guo12], and brain wave control [Reference Shi, Wang and Zhang13]. Among these control methods, data glove can provide better feelings for operators, because it makes the control of UAV more intuitive and can accurately recognize dynamic gestures in complex environment with less computation [Reference Kumar, Verma and Prasad14, Reference Luzhnica, Simon, Lex and Pammer15]. Also, data glove-based methods cannot be affected by the occlusion problem, which is a critical issue in optic tracking-based systems. Furthermore, data gloves are widely used in many fields, such as robot arm control [Reference Fang, Sun, Liu and Guo12], sign language recognition [Reference Dong, Fang, Li, Sun and Liu16], and UAV control [Reference Mezzinolu and Karakse17]. For example, ref. [Reference Muezzinoglu and Karakose18] presents an intelligent human–UAV interaction approach in real time based on machine learning using wearable gloves; it used data gloves in the Multi-Mode UAV Human-Computer Interaction System.
Algorithm is the point of gesture recognition with data gloves. At present, commonly used algorithms include sensor fusion algorithm [Reference Lin, Lee, Yang, Lo, Lee and Chen19], closed-form reconstruction algorithm [Reference Han11], supervised learning algorithm [Reference Luzhnica, Simon, Lex and Pammer15], etc. Muezzinoglu and Karakose [Reference Muezzinoglu and Karakose18] compared decision tree, Nave Bayes, support vector machines, and k-nearest neighbor classification methods in the interaction between data gloves and UAV. Finally, experiments are needed to verify the control effect of the algorithm results of the data glove on the UAV. Compared with the simulation environment, using data glove to control UAV in the real environment is costly and dangerous, and the UAV experimental verification in the simulation environment has also been widely used. For example, Fernando et al. [Reference Fernando, De Silvia, De Zoysa, Dilshan and Munasinghe20] used Matlab Simulink to test the flight algorithm of quadrotor UAV; Meyer et al. [Reference Meyer, Sendobry, Kohlbrecher, Klingauf and von Stryk21] designed a comprehensive simulation system of quadrotor UAV using ROS and Gazebo; Udvardy et al. [Reference Udvardy, Beszedes, Toth, Foldi and Botos22] carried out obstacle avoidance simulation of UAV through CoppeliaSim; and Li et al. studied the glove-based virtual hand grasping for virtual mechanical assembly, with detailed definitions of the bending angles of grasping gestures for four types of parts [Reference Li, Xu, Ni and Wang23].
In this paper, we aim to realize virtual interaction and manipulation control of a hexacopter based on hand gesture recognition from a designed data glove, to provide an intuitive and visual real-time simulation system for flight control algorithm verification and external control equipment testing. The remainder of the paper is organized as follows. Section 2 describes the hand gesture recognition from a data glove. The design of virtual simulation system for hexacopter capture is presented in Section 3. Section 4 demonstrates the simulation test verification, while conclusions and future works are given in Section 5.
2. Hand gesture recognition from a data glove
2.1. Data glove with its hardware
The designed data glove is shown in Fig. 1, which consists of a STM32F103 microcontroller and 10 MPU6050 sensors. The MPU6050 sensors are connected to the microcontroller through the IIC bus for real-time detection of acceleration and angular velocity, while the microcontroller is connected to the upper computer through RS232. The original angular velocity and acceleration can be obtained by using the gyroscope and accelerometer of the MPU6050. On this basis, the current Euler angle of the object can be obtained by filtering and integrating the data. Here, we can directly use the digital motion processor to obtain the quaternion from the MPU6050 for simplification. By the transformation of Euler angle and quaternion, the Euler angle of the detected object can be obtained. The hand gesture recognition from the data glove mainly includes the recognition of different actions based on the figure bending and palm flip judgment.

Figure 1. Data glove with its hardware.
2.2. Finger bending and palm flip judgment
When recognizing the finger bending, the back of the hand is upwards initially, and the pitch angles of all sensors are zero. The schematic diagram of a bending finger is shown in Fig. 2, with the distal joint and the proximal joint corresponding to the distal MPU6050 and the proximal MPU6050 in Fig. 1, respectively.

Figure 2. Finger bending judgment diagram.
The pitch angles of the two fingers can be measured as
![]() ${\theta _ - }1$
and
${\theta _ - }1$
and
![]() ${\theta _ - }2$
by the MPU6050 sensors, respectively. Then, the
${\theta _ - }2$
by the MPU6050 sensors, respectively. Then, the
![]() ${\theta _ - }3$
can be obtained by using (1).
${\theta _ - }3$
can be obtained by using (1).
To simply the recognition process, the figure is thought to be curved when the angle between two fingers is between
![]() $60^\circ$
and
$60^\circ$
and
![]() $120^\circ$
, while the figure is considered to be in a straight state when the angle between two fingers is between
$120^\circ$
, while the figure is considered to be in a straight state when the angle between two fingers is between
![]() $0^\circ$
and
$0^\circ$
and
![]() $20^\circ$
. When recognizing the palm flip, the back of the hand is upwards initially, and the roll angles of all sensors are zero. The mean value of the roll angle of the remaining sensors except the thumb is taken as the flip angle of the hand gesture.
$20^\circ$
. When recognizing the palm flip, the back of the hand is upwards initially, and the roll angles of all sensors are zero. The mean value of the roll angle of the remaining sensors except the thumb is taken as the flip angle of the hand gesture.
2.3. Recognition of different actions
Based on the recognition of figure bending and palm flip, and the relationship of the hand joints, we define a set of concise instruction gestures to quantify the different hand gestures in the program in order to realize the virtual simulation control of a hexacopter. The developed hand gestures are shown in Fig. 3, and the palm roll angle interval is
![]() $\left [{ -{{15}^ \circ } \sim{{15}^ \circ }} \right ]$
with finger bend command “11111” for the mobile ready gesture (The movement of forward, backward, left, right, up, and down can be realized by modifying the parameters in the control command); the back of hand roll angle interval is
$\left [{ -{{15}^ \circ } \sim{{15}^ \circ }} \right ]$
with finger bend command “11111” for the mobile ready gesture (The movement of forward, backward, left, right, up, and down can be realized by modifying the parameters in the control command); the back of hand roll angle interval is
![]() $\left [{ -{{15}^ \circ } \sim{{15}^ \circ }} \right ]$
with finger bend command “11111” for the grab gesture; the back of hand roll angle interval is
$\left [{ -{{15}^ \circ } \sim{{15}^ \circ }} \right ]$
with finger bend command “11111” for the grab gesture; the back of hand roll angle interval is
![]() $\left [{ -{{15}^ \circ } \sim{{15}^ \circ }} \right ]$
with finger bend command “11100” for the loosen gesture; the palm roll angle interval is
$\left [{ -{{15}^ \circ } \sim{{15}^ \circ }} \right ]$
with finger bend command “11100” for the loosen gesture; the palm roll angle interval is
![]() $\left [{ -{{195}^ \circ } \sim -{{165}^ \circ }} \right ]$
with finger bend command “11111” for the landing gesture; the palm pitch angle range interval is
$\left [{ -{{195}^ \circ } \sim -{{165}^ \circ }} \right ]$
with finger bend command “11111” for the landing gesture; the palm pitch angle range interval is
![]() $\left [{{{60}^ \circ } \sim{{100}^ \circ }} \right ]$
with finger bend command “00111” for the takeoff gesture; and the palm roll angle interval is
$\left [{{{60}^ \circ } \sim{{100}^ \circ }} \right ]$
with finger bend command “00111” for the takeoff gesture; and the palm roll angle interval is
![]() $\left [{ -{{195}^ \circ } \sim -{{165}^ \circ }} \right ]$
with finger bend command “11100” for the hover gesture.
$\left [{ -{{195}^ \circ } \sim -{{165}^ \circ }} \right ]$
with finger bend command “11100” for the hover gesture.

Figure 3. Recognition of different actions.
When the gesture of the data glove is recognized, it is mapped to the corresponding posture of the hexacopter, and the command is sent to the simulation software through the serial port on the data glove. After the hexacopter receives the gesture instruction, it analyzes and executes the corresponding action.
3. Model design and virtual simulation development for hexacopter capture
3.1. Model design of hexacopter and manipulator
The 3D model of the hexacopter is shown in Fig. 4(a), with a size of 600 mm; the manipulator is shown in Fig. 4(b), consisting of a base, four rotary joints, and the connecting rods, and its end-effector is a clamping device.

Figure 4. (a) 3D models of hexacopter; (b) 3D models of manipulator.

Figure 5. Simplified model of a hexacopter.
3.1.1. Model design of the hexacopter
The simplified model of a hexacopter is shown in Fig. 5. It includes a central flight control unit, three pairs of rigid arms, rotors, and motors. Each pair of rotors are evenly distributed at a distance of
![]() $60^\circ$
, and at the same height, with the same distance from the center. The rotors
$60^\circ$
, and at the same height, with the same distance from the center. The rotors
![]() $1$
,
$1$
,
![]() $3$
, and
$3$
, and
![]() $5$
rotate clockwise, while rotors
$5$
rotate clockwise, while rotors
![]() $2$
,
$2$
,
![]() $4$
, and
$4$
, and
![]() $6$
rotate counterclockwise. The reason for this setting is to counteract the torque effect and gyro effect and maintain the conservation of torque to ensure flight stability.
$6$
rotate counterclockwise. The reason for this setting is to counteract the torque effect and gyro effect and maintain the conservation of torque to ensure flight stability.
To establish the kinematics model of the hexacopter, we first need to assume the followings:
-
The whole body of the hexacopter is rigid body and will not undergo elastic deformation.
-
The surrounding environment is close to the ideal state, ignoring various external disturbances.
-
The established body coordinate system coincides with the center of mass of the hexacopter.
For the hexacopter, we establish two coordinate systems, the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
and the world coordinate system
${O_q} -{X_q}{Y_q}{Z_q}$
and the world coordinate system
![]() ${O_w} -{X_w}{Y_w}{Z_w}$
, as shown in Fig. 6.
${O_w} -{X_w}{Y_w}{Z_w}$
, as shown in Fig. 6.

Figure 6. Schematic diagram of the coordinate system.
For the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
, each rotor of the hexacopter can generate lift force
${O_q} -{X_q}{Y_q}{Z_q}$
, each rotor of the hexacopter can generate lift force
![]() $F_i$
and moment
$F_i$
and moment
![]() $M_i$
, and their relationships with the rotation speed of the motors are given in (2), where
$M_i$
, and their relationships with the rotation speed of the motors are given in (2), where
![]() $k_b$
indicates the lift coefficient,
$k_b$
indicates the lift coefficient,
![]() $k_d$
represents the torque coefficient, and
$k_d$
represents the torque coefficient, and
![]() $i$
indicates the
$i$
indicates the
![]() $ith$
motor.
$ith$
motor.
 \begin{equation} \left \{{\begin{array}{*{20}{c}}{{F_i} ={k_b}r_i^2,{k_b} \ge 0}\\ \\[-7pt] {{M_i} ={k_d}r_i^2,{k_d} \ge 0} \end{array}} \right. \end{equation}
\begin{equation} \left \{{\begin{array}{*{20}{c}}{{F_i} ={k_b}r_i^2,{k_b} \ge 0}\\ \\[-7pt] {{M_i} ={k_d}r_i^2,{k_d} \ge 0} \end{array}} \right. \end{equation}
Here, we define the Euler angle of the hexacopter as
![]() $\eta = \left [{\begin{array}{*{20}{c}} \phi &\quad \theta &\quad \psi \end{array}} \right ]$
, where
$\eta = \left [{\begin{array}{*{20}{c}} \phi &\quad \theta &\quad \psi \end{array}} \right ]$
, where
![]() $\phi$
is the roll angle,
$\phi$
is the roll angle,
![]() $\theta$
is the pitch angle, and
$\theta$
is the pitch angle, and
![]() $\psi$
is the yaw angle. The angular velocity is
$\psi$
is the yaw angle. The angular velocity is
![]() $\Omega = \left [{\begin{array}{*{20}{c}} p&\quad q&\quad r \end{array}} \right ]$
, so the transformation matrix
$\Omega = \left [{\begin{array}{*{20}{c}} p&\quad q&\quad r \end{array}} \right ]$
, so the transformation matrix
![]() $R$
from the body coordinate system
$R$
from the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
to the world coordinate system
${O_q} -{X_q}{Y_q}{Z_q}$
to the world coordinate system
![]() ${O_w} -{X_w}{Y_w}{Z_w}$
can be established, as given in (3).
${O_w} -{X_w}{Y_w}{Z_w}$
can be established, as given in (3).
 \begin{equation} R = \left [{\begin{array}{c@{\quad}c@{\quad}c}{\cos \theta \cos \psi }&{\sin \theta \cos \psi \sin \phi - \sin \psi \cos \phi }&{\sin \theta \cos \psi \cos \phi + \sin \psi \sin \phi }\\ \\[-8pt]
{\cos \theta \cos \psi }&{\sin \theta \sin \psi \sin \phi + \cos \psi \cos \phi }&{\sin \theta \sin \psi \cos \phi - \cos \psi \sin \phi }\\ \\[-8pt]
{ - \sin \theta }&{\cos \theta \sin \phi }&{\cos \theta \cos \phi } \end{array}} \right ] \end{equation}
\begin{equation} R = \left [{\begin{array}{c@{\quad}c@{\quad}c}{\cos \theta \cos \psi }&{\sin \theta \cos \psi \sin \phi - \sin \psi \cos \phi }&{\sin \theta \cos \psi \cos \phi + \sin \psi \sin \phi }\\ \\[-8pt]
{\cos \theta \cos \psi }&{\sin \theta \sin \psi \sin \phi + \cos \psi \cos \phi }&{\sin \theta \sin \psi \cos \phi - \cos \psi \sin \phi }\\ \\[-8pt]
{ - \sin \theta }&{\cos \theta \sin \phi }&{\cos \theta \cos \phi } \end{array}} \right ] \end{equation}
Ignoring the air resistance, the total lift of the hexacopter
![]() $F_q$
in the body coordinate system is given in (4).
$F_q$
in the body coordinate system is given in (4).
Then, the total lift of the hexacopter
![]() $F_w$
converted from the body coordinate system
$F_w$
converted from the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
to the world coordinate system
${O_q} -{X_q}{Y_q}{Z_q}$
to the world coordinate system
![]() ${O_w} -{X_w}{Y_w}{Z_w}$
is given in (5).
${O_w} -{X_w}{Y_w}{Z_w}$
is given in (5).
 \begin{equation}{F_w} = R{F_q} = \left [{\begin{array}{*{20}{c}}{\sin \theta \cos \psi \cos \phi + \sin \psi \sin \phi }\\ \\[-8pt]
{\sin \theta \sin \psi \cos \phi - \cos \psi \sin \phi }\\ \\[-8pt]
{\cos \theta \cos \phi } \end{array}} \right ]\sum \limits _{i = 1}^6{{k_b}} r_i^2 \end{equation}
\begin{equation}{F_w} = R{F_q} = \left [{\begin{array}{*{20}{c}}{\sin \theta \cos \psi \cos \phi + \sin \psi \sin \phi }\\ \\[-8pt]
{\sin \theta \sin \psi \cos \phi - \cos \psi \sin \phi }\\ \\[-8pt]
{\cos \theta \cos \phi } \end{array}} \right ]\sum \limits _{i = 1}^6{{k_b}} r_i^2 \end{equation}
The force of the hexacopter
![]() $F_g$
in the world coordinate system
$F_g$
in the world coordinate system
![]() ${O_w} -{X_w}{Y_w}{Z_w}$
is given in (6).
${O_w} -{X_w}{Y_w}{Z_w}$
is given in (6).
where
![]() $m$
represents the mass of the hexacopter,
$m$
represents the mass of the hexacopter,
![]() $g$
represents the acceleration of gravity, and
$g$
represents the acceleration of gravity, and
![]() $E_z$
represents the z-axis unit vector of the world coordinate system. According to Newton’s second law, the linear displacement equation can be obtained by combining (3), (5), and (6), as given in (7).
$E_z$
represents the z-axis unit vector of the world coordinate system. According to Newton’s second law, the linear displacement equation can be obtained by combining (3), (5), and (6), as given in (7).
 \begin{equation} \left \{{\begin{array}{*{20}{c}}{\ddot x = \dfrac{{\sum \limits _{i = 1}^6{{F_i}\left ({\sin \theta \cos \psi \cos \phi + sin\psi sin\phi } \right )} }}{m}}\\ \\[-8pt]
{\ddot y = \dfrac{{\sum \limits _{i = 1}^6{{F_i}\left ({\sin \theta \sin \psi \cos \phi - \cos \psi sin\phi } \right )} }}{m}}\\ \\[-8pt]
{\ddot z = \dfrac{{\sum \limits _{i = 1}^6{{F_i}\left ({\cos \theta \cos \phi - g} \right )} }}{m}} \end{array}} \right. \end{equation}
\begin{equation} \left \{{\begin{array}{*{20}{c}}{\ddot x = \dfrac{{\sum \limits _{i = 1}^6{{F_i}\left ({\sin \theta \cos \psi \cos \phi + sin\psi sin\phi } \right )} }}{m}}\\ \\[-8pt]
{\ddot y = \dfrac{{\sum \limits _{i = 1}^6{{F_i}\left ({\sin \theta \sin \psi \cos \phi - \cos \psi sin\phi } \right )} }}{m}}\\ \\[-8pt]
{\ddot z = \dfrac{{\sum \limits _{i = 1}^6{{F_i}\left ({\cos \theta \cos \phi - g} \right )} }}{m}} \end{array}} \right. \end{equation}
Define the vector
![]() $M_q$
in the body coordinate system
$M_q$
in the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
, as given in (8).
${O_q} -{X_q}{Y_q}{Z_q}$
, as given in (8).
where
![]() $J_b$
is the moment of inertia matrix of the hexacopter, and the angular velocities corresponding to the three anglers in the body coordinate system
$J_b$
is the moment of inertia matrix of the hexacopter, and the angular velocities corresponding to the three anglers in the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
are
${O_q} -{X_q}{Y_q}{Z_q}$
are
![]() $p$
,
$p$
,
![]() $q$
, and
$q$
, and
![]() $r$
. We can get (9), where the sec is the abbreviation of secant.
$r$
. We can get (9), where the sec is the abbreviation of secant.
 \begin{equation} \left [{\begin{array}{*{20}{c}}{\dot \phi }\\ \\[-9pt]
{\dot \theta }\\ \\[-9pt]
{\dot \psi } \end{array}} \right ] = \left [{\begin{array}{c@{\quad}c@{\quad}c} 1&{\sin \theta \tan \theta }&{\cos \phi \tan \theta }\\ \\[-9pt]
0&{\cos \phi }&{ - \sin \phi }\\ \\[-9pt]
0&{\sin \phi \sec \theta }&{\cos \phi \sec \theta } \end{array}} \right ]\left [{\begin{array}{c} p\\ \\[-9pt]
q\\ \\[-9pt]
r \end{array}} \right ] \end{equation}
\begin{equation} \left [{\begin{array}{*{20}{c}}{\dot \phi }\\ \\[-9pt]
{\dot \theta }\\ \\[-9pt]
{\dot \psi } \end{array}} \right ] = \left [{\begin{array}{c@{\quad}c@{\quad}c} 1&{\sin \theta \tan \theta }&{\cos \phi \tan \theta }\\ \\[-9pt]
0&{\cos \phi }&{ - \sin \phi }\\ \\[-9pt]
0&{\sin \phi \sec \theta }&{\cos \phi \sec \theta } \end{array}} \right ]\left [{\begin{array}{c} p\\ \\[-9pt]
q\\ \\[-9pt]
r \end{array}} \right ] \end{equation}
The three components of the vector
![]() $M_q$
represent the torque of the three coordinate axes in the body coordinate system
$M_q$
represent the torque of the three coordinate axes in the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
, respectively, as given in (10).
${O_q} -{X_q}{Y_q}{Z_q}$
, respectively, as given in (10).
And, the
![]() $A$
is given in (11).
$A$
is given in (11).
 \begin{equation} A = \left [{\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}{{k_b}}&{\frac{1}{2}{k_b}l}&{ - \frac{1}{2}{k_b}l}&{ -{k_b}l}&{ - \frac{1}{2}{k_b}l}&{\frac{1}{2}{k_b}l}\\ \\[-8pt]
0&{ - \frac{{\sqrt 3 }}{2}{k_b}l}&{ - \frac{{\sqrt 3 }}{2}{k_b}l}&0&{\frac{{\sqrt 3 }}{2}{k_b}l}&{\frac{{\sqrt 3 }}{2}{k_b}l}\\ \\[-8pt]
{{k_d}}&{ -{k_d}}&{{k_d}}&{ -{k_d}}&{{k_d}}&{ -{k_d}} \end{array}} \right ] \end{equation}
\begin{equation} A = \left [{\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}{{k_b}}&{\frac{1}{2}{k_b}l}&{ - \frac{1}{2}{k_b}l}&{ -{k_b}l}&{ - \frac{1}{2}{k_b}l}&{\frac{1}{2}{k_b}l}\\ \\[-8pt]
0&{ - \frac{{\sqrt 3 }}{2}{k_b}l}&{ - \frac{{\sqrt 3 }}{2}{k_b}l}&0&{\frac{{\sqrt 3 }}{2}{k_b}l}&{\frac{{\sqrt 3 }}{2}{k_b}l}\\ \\[-8pt]
{{k_d}}&{ -{k_d}}&{{k_d}}&{ -{k_d}}&{{k_d}}&{ -{k_d}} \end{array}} \right ] \end{equation}
3.1.2. Dynamics modeling of the manipulator
The manipulator mounted under the hexacopter will cause the center of gravity of the entire system to change during the movement, and the mass of the object grabbed by the manipulator will also affect the attitude of the hexacopter. In general, the fetching operation occurs when the hexacopter is hovering, so the motion analysis of the manipulator can be simplified to the motion analysis of its center of mass.
Define the position of the center of mass of the hexacopter in the world coordinate system
![]() ${O_w} -{X_w}{Y_w}{Z_w}$
as
${O_w} -{X_w}{Y_w}{Z_w}$
as
![]() ${}^w{P_u}$
, the position of the center of mass of the manipulator in the body coordinate system
${}^w{P_u}$
, the position of the center of mass of the manipulator in the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
as
${O_q} -{X_q}{Y_q}{Z_q}$
as
![]() ${}^q{P_c} ={\left [{\begin{array}{*{20}{c}}{{x_\textrm{com}}}&{{y_\textrm{com}}}&{{z_\textrm{com}}} \end{array}} \right ]^T}$
which can be converted to the world coordinate system
${}^q{P_c} ={\left [{\begin{array}{*{20}{c}}{{x_\textrm{com}}}&{{y_\textrm{com}}}&{{z_\textrm{com}}} \end{array}} \right ]^T}$
which can be converted to the world coordinate system
![]() ${O_w} -{X_w}{Y_w}{Z_w}$
, as given in (12).
${O_w} -{X_w}{Y_w}{Z_w}$
, as given in (12).
In the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
, the absolute velocity of the center of mass of the manipulator is given in (13), where the
${O_q} -{X_q}{Y_q}{Z_q}$
, the absolute velocity of the center of mass of the manipulator is given in (13), where the
![]() $q_v$
is the three-axis speed in the body coordinate system.
$q_v$
is the three-axis speed in the body coordinate system.
Convert the gravity of the manipulator to the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
, as given in (14).
${O_q} -{X_q}{Y_q}{Z_q}$
, as given in (14).
 \begin{equation}{m_c}g\left [{\begin{array}{*{20}{c}}{ - \sin \theta }\\ \\[-8pt]
{\sin \phi \cos \theta }\\ \\[-8pt]
{\cos \phi \cos \theta } \end{array}} \right ] -{m_c}\left ({{}^q{v_c} + \Omega \times{}^q{v_c}} \right ) ={F_c} \end{equation}
\begin{equation}{m_c}g\left [{\begin{array}{*{20}{c}}{ - \sin \theta }\\ \\[-8pt]
{\sin \phi \cos \theta }\\ \\[-8pt]
{\cos \phi \cos \theta } \end{array}} \right ] -{m_c}\left ({{}^q{v_c} + \Omega \times{}^q{v_c}} \right ) ={F_c} \end{equation}
where
![]() $F_c$
represents the force of the manipulator on the joint of the hexacopter in the body coordinate system
$F_c$
represents the force of the manipulator on the joint of the hexacopter in the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
. From the moment balance, we can get (15), where
${O_q} -{X_q}{Y_q}{Z_q}$
. From the moment balance, we can get (15), where
![]() ${}^q{P_L}$
is the position vector of the joint in the body coordinate system
${}^q{P_L}$
is the position vector of the joint in the body coordinate system
![]() ${O_q} -{X_q}{Y_q}{Z_q}$
.
${O_q} -{X_q}{Y_q}{Z_q}$
.
3.2. Virtual simulation development
The simulation software we use is
![]() $CoppeliaSim$
, and the physics engine used in this simulation experiment is the
$CoppeliaSim$
, and the physics engine used in this simulation experiment is the
![]() $Bullet2.78$
physics library, which can simulate structures including rigid bodies, soft bodies, and elastic bodies, in terms of dynamics, and also has a
$Bullet2.78$
physics library, which can simulate structures including rigid bodies, soft bodies, and elastic bodies, in terms of dynamics, and also has a
![]() $3D$
boundary collision function.
$3D$
boundary collision function.
For the flight control simulation in the CoppeliaSim software, the first step is to obtain the handle of each object through
![]() $sim.getObjectHandle()$
, which can be a model, sensor or joint, etc., so that various parameters can be passed to it to achieve the corresponding model object control. Then, the kinematics information of the hexacopter can be obtained through the Application Programming Interface function library encapsulated in the software. For example, the position information of the hexacopter and the target in the inertial coordinate system can be obtained by
$sim.getObjectHandle()$
, which can be a model, sensor or joint, etc., so that various parameters can be passed to it to achieve the corresponding model object control. Then, the kinematics information of the hexacopter can be obtained through the Application Programming Interface function library encapsulated in the software. For example, the position information of the hexacopter and the target in the inertial coordinate system can be obtained by
![]() $sim.getObjectPosition()$
. The velocity information of the hexacopter and the target can be obtained by
$sim.getObjectPosition()$
. The velocity information of the hexacopter and the target can be obtained by
![]() $sim.getObjectVelocity()$
. The attitude matrix of the hexacopter in the inertial coordinate system can be obtained through
$sim.getObjectVelocity()$
. The attitude matrix of the hexacopter in the inertial coordinate system can be obtained through
![]() $sim.getObjectOrientation()$
. The transformation matrix from body coordinate system to inertial coordinate system can be obtained through
$sim.getObjectOrientation()$
. The transformation matrix from body coordinate system to inertial coordinate system can be obtained through
![]() $sim.getObjectMatrix()$
. This information is used as the input to perform vertical control, horizontal control, and rotation control, respectively, so as to solve the lift and torque that each motor of the hexacopter should have. Finally, it is assigned to the six rotor motors through
$sim.getObjectMatrix()$
. This information is used as the input to perform vertical control, horizontal control, and rotation control, respectively, so as to solve the lift and torque that each motor of the hexacopter should have. Finally, it is assigned to the six rotor motors through
![]() $sim.addForceAndTorque()$
, which realizes the flight control of the hexacopter in the simulation software.
$sim.addForceAndTorque()$
, which realizes the flight control of the hexacopter in the simulation software.
For the control simulation of the manipulator, the first is to obtain the handle of each rotation joint through
![]() $sim.getObjectHandle()$
and then to set the initial position of each joint and the range of the rotation value. After that, using
$sim.getObjectHandle()$
and then to set the initial position of each joint and the range of the rotation value. After that, using
![]() $sim.rmlMoveToJointPosition()$
to assign all the set values to each joint through, so that each joint can be driven to move at the same time. The grabbing of the clamping device can be controlled by the
$sim.rmlMoveToJointPosition()$
to assign all the set values to each joint through, so that each joint can be driven to move at the same time. The grabbing of the clamping device can be controlled by the
![]() $sim.setintegerSignal()$
, and the grabbing device is closed when the acquired signal is
$sim.setintegerSignal()$
, and the grabbing device is closed when the acquired signal is
![]() $1$
, while the grabbing device is released when the acquired signal is
$1$
, while the grabbing device is released when the acquired signal is
![]() $0$
. As shown in Fig. 7, the manipulator can be controlled to perform different actions by setting the angle value of each rotary joint separately.
$0$
. As shown in Fig. 7, the manipulator can be controlled to perform different actions by setting the angle value of each rotary joint separately.

Figure 7. Motion control of the manipulator in
![]() $CoppeliaSim$
.
$CoppeliaSim$
.
4. Simulation test verification
4.1. Virtual simulation experiment of hexacopter grasping
Before the virtual simulation control of a hexacopter based on hand gesture recognition from a data glove, we simulated the virtual experiment of hexacopter grasping in
![]() $CoppeliaSim$
. Due to the size limitation of the gripping device of the manipulator, a cup was used as the grasping targets of this experiment, and we use the simulation camera under the hexacopter to determine the relative position of the target and determine the timing of grasping during the grasping process. Figure 8 shows the entire process of grasping simulation, with the simulation time of about
$CoppeliaSim$
. Due to the size limitation of the gripping device of the manipulator, a cup was used as the grasping targets of this experiment, and we use the simulation camera under the hexacopter to determine the relative position of the target and determine the timing of grasping during the grasping process. Figure 8 shows the entire process of grasping simulation, with the simulation time of about
![]() $10\,\textrm{s}$
. The first three sub-figures are the
$10\,\textrm{s}$
. The first three sub-figures are the
![]() $3rd$
,
$3rd$
,
![]() $7th$
, and
$7th$
, and
![]() $10th$
s, and the last one is the observation picture under different angles. Through Fig. 8, we can intuitively see that the entire grabbing process is smooth and fast. Of course, the moment of grabbing will also have a certain impact on the flying attitude of the hexacopter along the variations of the weight of the grabbed items. During the simulation, it was observed that the manipulator will shake to a certain extent due to the flying attitude of the hexacopter during the grasping process. @@In order to more accurately observe the grasping accuracy of the manipulator, a dummy point is added to the endpoint of the manipulator. And a chart is added to record the position and angle value of the endpoint of the manipulator.
$10th$
s, and the last one is the observation picture under different angles. Through Fig. 8, we can intuitively see that the entire grabbing process is smooth and fast. Of course, the moment of grabbing will also have a certain impact on the flying attitude of the hexacopter along the variations of the weight of the grabbed items. During the simulation, it was observed that the manipulator will shake to a certain extent due to the flying attitude of the hexacopter during the grasping process. @@In order to more accurately observe the grasping accuracy of the manipulator, a dummy point is added to the endpoint of the manipulator. And a chart is added to record the position and angle value of the endpoint of the manipulator.

Figure 8. Simulation of cup grabbing process in
![]() $CoppeliaSim$
.
$CoppeliaSim$
.
Figure 9 shows the three-axis position of the endpoint of the manipulator during grasping simulation.

Figure 9. Three-axis position of the end point of the manipulator.
It can be seen that although the fluctuation range of the three-axis position is within
![]() $ \pm 0.05$
m, the details are different; the position deviation of the
$ \pm 0.05$
m, the details are different; the position deviation of the
![]() $x\textrm{-axis}$
is the largest, it is judged to be caused by the influence of the yaw angle of the hexacopter, the deviation of the
$x\textrm{-axis}$
is the largest, it is judged to be caused by the influence of the yaw angle of the hexacopter, the deviation of the
![]() $y\textrm{-axis}$
is moderate, and the deviation of the
$y\textrm{-axis}$
is moderate, and the deviation of the
![]() $z\textrm{-axis}$
is the smallest, because it is related to the height control of the hexacopter. Therefore, the grasping accuracy of the manipulator is greatly affected by the flight control attitude of the hexacopter. From this experiment, we can know that the deviation range of the three axes is within
$z\textrm{-axis}$
is the smallest, because it is related to the height control of the hexacopter. Therefore, the grasping accuracy of the manipulator is greatly affected by the flight control attitude of the hexacopter. From this experiment, we can know that the deviation range of the three axes is within
![]() $ \pm 0.05$
m, which is within the acceptable range.
$ \pm 0.05$
m, which is within the acceptable range.
4.2. Virtual flight control experiment of hexacopter based on data glove
To test the effectiveness of the designed virtual flight control performance of hexacopter, we connected the data glove to the personal computer, as shown in Fig. 10.

Figure 10. System of virtual flight control experiment.

Figure 11. Snapshot to illustrate the relationship using the data glove to control the manipulator.
As we mentioned above, the MPU6050 sensors deployed on the data glove were used to obtain the attitude and acceleration data of the hands and to express different gestures with different characteristics. A total of
![]() $10$
experimenters were invited to participate in the data glove test, and in the experiment, the experimenter worn the data glove and controlled
$10$
experimenters were invited to participate in the data glove test, and in the experiment, the experimenter worn the data glove and controlled
![]() $10$
gestures including: flight commands for take-off, landing, and hover; forward, backward, left, right, up, and down movement commands; grasp and release gripper control order to perform the test, each person repeated the test
$10$
gestures including: flight commands for take-off, landing, and hover; forward, backward, left, right, up, and down movement commands; grasp and release gripper control order to perform the test, each person repeated the test
![]() $10$
times on the same gesture, for a total of
$10$
times on the same gesture, for a total of
![]() $110$
tests per person. The data were uploaded to the upper computer through the serial port; the instructions from the data glove were also sent to
$110$
tests per person. The data were uploaded to the upper computer through the serial port; the instructions from the data glove were also sent to
![]() $CoppeliaSim$
through the serial port. The snapshot during the experiment to illustrate the relationship using the data glove to control the manipulator is shown in Fig. 11.
$CoppeliaSim$
through the serial port. The snapshot during the experiment to illustrate the relationship using the data glove to control the manipulator is shown in Fig. 11.
One trajectory of the hexacopter flying in the
![]() $CoppeliaSim$
experiment by using data glove is shown in Fig. 12. What needs illustration is that, for the data glove, we need to place the palm flat for initialization before each use, and calibration is not required before each use.
$CoppeliaSim$
experiment by using data glove is shown in Fig. 12. What needs illustration is that, for the data glove, we need to place the palm flat for initialization before each use, and calibration is not required before each use.

Figure 12. Flying trajectory in
![]() $CoppeliaSim$
.
$CoppeliaSim$
.
For the manipulator control using the data glove, as shown in Fig. 13, the grasping and loosening operations can be realized.

Figure 13. Manipulator control in
![]() $CoppeliaSim$
using data glove.
$CoppeliaSim$
using data glove.
4.3. Discussion
In order to be able to quantitatively describe the performance of virtual control of the hexacopter and the manipulator by using data gloves, we conducted a statistical analysis of the test results, as given in Table I, from which we can see that the overall recognition rate is 84.3%, indicating that the data glove produced has the ability to recognize gestures, but its recognition performance is not superior. In gesture recognition, the recognition rate of static gestures is relatively higher than that of dynamic gestures. Among the static gestures which is the top five gestures in Table I, the hover gesture has the highest recognition rate. The average correct rate of static gestures can reach 94%. And the lowest recognition rate of dynamic gestures which is the last six gestures in Table I is upward movement, and the average recognition rate of dynamic gestures is only 76.1%.
Table I. Statistical results of the experiments (the number of successful tests out of 10).

Although the results are satisfactory, the accuracy of gesture recognition is not very high, which may be caused by the following reasons.
-
(1) The accuracy of the three attitude angles measured by the sensor is not high, and there will be a large deviation from the true value, especially in the process of hand movement and turning, the MPU6050 measurement data will have a large deviation because the fingers and the back of the hand are irregular.
-
(2) There is a certain error between the data measured by the sensor fixed on the glove and the actual finger posture angle.
-
(3) The test shows that the accuracy of dynamic gestures is low. The reason is that the hand movement will be accompanied by interference such as jitter, which causes the measured acceleration data to contain both the real motion direction data and the uncertain jitter direction data.
-
(4) The main clock frequency of STM32F103 is
 $72M$
; it is still difficult to read and process 11 sensor data, the frame information sent per unit time is not enough, and there is a large delay in motion gesture recognition.
$72M$
; it is still difficult to read and process 11 sensor data, the frame information sent per unit time is not enough, and there is a large delay in motion gesture recognition. -
(5) Different gestures have some different recognition rate; the reason for this is that for static gestures recognition, the wearing position of the MPU6050 for different people is not exactly the same because the size of the palm is different. The ideal situation is that the sensor on the glove is parallel to the fingers of the straight palm, while the sensor will be offset at different angles due to the different size of the hand. Although the program has a certain error tolerance for the sensor offset, it fails to cover all possible situations, resulting in inaccurate judgment of the final result. For dynamic gesture recognition, the sensitivity of the MPU6050 used in the glove is inconsistent with the up, down, left, and right, front, and back. For example, the up and down jitter occurs during the left and right movement, and the data changes in the up and down direction will be particularly large if the sensitivity to the up and down movement is high, which can lead to large deviations compared with the actual situation. Although this problem can be improved by optimizing the program, it still exists.
5. Conclusions and future works
To provide an intuitive and visual real-time simulation for flight control algorithm verification and external control equipment testing, we studied the virtual interaction and manipulation control of a hexacopter based on hand gesture recognition from a data glove. The hand gesture recognition is studied, and the virtual simulation experiment of hexacopter grasping and virtual flight control experiment were conducted, respectively. The results are satisfactory, although the accuracy of gesture recognition is not very high.
Future research work will mainly focus on how to improve the recognition rate and the response speed of the system.
Authors’ contributions
HH, FS, and MD conceived and designed the study. DW and ZL conducted the virtual interaction and manipulation control, and performed statistical analyses. HH, DW, and ZL wrote the article. FS and MD reviewed and edited the manuscript.
Financial support
The authors are grateful for the support by the Major Project of the National Natural Science Foundation of China (No. 62173233, 61803267), the basic Research Project of Shenzhen Basic Research Special Project (Natural Science Foundation) (No.20210316104110002), the Guangdong Basic and Applied Basic Research Foundation (No. 2021A1515011582), the Shenzhen Science and Technology Innovation Commission project (JSGG20180508152022006), the support of Young Teachers Scientific Research Project of Shenzhen University, and the 2021 National Undergraduate Training Programs for Innovation and Entrepreneurship (No. 202110590023).
Conflicts of interest
The authors declare that they have no conflict of interest.
Ethical considerations
None.