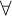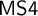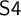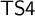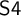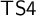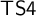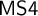1 Introduction
It is well known that, unlike classical quantifiers, the interpretation of intuitionistic quantifiers is non-symmetric in that
![]() $\forall x A$
is true at a world w iff A is true at every object a in the domain
$\forall x A$
is true at a world w iff A is true at every object a in the domain
![]() $D_v$
of every world
$D_v$
of every world
![]() $v$
accessible from
$v$
accessible from
![]() $w$
, while
$w$
, while
![]() $\exists x A$
is true at
$\exists x A$
is true at
![]() $w$
iff A is true at some object a in the domain
$w$
iff A is true at some object a in the domain
![]() $D_w$
of
$D_w$
of
![]() $w$
. This non-symmetry is also evident in the Gödel translation of the intuitionistic predicate calculus
$w$
. This non-symmetry is also evident in the Gödel translation of the intuitionistic predicate calculus
![]() ${\sf IQC}$
into the predicate
${\sf IQC}$
into the predicate
![]() ${\sf S4}$
, denoted
${\sf S4}$
, denoted
![]() ${\sf QS4}$
, since
${\sf QS4}$
, since
![]() $\forall xA$
is translated as
$\forall xA$
is translated as
![]() $\Box \forall x A^t$
while
$\Box \forall x A^t$
while
![]() $\exists x A$
as
$\exists x A$
as
![]() $\exists x A^t$
, where
$\exists x A^t$
, where
![]() $A^t$
is the translation of A.
$A^t$
is the translation of A.

Fig. 1 Diagram of translations.
Our aim is to provide a more symmetric temporal interpretation of intuitionistic quantifiers as “always in the future” (for
![]() $\forall $
) and “sometime in the past” (for
$\forall $
) and “sometime in the past” (for
![]() $\exists $
). In this paper we restrict our attention to monadic quantifiers (that quantify over one fixed variable), but in Section 7 we discuss the connection to the full predicate case, which is treated in detail in [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4]. One of the main reasons to treat the monadic case separately is because it gives rise to a new temporal system
$\exists $
). In this paper we restrict our attention to monadic quantifiers (that quantify over one fixed variable), but in Section 7 we discuss the connection to the full predicate case, which is treated in detail in [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4]. One of the main reasons to treat the monadic case separately is because it gives rise to a new temporal system
![]() ${\sf TS4}$
(see below).
${\sf TS4}$
(see below).
It is well known that the monadic fragment of
![]() ${\sf IQC}$
is axiomatized by Prior’s monadic intuitionistic propositional calculus
${\sf IQC}$
is axiomatized by Prior’s monadic intuitionistic propositional calculus
![]() ${\sf MIPC}$
[Reference Bull8, Reference Ono and Suzuki25]. The monadic fragment of
${\sf MIPC}$
[Reference Bull8, Reference Ono and Suzuki25]. The monadic fragment of
![]() ${\sf QS4}$
was studied by Fischer-Servi [Reference Fischer-Servi14] who showed that the Gödel translation of
${\sf QS4}$
was studied by Fischer-Servi [Reference Fischer-Servi14] who showed that the Gödel translation of
![]() ${\sf IQC}$
into
${\sf IQC}$
into
![]() ${\sf QS4}$
restricts to the monadic case. We denote the monadic fragment of
${\sf QS4}$
restricts to the monadic case. We denote the monadic fragment of
![]() ${\sf QS4}$
by
${\sf QS4}$
by
![]() ${\sf MS4}$
. One of our main contributions is to introduce a tense counterpart of
${\sf MS4}$
. One of our main contributions is to introduce a tense counterpart of
![]() ${\sf MS4}$
, denoted by
${\sf MS4}$
, denoted by
![]() ${\sf TS4}$
, and prove that a modification of the Gödel translation embeds
${\sf TS4}$
, and prove that a modification of the Gödel translation embeds
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf TS4}$
fully and faithfully. This allows us to give the desired temporal interpretation of monadic intuitionistic quantifiers as “always in the future” (for
${\sf TS4}$
fully and faithfully. This allows us to give the desired temporal interpretation of monadic intuitionistic quantifiers as “always in the future” (for
![]() $\forall $
) and “sometime in the past” (for
$\forall $
) and “sometime in the past” (for
![]() $\exists $
).
$\exists $
).
While
![]() ${\sf MS4}$
and
${\sf MS4}$
and
![]() ${\sf TS4}$
are not comparable, we introduce a common extension, which we denote by
${\sf TS4}$
are not comparable, we introduce a common extension, which we denote by
![]() ${\sf MS4.t}$
. The system
${\sf MS4.t}$
. The system
![]() ${\sf MS4.t}$
can be thought of as a tense extension of
${\sf MS4.t}$
can be thought of as a tense extension of
![]() ${\sf MS4}$
. We prove that there exist full and faithful translations of
${\sf MS4}$
. We prove that there exist full and faithful translations of
![]() ${\sf MIPC}$
,
${\sf MIPC}$
,
![]() ${\sf MS4}$
, and
${\sf MS4}$
, and
![]() ${\sf TS4}$
into
${\sf TS4}$
into
![]() ${\sf MS4.t}$
, yielding the diagram in Figure 1. The Gödel translation is denoted by
${\sf MS4.t}$
, yielding the diagram in Figure 1. The Gödel translation is denoted by
![]() $(\:)^t$
, our new translation by
$(\:)^t$
, our new translation by
![]() $(\:)^\natural $
, and the three translations into
$(\:)^\natural $
, and the three translations into
![]() ${\sf MS4.t}$
by
${\sf MS4.t}$
by
![]() $(\:)^\# $
,
$(\:)^\# $
,
![]() $(\:)^\flat$
, and
$(\:)^\flat$
, and
![]() $(\:)^\dagger $
, respectively.
$(\:)^\dagger $
, respectively.
We prove these results by employing relational semantics. In addition, we utilize algebraic semantics to prove that
![]() ${\sf MS4.t}$
has the fmp. It is then an easy consequence of the fullness and faithfulness of the translations considered that the other systems also have the fmp. That
${\sf MS4.t}$
has the fmp. It is then an easy consequence of the fullness and faithfulness of the translations considered that the other systems also have the fmp. That
![]() ${\sf MIPC}$
has the fmp was proved in [Reference Bull7], but the proof contained a gap, which was corrected in [Reference Fischer-Servi15, Reference Ono23]. The fmp for
${\sf MIPC}$
has the fmp was proved in [Reference Bull7], but the proof contained a gap, which was corrected in [Reference Fischer-Servi15, Reference Ono23]. The fmp for
![]() ${\sf MS4}$
follows from the results in [Reference Gabbay and Shehtman17, Sec. 12]. An advantage of our approach is in that it provides a uniform means for proving the fmp for all four systems in Figure 1.
${\sf MS4}$
follows from the results in [Reference Gabbay and Shehtman17, Sec. 12]. An advantage of our approach is in that it provides a uniform means for proving the fmp for all four systems in Figure 1.
In [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4] we extended the translation of
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf MS4.t}$
to the predicate setting.Footnote
1
We showed that the same interpretation of intuitionistic quantifiers can be realized via a full and faithful translation of
${\sf MS4.t}$
to the predicate setting.Footnote
1
We showed that the same interpretation of intuitionistic quantifiers can be realized via a full and faithful translation of
![]() ${\sf IQC}$
into a version of predicate
${\sf IQC}$
into a version of predicate
![]() ${\sf S4.t}$
that can be thought of as a predicate analogue of
${\sf S4.t}$
that can be thought of as a predicate analogue of
![]() ${\sf MS4.t}$
. We conclude this paper by comparing the translations investigated here with those studied in [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4].
${\sf MS4.t}$
. We conclude this paper by comparing the translations investigated here with those studied in [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4].
2 Logics of interest
In this section we present our four main logics of interest (see Figure 1). We start by recalling the monadic intuitionistic propositional calculus
![]() ${\sf MIPC}$
. This system was introduced by Prior [Reference Prior26, p. 38] and it was shown by Bull [Reference Bull8] that
${\sf MIPC}$
. This system was introduced by Prior [Reference Prior26, p. 38] and it was shown by Bull [Reference Bull8] that
![]() ${\sf MIPC}$
axiomatizes the monadic fragment of the intuitionistic predicate calculus
${\sf MIPC}$
axiomatizes the monadic fragment of the intuitionistic predicate calculus
![]() ${\sf IQC}$
.Footnote
2
For this reason we denote the modalities of
${\sf IQC}$
.Footnote
2
For this reason we denote the modalities of
![]() ${\sf MIPC}$
by
${\sf MIPC}$
by
![]() $\forall $
and
$\forall $
and
![]() $\exists $
. Let
$\exists $
. Let
![]() $\mathcal L$
be the propositional language and let
$\mathcal L$
be the propositional language and let
![]() $\mathcal L_{\forall \exists }$
be the extension of
$\mathcal L_{\forall \exists }$
be the extension of
![]() $\mathcal L$
with two modalities
$\mathcal L$
with two modalities
![]() $\forall $
and
$\forall $
and
![]() $\exists $
.
$\exists $
.
Definition 2.1. The monadic intuitionistic propositional calculus
![]() ${\sf MIPC}$
is the intuitionistic modal logic in the propositional modal language
${\sf MIPC}$
is the intuitionistic modal logic in the propositional modal language
![]() $\mathcal L_{\forall \exists }$
containing
$\mathcal L_{\forall \exists }$
containing
-
1. all theorems of the intuitionistic propositional calculus
 ${\sf IPC}$
;
${\sf IPC}$
; -
2. the
 ${\sf S4}$
-axioms for
${\sf S4}$
-axioms for
 $\forall $
:
$\forall $
:-
(a)
 $\forall (p\land q)\leftrightarrow (\forall p\land \forall q)$
,
$\forall (p\land q)\leftrightarrow (\forall p\land \forall q)$
, -
(b)
 $\forall p \rightarrow p$
,
$\forall p \rightarrow p$
, -
(c)
 $\forall p \rightarrow \forall \forall p$
;
$\forall p \rightarrow \forall \forall p$
;
-
-
3. the
 ${\sf S5}$
-axioms for
${\sf S5}$
-axioms for
 $\exists $
:
$\exists $
:-
(a)
 $\exists (p\vee q)\leftrightarrow (\exists p\vee \exists q)$
,
$\exists (p\vee q)\leftrightarrow (\exists p\vee \exists q)$
, -
(b)
 $p \rightarrow \exists p$
,
$p \rightarrow \exists p$
, -
(c)
 $\exists \exists p \rightarrow \exists p$
,
$\exists \exists p \rightarrow \exists p$
, -
(d)
 $(\exists p \land \exists q) \rightarrow \exists (\exists p \land q)$
;
$(\exists p \land \exists q) \rightarrow \exists (\exists p \land q)$
;
-
-
4. the axioms connecting
 $\forall $
and
$\forall $
and
 $\exists $
:
$\exists $
:-
(a)
 $\exists \forall p\leftrightarrow \forall p$
,
$\exists \forall p\leftrightarrow \forall p$
, -
(b)
 $\exists p \leftrightarrow \forall \exists p$
;
$\exists p \leftrightarrow \forall \exists p$
;
-
and closed under the rules of modus ponens, substitution, and necessitation
![]() $(\varphi / \forall \varphi )$
.
$(\varphi / \forall \varphi )$
.
Remark 2.2. There are several equivalent axiomatizations of
![]() ${\sf MIPC}$
(see, e.g., [Reference Bezhanishvili2, Lemma 2]).
${\sf MIPC}$
(see, e.g., [Reference Bezhanishvili2, Lemma 2]).
We next recall the monadic extension of
![]() ${\sf S4}$
studied by Fischer-Servi [Reference Fischer-Servi14] who showed that it axiomatizes the monadic fragment of the predicate
${\sf S4}$
studied by Fischer-Servi [Reference Fischer-Servi14] who showed that it axiomatizes the monadic fragment of the predicate
![]() ${\sf S4}$
. Let
${\sf S4}$
. Let
![]() $\mathcal L_{\Box \forall }$
be the propositional bimodal language with two modal operators
$\mathcal L_{\Box \forall }$
be the propositional bimodal language with two modal operators
![]() $\Box $
and
$\Box $
and
![]() $\forall $
. As usual,
$\forall $
. As usual,
![]() $\Diamond $
is an abbreviation for
$\Diamond $
is an abbreviation for
![]() $\neg \Box \neg $
and
$\neg \Box \neg $
and
![]() $\exists $
is an abbreviation for
$\exists $
is an abbreviation for
![]() $\neg \forall \neg $
.
$\neg \forall \neg $
.
Definition 2.3. The monadic
![]() $\sf S4$
, denoted
$\sf S4$
, denoted
![]() ${\sf MS4}$
, is the smallest bimodal logic containing all theorems of the classical propositional calculus
${\sf MS4}$
, is the smallest bimodal logic containing all theorems of the classical propositional calculus
![]() ${\sf CPC}$
, the
${\sf CPC}$
, the
![]() $\sf S4$
-axioms for
$\sf S4$
-axioms for
![]() $\Box $
, the
$\Box $
, the
![]() $\sf S5$
-axioms for
$\sf S5$
-axioms for
![]() $\forall $
, the left commutativity axiom
$\forall $
, the left commutativity axiom
and closed under modus ponens, substitution,
![]() $\Box $
-necessitation, and
$\Box $
-necessitation, and
![]() $\forall $
-necessitation.
$\forall $
-necessitation.
Remark 2.4. Recalling the definition of fusion of two logics (see [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16]),
![]() ${\sf MS4}$
is obtained from the fusion
${\sf MS4}$
is obtained from the fusion
![]() ${\sf S4}\otimes {\sf S5}$
by adding the left commutativity axiom
${\sf S4}\otimes {\sf S5}$
by adding the left commutativity axiom
![]() $\Box \forall p \rightarrow \forall \Box p$
which is the monadic version of the converse Barcan formula. The monadic version of the Barcan formula is the right commutativity axiom
$\Box \forall p \rightarrow \forall \Box p$
which is the monadic version of the converse Barcan formula. The monadic version of the Barcan formula is the right commutativity axiom
![]() $\forall \Box p \rightarrow \Box \forall p$
. Adding it to
$\forall \Box p \rightarrow \Box \forall p$
. Adding it to
![]() ${\sf MS4}$
yields the product logic
${\sf MS4}$
yields the product logic
![]() $\sf S4 \times \sf S5$
; see [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16, Chap. 5] for details.
$\sf S4 \times \sf S5$
; see [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16, Chap. 5] for details.
The following lemma will be useful in Section 3.
Lemma 2.5. An equivalent axiomatization of
![]() ${\sf MS4}$
is obtained by replacing the left commutativity axiom
${\sf MS4}$
is obtained by replacing the left commutativity axiom
![]() $\Box \forall p \to \forall \Box p$
by
$\Box \forall p \to \forall \Box p$
by
![]() $\exists \Box p \to \Box \exists p$
.
$\exists \Box p \to \Box \exists p$
.
Proof. We show that
![]() ${\sf MS4}\vdash \exists \Box p \to \Box \exists p$
. That
${\sf MS4}\vdash \exists \Box p \to \Box \exists p$
. That
![]() $\exists \Box p \to \Box \exists p$
together with the other axioms of
$\exists \Box p \to \Box \exists p$
together with the other axioms of
![]() ${\sf MS4}$
implies
${\sf MS4}$
implies
![]() $\Box \forall p \to \forall \Box p$
is proved similarly. Since
$\Box \forall p \to \forall \Box p$
is proved similarly. Since
![]() $\forall $
is an
$\forall $
is an
![]() ${\sf S5}$
-modality,
${\sf S5}$
-modality,
![]() $\Box \exists p \to \Box \forall \exists p$
is a theorem of
$\Box \exists p \to \Box \forall \exists p$
is a theorem of
![]() ${\sf MS4}$
. By the left commutativity axiom,
${\sf MS4}$
. By the left commutativity axiom,
![]() $\Box \forall \exists p \to \forall \Box \exists p$
is also a theorem of
$\Box \forall \exists p \to \forall \Box \exists p$
is also a theorem of
![]() ${\sf MS4}$
. So
${\sf MS4}$
. So
![]() ${\sf MS4}\vdash \Box \exists p \to \forall \Box \exists p$
, and hence
${\sf MS4}\vdash \Box \exists p \to \forall \Box \exists p$
, and hence
![]() ${\sf MS4}\vdash \exists \Box \exists p \to \exists \forall \Box \exists p$
. But
${\sf MS4}\vdash \exists \Box \exists p \to \exists \forall \Box \exists p$
. But
![]() $\exists \Box p \to \exists \Box \exists p$
,
$\exists \Box p \to \exists \Box \exists p$
,
![]() $\exists \forall \Box \exists p \to \forall \Box \exists p$
, and
$\exists \forall \Box \exists p \to \forall \Box \exists p$
, and
![]() $\forall \Box \exists p \to \Box \exists p$
are all theorems of
$\forall \Box \exists p \to \Box \exists p$
are all theorems of
![]() ${\sf MS4}$
because
${\sf MS4}$
because
![]() $\forall $
is an
$\forall $
is an
![]() ${\sf S5}$
-modality. Thus,
${\sf S5}$
-modality. Thus,
![]() ${\sf MS4}\vdash \exists \Box p \to \Box \exists p$
, concluding the proof.
${\sf MS4}\vdash \exists \Box p \to \Box \exists p$
, concluding the proof.
To introduce our main tense logic
![]() ${\sf TS4}$
, we first need to recall the tense logic
${\sf TS4}$
, we first need to recall the tense logic
![]() ${\sf S4.t}$
. Let
${\sf S4.t}$
. Let
![]() $\mathcal L_T$
be the propositional tense language with two modalities
$\mathcal L_T$
be the propositional tense language with two modalities
![]() ${[F]}$
and
${[F]}$
and
![]() ${[P]}$
. As usual,
${[P]}$
. As usual,
![]() ${[F]}$
is interpreted as “always in the future” and
${[F]}$
is interpreted as “always in the future” and
![]() ${[P]}$
as “always in the past.” We use the following standard abbreviations:
${[P]}$
as “always in the past.” We use the following standard abbreviations:
![]() ${\langle F \rangle }$
for
${\langle F \rangle }$
for
![]() $\neg {[F]} \neg $
and
$\neg {[F]} \neg $
and
![]() ${\langle P \rangle }$
for
${\langle P \rangle }$
for
![]() $\neg {[P]} \neg $
. Then
$\neg {[P]} \neg $
. Then
![]() ${\langle F \rangle }$
is interpreted as “sometime in the future” and
${\langle F \rangle }$
is interpreted as “sometime in the future” and
![]() ${\langle P \rangle }$
as “sometime in the past.”
${\langle P \rangle }$
as “sometime in the past.”
Definition 2.6. Let
![]() ${\sf S4.t}$
be the smallest bimodal logic containing all theorems of the classical propositional calculus
${\sf S4.t}$
be the smallest bimodal logic containing all theorems of the classical propositional calculus
![]() ${\sf CPC}$
, the
${\sf CPC}$
, the
![]() ${\sf S4}$
-axioms for
${\sf S4}$
-axioms for
![]() ${[F]}$
and
${[F]}$
and
![]() ${[P]}$
, the tense axioms
${[P]}$
, the tense axioms
and closed under modus ponens, substitution,
![]() ${[F]}$
-necessitation, and
${[F]}$
-necessitation, and
![]() ${[P]}$
-necessitation.
${[P]}$
-necessitation.
Remark 2.7. The system
![]() ${\sf S4.t}$
is the extension of the least tense logic
${\sf S4.t}$
is the extension of the least tense logic
![]() $\sf K.t$
in which both tense modalities satisfy the
$\sf K.t$
in which both tense modalities satisfy the
![]() ${\sf S4}$
-axioms. It was studied by several authors. Esakia [Reference Esakia10] showed that the Gödel translation can be extended to embed the Heyting–Brouwer logic
${\sf S4}$
-axioms. It was studied by several authors. Esakia [Reference Esakia10] showed that the Gödel translation can be extended to embed the Heyting–Brouwer logic
![]() $\sf HB$
of Rauszer [Reference Rauszer28] into
$\sf HB$
of Rauszer [Reference Rauszer28] into
![]() ${\sf S4.t}$
fully and faithfully. The language of
${\sf S4.t}$
fully and faithfully. The language of
![]() $\sf HB$
is obtained by enriching the language of
$\sf HB$
is obtained by enriching the language of
![]() $\sf IPC$
by an additional connective of coimplication, and the logic
$\sf IPC$
by an additional connective of coimplication, and the logic
![]() $\sf HB$
is the extension of
$\sf HB$
is the extension of
![]() $\sf IPC$
by the axioms for coimplication, which are dual to the axioms for implication. Wolter [Reference Wolter31] extended the celebrated Blok–Esakia theorem to this setting.
$\sf IPC$
by the axioms for coimplication, which are dual to the axioms for implication. Wolter [Reference Wolter31] extended the celebrated Blok–Esakia theorem to this setting.
We are ready to define
![]() ${\sf TS4}$
by combining
${\sf TS4}$
by combining
![]() ${\sf S4}$
and
${\sf S4}$
and
![]() ${\sf S4.t}$
. In Section 4 we will translate
${\sf S4.t}$
. In Section 4 we will translate
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf TS4}$
fully and faithfully. We will use
${\sf TS4}$
fully and faithfully. We will use
![]() ${\sf S4}$
to translate intuitionistic connectives and
${\sf S4}$
to translate intuitionistic connectives and
![]() ${\sf S4.t}$
to translate monadic intuitionistic quantifiers. Let
${\sf S4.t}$
to translate monadic intuitionistic quantifiers. Let
![]() $\mathcal {ML}$
be the multimodal propositional language with three modalities
$\mathcal {ML}$
be the multimodal propositional language with three modalities
![]() $\Box $
,
$\Box $
,
![]() ${[F]}$
, and
${[F]}$
, and
![]() ${[P]}$
. We use
${[P]}$
. We use
![]() $\Diamond $
,
$\Diamond $
,
![]() ${\langle F \rangle }$
, and
${\langle F \rangle }$
, and
![]() ${\langle P \rangle }$
as usual abbreviations.
${\langle P \rangle }$
as usual abbreviations.
Definition 2.8. The logic
![]() ${\sf TS4}$
is the least multimodal logic containing all theorems of the classical propositional calculus
${\sf TS4}$
is the least multimodal logic containing all theorems of the classical propositional calculus
![]() ${\sf CPC}$
, the
${\sf CPC}$
, the
![]() ${\sf S4}$
-axioms for
${\sf S4}$
-axioms for
![]() $\Box $
,
$\Box $
,
![]() ${[F]}$
, and
${[F]}$
, and
![]() ${[P]}$
, the tense axioms for
${[P]}$
, the tense axioms for
![]() ${[F]}$
and
${[F]}$
and
![]() ${[P]}$
, the connecting axioms
${[P]}$
, the connecting axioms
and closed under modus ponens, substitution, and three necessitation rules (for
![]() $\Box $
,
$\Box $
,
![]() ${[F]}$
, and
${[F]}$
, and
![]() ${[P]}$
).
${[P]}$
).
Our final logic of interest is the monadic tense logic
![]() ${\sf MS4.t}$
which is obtained by combining
${\sf MS4.t}$
which is obtained by combining
![]() ${\sf MS4}$
and
${\sf MS4}$
and
![]() ${\sf S4.t}$
. As we will see, both
${\sf S4.t}$
. As we will see, both
![]() ${\sf MS4}$
and
${\sf MS4}$
and
![]() ${\sf TS4}$
translate fully and faithfully into
${\sf TS4}$
translate fully and faithfully into
![]() ${\sf MS4.t}$
. In order to avoid confusion between the tense modalities of
${\sf MS4.t}$
. In order to avoid confusion between the tense modalities of
![]() ${\sf TS4}$
and
${\sf TS4}$
and
![]() ${\sf MS4.t}$
, we denote the tense modalities of
${\sf MS4.t}$
, we denote the tense modalities of
![]() ${\sf MS4.t}$
by
${\sf MS4.t}$
by
![]() $\Box _F$
and
$\Box _F$
and
![]() $\Box _P$
. Let
$\Box _P$
. Let
![]() $\mathcal L_{T\forall }$
be the propositional language with the tense modalities
$\mathcal L_{T\forall }$
be the propositional language with the tense modalities
![]() $\Box _F$
and
$\Box _F$
and
![]() $\Box _P$
, and the monadic modality
$\Box _P$
, and the monadic modality
![]() $\forall $
.
$\forall $
.
Definition 2.9. The tense
![]() ${\sf MS4}$
, denoted
${\sf MS4}$
, denoted
![]() ${\sf MS4.t}$
, is the least multimodal logic containing all theorems of the classical propositional calculus
${\sf MS4.t}$
, is the least multimodal logic containing all theorems of the classical propositional calculus
![]() ${\sf CPC}$
, the
${\sf CPC}$
, the
![]() ${\sf S4.t}$
-axioms for
${\sf S4.t}$
-axioms for
![]() $\Box _F$
and
$\Box _F$
and
![]() $\Box _P$
, the
$\Box _P$
, the
![]() ${\sf S5}$
-axioms for
${\sf S5}$
-axioms for
![]() $\forall $
, the left commutativity axiom
$\forall $
, the left commutativity axiom
and closed under modus ponens, substitution, and the necessitation rules (for
![]() $\Box _F$
,
$\Box _F$
,
![]() $\Box _P$
, and
$\Box _P$
, and
![]() $\forall $
).
$\forall $
).
Remark 2.10. We can think of
![]() ${\sf MS4.t}$
as a tense extension of
${\sf MS4.t}$
as a tense extension of
![]() ${\sf MS4}$
. It is worth stressing that
${\sf MS4}$
. It is worth stressing that
![]() ${\sf MS4.t}$
is not the monadic fragment of the standard predicate extension
${\sf MS4.t}$
is not the monadic fragment of the standard predicate extension
![]() ${\sf QS4.t}$
of
${\sf QS4.t}$
of
![]() ${\sf S4.t}$
. To see this, it is well known that the Barcan formula
${\sf S4.t}$
. To see this, it is well known that the Barcan formula
![]() $\forall x \Box _F \varphi \to \Box _F \forall x \varphi $
and the converse Barcan formula
$\forall x \Box _F \varphi \to \Box _F \forall x \varphi $
and the converse Barcan formula
![]() $\Box _F \forall x \varphi \to \forall x \Box _F \varphi $
are both theorems of any tense predicate logic containing the standard axioms of first-order logic. Therefore, both are theorems of
$\Box _F \forall x \varphi \to \forall x \Box _F \varphi $
are both theorems of any tense predicate logic containing the standard axioms of first-order logic. Therefore, both are theorems of
![]() ${\sf QS4.t}$
. Thus, the monadic fragment of
${\sf QS4.t}$
. Thus, the monadic fragment of
![]() ${\sf QS4.t}$
contains both the left commutativity axiom
${\sf QS4.t}$
contains both the left commutativity axiom
![]() $\Box _F \forall p \to \forall \Box _F p$
and the right commutativity axiom
$\Box _F \forall p \to \forall \Box _F p$
and the right commutativity axiom
![]() $\forall \Box _F p \to \Box _F \forall p$
. On the other hand, it is easy to see (e.g., using the Kripke semantics for
$\forall \Box _F p \to \Box _F \forall p$
. On the other hand, it is easy to see (e.g., using the Kripke semantics for
![]() ${\sf MS4.t}$
which we will define in the next section) that, while
${\sf MS4.t}$
which we will define in the next section) that, while
![]() ${\sf MS4.t}$
contains the left commutativity axiom, the right commutativity axiom is not provable in
${\sf MS4.t}$
contains the left commutativity axiom, the right commutativity axiom is not provable in
![]() ${\sf MS4.t}$
.
${\sf MS4.t}$
.
3 Relational semantics
In this section we investigate the relational semantics for
![]() ${\sf MIPC}$
,
${\sf MIPC}$
,
![]() ${\sf MS4}$
,
${\sf MS4}$
,
![]() ${\sf TS4}$
, and
${\sf TS4}$
, and
![]() ${\sf MS4.t}$
. The relational semantics for
${\sf MS4.t}$
. The relational semantics for
![]() ${\sf MIPC}$
and
${\sf MIPC}$
and
![]() ${\sf MS4}$
have already been studied in the literature, and the relational semantics for
${\sf MS4}$
have already been studied in the literature, and the relational semantics for
![]() ${\sf TS4}$
and
${\sf TS4}$
and
![]() ${\sf MS4.t}$
are obtained by a straightforward adaptation.
${\sf MS4.t}$
are obtained by a straightforward adaptation.
Definition 3.1. Let R be a quasi-order (reflexive and transitive relation) on a set X. As usual, for
![]() $x\in X$
, we write
$x\in X$
, we write
and for
![]() $A\subseteq X$
, we write
$A\subseteq X$
, we write
We say that
![]() $A \subseteq X$
is an R-upset if
$A \subseteq X$
is an R-upset if
![]() $R[A]=A$
and that it is an R-downset if
$R[A]=A$
and that it is an R-downset if
![]() $R^{-1}[A]=A$
.
$R^{-1}[A]=A$
.
We first describe the relational semantics for
![]() ${\sf MIPC}$
. There are several such (see, e.g., [Reference Bezhanishvili3]), but we concentrate on the one introduced by Ono [Reference Ono23].
${\sf MIPC}$
. There are several such (see, e.g., [Reference Bezhanishvili3]), but we concentrate on the one introduced by Ono [Reference Ono23].
Definition 3.2. An
![]() ${\sf MIPC}$
-frame is a triple
${\sf MIPC}$
-frame is a triple
![]() $\mathfrak F=(X,R,Q)$
where X is a set, R is a partial order, Q is a quasi-order, and the following two conditions are satisfied:
$\mathfrak F=(X,R,Q)$
where X is a set, R is a partial order, Q is a quasi-order, and the following two conditions are satisfied:
-
(O1)
 $R \subseteq Q$
,
$R \subseteq Q$
, -
(O2)
 $x Q y \Rightarrow (\exists z)(x R z \; \& \; z E_Q y)$
(see Figure 2).
$x Q y \Rightarrow (\exists z)(x R z \; \& \; z E_Q y)$
(see Figure 2).
Here
![]() $E_Q$
is the equivalence relation defined by
$E_Q$
is the equivalence relation defined by
![]() $x E_Q y$
iff
$x E_Q y$
iff
![]() $x Q y$
and
$x Q y$
and
![]() $y Q x$
.
$y Q x$
.
Remark 3.3. If U is an R-upset of an
![]() ${\sf MIPC}$
-frame
${\sf MIPC}$
-frame
![]() $\mathfrak {F}$
, then Condition (O2) implies that
$\mathfrak {F}$
, then Condition (O2) implies that
![]() $E_Q[U]=Q[U]$
. This motivates our interpretation of
$E_Q[U]=Q[U]$
. This motivates our interpretation of
![]() $\exists $
as “sometime in the past.” Indeed, taking
$\exists $
as “sometime in the past.” Indeed, taking
![]() $Q[U]$
is the standard way to associate an operator on
$Q[U]$
is the standard way to associate an operator on
![]() $\wp (X)$
to the tense modality “sometime in the past” (see, e.g., [Reference Thomason30, p. 151]).
$\wp (X)$
to the tense modality “sometime in the past” (see, e.g., [Reference Thomason30, p. 151]).

Fig. 2 Condition (O2).
Definition 3.4. A valuation on an
![]() ${\sf MIPC}$
-frame
${\sf MIPC}$
-frame
![]() $\mathfrak F=(X,R,Q)$
is a map
$\mathfrak F=(X,R,Q)$
is a map
![]() $v$
associating an R-upset of
$v$
associating an R-upset of
![]() $\mathfrak F$
to any propositional letter of
$\mathfrak F$
to any propositional letter of
![]() $\mathcal L_{\forall \exists }$
. The connectives
$\mathcal L_{\forall \exists }$
. The connectives
![]() $\wedge ,\vee ,\to ,\neg $
are then interpreted as in intuitionistic Kripke frames, and
$\wedge ,\vee ,\to ,\neg $
are then interpreted as in intuitionistic Kripke frames, and
![]() $\forall ,\exists $
are interpreted as
$\forall ,\exists $
are interpreted as
As usual, we say that
![]() $\varphi $
is valid in
$\varphi $
is valid in
![]() $\mathfrak F$
, and write
$\mathfrak F$
, and write
![]() $\mathfrak F \vDash \varphi $
, if
$\mathfrak F \vDash \varphi $
, if
![]() $x \vDash _v \varphi $
for every valuation
$x \vDash _v \varphi $
for every valuation
![]() $v$
and every
$v$
and every
![]() $x \in X$
.
$x \in X$
.
It is well known that
![]() ${\sf MIPC}$
is a canonical logic (see, e.g., [Reference Bezhanishvili3, Sec. 6]). Thus, we have:
${\sf MIPC}$
is a canonical logic (see, e.g., [Reference Bezhanishvili3, Sec. 6]). Thus, we have:
Theorem 3.5.
![]() ${\sf MIPC}$
is a canonical logic, and hence it is sound and complete with respect to its relational semantics. Therefore,
${\sf MIPC}$
is a canonical logic, and hence it is sound and complete with respect to its relational semantics. Therefore,
Remark 3.6. In addition,
![]() ${\sf MIPC}$
has the fmp [Reference Bull7, Reference Fischer-Servi15, Reference Ono23] and hence is decidable. As we will see in Section 6, the fmp of
${\sf MIPC}$
has the fmp [Reference Bull7, Reference Fischer-Servi15, Reference Ono23] and hence is decidable. As we will see in Section 6, the fmp of
![]() ${\sf MIPC}$
can be derived from the fmp of
${\sf MIPC}$
can be derived from the fmp of
![]() ${\sf MS4.t}$
.
${\sf MS4.t}$
.
The relational semantics for
![]() ${\sf MS4}$
was introduced by Esakia [Reference Esakia12].
${\sf MS4}$
was introduced by Esakia [Reference Esakia12].
Definition 3.7. An
![]() ${\sf MS4}$
-frame is a triple
${\sf MS4}$
-frame is a triple
![]() $\mathfrak F=(X,R,E)$
where X is a set, R is a quasi-order, E is an equivalence relation, and the following commutativity condition is satisfied (see
Figure 3
):
$\mathfrak F=(X,R,E)$
where X is a set, R is a quasi-order, E is an equivalence relation, and the following commutativity condition is satisfied (see
Figure 3
):

Fig. 3 Condition (E).
Definition 3.8. A valuation on an
![]() ${\sf MS4}$
-frame
${\sf MS4}$
-frame
![]() $\mathfrak F=(X,R,E)$
is a map
$\mathfrak F=(X,R,E)$
is a map
![]() $v$
associating a subset of X to each propositional letter of
$v$
associating a subset of X to each propositional letter of
![]() $\mathcal L_{\Box \forall }$
. The Boolean connectives are interpreted as usual, and
$\mathcal L_{\Box \forall }$
. The Boolean connectives are interpreted as usual, and
By Lemma 2.5, in the axiomatization of
![]() ${\sf MS4}$
, the left commutativity axiom
${\sf MS4}$
, the left commutativity axiom
![]() $\Box \forall p \to \forall \Box p$
can be replaced by
$\Box \forall p \to \forall \Box p$
can be replaced by
![]() $\exists \Box p \to \Box \exists p$
. Therefore,
$\exists \Box p \to \Box \exists p$
. Therefore,
![]() ${\sf MS4}$
can be axiomatized by Sahlqvist formulas (see, e.g., [Reference Blackburn, de Rijke and Venema5, Sec. 3.6]). Thus, by the Sahlqvist completeness theorem (see, e.g., [Reference Blackburn, de Rijke and Venema5, Theorem 4.42]), it is sound and complete with respect to its relational semantics:
${\sf MS4}$
can be axiomatized by Sahlqvist formulas (see, e.g., [Reference Blackburn, de Rijke and Venema5, Sec. 3.6]). Thus, by the Sahlqvist completeness theorem (see, e.g., [Reference Blackburn, de Rijke and Venema5, Theorem 4.42]), it is sound and complete with respect to its relational semantics:
Theorem 3.9.
![]() ${\sf MS4}$
is a Sahlqvist logic, and hence it is sound and complete with respect to its relational semantics. Therefore,
${\sf MS4}$
is a Sahlqvist logic, and hence it is sound and complete with respect to its relational semantics. Therefore,
Remark 3.10. In addition,
![]() ${\sf MS4}$
has the fmp and is decidable. This can be derived from the results in [Reference Gabbay and Shehtman17, Sec. 12] (see also [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16, Theorems 6.52 and 9.12]). As we will see in Section 6, the fmp of
${\sf MS4}$
has the fmp and is decidable. This can be derived from the results in [Reference Gabbay and Shehtman17, Sec. 12] (see also [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16, Theorems 6.52 and 9.12]). As we will see in Section 6, the fmp of
![]() ${\sf MS4}$
can also be derived from the fmp of
${\sf MS4}$
can also be derived from the fmp of
![]() ${\sf MS4.t}$
.
${\sf MS4.t}$
.
We next recall the relational semantics for
![]() ${\sf S4.t}$
.
${\sf S4.t}$
.
Definition 3.11. An
![]() ${\sf S4.t}$
-frame is a pair
${\sf S4.t}$
-frame is a pair
![]() $\mathfrak {F}=(X,Q)$
where X is a set and Q is a quasi-order on X.
$\mathfrak {F}=(X,Q)$
where X is a set and Q is a quasi-order on X.
Remark 3.12. While
![]() ${\sf S4.t}$
-frames coincide with
${\sf S4.t}$
-frames coincide with
![]() ${\sf S4}$
-frames, the difference is in the interpretation of the modalities as we use Q to interpret
${\sf S4}$
-frames, the difference is in the interpretation of the modalities as we use Q to interpret
![]() ${[F]}$
and its inverse relation
${[F]}$
and its inverse relation
![]() to interpret
to interpret
![]() ${[P]}$
.
${[P]}$
.
Definition 3.13. A valuation on an
![]() ${\sf S4.t}$
-frame
${\sf S4.t}$
-frame
![]() $\mathfrak F=(X,Q)$
is a map
$\mathfrak F=(X,Q)$
is a map
![]() $v$
associating a subset of X to each propositional letter of
$v$
associating a subset of X to each propositional letter of
![]() $\mathcal L_T$
. The Boolean connectives are interpreted as usual, and the tense modalities are interpreted as
$\mathcal L_T$
. The Boolean connectives are interpreted as usual, and the tense modalities are interpreted as
Remark 3.14. It is straightforward to see that all the axioms of
![]() ${\sf S4.t}$
are Sahlqvist formulas. Therefore,
${\sf S4.t}$
are Sahlqvist formulas. Therefore,
![]() ${\sf S4.t}$
is a Sahlqvist logic, and hence it is sound and complete with respect to its relational semantics. That
${\sf S4.t}$
is a Sahlqvist logic, and hence it is sound and complete with respect to its relational semantics. That
![]() ${\sf S4.t}$
has the fmp follows from [Reference Segerberg29, pp. 313–314] (see also [Reference Goldblatt18, p. 44] and Remark 6.18(3)).
${\sf S4.t}$
has the fmp follows from [Reference Segerberg29, pp. 313–314] (see also [Reference Goldblatt18, p. 44] and Remark 6.18(3)).
We now introduce the relational semantics for
![]() ${\sf TS4}$
.
${\sf TS4}$
.
Definition 3.15. A
![]() ${\sf TS4}$
-frame is a triple
${\sf TS4}$
-frame is a triple
![]() $\mathfrak F=(X,R,Q)$
where X is a set and
$\mathfrak F=(X,R,Q)$
where X is a set and
![]() $R,Q$
are quasi-orders on X satisfying Conditions (O1) and (O2).
$R,Q$
are quasi-orders on X satisfying Conditions (O1) and (O2).
It follows that
![]() ${\sf TS4}$
-frames are a version of
${\sf TS4}$
-frames are a version of
![]() ${\sf MIPC}$
-frames, where the relation R is a quasi-order. We interpret
${\sf MIPC}$
-frames, where the relation R is a quasi-order. We interpret
![]() $\Box $
using R, and
$\Box $
using R, and
![]() ${[F]}$
,
${[F]}$
,
![]() ${[P]}$
using Q and its inverse
${[P]}$
using Q and its inverse
![]() .
.
Definition 3.16. A valuation on a
![]() ${\sf TS4}$
-frame
${\sf TS4}$
-frame
![]() $\mathfrak F=(X,R,Q)$
is a map
$\mathfrak F=(X,R,Q)$
is a map
![]() $v$
associating a subset of X to each propositional letter of
$v$
associating a subset of X to each propositional letter of
![]() $\mathcal {ML}$
. The Boolean connectives are interpreted as usual, and the modalities
$\mathcal {ML}$
. The Boolean connectives are interpreted as usual, and the modalities
![]() $\Box $
,
$\Box $
,
![]() ${[F]}$
, and
${[F]}$
, and
![]() ${[P]}$
are interpreted as
${[P]}$
are interpreted as
 $$ \begin{align*} \begin{array}{l c l} x \vDash_v \Box \varphi & \text{ iff } & (\forall y \in X) (x R y \Rightarrow y \vDash_v \varphi ), \\ x \vDash_v {[F]} \varphi & \text{ iff } & (\forall y \in X) (x Q y \Rightarrow y \vDash_v \varphi ), \\ x \vDash_v {[P]} \varphi & \text{ iff } & (\forall y \in X) (y Q x \Rightarrow y \vDash_v \varphi ). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l c l} x \vDash_v \Box \varphi & \text{ iff } & (\forall y \in X) (x R y \Rightarrow y \vDash_v \varphi ), \\ x \vDash_v {[F]} \varphi & \text{ iff } & (\forall y \in X) (x Q y \Rightarrow y \vDash_v \varphi ), \\ x \vDash_v {[P]} \varphi & \text{ iff } & (\forall y \in X) (y Q x \Rightarrow y \vDash_v \varphi ). \end{array} \end{align*} $$
Consequently,
 $$ \begin{align*} \begin{array}{l c l} x \vDash_v \Diamond \varphi & \text{ iff } & (\exists y \in X) (x R y \; \& \; y \vDash_v \varphi ),\\ x \vDash_v {\langle F \rangle} \varphi & \text{ iff } & (\exists y \in X) (x Q y \; \& \; y \vDash_v \varphi ),\\ x \vDash_v {\langle P \rangle} \varphi & \text{ iff } & (\exists y \in X) (y Q x \; \& \; y \vDash_v \varphi ). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l c l} x \vDash_v \Diamond \varphi & \text{ iff } & (\exists y \in X) (x R y \; \& \; y \vDash_v \varphi ),\\ x \vDash_v {\langle F \rangle} \varphi & \text{ iff } & (\exists y \in X) (x Q y \; \& \; y \vDash_v \varphi ),\\ x \vDash_v {\langle P \rangle} \varphi & \text{ iff } & (\exists y \in X) (y Q x \; \& \; y \vDash_v \varphi ). \end{array} \end{align*} $$
Remark 3.17. It is straightforward to check that if
![]() $(X,R,Q)$
is a
$(X,R,Q)$
is a
![]() ${\sf TS4}$
-frame, then
${\sf TS4}$
-frame, then
![]() $(X,R,E_Q)$
is an
$(X,R,E_Q)$
is an
![]() ${\sf MS4}$
-frame, and that if
${\sf MS4}$
-frame, and that if
![]() $(X,R,E)$
is an
$(X,R,E)$
is an
![]() ${\sf MS4}$
-frame, then
${\sf MS4}$
-frame, then
![]() $(X,R,Q_E)$
is a
$(X,R,Q_E)$
is a
![]() ${\sf TS4}$
-frame, where
${\sf TS4}$
-frame, where
![]() $Q_E$
is defined by
$Q_E$
is defined by
If
![]() $(X,R,Q)$
is a
$(X,R,Q)$
is a
![]() ${\sf TS4}$
-frame, by definition we have that
${\sf TS4}$
-frame, by definition we have that
Thus,
![]() $Q=Q_{E_Q}$
. On the other hand, there exist
$Q=Q_{E_Q}$
. On the other hand, there exist
![]() ${\sf MS4}$
-frames
${\sf MS4}$
-frames
![]() $(X,R,E)$
such that
$(X,R,E)$
such that
![]() $E\ne E_{Q_E}$
(see [Reference Bezhanishvili3, p. 24]). Therefore, this correspondence is not a bijection.
$E\ne E_{Q_E}$
(see [Reference Bezhanishvili3, p. 24]). Therefore, this correspondence is not a bijection.
Since all
![]() ${\sf TS4}$
-axioms are Sahlqvist formulas, we have:
${\sf TS4}$
-axioms are Sahlqvist formulas, we have:
Theorem 3.18.
![]() ${\sf TS4}$
is a Sahlqvist logic, and hence it is sound and complete with respect to its relational semantics. Therefore,
${\sf TS4}$
is a Sahlqvist logic, and hence it is sound and complete with respect to its relational semantics. Therefore,
Remark 3.19. In Section 6 we will see that
![]() ${\sf TS4}$
has the fmp and hence is decidable.
${\sf TS4}$
has the fmp and hence is decidable.
Finally, we introduce the relational semantics for
![]() ${\sf MS4.t}$
. As with
${\sf MS4.t}$
. As with
![]() $\sf S4$
and
$\sf S4$
and
![]() $\sf S4.t$
, we have that
$\sf S4.t$
, we have that
![]() ${\sf MS4.t}$
-frames are simply
${\sf MS4.t}$
-frames are simply
![]() ${\sf MS4}$
-frames, the difference is in interpreting tense modalities.
${\sf MS4}$
-frames, the difference is in interpreting tense modalities.
Definition 3.20. A valuation on an
![]() ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
![]() $\mathfrak F=(X,R,E)$
is a map
$\mathfrak F=(X,R,E)$
is a map
![]() $v$
associating a subset of X to each propositional letter of
$v$
associating a subset of X to each propositional letter of
![]() $\mathcal L_{T\forall }$
. The Boolean connectives are interpreted as usual, and
$\mathcal L_{T\forall }$
. The Boolean connectives are interpreted as usual, and
 $$ \begin{align*} \begin{array}{l c l} \mathfrak{F}, x \vDash_v \Box_F \varphi & \text{ iff } & (\forall y \in X) (x R y \Rightarrow y \vDash_v \varphi ), \\ \mathfrak{F}, x \vDash_v \Box_P \varphi & \text{ iff } & (\forall y \in X) (y R x \Rightarrow y \vDash_v \varphi ), \\ \mathfrak{F}, x \vDash_v \forall \varphi & \text{ iff } & (\forall y \in X) (x E y \Rightarrow y \vDash_v \varphi). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l c l} \mathfrak{F}, x \vDash_v \Box_F \varphi & \text{ iff } & (\forall y \in X) (x R y \Rightarrow y \vDash_v \varphi ), \\ \mathfrak{F}, x \vDash_v \Box_P \varphi & \text{ iff } & (\forall y \in X) (y R x \Rightarrow y \vDash_v \varphi ), \\ \mathfrak{F}, x \vDash_v \forall \varphi & \text{ iff } & (\forall y \in X) (x E y \Rightarrow y \vDash_v \varphi). \end{array} \end{align*} $$
Since both
![]() ${\sf MS4}$
and
${\sf MS4}$
and
![]() ${\sf S4.t}$
are Sahlqvist logics, so is
${\sf S4.t}$
are Sahlqvist logics, so is
![]() ${\sf MS4.t}$
. Thus, we have:
${\sf MS4.t}$
. Thus, we have:
Theorem 3.21.
![]() ${\sf MS4.t}$
is a Sahlqvist logic, and hence it is sound and complete with respect to its relational semantics. Therefore,
${\sf MS4.t}$
is a Sahlqvist logic, and hence it is sound and complete with respect to its relational semantics. Therefore,
In Section 6 we will prove that
![]() ${\sf MS4.t}$
has the fmp and hence is decidable.
${\sf MS4.t}$
has the fmp and hence is decidable.
4 The four translations
In this section we define the translations of Figure 1 and show that they are full and faithful by using relational semantics. We start by recalling that the Gödel translation of
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf MS4}$
is defined by
${\sf MS4}$
is defined by
 $$ \begin{align*} \bot^t &= \bot,\\ p^t &= \Box p \quad \mbox{for each propositional letter } p, \\ (\varphi \land \psi)^t &= \varphi^t \land \psi^t, \\ (\varphi \lor \psi)^t &= \varphi^t \lor \psi^t, \\ (\varphi \to \psi)^t &= \Box (\neg \varphi^t \lor \psi^t), \\ (\forall \varphi)^t &= \Box \forall \varphi^t, \\ (\exists \varphi)^t &= \exists \varphi^t. \end{align*} $$
$$ \begin{align*} \bot^t &= \bot,\\ p^t &= \Box p \quad \mbox{for each propositional letter } p, \\ (\varphi \land \psi)^t &= \varphi^t \land \psi^t, \\ (\varphi \lor \psi)^t &= \varphi^t \lor \psi^t, \\ (\varphi \to \psi)^t &= \Box (\neg \varphi^t \lor \psi^t), \\ (\forall \varphi)^t &= \Box \forall \varphi^t, \\ (\exists \varphi)^t &= \exists \varphi^t. \end{align*} $$
Definition 4.1. The translation
![]() $(-)^\natural : {\sf MIPC} \to {\sf TS4}$
is defined as
$(-)^\natural : {\sf MIPC} \to {\sf TS4}$
is defined as
![]() $(-)^t$
on propositional letters,
$(-)^t$
on propositional letters,
![]() $\bot $
,
$\bot $
,
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
, and
$\vee $
, and
![]() $\to $
; and for
$\to $
; and for
![]() $\forall $
and
$\forall $
and
![]() $\exists $
we set:
$\exists $
we set:
 $$ \begin{align*} (\forall \varphi)^\natural &= {[F]} \varphi^\natural,\\ (\exists \varphi)^\natural &= {\langle P \rangle} \varphi^\natural. \end{align*} $$
$$ \begin{align*} (\forall \varphi)^\natural &= {[F]} \varphi^\natural,\\ (\exists \varphi)^\natural &= {\langle P \rangle} \varphi^\natural. \end{align*} $$
Remark 4.2. Thus,
![]() $(-)^\natural $
realizes the desired temporal interpretation of the intuitionistic monadic quantifiers:
$(-)^\natural $
realizes the desired temporal interpretation of the intuitionistic monadic quantifiers:
![]() $\forall $
as “always in the future” and
$\forall $
as “always in the future” and
![]() $\exists $
as “sometime in the past.”
$\exists $
as “sometime in the past.”
Definition 4.3. The translation
![]() $(-)^\dagger : {\sf TS4} \to {\sf MS4.t}$
is defined by
$(-)^\dagger : {\sf TS4} \to {\sf MS4.t}$
is defined by
 $$ \begin{align*} p^\dagger &=p \quad \mbox{ for each propositional letter}\ p,\\ (\varphi \circ \psi)^\dagger &= \varphi^\dagger \circ \psi^\dagger \quad \mbox{for } \circ= \wedge, \vee,\\ (\neg \varphi)^\dagger & =\neg \varphi^\dagger,\\ (\Box \varphi)^\dagger &=\Box_F \varphi^\dagger,\\ ({[F]} \varphi)^\dagger &=\Box_F \forall \varphi^\dagger,\\ ({[P]} \varphi)^\dagger &=\forall \Box_P \varphi^\dagger. \end{align*} $$
$$ \begin{align*} p^\dagger &=p \quad \mbox{ for each propositional letter}\ p,\\ (\varphi \circ \psi)^\dagger &= \varphi^\dagger \circ \psi^\dagger \quad \mbox{for } \circ= \wedge, \vee,\\ (\neg \varphi)^\dagger & =\neg \varphi^\dagger,\\ (\Box \varphi)^\dagger &=\Box_F \varphi^\dagger,\\ ({[F]} \varphi)^\dagger &=\Box_F \forall \varphi^\dagger,\\ ({[P]} \varphi)^\dagger &=\forall \Box_P \varphi^\dagger. \end{align*} $$
Remark 4.4.
-
1. The translation
 $(-)^\dagger : {\sf TS4} \to {\sf MS4.t}$
is suggested by the correspondence between
$(-)^\dagger : {\sf TS4} \to {\sf MS4.t}$
is suggested by the correspondence between
 ${\sf TS4}$
-frames and
${\sf TS4}$
-frames and
 ${\sf MS4}$
-frames described in Remark 3.17. Each
${\sf MS4}$
-frames described in Remark 3.17. Each
 ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
 $\mathfrak {F}=(X,R,E)$
is an
$\mathfrak {F}=(X,R,E)$
is an
 ${\sf MS4}$
-frame, the relation
${\sf MS4}$
-frame, the relation
 $Q_E$
on the corresponding
$Q_E$
on the corresponding
 ${\sf TS4}$
-frame is the composition of R and E, and the inverse relation
${\sf TS4}$
-frame is the composition of R and E, and the inverse relation
 is the composition of E and
is the composition of E and
 . Therefore, the modalities
. Therefore, the modalities
 ${[F]}$
and
${[F]}$
and
 ${[P]}$
are translated as
${[P]}$
are translated as
 $\Box _F \forall $
and
$\Box _F \forall $
and
 $\forall \Box _P$
, respectively. Notice that, since
$\forall \Box _P$
, respectively. Notice that, since
 ${\sf MS4}$
lacks a modality corresponding to the relation
${\sf MS4}$
lacks a modality corresponding to the relation
 , we are not able to translate
, we are not able to translate
 ${\sf TS4}$
into
${\sf TS4}$
into
 ${\sf MS4}$
.
${\sf MS4}$
. -
2. It is natural to consider a modification of
 $(-)^\dagger :{\sf TS4} \to {\sf MS4.t}$
where
$(-)^\dagger :{\sf TS4} \to {\sf MS4.t}$
where
 ${[P]}$
is translated as
${[P]}$
is translated as
 $\Box _P \forall $
. However, such a modification does not result in a faithful translation. Nevertheless, as we will see in Section 5, its composition with
$\Box _P \forall $
. However, such a modification does not result in a faithful translation. Nevertheless, as we will see in Section 5, its composition with
 $(-)^\natural :{\sf MIPC} \to {\sf TS4}$
is full and faithful.
$(-)^\natural :{\sf MIPC} \to {\sf TS4}$
is full and faithful.
The translation of
![]() ${\sf MS4}$
into
${\sf MS4}$
into
![]() ${\sf MS4.t}$
reflects that
${\sf MS4.t}$
reflects that
![]() ${\sf MS4.t}$
is a tense extension of
${\sf MS4.t}$
is a tense extension of
![]() ${\sf MS4}$
.
${\sf MS4}$
.
Definition 4.5. The translation
![]() $(-)^\# : {\sf MS4} \to {\sf MS4.t}$
replaces in each formula
$(-)^\# : {\sf MS4} \to {\sf MS4.t}$
replaces in each formula
![]() $\varphi $
of
$\varphi $
of
![]() $\mathcal {L}_{\Box \forall }$
every occurrence of
$\mathcal {L}_{\Box \forall }$
every occurrence of
![]() $\Box $
with
$\Box $
with
![]() $\Box _F$
.
$\Box _F$
.
We show that these four translations are full and faithful by using relational semantics. For this we first need to generalize the well-known notion of the skeleton of an
![]() ${\sf S4}$
-frame (see, e.g., [Reference Chagrov and Zakharyaschev9, Sec. 3.9]).
${\sf S4}$
-frame (see, e.g., [Reference Chagrov and Zakharyaschev9, Sec. 3.9]).
Definition 4.6.
-
1. If R is a quasi-order on a set X, we define
 $\sim $
to be the equivalence relation on X given by We let
$\sim $
to be the equivalence relation on X given by We let $$ \begin{align*} x \sim y \mbox{ iff } xRy \mbox{ and } yRx. \end{align*} $$
$$ \begin{align*} x \sim y \mbox{ iff } xRy \mbox{ and } yRx. \end{align*} $$
 $X'$
be the set of equivalence classes of
$X'$
be the set of equivalence classes of
 $\sim $
, and define
$\sim $
, and define
 $R'$
on
$R'$
on
 $X'$
by
$X'$
by  $$ \begin{align*} [x] R' [y] \mbox{ iff } xRy. \end{align*} $$
$$ \begin{align*} [x] R' [y] \mbox{ iff } xRy. \end{align*} $$
-
2. Let
 $\mathfrak F=(X,R,E)$
be an
$\mathfrak F=(X,R,E)$
be an
 ${\sf MS4}$
-frame. Recall that
${\sf MS4}$
-frame. Recall that
 $Q_E$
is defined on X by
$Q_E$
is defined on X by
 $x Q_E y$
iff
$x Q_E y$
iff
 $(\exists z \in X )(xRz \ \& \ zEy)$
(see Remark 3.17). Define
$(\exists z \in X )(xRz \ \& \ zEy)$
(see Remark 3.17). Define
 $Q'$
on
$Q'$
on
 $X'$
by We call
$X'$
by We call $$ \begin{align*} [x] Q' [y] \mbox{ iff } xQ_Ey. \end{align*} $$
$$ \begin{align*} [x] Q' [y] \mbox{ iff } xQ_Ey. \end{align*} $$
 $\mathfrak {F}^t=(X',R',Q')$
the skeleton of the
$\mathfrak {F}^t=(X',R',Q')$
the skeleton of the
 ${\sf MS4}$
-frame
${\sf MS4}$
-frame
 $\mathfrak {F}$
.
$\mathfrak {F}$
.
-
3. Let
 $\mathfrak F=(X,R,Q)$
be a
$\mathfrak F=(X,R,Q)$
be a
 ${\sf TS4}$
-frame. Define
${\sf TS4}$
-frame. Define
 $Q'$
on
$Q'$
on
 $X'$
by We call
$X'$
by We call $$ \begin{align*} [x] Q' [y] \mbox{ iff } xQy. \end{align*} $$
$$ \begin{align*} [x] Q' [y] \mbox{ iff } xQy. \end{align*} $$
 $\mathfrak {F}^\natural =(X',R',Q')$
the skeleton of the
$\mathfrak {F}^\natural =(X',R',Q')$
the skeleton of the
 ${\sf TS4}$
-frame
${\sf TS4}$
-frame
 $\mathfrak {F}$
.
$\mathfrak {F}$
.
-
4. For an
 ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
 $\mathfrak F=(X,R,E)$
let
$\mathfrak F=(X,R,E)$
let
 $\mathfrak {F}^\dagger = (X,R,Q_E)$
where
$\mathfrak {F}^\dagger = (X,R,Q_E)$
where
 $Q_E$
is defined as in (2).
$Q_E$
is defined as in (2).
Remark 4.7. If a
![]() ${\sf TS4}$
-frame
${\sf TS4}$
-frame
![]() $\mathfrak {F}=(X,R,Q)$
is such that R is a partial order, then
$\mathfrak {F}=(X,R,Q)$
is such that R is a partial order, then
![]() $\mathfrak {F}$
is isomorphic to its skeleton
$\mathfrak {F}$
is isomorphic to its skeleton
![]() $\mathfrak {F}^\natural $
. However, we cannot always recover an
$\mathfrak {F}^\natural $
. However, we cannot always recover an
![]() ${\sf MS4}$
-frame
${\sf MS4}$
-frame
![]() $\mathfrak {F}=(X,R,E)$
from its skeleton
$\mathfrak {F}=(X,R,E)$
from its skeleton
![]() $\mathfrak {F}^t$
even if R is a partial order. Indeed, it is not always the case that
$\mathfrak {F}^t$
even if R is a partial order. Indeed, it is not always the case that
![]() $E=E_{Q_E}$
. Nonetheless, if
$E=E_{Q_E}$
. Nonetheless, if
![]() $\mathfrak {F}$
is canonical (and in particular finite) and R is a partial order, then
$\mathfrak {F}$
is canonical (and in particular finite) and R is a partial order, then
![]() $E=E_{Q_E}$
; see [Reference Bezhanishvili3, Sec. 2] for details.
$E=E_{Q_E}$
; see [Reference Bezhanishvili3, Sec. 2] for details.
Proposition 4.8.
-
1. If
 $\mathfrak F$
is an
$\mathfrak F$
is an
 ${\sf MS4}$
-frame, then
${\sf MS4}$
-frame, then
 $\mathfrak {F}^t$
is an
$\mathfrak {F}^t$
is an
 ${\sf MIPC}$
-frame.
${\sf MIPC}$
-frame. -
2. If
 $\mathfrak F$
is a
$\mathfrak F$
is a
 ${\sf TS4}$
-frame, then
${\sf TS4}$
-frame, then
 $\mathfrak {F}^\natural $
is an
$\mathfrak {F}^\natural $
is an
 ${\sf MIPC}$
-frame.
${\sf MIPC}$
-frame. -
3. If
 $\mathfrak F$
is an
$\mathfrak F$
is an
 ${\sf MS4.t}$
-frame, then
${\sf MS4.t}$
-frame, then
 $\mathfrak {F}^\dagger $
is a
$\mathfrak {F}^\dagger $
is a
 ${\sf TS4}$
-frame.
${\sf TS4}$
-frame.
Proof. (1). It is well known that
![]() $(X',R')$
is an intuitionistic Kripke frame. That
$(X',R')$
is an intuitionistic Kripke frame. That
![]() $Q'$
is well defined follows from Condition (E). Showing that
$Q'$
is well defined follows from Condition (E). Showing that
![]() $Q'$
is a quasi-order and that (O1), (O2) hold in
$Q'$
is a quasi-order and that (O1), (O2) hold in
![]() $\mathfrak {F}^t$
is straightforward.
$\mathfrak {F}^t$
is straightforward.
(2). We have that
![]() $Q'$
is well defined on
$Q'$
is well defined on
![]() $X'$
because
$X'$
because
![]() $R \subseteq Q$
in
$R \subseteq Q$
in
![]() $\mathfrak {F}$
. Showing that
$\mathfrak {F}$
. Showing that
![]() $Q'$
is a quasi-order and that (O1), (O2) hold in
$Q'$
is a quasi-order and that (O1), (O2) hold in
![]() $\mathfrak {F}^\natural $
is straightforward.
$\mathfrak {F}^\natural $
is straightforward.
(3). Since
![]() ${\sf MS4.t}$
-frames coincide with
${\sf MS4.t}$
-frames coincide with
![]() ${\sf MS4}$
-frames, it follows from Remark 3.17 that
${\sf MS4}$
-frames, it follows from Remark 3.17 that
![]() $\mathfrak {F}^\dagger $
is a
$\mathfrak {F}^\dagger $
is a
![]() ${\sf TS4}$
-frame.
${\sf TS4}$
-frame.
It is well known that an
![]() ${\sf S4}$
-frame validates the Gödel translation of an intuitionistic formula
${\sf S4}$
-frame validates the Gödel translation of an intuitionistic formula
![]() $\varphi $
iff its skeleton validates
$\varphi $
iff its skeleton validates
![]() $\varphi $
(see, e.g., [Reference Chagrov and Zakharyaschev9, Corollary 3.82]). We will prove in Proposition 4.11 that analogous results hold for the four translations defined in this section. For this we need the following technical lemma.
$\varphi $
(see, e.g., [Reference Chagrov and Zakharyaschev9, Corollary 3.82]). We will prove in Proposition 4.11 that analogous results hold for the four translations defined in this section. For this we need the following technical lemma.
Lemma 4.9. For any formula
![]() $\chi $
of
$\chi $
of
![]() $\mathcal L_{\forall \exists }$
, we have
$\mathcal L_{\forall \exists }$
, we have
Consequently, if
![]() $\mathfrak {F}=(X,R,E)$
is an
$\mathfrak {F}=(X,R,E)$
is an
![]() ${\sf MS4}$
-frame and
${\sf MS4}$
-frame and
![]() $v$
a valuation on
$v$
a valuation on
![]() $\mathfrak {F}$
, then the set of points
$\mathfrak {F}$
, then the set of points
![]() $x\in X$
such that
$x\in X$
such that
![]() $\mathfrak {F}, x \vDash _v \chi ^t$
forms an R-upset of
$\mathfrak {F}, x \vDash _v \chi ^t$
forms an R-upset of
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
Proof. We prove that
![]() ${\sf MS4} \vdash \chi ^t \to \Box \chi ^t$
by induction on the complexity of
${\sf MS4} \vdash \chi ^t \to \Box \chi ^t$
by induction on the complexity of
![]() $\chi $
. This is obvious when
$\chi $
. This is obvious when
![]() $\chi =\bot $
. The cases when
$\chi =\bot $
. The cases when
![]() $\chi $
is p,
$\chi $
is p,
![]() $\varphi \to \psi $
, or
$\varphi \to \psi $
, or
![]() $\forall \varphi $
follow from the axiom
$\forall \varphi $
follow from the axiom
![]() $\Box \varphi \to \Box \Box \varphi $
. We next consider the cases when
$\Box \varphi \to \Box \Box \varphi $
. We next consider the cases when
![]() $\chi $
is
$\chi $
is
![]() $\varphi \wedge \psi $
or
$\varphi \wedge \psi $
or
![]() $\varphi \vee \psi $
. Suppose that the claim is true for
$\varphi \vee \psi $
. Suppose that the claim is true for
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, so
$\psi $
, so
![]() $\varphi ^t \to \Box \varphi ^t$
and
$\varphi ^t \to \Box \varphi ^t$
and
![]() $\psi ^t \to \Box \psi ^t$
are theorems of
$\psi ^t \to \Box \psi ^t$
are theorems of
![]() ${\sf MS4}$
. Then
${\sf MS4}$
. Then
![]() $\varphi ^t \wedge \psi ^t \to \Box (\varphi ^t \wedge \psi ^t)$
and
$\varphi ^t \wedge \psi ^t \to \Box (\varphi ^t \wedge \psi ^t)$
and
![]() $\varphi ^t \vee \psi ^t \to \Box (\varphi ^t \vee \psi ^t)$
are also theorems of
$\varphi ^t \vee \psi ^t \to \Box (\varphi ^t \vee \psi ^t)$
are also theorems of
![]() ${\sf MS4}$
. Finally, if
${\sf MS4}$
. Finally, if
![]() $\chi $
is
$\chi $
is
![]() $\exists \varphi $
and
$\exists \varphi $
and
![]() ${\sf MS4} \vdash \varphi ^t\to \Box \varphi ^t$
, then
${\sf MS4} \vdash \varphi ^t\to \Box \varphi ^t$
, then
![]() ${\sf MS4} \vdash \exists \varphi ^t \to \exists \Box \varphi ^t$
. Therefore, since
${\sf MS4} \vdash \exists \varphi ^t \to \exists \Box \varphi ^t$
. Therefore, since
![]() ${\sf MS4} \vdash \exists \Box \varphi ^t \to \Box \exists \varphi ^t$
by Lemma 2.5, we conclude that
${\sf MS4} \vdash \exists \Box \varphi ^t \to \Box \exists \varphi ^t$
by Lemma 2.5, we conclude that
![]() ${\sf MS4} \vdash \exists \varphi ^t \to \Box \exists \varphi ^t$
.
${\sf MS4} \vdash \exists \varphi ^t \to \Box \exists \varphi ^t$
.
Let
![]() $\mathfrak {F}=(X,R,E)$
be an
$\mathfrak {F}=(X,R,E)$
be an
![]() ${\sf MS4}$
-frame,
${\sf MS4}$
-frame,
![]() $v$
a valuation of
$v$
a valuation of
![]() $\mathfrak {F}$
, and
$\mathfrak {F}$
, and
![]() $x\in X$
. Since
$x\in X$
. Since
![]() ${\sf MS4} \vdash \chi ^t \to \Box \chi ^t$
, if
${\sf MS4} \vdash \chi ^t \to \Box \chi ^t$
, if
![]() $\mathfrak {F}, x \vDash _v \chi ^t$
, then
$\mathfrak {F}, x \vDash _v \chi ^t$
, then
![]() $\mathfrak {F}, x \vDash _v \Box \chi ^t$
. Therefore, for each y such that
$\mathfrak {F}, x \vDash _v \Box \chi ^t$
. Therefore, for each y such that
![]() $xRy$
we have
$xRy$
we have
![]() $\mathfrak {F}, y \vDash _v \chi ^t$
. Thus,
$\mathfrak {F}, y \vDash _v \chi ^t$
. Thus,
![]() $\{ x \in X \mid \mathfrak {F}, x \vDash _v \chi ^t \}$
is an R-upset.
$\{ x \in X \mid \mathfrak {F}, x \vDash _v \chi ^t \}$
is an R-upset.
The next result generalizes to our setting a well-known correspondence result [Reference Chagrov and Zakharyaschev9, Lemma 3.81] between
![]() ${\sf IPC}$
-models and
${\sf IPC}$
-models and
![]() ${\sf S4}$
-models.
${\sf S4}$
-models.
Proposition 4.10.
-
1. For each valuation
 $v$
on an
$v$
on an
 ${\sf MS4}$
-frame
${\sf MS4}$
-frame
 $\mathfrak {F}$
there is a valuation
$\mathfrak {F}$
there is a valuation
 $v'$
on
$v'$
on
 $\mathfrak {F}^t$
such that for each
$\mathfrak {F}^t$
such that for each
 $x\in \mathfrak F$
and
$x\in \mathfrak F$
and
 $\mathcal {L}_{\forall \exists }$
-formula
$\mathcal {L}_{\forall \exists }$
-formula
 $\varphi $
, we have
$\varphi $
, we have  $$ \begin{align*} \mathfrak{F}^t, [x] \vDash_{v'} \varphi \ \mbox{ iff } \ \mathfrak{F}, x \vDash_v \varphi^t. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^t, [x] \vDash_{v'} \varphi \ \mbox{ iff } \ \mathfrak{F}, x \vDash_v \varphi^t. \end{align*} $$
-
2. For each valuation
 $v$
on a
$v$
on a
 ${\sf TS4}$
-frame
${\sf TS4}$
-frame
 $\mathfrak {F}$
there is a valuation
$\mathfrak {F}$
there is a valuation
 $v'$
on
$v'$
on
 $\mathfrak {F}^\natural $
such that for each
$\mathfrak {F}^\natural $
such that for each
 $x \in \mathfrak {F}$
and
$x \in \mathfrak {F}$
and
 $\mathcal {L}_{\forall \exists }$
-formula
$\mathcal {L}_{\forall \exists }$
-formula
 $\varphi $
, we have
$\varphi $
, we have  $$ \begin{align*} \mathfrak{F^\natural}, [x] \vDash_{v'} \varphi \ \mbox{ iff } \ \mathfrak{F},x \vDash_{v} \varphi^\natural. \end{align*} $$
$$ \begin{align*} \mathfrak{F^\natural}, [x] \vDash_{v'} \varphi \ \mbox{ iff } \ \mathfrak{F},x \vDash_{v} \varphi^\natural. \end{align*} $$
-
3. Each valuation
 $v$
on an
$v$
on an
 ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
 $\mathfrak {F}$
is also a valuation on
$\mathfrak {F}$
is also a valuation on
 $\mathfrak {F}^\dagger $
and for each
$\mathfrak {F}^\dagger $
and for each
 $x \in \mathfrak {F}$
and
$x \in \mathfrak {F}$
and
 $\mathcal {ML}$
-formula
$\mathcal {ML}$
-formula
 $\varphi $
, we have
$\varphi $
, we have  $$ \begin{align*} \mathfrak{F^\dagger}, x \vDash_v \varphi \ \mbox{ iff } \ \mathfrak{F},x \vDash_v \varphi^\dagger. \end{align*} $$
$$ \begin{align*} \mathfrak{F^\dagger}, x \vDash_v \varphi \ \mbox{ iff } \ \mathfrak{F},x \vDash_v \varphi^\dagger. \end{align*} $$
-
4. Each valuation
 $v$
on an
$v$
on an
 ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
 $\mathfrak {F}$
is also a valuation on
$\mathfrak {F}$
is also a valuation on
 $\mathfrak {F}$
as an
$\mathfrak {F}$
as an
 ${\sf MS4}$
-frame and for each
${\sf MS4}$
-frame and for each
 $x \in \mathfrak {F}$
and
$x \in \mathfrak {F}$
and
 $\mathcal L_{\Box \forall }$
-formula
$\mathcal L_{\Box \forall }$
-formula
 $\varphi $
, we have
$\varphi $
, we have  $$ \begin{align*} \mathfrak{F}, x \vDash_v \varphi \ \mbox{ iff } \ \mathfrak{F},x \vDash_v \varphi^\#. \end{align*} $$
$$ \begin{align*} \mathfrak{F}, x \vDash_v \varphi \ \mbox{ iff } \ \mathfrak{F},x \vDash_v \varphi^\#. \end{align*} $$
Proof. (1). Define
![]() $v'$
on
$v'$
on
![]() $\mathfrak {F}^t$
by
$\mathfrak {F}^t$
by
![]() $v'(p)=\{ [x] \in X' \mid R[x] \subseteq v(p)\}$
. It is easy to see that
$v'(p)=\{ [x] \in X' \mid R[x] \subseteq v(p)\}$
. It is easy to see that
![]() $v'$
is well defined. We show that
$v'$
is well defined. We show that
![]() $\mathfrak {F}^t, [x] \vDash _{v'} \varphi $
iff
$\mathfrak {F}^t, [x] \vDash _{v'} \varphi $
iff
![]() $\mathfrak {F},x \vDash _v \varphi ^t$
by induction on the complexity of
$\mathfrak {F},x \vDash _v \varphi ^t$
by induction on the complexity of
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $v'(p)= \{ [x] \mid \mathfrak {F},x \vDash _v \Box p \}$
, the claim is obvious when
$v'(p)= \{ [x] \mid \mathfrak {F},x \vDash _v \Box p \}$
, the claim is obvious when
![]() $\varphi $
is a propositional letter. We prove the claim for
$\varphi $
is a propositional letter. We prove the claim for
![]() $\varphi $
of the form
$\varphi $
of the form
![]() $\forall \psi $
and
$\forall \psi $
and
![]() $\exists \psi $
since the other cases are well known (see, e.g., [Reference Chagrov and Zakharyaschev9, Lemma 3.81]). Suppose
$\exists \psi $
since the other cases are well known (see, e.g., [Reference Chagrov and Zakharyaschev9, Lemma 3.81]). Suppose
![]() $\varphi =\forall \psi $
. By the definition of
$\varphi =\forall \psi $
. By the definition of
![]() $Q'$
and induction hypothesis, we have
$Q'$
and induction hypothesis, we have
 $$ \begin{align*} \mathfrak{F}^t, [x] \vDash_{v'} \forall \psi &\mbox{ iff } (\forall [y] \in X')([x]Q'[y] \, \Rightarrow \, \mathfrak{F}^t, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } (\forall y \in X)(xQ_Ey \, \Rightarrow \, \mathfrak{F}^t, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } (\forall y \in X)(xQ_Ey \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^t). \end{align*} $$
$$ \begin{align*} \mathfrak{F}^t, [x] \vDash_{v'} \forall \psi &\mbox{ iff } (\forall [y] \in X')([x]Q'[y] \, \Rightarrow \, \mathfrak{F}^t, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } (\forall y \in X)(xQ_Ey \, \Rightarrow \, \mathfrak{F}^t, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } (\forall y \in X)(xQ_Ey \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^t). \end{align*} $$
On the other hand,
 $$ \begin{align*} \mathfrak{F}, x \vDash_v (\forall \psi)^t &\mbox{ iff } \mathfrak{F}, x \vDash_v \Box \forall \psi^t\\ &\mbox{ iff } (\forall z \in X)(xRz \, \Rightarrow \, (\forall y \in X)(zEy \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^t))\\ &\mbox{ iff } (\forall y \in X)(xQ_Ey \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^t). \end{align*} $$
$$ \begin{align*} \mathfrak{F}, x \vDash_v (\forall \psi)^t &\mbox{ iff } \mathfrak{F}, x \vDash_v \Box \forall \psi^t\\ &\mbox{ iff } (\forall z \in X)(xRz \, \Rightarrow \, (\forall y \in X)(zEy \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^t))\\ &\mbox{ iff } (\forall y \in X)(xQ_Ey \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^t). \end{align*} $$
Thus,
![]() $\mathfrak {F}^t, [x] \vDash _{v'} \forall \psi $
iff
$\mathfrak {F}^t, [x] \vDash _{v'} \forall \psi $
iff
![]() $\mathfrak {F}, x \vDash _v (\forall \psi )^t$
.
$\mathfrak {F}, x \vDash _v (\forall \psi )^t$
.
Suppose
![]() $\varphi =\exists \psi $
. As noted in Remark 3.3,
$\varphi =\exists \psi $
. As noted in Remark 3.3,
![]() $Q'$
and
$Q'$
and
![]() $E_{Q'}$
coincide on
$E_{Q'}$
coincide on
![]() $R'$
-upsets, and it is straightforward to see by induction that the set
$R'$
-upsets, and it is straightforward to see by induction that the set
![]() $\{ [y] \mid \mathfrak {F}^t, [y] \vDash _{v'} \psi \}$
is an
$\{ [y] \mid \mathfrak {F}^t, [y] \vDash _{v'} \psi \}$
is an
![]() $R'$
-upset. Therefore, by the induction hypothesis,
$R'$
-upset. Therefore, by the induction hypothesis,
 $$ \begin{align*} \mathfrak{F}^t, [x] \vDash_{v'} \exists \psi &\mbox{ iff } (\exists [y] \in X')([x]E_{Q'}[y] \; \& \; \mathfrak{F}^t, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } [x] \in E_{Q'}[\{ [y] \mid \mathfrak{F}^t, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } [x] \in Q'[\{ [y] \mid \mathfrak{F}^t, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } x \in Q_E[\{ y \mid \mathfrak{F}^t, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } x \in Q_E[\{ y \mid \mathfrak{F}, y \vDash_v \psi^t \}]. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^t, [x] \vDash_{v'} \exists \psi &\mbox{ iff } (\exists [y] \in X')([x]E_{Q'}[y] \; \& \; \mathfrak{F}^t, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } [x] \in E_{Q'}[\{ [y] \mid \mathfrak{F}^t, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } [x] \in Q'[\{ [y] \mid \mathfrak{F}^t, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } x \in Q_E[\{ y \mid \mathfrak{F}^t, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } x \in Q_E[\{ y \mid \mathfrak{F}, y \vDash_v \psi^t \}]. \end{align*} $$
On the other hand, since
![]() $\{ y \mid \mathfrak {F}, y \vDash _v \psi ^t \}$
is an R-upset (see Lemma 4.9), and E and
$\{ y \mid \mathfrak {F}, y \vDash _v \psi ^t \}$
is an R-upset (see Lemma 4.9), and E and
![]() $Q_E$
coincide on R-upsets, we have
$Q_E$
coincide on R-upsets, we have
 $$ \begin{align*} \mathfrak{F}, x \vDash_v (\exists \psi)^t &\mbox{ iff } \mathfrak{F}, x \vDash_v \exists \psi^t \\ &\mbox{ iff } (\exists y \in X)(xEy \; \& \; \mathfrak{F}, y \vDash_v \psi^t)\\ &\mbox{ iff } x \in E[\{ y \mid \mathfrak{F}, y \vDash_v \psi^t \}]\\ &\mbox{ iff } x \in Q_E[\{ y \mid \mathfrak{F}, y \vDash_v \psi^t \}]. \end{align*} $$
$$ \begin{align*} \mathfrak{F}, x \vDash_v (\exists \psi)^t &\mbox{ iff } \mathfrak{F}, x \vDash_v \exists \psi^t \\ &\mbox{ iff } (\exists y \in X)(xEy \; \& \; \mathfrak{F}, y \vDash_v \psi^t)\\ &\mbox{ iff } x \in E[\{ y \mid \mathfrak{F}, y \vDash_v \psi^t \}]\\ &\mbox{ iff } x \in Q_E[\{ y \mid \mathfrak{F}, y \vDash_v \psi^t \}]. \end{align*} $$
Thus,
![]() $\mathfrak {F}^t, [x] \vDash _{v'} \exists \psi $
iff
$\mathfrak {F}^t, [x] \vDash _{v'} \exists \psi $
iff
![]() $\mathfrak {F}, x \vDash _v (\exists \psi )^t$
.
$\mathfrak {F}, x \vDash _v (\exists \psi )^t$
.
(2). As in (1) we define
![]() $v'$
by
$v'$
by
![]() $v'(p)=\{ [x] \in X' \mid R[x] \subseteq v(p)\}$
. We show that
$v'(p)=\{ [x] \in X' \mid R[x] \subseteq v(p)\}$
. We show that
![]() $\mathfrak {F^\natural }, [x] \vDash _{v'} \varphi $
iff
$\mathfrak {F^\natural }, [x] \vDash _{v'} \varphi $
iff
![]() $\mathfrak {F},x \vDash _{v} \varphi ^\natural $
by induction on the complexity of
$\mathfrak {F},x \vDash _{v} \varphi ^\natural $
by induction on the complexity of
![]() $\varphi $
. It is sufficient to only consider the cases when
$\varphi $
. It is sufficient to only consider the cases when
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\forall \psi $
or
$\forall \psi $
or
![]() $\exists \psi $
. Suppose
$\exists \psi $
. Suppose
![]() $\varphi =\forall \psi $
. Then by the definition of
$\varphi =\forall \psi $
. Then by the definition of
![]() $Q'$
and induction hypothesis,
$Q'$
and induction hypothesis,
 $$ \begin{align*} \mathfrak{F}^\natural, [x] \vDash_{v'} \forall \psi &\mbox{ iff } (\forall [y] \in X')([x]Q'[y] \, \Rightarrow \, \mathfrak{F}^\natural, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } (\forall y \in X)(xQy \, \Rightarrow \, \mathfrak{F}^\natural, [y] \vDash_{v'} \psi) \\ &\mbox{ iff } (\forall y \in X)(xQy \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^\natural) \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v {[F]} \psi^\natural \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v (\forall \psi)^\natural. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^\natural, [x] \vDash_{v'} \forall \psi &\mbox{ iff } (\forall [y] \in X')([x]Q'[y] \, \Rightarrow \, \mathfrak{F}^\natural, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } (\forall y \in X)(xQy \, \Rightarrow \, \mathfrak{F}^\natural, [y] \vDash_{v'} \psi) \\ &\mbox{ iff } (\forall y \in X)(xQy \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^\natural) \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v {[F]} \psi^\natural \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v (\forall \psi)^\natural. \end{align*} $$
Suppose
![]() $\varphi =\exists \psi $
. As noted in Remark 3.3,
$\varphi =\exists \psi $
. As noted in Remark 3.3,
![]() $Q'$
and
$Q'$
and
![]() $E_{Q'}$
coincide on
$E_{Q'}$
coincide on
![]() $R'$
-upsets. Since the set
$R'$
-upsets. Since the set
![]() $\{ [y] \mid \mathfrak {F}^\natural , [y] \vDash _{v'} \psi \}$
is an
$\{ [y] \mid \mathfrak {F}^\natural , [y] \vDash _{v'} \psi \}$
is an
![]() $R'$
-upset, by the induction hypothesis, we have
$R'$
-upset, by the induction hypothesis, we have
 $$ \begin{align*} \mathfrak{F}^\natural, [x] \vDash_{v'} \exists \psi &\mbox{ iff } (\exists [y] \in X')([x]E_{Q'}[y] \; \& \; \mathfrak{F}^\natural, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } [x] \in E_{Q'}[\{ [y] \mid \mathfrak{F}^\natural, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } [x] \in Q'[\{ [y] \mid \mathfrak{F}^\natural, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } x \in Q[\{ y \mid \mathfrak{F}^\natural, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } x \in Q[\{ y \mid \mathfrak{F}, y \vDash_v \psi^\natural \}] \\ &\mbox{ iff } (\exists y \in X)(yQx \; \& \; \mathfrak{F}, y \vDash_v \psi^\natural) \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v {\langle P \rangle} \psi^\natural \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v (\exists \psi)^\natural. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^\natural, [x] \vDash_{v'} \exists \psi &\mbox{ iff } (\exists [y] \in X')([x]E_{Q'}[y] \; \& \; \mathfrak{F}^\natural, [y] \vDash_{v'} \psi)\\ &\mbox{ iff } [x] \in E_{Q'}[\{ [y] \mid \mathfrak{F}^\natural, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } [x] \in Q'[\{ [y] \mid \mathfrak{F}^\natural, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } x \in Q[\{ y \mid \mathfrak{F}^\natural, [y] \vDash_{v'} \psi \}]\\ &\mbox{ iff } x \in Q[\{ y \mid \mathfrak{F}, y \vDash_v \psi^\natural \}] \\ &\mbox{ iff } (\exists y \in X)(yQx \; \& \; \mathfrak{F}, y \vDash_v \psi^\natural) \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v {\langle P \rangle} \psi^\natural \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v (\exists \psi)^\natural. \end{align*} $$
(3). It is clear that if v is a valuation on
![]() $\mathfrak {F}$
, then v is also a valuation on
$\mathfrak {F}$
, then v is also a valuation on
![]() $\mathfrak {F}^\dagger $
. We show that
$\mathfrak {F}^\dagger $
. We show that
![]() $\mathfrak {F}^\dagger , x \vDash _v \varphi $
iff
$\mathfrak {F}^\dagger , x \vDash _v \varphi $
iff
![]() $\mathfrak {F},x \vDash _v \varphi ^\dagger $
by induction on the complexity of
$\mathfrak {F},x \vDash _v \varphi ^\dagger $
by induction on the complexity of
![]() $\varphi $
. The only nontrivial cases are when
$\varphi $
. The only nontrivial cases are when
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\Box \psi $
,
$\Box \psi $
,
![]() ${[F]} \psi $
, and
${[F]} \psi $
, and
![]() ${[P]} \psi $
. Suppose
${[P]} \psi $
. Suppose
![]() $\varphi =\Box \psi $
. Then, by the induction hypothesis,
$\varphi =\Box \psi $
. Then, by the induction hypothesis,
 $$ \begin{align*} \mathfrak{F}^\dagger, x \vDash_v \Box \psi &\mbox{ iff } (\forall y \in X)(xRy \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi)\\ &\mbox{ iff } (\forall y \in X)(xRy \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^\dagger) \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v \Box_F \psi^\dagger\\ &\mbox{ iff } \mathfrak{F}, x \vDash_v (\Box \psi)^\dagger. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^\dagger, x \vDash_v \Box \psi &\mbox{ iff } (\forall y \in X)(xRy \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi)\\ &\mbox{ iff } (\forall y \in X)(xRy \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^\dagger) \\ &\mbox{ iff } \mathfrak{F}, x \vDash_v \Box_F \psi^\dagger\\ &\mbox{ iff } \mathfrak{F}, x \vDash_v (\Box \psi)^\dagger. \end{align*} $$
Suppose
![]() $\varphi ={[F]} \psi $
. Then, by the induction hypothesis,
$\varphi ={[F]} \psi $
. Then, by the induction hypothesis,
 $$ \begin{align*} \mathfrak{F}^\dagger, x \vDash_v {[F]} \psi &\mbox{ iff } (\forall y \in X)(x Q_E y \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi)\\&\mbox{ iff } (\forall z \in X)(xRz \, \Rightarrow \, (\forall y \in X)(zEy \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi))\\&\mbox{ iff } (\forall z \in X)(xRz \, \Rightarrow \, (\forall y \in X)(zEy \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^\dagger)) \\&\mbox{ iff } (\forall z \in X)(xRz \, \Rightarrow \, \mathfrak{F}, z \vDash \forall \psi^\dagger)\\&\mbox{ iff } \mathfrak{F}, x \vDash_v \Box_F \forall \psi^\dagger\\&\mbox{ iff } \mathfrak{F}, x \vDash_v ({[F]} \psi)^\dagger. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^\dagger, x \vDash_v {[F]} \psi &\mbox{ iff } (\forall y \in X)(x Q_E y \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi)\\&\mbox{ iff } (\forall z \in X)(xRz \, \Rightarrow \, (\forall y \in X)(zEy \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi))\\&\mbox{ iff } (\forall z \in X)(xRz \, \Rightarrow \, (\forall y \in X)(zEy \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^\dagger)) \\&\mbox{ iff } (\forall z \in X)(xRz \, \Rightarrow \, \mathfrak{F}, z \vDash \forall \psi^\dagger)\\&\mbox{ iff } \mathfrak{F}, x \vDash_v \Box_F \forall \psi^\dagger\\&\mbox{ iff } \mathfrak{F}, x \vDash_v ({[F]} \psi)^\dagger. \end{align*} $$
Suppose
![]() $\varphi ={[P]} \psi $
. Then, by the induction hypothesis,
$\varphi ={[P]} \psi $
. Then, by the induction hypothesis,
 $$ \begin{align*} \mathfrak{F}^\dagger, x \vDash_v {[P]} \psi &\mbox{ iff } (\forall y \in X)(y Q_E x \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi)\\&\mbox{ iff } (\forall y,z \in X)(yRz \ \& \ zEx \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi)\\&\mbox{ iff } (\forall z \in X)(zEx \, \Rightarrow \, (\forall y \in X)(yRz \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi))\\&\mbox{ iff } (\forall z \in X)(zEx \, \Rightarrow \, (\forall y \in X)(yRz \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^\dagger)) \\&\mbox{ iff } (\forall z \in X)(xEz \, \Rightarrow \, \mathfrak{F}, z \vDash \Box_P \psi^\dagger)\\&\mbox{ iff } \mathfrak{F}, x \vDash_v \forall \Box_P \psi^\dagger\\&\mbox{ iff } \mathfrak{F}, x \vDash_v ({[P]} \psi)^\dagger. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^\dagger, x \vDash_v {[P]} \psi &\mbox{ iff } (\forall y \in X)(y Q_E x \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi)\\&\mbox{ iff } (\forall y,z \in X)(yRz \ \& \ zEx \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi)\\&\mbox{ iff } (\forall z \in X)(zEx \, \Rightarrow \, (\forall y \in X)(yRz \, \Rightarrow \, \mathfrak{F}^\dagger, y \vDash_v \psi))\\&\mbox{ iff } (\forall z \in X)(zEx \, \Rightarrow \, (\forall y \in X)(yRz \, \Rightarrow \, \mathfrak{F}, y \vDash_v \psi^\dagger)) \\&\mbox{ iff } (\forall z \in X)(xEz \, \Rightarrow \, \mathfrak{F}, z \vDash \Box_P \psi^\dagger)\\&\mbox{ iff } \mathfrak{F}, x \vDash_v \forall \Box_P \psi^\dagger\\&\mbox{ iff } \mathfrak{F}, x \vDash_v ({[P]} \psi)^\dagger. \end{align*} $$
(4). This is an immediate consequence of the definition of
![]() $(-)^\#$
and the relational semantics for
$(-)^\#$
and the relational semantics for
![]() ${\sf MS4}$
and
${\sf MS4}$
and
![]() ${\sf MS4.t}$
.
${\sf MS4.t}$
.
Proposition 4.11.
-
1. For each
 ${\sf MS4}$
-frame
${\sf MS4}$
-frame
 $\mathfrak {F}$
and
$\mathfrak {F}$
and
 $\mathcal {L}_{\forall \exists }$
-formula
$\mathcal {L}_{\forall \exists }$
-formula
 $\varphi $
, we have
$\varphi $
, we have  $$ \begin{align*} \mathfrak{F}^t \vDash \varphi \ \mbox{ iff } \ \mathfrak{F} \vDash \varphi^t. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^t \vDash \varphi \ \mbox{ iff } \ \mathfrak{F} \vDash \varphi^t. \end{align*} $$
-
2. For each
 ${\sf TS4}$
-frame
${\sf TS4}$
-frame
 $\mathfrak {F}$
and
$\mathfrak {F}$
and
 $\mathcal {L}_{\forall \exists }$
-formula
$\mathcal {L}_{\forall \exists }$
-formula
 $\varphi $
, we have
$\varphi $
, we have  $$ \begin{align*} \mathfrak{F}^\natural \vDash \varphi \ \mbox{ iff } \ \mathfrak{F} \vDash \varphi^\natural. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^\natural \vDash \varphi \ \mbox{ iff } \ \mathfrak{F} \vDash \varphi^\natural. \end{align*} $$
-
3. For each
 ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
 $\mathfrak {F}$
and
$\mathfrak {F}$
and
 $\mathcal {ML}$
-formula
$\mathcal {ML}$
-formula
 $\varphi $
, we have
$\varphi $
, we have  $$ \begin{align*} \mathfrak{F}^\dagger \vDash \varphi \ \mbox{ iff } \ \mathfrak{F} \vDash \varphi^\dagger. \end{align*} $$
$$ \begin{align*} \mathfrak{F}^\dagger \vDash \varphi \ \mbox{ iff } \ \mathfrak{F} \vDash \varphi^\dagger. \end{align*} $$
-
4. For each
 ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
 $\mathfrak {F}$
and
$\mathfrak {F}$
and
 $\mathcal L_{\Box \forall }$
-formula
$\mathcal L_{\Box \forall }$
-formula
 $\varphi $
, we have
$\varphi $
, we have  $$ \begin{align*} \mathfrak{F} \vDash \varphi \ \mbox{ iff } \ \mathfrak{F} \vDash \varphi^\#. \end{align*} $$
$$ \begin{align*} \mathfrak{F} \vDash \varphi \ \mbox{ iff } \ \mathfrak{F} \vDash \varphi^\#. \end{align*} $$
Proof. We only prove (2) since the proofs of (1), (3), and (4) are similar. If
![]() $\mathfrak {F} \nvDash \varphi ^\natural $
, then there is a valuation
$\mathfrak {F} \nvDash \varphi ^\natural $
, then there is a valuation
![]() $v$
on
$v$
on
![]() $\mathfrak {F}$
such that
$\mathfrak {F}$
such that
![]() $\mathfrak {F}, x \nvDash _v \varphi ^\natural $
for some
$\mathfrak {F}, x \nvDash _v \varphi ^\natural $
for some
![]() $x \in X$
. By Proposition 4.10(2),
$x \in X$
. By Proposition 4.10(2),
![]() $v'$
is a valuation on
$v'$
is a valuation on
![]() $\mathfrak {F}^\natural $
such that
$\mathfrak {F}^\natural $
such that
![]() $\mathfrak {F}^\natural , [x] \nvDash _{v'} \varphi $
. Therefore,
$\mathfrak {F}^\natural , [x] \nvDash _{v'} \varphi $
. Therefore,
![]() $\mathfrak {F}^\natural \nvDash \varphi $
. If
$\mathfrak {F}^\natural \nvDash \varphi $
. If
![]() $\mathfrak {F}^\natural \nvDash \varphi $
, then there is a valuation
$\mathfrak {F}^\natural \nvDash \varphi $
, then there is a valuation
![]() $w$
on
$w$
on
![]() $\mathfrak {F}^\natural $
and
$\mathfrak {F}^\natural $
and
![]() $[x] \in X'$
such that
$[x] \in X'$
such that
![]() $\mathfrak {F}^\natural , [x] \nvDash _w \varphi $
. Let
$\mathfrak {F}^\natural , [x] \nvDash _w \varphi $
. Let
![]() $v$
be the valuation on
$v$
be the valuation on
![]() $\mathfrak {F}$
given by
$\mathfrak {F}$
given by
![]() $v(p)=\{x \mid [x] \in w(p)\}$
. Since
$v(p)=\{x \mid [x] \in w(p)\}$
. Since
![]() $\mathfrak {F}^\natural $
is an
$\mathfrak {F}^\natural $
is an
![]() ${\sf MIPC}$
-frame,
${\sf MIPC}$
-frame,
![]() $w(p)$
is an
$w(p)$
is an
![]() $R'$
-upset of
$R'$
-upset of
![]() $\mathfrak {F}^\natural $
for each p. So
$\mathfrak {F}^\natural $
for each p. So
![]() $v(p)$
is an R-upset of
$v(p)$
is an R-upset of
![]() $\mathfrak {F}$
for each p. Therefore,
$\mathfrak {F}$
for each p. Therefore,
![]() $w=v'$
because
$w=v'$
because
Thus,
![]() $\mathfrak {F}^\natural , [x] \nvDash _{v'} \varphi $
. By Proposition 4.10(2),
$\mathfrak {F}^\natural , [x] \nvDash _{v'} \varphi $
. By Proposition 4.10(2),
![]() $\mathfrak {F}, x \nvDash _v \varphi ^\natural $
. Consequently,
$\mathfrak {F}, x \nvDash _v \varphi ^\natural $
. Consequently,
![]() $\mathfrak {F} \nvDash \varphi ^\natural $
.
$\mathfrak {F} \nvDash \varphi ^\natural $
.
In order to show that the translations are full, we also need the following result, which generalizes to our setting a well-known fact that each
![]() ${\sf IPC}$
-frame is the skeleton of an
${\sf IPC}$
-frame is the skeleton of an
![]() ${\sf S4}$
-frame.
${\sf S4}$
-frame.
Proposition 4.12.
-
1. For each
 ${\sf MIPC}$
-frame
${\sf MIPC}$
-frame
 $\mathfrak {G}$
there is an
$\mathfrak {G}$
there is an
 ${\sf MS4}$
-frame
${\sf MS4}$
-frame
 $\mathfrak {F}$
such that
$\mathfrak {F}$
such that
 $\mathfrak {G}$
is isomorphic to
$\mathfrak {G}$
is isomorphic to
 $\mathfrak {F}^t$
.
$\mathfrak {F}^t$
. -
2. Each
 ${\sf MIPC}$
-frame
${\sf MIPC}$
-frame
 $\mathfrak {G}$
is also a
$\mathfrak {G}$
is also a
 ${\sf TS4}$
-frame and
${\sf TS4}$
-frame and
 $\mathfrak {G}^\natural $
is isomorphic to
$\mathfrak {G}^\natural $
is isomorphic to
 $\mathfrak {G}$
.
$\mathfrak {G}$
. -
3. For each
 ${\sf TS4}$
-frame
${\sf TS4}$
-frame
 $\mathfrak {G}$
there is an
$\mathfrak {G}$
there is an
 ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
 $\mathfrak {F}$
such that
$\mathfrak {F}$
such that
 $\mathfrak {G}=\mathfrak {F}^\dagger $
.
$\mathfrak {G}=\mathfrak {F}^\dagger $
.
Proof. (1). Let
![]() $\mathfrak {G}=(X,R,Q)$
be an
$\mathfrak {G}=(X,R,Q)$
be an
![]() ${\sf MIPC}$
-frame. We show that
${\sf MIPC}$
-frame. We show that
![]() $\mathfrak {F}=(X,R,E_Q)$
is an
$\mathfrak {F}=(X,R,E_Q)$
is an
![]() ${\sf MS4}$
-frame. If
${\sf MS4}$
-frame. If
![]() $xE_Qy$
and
$xE_Qy$
and
![]() $yRz$
, then by definition of
$yRz$
, then by definition of
![]() $E_Q$
and Condition (O1),
$E_Q$
and Condition (O1),
![]() $xQy$
and
$xQy$
and
![]() $yQz$
. Since Q is transitive,
$yQz$
. Since Q is transitive,
![]() $xQz$
. Condition (O2) then implies that there is
$xQz$
. Condition (O2) then implies that there is
![]() $u \in X$
with
$u \in X$
with
![]() $xRu$
and
$xRu$
and
![]() $u E_Q z$
. Thus,
$u E_Q z$
. Thus,
![]() $\mathfrak F$
is an
$\mathfrak F$
is an
![]() ${\sf MS4}$
-frame. Since R is a partial order, it is an immediate consequence of Definition 4.6(1) that
${\sf MS4}$
-frame. Since R is a partial order, it is an immediate consequence of Definition 4.6(1) that
![]() $\sim $
is the identity relation. It follows from Condition (O2) that
$\sim $
is the identity relation. It follows from Condition (O2) that
![]() $Q=Q_{E_Q}$
. Hence,
$Q=Q_{E_Q}$
. Hence,
![]() $\mathfrak {G}$
is isomorphic to
$\mathfrak {G}$
is isomorphic to
![]() $\mathfrak {F}^t$
.
$\mathfrak {F}^t$
.
(2). Let
![]() $\mathfrak {G}=(X,R,Q)$
be an
$\mathfrak {G}=(X,R,Q)$
be an
![]() ${\sf MIPC}$
-frame. It is clear from the definition of
${\sf MIPC}$
-frame. It is clear from the definition of
![]() ${\sf TS4}$
-frames that
${\sf TS4}$
-frames that
![]() $\mathfrak {G}$
is also a
$\mathfrak {G}$
is also a
![]() ${\sf TS4}$
-frame. Since R is a partial order,
${\sf TS4}$
-frame. Since R is a partial order,
![]() $\sim $
is the identity relation. Therefore,
$\sim $
is the identity relation. Therefore,
![]() $\mathfrak {G}$
is isomorphic to
$\mathfrak {G}$
is isomorphic to
![]() $\mathfrak {G}^\natural $
.
$\mathfrak {G}^\natural $
.
(3). Let
![]() $\mathfrak {G}=(X,R,Q)$
be a
$\mathfrak {G}=(X,R,Q)$
be a
![]() ${\sf TS4}$
-frame. As we observed in Remark 3.17,
${\sf TS4}$
-frame. As we observed in Remark 3.17,
![]() $\mathfrak {F}=(X,R,E_Q)$
is an
$\mathfrak {F}=(X,R,E_Q)$
is an
![]() ${\sf MS4}$
-frame, and so an
${\sf MS4}$
-frame, and so an
![]() ${\sf MS4.t}$
-frame. By definition of
${\sf MS4.t}$
-frame. By definition of
![]() ${\sf TS4}$
-frames we have that
${\sf TS4}$
-frames we have that
![]() $Q=Q_{E_Q}$
, and hence
$Q=Q_{E_Q}$
, and hence
![]() $\mathfrak {G}=\mathfrak {F}^\dagger $
.
$\mathfrak {G}=\mathfrak {F}^\dagger $
.
We are ready to prove the main result of this section that the four translations are full and faithful. That the Gödel translation of
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf MS4}$
is full and faithful was first observed by Fischer-Servi [Reference Fischer-Servi14] using the translations of
${\sf MS4}$
is full and faithful was first observed by Fischer-Servi [Reference Fischer-Servi14] using the translations of
![]() ${\sf MIPC}$
and
${\sf MIPC}$
and
![]() ${\sf MS4}$
into
${\sf MS4}$
into
![]() ${\sf IQC}$
and
${\sf IQC}$
and
![]() ${\sf QS4}$
, respectively, and the predicate version of the Gödel translation. In [Reference Fischer-Servi15] she gave a different proof of this result, using that
${\sf QS4}$
, respectively, and the predicate version of the Gödel translation. In [Reference Fischer-Servi15] she gave a different proof of this result, using that
![]() ${\sf MIPC}$
has the fmp. Our proof utilizes the relational semantics and generalizes the semantic proof that the Gödel translation of
${\sf MIPC}$
has the fmp. Our proof utilizes the relational semantics and generalizes the semantic proof that the Gödel translation of
![]() ${\sf IPC}$
into
${\sf IPC}$
into
![]() ${\sf S4}$
is full and faithful (see, e.g., [Reference Chagrov and Zakharyaschev9, Sec. 3.9]).
${\sf S4}$
is full and faithful (see, e.g., [Reference Chagrov and Zakharyaschev9, Sec. 3.9]).
Theorem 4.13.
-
1. The Gödel translation
 $(-)^t$
of
$(-)^t$
of
 ${\sf MIPC}$
into
${\sf MIPC}$
into
 ${\sf MS4}$
is full and faithful; that is,
${\sf MS4}$
is full and faithful; that is,  $$ \begin{align*} {\sf MIPC} \vdash\varphi \quad \mbox{ iff } \quad {\sf MS4} \vdash \varphi^t. \end{align*} $$
$$ \begin{align*} {\sf MIPC} \vdash\varphi \quad \mbox{ iff } \quad {\sf MS4} \vdash \varphi^t. \end{align*} $$
-
2. The translation
 $(-)^\natural $
of
$(-)^\natural $
of
 ${\sf MIPC}$
into
${\sf MIPC}$
into
 ${\sf TS4}$
is full and faithful; that is,
${\sf TS4}$
is full and faithful; that is,  $$ \begin{align*} {\sf MIPC} \vdash\varphi \quad \mbox{ iff } \quad {\sf TS4} \vdash\varphi^\natural. \end{align*} $$
$$ \begin{align*} {\sf MIPC} \vdash\varphi \quad \mbox{ iff } \quad {\sf TS4} \vdash\varphi^\natural. \end{align*} $$
-
3. The translation
 $(-)^\dagger $
of
$(-)^\dagger $
of
 ${\sf TS4}$
into
${\sf TS4}$
into
 ${\sf MS4.t}$
is full and faithful; that is,
${\sf MS4.t}$
is full and faithful; that is,  $$ \begin{align*} \begin{array}{l c l} {\sf TS4} \vdash \varphi & \mbox{ iff } & {\sf MS4.t} \vdash \varphi^\dagger. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l c l} {\sf TS4} \vdash \varphi & \mbox{ iff } & {\sf MS4.t} \vdash \varphi^\dagger. \end{array} \end{align*} $$
-
4. The translation
 $(-)^\#$
of
$(-)^\#$
of
 ${\sf MS4}$
into
${\sf MS4}$
into
 ${\sf MS4.t}$
is full and faithful; that is,
${\sf MS4.t}$
is full and faithful; that is,  $$ \begin{align*} \begin{array}{l c l} {\sf MS4} \vdash \varphi & \mbox{ iff } & {\sf MS4.t} \vdash \varphi^\#. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l c l} {\sf MS4} \vdash \varphi & \mbox{ iff } & {\sf MS4.t} \vdash \varphi^\#. \end{array} \end{align*} $$
Proof. We prove (2). For faithfulness, suppose that
![]() ${\sf TS4} \nvdash \varphi ^\natural $
. By Theorem 3.18, there is a
${\sf TS4} \nvdash \varphi ^\natural $
. By Theorem 3.18, there is a
![]() ${\sf TS4}$
-frame
${\sf TS4}$
-frame
![]() $\mathfrak {F}$
such that
$\mathfrak {F}$
such that
![]() $\mathfrak {F} \nvDash \varphi ^\natural $
. By Propositions 4.8(2) and 4.11(2),
$\mathfrak {F} \nvDash \varphi ^\natural $
. By Propositions 4.8(2) and 4.11(2),
![]() $\mathfrak {F}^\natural $
is an
$\mathfrak {F}^\natural $
is an
![]() ${\sf MIPC}$
-frame and
${\sf MIPC}$
-frame and
![]() $\mathfrak {F}^\natural \nvDash \varphi $
. Thus, by Theorem 3.5,
$\mathfrak {F}^\natural \nvDash \varphi $
. Thus, by Theorem 3.5,
![]() ${\sf MIPC} \nvdash \varphi $
. For fullness, let
${\sf MIPC} \nvdash \varphi $
. For fullness, let
![]() ${\sf MIPC} \nvdash \varphi $
. Then there is an
${\sf MIPC} \nvdash \varphi $
. Then there is an
![]() ${\sf MIPC}$
-frame
${\sf MIPC}$
-frame
![]() $\mathfrak {G}$
such that
$\mathfrak {G}$
such that
![]() $\mathfrak {G} \nvDash \varphi $
. By Proposition 4.12(2), there is a
$\mathfrak {G} \nvDash \varphi $
. By Proposition 4.12(2), there is a
![]() ${\sf TS4}$
-frame
${\sf TS4}$
-frame
![]() $\mathfrak{F}$
such that
$\mathfrak{F}$
such that
![]() $\mathfrak {G}$
is isomorphic to
$\mathfrak {G}$
is isomorphic to
![]() $\mathfrak {F}^\natural $
. Therefore,
$\mathfrak {F}^\natural $
. Therefore,
![]() $\mathfrak {F}^\natural \nvDash \varphi $
. Proposition 4.11(2) implies that
$\mathfrak {F}^\natural \nvDash \varphi $
. Proposition 4.11(2) implies that
![]() $\mathfrak {F} \nvDash \varphi ^\natural $
. Thus,
$\mathfrak {F} \nvDash \varphi ^\natural $
. Thus,
![]() ${\sf TS4} \nvdash \varphi ^\natural $
.
${\sf TS4} \nvdash \varphi ^\natural $
.
The proofs of (1), (3), and (4) are obtained analogously using Theorems 3.5, 3.9, 3.18, and 3.21, and Propositions 4.8, 4.11, and 4.12.
5 Compositions of the translations
In this section we show that the translations introduced in the previous section form a commutative diagram up to logical equivalence.
We denote the composition of
![]() $(-)^\#$
and
$(-)^\#$
and
![]() $(-)^t$
by
$(-)^t$
by
![]() $(-)^{t \#}$
, and the composition of
$(-)^{t \#}$
, and the composition of
![]() $(-)^\dagger $
and
$(-)^\dagger $
and
![]() $(-)^\natural $
by
$(-)^\natural $
by
![]() $(-)^{\natural \dagger }$
. Since we proved that all these four translations are full and faithful, we also have that
$(-)^{\natural \dagger }$
. Since we proved that all these four translations are full and faithful, we also have that
![]() $(-)^{t \#}$
and
$(-)^{t \#}$
and
![]() $(-)^{\natural \dagger }$
are full and faithful translations of
$(-)^{\natural \dagger }$
are full and faithful translations of
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf MS4.t}$
. We have thus obtained the following diagram of full and faithful translations. We next show that this diagram is commutative up to logical equivalence in
${\sf MS4.t}$
. We have thus obtained the following diagram of full and faithful translations. We next show that this diagram is commutative up to logical equivalence in
![]() ${\sf MS4.t}$
.
${\sf MS4.t}$
.

Lemma 5.1. For each formula
![]() $\varphi $
of
$\varphi $
of
![]() $\mathcal L_{\forall \exists }$
, we have
$\mathcal L_{\forall \exists }$
, we have
Proof. By Lemma 4.9 and Theorem 4.13(4),
![]() ${\sf MS4.t} \vdash \varphi ^{t \#} \to \Box _F \varphi ^{t \#}$
. Therefore,
${\sf MS4.t} \vdash \varphi ^{t \#} \to \Box _F \varphi ^{t \#}$
. Therefore,
![]() ${\sf MS4.t} \vdash \Diamond _P \varphi ^{t \#} \to \Diamond _P \Box _F \varphi ^{t \#}$
. The tense axiom then gives
${\sf MS4.t} \vdash \Diamond _P \varphi ^{t \#} \to \Diamond _P \Box _F \varphi ^{t \#}$
. The tense axiom then gives
![]() ${\sf MS4.t} \vdash \Diamond _P \varphi ^{t \#} \to \varphi ^{t \#}$
. Thus,
${\sf MS4.t} \vdash \Diamond _P \varphi ^{t \#} \to \varphi ^{t \#}$
. Thus,
![]() ${\sf MS4.t} \vdash \varphi ^{t \#} \leftrightarrow \Diamond _P \varphi ^{t \#}$
.
${\sf MS4.t} \vdash \varphi ^{t \#} \leftrightarrow \Diamond _P \varphi ^{t \#}$
.
Theorem 5.2. For each
![]() $\mathcal L_{\forall \exists }$
-formula
$\mathcal L_{\forall \exists }$
-formula
![]() $\chi $
we have
$\chi $
we have
Proof. The two compositions compare as follows:
 $$ \begin{align*} &\bot^{t \#}=\bot && \bot^{\natural \dagger}=\bot \\ &p^{t \#}=\Box_F p && p^{\natural \dagger}=\Box_F p \\ &(\varphi \wedge \psi)^{t \#}= \varphi^{t \#} \wedge \psi^{t \#} \qquad && (\varphi \wedge \psi)^{\natural \dagger}= \varphi^{\natural \dagger} \wedge \psi^{\natural \dagger} \\ &(\varphi \vee \psi)^{t \#}= \varphi^{t \#} \vee \psi^{t \#} \qquad && (\varphi \vee \psi)^{\natural \dagger}= \varphi^{\natural \dagger} \vee \psi^{\natural \dagger} \\ &(\varphi \to \psi)^{t \#}= \Box_F(\neg \varphi^{t \#} \vee \psi^{t \#}) \qquad && (\varphi \to \psi)^{\natural \dagger}= \Box_F(\neg \varphi^{\natural \dagger} \vee \psi^{\natural \dagger}) \\ &(\forall \varphi)^{t \#}= \Box_F \forall \varphi^{t \#} && (\forall \varphi)^{\natural \dagger}= \Box_F \forall \varphi^{\natural \dagger} \\ &(\exists \varphi)^{t \#}= \exists \varphi^{t \#} && (\exists \varphi)^{\natural \dagger}= ({\langle P \rangle} \varphi^\natural)^\dagger= (\neg {[P]} \neg \varphi^\natural)^\dagger \\ & && \hphantom{(\exists \varphi)^{\natural \dagger}} = \neg \forall \Box_P \neg \varphi^{\natural \dagger}. \end{align*} $$
$$ \begin{align*} &\bot^{t \#}=\bot && \bot^{\natural \dagger}=\bot \\ &p^{t \#}=\Box_F p && p^{\natural \dagger}=\Box_F p \\ &(\varphi \wedge \psi)^{t \#}= \varphi^{t \#} \wedge \psi^{t \#} \qquad && (\varphi \wedge \psi)^{\natural \dagger}= \varphi^{\natural \dagger} \wedge \psi^{\natural \dagger} \\ &(\varphi \vee \psi)^{t \#}= \varphi^{t \#} \vee \psi^{t \#} \qquad && (\varphi \vee \psi)^{\natural \dagger}= \varphi^{\natural \dagger} \vee \psi^{\natural \dagger} \\ &(\varphi \to \psi)^{t \#}= \Box_F(\neg \varphi^{t \#} \vee \psi^{t \#}) \qquad && (\varphi \to \psi)^{\natural \dagger}= \Box_F(\neg \varphi^{\natural \dagger} \vee \psi^{\natural \dagger}) \\ &(\forall \varphi)^{t \#}= \Box_F \forall \varphi^{t \#} && (\forall \varphi)^{\natural \dagger}= \Box_F \forall \varphi^{\natural \dagger} \\ &(\exists \varphi)^{t \#}= \exists \varphi^{t \#} && (\exists \varphi)^{\natural \dagger}= ({\langle P \rangle} \varphi^\natural)^\dagger= (\neg {[P]} \neg \varphi^\natural)^\dagger \\ & && \hphantom{(\exists \varphi)^{\natural \dagger}} = \neg \forall \Box_P \neg \varphi^{\natural \dagger}. \end{align*} $$
Thus, they are identical except the
![]() $\exists $
-clause. Therefore, to prove that
$\exists $
-clause. Therefore, to prove that
![]() ${\sf MS4.t} \vdash \chi ^{t \#} \leftrightarrow \chi ^{\natural \dagger }$
it is sufficient to prove that
${\sf MS4.t} \vdash \chi ^{t \#} \leftrightarrow \chi ^{\natural \dagger }$
it is sufficient to prove that
![]() ${\sf MS4.t} \vdash \varphi ^{t \#} \leftrightarrow \varphi ^{\natural \dagger }$
implies
${\sf MS4.t} \vdash \varphi ^{t \#} \leftrightarrow \varphi ^{\natural \dagger }$
implies
![]() ${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \neg \forall \Box _P \neg \varphi ^{\natural \dagger }$
. Since
${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \neg \forall \Box _P \neg \varphi ^{\natural \dagger }$
. Since
![]() ${\sf MS4.t} \vdash \neg \forall \Box _P \neg \varphi ^{\natural \dagger } \leftrightarrow \exists \Diamond _P \varphi ^{\natural \dagger }$
, it is enough to prove that
${\sf MS4.t} \vdash \neg \forall \Box _P \neg \varphi ^{\natural \dagger } \leftrightarrow \exists \Diamond _P \varphi ^{\natural \dagger }$
, it is enough to prove that
![]() ${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \exists \Diamond _P \varphi ^{\natural \dagger }$
. From the assumption
${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \exists \Diamond _P \varphi ^{\natural \dagger }$
. From the assumption
![]() ${\sf MS4.t} \vdash \varphi ^{t \#} \leftrightarrow \varphi ^{\natural \dagger }$
it follows that
${\sf MS4.t} \vdash \varphi ^{t \#} \leftrightarrow \varphi ^{\natural \dagger }$
it follows that
![]() ${\sf MS4.t} \vdash \exists \Diamond _P \varphi ^{t \#} \leftrightarrow \exists \Diamond _P \varphi ^{\natural \dagger }$
. By Lemma 5.1,
${\sf MS4.t} \vdash \exists \Diamond _P \varphi ^{t \#} \leftrightarrow \exists \Diamond _P \varphi ^{\natural \dagger }$
. By Lemma 5.1,
![]() ${\sf MS4.t} \vdash \varphi ^{t \#} \leftrightarrow \Diamond _P \varphi ^{t \#}$
and hence
${\sf MS4.t} \vdash \varphi ^{t \#} \leftrightarrow \Diamond _P \varphi ^{t \#}$
and hence
![]() ${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \exists \Diamond _P \varphi ^{t \#}$
. Thus,
${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \exists \Diamond _P \varphi ^{t \#}$
. Thus,
![]() ${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \exists \Diamond _P \varphi ^{\natural \dagger }$
.
${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \exists \Diamond _P \varphi ^{\natural \dagger }$
.
As we pointed out in Remark 4.4(2), there is another natural translation of
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf MS4.t}$
.
${\sf MS4.t}$
.
Definition 5.3. Let
![]() $(-)^\flat :{\sf MIPC} \to {\sf MS4.t}$
be the translation that differs from
$(-)^\flat :{\sf MIPC} \to {\sf MS4.t}$
be the translation that differs from
![]() $(-)^{t \#}$
and
$(-)^{t \#}$
and
![]() $(-)^{\natural \dagger }$
only in the
$(-)^{\natural \dagger }$
only in the
![]() $\exists $
-clause:
$\exists $
-clause:
The translation
![]() $(-)^\flat $
provides a temporal interpretation of intuitionistic monadic quantifiers that is similar to the translation
$(-)^\flat $
provides a temporal interpretation of intuitionistic monadic quantifiers that is similar to the translation
![]() $(-)^\natural $
(see also Section 7).
$(-)^\natural $
(see also Section 7).
Theorem 5.4. For each
![]() $\mathcal L_{\forall \exists }$
-formula
$\mathcal L_{\forall \exists }$
-formula
![]() $\chi $
we have
$\chi $
we have
Consequently, the translation
![]() $(-)^\flat $
of
$(-)^\flat $
of
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf MS4.t}$
is full and faithful.
${\sf MS4.t}$
is full and faithful.
Proof. The translations
![]() $(-)^\flat $
and
$(-)^\flat $
and
![]() $(-)^{t \#}$
are identical except the
$(-)^{t \#}$
are identical except the
![]() $\exists $
-clause. Therefore, to prove that
$\exists $
-clause. Therefore, to prove that
![]() ${\sf MS4.t} \vdash \chi ^\flat \leftrightarrow \chi ^{t \#}$
it is sufficient to prove that
${\sf MS4.t} \vdash \chi ^\flat \leftrightarrow \chi ^{t \#}$
it is sufficient to prove that
![]() ${\sf MS4.t} \vdash \varphi ^\flat \leftrightarrow \varphi ^{t \#}$
implies
${\sf MS4.t} \vdash \varphi ^\flat \leftrightarrow \varphi ^{t \#}$
implies
![]() ${\sf MS4.t} \vdash \Diamond _P \exists \varphi ^\flat \leftrightarrow \exists \varphi ^{t \#}$
. By Lemma 5.1,
${\sf MS4.t} \vdash \Diamond _P \exists \varphi ^\flat \leftrightarrow \exists \varphi ^{t \#}$
. By Lemma 5.1,
![]() ${\sf MS4.t} \vdash (\exists \varphi )^{t \#} \leftrightarrow \Diamond _P (\exists \varphi )^{t \#}$
which means
${\sf MS4.t} \vdash (\exists \varphi )^{t \#} \leftrightarrow \Diamond _P (\exists \varphi )^{t \#}$
which means
![]() ${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \Diamond _P \exists \varphi ^{t \#}$
. From the assumption
${\sf MS4.t} \vdash \exists \varphi ^{t \#} \leftrightarrow \Diamond _P \exists \varphi ^{t \#}$
. From the assumption
![]() ${\sf MS4.t} \vdash \varphi ^\flat \leftrightarrow \varphi ^{t \#}$
it follows that
${\sf MS4.t} \vdash \varphi ^\flat \leftrightarrow \varphi ^{t \#}$
it follows that
![]() ${\sf MS4.t} \vdash \Diamond _P \exists \varphi ^\flat \leftrightarrow \exists \varphi ^{t \#}$
. Since
${\sf MS4.t} \vdash \Diamond _P \exists \varphi ^\flat \leftrightarrow \exists \varphi ^{t \#}$
. Since
![]() $(-)^{t \#}$
is full and faithful, we conclude that
$(-)^{t \#}$
is full and faithful, we conclude that
![]() $(-)^\flat $
is full and faithful as well.
$(-)^\flat $
is full and faithful as well.
As a result, we obtain the following diagram of full and faithful translations that is commutative up to logical equivalence in
![]() ${\sf MS4.t}$
:
${\sf MS4.t}$
:

6 Finite model property
In this section we give a uniform proof of the fmp for the four logics studied in this paper. Our strategy is to first establish the fmp for
![]() ${\sf MS4.t}$
via algebraic methods, and then use the full and faithful translations to conclude that the other three logics also have the fmp.
${\sf MS4.t}$
via algebraic methods, and then use the full and faithful translations to conclude that the other three logics also have the fmp.
The algebraic semantics for
![]() ${\sf MS4.t}$
is given by
${\sf MS4.t}$
is given by
![]() ${\sf MS4.t}$
-algebras. To define these algebras, we first recall the definition of
${\sf MS4.t}$
-algebras. To define these algebras, we first recall the definition of
![]() ${\sf S4}$
-algebras,
${\sf S4}$
-algebras,
![]() ${\sf S5}$
-algebras, and
${\sf S5}$
-algebras, and
![]() ${\sf S4.t}$
-algebras, which provide algebraic semantics for
${\sf S4.t}$
-algebras, which provide algebraic semantics for
![]() ${\sf S4}$
,
${\sf S4}$
,
![]() ${\sf S5}$
, and
${\sf S5}$
, and
![]() ${\sf S4.t}$
, respectively.
${\sf S4.t}$
, respectively.
![]() ${\sf S4}$
-algebras are known under various names. They were first introduced by McKinsey and Tarski [Reference McKinsey and Tarski22] under the name of closure algebras. Rasiowa and Sikorski [Reference Rasiowa and Sikorski27] call them topological Boolean algebras and Blok [Reference Blok6] calls them interior algebras.
${\sf S4}$
-algebras are known under various names. They were first introduced by McKinsey and Tarski [Reference McKinsey and Tarski22] under the name of closure algebras. Rasiowa and Sikorski [Reference Rasiowa and Sikorski27] call them topological Boolean algebras and Blok [Reference Blok6] calls them interior algebras.
![]() ${\sf S5}$
-algebras were first introduced by Halmos [Reference Halmos20] under the name of monadic algebras, and
${\sf S5}$
-algebras were first introduced by Halmos [Reference Halmos20] under the name of monadic algebras, and
![]() ${\sf S4.t}$
-algebras by Esakia [Reference Esakia11] under the name of
${\sf S4.t}$
-algebras by Esakia [Reference Esakia11] under the name of
![]() ${\sf S4}^2$
-algebras.
${\sf S4}^2$
-algebras.
Definition 6.1. Let B be a Boolean algebra.
-
1. A unary function
 $\Box :B\to B$
is an interior operator on B if for all
$\Box :B\to B$
is an interior operator on B if for all $$ \begin{align*} \Box(a\wedge b) = \Box a \wedge \Box b, \qquad \Box 1 =1, \qquad \Box a \leq a, \qquad \Box a \leq \Box \Box a, \end{align*} $$
$$ \begin{align*} \Box(a\wedge b) = \Box a \wedge \Box b, \qquad \Box 1 =1, \qquad \Box a \leq a, \qquad \Box a \leq \Box \Box a, \end{align*} $$
 $a,b \in B$
.
$a,b \in B$
.
-
2. An
 ${\sf S4}$
-algebra is a pair
${\sf S4}$
-algebra is a pair
 $\mathfrak {B}=(B, \Box )$
where B is a Boolean algebra and
$\mathfrak {B}=(B, \Box )$
where B is a Boolean algebra and
 $\Box $
is an interior operator on B.
$\Box $
is an interior operator on B. -
3. An
 ${\sf S5}$
-algebra is an
${\sf S5}$
-algebra is an
 ${\sf S4}$
-algebra
${\sf S4}$
-algebra
 $\mathfrak {B}=(B, \forall )$
that in addition satisfies
$\mathfrak {B}=(B, \forall )$
that in addition satisfies
 $a \leq \forall \exists a$
for all
$a \leq \forall \exists a$
for all
 $a \in B$
, where
$a \in B$
, where
 $\exists $
denotes the dual operator
$\exists $
denotes the dual operator
 $\neg \forall \neg $
.
$\neg \forall \neg $
. -
4. An
 ${\sf S4.t}$
-algebra is a triple
${\sf S4.t}$
-algebra is a triple
 $\mathfrak {B}=(B, \Box _F, \Box _P)$
where B is a Boolean algebra and
$\mathfrak {B}=(B, \Box _F, \Box _P)$
where B is a Boolean algebra and
 $\Box _F, \Box _P$
are interior operators on B such that (PF)
$\Box _F, \Box _P$
are interior operators on B such that (PF) $$ \begin{align} a \le \Box_P \Diamond_F a, \end{align} $$
(FP)for all
$$ \begin{align} a \le \Box_P \Diamond_F a, \end{align} $$
(FP)for all $$ \begin{align} a \le \Box_F \Diamond_P a, \end{align} $$
$$ \begin{align} a \le \Box_F \Diamond_P a, \end{align} $$
 $a \in B$
, where
$a \in B$
, where
 $\Diamond _F=\neg \Box _F \neg $
and
$\Diamond _F=\neg \Box _F \neg $
and
 $\Diamond _P=\neg \Box _P \neg $
.
$\Diamond _P=\neg \Box _P \neg $
.
![]() ${\sf MS4.t}$
-algebras are obtained by combining
${\sf MS4.t}$
-algebras are obtained by combining
![]() ${\sf S4.t}$
-algebras and
${\sf S4.t}$
-algebras and
![]() ${\sf S5}$
-algebras.
${\sf S5}$
-algebras.
Definition 6.2. An
![]() ${\sf MS4.t}$
-algebra is a tuple
${\sf MS4.t}$
-algebra is a tuple
![]() $\mathfrak B=(B, \Box _F, \Box _P, \forall )$
where
$\mathfrak B=(B, \Box _F, \Box _P, \forall )$
where
-
1.
 $(B, \Box _F, \Box _P)$
is an
$(B, \Box _F, \Box _P)$
is an
 ${\sf S4.t}$
-algebra,
${\sf S4.t}$
-algebra, -
2.
 $(B, \forall )$
is an
$(B, \forall )$
is an
 ${\sf S5}$
-algebra,
${\sf S5}$
-algebra, -
3.
 $\Box _F \forall a \leq \forall \Box _F a$
for each
$\Box _F \forall a \leq \forall \Box _F a$
for each
 $a\in B$
.
$a\in B$
.
Validity of
![]() $\mathcal L_{T\forall }$
-formulas in
$\mathcal L_{T\forall }$
-formulas in
![]() ${\sf MS4.t}$
-algebras is defined in the usual way (see, e.g., [Reference Chagrov and Zakharyaschev9, Reference Rasiowa and Sikorski27]). If a formula
${\sf MS4.t}$
-algebras is defined in the usual way (see, e.g., [Reference Chagrov and Zakharyaschev9, Reference Rasiowa and Sikorski27]). If a formula
![]() $\varphi $
is valid in an
$\varphi $
is valid in an
![]() ${\sf MS4.t}$
-algebra
${\sf MS4.t}$
-algebra
![]() $\mathfrak {B}$
, we write
$\mathfrak {B}$
, we write
![]() $\mathfrak B \vDash \varphi $
. The standard Lindenbaum–Tarski construction (see, e.g., [Reference Rasiowa and Sikorski27, Chap. VI]) yields the following:
$\mathfrak B \vDash \varphi $
. The standard Lindenbaum–Tarski construction (see, e.g., [Reference Rasiowa and Sikorski27, Chap. VI]) yields the following:
Theorem 6.3.
![]() ${\sf MS4.t}$
is sound and complete with respect to its algebraic semantics. Therefore,
${\sf MS4.t}$
is sound and complete with respect to its algebraic semantics. Therefore,
Definition 6.4. Let
![]() $\mathfrak B=(B, \Box _F, \Box _P, \forall )$
be an
$\mathfrak B=(B, \Box _F, \Box _P, \forall )$
be an
![]() ${\sf MS4.t}$
-algebra. We define
${\sf MS4.t}$
-algebra. We define
-
1.
 $H_F:=\{a \in B \mid \Box _F a=a\}$
to be the set of
$H_F:=\{a \in B \mid \Box _F a=a\}$
to be the set of
 $\Box _F$
-fixpoints,
$\Box _F$
-fixpoints, -
2.
 $H_P:=\{a \in B \mid \Box _P a=a\}$
to be the set of
$H_P:=\{a \in B \mid \Box _P a=a\}$
to be the set of
 $\Box _P$
-fixpoints,
$\Box _P$
-fixpoints, -
3.
 $B_0:=\{a \in B \mid \forall a=a\}$
to be the set of
$B_0:=\{a \in B \mid \forall a=a\}$
to be the set of
 $\forall $
-fixpoints.
$\forall $
-fixpoints.
Remark 6.5.
-
1. It is well known (see, e.g., [Reference Esakia13, Proposition 2.2.4]) that
 $H_F$
and
$H_F$
and
 $H_P$
with the restricted order from B are both Heyting algebras that are bounded sublattices of B. Moreover, it follows from Definition 6.1(4) that
$H_P$
with the restricted order from B are both Heyting algebras that are bounded sublattices of B. Moreover, it follows from Definition 6.1(4) that
 $H_F$
coincides with the set of
$H_F$
coincides with the set of
 $\Diamond _P$
-fixpoints and
$\Diamond _P$
-fixpoints and
 $H_P$
with the set of
$H_P$
with the set of
 $\Diamond _F$
-fixpoints. Furthermore,
$\Diamond _F$
-fixpoints. Furthermore,
 $\neg $
maps
$\neg $
maps
 $H_F$
to
$H_F$
to
 $H_P$
and vice versa. Indeed, if
$H_P$
and vice versa. Indeed, if
 $a \in H_F$
, then
$a \in H_F$
, then
 $a = \Box _F a$
. By (PF),
$a = \Box _F a$
. By (PF),
 $\Diamond _P a = \Diamond _P \Box _F a \le a$
, so
$\Diamond _P a = \Diamond _P \Box _F a \le a$
, so
 $\Diamond _P a = a$
, and hence
$\Diamond _P a = a$
, and hence
 $\Box _P \neg a =\neg \Diamond _P a= \neg a$
. Therefore,
$\Box _P \neg a =\neg \Diamond _P a= \neg a$
. Therefore,
 $\neg a \in H_P$
. Similarly, if
$\neg a \in H_P$
. Similarly, if
 $a \in H_P$
, then
$a \in H_P$
, then
 $\neg a \in H_F$
. Thus,
$\neg a \in H_F$
. Thus,
 $\neg $
is a dual isomorphism between
$\neg $
is a dual isomorphism between
 $H_F$
and
$H_F$
and
 $H_P$
.
$H_P$
. -
2. It is easy to see that
 $B_0$
is an
$B_0$
is an
 ${\sf S4}$
-subalgebra of
${\sf S4}$
-subalgebra of
 $(B, \Box _F)$
because the inequality
$(B, \Box _F)$
because the inequality
 $\Box _F \forall a \leq \forall \Box _F a$
, which corresponds to the left commutativity axiom, is equivalent to the equality
$\Box _F \forall a \leq \forall \Box _F a$
, which corresponds to the left commutativity axiom, is equivalent to the equality
 $\forall \Box _F \forall a = \Box _F \forall a$
.
$\forall \Box _F \forall a = \Box _F \forall a$
.
We now prove that
![]() ${\sf MS4.t}$
has the fmp. For this we must show that if
${\sf MS4.t}$
has the fmp. For this we must show that if
![]() ${\sf MS4.t}\not \vdash \varphi $
, then
${\sf MS4.t}\not \vdash \varphi $
, then
![]() $\varphi $
is refuted on a finite
$\varphi $
is refuted on a finite
![]() ${\sf MS4.t}$
-algebra.
${\sf MS4.t}$
-algebra.
Definition 6.6. Let
![]() $\mathfrak {B}=(B, \Box _F, \Box _P, \forall )$
be an
$\mathfrak {B}=(B, \Box _F, \Box _P, \forall )$
be an
![]() ${\sf MS4.t}$
-algebra and
${\sf MS4.t}$
-algebra and
![]() $S \subseteq B$
a finite subset. Then
$S \subseteq B$
a finite subset. Then
![]() $(B, \forall )$
is an
$(B, \forall )$
is an
![]() ${\sf S5}$
-algebra. Let
${\sf S5}$
-algebra. Let
![]() $(B', \forall ')$
be the
$(B', \forall ')$
be the
![]() ${\sf S5}$
-subalgebra of
${\sf S5}$
-subalgebra of
![]() $(B, \forall )$
generated by S. It is well known (see [Reference Bass1]) that
$(B, \forall )$
generated by S. It is well known (see [Reference Bass1]) that
![]() $(B', \forall ')$
is finite. Define
$(B', \forall ')$
is finite. Define
![]() $\Box _F'$
and
$\Box _F'$
and
![]() $\Box _P'$
on
$\Box _P'$
on
![]() $B'$
by
$B'$
by
 $$ \begin{align*} \Box_F' a &= \bigvee \{ b \in B'\cap H_F \mid b \leq a \}, \\ \Box_P' a &= \bigvee \{ b \in B'\cap H_P \mid b \leq a \}. \end{align*} $$
$$ \begin{align*} \Box_F' a &= \bigvee \{ b \in B'\cap H_F \mid b \leq a \}, \\ \Box_P' a &= \bigvee \{ b \in B'\cap H_P \mid b \leq a \}. \end{align*} $$
We denote
![]() $(B', \Box _F', \Box _P', \forall ')$
by
$(B', \Box _F', \Box _P', \forall ')$
by
![]() $\mathfrak {B}_S$
.
$\mathfrak {B}_S$
.
Lemma 6.7.
![]() $\mathfrak {B}_S$
is an
$\mathfrak {B}_S$
is an
![]() ${\sf MS4.t}$
-algebra.
${\sf MS4.t}$
-algebra.
Proof.
![]() $(B',\forall ')$
is an
$(B',\forall ')$
is an
![]() ${\sf S5}$
-algebra by definition. Since
${\sf S5}$
-algebra by definition. Since
![]() $(B, \Box _F)$
and
$(B, \Box _F)$
and
![]() $(B, \Box _P)$
are both
$(B, \Box _P)$
are both
![]() ${\sf S4}$
-algebras, a standard argument (see [Reference McKinsey and Tarski22, Lemma 4.14]) shows that
${\sf S4}$
-algebras, a standard argument (see [Reference McKinsey and Tarski22, Lemma 4.14]) shows that
![]() $(B', \Box _F')$
and
$(B', \Box _F')$
and
![]() $(B', \Box _P')$
are also
$(B', \Box _P')$
are also
![]() ${\sf S4}$
-algebras. We show that
${\sf S4}$
-algebras. We show that
![]() $(B', \Box _F', \Box _P')$
is an
$(B', \Box _F', \Box _P')$
is an
![]() ${\sf S4.t}$
-algebra. As noted in Remark 6.5(1),
${\sf S4.t}$
-algebra. As noted in Remark 6.5(1),
![]() $\neg $
is a dual isomorphism between the algebras
$\neg $
is a dual isomorphism between the algebras
![]() $H_F$
and
$H_F$
and
![]() $H_P$
of
$H_P$
of
![]() $\Box _F$
-fixpoints and
$\Box _F$
-fixpoints and
![]() $\Box _P$
-fixpoints of
$\Box _P$
-fixpoints of
![]() $\mathfrak {B}$
. Therefore,
$\mathfrak {B}$
. Therefore,
 $$ \begin{align*} \Diamond_F' a := \neg \Box_F' \neg a & = \neg \bigvee \{ b \in B'\cap H_F \mid b \leq \neg a \} \\ & = \neg \bigvee \{ b \in B'\cap H_F \mid a \leq \neg b \} \\ & = \bigwedge \{ \neg b \mid b \in B'\cap H_F, \; a \leq \neg b \} \\ & = \bigwedge \{ c \in B' \cap H_P \mid a \leq c \}. \end{align*} $$
$$ \begin{align*} \Diamond_F' a := \neg \Box_F' \neg a & = \neg \bigvee \{ b \in B'\cap H_F \mid b \leq \neg a \} \\ & = \neg \bigvee \{ b \in B'\cap H_F \mid a \leq \neg b \} \\ & = \bigwedge \{ \neg b \mid b \in B'\cap H_F, \; a \leq \neg b \} \\ & = \bigwedge \{ c \in B' \cap H_P \mid a \leq c \}. \end{align*} $$
Since this meet is finite and
![]() $\Box _P$
commutes with finite meets, we obtain
$\Box _P$
commutes with finite meets, we obtain
 $$ \begin{align*} \Box_P \Diamond_F' a & = \Box_P \left( \bigwedge \{ c \in B' \cap H_P \mid a \leq c \} \right) \\ & = \bigwedge \{ \Box_P c \mid c \in B' \cap H_P , \; a \leq c \} \\ & = \bigwedge \{ c \in B' \cap H_P \mid a \leq c \} \\ & = \Diamond_F' a. \end{align*} $$
$$ \begin{align*} \Box_P \Diamond_F' a & = \Box_P \left( \bigwedge \{ c \in B' \cap H_P \mid a \leq c \} \right) \\ & = \bigwedge \{ \Box_P c \mid c \in B' \cap H_P , \; a \leq c \} \\ & = \bigwedge \{ c \in B' \cap H_P \mid a \leq c \} \\ & = \Diamond_F' a. \end{align*} $$
Thus,
![]() $\Diamond _F' a \in B' \cap H_P $
which yields
$\Diamond _F' a \in B' \cap H_P $
which yields
Similarly, we have that
![]() $\Diamond _P' a = \bigwedge \{ c \in B' \cap H_F \mid a \leq c \}$
from which we deduce that
$\Diamond _P' a = \bigwedge \{ c \in B' \cap H_F \mid a \leq c \}$
from which we deduce that
![]() $\Box _F' \Diamond _P' a = \Diamond _P' a$
. This implies that
$\Box _F' \Diamond _P' a = \Diamond _P' a$
. This implies that
![]() $a \le \Box _P' \Diamond _F' a$
and
$a \le \Box _P' \Diamond _F' a$
and
![]() $a \le \Box _F' \Diamond _P' a$
. Consequently,
$a \le \Box _F' \Diamond _P' a$
. Consequently,
![]() $(B, \Box _F', \Box _P')$
is an
$(B, \Box _F', \Box _P')$
is an
![]() ${\sf S4.t}$
-algebra.
${\sf S4.t}$
-algebra.
It remains to show that
![]() $\Box _F' \forall ' a \le \forall ' \Box _F' a$
holds in
$\Box _F' \forall ' a \le \forall ' \Box _F' a$
holds in
![]() $\mathfrak {B}_S$
. For this it is sufficient to show that the set
$\mathfrak {B}_S$
. For this it is sufficient to show that the set
![]() $B_0':=B' \cap B_0$
of the
$B_0':=B' \cap B_0$
of the
![]() $\forall '$
-fixpoints of
$\forall '$
-fixpoints of
![]() $B'$
is an
$B'$
is an
![]() ${\sf S4}$
-subalgebra of
${\sf S4}$
-subalgebra of
![]() $(B', \Box _F')$
because then
$(B', \Box _F')$
because then
![]() $\Box _F' \forall ' a=\forall ' \Box _F' \forall ' a \le \forall ' \Box _F' a$
. Suppose that
$\Box _F' \forall ' a=\forall ' \Box _F' \forall ' a \le \forall ' \Box _F' a$
. Suppose that
![]() $d \in B_0'$
. By definition,
$d \in B_0'$
. By definition,
![]() $\Box _F' d = \bigvee \{ b \in B'\cap H_F \mid b \leq d \}$
. Let
$\Box _F' d = \bigvee \{ b \in B'\cap H_F \mid b \leq d \}$
. Let
![]() $b \in B'\cap H_F$
. It follows from Lemma 2.5 that
$b \in B'\cap H_F$
. It follows from Lemma 2.5 that
![]() $\exists b = \exists \Box _F b =\Box _F \exists \Box _F b = \Box _F \exists b$
. Therefore,
$\exists b = \exists \Box _F b =\Box _F \exists \Box _F b = \Box _F \exists b$
. Therefore,
![]() $\exists b \in B' \cap H_F$
. Moreover,
$\exists b \in B' \cap H_F$
. Moreover,
![]() $b \le \exists b$
and
$b \le \exists b$
and
![]() $b \le d$
imply
$b \le d$
imply
![]() $\exists b \le \exists d = d$
. Thus,
$\exists b \le \exists d = d$
. Thus,
![]() $\Box _F' d = \bigvee \{ \exists b \mid b \in B'\cap H_F, \; b \leq d \}$
. Since
$\Box _F' d = \bigvee \{ \exists b \mid b \in B'\cap H_F, \; b \leq d \}$
. Since
![]() $(B', \forall ')$
is an
$(B', \forall ')$
is an
![]() ${\sf S5}$
-algebra,
${\sf S5}$
-algebra,
![]() $B_0'$
is the set of
$B_0'$
is the set of
![]() $\exists '$
-fixpoints of
$\exists '$
-fixpoints of
![]() $B'$
and is closed under finite joins. Consequently,
$B'$
and is closed under finite joins. Consequently,
![]() $\Box _F' d \in B_0'$
.
$\Box _F' d \in B_0'$
.
Theorem 6.8.
![]() ${\sf MS4.t}$
has the fmp.
${\sf MS4.t}$
has the fmp.
Proof. By Theorem 6.3, it is sufficient to prove that each
![]() $\mathcal L_{T\forall }$
-formula
$\mathcal L_{T\forall }$
-formula
![]() $\varphi $
refuted on some
$\varphi $
refuted on some
![]() ${\sf MS4.t}$
-algebra is also refuted on a finite
${\sf MS4.t}$
-algebra is also refuted on a finite
![]() ${\sf MS4.t}$
-algebra. Let
${\sf MS4.t}$
-algebra. Let
![]() $t(x_1, \ldots , x_n)$
be the term in the language of
$t(x_1, \ldots , x_n)$
be the term in the language of
![]() ${\sf MS4.t}$
-algebras that corresponds to
${\sf MS4.t}$
-algebras that corresponds to
![]() $\varphi $
, and suppose there is an
$\varphi $
, and suppose there is an
![]() ${\sf MS4.t}$
-algebra
${\sf MS4.t}$
-algebra
![]() $\mathfrak {B}=(B, \Box _F, \Box _P, \forall )$
and
$\mathfrak {B}=(B, \Box _F, \Box _P, \forall )$
and
![]() $a_1, \ldots , a_n \in B$
such that
$a_1, \ldots , a_n \in B$
such that
![]() $t(a_1, \ldots , a_n) \neq 1$
in
$t(a_1, \ldots , a_n) \neq 1$
in
![]() $\mathfrak {B}$
. Let
$\mathfrak {B}$
. Let
Then S is a finite subset of B. Therefore, by Lemma 6.7,
![]() $\mathfrak {B}_S=(B', \Box _F', \Box _P', \forall )$
is a finite
$\mathfrak {B}_S=(B', \Box _F', \Box _P', \forall )$
is a finite
![]() ${\sf MS4.t}$
-algebra. It follows from the definition of
${\sf MS4.t}$
-algebra. It follows from the definition of
![]() $\Box _F'$
that, for each
$\Box _F'$
that, for each
![]() $b \in B'$
, if
$b \in B'$
, if
![]() $\Box _F b \in B'$
, then
$\Box _F b \in B'$
, then
![]() $\Box _F' b= \Box _F b$
. Similarly, if
$\Box _F' b= \Box _F b$
. Similarly, if
![]() $\Box _P b \in B'$
, then
$\Box _P b \in B'$
, then
![]() $\Box _P' b= \Box _P b$
. Thus, for each subterm
$\Box _P' b= \Box _P b$
. Thus, for each subterm
![]() $t'$
of t, the computation of
$t'$
of t, the computation of
![]() $t'$
in
$t'$
in
![]() $\mathfrak {B}_S$
is the same as that in
$\mathfrak {B}_S$
is the same as that in
![]() $\mathfrak {B}$
. Consequently,
$\mathfrak {B}$
. Consequently,
![]() $t(a_1, \ldots , a_n) \neq 1$
in
$t(a_1, \ldots , a_n) \neq 1$
in
![]() $\mathfrak {B}_S$
, and we have found a finite
$\mathfrak {B}_S$
, and we have found a finite
![]() ${\sf MS4.t}$
-algebra refuting
${\sf MS4.t}$
-algebra refuting
![]() $\varphi $
.
$\varphi $
.
We conclude this section by showing that the fmp for
![]() ${\sf TS4}$
,
${\sf TS4}$
,
![]() ${\sf MS4}$
, and
${\sf MS4}$
, and
![]() ${\sf MIPC}$
can be obtained as a consequence of Theorem 6.8 via the full and faithful translations into
${\sf MIPC}$
can be obtained as a consequence of Theorem 6.8 via the full and faithful translations into
![]() ${\sf MS4.t}$
described in Section 4. In order to do so, we state the fmp of
${\sf MS4.t}$
described in Section 4. In order to do so, we state the fmp of
![]() ${\sf MS4.t}$
in terms of
${\sf MS4.t}$
in terms of
![]() ${\sf MS4.t}$
-frames thanks to the correspondence between finite
${\sf MS4.t}$
-frames thanks to the correspondence between finite
![]() ${\sf MS4.t}$
-algebras and finite
${\sf MS4.t}$
-algebras and finite
![]() ${\sf MS4.t}$
-frames. In fact, we will obtain such a correspondence as a consequence of a representation result for
${\sf MS4.t}$
-frames. In fact, we will obtain such a correspondence as a consequence of a representation result for
![]() ${\sf MS4.t}$
-algebras.
${\sf MS4.t}$
-algebras.
Definition 6.9. Let R be a quasi-order on a set X and
![]() $A \subseteq X$
. We define
$A \subseteq X$
. We define
If
is the inverse relation of R, we have
If E is an equivalence relation on X, we use the notation
Proposition 6.10. For each
![]() ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
![]() $\mathfrak F=(X,R,E)$
we have that
$\mathfrak F=(X,R,E)$
we have that
![]() is an
is an
![]() ${\sf MS4.t}$
-algebra.
${\sf MS4.t}$
-algebra.
Proof. Since R is a quasi-order, so is
![]() , and hence
, and hence
![]() $(\wp (X),\Box _R)$
and
$(\wp (X),\Box _R)$
and
![]() are
are
![]() ${\sf S4}$
-algebras; and since E is an equivalence relation,
${\sf S4}$
-algebras; and since E is an equivalence relation,
![]() $(\wp (X),\forall _E)$
is an
$(\wp (X),\forall _E)$
is an
![]() ${\sf S5}$
-algebra (see [Reference Jónsson and Tarski21, Theorem 3.5]). In addition, the commutativity condition yields that
${\sf S5}$
-algebra (see [Reference Jónsson and Tarski21, Theorem 3.5]). In addition, the commutativity condition yields that
![]() $\Box _R \forall _E (A) \leq \forall _E \Box _R (A)$
for each
$\Box _R \forall _E (A) \leq \forall _E \Box _R (A)$
for each
![]() $A \in \wp (X)$
. A standard argument (see [Reference Jónsson and Tarski21, Theorem 3.6]) gives that
$A \in \wp (X)$
. A standard argument (see [Reference Jónsson and Tarski21, Theorem 3.6]) gives that
![]() $\Box _R$
and
$\Box _R$
and
![]() satisfy (PF) and (FP). Therefore,
satisfy (PF) and (FP). Therefore,
![]() $\mathfrak F^+$
is an
$\mathfrak F^+$
is an
![]() ${\sf MS4.t}$
-algebra.
${\sf MS4.t}$
-algebra.
Remark 6.11. If
![]() $\mathfrak B=\mathfrak F^+$
, then the elements of
$\mathfrak B=\mathfrak F^+$
, then the elements of
![]() $H_F$
and
$H_F$
and
![]() $H_P$
are, respectively, the R-upsets and R-downsets of
$H_P$
are, respectively, the R-upsets and R-downsets of
![]() $\mathfrak {F}$
, and the elements of
$\mathfrak {F}$
, and the elements of
![]() $B_0$
are the E-saturated subsets of
$B_0$
are the E-saturated subsets of
![]() $\mathfrak {F}$
(that is, unions of E-equivalence classes).
$\mathfrak {F}$
(that is, unions of E-equivalence classes).
We next prove that each
![]() ${\sf MS4.t}$
-algebra is represented as a subalgebra of
${\sf MS4.t}$
-algebra is represented as a subalgebra of
![]() $\mathfrak F^+$
for some
$\mathfrak F^+$
for some
![]() ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
![]() $\mathfrak F$
.
$\mathfrak F$
.
Definition 6.12. Let
![]() $\mathfrak B=(B, \Box _F, \Box _P, \forall )$
be an
$\mathfrak B=(B, \Box _F, \Box _P, \forall )$
be an
![]() ${\sf MS4.t}$
-algebra. The canonical frame of
${\sf MS4.t}$
-algebra. The canonical frame of
![]() $\mathfrak B$
is the frame
$\mathfrak B$
is the frame
![]() $\mathfrak B_+=(X_{\mathfrak B},R_{\mathfrak B},E_{\mathfrak B})$
where
$\mathfrak B_+=(X_{\mathfrak B},R_{\mathfrak B},E_{\mathfrak B})$
where
![]() $X_{\mathfrak B}$
is the set of ultrafilters of B,
$X_{\mathfrak B}$
is the set of ultrafilters of B,
![]() $x R_{\mathfrak B} y$
iff
$x R_{\mathfrak B} y$
iff
![]() $x\cap H_F \subseteq y$
iff
$x\cap H_F \subseteq y$
iff
![]() $y\cap H_P \subseteq x$
, and
$y\cap H_P \subseteq x$
, and
![]() $x E_{\mathfrak B} y$
iff
$x E_{\mathfrak B} y$
iff
![]() $x\cap B_0 = y\cap B_0$
.
$x\cap B_0 = y\cap B_0$
.
Lemma 6.13. If
![]() $\mathfrak B$
is an
$\mathfrak B$
is an
![]() ${\sf MS4.t}$
-algebra, then
${\sf MS4.t}$
-algebra, then
![]() $\mathfrak B_+$
is an
$\mathfrak B_+$
is an
![]() ${\sf MS4.t}$
-frame.
${\sf MS4.t}$
-frame.
Proof. Since
![]() $(B,\Box _F)$
is an
$(B,\Box _F)$
is an
![]() ${\sf S4}$
-algebra, we have that
${\sf S4}$
-algebra, we have that
![]() $R_{\mathfrak B}$
is a quasi-order (see [Reference Jónsson and Tarski21, Theorem 3.14]); and since
$R_{\mathfrak B}$
is a quasi-order (see [Reference Jónsson and Tarski21, Theorem 3.14]); and since
![]() $(B,\forall )$
is an
$(B,\forall )$
is an
![]() ${\sf S5}$
-algebra,
${\sf S5}$
-algebra,
![]() $E_{\mathfrak B}$
is an equivalence relation (see [Reference Jónsson and Tarski21, Theorem 3.18]). It remains to show that Definition 3.7(E) is satisfied. Let
$E_{\mathfrak B}$
is an equivalence relation (see [Reference Jónsson and Tarski21, Theorem 3.18]). It remains to show that Definition 3.7(E) is satisfied. Let
![]() $x,y,z \in X_{\mathfrak B}$
be such that
$x,y,z \in X_{\mathfrak B}$
be such that
![]() $x E_{\mathfrak B} y$
and
$x E_{\mathfrak B} y$
and
![]() $y R_{\mathfrak B} z$
. This means that
$y R_{\mathfrak B} z$
. This means that
![]() $x \cap B_0=y \cap B_0$
and
$x \cap B_0=y \cap B_0$
and
![]() $y \cap H_F \subseteq z$
. Let F be the filter of
$y \cap H_F \subseteq z$
. Let F be the filter of
![]() $\mathfrak B$
generated by
$\mathfrak B$
generated by
![]() $(x \cap H_F) \cup (z \cap B_0)$
. We show that F is proper. Otherwise, since
$(x \cap H_F) \cup (z \cap B_0)$
. We show that F is proper. Otherwise, since
![]() $x \cap H_F$
and
$x \cap H_F$
and
![]() $z \cap B_0$
are closed under finite meets, there are
$z \cap B_0$
are closed under finite meets, there are
![]() $a \in x \cap H_F$
and
$a \in x \cap H_F$
and
![]() $b \in z \cap B_0$
such that
$b \in z \cap B_0$
such that
![]() $a \land b =0$
. Therefore,
$a \land b =0$
. Therefore,
![]() $a \le \neg b$
. Thus,
$a \le \neg b$
. Thus,
![]() $a = \Box _F a \le \Box _F \neg b$
, so
$a = \Box _F a \le \Box _F \neg b$
, so
![]() $\Box _F \neg b \in x$
. Since
$\Box _F \neg b \in x$
. Since
![]() $B_0$
is an
$B_0$
is an
![]() ${\sf S4}$
-subalgebra of
${\sf S4}$
-subalgebra of
![]() $(B, \Box _F)$
(see Remark 6.5(2)) and
$(B, \Box _F)$
(see Remark 6.5(2)) and
![]() $b \in B_0$
, we have
$b \in B_0$
, we have
![]() $\Box _F \neg b \in B_0$
. This yields
$\Box _F \neg b \in B_0$
. This yields
![]() $\Box _F \neg b \in x \cap B_0=y \cap B_0$
, which implies
$\Box _F \neg b \in x \cap B_0=y \cap B_0$
, which implies
![]() $\Box _F \neg b \in y \cap H_F \subseteq z$
. Therefore,
$\Box _F \neg b \in y \cap H_F \subseteq z$
. Therefore,
![]() $\neg b \in z$
which contradicts
$\neg b \in z$
which contradicts
![]() $b \in z$
. Thus, F is proper, and so there is an ultrafilter u of B such that
$b \in z$
. Thus, F is proper, and so there is an ultrafilter u of B such that
![]() $F\subseteq u$
. Consequently,
$F\subseteq u$
. Consequently,
![]() $x\cap H_F\subseteq u$
and
$x\cap H_F\subseteq u$
and
![]() $z\cap B_0\subseteq u\cap B_0$
. Since
$z\cap B_0\subseteq u\cap B_0$
. Since
![]() $z \cap B_0$
and
$z \cap B_0$
and
![]() $u \cap B_0$
are both ultrafilters of
$u \cap B_0$
are both ultrafilters of
![]() $B_0$
, we conclude that
$B_0$
, we conclude that
![]() $z\cap B_0= u\cap B_0$
. Thus, there is
$z\cap B_0= u\cap B_0$
. Thus, there is
![]() $u\in X_{\mathfrak B}$
with
$u\in X_{\mathfrak B}$
with
![]() $xR_{\mathfrak B}u$
and
$xR_{\mathfrak B}u$
and
![]() $uE_{\mathfrak B}z$
.
$uE_{\mathfrak B}z$
.
Definition 6.14. Let
![]() $\mathfrak {B}$
be an
$\mathfrak {B}$
be an
![]() ${\sf MS4.t}$
-algebra. The Stone map
${\sf MS4.t}$
-algebra. The Stone map
![]() $\beta :\mathfrak B\to (\mathfrak B_+)^+$
is defined by
$\beta :\mathfrak B\to (\mathfrak B_+)^+$
is defined by
It follows from Jónsson-Tarski duality that
![]() $\beta$
is a 1-1 homomorphism of
$\beta$
is a 1-1 homomorphism of
![]() $\mathsf{MS4.t}$
-algebras, and that it is an isomorphism if
$\mathsf{MS4.t}$
-algebras, and that it is an isomorphism if
![]() $\mathfrak{B}$
is finite. Thus, we obtain the following representation theorem for
$\mathfrak{B}$
is finite. Thus, we obtain the following representation theorem for
![]() ${\sf MS4.t}$
-algebras.
${\sf MS4.t}$
-algebras.
Theorem 6.15 (Representation theorem)
Let
![]() $\mathfrak {B}$
be an
$\mathfrak {B}$
be an
![]() ${\sf MS4.t}$
-algebra.
${\sf MS4.t}$
-algebra.
-
1.
 $\mathfrak {B}$
is isomorphic to a subalgebra of
$\mathfrak {B}$
is isomorphic to a subalgebra of
 $(\mathfrak B_+)^+$
.
$(\mathfrak B_+)^+$
. -
2. When
 $\mathfrak {B}$
is finite, its embedding into
$\mathfrak {B}$
is finite, its embedding into
 $(\mathfrak B_+)^+$
is an isomorphism.
$(\mathfrak B_+)^+$
is an isomorphism.
Remark 6.16. As usual, to recover the image of the embedding of
![]() $\mathfrak {B}$
into
$\mathfrak {B}$
into
![]() $(\mathfrak B_+)^+$
we need to endow
$(\mathfrak B_+)^+$
we need to endow
![]() $\mathfrak B_+$
with a Stone topology (see, e.g., [Reference Esakia13, Definition 3.3.3]). This leads to the notion of perfect
$\mathfrak B_+$
with a Stone topology (see, e.g., [Reference Esakia13, Definition 3.3.3]). This leads to the notion of perfect
![]() ${\sf MS4.t}$
-frames and a duality between the categories of
${\sf MS4.t}$
-frames and a duality between the categories of
![]() ${\sf MS4.t}$
-algebras and perfect
${\sf MS4.t}$
-algebras and perfect
![]() ${\sf MS4.t}$
-frames.
${\sf MS4.t}$
-frames.
Thanks to the representation theorem, the fmp of
![]() ${\sf MS4.t}$
can be equivalently stated as follows: if
${\sf MS4.t}$
can be equivalently stated as follows: if
![]() $\varphi $
is not a theorem of
$\varphi $
is not a theorem of
![]() ${\sf MS4.t}$
, then it is refuted in a finite
${\sf MS4.t}$
, then it is refuted in a finite
![]() ${\sf MS4.t}$
-frame. We now obtain the fmp of
${\sf MS4.t}$
-frame. We now obtain the fmp of
![]() ${\sf TS4}$
,
${\sf TS4}$
,
![]() ${\sf MS4}$
, and
${\sf MS4}$
, and
![]() ${\sf MIPC}$
as a consequence of the fmp of
${\sf MIPC}$
as a consequence of the fmp of
![]() ${\sf MS4.t}$
.
${\sf MS4.t}$
.
Theorem 6.17.
-
1.
 ${\sf TS4}$
has the fmp.
${\sf TS4}$
has the fmp. -
2.
 ${\sf MS4}$
has the fmp.
${\sf MS4}$
has the fmp. -
3.
 ${\sf MIPC}$
has the fmp.
${\sf MIPC}$
has the fmp.
Proof. (1). Suppose that
![]() ${\sf TS4} \nvdash \varphi $
. By Theorem 4.13(3),
${\sf TS4} \nvdash \varphi $
. By Theorem 4.13(3),
![]() ${\sf MS4.t} \nvdash \varphi ^\dagger $
. Since
${\sf MS4.t} \nvdash \varphi ^\dagger $
. Since
![]() ${\sf MS4.t}$
has the fmp, there is a finite
${\sf MS4.t}$
has the fmp, there is a finite
![]() ${\sf MS4.t}$
-frame
${\sf MS4.t}$
-frame
![]() $\mathfrak {F}$
such that
$\mathfrak {F}$
such that
![]() $\mathfrak {F} \nvDash \varphi ^\dagger $
. By Proposition 4.11(3),
$\mathfrak {F} \nvDash \varphi ^\dagger $
. By Proposition 4.11(3),
![]() $\mathfrak {F}^\dagger \nvDash \varphi $
. We have thus obtained a finite
$\mathfrak {F}^\dagger \nvDash \varphi $
. We have thus obtained a finite
![]() ${\sf TS4}$
-frame
${\sf TS4}$
-frame
![]() $\mathfrak {F}^\dagger $
refuting
$\mathfrak {F}^\dagger $
refuting
![]() $\varphi $
.
$\varphi $
.
(2). Similar to the proof of (1) but uses the translation
![]() $(-)^\# : {\sf MS4} \to {\sf MS4.t}$
instead of
$(-)^\# : {\sf MS4} \to {\sf MS4.t}$
instead of
![]() $(-)^\dagger $
.
$(-)^\dagger $
.
(3). Similar to the proof of (1) but uses the composition
![]() $(-)^{t \#}: {\sf MIPC} \to {\sf MS4.t}$
instead of
$(-)^{t \#}: {\sf MIPC} \to {\sf MS4.t}$
instead of
![]() $(-)^\dagger $
. Alternatively, we can use the translation
$(-)^\dagger $
. Alternatively, we can use the translation
![]() $(-)^{\natural \dagger }$
of
$(-)^{\natural \dagger }$
of
![]() ${\sf MIPC}$
into
${\sf MIPC}$
into
![]() ${\sf MS4.t}$
.
${\sf MS4.t}$
.
Remark 6.18.
-
1. That
 ${\sf MIPC}$
has the fmp was first established by Bull [Reference Bull7] using algebraic semantics. His proof contained a gap, which was corrected independently by Fischer-Servi [Reference Fischer-Servi15] and Ono [Reference Ono23]. A semantic proof is given in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16], which is based on a technique developed by Grefe [Reference Grefe, Kracht, de Rijke, Wansing and Zakharyaschev19].
${\sf MIPC}$
has the fmp was first established by Bull [Reference Bull7] using algebraic semantics. His proof contained a gap, which was corrected independently by Fischer-Servi [Reference Fischer-Servi15] and Ono [Reference Ono23]. A semantic proof is given in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16], which is based on a technique developed by Grefe [Reference Grefe, Kracht, de Rijke, Wansing and Zakharyaschev19]. -
2. The fmp for
 ${\sf MS4}$
can be derived from the results in [Reference Gabbay and Shehtman17, Sec. 12] (see also [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16, Theorems 6.52 and 9.12]). The proof given above is more direct.
${\sf MS4}$
can be derived from the results in [Reference Gabbay and Shehtman17, Sec. 12] (see also [Reference Gabbay, Kurucz, Wolter and Zakharyaschev16, Theorems 6.52 and 9.12]). The proof given above is more direct. -
3. The proof of the fmp for
 ${\sf MS4.t}$
contains the proof of the fmp for
${\sf MS4.t}$
contains the proof of the fmp for
 ${\sf S4.t}$
, but the latter is known (see [Reference Segerberg29, pp. 313–314] or [Reference Goldblatt18, p. 44]). In fact,
${\sf S4.t}$
, but the latter is known (see [Reference Segerberg29, pp. 313–314] or [Reference Goldblatt18, p. 44]). In fact,
 ${\sf MS4.t}$
is a conservative extension of
${\sf MS4.t}$
is a conservative extension of
 ${\sf S4.t}$
.
${\sf S4.t}$
.
7 Connection with the full predicate case
In [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4] we studied a translation that is the predicate analogue of the translation
![]() $(-)^\flat: \mathsf{MIPC} \to \mathsf{MS4.t}$
. We proved that this translation embeds
$(-)^\flat: \mathsf{MIPC} \to \mathsf{MS4.t}$
. We proved that this translation embeds
![]() ${\sf IQC}$
fully and faithfully into a weakening of the tense predicate logic
${\sf IQC}$
fully and faithfully into a weakening of the tense predicate logic
![]() ${\sf QS4.t}$
. This weakening is necessary since
${\sf QS4.t}$
. This weakening is necessary since
![]() ${\sf QS4.t}$
proves the Barcan formula for both
${\sf QS4.t}$
proves the Barcan formula for both
![]() $\Box _F$
and
$\Box _F$
and
![]() $\Box _P$
, so Kripke frames of
$\Box _P$
, so Kripke frames of
![]() ${\sf QS4.t}$
have constant domains, and hence they validate the translation of the constant domain axiom
${\sf QS4.t}$
have constant domains, and hence they validate the translation of the constant domain axiom
![]() $\forall x(A\vee B)\to (A\vee \forall x B)$
, where x is not free in A. Since this is not provable in
$\forall x(A\vee B)\to (A\vee \forall x B)$
, where x is not free in A. Since this is not provable in
![]() ${\sf IQC}$
, the translation cannot be full. Instead we considered the tense predicate logic
${\sf IQC}$
, the translation cannot be full. Instead we considered the tense predicate logic
![]() ${\sf Q^\circ S4.t}$
in which the universal instantiation axiom
${\sf Q^\circ S4.t}$
in which the universal instantiation axiom
![]() $\forall x A \to A(y/x)$
is replaced by its weakened version
$\forall x A \to A(y/x)$
is replaced by its weakened version
![]() $\forall y(\forall x A \to A(y/x))$
. The main result of [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4] proves that
$\forall y(\forall x A \to A(y/x))$
. The main result of [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4] proves that
![]() ${\sf IQC}$
translates fully and faithfully into
${\sf IQC}$
translates fully and faithfully into
![]() ${\sf Q^\circ S4.t}$
(provided the translation is restricted to sentences).
${\sf Q^\circ S4.t}$
(provided the translation is restricted to sentences).
It is natural to investigate the relationship between
![]() ${\sf MS4.t}$
and predicate extensions of
${\sf MS4.t}$
and predicate extensions of
![]() ${\sf S4.t}$
. As we already pointed out in Remark 2.10,
${\sf S4.t}$
. As we already pointed out in Remark 2.10,
![]() ${\sf MS4.t}$
is not the monadic fragment of
${\sf MS4.t}$
is not the monadic fragment of
![]() ${\sf QS4.t}$
. In addition,
${\sf QS4.t}$
. In addition,
![]() ${\sf MS4.t}$
cannot be the monadic fragment of
${\sf MS4.t}$
cannot be the monadic fragment of
![]() ${\sf Q^\circ S4.t}$
either since the formula
${\sf Q^\circ S4.t}$
either since the formula
![]() $\forall x A \to A$
is not in general provable in
$\forall x A \to A$
is not in general provable in
![]() ${\sf Q^\circ S4.t}$
, whereas
${\sf Q^\circ S4.t}$
, whereas
![]() $\forall \varphi \to \varphi $
is provable in
$\forall \varphi \to \varphi $
is provable in
![]() ${\sf MS4.t}$
. On the other hand, call a formula
${\sf MS4.t}$
. On the other hand, call a formula
![]() $\varphi $
(in the language of
$\varphi $
(in the language of
![]() ${\sf MS4.t}$
) bounded if each occurrence of a propositional letter in
${\sf MS4.t}$
) bounded if each occurrence of a propositional letter in
![]() $\varphi $
is under the scope of
$\varphi $
is under the scope of
![]() $\forall $
. Bounded formulas play the same role as sentences of
$\forall $
. Bounded formulas play the same role as sentences of
![]() ${\sf Q^\circ S4.t}$
containing only one fixed variable. It is quite plausible that for a bounded formula
${\sf Q^\circ S4.t}$
containing only one fixed variable. It is quite plausible that for a bounded formula
![]() $\varphi $
we have
$\varphi $
we have
![]() ${\sf MS4.t}\vdash \varphi $
iff
${\sf MS4.t}\vdash \varphi $
iff
![]() ${\sf Q^\circ S4.t}$
proves the translation of
${\sf Q^\circ S4.t}$
proves the translation of
![]() $\varphi $
where each occurrence of a propositional letter p is replaced with the unary predicate
$\varphi $
where each occurrence of a propositional letter p is replaced with the unary predicate
![]() $P(x)$
and
$P(x)$
and
![]() $\forall $
is replaced with
$\forall $
is replaced with
![]() $\forall x$
(for a similar translation of
$\forall x$
(for a similar translation of
![]() $\sf MIPC$
and its extensions into
$\sf MIPC$
and its extensions into
![]() ${\sf IQC}$
and its extensions, see [Reference Ono24]). If true, this would yield that the monadic sentences provable in
${\sf IQC}$
and its extensions, see [Reference Ono24]). If true, this would yield that the monadic sentences provable in
![]() ${\sf Q^\circ S4.t}$
are exactly the bounded formulas
${\sf Q^\circ S4.t}$
are exactly the bounded formulas
![]() $\varphi $
provable in
$\varphi $
provable in
![]() ${\sf MS4.t}$
. It would also yield that restricting the translation
${\sf MS4.t}$
. It would also yield that restricting the translation
![]() ${\sf IQC} \to {\sf Q^\circ S4.t}$
of [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4] to the monadic setting gives the translation
${\sf IQC} \to {\sf Q^\circ S4.t}$
of [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4] to the monadic setting gives the translation
![]() $(-)^\flat :{\sf MIPC} \to {\sf MS4.t}$
for bounded formulas.
$(-)^\flat :{\sf MIPC} \to {\sf MS4.t}$
for bounded formulas.
It is natural to seek an axiomatization of the full monadic fragment of
![]() ${\sf Q^\circ S4.t}$
. Note that in this fragment
${\sf Q^\circ S4.t}$
. Note that in this fragment
![]() $\forall $
does not behave like an
$\forall $
does not behave like an
![]() ${\sf S5}$
-modality. For example,
${\sf S5}$
-modality. For example,
![]() $\forall \varphi \to \varphi $
is not in general a theorem of this fragment.
$\forall \varphi \to \varphi $
is not in general a theorem of this fragment.
Finally, the translation
![]() $(-)^\#: {\sf MS4} \to {\sf MS4.t}$
suggests a translation of
$(-)^\#: {\sf MS4} \to {\sf MS4.t}$
suggests a translation of
![]() ${\sf QS4}$
into
${\sf QS4}$
into
![]() ${\sf Q^\circ S4.t}$
which replaces each occurrence of
${\sf Q^\circ S4.t}$
which replaces each occurrence of
![]() $\Box $
with
$\Box $
with
![]() $\Box _F$
. It is easy to see that for sentences this translation is full and faithful. Composing it with the standard Gödel translation of
$\Box _F$
. It is easy to see that for sentences this translation is full and faithful. Composing it with the standard Gödel translation of
![]() ${\sf IQC}$
into
${\sf IQC}$
into
![]() ${\sf QS4}$
yields a translation
${\sf QS4}$
yields a translation
![]() ${\sf IQC} \to {\sf Q^\circ S4.t}$
which is different from the translation of [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4]. This translation restricts to the translation
${\sf IQC} \to {\sf Q^\circ S4.t}$
which is different from the translation of [Reference Bezhanishvili, Carai, Olivetti, Verbrugge, Negri and Sandu4]. This translation restricts to the translation
![]() $(-)^{t \#}: {\sf MIPC} \to {\sf MS4.t}$
for bounded formulas. Thus, the upper part of the diagram of Section 4 extends to the predicate case.
$(-)^{t \#}: {\sf MIPC} \to {\sf MS4.t}$
for bounded formulas. Thus, the upper part of the diagram of Section 4 extends to the predicate case.
On the other hand, we do not see a natural way to interpret the tense modalities of
![]() ${\sf TS4}$
as monadic quantifiers, and hence we cannot think of a natural predicate logic which could take the role of
${\sf TS4}$
as monadic quantifiers, and hence we cannot think of a natural predicate logic which could take the role of
![]() ${\sf TS4}$
in the diagram of Section 4. Thus, the lower part of the diagram does not seem to have a natural extension to the predicate case. Nevertheless, we can consider the predicate analogue of the translation
${\sf TS4}$
in the diagram of Section 4. Thus, the lower part of the diagram does not seem to have a natural extension to the predicate case. Nevertheless, we can consider the predicate analogue of the translation
![]() $(-)^{\natural \dagger }:{\sf MIPC} \to {\sf MS4.t}$
. Arguing as in Theorems 5.2 and 5.4 yields a translation of
$(-)^{\natural \dagger }:{\sf MIPC} \to {\sf MS4.t}$
. Arguing as in Theorems 5.2 and 5.4 yields a translation of
![]() ${\sf IQC}$
into
${\sf IQC}$
into
![]() ${\sf Q^\circ S4.t}$
that is full and faithful on sentences and coincides, up to logical equivalence in
${\sf Q^\circ S4.t}$
that is full and faithful on sentences and coincides, up to logical equivalence in
![]() ${\sf Q^\circ S4.t}$
, with the other two predicate translations described in this section.
${\sf Q^\circ S4.t}$
, with the other two predicate translations described in this section.
We thus obtain the following diagram in the predicate case which is commutative up to logical equivalence in
![]() ${\sf Q^\circ S4.t}$
.
${\sf Q^\circ S4.t}$
.

Acknowledgments
We would like to thank Ilya Shapirovsky for simplifying the proofs in Section 3 and for pointing out some references. We would also like to thank the referee for the comments that have improved the presentation of the paper.