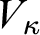Set-theoretic potentialism is the view in the philosophy of mathematics that the universe of set theory is never fully completed, but rather unfolds gradually as parts of it increasingly come into existence or become accessible to us. On this view, the outer or upper reaches of the set-theoretic universe have merely potential rather than actual existence, in the sense that one can always form additional sets from that realm, as many as desired, but the task is never completed. For example, height potentialism is the view that the universe is never fully completed with respect to height: new ordinals come into existence as the known part of the universe grows ever taller. Width potentialism holds that the universe may grow outward, as with forcing, so that already-existing sets can potentially gain new subsets in a larger universe. One commonly held view among set theorists is height potentialism combined with width actualism, whereby the universe grows only upward rather than outward, and so at any moment the part of the universe currently known to us is a rank initial segment
![]() $V_\alpha $
of the potential yet-to-be-revealed higher parts of the universe.Footnote
1
Such a perspective might even be attractive to a Platonistically inclined large-cardinal set theorist, who wants to hold that there are many large cardinals, but who also is willing at any moment to upgrade to a taller universe with even larger large cardinals than had previously been mentioned. Meanwhile, the width-potentialist height-actualist view may be attractive for those who wish to hold a potentialist account of forcing over the set-theoretic universe V. On the height-and-width-potentialist view, one views the universe as growing with respect to both height and width.Footnote
2
A set-theoretic monist, in contrast, with an ontology having only a single fully existing universe, will be an actualist with respect to both width and height. The second author has described various potentialist views in [Reference Linnebo20, Reference Linnebo and Shapiro21].
$V_\alpha $
of the potential yet-to-be-revealed higher parts of the universe.Footnote
1
Such a perspective might even be attractive to a Platonistically inclined large-cardinal set theorist, who wants to hold that there are many large cardinals, but who also is willing at any moment to upgrade to a taller universe with even larger large cardinals than had previously been mentioned. Meanwhile, the width-potentialist height-actualist view may be attractive for those who wish to hold a potentialist account of forcing over the set-theoretic universe V. On the height-and-width-potentialist view, one views the universe as growing with respect to both height and width.Footnote
2
A set-theoretic monist, in contrast, with an ontology having only a single fully existing universe, will be an actualist with respect to both width and height. The second author has described various potentialist views in [Reference Linnebo20, Reference Linnebo and Shapiro21].
Our project here is to analyze and understand more precisely the modal commitments of various set-theoretic potentialist views. We shall restrict ourselves in this analysis, however, to forms of potentialism based on classical modal logic.Footnote 3 After developing a general model-theoretic account of the semantics of potentialism in Section 1 and providing tools in Section 2 for establishing both lower and upper bounds on the modal validities for various kinds of potentialist contexts, we shall use those tools in Section 3 to settle exactly the propositional modal validities for several natural kinds of set-theoretic height and width potentialism.
The various kinds of set-theoretic potentialism validate in each case a specific corresponding modal theory, which expresses the fundamental principles or potentialist philosophy of that conception. Set-theoretic rank-potentialism and Grothendieck–Zermelo potentialism, for example, validate precisely S4.3 and exhibit what could be described as a character of linear inevitability: the central axiom (.3) can be interpreted as a linearity assertion; the finite pre-linear Kripke frames are complete for S4.3; and the worlds in these potentialist systems are linearly ordered. Forcing potentialism and countable-transitive model potentialism, in contrast, exhibit a character of directed convergence, with the validities being exactly S4.2, whose central axiom expresses the idea that any two possibilities can be brought together again in a common further possibility, but without any presumption of linearity. Some systems validate S5, whose central axiom
![]() expresses maximality or completeness, where any statement that could become permanent has already been made permanent. Meanwhile, the potentialist systems validating only S4, as in [Reference Hamkins13, Reference Hamkins and Woodin17], exhibit a far more radical branching character, one in which fundamental bifurcations in possibility are revealed as the universe unfolds in one manner as opposed to another incompatible manner.
expresses maximality or completeness, where any statement that could become permanent has already been made permanent. Meanwhile, the potentialist systems validating only S4, as in [Reference Hamkins13, Reference Hamkins and Woodin17], exhibit a far more radical branching character, one in which fundamental bifurcations in possibility are revealed as the universe unfolds in one manner as opposed to another incompatible manner.
Thus, there is a watershed between S4 on the one hand and S4.2 and above on the other. Only in the latter group of theories does the potentialist translation of Theorem 1 (and the mirroring theorem of [Reference Linnebo20]) work as it should; this breaks down when the logic is below S4.2. The first author argues in [Reference Hamkins13, sec. 7] that the convergent forms of potentialism can be seen as implicitly actualist, although the second author counters this with concerns of higher-order logic [Reference Linnebo and Shapiro21, sec. 7].
Let us also briefly mention the strong affinities between set-theoretic potentialism and set-theoretic pluralism, particularly with the various set-theoretic multiverse conceptions currently in the literature, such as those of the first author [Reference Gitman and Hamkins5, Reference Hamkins7, Reference Hamkins8, Reference Hamkins10]. Potentialists may regard themselves mainly as providing an account of truth ultimately for a single universe, gradually revealed, the limit of their potentialist system. Nevertheless, the universe fragments of their potentialist account can often naturally be taken as universes in their own right, connected by the potentialist modalities, and in this way, every potentialist system can be viewed as a multiverse. Indeed, the potentialist systems we analyze in this article—including rank potentialism, forcing potentialism, generic-multiverse potentialism, countable-transitive-model potentialism, and countable-model potentialism—each align with corresponding natural multiverse conceptions. Because of this, we take the results of this article as providing not only an analysis of the modal commitments of set-theoretic potentialism, but also an analysis of the modal commitments of various particular set-theoretic multiverse conceptions. Indeed, one might say that it is possible (ahem), in another world, for this article to have been entitled, “The modal logic of various set-theoretic multiverse conceptions.”
1 The semantics of potentialism
Although we are motivated by the case of set-theoretic potentialism, the potentialist idea itself is far more general, and can be carried out in a general model-theoretic context. For example, the potentialist account of arithmetic is deeply connected with the classical debates surrounding potential as opposed to actual infinity, and indeed, perhaps it is in those classical debates where one finds the origin of potentialism. More generally, one can provide a potentialist account of truth in the context of essentially any kind of structure in any language or theory.
Allow us therefore to lay out a general model-theoretic account of what we call the semantics of potentialism. Suppose that
![]() $\mathcal {W}$
is a collection of structures in a common signature
$\mathcal {W}$
is a collection of structures in a common signature
![]() $\mathcal {L}$
—we shall call them worlds—and that
$\mathcal {L}$
—we shall call them worlds—and that
![]() $\mathcal {W}$
is equipped with an accessibility relation, making it a Kripke model of
$\mathcal {W}$
is equipped with an accessibility relation, making it a Kripke model of
![]() $\mathcal {L}$
-structures. We say that
$\mathcal {L}$
-structures. We say that
![]() $\mathcal {W}$
is a potentialist system, if the accessibility relation is reflexive and transitive and if, furthermore, whenever one world accesses another in
$\mathcal {W}$
is a potentialist system, if the accessibility relation is reflexive and transitive and if, furthermore, whenever one world accesses another in
![]() $\mathcal {W}$
, then the domain of the first world is contained within that of the second. Thus, a potentialist system is a reflexive transitive Kripke model of
$\mathcal {W}$
, then the domain of the first world is contained within that of the second. Thus, a potentialist system is a reflexive transitive Kripke model of
![]() $\mathcal {L}$
-structures, in which the accessibility relation is inflationary in the domains of the structures, so that the individuals of a world continue to exist in any accessed new world. The main idea of potentialism is that any particular world W regards the individuals of W as the actually existing individuals or objects, and those in the larger yet-to-be-accessed worlds have merely a potential existence; but we may regard those potentially existing objects as actually existing, if we should simply move to the context and perspective of those larger worlds.
$\mathcal {L}$
-structures, in which the accessibility relation is inflationary in the domains of the structures, so that the individuals of a world continue to exist in any accessed new world. The main idea of potentialism is that any particular world W regards the individuals of W as the actually existing individuals or objects, and those in the larger yet-to-be-accessed worlds have merely a potential existence; but we may regard those potentially existing objects as actually existing, if we should simply move to the context and perspective of those larger worlds.
We shall be principally interested in the case where
![]() $\mathcal {L}$
is a first-order language and these are first-order structures, such as in the case of set-theoretic potentialism. Meanwhile, the ideas do readily generalize to nearly any kind of structure, using infinitary or higher-order logics, among others.
$\mathcal {L}$
is a first-order language and these are first-order structures, such as in the case of set-theoretic potentialism. Meanwhile, the ideas do readily generalize to nearly any kind of structure, using infinitary or higher-order logics, among others.
An important case of potentialism occurs when the accessibility relation of
![]() $\mathcal {W}$
is precisely the substructure relation on the family of structures. In particular, for any class
$\mathcal {W}$
is precisely the substructure relation on the family of structures. In particular, for any class
![]() $\mathcal {W}$
of
$\mathcal {W}$
of
![]() $\mathcal {L}$
-structures, we may place the potentialist accessibility relation on
$\mathcal {L}$
-structures, we may place the potentialist accessibility relation on
![]() $\mathcal {W}$
, by which world W accesses U if and only if W is a substructure of U, so the domain of W is contained within that of U and they agree on the atomic facts about individuals in W. In this way, any class of
$\mathcal {W}$
, by which world W accesses U if and only if W is a substructure of U, so the domain of W is contained within that of U and they agree on the atomic facts about individuals in W. In this way, any class of
![]() $\mathcal {L}$
-structures can be viewed as a potentialist system.
$\mathcal {L}$
-structures can be viewed as a potentialist system.
The semantics of potentialism for any potentialist system is defined, of course, in the usual Kripkean manner for assertions in the potentialist language
![]() $\mathcal {L}^\Diamond $
, which augments
$\mathcal {L}^\Diamond $
, which augments
![]() $\mathcal {L}$
with the modal operators
$\mathcal {L}$
with the modal operators
![]() and
and
![]() . Namely, we define recursively what it means to say that an
. Namely, we define recursively what it means to say that an
![]() $\mathcal {L}^\Diamond $
-formula
$\mathcal {L}^\Diamond $
-formula
![]() $\varphi $
is true at a world
$\varphi $
is true at a world
![]() $W\in \mathcal {W}$
with parameters
$W\in \mathcal {W}$
with parameters
![]() $a_0,\dots ,a_n\in W$
, written:
$a_0,\dots ,a_n\in W$
, written:
Specifically, an atomic assertion
![]() $\varphi (a_0,\dots ,a_n)$
is true at world W in
$\varphi (a_0,\dots ,a_n)$
is true at world W in
![]() $\mathcal {W}$
for parameters
$\mathcal {W}$
for parameters
![]() $a_0,\dots ,a_n\in W$
just in case the corresponding atomic fact is true in W in the usual Tarskian sense of
$a_0,\dots ,a_n\in W$
just in case the corresponding atomic fact is true in W in the usual Tarskian sense of
![]() $\mathcal {L}$
-satisfaction. The truth definition extends through Boolean combinations in the usual Tarskian manner, so that
$\mathcal {L}$
-satisfaction. The truth definition extends through Boolean combinations in the usual Tarskian manner, so that
![]() $W\models _{\mathcal {W}}(\varphi \wedge \psi )(a_0,\dots ,a_n)$
just in case both
$W\models _{\mathcal {W}}(\varphi \wedge \psi )(a_0,\dots ,a_n)$
just in case both
![]() $\varphi (a_0,\dots ,a_n)$
and
$\varphi (a_0,\dots ,a_n)$
and
![]() $\psi (a_0,\dots ,a_n)$
are true separately at world W in
$\psi (a_0,\dots ,a_n)$
are true separately at world W in
![]() $\mathcal {W}$
; and
$\mathcal {W}$
; and
![]() $\neg \varphi (a_0,\dots ,a_n)$
is true at world W just in case
$\neg \varphi (a_0,\dots ,a_n)$
is true at world W just in case
![]() $\varphi (a_0,\dots ,a_n)$
is not true at W. Quantifiers are handled by quantifying only over the current actual individuals, that is, over the objects of the current possible world, so that
$\varphi (a_0,\dots ,a_n)$
is not true at W. Quantifiers are handled by quantifying only over the current actual individuals, that is, over the objects of the current possible world, so that
![]() $W\models _{\mathcal {W}}\exists x\, \varphi (x,a_0,\dots ,a_n)$
just in case there is some
$W\models _{\mathcal {W}}\exists x\, \varphi (x,a_0,\dots ,a_n)$
just in case there is some
![]() $a\in W$
for which
$a\in W$
for which
![]() $W\models _{\mathcal {W}}\varphi (a,a_0,\dots ,a_n)$
. The modal semantics are determined by the potentialist accessibility relation, so that
$W\models _{\mathcal {W}}\varphi (a,a_0,\dots ,a_n)$
. The modal semantics are determined by the potentialist accessibility relation, so that
![]() if and only if W can access some world
if and only if W can access some world
![]() $U\in \mathcal {W}$
for which
$U\in \mathcal {W}$
for which
![]() $U\models _{\mathcal {W}}\varphi (a_0,\dots ,a_n)$
. Similarly,
$U\models _{\mathcal {W}}\varphi (a_0,\dots ,a_n)$
. Similarly,
![]() is true at world W just in case
is true at world W just in case
![]() $\varphi (a_0,\dots ,a_n)$
is true at all such accessed worlds U in
$\varphi (a_0,\dots ,a_n)$
is true at all such accessed worlds U in
![]() $\mathcal {W}$
. Notice that since the domains of the possible worlds are inflationary along the accessibility relation, there is no need to worry about parameters ceasing to exist in connection with the clauses just mentioned for the modal operators; thus, we avoid what can otherwise often be a troublesome matter for modal semantics. In this way, any collection
$\mathcal {W}$
. Notice that since the domains of the possible worlds are inflationary along the accessibility relation, there is no need to worry about parameters ceasing to exist in connection with the clauses just mentioned for the modal operators; thus, we avoid what can otherwise often be a troublesome matter for modal semantics. In this way, any collection
![]() $\mathcal {W}$
of
$\mathcal {W}$
of
![]() $\mathcal {L}$
-structures in the same language determines a corresponding potentialist semantics in the modal-equipped language
$\mathcal {L}$
-structures in the same language determines a corresponding potentialist semantics in the modal-equipped language
![]() $\mathcal {L}^\Diamond $
using the potentialist accessibility relation.
$\mathcal {L}^\Diamond $
using the potentialist accessibility relation.
For sufficiently coherent collections of structures
![]() $\mathcal {W}$
, the potentialist approach to truth can interact in a meaningful way with the usual Tarskian account of truth in a kind of limit structure. Namely, we define that a potentialist system
$\mathcal {W}$
, the potentialist approach to truth can interact in a meaningful way with the usual Tarskian account of truth in a kind of limit structure. Namely, we define that a potentialist system
![]() $\mathcal {W}$
of
$\mathcal {W}$
of
![]() $\mathcal {L}$
-structures provides a potentialist account of a particular
$\mathcal {L}$
-structures provides a potentialist account of a particular
![]() $\mathcal {L}$
-structure M, if every world W in
$\mathcal {L}$
-structure M, if every world W in
![]() $\mathcal {W}$
is a substructure of M and furthermore, for every such W and every individual
$\mathcal {W}$
is a substructure of M and furthermore, for every such W and every individual
![]() $a\in M$
, there is a world
$a\in M$
, there is a world
![]() $U\in \mathcal {W}$
accessed by W with
$U\in \mathcal {W}$
accessed by W with
![]() $a\in U$
. In other words, any world W in
$a\in U$
. In other words, any world W in
![]() $\mathcal {W}$
can be extended so as to accommodate any given individual of M. This can be seen as a weak form of directedness.Footnote
4
We shall also say in this case that
$\mathcal {W}$
can be extended so as to accommodate any given individual of M. This can be seen as a weak form of directedness.Footnote
4
We shall also say in this case that
![]() $\mathcal {W}$
converges to M or that M is the limit of
$\mathcal {W}$
converges to M or that M is the limit of
![]() $\mathcal {W}$
. When
$\mathcal {W}$
. When
![]() $\mathcal {W}$
has a limit structure M, the worlds of
$\mathcal {W}$
has a limit structure M, the worlds of
![]() $\mathcal {W}$
must all agree with M on the atomic truths and therefore also with each other. Since any given world in
$\mathcal {W}$
must all agree with M on the atomic truths and therefore also with each other. Since any given world in
![]() $\mathcal {W}$
can be enlarged so as to encompass any given individual of M, it follows that the domain of M is the union of the domains of the worlds in
$\mathcal {W}$
can be enlarged so as to encompass any given individual of M, it follows that the domain of M is the union of the domains of the worlds in
![]() $\mathcal {W}$
. So the limit structure M is completely determined by the collection of structures
$\mathcal {W}$
. So the limit structure M is completely determined by the collection of structures
![]() $\mathcal {W}$
providing the potentialist account of it. Clearly, a given structure might have many different potentialist accounts.
$\mathcal {W}$
providing the potentialist account of it. Clearly, a given structure might have many different potentialist accounts.
Without referring directly to any limit structure, we say that a collection
![]() $\mathcal {W}$
of
$\mathcal {W}$
of
![]() $\mathcal {L}$
-structures is coherent, if the structures in
$\mathcal {L}$
-structures is coherent, if the structures in
![]() $\mathcal {W}$
agree on atomic truth and every structure in
$\mathcal {W}$
agree on atomic truth and every structure in
![]() $\mathcal {W}$
can be extended in
$\mathcal {W}$
can be extended in
![]() $\mathcal {W}$
so as to accommodate any individual arising in any of the other structures. This is equivalent, of course, to saying that
$\mathcal {W}$
so as to accommodate any individual arising in any of the other structures. This is equivalent, of course, to saying that
![]() $\mathcal {W}$
converges to a limit structure M, which is simply the union of the structures of
$\mathcal {W}$
converges to a limit structure M, which is simply the union of the structures of
![]() $\mathcal {W}$
. For example, in the case of potential infinity, a coherent collection of
$\mathcal {W}$
. For example, in the case of potential infinity, a coherent collection of
![]() $\mathcal {L}$
-structures can be regarded as a collection of finite approximations of some potentially infinite limit structure. More generally, a coherent collection of structures can be regard as an approximation of some incompletable limit structure in terms of its completable parts.
$\mathcal {L}$
-structures can be regarded as a collection of finite approximations of some potentially infinite limit structure. More generally, a coherent collection of structures can be regard as an approximation of some incompletable limit structure in terms of its completable parts.
For any assertion
![]() $\psi $
in the underlying language
$\psi $
in the underlying language
![]() $\mathcal {L}$
, consider the potentialist translation
$\mathcal {L}$
, consider the potentialist translation
![]() $\psi ^\Diamond $
, which will be the assertion in the language
$\psi ^\Diamond $
, which will be the assertion in the language
![]() $\mathcal {L}^\Diamond $
arising when one replaces every instance of
$\mathcal {L}^\Diamond $
arising when one replaces every instance of
![]() $\exists x$
with
$\exists x$
with
![]() and every instance of
and every instance of
![]() $\forall x$
with
$\forall x$
with
![]() . It is through this translation, in light of Theorem 1, that the potentialist can refer to truth in the limit structure, without having that structure explicitly as a part of his or her ontology [Reference Linnebo20].
. It is through this translation, in light of Theorem 1, that the potentialist can refer to truth in the limit structure, without having that structure explicitly as a part of his or her ontology [Reference Linnebo20].
Theorem 1. If
![]() $\mathcal {W}$
provides a potentialist account of a structure M, then truth in M is equivalent to potentialist truth at the worlds of
$\mathcal {W}$
provides a potentialist account of a structure M, then truth in M is equivalent to potentialist truth at the worlds of
![]() $\mathcal {W}$
. Namely, for any
$\mathcal {W}$
. Namely, for any
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\psi $
and any
$\psi $
and any
![]() $a_0,\dots ,a_n\in M$
, we have:
$a_0,\dots ,a_n\in M$
, we have:
for any
![]() $W\in \mathcal {W}$
in which the individuals
$W\in \mathcal {W}$
in which the individuals
![]() $a_0,\dots ,a_n$
exist.
$a_0,\dots ,a_n$
exist.
Proof. This is proved by a simple induction on formulas
![]() $\psi $
in the language of
$\psi $
in the language of
![]() $\mathcal {L}$
. The claim is immediate for atomic assertions, since every
$\mathcal {L}$
. The claim is immediate for atomic assertions, since every
![]() $W\in \mathcal {W}$
is a submodel of M, and the case of Boolean connectives is also easy. For quantifiers, the point is that asserting
$W\in \mathcal {W}$
is a submodel of M, and the case of Boolean connectives is also easy. For quantifiers, the point is that asserting
![]() $\exists x$
from the perspective of M is exactly asserting
$\exists x$
from the perspective of M is exactly asserting
![]() from the perspective of W in the potentialist semantics, because the witness x might not yet exist in W, but if it does exist in M then it will exist in some U extending W by the definition of what it means for
from the perspective of W in the potentialist semantics, because the witness x might not yet exist in W, but if it does exist in M then it will exist in some U extending W by the definition of what it means for
![]() $\mathcal {W}$
to provide a potentialist account of M. Similarly, asserting
$\mathcal {W}$
to provide a potentialist account of M. Similarly, asserting
![]() $\forall x$
in M amounts to
$\forall x$
in M amounts to
![]() in W with respect to the potentialist semantics.
in W with respect to the potentialist semantics.
Let us now discuss what it means for a modal assertion
![]() $\varphi (p_0,\dots ,p_n)$
to be valid with respect to a potentialist system
$\varphi (p_0,\dots ,p_n)$
to be valid with respect to a potentialist system
![]() $\mathcal {W}$
. In a general case, this concept applies to assertions
$\mathcal {W}$
. In a general case, this concept applies to assertions
![]() $\varphi (p_0,\dots ,p_n)$
in the language
$\varphi (p_0,\dots ,p_n)$
in the language
![]() $\mathcal {L}^\Diamond (p_0,p_1,\dots )$
, which expands
$\mathcal {L}^\Diamond (p_0,p_1,\dots )$
, which expands
![]() $\mathcal {L}^\Diamond $
with propositional variables
$\mathcal {L}^\Diamond $
with propositional variables
![]() $p_0,p_1,\dots $
, treated syntactically as atomic formulas. A central case for us, however, will be the validities
$p_0,p_1,\dots $
, treated syntactically as atomic formulas. A central case for us, however, will be the validities
![]() $\varphi (p_0,\dots ,p_n)$
that are expressible in the more restricted language of propositional modal logic, using only the propositional variables, logical connectives and modal operators (but no quantifiers, relations or terms). For example, we shall consider the well-known modal theories S4, S4.2, S4.3 and S5, which are expressed in propositional modal logic.
$\varphi (p_0,\dots ,p_n)$
that are expressible in the more restricted language of propositional modal logic, using only the propositional variables, logical connectives and modal operators (but no quantifiers, relations or terms). For example, we shall consider the well-known modal theories S4, S4.2, S4.3 and S5, which are expressed in propositional modal logic.
A modal assertion
![]() $\varphi (p_0,\dots ,p_n)$
is valid at a world W in
$\varphi (p_0,\dots ,p_n)$
is valid at a world W in
![]() $\mathcal {W}$
for a certain class of assertions, if all the resulting substitution instances
$\mathcal {W}$
for a certain class of assertions, if all the resulting substitution instances
![]() $\varphi (\psi _0,\dots ,\psi _n)$
, where assertion
$\varphi (\psi _0,\dots ,\psi _n)$
, where assertion
![]() $\psi _i$
from the allowed class is substituted for the propositional variable
$\psi _i$
from the allowed class is substituted for the propositional variable
![]() $p_i$
, are true at W. For example, we shall consider cases where a modal assertion
$p_i$
, are true at W. For example, we shall consider cases where a modal assertion
![]() $\varphi (p_0,\dots ,p_n)$
is valid for sentences in the underlying language
$\varphi (p_0,\dots ,p_n)$
is valid for sentences in the underlying language
![]() $\mathcal {L}$
, or in the potentialist language
$\mathcal {L}$
, or in the potentialist language
![]() $\mathcal {L}^\Diamond $
, or in these languages with parameters allowed from W. Let us denote by
$\mathcal {L}^\Diamond $
, or in these languages with parameters allowed from W. Let us denote by
![]() $\mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L})$
the set of modal propositional validities at W in
$\mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L})$
the set of modal propositional validities at W in
![]() $\mathcal {W}$
with respect to assertions from the language
$\mathcal {W}$
with respect to assertions from the language
![]() $\mathcal {L}$
, not allowing extra parameters from W; and we shall write
$\mathcal {L}$
, not allowing extra parameters from W; and we shall write
![]() $\mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L}_W)$
for the corresponding set of validities with respect to
$\mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L}_W)$
for the corresponding set of validities with respect to
![]() $\mathcal {L}$
-assertions, where now parameters from W are allowed. Clearly, it is a more severe requirement generally for a modal formula to be valid with respect to a larger collection of assertions, and so:
$\mathcal {L}$
-assertions, where now parameters from W are allowed. Clearly, it is a more severe requirement generally for a modal formula to be valid with respect to a larger collection of assertions, and so:
In particular, allowing parameters results in possibly fewer validities:
We say that a propositional modal assertion
![]() $\varphi $
is valid in
$\varphi $
is valid in
![]() $\mathcal {W}$
for substitution instances from
$\mathcal {W}$
for substitution instances from
![]() $\mathcal {L}$
if it is valid at every world of
$\mathcal {L}$
if it is valid at every world of
![]() $\mathcal {W}$
. Let
$\mathcal {W}$
. Let
![]() $\mathord {\textrm {Val}}_{\mathcal {W}}(\mathcal {L})$
be the resulting set of validities. It can happen that the worlds of
$\mathord {\textrm {Val}}_{\mathcal {W}}(\mathcal {L})$
be the resulting set of validities. It can happen that the worlds of
![]() $\mathcal {W}$
do not all exhibit the same validities, and in this case, some individual worlds will exhibit more validities than the system does as a whole. For example, in set-theoretic rank potentialism (see Section 3.2), the modal assertions valid at all worlds are precisely those in S4.3, but individual worlds can validate S5, which goes beyond S4.3.
$\mathcal {W}$
do not all exhibit the same validities, and in this case, some individual worlds will exhibit more validities than the system does as a whole. For example, in set-theoretic rank potentialism (see Section 3.2), the modal assertions valid at all worlds are precisely those in S4.3, but individual worlds can validate S5, which goes beyond S4.3.
In the potentialist semantics, it is natural to consider the converse Barcan formula scheme
, having substitution instances
The following theorem lays out some easy potentialist validities, depending in some cases on the nature of
![]() $\mathcal {W}$
.
$\mathcal {W}$
.
Theorem 2. Suppose that
![]() $\mathcal {W}$
is any potentialist system of structures in a common language
$\mathcal {W}$
is any potentialist system of structures in a common language
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
-
(1) The modal theory S4 is valid at every world of
 $\mathcal {W}$
.
$\mathcal {W}$
. -
(2) The converse Barcan formula is valid at every world of
 $\mathcal {W}$
.
$\mathcal {W}$
. -
(3) If the accessibility relation of
 $\mathcal {W}$
is directed, then the modal theory S4.2 is valid at every world of
$\mathcal {W}$
is directed, then the modal theory S4.2 is valid at every world of
 $\mathcal {W}$
.
$\mathcal {W}$
. -
(4) If the accessibility relation of
 $\mathcal {W}$
is linearly ordered, then the modal theory S4.3 is valid at every world of
$\mathcal {W}$
is linearly ordered, then the modal theory S4.3 is valid at every world of
 $\mathcal {W}$
.
$\mathcal {W}$
.
In each case, the validities hold for all assertions in
![]() $\mathcal {L}^\Diamond $
, with parameters.
$\mathcal {L}^\Diamond $
, with parameters.
Proof. This is a standard elementary exercise in Kripke semantics, and so we leave most of the details to the reader. Statement 1 holds because the potentialist accessibility relation is reflexive and transitive; Statement 2 holds because the domains of the worlds increase monotonically with the accessibility relation; Statement 3 holds because the directedness of the accessibility relation leads immediately to the validity of the .2 axiom
![]() ; and Statement 4 holds because linearity of the accessibility relation causes the validity of the .3 axiom
; and Statement 4 holds because linearity of the accessibility relation causes the validity of the .3 axiom
![]() .
.
We should like to emphasize that Theorem 2 concerns only lower bounds on the modal validities of a potentialist system, and it is possible in general for a potentialist system
![]() $\mathcal {W}$
to exhibit more validities than would be indicated by this theorem, as we shall discuss at length for various systems later in this article.
$\mathcal {W}$
to exhibit more validities than would be indicated by this theorem, as we shall discuss at length for various systems later in this article.
2 Some tools for studying modal validities
So let us now turn to the harder question of upper bounds on the modal validities; we should like to identify useful criteria for establishing that the valid principles of potentialism for a given potentialist system
![]() $\mathcal {W}$
are contained in a certain modal theory. Using these criteria, we shall be able to determine in many cases the exact collection of modal validities for a given potentialist account. Our analysis will make use of the tools developed in [Reference Hamkins, Leibman and Löwe14–Reference Hamkins, Löwe and Lodaya16] for the case of the modal logic of forcing; the forcing modality was introduced in [Reference Hamkins6]. One of the important insights of that earlier work was that the existence of certain kinds of control statements, which are easy to work with and recognize—switches, buttons, dials and ratchets—enable one to place definite upper bounds on the modal validities of a world.
$\mathcal {W}$
are contained in a certain modal theory. Using these criteria, we shall be able to determine in many cases the exact collection of modal validities for a given potentialist account. Our analysis will make use of the tools developed in [Reference Hamkins, Leibman and Löwe14–Reference Hamkins, Löwe and Lodaya16] for the case of the modal logic of forcing; the forcing modality was introduced in [Reference Hamkins6]. One of the important insights of that earlier work was that the existence of certain kinds of control statements, which are easy to work with and recognize—switches, buttons, dials and ratchets—enable one to place definite upper bounds on the modal validities of a world.
To begin with an easy case, following [Reference Hamkins and Löwe15], we say that an assertion s is a switch in a Kripke model
![]() $\mathcal {W}$
, if both
$\mathcal {W}$
, if both
![]() and
and
![]() are true at every world. A little more generally, s is a switch at a particular world W, if
are true at every world. A little more generally, s is a switch at a particular world W, if
![]() and
and
![]() hold in all the worlds one can reach from W. Thus, a switch is an assertion that can be successively turned on and off as much as one likes, by accessing new worlds in the Kripke model. A family of switches
hold in all the worlds one can reach from W. Thus, a switch is an assertion that can be successively turned on and off as much as one likes, by accessing new worlds in the Kripke model. A family of switches
![]() $\left \langle s_0,s_1,\ldots \right \rangle $
is independent, if one can always flip the truth values of any finitely many of the switches so as to realize any desired finite pattern of truth. If a world W has independent switches, then they remain independent in any accessed world.
$\left \langle s_0,s_1,\ldots \right \rangle $
is independent, if one can always flip the truth values of any finitely many of the switches so as to realize any desired finite pattern of truth. If a world W has independent switches, then they remain independent in any accessed world.
Theorem 3. If
![]() $\mathcal {W}$
is Kripke model and world W admits arbitrarily large finite collections of independent switches, then the propositional modal assertions valid at W are contained in the modal theory S5.
$\mathcal {W}$
is Kripke model and world W admits arbitrarily large finite collections of independent switches, then the propositional modal assertions valid at W are contained in the modal theory S5.
In particular, if the switches work throughout
![]() $\mathcal {W}$
, as they do in many of our applications, then the validities of every world of
$\mathcal {W}$
, as they do in many of our applications, then the validities of every world of
![]() $\mathcal {W}$
are contained within S5.
$\mathcal {W}$
are contained within S5.
Proof. This argument follows the main idea of [Reference Hamkins, Leibman and Löwe14, theorem 10], using the labeling idea of [Reference Hamkins, Leibman and Löwe14, lemma 9] and going back to the methods of [Reference Hamkins and Löwe15, theorem 6]. Those results were stated specifically for the case of forcing and models of set theory, but the point here is that the same idea works generally in any Kripke model. So we refer the reader to that presentation, but let us also briefly explain the details. Suppose that
![]() $\mathcal {W}$
is a Kripke model which admits arbitrarily large finite collections of independent switches at world W. Let us consider W as the initial world of
$\mathcal {W}$
is a Kripke model which admits arbitrarily large finite collections of independent switches at world W. Let us consider W as the initial world of
![]() $\mathcal {W}$
and assume without loss that every world of
$\mathcal {W}$
and assume without loss that every world of
![]() $\mathcal {W}$
can be reached from W by successive applications of the accessibility relation. If
$\mathcal {W}$
can be reached from W by successive applications of the accessibility relation. If
![]() $\varphi (p_0,\dots ,p_n)$
is any propositional modal assertion not in S5, then it is known to fail at a world w in some finite propositional Kripke model M whose accessibility relation is the complete binary relation (all worlds access all worlds). By duplicating some worlds of M, if necessary, we may assume that the number of worlds is a power of 2:
$\varphi (p_0,\dots ,p_n)$
is any propositional modal assertion not in S5, then it is known to fail at a world w in some finite propositional Kripke model M whose accessibility relation is the complete binary relation (all worlds access all worlds). By duplicating some worlds of M, if necessary, we may assume that the number of worlds is a power of 2:
![]() $\left \langle w_j\mid j<2^m\right \rangle $
. Let
$\left \langle w_j\mid j<2^m\right \rangle $
. Let
![]() $\left \langle s_k\mid k<m\right \rangle $
be an independent family of m switches for
$\left \langle s_k\mid k<m\right \rangle $
be an independent family of m switches for
![]() $\mathcal {W}$
. We shall simulate a copy of M inside
$\mathcal {W}$
. We shall simulate a copy of M inside
![]() $\mathcal {W}$
as follows. For each
$\mathcal {W}$
as follows. For each
![]() $j<2^m$
, let
$j<2^m$
, let
![]() $\bar s_j$
be the Boolean combination of the switches
$\bar s_j$
be the Boolean combination of the switches
![]() $s_k$
that accords with the same pattern as the binary bits of the number j. We associate each world
$s_k$
that accords with the same pattern as the binary bits of the number j. We associate each world
![]() $w_j$
in M with the worlds W in
$w_j$
in M with the worlds W in
![]() $\mathcal {W}$
for which
$\mathcal {W}$
for which
![]() $\bar s_j$
holds. We may assume that world W in
$\bar s_j$
holds. We may assume that world W in
![]() $\mathcal {W}$
is associated with world w in M. Since the switch patterns
$\mathcal {W}$
is associated with world w in M. Since the switch patterns
![]() $\bar s_j$
are mutually exclusive and exhaustive, this association amounts to a partition of the worlds of
$\bar s_j$
are mutually exclusive and exhaustive, this association amounts to a partition of the worlds of
![]() $\mathcal {W}$
, with one piece of the partition associated with each world
$\mathcal {W}$
, with one piece of the partition associated with each world
![]() $w_j$
in M. For each propositional variable p appearing in
$w_j$
in M. For each propositional variable p appearing in
![]() $\varphi $
, let
$\varphi $
, let
![]() $\psi _p=\bigvee \{{\bar s_j\mid (M,w_j)\models p}\}$
. Thus,
$\psi _p=\bigvee \{{\bar s_j\mid (M,w_j)\models p}\}$
. Thus,
![]() $\psi _p$
is true in a world
$\psi _p$
is true in a world
![]() $U\in \mathcal {W}$
just in case p is true in the world u of M with which U is associated. One may now prove by induction on formulas
$U\in \mathcal {W}$
just in case p is true in the world u of M with which U is associated. One may now prove by induction on formulas
![]() $\phi $
in propositional modal logic that
$\phi $
in propositional modal logic that
whenever u is associated with U, or in other words, whenever the pattern of switches
![]() $\bar s_j$
is true in W, where
$\bar s_j$
is true in W, where
![]() $w=w_j$
. Since
$w=w_j$
. Since
![]() $\varphi $
fails at a world of M, we have therefore found a failing substitution instance of
$\varphi $
fails at a world of M, we have therefore found a failing substitution instance of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathcal {W}$
.
$\mathcal {W}$
.
For a related formulation, let us say that a (possibly infinite) list of statements
![]() $d_0,d_1,d_2,\dots $
is a dial in a Kripke model
$d_0,d_1,d_2,\dots $
is a dial in a Kripke model
![]() $\mathcal {W}$
, if every world in
$\mathcal {W}$
, if every world in
![]() $\mathcal {W}$
satisfies exactly one of the statements
$\mathcal {W}$
satisfies exactly one of the statements
![]() $d_i$
and furthermore, every world can access another world with any prescribed dial value. So you can adjust the dial as you like. If a world satisfies
$d_i$
and furthermore, every world can access another world with any prescribed dial value. So you can adjust the dial as you like. If a world satisfies
![]() $d_i$
, then we shall say that the dial value is i in that world. The following argument shows how to translate between dials and independent switches. Notice that from any larger dial or from an infinite dial, we can construct smaller dials of any given size, simply by keeping any desired fewer finite number of dial statements and adding the statement that none of them holds.
$d_i$
, then we shall say that the dial value is i in that world. The following argument shows how to translate between dials and independent switches. Notice that from any larger dial or from an infinite dial, we can construct smaller dials of any given size, simply by keeping any desired fewer finite number of dial statements and adding the statement that none of them holds.
Theorem 4. A Kripke model
![]() $\mathcal {W}$
admits arbitrarily large finite families of independent switches if and only if it admits arbitrarily large finite dials.
$\mathcal {W}$
admits arbitrarily large finite families of independent switches if and only if it admits arbitrarily large finite dials.
Proof. If
![]() $\left \langle s_i\mid i<m\right \rangle $
is an independent family of switches, then for each
$\left \langle s_i\mid i<m\right \rangle $
is an independent family of switches, then for each
![]() $j<2^m$
, let
$j<2^m$
, let
![]() $d_j$
be the assertion that the switch pattern of the
$d_j$
be the assertion that the switch pattern of the
![]() $s_i$
conforms exactly with the binary digits of j. Since every world exhibits some unique pattern for the switches, these form a mutually exclusive partition of truth; and since the switches are independent, any world can access another world realizing any given dial value
$s_i$
conforms exactly with the binary digits of j. Since every world exhibits some unique pattern for the switches, these form a mutually exclusive partition of truth; and since the switches are independent, any world can access another world realizing any given dial value
![]() $d_j$
. Conversely, if
$d_j$
. Conversely, if
![]() $\left \langle d_j\mid j<n\right \rangle $
is a dial with
$\left \langle d_j\mid j<n\right \rangle $
is a dial with
![]() $2^m\leq n$
, then let
$2^m\leq n$
, then let
![]() $s_i$
assert that one of the
$s_i$
assert that one of the
![]() $d_j$
’s holds, where the
$d_j$
’s holds, where the
![]() $i^{\textrm {th}}$
bit of j is
$i^{\textrm {th}}$
bit of j is
![]() $1$
. These are independent switches, precisely because any desired dial value is possible.
$1$
. These are independent switches, precisely because any desired dial value is possible.
Let us discuss a few more types of control statements. Following [Reference Hamkins and Löwe15], a button in any Kripke model
![]() $\mathcal {W}$
is a statement b such that
$\mathcal {W}$
is a statement b such that
![]() is true at every world. The button is pushed at a world if
is true at every world. The button is pushed at a world if
![]() holds at that world, and otherwise unpushed. A pure button is a button b for which
holds at that world, and otherwise unpushed. A pure button is a button b for which
![]() is true at every world, so that pushing the button is the same as making it become true. In S4, if b is an unpushed button, then
is true at every world, so that pushing the button is the same as making it become true. In S4, if b is an unpushed button, then
![]() is an unpushed pure button. A family of buttons and switches is independent in a Kripke model
is an unpushed pure button. A family of buttons and switches is independent in a Kripke model
![]() $\mathcal {W}$
, if there is a world at which the buttons are unpushed, and every world W accesses a world U in which any additional button may be pushed, without pushing any other as-yet unpushed buttons from the family, while also setting any finitely many of the switches so as to have any desired pattern in U. And similarly with dials.
$\mathcal {W}$
, if there is a world at which the buttons are unpushed, and every world W accesses a world U in which any additional button may be pushed, without pushing any other as-yet unpushed buttons from the family, while also setting any finitely many of the switches so as to have any desired pattern in U. And similarly with dials.
Theorem 5. If
![]() $\mathcal {W}$
is a Kripke model that admits arbitrarily large finite families of independent buttons and switches, or independent buttons independent of a dial, then the propositional modal validities of
$\mathcal {W}$
is a Kripke model that admits arbitrarily large finite families of independent buttons and switches, or independent buttons independent of a dial, then the propositional modal validities of
![]() $\mathcal {W}$
are contained in S4.2. The validities of any particular world in which the buttons are not yet pushed are contained in S4.2, and in any case, are contained in S5.
$\mathcal {W}$
are contained in S4.2. The validities of any particular world in which the buttons are not yet pushed are contained in S4.2, and in any case, are contained in S5.
Proof. This argument follows [Reference Hamkins, Leibman and Löwe14, theorem 13], which extended the main technique of [Reference Hamkins and Löwe15]. That earlier result was stated only in the case of models of set theory, but the idea works generally in any Kripke model. Let us briefly describe the details. If
![]() $\varphi (p_0,\dots ,p_k)$
is any propositional modal assertion not in S4.2, then by [Reference Hamkins and Löwe15, theorem 11] it fails at some world in a Kripke model M whose frame is a finite pre-Boolean algebra. (A pre-Boolean algebra is a partial pre-order
$\varphi (p_0,\dots ,p_k)$
is any propositional modal assertion not in S4.2, then by [Reference Hamkins and Löwe15, theorem 11] it fails at some world in a Kripke model M whose frame is a finite pre-Boolean algebra. (A pre-Boolean algebra is a partial pre-order
![]() $(B, \leq )$
whose quotient order
$(B, \leq )$
whose quotient order
![]() $B / \equiv $
is a Boolean algebra, where
$B / \equiv $
is a Boolean algebra, where
![]() $a\equiv b\mathrel {\Longleftrightarrow } a\leq b\leq a$
is the induced equivalence relation; we shall subsequently refer to the equivalence classes as the ‘clusters’ of the Kripke model.) We may assume without loss by duplicating worlds that the clusters of M have uniform size m, and let n be the number of atomic clusters, that is, the number of atoms in the quotient Boolean algebra. We may therefore index the worlds of M as
$a\equiv b\mathrel {\Longleftrightarrow } a\leq b\leq a$
is the induced equivalence relation; we shall subsequently refer to the equivalence classes as the ‘clusters’ of the Kripke model.) We may assume without loss by duplicating worlds that the clusters of M have uniform size m, and let n be the number of atomic clusters, that is, the number of atoms in the quotient Boolean algebra. We may therefore index the worlds of M as
![]() $w^a_j$
, where
$w^a_j$
, where
![]() $j<m$
and
$j<m$
and
![]() $a\subseteq n$
, where
$a\subseteq n$
, where
![]() $w^a_j$
accesses
$w^a_j$
accesses
![]() $w^b_i$
just in case
$w^b_i$
just in case
![]() $a\subseteq b$
. Fix an independent family of n buttons
$a\subseteq b$
. Fix an independent family of n buttons
![]() $\left \langle b_i\mid i<n\right \rangle $
and a dial
$\left \langle b_i\mid i<n\right \rangle $
and a dial
![]() $\left \langle d_j\mid k<m\right \rangle $
of length m (use the switches to construct a dial if necessary). For each world
$\left \langle d_j\mid k<m\right \rangle $
of length m (use the switches to construct a dial if necessary). For each world
![]() $w^a_j$
, let
$w^a_j$
, let
 $\Phi _{w^a_j}=(\bigwedge _{i\in a}b_i)\wedge (\bigwedge _{i\notin a}\neg b_i)\wedge d_j$
, which asserts that the pushed buttons are exactly those indexed in a and the dial value is j. The independence of the buttons and the dial ensures that these assertions are mutually exclusive and a partition of truth, and furthermore that the worlds of
$\Phi _{w^a_j}=(\bigwedge _{i\in a}b_i)\wedge (\bigwedge _{i\notin a}\neg b_i)\wedge d_j$
, which asserts that the pushed buttons are exactly those indexed in a and the dial value is j. The independence of the buttons and the dial ensures that these assertions are mutually exclusive and a partition of truth, and furthermore that the worlds of
![]() $\mathcal {W}$
in which
$\mathcal {W}$
in which
 $\Phi _{w^a_j}$
holds can access worlds with
$\Phi _{w^a_j}$
holds can access worlds with
 $\Phi _{w^b_i}$
just in case
$\Phi _{w^b_i}$
just in case
![]() $a\subseteq b$
. We associate each world
$a\subseteq b$
. We associate each world
![]() $w^a_j$
of M with the worlds
$w^a_j$
of M with the worlds
![]() $W\in \mathcal {W}$
in which
$W\in \mathcal {W}$
in which
 $\Phi _{w^a_j}$
is true. For each propositional variable p in
$\Phi _{w^a_j}$
is true. For each propositional variable p in
![]() $\varphi $
, let
$\varphi $
, let
 $\psi _p=\bigvee \{{\Phi _{w^a_j}\mid (M,w^a_j)\models p}\}$
, which will be true in a world W of
$\psi _p=\bigvee \{{\Phi _{w^a_j}\mid (M,w^a_j)\models p}\}$
, which will be true in a world W of
![]() $\mathcal {W}$
just in case W is associated with a world w in M in which p is true. One can now verify that
$\mathcal {W}$
just in case W is associated with a world w in M in which p is true. One can now verify that
whenever world w in M is associated with world W in
![]() $\mathcal {W}$
. This is because it is true for the propositional variables and is easily preserved by logical connectives, and furthermore because the accessibility relation of M is exactly simulated via the association as we described. Since the original modal assertion
$\mathcal {W}$
. This is because it is true for the propositional variables and is easily preserved by logical connectives, and furthermore because the accessibility relation of M is exactly simulated via the association as we described. Since the original modal assertion
![]() $\varphi (p_0,\dots ,p_n)$
fails at a world of M, we have therefore provided a substitution instance of
$\varphi (p_0,\dots ,p_n)$
fails at a world of M, we have therefore provided a substitution instance of
![]() $\varphi $
that fails at the associated worlds W of
$\varphi $
that fails at the associated worlds W of
![]() $\mathcal {W}$
, and so
$\mathcal {W}$
, and so
![]() $\varphi $
is not valid in
$\varphi $
is not valid in
![]() $\mathcal {W}$
.
$\mathcal {W}$
.
Finally, since the independent switches remain operable even after all the buttons are pushed, each individual world of
![]() $\mathcal {W}$
has its validities contained in S5 by Theorem 3.
$\mathcal {W}$
has its validities contained in S5 by Theorem 3.
Following [Reference Hamkins, Leibman and Löwe14], a ratchet for a Kripke model
![]() $\mathcal {W}$
at a world W is a sequence of assertions
$\mathcal {W}$
at a world W is a sequence of assertions
![]() $r_1$
,
$r_1$
,
![]() $r_2,\ldots , r_n$
, such that each
$r_2,\ldots , r_n$
, such that each
![]() $r_i$
is an unpushed button in W, each statement
$r_i$
is an unpushed button in W, each statement
![]() $r_i$
necessarily implies all the previous statements
$r_i$
necessarily implies all the previous statements
![]() $r_j$
for
$r_j$
for
![]() $j<i$
and over any world in which
$j<i$
and over any world in which
![]() $r_i$
is not yet true, it can become true in some accessible world in which
$r_i$
is not yet true, it can become true in some accessible world in which
![]() $r_{i+1}$
is not true; in this case, we say that the ratchet volume is i in that accessed world. The idea of the ratchet, of course, is that it is unidirectional: the ratchet volume can only go up, never down. It is sometimes convenient to append a tautologically true statement
$r_{i+1}$
is not true; in this case, we say that the ratchet volume is i in that accessed world. The idea of the ratchet, of course, is that it is unidirectional: the ratchet volume can only go up, never down. It is sometimes convenient to append a tautologically true statement
![]() $r_0$
at the beginning and say that the ratchet volume is
$r_0$
at the beginning and say that the ratchet volume is
![]() $0$
in the initial world W. A ratchet is mutually independent with an independent family of switches, if in every world, one can achieve any finite pattern for the switches in an accessed world, without increasing the ratchet volume; and similarly with a dial.
$0$
in the initial world W. A ratchet is mutually independent with an independent family of switches, if in every world, one can achieve any finite pattern for the switches in an accessed world, without increasing the ratchet volume; and similarly with a dial.
Theorem 6. If
![]() $\mathcal {W}$
is Kripke model having arbitrarily large finite ratchets mutually independent with arbitrarily large families of independent switches
$\mathcal {W}$
is Kripke model having arbitrarily large finite ratchets mutually independent with arbitrarily large families of independent switches
![]() $($
or with an arbitrarily large finite dial
$($
or with an arbitrarily large finite dial
![]() $)$
, then the propositional modal validities of
$)$
, then the propositional modal validities of
![]() $\mathcal {W}$
are contained in S4.3. The validities of any particular world with ratchet volume zero are contained in S4.3 and, in any case, the validities of each world are contained in S5.
$\mathcal {W}$
are contained in S4.3. The validities of any particular world with ratchet volume zero are contained in S4.3 and, in any case, the validities of each world are contained in S5.
Proof. This argument builds on [Reference Hamkins, Leibman and Löwe14, theorems 11], although again those results were stated only for models of set theory, whereas the same idea works with respect to any Kripke model. Let us briefly sketch the argument. If a modal assertion
![]() $\varphi (p_0,\dots ,p_n)$
is not in S4.3, then since the finite linear pre-orders are a complete set of frames for S4.3, it follows that
$\varphi (p_0,\dots ,p_n)$
is not in S4.3, then since the finite linear pre-orders are a complete set of frames for S4.3, it follows that
![]() $\varphi $
fails at an initial world in a finite Kripke model whose frame is a finite linear pre-order (a finite chain of clusters of worlds, with each world in a cluster accessing all worlds in that cluster and any world in any higher cluster). Let
$\varphi $
fails at an initial world in a finite Kripke model whose frame is a finite linear pre-order (a finite chain of clusters of worlds, with each world in a cluster accessing all worlds in that cluster and any world in any higher cluster). Let
![]() $n+1$
be the number of clusters, and we may assume without loss that each cluster has uniform size m. So the worlds of M can be described as
$n+1$
be the number of clusters, and we may assume without loss that each cluster has uniform size m. So the worlds of M can be described as
![]() $w^i_j$
, where
$w^i_j$
, where
![]() $i\leq n$
and
$i\leq n$
and
![]() $j<m$
. Let
$j<m$
. Let
![]() $r_0,r_1,\dots ,r_n$
be a ratchet in
$r_0,r_1,\dots ,r_n$
be a ratchet in
![]() $\mathcal {W}$
of length n, mutually independent with a dial
$\mathcal {W}$
of length n, mutually independent with a dial
![]() $\left \langle d_j\mid j<m\right \rangle $
(use switches to construct a dial if necessary). For each world
$\left \langle d_j\mid j<m\right \rangle $
(use switches to construct a dial if necessary). For each world
![]() $w^i_j$
in M, let
$w^i_j$
in M, let
 $\Phi _{w^i_j}=r_i\wedge d_j$
be the assertion expressing that the ratchet volume is i and the dial value is j, and we associate world
$\Phi _{w^i_j}=r_i\wedge d_j$
be the assertion expressing that the ratchet volume is i and the dial value is j, and we associate world
![]() $w^i_j$
with the words W in
$w^i_j$
with the words W in
![]() $\mathcal {W}$
satisfying
$\mathcal {W}$
satisfying
 $\Phi _{w^i_j}$
. The assumptions on the ratchet and dial ensure that a world in
$\Phi _{w^i_j}$
. The assumptions on the ratchet and dial ensure that a world in
![]() $\mathcal {W}$
satisfying
$\mathcal {W}$
satisfying
 $\Phi _{w^i_j}$
can access those worlds in
$\Phi _{w^i_j}$
can access those worlds in
![]() $\mathcal {W}$
that satisfy some
$\mathcal {W}$
that satisfy some
 $\Phi _{w^{i'}_{j'}}$
, exactly for
$\Phi _{w^{i'}_{j'}}$
, exactly for
![]() $i\leq i'$
. Thus, the
$i\leq i'$
. Thus, the
![]() $\Phi _w$
assertions partition the worlds of
$\Phi _w$
assertions partition the worlds of
![]() $\mathcal {W}$
in a way that exactly mimics the accessibility relation of M. For every propositional variable p appearing in
$\mathcal {W}$
in a way that exactly mimics the accessibility relation of M. For every propositional variable p appearing in
![]() $\varphi $
, let
$\varphi $
, let
![]() $\psi _p=\bigvee \{{\Phi _w\mid (M,w)\models p}\}$
, which holds exactly in the worlds of
$\psi _p=\bigvee \{{\Phi _w\mid (M,w)\models p}\}$
, which holds exactly in the worlds of
![]() $\mathcal {W}$
that are associated with a world of M in which p is true. It now follows by induction on formulas that
$\mathcal {W}$
that are associated with a world of M in which p is true. It now follows by induction on formulas that
whenever W is a world in
![]() $\mathcal {W}$
associated with world w in M. Since
$\mathcal {W}$
associated with world w in M. Since
![]() $\varphi $
fails at an initial world of M, this therefore provides a substitution instance of
$\varphi $
fails at an initial world of M, this therefore provides a substitution instance of
![]() $\varphi $
that fails at any world of
$\varphi $
that fails at any world of
![]() $\mathcal {W}$
with zero ratchet volume. So the validities of
$\mathcal {W}$
with zero ratchet volume. So the validities of
![]() $\mathcal {W}$
are contained among S4.3.
$\mathcal {W}$
are contained among S4.3.
Meanwhile, because the switches remain operable even after the ratchet is used up, every individual world of
![]() $\mathcal {W}$
has its validities contained in S5 by Theorem 3.
$\mathcal {W}$
has its validities contained in S5 by Theorem 3.
For the set-theoretic structures that we have in mind for our application, it often happens that one can define much longer transfinite ratchets, and these can eliminate the need for switches. So let us describe how that works. Suppose that
![]() $\mathcal {W}$
is a potentialist system forming a coherent collection of transitive set models of some weak set theory, whose limit model is U. Assume furthermore that the ordinals of U have limit ordinal height at least
$\mathcal {W}$
is a potentialist system forming a coherent collection of transitive set models of some weak set theory, whose limit model is U. Assume furthermore that the ordinals of U have limit ordinal height at least
![]() $\omega ^2$
and that the models are able to carry out simple ordinal arithmetic. Generalizing the terminology of [Reference Hamkins, Leibman and Löwe14], let us say that
$\omega ^2$
and that the models are able to carry out simple ordinal arithmetic. Generalizing the terminology of [Reference Hamkins, Leibman and Löwe14], let us say that
![]() $\mathcal {W}$
admits a long ratchet starting at world W, if there are a sequence of statements
$\mathcal {W}$
admits a long ratchet starting at world W, if there are a sequence of statements
![]() $r_\alpha $
for
$r_\alpha $
for
![]() $\alpha \in \mathord {{\textrm {Ord}}}^U$
, each an unpushed button in W, such that each
$\alpha \in \mathord {{\textrm {Ord}}}^U$
, each an unpushed button in W, such that each
![]() $r_\alpha $
necessarily implies all earlier
$r_\alpha $
necessarily implies all earlier
![]() $r_\beta $
for
$r_\beta $
for
![]() $\beta <\alpha $
, no world satisfies all the
$\beta <\alpha $
, no world satisfies all the
![]() $r_\alpha $
and in any world in which
$r_\alpha $
and in any world in which
![]() $r_\alpha $
is not yet true (perhaps because
$r_\alpha $
is not yet true (perhaps because
![]() $\alpha $
does not yet exist in that world), then there is an accessible world in which
$\alpha $
does not yet exist in that world), then there is an accessible world in which
![]() $\alpha $
exists and
$\alpha $
exists and
![]() $r_\alpha $
is true, but
$r_\alpha $
is true, but
![]() $r_{\alpha +1}$
is not true (perhaps because
$r_{\alpha +1}$
is not true (perhaps because
![]() $\alpha +1$
does not yet exist). The ratchet is uniform if there is a formula
$\alpha +1$
does not yet exist). The ratchet is uniform if there is a formula
![]() $\eta $
such that
$\eta $
such that
![]() $r_\alpha =\eta (\alpha )$
, expressed with parameter
$r_\alpha =\eta (\alpha )$
, expressed with parameter
![]() $\alpha $
. It is not expected necessarily that the worlds of
$\alpha $
. It is not expected necessarily that the worlds of
![]() $\mathcal {W}$
each have all the ordinals
$\mathcal {W}$
each have all the ordinals
![]() $\alpha $
of the limit model.
$\alpha $
of the limit model.
The main observation, originally made by George Leibman, is that a uniform long ratchet can be used as in [Reference Hamkins, Leibman and Löwe14, theorem 12] to provide an arbitrarily large finite ratchet mutually independent with as many finitely many independent switches as desired or with a dial. Basically, ordinals of the form
![]() $\omega \cdot k+j$
are viewed as having simulated ratchet volume k and dial value
$\omega \cdot k+j$
are viewed as having simulated ratchet volume k and dial value
![]() $j\mod m$
, or switch values given by the binary digits of j. Thus, one can view the assertion
$j\mod m$
, or switch values given by the binary digits of j. Thus, one can view the assertion
![]() $r_{\omega \cdot k+j}$
as expressing simulated volume k and dial value
$r_{\omega \cdot k+j}$
as expressing simulated volume k and dial value
![]() $j\mod m$
, and the point is that you can change the dial value to any desired number below m, without increasing the simulated ratchet volume, simply by increasing
$j\mod m$
, and the point is that you can change the dial value to any desired number below m, without increasing the simulated ratchet volume, simply by increasing
![]() $r_\alpha $
while staying in the same
$r_\alpha $
while staying in the same
![]() $\omega $
-block of ordinals. For ordinals above
$\omega $
-block of ordinals. For ordinals above
![]() $\omega ^2$
, one views them as
$\omega ^2$
, one views them as
![]() $\lambda +j$
for some limit ordinal
$\lambda +j$
for some limit ordinal
![]() $\lambda $
, and then takes
$\lambda $
, and then takes
![]() $r_{\lambda +j}$
as asserting the top ratchet volume with dial value
$r_{\lambda +j}$
as asserting the top ratchet volume with dial value
![]() $j\mod m$
. Thus, a uniform long ratchet provides arbitrarily long finite ratchets mutually independent with arbitrarily large dials or switches. Note that although the long ratchet
$j\mod m$
. Thus, a uniform long ratchet provides arbitrarily long finite ratchets mutually independent with arbitrarily large dials or switches. Note that although the long ratchet
![]() $r_\alpha $
itself uses the ordinals
$r_\alpha $
itself uses the ordinals
![]() $\alpha $
as parameters, the ratchet volume in any world is a definable ordinal (or
$\alpha $
as parameters, the ratchet volume in any world is a definable ordinal (or
![]() $\mathord {{\textrm {Ord}}}$
itself in that world) and we may therefore definably extract the corresponding finite ratchet and dial values without need for any parameter. We therefore may deduce:
$\mathord {{\textrm {Ord}}}$
itself in that world) and we may therefore definably extract the corresponding finite ratchet and dial values without need for any parameter. We therefore may deduce:
Theorem 7. If
![]() $\mathcal {W}$
is potentialist system of transitive models of set theory admitting a uniform long ratchet, then at the worlds of
$\mathcal {W}$
is potentialist system of transitive models of set theory admitting a uniform long ratchet, then at the worlds of
![]() $\mathcal {W}$
where the ratchet has not yet started to crank, the modal validities are contained within the modal theory S4.3, and the validities of any particular world of
$\mathcal {W}$
where the ratchet has not yet started to crank, the modal validities are contained within the modal theory S4.3, and the validities of any particular world of
![]() $\mathcal {W}$
is contained within S5.
$\mathcal {W}$
is contained within S5.
In the previous several theorems, where we provided upper bounds on the propositional modal validities of a given Kripke model, we should like to point out that the failing substitution instances we constructed were of the form
![]() $\varphi (\psi _{p_0},\dots ,\psi _{p_n})$
, where the sentences
$\varphi (\psi _{p_0},\dots ,\psi _{p_n})$
, where the sentences
![]() $\psi _p$
were various Boolean combinations of the switch, button and ratchet assertions appearing in the hypotheses of the theorems. In particular, in the case that the Kripke model
$\psi _p$
were various Boolean combinations of the switch, button and ratchet assertions appearing in the hypotheses of the theorems. In particular, in the case that the Kripke model
![]() $\mathcal {W}$
is a collection of
$\mathcal {W}$
is a collection of
![]() $\mathcal {L}$
-structures under the potentialist semantics and the control statements are
$\mathcal {L}$
-structures under the potentialist semantics and the control statements are
![]() $\mathcal {L}$
-sentences, then the arguments show that we achieve the upper bound modal theories S4.3, S4.2 with respect to
$\mathcal {L}$
-sentences, then the arguments show that we achieve the upper bound modal theories S4.3, S4.2 with respect to
![]() $\mathcal {L}$
-substitutions. These arguments therefore provide a slightly stronger result than achieving the upper bounds with respect to
$\mathcal {L}$
-substitutions. These arguments therefore provide a slightly stronger result than achieving the upper bounds with respect to
![]() $\mathcal {L}^\Diamond $
-substitutions, since otherwise the possibility might remain that there could be additional validities that work with respect to
$\mathcal {L}^\Diamond $
-substitutions, since otherwise the possibility might remain that there could be additional validities that work with respect to
![]() $\mathcal {L}$
-substitutions, even if the stated bound is optimal for
$\mathcal {L}$
-substitutions, even if the stated bound is optimal for
![]() $\mathcal {L}^\Diamond $
-substitutions. This observation is relevant for the applications in the next section to the case of set-theoretic potentialism, where in most cases we are able to construct the relevant control statements in the language
$\mathcal {L}^\Diamond $
-substitutions. This observation is relevant for the applications in the next section to the case of set-theoretic potentialism, where in most cases we are able to construct the relevant control statements in the language
![]() $\mathcal {L}$
rather than only in
$\mathcal {L}$
rather than only in
![]() $\mathcal {L}^\Diamond $
. Nevertheless, in a few cases in Section 3 we will need the extra power of
$\mathcal {L}^\Diamond $
. Nevertheless, in a few cases in Section 3 we will need the extra power of
![]() $\mathcal {L}^\Diamond $
in order to achieve the desired control statements.
$\mathcal {L}^\Diamond $
in order to achieve the desired control statements.
3 Set-theoretic potentialism
3.1 Introduction
Let us now turn specifically to set-theoretic potentialism, our motivating focus. We shall introduce and consider several natural kinds of set-theoretic potentialism, and for each of them, we shall use the results of the previous section in order to identify exactly what are the modal validities of that variety of potentialism, and under what circumstances a particular world might exhibit a stronger collection of validities. We are particularly interested in identifying instances of the potentialist maximality principle, which occurs when S5 is valid at a world.
It may be useful to clarify the dialectic of the article. We are analyzing various kinds of set-theoretic potentialism, but for most of the work we do so only as far as they are simulated from the perspective of ZFC set theory, which we shall use as our background theory. This choice of background theory is reasonable in light of its familiarity and because it is acceptable to actualists and potentialists alike. After all, since ZFC is a non-modal theory, it doesn’t take a stand on whether its universe V should be regarded as fully completed or as incompletable and merely potential. The former option is suggested when the language of ZFC is taken at face value, while the latter is permissible when we adopt the modal translation of the language of ZFC described in Theorem 1.
For each of the kinds of set-theoretic potentialism we shall consider, it turns out that the collection of modal validities can depend on a great variety of contextual choices: on the particular world that is considered, on the language that is used, on the modal vocabulary that is allowed, and on the parameters that are allowed. For example, it is possible that a world W validates S5 with respect to substitution instances by sentences in the language of set theory, but only S4.3 when parameters or modal vocabulary are allowed. For this reason, it becomes somewhat fussy or technical to provide a full account of the situation, but we have nevertheless strived to do so.
The most restrictive language we consider is the language of set theory
![]() $\mathcal {L}_\in $
, which beyond the logical vocabulary has only the set-membership relation
$\mathcal {L}_\in $
, which beyond the logical vocabulary has only the set-membership relation
![]() $\in $
; the most generous language is generally
$\in $
; the most generous language is generally
 $\mathcal {L}_{\in ,W}^\Diamond $
, which also allows the modal operators and arbitrary parameters from the world W being considered. Since as we mentioned earlier, it is a more severe requirement for a propositional modal assertion to be valid with respect to substitution instances from a more expressive language, it follows in general that we have the following inclusions for any world W in any potentialist system.
$\mathcal {L}_{\in ,W}^\Diamond $
, which also allows the modal operators and arbitrary parameters from the world W being considered. Since as we mentioned earlier, it is a more severe requirement for a propositional modal assertion to be valid with respect to substitution instances from a more expressive language, it follows in general that we have the following inclusions for any world W in any potentialist system.

As a preview, the following table briefly summarizes our main conclusions for the main kinds of set-theoretic potentialism that we consider. Details and additional cases can be found in the rest of the section.
-
Rank-potentialism
 $\mathcal {V}=\{{V_\beta \mid \beta \in \mathord {{\textrm {Ord}}}}\}$
$\mathcal {V}=\{{V_\beta \mid \beta \in \mathord {{\textrm {Ord}}}}\}$
 true in some larger
true in some larger
 $V_\beta $
height potentialist, width actualist
$V_\beta $
height potentialist, width actualist
 $S4.3 \subseteq \mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}^\Diamond _{\in ,V_\beta }) \subseteq \mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}_\in ) \subseteq S5$
$S4.3 \subseteq \mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}^\Diamond _{\in ,V_\beta }) \subseteq \mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}_\in ) \subseteq S5$
-
Grothendieck–Zermelo potentialism
 $\mathcal {Z}=\{{V_\kappa \mid \kappa \text { inaccessible}}\}$
$\mathcal {Z}=\{{V_\kappa \mid \kappa \text { inaccessible}}\}$
 true in some larger inaccessible
true in some larger inaccessible
 $V_\kappa $
height potentialist, width actualist
$V_\kappa $
height potentialist, width actualist
 $ S4.3 \subseteq \mathord {\textrm {Val}}_{\mathcal {Z}}(V_\kappa ,\mathcal {L}^\Diamond _{\in ,V_\kappa }) \subseteq \mathord {\textrm {Val}}_{\mathcal {Z}}(V_\kappa ,\mathcal {L}_\in ) \subseteq S5$
$ S4.3 \subseteq \mathord {\textrm {Val}}_{\mathcal {Z}}(V_\kappa ,\mathcal {L}^\Diamond _{\in ,V_\kappa }) \subseteq \mathord {\textrm {Val}}_{\mathcal {Z}}(V_\kappa ,\mathcal {L}_\in ) \subseteq S5$
-
Transitive-set potentialism
 $\mathcal {T}=\{{W\mid W\text { transitive}}\}$
$\mathcal {T}=\{{W\mid W\text { transitive}}\}$
 true in some larger transitive set height potentialist, width potentialist
true in some larger transitive set height potentialist, width potentialist
 $S4.2 \subseteq \mathord {\textrm {Val}}_{\mathcal {T}}(W,\mathcal {L}_{\in ,W}^\Diamond ) \subseteq \mathord {\textrm {Val}}_{\mathcal {T}}(W,\mathcal {L}_\in ) \subseteq S5$
$S4.2 \subseteq \mathord {\textrm {Val}}_{\mathcal {T}}(W,\mathcal {L}_{\in ,W}^\Diamond ) \subseteq \mathord {\textrm {Val}}_{\mathcal {T}}(W,\mathcal {L}_\in ) \subseteq S5$
-
Forcing potentialism
 $\mathcal {M}=\{{V[G]\mid G\text { is }V\text {-generic}}\}$
$\mathcal {M}=\{{V[G]\mid G\text { is }V\text {-generic}}\}$
 true in some forcing extension height actualist, width potentialist
true in some forcing extension height actualist, width potentialist
 $S4.2 = \mathord {\textrm {Val}}_{\mathcal {M}}(W,\mathcal {L}_{\in ,W}) \subseteq \mathord {\textrm {Val}}_{\mathcal {M}}(W,\mathcal {L}_\in ) \subseteq S5$
$S4.2 = \mathord {\textrm {Val}}_{\mathcal {M}}(W,\mathcal {L}_{\in ,W}) \subseteq \mathord {\textrm {Val}}_{\mathcal {M}}(W,\mathcal {L}_\in ) \subseteq S5$
-
Countable-transitive model potentialism
 $\mathcal {C}=\{{M\mid M\models {\textrm {ZFC}},\text { countable, transitive}}\}$
$\mathcal {C}=\{{M\mid M\models {\textrm {ZFC}},\text { countable, transitive}}\}$
 true in some larger countable transitive model of ZFC height potentialist, width potentialist
true in some larger countable transitive model of ZFC height potentialist, width potentialist
 $S4.2 = \mathord {\textrm {Val}}_{\mathcal {C}}(W,\mathcal {L}_{\in ,W}) \subseteq \mathord {\textrm {Val}}_{\mathcal {C}}(W,\mathcal {L}_\in ) \subseteq S5$
$S4.2 = \mathord {\textrm {Val}}_{\mathcal {C}}(W,\mathcal {L}_{\in ,W}) \subseteq \mathord {\textrm {Val}}_{\mathcal {C}}(W,\mathcal {L}_\in ) \subseteq S5$
-
Countable-model potentialism
 $\mathcal {W}=\{{M\mid M\models {\textrm {ZFC}},\text { countable}}\}$
$\mathcal {W}=\{{M\mid M\models {\textrm {ZFC}},\text { countable}}\}$
 true in some larger countable model of ZFC height potentialist, width potentialist
true in some larger countable model of ZFC height potentialist, width potentialist
 $S4.3 = \mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L}_{\in ,W}^\diamond ) = \mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L}_{\in ,W}) \subseteq \mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L}_\in ) \subseteq S5$
$S4.3 = \mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L}_{\in ,W}^\diamond ) = \mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L}_{\in ,W}) \subseteq \mathord {\textrm {Val}}_{\mathcal {W}}(W,\mathcal {L}_\in ) \subseteq S5$
In each case, the indicated lower and upper bounds are realized in particular worlds, usually in the strongest possible way that is consistent with the stated inclusions, although in some cases, this is proved only under additional mild technical hypotheses. Indeed, some of the potentialist accounts are only undertaken with additional set-theoretic assumptions going beyond ZFC. For example, the Grothendieck–Zermelo account of potentialism is interesting mainly only under the assumption that there are a proper class of inaccessible cardinals, and countable-transitive-model potentialism is more robust under the assumption that every real is an element of a countable transitive model of set theory, which can be thought of as a mild large-cardinal assumption.
We shall now consider the various forms of potentialism in detail, and not only the ones mentioned above but also further variations. Since the subsections are largely independent of one another, readers may choose to focus on the forms of potentialism they happen to find most interesting.
3.2 Set-theoretic rank potentialism
Let us begin with a very natural case of height potentialism combined with width actualism, namely, the case of set-theoretic rank potentialism, constituted by the worlds
These worlds
![]() $V_\beta $
are the rank-initial segments of the cumulative set-theoretic hierarchy, and the potentialist modality here is “true in some larger rank-initial segment of the universe,” so that
$V_\beta $
are the rank-initial segments of the cumulative set-theoretic hierarchy, and the potentialist modality here is “true in some larger rank-initial segment of the universe,” so that
![]() is true at some
is true at some
![]() $V_\beta $
, if
$V_\beta $
, if
![]() $\varphi $
is true in some larger
$\varphi $
is true in some larger
![]() $V_\delta $
. This system clearly provides a potentialist account of its limit, the full background set-theoretic universe V.
$V_\delta $
. This system clearly provides a potentialist account of its limit, the full background set-theoretic universe V.
Theorem 8. In set-theoretic rank potentialism
![]() $\mathcal {V}$
, every world
$\mathcal {V}$
, every world
![]() $V_\beta $
obeys
$V_\beta $
obeys
 $$ \begin{align*} S4.3 \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_{\in,V_\beta}) \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}_\in) \subseteq S5. \end{align*} $$
$$ \begin{align*} S4.3 \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_{\in,V_\beta}) \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}_\in) \subseteq S5. \end{align*} $$
In other words, S4.3 is valid in every world for these languages and the validities of every world are contained within S5.
Proof. Since the rank-initial segments
![]() $V_\beta $
are linearly ordered, it follows by Theorem 2 that every assertion in S4.3 is valid for rank potentialism, with respect to any language, verifying the first inclusion. The central inclusion
$V_\beta $
are linearly ordered, it follows by Theorem 2 that every assertion in S4.3 is valid for rank potentialism, with respect to any language, verifying the first inclusion. The central inclusion
 $\mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}^\Diamond _{\in ,V_\beta })\subseteq \mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}_\in )$
follows from the fact that it is a less severe requirement for a propositional modal assertion to be valid with respect to less expressive language. Finally, to show the last inclusion
$\mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}^\Diamond _{\in ,V_\beta })\subseteq \mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}_\in )$
follows from the fact that it is a less severe requirement for a propositional modal assertion to be valid with respect to less expressive language. Finally, to show the last inclusion
![]() $\mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}_\in )\subseteq S5$
, it suffices by Theorems 3 and 4 to show that we have an infinite dial that works in all these worlds. For
$\mathord {\textrm {Val}}_{\mathcal {V}}(V_\beta ,\mathcal {L}_\in )\subseteq S5$
, it suffices by Theorems 3 and 4 to show that we have an infinite dial that works in all these worlds. For
![]() $j<\omega $
, let
$j<\omega $
, let
![]() $d_j$
be the assertion that the height of the ordinals is
$d_j$
be the assertion that the height of the ordinals is
![]() $\lambda +j$
, where
$\lambda +j$
, where
![]() $\lambda $
is a limit ordinal or zero. So
$\lambda $
is a limit ordinal or zero. So
![]() $d_j$
is true in
$d_j$
is true in
![]() $V_\beta $
if and only if
$V_\beta $
if and only if
![]() $\beta =\lambda +j$
for some limit ordinal
$\beta =\lambda +j$
for some limit ordinal
![]() $\lambda $
or zero. These statements are expressible in the language of set theory
$\lambda $
or zero. These statements are expressible in the language of set theory
![]() $\mathcal {L}_\in $
without parameters or modal vocabulary. And they form a dial, because every ordinal
$\mathcal {L}_\in $
without parameters or modal vocabulary. And they form a dial, because every ordinal
![]() $\beta $
is uniquely expressed as
$\beta $
is uniquely expressed as
![]() $\lambda +j$
for some limit ordinal
$\lambda +j$
for some limit ordinal
![]() $\lambda $
or zero and some finite
$\lambda $
or zero and some finite
![]() $j<\omega $
, and from any
$j<\omega $
, and from any
![]() $V_\beta $
we can extend to a larger
$V_\beta $
we can extend to a larger
![]() $V_{\lambda +j}$
so as to realize any desired j.
$V_{\lambda +j}$
so as to realize any desired j.
Theorem 9. The lower bound of Theorem 8 is sharp, for there are some worlds
![]() $V_\beta $
in the rank-potentialist system
$V_\beta $
in the rank-potentialist system
![]() $\mathcal {V}$
with
$\mathcal {V}$
with
 $$ \begin{align*}S4.3 = \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_{\in,V_\beta})= \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}_\in).\end{align*} $$
$$ \begin{align*}S4.3 = \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_{\in,V_\beta})= \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}_\in).\end{align*} $$
Proof. Let
![]() $r_k$
be the assertion that the ordinal
$r_k$
be the assertion that the ordinal
![]() $\omega \cdot k$
exists. These statements are expressible in the language of set theory without parameters, since
$\omega \cdot k$
exists. These statements are expressible in the language of set theory without parameters, since
![]() $r_k$
is equivalent in any
$r_k$
is equivalent in any
![]() $V_\beta $
to the assertion that there are at least k distinct limit ordinals. The statements constitute a ratchet for the system of rank potentialism, since once the ordinal
$V_\beta $
to the assertion that there are at least k distinct limit ordinals. The statements constitute a ratchet for the system of rank potentialism, since once the ordinal
![]() $\omega \cdot k$
exists in
$\omega \cdot k$
exists in
![]() $V_\beta $
, then all smaller
$V_\beta $
, then all smaller
![]() $\omega \cdot r$
also exist; they continue to exist in all larger
$\omega \cdot r$
also exist; they continue to exist in all larger
![]() $V_\delta $
; and if
$V_\delta $
; and if
![]() $\omega \cdot k$
does not yet exist in
$\omega \cdot k$
does not yet exist in
![]() $V_\beta $
, then we can extend
$V_\beta $
, then we can extend
![]() $V_\beta $
to
$V_\beta $
to
![]() $V_{\omega \cdot k+1}$
, where
$V_{\omega \cdot k+1}$
, where
![]() $\omega \cdot k$
exists but
$\omega \cdot k$
exists but
![]() $\omega \cdot (k+1)$
does not yet exist. For any fixed
$\omega \cdot (k+1)$
does not yet exist. For any fixed
![]() $n<\omega $
and any
$n<\omega $
and any
![]() $i<n$
, let
$i<n$
, let
![]() $d_i^*$
assert that the dial value
$d_i^*$
assert that the dial value
![]() $d_j$
of the previous theorem has
$d_j$
of the previous theorem has
![]() $i=j\mod n$
. That is, we use the dial values of the previous theorem modulo n. The point is that we can realize any dial value for
$i=j\mod n$
. That is, we use the dial values of the previous theorem modulo n. The point is that we can realize any dial value for
![]() $d_i^*$
without raising the ratchet volume, since we simply move to the next block of size n, and so we have independent ratchet and dials of any desired size, and these are expressible in the language of set theory without parameters or modal operators. It follows by Theorem 6 that the validities of
$d_i^*$
without raising the ratchet volume, since we simply move to the next block of size n, and so we have independent ratchet and dials of any desired size, and these are expressible in the language of set theory without parameters or modal operators. It follows by Theorem 6 that the validities of
![]() $V_\beta $
for the language of set theory are precisely S4.3, for sufficiently small
$V_\beta $
for the language of set theory are precisely S4.3, for sufficiently small
![]() $\beta $
, as desired.
$\beta $
, as desired.
We could have alternatively proved Theorem 9 by using a long ratchet and applying Theorem 7. Indeed, the proof we gave amounts to using the method described in Theorem 7 with the ratchet
![]() $r_\alpha =$
“
$r_\alpha =$
“
![]() $\alpha $
exists.”
$\alpha $
exists.”
Corollary 10. The modal logic of rank potentialism with respect to the language of set theory—the propositional modal assertions valid in all worlds—is exactly
![]() $\mathord {\textrm {Val}}_{\mathcal {V}}(\mathcal {L}_\in ) = S4.3$
. Furthermore,
$\mathord {\textrm {Val}}_{\mathcal {V}}(\mathcal {L}_\in ) = S4.3$
. Furthermore,
![]() $\mathord {\textrm {Val}}_{\mathcal {V}}(\mathcal {L}^+_\in ) = S4.3$
for any language
$\mathord {\textrm {Val}}_{\mathcal {V}}(\mathcal {L}^+_\in ) = S4.3$
for any language
![]() $\mathcal {L}^+_\in $
extending the language of set theory
$\mathcal {L}^+_\in $
extending the language of set theory
![]() $\mathcal {L}_\in $
by parameters, relations or modal vocabulary.
$\mathcal {L}_\in $
by parameters, relations or modal vocabulary.
Proof. Theorems 8 and 9 show that S4.3 is valid in all rank-potentialist worlds
![]() $V_\beta $
, and there is some world realizing only the validities in S4.3. So it is precisely S4.3 that is valid in all worlds, and consequently
$V_\beta $
, and there is some world realizing only the validities in S4.3. So it is precisely S4.3 that is valid in all worlds, and consequently
![]() $\mathord {\textrm {Val}}_{\mathcal {V}}(\mathcal {L}_\in ) = S4.3$
. It follows by Theorem 2 that
$\mathord {\textrm {Val}}_{\mathcal {V}}(\mathcal {L}_\in ) = S4.3$
. It follows by Theorem 2 that
![]() $\mathord {\textrm {Val}}_{\mathcal {V}}(\mathcal {L}_\in ^+) = S4.3$
for any extension of the language, since the
$\mathord {\textrm {Val}}_{\mathcal {V}}(\mathcal {L}_\in ^+) = S4.3$
for any extension of the language, since the
![]() $V_\beta $
are linearly ordered.
$V_\beta $
are linearly ordered.
Let us turn now to the upper bound of Theorem 8, which also is sharp. Indeed, it is sharp in a way that we find interesting and attractive, for the worlds realizing the upper bound fulfill what we call the potentialist maximality principle, an interesting set-theoretic principle of its own.
Definition 11. Let us define that a world W in a potentialist system
![]() $\mathcal {W}$
fulfills the potentialist maximality principle for a class of assertions, if the modal theory S5 is valid at W for those assertions under the potentialist semantics.
$\mathcal {W}$
fulfills the potentialist maximality principle for a class of assertions, if the modal theory S5 is valid at W for those assertions under the potentialist semantics.
Since S4 is valid in any potentialist system by Theorem 2, the potentialist maximality principle amounts to the validity of Axiom 5
which expresses a kind of maximality principle, since it asserts that whenever assertion
![]() $\varphi $
is potentially necessarily true, then it is already actually true. Under this principle, the collection of potentially necessarily true statements that are actually true is maximized.
$\varphi $
is potentially necessarily true, then it is already actually true. Under this principle, the collection of potentially necessarily true statements that are actually true is maximized.
An ordinal
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _3$
-correct, if
$\Sigma _3$
-correct, if
![]() $V_\delta \prec _{\Sigma _3} V$
, meaning that
$V_\delta \prec _{\Sigma _3} V$
, meaning that
![]() $V_\delta $
and V agree on the truth of
$V_\delta $
and V agree on the truth of
![]() $\Sigma _3$
formulas with parameters from
$\Sigma _3$
formulas with parameters from
![]() $V_\delta $
. Any such ordinal
$V_\delta $
. Any such ordinal
![]() $\delta $
is a
$\delta $
is a
![]() $\beth $
-fixed point and a limit of such fixed points, and more. The usual proof of the Lévy–Montague reflection theorem shows that the class of all
$\beth $
-fixed point and a limit of such fixed points, and more. The usual proof of the Lévy–Montague reflection theorem shows that the class of all
![]() $\Sigma _3$
-correct cardinals, denoted
$\Sigma _3$
-correct cardinals, denoted
![]() $C^{(3)}$
, is closed and unbounded in the ordinals.
$C^{(3)}$
, is closed and unbounded in the ordinals.
Theorem 12. The following are equivalent for any ordinal
![]() $\delta$
:
$\delta$
:
-
(1)
 $V_\delta $
satisfies the rank-potentialism maximality principle for assertions in the language of set theory with parameters from
$V_\delta $
satisfies the rank-potentialism maximality principle for assertions in the language of set theory with parameters from
 $V_\delta $
. That is,
$V_\delta $
. That is,  $$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{V}}(V_\delta,\mathcal{L}_{\in,V_\delta})=S5.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{V}}(V_\delta,\mathcal{L}_{\in,V_\delta})=S5.\end{align*} $$
-
(2)
 $\delta $
is
$\delta $
is
 $\Sigma _3$
-correct.
$\Sigma _3$
-correct.
Proof. (
![]() $2\mathrel {\rightarrow } 1$
) Assume that
$2\mathrel {\rightarrow } 1$
) Assume that
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _3$
-correct. Since we already know that S4.3 is valid at
$\Sigma _3$
-correct. Since we already know that S4.3 is valid at
![]() $V_\delta $
, it suffices to verify the validity of Axiom 5. So suppose that
$V_\delta $
, it suffices to verify the validity of Axiom 5. So suppose that
![]() for some assertion
for some assertion
![]() $\varphi $
in the language of set theory with parameters
$\varphi $
in the language of set theory with parameters
![]() $\vec a\in V_\delta $
, using the rank-potentialist semantics. This means that there is some
$\vec a\in V_\delta $
, using the rank-potentialist semantics. This means that there is some
![]() $\lambda \geq \delta $
, such that for all
$\lambda \geq \delta $
, such that for all
![]() $\theta \geq \lambda $
we have
$\theta \geq \lambda $
we have
![]() $V_\theta \models \varphi (\vec a)$
. The assertion
$V_\theta \models \varphi (\vec a)$
. The assertion
![]() $\exists \lambda \,\forall \theta \geq \lambda \,V_\theta \models \varphi (\vec a)$
has complexity
$\exists \lambda \,\forall \theta \geq \lambda \,V_\theta \models \varphi (\vec a)$
has complexity
![]() $\Sigma _3(\vec a)$
in the language of set theory,Footnote
5
and so this assertion must be true in
$\Sigma _3(\vec a)$
in the language of set theory,Footnote
5
and so this assertion must be true in
![]() $V_\delta $
, thereby verifying this instance of S5. And so the potentialist maximality principle is true at
$V_\delta $
, thereby verifying this instance of S5. And so the potentialist maximality principle is true at
![]() $V_\delta $
for assertions in the language of set theory with parameters from
$V_\delta $
for assertions in the language of set theory with parameters from
![]() $V_\delta $
.
$V_\delta $
.
(
![]() $1\mathrel {\rightarrow } 2$
) Conversely, assume that S5 is valid in
$1\mathrel {\rightarrow } 2$
) Conversely, assume that S5 is valid in
![]() $V_\delta $
for assertions in the language of set theory with parameters in
$V_\delta $
for assertions in the language of set theory with parameters in
![]() $V_\delta $
. This implies that
$V_\delta $
. This implies that
![]() $\delta $
is a
$\delta $
is a
![]() $\beth $
-fixed point, since for any ordinal
$\beth $
-fixed point, since for any ordinal
![]() $\alpha $
it is possibly necessary that
$\alpha $
it is possibly necessary that
![]() $\beth _\alpha $
exists (one need only grow the universe sufficiently tall), and therefore, for any
$\beth _\alpha $
exists (one need only grow the universe sufficiently tall), and therefore, for any
![]() $\alpha <\delta $
we know that
$\alpha <\delta $
we know that
![]() $\beth _\alpha $
exists already in
$\beth _\alpha $
exists already in
![]() $V_\delta $
, and so
$V_\delta $
, and so
![]() $\delta =\beth _\delta $
. This implies
$\delta =\beth _\delta $
. This implies
![]() $V_\delta =H_\delta $
and so
$V_\delta =H_\delta $
and so
![]() $V_\delta \prec _{\Sigma _1} V$
by the Lévy reflection theorem; so
$V_\delta \prec _{\Sigma _1} V$
by the Lévy reflection theorem; so
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _1$
-correct. A similar argument works more generally to establish
$\Sigma _1$
-correct. A similar argument works more generally to establish
![]() $\Sigma _3$
-correctness. Specifically, suppose that a
$\Sigma _3$
-correctness. Specifically, suppose that a
![]() $\Sigma _3$
assertion holds in V, using some parameters
$\Sigma _3$
assertion holds in V, using some parameters
![]() $\vec a\in V_\delta $
. Every
$\vec a\in V_\delta $
. Every
![]() $\Sigma _3$
assertion is equivalent to an assertion of the form
$\Sigma _3$
assertion is equivalent to an assertion of the form
![]() $\exists x\forall \beta \,V_\beta \models \psi (x,\vec a)$
. Thus,
$\exists x\forall \beta \,V_\beta \models \psi (x,\vec a)$
. Thus,
![]() , since one need only grow the universe sufficiently tall until the witness x is found. By S5, we may conclude that
, since one need only grow the universe sufficiently tall until the witness x is found. By S5, we may conclude that
![]() $V_\delta \models \exists x\forall \beta \, V_\beta \models \psi (x,\vec a)$
, showing that the
$V_\delta \models \exists x\forall \beta \, V_\beta \models \psi (x,\vec a)$
, showing that the
![]() $\Sigma _3$
assertion holds in
$\Sigma _3$
assertion holds in
![]() $V_\delta $
. So
$V_\delta $
. So
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _3$
-correct, as desired.
$\Sigma _3$
-correct, as desired.
Corollary 13. The upper bound of Theorem 8 is sharp, for there are worlds
![]() $V_\delta $
with
$V_\delta $
with
Proof. Theorem 12 shows that this is true for any
![]() $\Sigma _3$
-correct cardinal
$\Sigma _3$
-correct cardinal
![]() $\delta $
, and there is a proper-class club of such cardinals.
$\delta $
, and there is a proper-class club of such cardinals.
The maximality principle for the full potentialist language
![]() $\mathcal {L}_\in ^\Diamond $
, not just the language
$\mathcal {L}_\in ^\Diamond $
, not just the language
![]() $\mathcal {L}_\in $
of set theory, turns out to be strictly stronger. Indeed, the following theorem shows that the full maximality principle at a world
$\mathcal {L}_\in $
of set theory, turns out to be strictly stronger. Indeed, the following theorem shows that the full maximality principle at a world
![]() $V_\delta $
reveals that this
$V_\delta $
reveals that this
![]() $V_\delta $
is in a sense a miniature replica of the full ambient universe V in which it sits, having all the same truths about the objects in
$V_\delta $
is in a sense a miniature replica of the full ambient universe V in which it sits, having all the same truths about the objects in
![]() $V_\delta $
. A cardinal
$V_\delta $
. A cardinal
![]() $\delta $
is correct, if it is
$\delta $
is correct, if it is
![]() $\Sigma _n$
-correct for every n, or in other words, if it realizes the scheme
$\Sigma _n$
-correct for every n, or in other words, if it realizes the scheme
![]() $V_\delta \prec V$
. In light of Tarski’s theorem on the non-definability of truth, this concept is not expressible as a single assertion in the language of set theory, although it can be expressed as a scheme of statements, the assertion that
$V_\delta \prec V$
. In light of Tarski’s theorem on the non-definability of truth, this concept is not expressible as a single assertion in the language of set theory, although it can be expressed as a scheme of statements, the assertion that
![]() $\delta $
realizes a certain type.
$\delta $
realizes a certain type.
Theorem 14. The following schemes are equivalent for any ordinal
![]() $\delta $
:
$\delta $
:
-
(1)
 $V_\delta $
satisfies the rank-potentialist maximality principle for assertions in the potentialist language
$V_\delta $
satisfies the rank-potentialist maximality principle for assertions in the potentialist language
 $\mathcal {L}_{\in ,V_\delta }^\Diamond $
allowing parameters from
$\mathcal {L}_{\in ,V_\delta }^\Diamond $
allowing parameters from
 $V_\delta $
. That is,
$V_\delta $
. That is,  $$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{V}}(V_\delta,\mathcal{L}_{\in,V_\delta}^\Diamond)=S5.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{V}}(V_\delta,\mathcal{L}_{\in,V_\delta}^\Diamond)=S5.\end{align*} $$
-
(2)
 $\delta $
is a correct cardinal.
$\delta $
is a correct cardinal.
Proof. (
![]() $2\mathrel {\rightarrow } 1$
) Assume that
$2\mathrel {\rightarrow } 1$
) Assume that
![]() $\delta $
is correct, so that we have the scheme
$\delta $
is correct, so that we have the scheme
![]() $V_\delta \prec V$
, and suppose that
$V_\delta \prec V$
, and suppose that
![]() is true at
is true at
![]() $V_\delta $
, where
$V_\delta $
, where
![]() $\varphi $
is an assertion in the potentialist language
$\varphi $
is an assertion in the potentialist language
![]() $\mathcal {L}_\in ^\Diamond $
and
$\mathcal {L}_\in ^\Diamond $
and
![]() $\vec a\in V_\delta $
. Thus,
$\vec a\in V_\delta $
. Thus,
![]() $\exists \lambda \forall \theta \geq \lambda \, V_\theta \models \varphi (\vec a)$
is true in V. Since the rank-potentialist modalities are expressible in the language of set theory, it follows from the
$\exists \lambda \forall \theta \geq \lambda \, V_\theta \models \varphi (\vec a)$
is true in V. Since the rank-potentialist modalities are expressible in the language of set theory, it follows from the
![]() $V_\delta \prec V$
scheme that
$V_\delta \prec V$
scheme that
![]() $V_\delta \models \exists \lambda \forall \theta \geq \lambda \, V_\theta \models \varphi (\vec a)$
. Note that since
$V_\delta \models \exists \lambda \forall \theta \geq \lambda \, V_\theta \models \varphi (\vec a)$
. Note that since
![]() $V_\delta \prec V$
, it follows that
$V_\delta \prec V$
, it follows that
![]() $V_\delta $
and V agree on whether some particular
$V_\delta $
and V agree on whether some particular
![]() $V_\theta $
satisfies a given rank-potentialist assertion. Since
$V_\theta $
satisfies a given rank-potentialist assertion. Since
![]() $V_\delta \prec V$
, it follows that the witness
$V_\delta \prec V$
, it follows that the witness
![]() $\lambda <\delta $
also works in V, and so
$\lambda <\delta $
also works in V, and so
![]() $V_\delta \models \varphi (\vec a)$
, verifying this instance of S5. So
$V_\delta \models \varphi (\vec a)$
, verifying this instance of S5. So
![]() $V_\delta $
satisfies the desired potentialist maximality principle.
$V_\delta $
satisfies the desired potentialist maximality principle.
(
![]() $1\mathrel {\rightarrow } 2$
) Conversely, suppose that S5 holds at
$1\mathrel {\rightarrow } 2$
) Conversely, suppose that S5 holds at
![]() $V_\delta $
for assertions in the potentialist language
$V_\delta $
for assertions in the potentialist language
![]() $\mathcal {L}_\in ^\Diamond $
with parameters in
$\mathcal {L}_\in ^\Diamond $
with parameters in
![]() $V_\delta $
. We know from Statement 1 that
$V_\delta $
. We know from Statement 1 that
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _3$
correct. Suppose that
$\Sigma _3$
correct. Suppose that
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _n$
-correct, and that a
$\Sigma _n$
-correct, and that a
![]() $\Sigma _{n+1}$
assertion is true in V. So
$\Sigma _{n+1}$
assertion is true in V. So
![]() $V\models \exists x\,\psi (x,\vec a)$
, where
$V\models \exists x\,\psi (x,\vec a)$
, where
![]() $\psi $
has complexity
$\psi $
has complexity
![]() $\Pi _n$
. By Theorem 1, the set-theoretic assertion
$\Pi _n$
. By Theorem 1, the set-theoretic assertion
![]() $\psi (x,\vec a)$
is true in V if and only if
$\psi (x,\vec a)$
is true in V if and only if
![]() $\psi ^\Diamond (x,\vec a)$
is true at any
$\psi ^\Diamond (x,\vec a)$
is true at any
![]() $V_\beta $
containing x and
$V_\beta $
containing x and
![]() $\vec a$
. Thus,
$\vec a$
. Thus,
![]() , since once one goes high enough, the witness x from V will exists. By S5, therefore, there is
, since once one goes high enough, the witness x from V will exists. By S5, therefore, there is
![]() $x\in V_\delta $
with
$x\in V_\delta $
with
![]() $V_\delta \models \psi ^\Diamond (x,\vec a)$
, which means that
$V_\delta \models \psi ^\Diamond (x,\vec a)$
, which means that
![]() $V\models \psi (x,\vec a)$
, and so we have found the desired witness x inside
$V\models \psi (x,\vec a)$
, and so we have found the desired witness x inside
![]() $V_\delta $
. So
$V_\delta $
. So
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _{n+1}$
-correct, as desired.
$\Sigma _{n+1}$
-correct, as desired.
Although ZFC proves that there are numerous
![]() $\Sigma _3$
-correct cardinals
$\Sigma _3$
-correct cardinals
![]() $\delta $
and therefore numerous instances
$\delta $
and therefore numerous instances
![]() $V_\delta $
of the potentialist maximality principle for assertions in the language of set theory with parameters, it is meanwhile not provable in ZFC, if consistent, that there is a cardinal
$V_\delta $
of the potentialist maximality principle for assertions in the language of set theory with parameters, it is meanwhile not provable in ZFC, if consistent, that there is a cardinal
![]() $\delta $
fulfilling the scheme
$\delta $
fulfilling the scheme
![]() $V_\delta \prec V$
, and so we do not necessarily have instances of the potentialist maximality principle in the full potentialist language of set theory
$V_\delta \prec V$
, and so we do not necessarily have instances of the potentialist maximality principle in the full potentialist language of set theory
![]() $\mathcal {L}_\in ^\Diamond $
with parameters. Meanwhile, the
$\mathcal {L}_\in ^\Diamond $
with parameters. Meanwhile, the
![]() $V_\delta \prec V$
scheme is equiconsistent with and indeed conservative over ZFC, for every model
$V_\delta \prec V$
scheme is equiconsistent with and indeed conservative over ZFC, for every model
![]() $M\models {\textrm {ZFC}}$
has an elementary extension in which this scheme is realized. To see this, consider the elementary diagram of M together with the scheme asserting
$M\models {\textrm {ZFC}}$
has an elementary extension in which this scheme is realized. To see this, consider the elementary diagram of M together with the scheme asserting
![]() $V_\delta \prec V$
, in the language with
$V_\delta \prec V$
, in the language with
![]() $\delta $
as a new constant symbol; every finite subtheory is satisfiable by the reflection theorem applied in M, and so by compactness there is an elementary extension of M with a correct cardinal (see also [Reference Hamkins6, lemma 5.4]).
$\delta $
as a new constant symbol; every finite subtheory is satisfiable by the reflection theorem applied in M, and so by compactness there is an elementary extension of M with a correct cardinal (see also [Reference Hamkins6, lemma 5.4]).
Note that each of the statements in Theorem 14 is a full scheme of assertions in the language of set theory. In particular, one cannot express the concept of “
![]() $\Sigma _n$
-correct for every n” by a single statement in the language of set theory; instead, one makes a separate assertion for each n in the metatheory. Similarly, the assertion that a modal assertion is valid for all
$\Sigma _n$
-correct for every n” by a single statement in the language of set theory; instead, one makes a separate assertion for each n in the metatheory. Similarly, the assertion that a modal assertion is valid for all
![]() $\mathcal {L}_\in ^\Diamond $
assertions is not a single assertion in the language of set theory, but one can assert all instances of it as a scheme. In order to formalize Theorem 14 in ZFC, therefore, we may view it as two theorem schemes, one proving every instance of Statement 2, assuming the theory expressed by Statement 1, and one proving every instance of Statement 1, assuming the theory expressed by Statement 2. This subtle formalization issue did not arise in Theorem 12, because the bounded complexity of the correctness assumption there and the fact that the arbitrary set-theoretic assertions are evaluated there only in various set structures
$\mathcal {L}_\in ^\Diamond $
assertions is not a single assertion in the language of set theory, but one can assert all instances of it as a scheme. In order to formalize Theorem 14 in ZFC, therefore, we may view it as two theorem schemes, one proving every instance of Statement 2, assuming the theory expressed by Statement 1, and one proving every instance of Statement 1, assuming the theory expressed by Statement 2. This subtle formalization issue did not arise in Theorem 12, because the bounded complexity of the correctness assumption there and the fact that the arbitrary set-theoretic assertions are evaluated there only in various set structures
![]() $V_\beta $
meant we could formalize it all as a single assertion in ZFC.
$V_\beta $
meant we could formalize it all as a single assertion in ZFC.
We expect (and suggest as a good graduate-student project) that one can provide a somewhat tighter analysis connecting the precise degree of correctness of
![]() $\delta $
and the modal-operator complexity of the assertions allowed to be substituted in the S5 axioms. For example, if
$\delta $
and the modal-operator complexity of the assertions allowed to be substituted in the S5 axioms. For example, if
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _4$
-correct, then S5 would be valid at world
$\Sigma _4$
-correct, then S5 would be valid at world
![]() $V_\delta $
with respect to substitution instances in the language
$V_\delta $
with respect to substitution instances in the language
![]() $\mathcal {L}_\in ^\Diamond $
having at most one modal operator at the front. As the correctness of
$\mathcal {L}_\in ^\Diamond $
having at most one modal operator at the front. As the correctness of
![]() $\delta $
improves, one can accommodate more complex modal assertions in the substitution instances, and Theorem 14 is simply the amalgamation of all these level-by-level results.
$\delta $
improves, one can accommodate more complex modal assertions in the substitution instances, and Theorem 14 is simply the amalgamation of all these level-by-level results.
Corollary 15. It is relatively consistent with ZFC that the upper bound of Theorem 8 is sharp in a stronger way, with a world
![]() $V_\delta $
having
$V_\delta $
having
 $$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{V}}(V_\delta,\mathcal{L}_{\in,V_\delta}^\Diamond)= \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}_\in)=S5.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{V}}(V_\delta,\mathcal{L}_{\in,V_\delta}^\Diamond)= \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}_\in)=S5.\end{align*} $$
Proof. Theorem 14 shows that this is true exactly at the (fully) correct cardinals
![]() $\delta $
. The existence of a correct cardinal is independent of but equiconsistent with ZFC.
$\delta $
. The existence of a correct cardinal is independent of but equiconsistent with ZFC.
3.3 Variations on set-theoretic rank potentialism
Some height-potentialists may prefer a more restrictive class of universe fragments. For example, perhaps one wants to consider
![]() $V_\beta $
only when
$V_\beta $
only when
![]() $\beta $
is itself a strong limit cardinal, or a
$\beta $
is itself a strong limit cardinal, or a
![]() $\Sigma _n$
-correct cardinal, or where
$\Sigma _n$
-correct cardinal, or where
![]() $V_\beta $
exhibits some other feature, such as satisfying some definable theory T. These situations are unified by the case where we have a proper class of ordinals
$V_\beta $
exhibits some other feature, such as satisfying some definable theory T. These situations are unified by the case where we have a proper class of ordinals
![]() $A\subseteq \mathord {{\textrm {Ord}}}$
and we consider the potentialist system
$A\subseteq \mathord {{\textrm {Ord}}}$
and we consider the potentialist system
Theorem 16. If
![]() $A\subseteq \mathord {{\textrm {Ord}}}$
is a definable proper class of ordinals in the set-theoretic universe V, and the definition of A is absolute to
$A\subseteq \mathord {{\textrm {Ord}}}$
is a definable proper class of ordinals in the set-theoretic universe V, and the definition of A is absolute to
![]() $V_\beta $
for all
$V_\beta $
for all
![]() $\beta \in A$
, then every world
$\beta \in A$
, then every world
![]() $V_\beta $
in the relativized rank-potentialist system
$V_\beta $
in the relativized rank-potentialist system
![]() $\mathcal {V}_A$
obeys
$\mathcal {V}_A$
obeys
 $$ \begin{align*}S4.3 \ \subseteq\ \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_{\in,V_\beta}) \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
$$ \begin{align*}S4.3 \ \subseteq\ \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_{\in,V_\beta}) \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
If A is definable but not necessarily absolute, then nevertheless every world obeys at least
 $$ \begin{align*}S4.3\ \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_{\in,V_\beta}) \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_\in) \subseteq S5.\end{align*} $$
$$ \begin{align*}S4.3\ \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_{\in,V_\beta}) \subseteq \mathord{\mathrm{Val}}_{\mathcal{V}}(V_\beta,\mathcal{L}^\Diamond_\in) \subseteq S5.\end{align*} $$
Furthermore, the lower bounds in each case are realized.
Proof. Since the worlds
![]() $V_\beta $
in
$V_\beta $
in
![]() $\mathcal {V}_A$
are linearly ordered, it follows that every assertion of S4.3 will be valid for the potentialist semantics with respect to any of the languages. To show that some worlds validate only S4.3, it suffices by Theorem 7 to find uniform long ratchets. Consider first the case where the definition of A is absolute to
$\mathcal {V}_A$
are linearly ordered, it follows that every assertion of S4.3 will be valid for the potentialist semantics with respect to any of the languages. To show that some worlds validate only S4.3, it suffices by Theorem 7 to find uniform long ratchets. Consider first the case where the definition of A is absolute to
![]() $V_\beta $
for every
$V_\beta $
for every
![]() $\beta \in A$
. For example, this would be true if A was the class of strong limit cardinals, or the class of
$\beta \in A$
. For example, this would be true if A was the class of strong limit cardinals, or the class of
![]() $\Sigma _n$
-correct cardinals, or if A was the class of
$\Sigma _n$
-correct cardinals, or if A was the class of
![]() $\beta $
for which
$\beta $
for which
![]() $V_\beta $
satisfied a certain specific c.e. theory T. For any ordinal
$V_\beta $
satisfied a certain specific c.e. theory T. For any ordinal
![]() $\alpha $
, let
$\alpha $
, let
![]() $r_\alpha $
be the assertion that there are at least
$r_\alpha $
be the assertion that there are at least
![]() $\alpha $
many ordinals in A. These statements are expressible in the language of set theory and they form a long ratchet, since once they are true in some
$\alpha $
many ordinals in A. These statements are expressible in the language of set theory and they form a long ratchet, since once they are true in some
![]() $V_\beta $
, they remain true in all taller models
$V_\beta $
, they remain true in all taller models
![]() $V_\delta $
, by the absoluteness assumption on A; they are all false in the smallest model
$V_\delta $
, by the absoluteness assumption on A; they are all false in the smallest model
![]() $V_\beta $
where
$V_\beta $
where
![]() $\beta $
is the least element of A; they have the necessary downward implications; and for any
$\beta $
is the least element of A; they have the necessary downward implications; and for any
![]() $\alpha $
, we can let
$\alpha $
, we can let
![]() $\beta $
be the
$\beta $
be the
![]() $(\alpha +1)^{\textrm {st}}$
element of A and observe that
$(\alpha +1)^{\textrm {st}}$
element of A and observe that
![]() $V_\beta $
thinks that there are precisely
$V_\beta $
thinks that there are precisely
![]() $\alpha $
many elements of A (again using the absoluteness of A); it follows that
$\alpha $
many elements of A (again using the absoluteness of A); it follows that
![]() $r_\alpha $
is true in
$r_\alpha $
is true in
![]() $V_\beta $
but not
$V_\beta $
but not
![]() $r_{\alpha +1}$
. Because we have therefore produced a uniform long ratchet, expressible in the language of set theory, it follows from Theorem 7 that the propositional modal validities of any sufficiently small world
$r_{\alpha +1}$
. Because we have therefore produced a uniform long ratchet, expressible in the language of set theory, it follows from Theorem 7 that the propositional modal validities of any sufficiently small world
![]() $V_\beta $
of
$V_\beta $
of
![]() $\mathcal {V}_A$
, that is, where the ratchets have not yet been cranked, will be exactly
$\mathcal {V}_A$
, that is, where the ratchets have not yet been cranked, will be exactly
 $$ \begin{align*}S4.3=\mathord{\mathrm{Val}}_{\mathcal{V}_A}(V_\beta,\mathcal{L}_{\in,V_\beta}^\Diamond)=\mathord{\mathrm{Val}}_{\mathcal{V}_A}(V_\beta,\mathcal{L}_\in),\end{align*} $$
$$ \begin{align*}S4.3=\mathord{\mathrm{Val}}_{\mathcal{V}_A}(V_\beta,\mathcal{L}_{\in,V_\beta}^\Diamond)=\mathord{\mathrm{Val}}_{\mathcal{V}_A}(V_\beta,\mathcal{L}_\in),\end{align*} $$
realizing the lower bound in a strong way. Furthermore, Theorem 7 also shows that every world of
![]() $\mathcal {V}_A$
will have its validities contained in S5, establishing the upper bound.
$\mathcal {V}_A$
will have its validities contained in S5, establishing the upper bound.
Consider now the case where A is definable, but not necessarily absolute to all these
![]() $V_\beta $
. In this case, the statements
$V_\beta $
. In this case, the statements
![]() $r_\alpha $
of the previous paragraph might not be a ratchet, since perhaps some
$r_\alpha $
of the previous paragraph might not be a ratchet, since perhaps some
![]() $V_\beta $
thinks wrongly that there are
$V_\beta $
thinks wrongly that there are
![]() $\alpha $
many elements of A, but a larger
$\alpha $
many elements of A, but a larger
![]() $V_\delta $
recognizes that many of those ordinals are not actually in A. Nevertheless, we can fix this problem simply by making our ratchet assertions in the potentialist modal language
$V_\delta $
recognizes that many of those ordinals are not actually in A. Nevertheless, we can fix this problem simply by making our ratchet assertions in the potentialist modal language
![]() $\mathcal {L}_\in ^\Diamond $
, rather than in the language of set theory. Specifically, for our ratchet statements, we use instead the assertion
$\mathcal {L}_\in ^\Diamond $
, rather than in the language of set theory. Specifically, for our ratchet statements, we use instead the assertion
![]() $\bar r_\alpha $
that asserts that there are
$\bar r_\alpha $
that asserts that there are
![]() $\alpha $
many ordinals
$\alpha $
many ordinals
![]() $\xi $
for which
$\xi $
for which
![]() $(\xi \in A)^\Diamond $
, using the potentialist translation of the definition of A in V. By Theorem 1, the assertion
$(\xi \in A)^\Diamond $
, using the potentialist translation of the definition of A in V. By Theorem 1, the assertion
![]() $(\xi \in A)^\Diamond $
in some
$(\xi \in A)^\Diamond $
in some
![]() $V_\beta $
is equivalent to
$V_\beta $
is equivalent to
![]() $\xi \in A$
in V, and so
$\xi \in A$
in V, and so
![]() $\bar r_\alpha $
is true in some
$\bar r_\alpha $
is true in some
![]() $V_\beta $
just in case there are at least
$V_\beta $
just in case there are at least
![]() $\alpha $
many elements of A below
$\alpha $
many elements of A below
![]() $\beta $
. (This is a sneaky trick, and the cost is that our analysis on the bounds will apply only for
$\beta $
. (This is a sneaky trick, and the cost is that our analysis on the bounds will apply only for
![]() $\mathcal {L}^\Diamond $
-substitution instances; it could be that additional validities hold when one considers only substitution instances in the language of set theory
$\mathcal {L}^\Diamond $
-substitution instances; it could be that additional validities hold when one considers only substitution instances in the language of set theory
![]() $\mathcal {L}_\in $
alone.) These revised statements in effect are able to refer via the potentialist translation to the actual class A, and they form a long ratchet for the same reasons that
$\mathcal {L}_\in $
alone.) These revised statements in effect are able to refer via the potentialist translation to the actual class A, and they form a long ratchet for the same reasons that
![]() $r_\alpha $
did in the previous paragraph. Thus, in any case, the modal validities of the smallest world of
$r_\alpha $
did in the previous paragraph. Thus, in any case, the modal validities of the smallest world of
![]() $\mathcal {V}_A$
is exactly S4.3 for assertions in the potentialist language, again realizing the lower bound, and every world has its validities for that language contained in S5, establishing the upper bound.
$\mathcal {V}_A$
is exactly S4.3 for assertions in the potentialist language, again realizing the lower bound, and every world has its validities for that language contained in S5, establishing the upper bound.
Let us turn now to the question of whether the upper bounds are realized, for which we shall undertake a similar analysis as in the case of set-theoretic rank potentialism. For any class A, a cardinal
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _3(A)$
-correct, if
$\Sigma _3(A)$
-correct, if
![]() $\left \langle V_\delta ,\in ,A\cap V_\delta \right \rangle \prec _{\Sigma _3}\left \langle V,\in ,A\right \rangle $
. The proofs of Theorems 12 and 14 can be adapted to establish the following.
$\left \langle V_\delta ,\in ,A\cap V_\delta \right \rangle \prec _{\Sigma _3}\left \langle V,\in ,A\right \rangle $
. The proofs of Theorems 12 and 14 can be adapted to establish the following.
Theorem 17. Suppose that A is a definable class of ordinals, which is absolute to
![]() $V_\delta $
for any
$V_\delta $
for any
![]() $\delta \in A$
. Then the following are equivalent for the potentialist semantics of
$\delta \in A$
. Then the following are equivalent for the potentialist semantics of
![]() $\mathcal {V}_A=\{{V_\beta \mid \beta \in A}\}$
.
$\mathcal {V}_A=\{{V_\beta \mid \beta \in A}\}$
.
-
(1)
 $V_\delta $
satisfies the potentialist maximality principle for assertions in the language of set theory with parameters in
$V_\delta $
satisfies the potentialist maximality principle for assertions in the language of set theory with parameters in
 $V_\delta $
.
$V_\delta $
. -
(2)
 $\delta $
is
$\delta $
is
 $\Sigma _3(A)$
-correct.
$\Sigma _3(A)$
-correct.
Theorem 18. Suppose that A is a definable class of ordinals. Then the following are equivalent for the potentialist semantics of
![]() $\mathcal {V}_A=\{{V_\beta \mid \beta \in A}\}$
.
$\mathcal {V}_A=\{{V_\beta \mid \beta \in A}\}$
.
-
(1)
 $V_\delta $
satisfies the potentialist maximality principle for assertions in the potentialist language of set theory
$V_\delta $
satisfies the potentialist maximality principle for assertions in the potentialist language of set theory
 $\mathcal {L}_\in ^\Diamond $
with parameters in
$\mathcal {L}_\in ^\Diamond $
with parameters in
 $V_\delta $
.
$V_\delta $
. -
(2)
 $\delta $
is a correct cardinal.
$\delta $
is a correct cardinal.
Thus, the upper bounds of Theorem 16 are sharp. Notice that we do not need the predicate for A in Theorem 18, since it is definable and we get the absoluteness of A to
![]() $V_\delta $
from
$V_\delta $
from
![]() $\Sigma _n$
-correctness, once n is large enough.
$\Sigma _n$
-correctness, once n is large enough.
Let us briefly generalize the analysis to the case of an arbitrary class
![]() $A\subseteq \mathord {{\textrm {Ord}}}$
, not necessarily definable, in Gödel–Bernays set theory GBC. Consider the potentialist system
$A\subseteq \mathord {{\textrm {Ord}}}$
, not necessarily definable, in Gödel–Bernays set theory GBC. Consider the potentialist system
 $\mathcal {W}_A=\{{\left \langle V_\beta ,\in ,A\cap \beta \right \rangle \mid \beta \in A}\}$
in the language of set theory with a predicate for A, a language we denote by
$\mathcal {W}_A=\{{\left \langle V_\beta ,\in ,A\cap \beta \right \rangle \mid \beta \in A}\}$
in the language of set theory with a predicate for A, a language we denote by
![]() $\mathcal {L}_\in (A)$
.
$\mathcal {L}_\in (A)$
.
Theorem 19. Every world W in
![]() $\mathcal {W}_A$
obeys
$\mathcal {W}_A$
obeys
 $$ \begin{align*}S4.3\ \subseteq\ \mathord{\mathrm{Val}}(W,\mathcal{L}^\Diamond_{\in}(A)_W)\ \subseteq\ \mathord{\mathrm{Val}}(W,\mathcal{L}_\in(A))\ \subseteq\ S5.\end{align*} $$
$$ \begin{align*}S4.3\ \subseteq\ \mathord{\mathrm{Val}}(W,\mathcal{L}^\Diamond_{\in}(A)_W)\ \subseteq\ \mathord{\mathrm{Val}}(W,\mathcal{L}_\in(A))\ \subseteq\ S5.\end{align*} $$
The lower bound is sharp, in that there are some worlds W with
 $$ \begin{align*}S4.3 = \mathord{\mathrm{Val}}(W,\mathcal{L}^\Diamond_\in(A)_W) = \mathord{\mathrm{Val}}(W,\mathcal{L}_\in(A)).\end{align*} $$
$$ \begin{align*}S4.3 = \mathord{\mathrm{Val}}(W,\mathcal{L}^\Diamond_\in(A)_W) = \mathord{\mathrm{Val}}(W,\mathcal{L}_\in(A)).\end{align*} $$
Proof. This is simply an adaptation of Theorem 16. Since we have added A explicitly to the structures, it is in effect absolute between these structures, and so we get the stronger conclusions of that theorem, but only in the language in which A is a predicate.
Some set-theorists may prefer to use the sets
![]() $H_\kappa $
, the collection of sets of hereditary size less than
$H_\kappa $
, the collection of sets of hereditary size less than
![]() $\kappa $
, for a regular cardinal
$\kappa $
, for a regular cardinal
![]() $\kappa $
, in place of the rank-initial segments
$\kappa $
, in place of the rank-initial segments
![]() $V_\beta $
, and the analysis in this case is basically the same.
$V_\beta $
, and the analysis in this case is basically the same.
Theorem 20. The previous theorems also hold if one uses the sets
![]() $H_\kappa $
for regular cardinals
$H_\kappa $
for regular cardinals
![]() $\kappa $
, in place of the rank-initial segments
$\kappa $
, in place of the rank-initial segments
![]() $V_\beta $
. In particular, the potentialist account consisting of all
$V_\beta $
. In particular, the potentialist account consisting of all
![]() $H_\kappa $
, or of
$H_\kappa $
, or of
![]() $H_\kappa $
for regular cardinals from some definable proper class A, is in each case precisely S4.3.
$H_\kappa $
for regular cardinals from some definable proper class A, is in each case precisely S4.3.
-
(1) S4.3 is valid for
 $H_\kappa $
-potentialism in every world
$H_\kappa $
-potentialism in every world
 $H_\kappa $
.
$H_\kappa $
. -
(2) Some worlds
 $H_\kappa $
validate only S4.3.
$H_\kappa $
validate only S4.3. -
(3) Every world
 $H_\kappa $
has its validities contained within S5.
$H_\kappa $
has its validities contained within S5.
Proof. The proof is essentially identical to the proofs of Theorems 8 and 9. Namely, the S4.3 assertions are valid since the
![]() $H_\kappa $
are linearly ordered. Conversely, one can define ratchets for the
$H_\kappa $
are linearly ordered. Conversely, one can define ratchets for the
![]() $H_\kappa $
by letting
$H_\kappa $
by letting
![]() $r_\alpha $
assert that there are
$r_\alpha $
assert that there are
![]() $\alpha $
many regular cardinals
$\alpha $
many regular cardinals
![]() $\kappa $
for which
$\kappa $
for which
![]() $H_\kappa $
is allowed as a universe fragment, using the potentialist translation as in the proof of Theorem 16. So there are worlds
$H_\kappa $
is allowed as a universe fragment, using the potentialist translation as in the proof of Theorem 16. So there are worlds
![]() $H_\kappa $
in which only S4.3 is valid, and meanwhile, every world has its validities within S5.
$H_\kappa $
in which only S4.3 is valid, and meanwhile, every world has its validities within S5.
Since
![]() $V_\delta =H_\delta $
for any
$V_\delta =H_\delta $
for any
![]() $\beth $
-fixed point
$\beth $
-fixed point
![]() $\delta $
, which happens on a closed unbounded class of cardinals, the differences between
$\delta $
, which happens on a closed unbounded class of cardinals, the differences between
![]() $V_\delta $
-potentialism and
$V_\delta $
-potentialism and
![]() $H_\delta $
-potentialism tend to evaporate once one has the idea to restrict the class of
$H_\delta $
-potentialism tend to evaporate once one has the idea to restrict the class of
![]() $\delta $
.
$\delta $
.
3.4 Grothendieck universe potentialism
In current mathematical practice, the potentialist perspective is well illustrated by the category-theoretic usage of Grothendieck universes, or Grothendieck–Zermelo universes, as we shall call them. These are the rank-initial segments of the cumulative hierarchy
![]() $V_\kappa $
, for an inaccessible cardinal
$V_\kappa $
, for an inaccessible cardinal
![]() $\kappa $
. Zermelo introduced and studied these universes in 1930 [Reference Zermelo28], proving that they are exactly the models of second-order set theory
$\kappa $
. Zermelo introduced and studied these universes in 1930 [Reference Zermelo28], proving that they are exactly the models of second-order set theory
![]() ${\textrm {ZFC}}_2$
, and they have been studied by set theorists continuously since that time—they form the beginnings of the intensely studied large cardinal hierarchy. For example, the consistency strength of a single Mahlo cardinal is strictly stronger than ZFC with a proper class of inaccessible cardinals. Grothendieck rediscovered these universes in the 1960s, also considering the empty universe
${\textrm {ZFC}}_2$
, and they have been studied by set theorists continuously since that time—they form the beginnings of the intensely studied large cardinal hierarchy. For example, the consistency strength of a single Mahlo cardinal is strictly stronger than ZFC with a proper class of inaccessible cardinals. Grothendieck rediscovered these universes in the 1960s, also considering the empty universe
![]() $\emptyset $
and
$\emptyset $
and
![]() $V_\omega $
as instances, and used them to serve as a suitable universe concept in category theory.
$V_\omega $
as instances, and used them to serve as a suitable universe concept in category theory.
In the category-theoretic practice, mathematical claims are made relative to a given universe, rather than to the entire set-theoretic universe, but one feels free at any time to move to a larger universe. This practice therefore illustrates almost perfectly the potentialist idea, and accords very well also with how Zermelo himself perceived his universes. With the second-order system
![]() ${\textrm {ZFC}}_2$
in mind, Zermelo wrote:
${\textrm {ZFC}}_2$
in mind, Zermelo wrote:
What appears as an ‘ultrafinite non- or super-set’ in one model is, in the succeeding model, a perfectly good, valid set with both a cardinal number and an ordinal type, and is itself a foundation stone for the construction of a new domain [Reference Zermelo28].
That is, what is a proper class from the point of view of one model of
![]() ${\textrm {ZFC}}_2$
is merely a set from the point of view of some extended model. Zermelo is thus explicitly viewing these
${\textrm {ZFC}}_2$
is merely a set from the point of view of some extended model. Zermelo is thus explicitly viewing these
![]() $V_\kappa $
as set-theoretic worlds.
$V_\kappa $
as set-theoretic worlds.
So let us refer to Grothendieck–Zermelo (GZ) potentialism as concerned with the potentialist system
Meanwhile, the Grothendieck universe axiom is the assertion that every set is an element of a Grothendieck–Zermelo universe, or equivalently, that the inaccessible cardinals are unbounded in the ordinals.
Theorem 21. Assume the Grothendieck universe axiom holds. Then Grothendieck–Zermelo potentialism provides a potentialist account of the set-theoretic universe V, and every Grothendieck–Zermelo universe W obeys
 $$ \begin{align*}S4.3 \ \subseteq\ \mathord{\mathrm{Val}}_{\mathcal{Z}}(W,\mathcal{L}^\Diamond_{\in,W}) \subseteq \mathord{\mathrm{Val}}_{\mathcal{Z}}(W,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
$$ \begin{align*}S4.3 \ \subseteq\ \mathord{\mathrm{Val}}_{\mathcal{Z}}(W,\mathcal{L}^\Diamond_{\in,W}) \subseteq \mathord{\mathrm{Val}}_{\mathcal{Z}}(W,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
The lower bound is sharp, in that some Grothendieck–Zermelo universes W obey
 $$ \begin{align*}S4.3 \ = \mathord{\mathrm{Val}}_{\mathcal{Z}}(W,\mathcal{L}^\Diamond_{\in,W}) = \mathord{\mathrm{Val}}_{\mathcal{Z}}(W,\mathcal{L}_\in).\end{align*} $$
$$ \begin{align*}S4.3 \ = \mathord{\mathrm{Val}}_{\mathcal{Z}}(W,\mathcal{L}^\Diamond_{\in,W}) = \mathord{\mathrm{Val}}_{\mathcal{Z}}(W,\mathcal{L}_\in).\end{align*} $$
Proof. This is an immediate consequence of Theorem 16. Note that because the class of inaccessible cardinals is absolute to
![]() $V_\kappa $
, we obtain the stronger conclusions of that theorem.
$V_\kappa $
, we obtain the stronger conclusions of that theorem.
Let us now turn to the sharpness of the upper bound, which is a statement with large cardinal strength. A cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\Sigma _n$
-reflecting, if it is inaccessible and
$\Sigma _n$
-reflecting, if it is inaccessible and
![]() $\Sigma _n$
-correct.
$\Sigma _n$
-correct.
Theorem 22. For any inaccessible cardinal
![]() $\kappa $
, the following are equivalent:
$\kappa $
, the following are equivalent:
-
(1) The Grothendieck universe axiom holds and
 $V_\kappa $
satisfies the GZ-potentialist maximality principle for assertions in the language of set theory with parameters from
$V_\kappa $
satisfies the GZ-potentialist maximality principle for assertions in the language of set theory with parameters from
 $V_\kappa $
. That is,
$V_\kappa $
. That is,  $$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{Z}}(V_\kappa,\mathcal{L}_{\in,V_\kappa})=S5.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{Z}}(V_\kappa,\mathcal{L}_{\in,V_\kappa})=S5.\end{align*} $$
-
(2)
 $\kappa $
is a
$\kappa $
is a
 $\Sigma _3$
-reflecting cardinal.
$\Sigma _3$
-reflecting cardinal.
Proof. (
![]() $2\to 1$
) Assume that
$2\to 1$
) Assume that
![]() $\kappa $
is a
$\kappa $
is a
![]() $\Sigma _3$
-reflecting cardinal. So
$\Sigma _3$
-reflecting cardinal. So
![]() $\kappa $
is inaccessible and
$\kappa $
is inaccessible and
![]() $V_\kappa $
is a Grothendieck–Zermelo universe. Since
$V_\kappa $
is a Grothendieck–Zermelo universe. Since
![]() $V_\kappa \prec _{\Sigma _3}V$
and V has an inaccessible cardinal, it follows that
$V_\kappa \prec _{\Sigma _3}V$
and V has an inaccessible cardinal, it follows that
![]() $V_\kappa $
must have an inaccessible cardinal. Similarly, for any
$V_\kappa $
must have an inaccessible cardinal. Similarly, for any
![]() $\beta <\kappa $
we know that V has an inaccessible cardinal above
$\beta <\kappa $
we know that V has an inaccessible cardinal above
![]() $\beta $
, and so
$\beta $
, and so
![]() $V_\kappa $
must agree. So the inaccessible cardinals are unbounded in
$V_\kappa $
must agree. So the inaccessible cardinals are unbounded in
![]() $\kappa $
. Thus,
$\kappa $
. Thus,
![]() $V_\kappa $
satisfies the Grothendieck universe axiom. This axiom is itself a
$V_\kappa $
satisfies the Grothendieck universe axiom. This axiom is itself a
![]() $\Pi _3$
assertion, and so it is true in V. So the Grothendieck universe axiom holds. Now suppose that
$\Pi _3$
assertion, and so it is true in V. So the Grothendieck universe axiom holds. Now suppose that
![]() holds at
holds at
![]() $V_\kappa $
in the GZ-potentialist semantics, where
$V_\kappa $
in the GZ-potentialist semantics, where
![]() $\varphi $
is an assertion in the language of set theory and
$\varphi $
is an assertion in the language of set theory and
![]() $\vec a\in V_\kappa $
. Thus, there is some inaccessible cardinal
$\vec a\in V_\kappa $
. Thus, there is some inaccessible cardinal
![]() $\lambda $
such that for all inaccessible cardinals
$\lambda $
such that for all inaccessible cardinals
![]() $\theta \geq \lambda $
we have
$\theta \geq \lambda $
we have
![]() $V_\theta \models \varphi $
. As before, this is a
$V_\theta \models \varphi $
. As before, this is a
![]() $\Sigma _3$
assertion, and so it is true in
$\Sigma _3$
assertion, and so it is true in
![]() $V_\kappa $
. So there is a
$V_\kappa $
. So there is a
![]() $\lambda <\kappa $
, such that every inaccessible cardinal
$\lambda <\kappa $
, such that every inaccessible cardinal
![]() $\theta \geq \lambda $
in
$\theta \geq \lambda $
in
![]() $V_\kappa $
has
$V_\kappa $
has
![]() $V_\theta \models \varphi (\vec a)$
. The assertion that
$V_\theta \models \varphi (\vec a)$
. The assertion that
![]() $\lambda $
has this property has complexity
$\lambda $
has this property has complexity
![]() $\Pi _2$
, and so this
$\Pi _2$
, and so this
![]() $\lambda $
also works in V. Therefore,
$\lambda $
also works in V. Therefore,
![]() $V_\kappa \models \varphi (\vec a)$
, verifying this instance of the maximality principle, as desired.
$V_\kappa \models \varphi (\vec a)$
, verifying this instance of the maximality principle, as desired.
(
![]() $1\to 2$
) Assume that the Grothendieck universe axiom holds and that the GZ-potentialist maximality principle is true at GZ-universe
$1\to 2$
) Assume that the Grothendieck universe axiom holds and that the GZ-potentialist maximality principle is true at GZ-universe
![]() $V_\kappa $
. In particular,
$V_\kappa $
. In particular,
![]() $\kappa $
is an inaccessible cardinal. So it is a
$\kappa $
is an inaccessible cardinal. So it is a
![]() $\beth $
-fixed point and therefore
$\beth $
-fixed point and therefore
![]() $\Sigma _1$
-correct. If a
$\Sigma _1$
-correct. If a
![]() $\Sigma _2$
assertion is true in V, then this is witnessed in all large enough
$\Sigma _2$
assertion is true in V, then this is witnessed in all large enough
![]() $V_\theta $
, including when
$V_\theta $
, including when
![]() $\theta $
is inaccessible, and so by the maximality principle, it is witnessed in
$\theta $
is inaccessible, and so by the maximality principle, it is witnessed in
![]() $V_\kappa $
, so
$V_\kappa $
, so
![]() $\kappa $
is
$\kappa $
is
![]() $\Sigma _2$
-correct. Finally, suppose that some
$\Sigma _2$
-correct. Finally, suppose that some
![]() $\Sigma _3$
-assertion is true. All such statements have the form
$\Sigma _3$
-assertion is true. All such statements have the form
![]() $\exists x\forall y\, \psi (x,y,\vec a)$
, where
$\exists x\forall y\, \psi (x,y,\vec a)$
, where
![]() $\psi $
has complexity
$\psi $
has complexity
![]() $\Sigma _1$
. This implies
$\Sigma _1$
. This implies
![]() at
at
![]() $V_\kappa $
, since once
$V_\kappa $
, since once
![]() $\lambda $
is large enough, then x will exist in
$\lambda $
is large enough, then x will exist in
![]() $V_\theta $
for any larger
$V_\theta $
for any larger
![]() $\theta $
. So by the maximality principle, we conclude that
$\theta $
. So by the maximality principle, we conclude that
![]() $V_\kappa \models \exists x\forall y\,\psi (x,y,\vec a)$
, verifying this instance of
$V_\kappa \models \exists x\forall y\,\psi (x,y,\vec a)$
, verifying this instance of
![]() $\Sigma _3$
-correctness. Since
$\Sigma _3$
-correctness. Since
![]() $\kappa $
is inaccessible, we have proved that
$\kappa $
is inaccessible, we have proved that
![]() $\kappa $
is
$\kappa $
is
![]() $\Sigma _3$
-reflecting.
$\Sigma _3$
-reflecting.
A cardinal
![]() $\kappa $
is reflecting, if it is inaccessible and correct, so that it realizes the scheme
$\kappa $
is reflecting, if it is inaccessible and correct, so that it realizes the scheme
![]() $V_\kappa \prec V$
. In other words, it is
$V_\kappa \prec V$
. In other words, it is
![]() $\Sigma _n$
-reflecting for every natural number n. As with the correct cardinals, this is not a first-order expressible concept, although it can be expressed as a scheme.
$\Sigma _n$
-reflecting for every natural number n. As with the correct cardinals, this is not a first-order expressible concept, although it can be expressed as a scheme.
Theorem 23. For any inaccessible cardinal
![]() $\kappa $
, the following are equivalent:
$\kappa $
, the following are equivalent:
-
(1) The Grothendieck universe axiom holds and
 $V_\kappa $
satisfies the GZ-potentialist maximality principle for assertions in the potentialist language
$V_\kappa $
satisfies the GZ-potentialist maximality principle for assertions in the potentialist language
 $\mathcal {L}_\in ^\Diamond $
with parameters from
$\mathcal {L}_\in ^\Diamond $
with parameters from
 $V_\kappa $
. That is,
$V_\kappa $
. That is,  $$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{Z}}(V_\kappa,\mathcal{L}_{\in,V_\kappa}^\Diamond)=S5.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{Z}}(V_\kappa,\mathcal{L}_{\in,V_\kappa}^\Diamond)=S5.\end{align*} $$
-
(2)
 $\kappa $
is a reflecting cardinal.
$\kappa $
is a reflecting cardinal.
3.5 Transitive-set potentialism
Consider next the potentialist account of V arising from the class of all transitive sets
Thus,
![]() is true at a transitive set W if there is another transitive set U with
is true at a transitive set W if there is another transitive set U with
![]() $W\subseteq U$
and
$W\subseteq U$
and
![]() $U\models _{\mathcal {T}}\psi $
. Let us call this transitive-set potentialism. Since transitive sets can grow both in height and in width, this form of potentialism can be viewed as a form both of height and width potentialism. But it does not exhibit potentiality equally in height and width, since any transitive set W can ultimately be completed with respect to width, by moving to the smallest
$U\models _{\mathcal {T}}\psi $
. Let us call this transitive-set potentialism. Since transitive sets can grow both in height and in width, this form of potentialism can be viewed as a form both of height and width potentialism. But it does not exhibit potentiality equally in height and width, since any transitive set W can ultimately be completed with respect to width, by moving to the smallest
![]() $V_\beta $
containing it, and then no additional subsets of sets in W will ever arise in
$V_\beta $
containing it, and then no additional subsets of sets in W will ever arise in
![]() $\mathcal {T}$
. Because of this, the transitive-set potentialist account is somewhat milder with respect to width potentialism than it is with respect to height potentialism: any set appearing in a universe fragment will eventually get all its possible subsets, after which time it will not grow in width any further, although the heights of the transitive sets never stabilize in this way, since every transitive set is included in another transitive set with additional larger ordinals. In this sense, worlds in transitive-set potentialism are width-completable in a way that they are not height-completable.
$\mathcal {T}$
. Because of this, the transitive-set potentialist account is somewhat milder with respect to width potentialism than it is with respect to height potentialism: any set appearing in a universe fragment will eventually get all its possible subsets, after which time it will not grow in width any further, although the heights of the transitive sets never stabilize in this way, since every transitive set is included in another transitive set with additional larger ordinals. In this sense, worlds in transitive-set potentialism are width-completable in a way that they are not height-completable.
Theorem 24. In transitive-set potentialism, every world W obeys
 $$ \begin{align*}S4.2 \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}}(W,\mathcal{L}_{\in,W}^\Diamond) \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}}(W,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
$$ \begin{align*}S4.2 \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}}(W,\mathcal{L}_{\in,W}^\Diamond) \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}}(W,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
The lower bound is sharp, in that some worlds W have
 $$ \begin{align*}S4.2 = \mathord{\mathrm{Val}}_{\mathcal{T}}(W,\mathcal{L}_{\in,W}^\Diamond) = \mathord{\mathrm{Val}}_{\mathcal{T}}(W,\mathcal{L}_\in).\end{align*} $$
$$ \begin{align*}S4.2 = \mathord{\mathrm{Val}}_{\mathcal{T}}(W,\mathcal{L}_{\in,W}^\Diamond) = \mathord{\mathrm{Val}}_{\mathcal{T}}(W,\mathcal{L}_\in).\end{align*} $$
Proof. Since the union of two transitive sets is transitive, it follows that the potentialist system of all transitive sets is directed and therefore by Theorem 2 every assertion of S4.2 is valid. To achieve S5 as an upper bound, it suffices by Theorems 3 and 4 to show that this system admits an infinite dial. For this, we can use the same dial
![]() $d_j$
as in Theorem 8, namely, the assertion
$d_j$
as in Theorem 8, namely, the assertion
![]() $d_j$
that the ordinals have the form
$d_j$
that the ordinals have the form
![]() $\lambda +j$
where
$\lambda +j$
where
![]() $\lambda $
is either a limit ordinal or zero. This is expressible by a sentence in the language of set theory, correctly interpreted inside any transitive set, and since any transitive set can be extended to any desired larger ordinal height, it forms a dial.
$\lambda $
is either a limit ordinal or zero. This is expressible by a sentence in the language of set theory, correctly interpreted inside any transitive set, and since any transitive set can be extended to any desired larger ordinal height, it forms a dial.
To show that the lower bound is sharp, it suffices by Theorem 5 to find an independent family of buttons, independent of this dial. For this, let
![]() $\left \langle B_k\mid k\in \omega \right \rangle $
be an infinite list of distinct arithmetically definable infinite, co-infinite sets of natural numbers. Let
$\left \langle B_k\mid k\in \omega \right \rangle $
be an infinite list of distinct arithmetically definable infinite, co-infinite sets of natural numbers. Let
![]() $b_k$
be the assertion, “
$b_k$
be the assertion, “
![]() $V_\omega $
exists and also
$V_\omega $
exists and also
![]() $B_k$
exists.” Note that this assertion is upward absolute for transitive sets, since if
$B_k$
exists.” Note that this assertion is upward absolute for transitive sets, since if
![]() $V_\omega $
and
$V_\omega $
and
![]() $B_k$
exist in some transitive set, then this will continue to be true in any larger transitive set. So each
$B_k$
exist in some transitive set, then this will continue to be true in any larger transitive set. So each
![]() $b_k$
is a button. Furthermore, these assertions form an independent family of buttons, since if M is any transitive set, then
$b_k$
is a button. Furthermore, these assertions form an independent family of buttons, since if M is any transitive set, then
![]() $M\cup V_\omega \cup \left \{{B_k}\right \}$
is the union of transitive sets and hence also transitive, and we have added
$M\cup V_\omega \cup \left \{{B_k}\right \}$
is the union of transitive sets and hence also transitive, and we have added
![]() $B_k$
without adding any other
$B_k$
without adding any other
![]() $B_j$
for
$B_j$
for
![]() $j\neq k$
. Since these buttons and dial values can be controlled independently of each other without interference, it follows by Theorem 5 that the modal validities in any world where infinitely many of the buttons are not yet pushed will be contained within and hence equal to S4.2, as desired.
$j\neq k$
. Since these buttons and dial values can be controlled independently of each other without interference, it follows by Theorem 5 that the modal validities in any world where infinitely many of the buttons are not yet pushed will be contained within and hence equal to S4.2, as desired.
The upper bound of Theorem 24 also is sharp, in light of the following two theorems.
Theorem 25. The following are equivalent in transitive-set potentialism.
-
(1) The potentialist maximality principle holds for world M for assertions in the language of set theory with parameters from M. That is,
 $$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{T}}(M,\mathcal{L}_{\in,M})=S5.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{T}}(M,\mathcal{L}_{\in,M})=S5.\end{align*} $$
-
(2)
 $M=V_\delta $
for some
$M=V_\delta $
for some
 $\Sigma _2$
-correct cardinal
$\Sigma _2$
-correct cardinal
 $\delta $
.
$\delta $
.
Proof. (
![]() $2\mathrel {\rightarrow } 1$
) Consider
$2\mathrel {\rightarrow } 1$
) Consider
![]() $M=V_\delta $
, where
$M=V_\delta $
, where
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _2$
-correct, and assume
$\Sigma _2$
-correct, and assume
![]() holds in M. So there is a transitive set N such that in all larger transitive sets
holds in M. So there is a transitive set N such that in all larger transitive sets
![]() $U\supseteq N$
, we have
$U\supseteq N$
, we have
![]() $U\models \varphi (\vec a)$
. This is a
$U\models \varphi (\vec a)$
. This is a
![]() $\Sigma _2$
assertion about
$\Sigma _2$
assertion about
![]() $\vec a$
, and so it must already be true in M. So there is transitive set
$\vec a$
, and so it must already be true in M. So there is transitive set
![]() $N\in M$
such that, inside M, every transitive
$N\in M$
such that, inside M, every transitive
![]() $U\supseteq N$
satisfies
$U\supseteq N$
satisfies
![]() $\varphi (\vec a)$
. This is a
$\varphi (\vec a)$
. This is a
![]() $\Pi _1$
-property about
$\Pi _1$
-property about
![]() $\vec a$
and this particular N, which therefore holds in V. Since M itself is such a transitive set, we conclude
$\vec a$
and this particular N, which therefore holds in V. Since M itself is such a transitive set, we conclude
![]() $M\models \varphi $
, as desired.
$M\models \varphi $
, as desired.
(
![]() $1\mathrel {\rightarrow } 2$
) Assume that the potentialist maximality principle holds in M for assertions in the language of set theory with parameters from M. First, we claim that M is correct about power sets. If a is any set in M, then we claim that
$1\mathrel {\rightarrow } 2$
) Assume that the potentialist maximality principle holds in M for assertions in the language of set theory with parameters from M. First, we claim that M is correct about power sets. If a is any set in M, then we claim that
![]() . In other words, the existence of the power set of a is possibly necessary. This is simply because once you move to a transitive set that has the actual power set of a, then it necessarily is the power set of a in all larger transitive sets. So M thinks
. In other words, the existence of the power set of a is possibly necessary. This is simply because once you move to a transitive set that has the actual power set of a, then it necessarily is the power set of a in all larger transitive sets. So M thinks
![]() $P(a)$
exists (that is, the power set relativized to M). If M does not have the actual power set of a, then there is some
$P(a)$
exists (that is, the power set relativized to M). If M does not have the actual power set of a, then there is some
![]() $u\subseteq a$
with
$u\subseteq a$
with
![]() $u\notin M$
, in which case
$u\notin M$
, in which case
![]() $M\cup \left \{{u}\right \}$
is a transitive set containing M, which does not think that the power set of a exists, contrary to this being necessary over M. So M computes the power sets correctly. A similar argument shows that M computes
$M\cup \left \{{u}\right \}$
is a transitive set containing M, which does not think that the power set of a exists, contrary to this being necessary over M. So M computes the power sets correctly. A similar argument shows that M computes
![]() $V_\alpha $
correctly for any ordinal
$V_\alpha $
correctly for any ordinal
![]() $\alpha \in M$
, since the existence of
$\alpha \in M$
, since the existence of
![]() $V_\alpha $
is possibly necessary, and M cannot have a fake version of some
$V_\alpha $
is possibly necessary, and M cannot have a fake version of some
![]() $V_\alpha $
, since in that case it would have to be wrong about some power sets. Also, for any set a it is possible necessary that
$V_\alpha $
, since in that case it would have to be wrong about some power sets. Also, for any set a it is possible necessary that
![]() $a\in V_\alpha $
for some ordinal
$a\in V_\alpha $
for some ordinal
![]() $\alpha $
, and so this is already true in M. Thus,
$\alpha $
, and so this is already true in M. Thus,
![]() $M=V_\delta $
for some ordinal
$M=V_\delta $
for some ordinal
![]() $\delta $
. To see that
$\delta $
. To see that
![]() $\delta $
must be
$\delta $
must be
![]() $\Sigma _2$
-correct, suppose that a
$\Sigma _2$
-correct, suppose that a
![]() $\Sigma _2$
assertion
$\Sigma _2$
assertion
![]() $\varphi (\vec a)$
is true in V. This is witnessed by the existence of some ordinal
$\varphi (\vec a)$
is true in V. This is witnessed by the existence of some ordinal
![]() $\beta $
for which
$\beta $
for which
![]() $V_\beta \models \psi (\vec a)$
for some assertion
$V_\beta \models \psi (\vec a)$
for some assertion
![]() $\psi $
. So it is possibly necessary that, “there is an ordinal
$\psi $
. So it is possibly necessary that, “there is an ordinal
![]() $\beta $
for which
$\beta $
for which
![]() $V_\beta $
exists and satisfies
$V_\beta $
exists and satisfies
![]() $\psi (\vec a)$
.” Thus, this must already be true in M, and so
$\psi (\vec a)$
.” Thus, this must already be true in M, and so
![]() $\varphi (\vec a)$
is true already in M, as desired. So
$\varphi (\vec a)$
is true already in M, as desired. So
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _2$
-correct.
$\Sigma _2$
-correct.
Theorem 26. The following are equivalent in transitive-set potentialism.
-
(1) The potentialist maximality principle holds for world M for assertions in the potentialist language
 $\mathcal {L}_\in ^\Diamond $
with parameters from M. That is,
$\mathcal {L}_\in ^\Diamond $
with parameters from M. That is,  $$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{T}}(M,\mathcal{L}_{\in,M}^\Diamond)=S5.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{T}}(M,\mathcal{L}_{\in,M}^\Diamond)=S5.\end{align*} $$
-
(2)
 $M\prec V$
. In other words,
$M\prec V$
. In other words,
 $M=V_\delta $
for a correct cardinal
$M=V_\delta $
for a correct cardinal
 $\delta $
, realizing the scheme
$\delta $
, realizing the scheme
 $V_\delta \prec V$
.
$V_\delta \prec V$
.
Proof. This is like the proof of Theorem 14 combined with the ideas of Theorem 25. If the maximality principle holds for world M in the potentialist language, then we know by Theorem 25 that
![]() $M=V_\delta $
for a
$M=V_\delta $
for a
![]() $\Sigma _2$
-correct cardinal
$\Sigma _2$
-correct cardinal
![]() $\delta $
. But since the transitive sets form a potentialist account of V in the manner of Theorem 1, we can as in Theorem 14 show that
$\delta $
. But since the transitive sets form a potentialist account of V in the manner of Theorem 1, we can as in Theorem 14 show that
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _n$
-correct for every n.
$\Sigma _n$
-correct for every n.
Conversely, assume that
![]() $M=V_\delta \prec V$
and
$M=V_\delta \prec V$
and
![]() holds in M, where
holds in M, where
![]() $\varphi $
is a
$\varphi $
is a
![]() $\mathcal {L}_\in ^\Diamond $
assertion. So there is a transitive set N, such that in all larger transitive sets
$\mathcal {L}_\in ^\Diamond $
assertion. So there is a transitive set N, such that in all larger transitive sets
![]() $U\supseteq N$
we have
$U\supseteq N$
we have
![]() $U\models \varphi (\vec a)$
. Since the existence of a such a set N and the potentialist semantics are expressible in the language of set theory, it follows from
$U\models \varphi (\vec a)$
. Since the existence of a such a set N and the potentialist semantics are expressible in the language of set theory, it follows from
![]() $M\prec V$
that there is such a set already in M, and consequently
$M\prec V$
that there is such a set already in M, and consequently
![]() $M\models \varphi (\vec a)$
, as desired.
$M\models \varphi (\vec a)$
, as desired.
Just as with rank potentialism, one may not want to allow all transitive sets, but only some, say, those that satisfy a given c.e. theory T. In this case, the collection of modal validities can depend on the theory and on the set-theoretic background.
Theorem 27. Suppose that T is a
![]() $($
sufficient
$($
sufficient
![]() $)$
c.e. theory and every set x in V is an element of a transitive model of T. Then the collection of all such models
$)$
c.e. theory and every set x in V is an element of a transitive model of T. Then the collection of all such models
provides a potentialist account of V. Furthermore, every world W in this system obeys
 $$ \begin{align*}S4.2 \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}_T}(W,\mathcal{L}_{\in,W}^\Diamond) \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}_T}(W,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
$$ \begin{align*}S4.2 \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}_T}(W,\mathcal{L}_{\in,W}^\Diamond) \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}_T}(W,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
Reaching toward the lower bound, there is a world W obeying
 $$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{T}_T}(W,\mathcal{L}_{\in,W}^\Diamond) \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}_T}(W,\mathcal{L}_\in)\subseteq S4.3.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}_{\mathcal{T}_T}(W,\mathcal{L}_{\in,W}^\Diamond) \subseteq \mathord{\mathrm{Val}}_{\mathcal{T}_T}(W,\mathcal{L}_\in)\subseteq S4.3.\end{align*} $$
Examples show that the modal validities true at every world of
![]() $\mathcal {T}_T$
can be exactly S4.2, exactly S4.3, or exactly some other intermediate modal theory, depending on the theory T and on the set-theoretic background V.
$\mathcal {T}_T$
can be exactly S4.2, exactly S4.3, or exactly some other intermediate modal theory, depending on the theory T and on the set-theoretic background V.
Proof. The collection of models
![]() $\mathcal {T}_T$
provides a potentialist account of V, since if
$\mathcal {T}_T$
provides a potentialist account of V, since if
![]() $W\in \mathcal {T}_T$
, then
$W\in \mathcal {T}_T$
, then
![]() $\left \langle W,\in \right \rangle $
is a substructure of
$\left \langle W,\in \right \rangle $
is a substructure of
![]() $\left \langle V,\in \right \rangle $
and if x is any set in V, then by the assumption on T we have a transitive model containing
$\left \langle V,\in \right \rangle $
and if x is any set in V, then by the assumption on T we have a transitive model containing
![]() $\{W,x\}$
as an element, which must therefore have
$\{W,x\}$
as an element, which must therefore have
![]() $W\subseteq U$
. So the weak directedness property is fulfilled. But actually, a similar argument shows that
$W\subseteq U$
. So the weak directedness property is fulfilled. But actually, a similar argument shows that
![]() $\mathcal {T}_T$
is fully directed: if
$\mathcal {T}_T$
is fully directed: if
![]() $W_0,W_1\in \mathcal {T}_T$
, then the assumption on T ensures that there is
$W_0,W_1\in \mathcal {T}_T$
, then the assumption on T ensures that there is
![]() $U\in \mathcal {T}_T$
with
$U\in \mathcal {T}_T$
with
![]() $\{W_0,W_1\}\in U$
, which ensures
$\{W_0,W_1\}\in U$
, which ensures
![]() $W_0,W_1\subseteq U$
, as desired. By Theorem 2, therefore, S4.2 is valid at every world for the potentialist account provided by
$W_0,W_1\subseteq U$
, as desired. By Theorem 2, therefore, S4.2 is valid at every world for the potentialist account provided by
![]() $\mathcal {T}_T$
, verifying Statement 1.
$\mathcal {T}_T$
, verifying Statement 1.
Meanwhile, observe that
![]() $\mathcal {T}_T$
is well-founded with respect to
$\mathcal {T}_T$
is well-founded with respect to
![]() $\in $
, and so for any ordinal
$\in $
, and so for any ordinal
![]() $\alpha $
, we may let
$\alpha $
, we may let
![]() $r_\alpha $
be the assertion, “the
$r_\alpha $
be the assertion, “the
![]() $\in $
-relation on the transitive models of T has rank at least
$\in $
-relation on the transitive models of T has rank at least
![]() $\alpha $
.” Our hypothesis in the theorem that T is sufficient is meant to ensure that models of T are able to refer to T by means of its arithmetic definition and are also able to calculate the rank of a well-founded relation (so even some very weak set theories suffice). Since the rank can never go down as the transitive sets get larger, it follows that each
$\alpha $
.” Our hypothesis in the theorem that T is sufficient is meant to ensure that models of T are able to refer to T by means of its arithmetic definition and are also able to calculate the rank of a well-founded relation (so even some very weak set theories suffice). Since the rank can never go down as the transitive sets get larger, it follows that each
![]() $r_\alpha $
will necessarily imply all earlier
$r_\alpha $
will necessarily imply all earlier
![]() $r_\beta $
for
$r_\beta $
for
![]() $\beta <\alpha $
. And if
$\beta <\alpha $
. And if
![]() $r_\alpha $
is not true in some transitive
$r_\alpha $
is not true in some transitive
![]() $W\models T$
, then we may simply extend W to a transitive set
$W\models T$
, then we may simply extend W to a transitive set
![]() $U\models T$
of rank
$U\models T$
of rank
![]() $\alpha +1$
, so that
$\alpha +1$
, so that
![]() $W\subseteq U$
and
$W\subseteq U$
and
![]() $U\models r_\alpha \wedge \neg r_{\alpha +1}$
. So this is a uniform long ratchet, and therefore by Theorem 7 any world in which this ratchet has not yet begun will have its validities contained within S4.3. And furthermore, the same theorem provides S5 as an upper bound for all the worlds.
$U\models r_\alpha \wedge \neg r_{\alpha +1}$
. So this is a uniform long ratchet, and therefore by Theorem 7 any world in which this ratchet has not yet begun will have its validities contained within S4.3. And furthermore, the same theorem provides S5 as an upper bound for all the worlds.
Let us now give some examples showing that various modal theories can arise, depending on the theory and on the set-theoretic background. For the easiest case, if we take the empty theory, then
![]() $\mathcal {T}_T$
is the same as the class
$\mathcal {T}_T$
is the same as the class
![]() $\mathcal {T}$
of all transitive sets, whose modal validities we have already established as S4.2 in Theorem 24. Next, assume
$\mathcal {T}$
of all transitive sets, whose modal validities we have already established as S4.2 in Theorem 24. Next, assume
![]() $V=L$
in the background theory, and consider the theory T consisting of the assertion “V=L,” so that the transitive models of this theory are exactly the models
$V=L$
in the background theory, and consider the theory T consisting of the assertion “V=L,” so that the transitive models of this theory are exactly the models
![]() $L_\alpha $
appearing in the constructibility hierarchy. These are linearly ordered, and so S4.3 is valid for this potentialist system, and the validities are contained within S4.3 by the previous paragraph, yielding exactly S4.3 as the common modal theory.
$L_\alpha $
appearing in the constructibility hierarchy. These are linearly ordered, and so S4.3 is valid for this potentialist system, and the validities are contained within S4.3 by the previous paragraph, yielding exactly S4.3 as the common modal theory.
Finally, assume
![]() $V=L$
in the background, and let’s describe a theory T for which the corresponding potentialist system
$V=L$
in the background, and let’s describe a theory T for which the corresponding potentialist system
![]() $\mathcal {T}_T$
exhibits modal validities strictly in between S4.2 and S4.3. Let
$\mathcal {T}_T$
exhibits modal validities strictly in between S4.2 and S4.3. Let
![]() ${\textrm {ZFC}}^*$
be a fixed finite fragment of
${\textrm {ZFC}}^*$
be a fixed finite fragment of
![]() ${\textrm {ZFC}}$
, which can prove the existence of the reals and which furthermore is invariant by Cohen-real forcing and by random-real forcing. Let T be the theory asserting that either (i)
${\textrm {ZFC}}$
, which can prove the existence of the reals and which furthermore is invariant by Cohen-real forcing and by random-real forcing. Let T be the theory asserting that either (i)
![]() ${\textrm {ZFC}}^*+V=L$
; or (ii)
${\textrm {ZFC}}^*+V=L$
; or (ii)
![]() ${\textrm {ZFC}}^*+V=L[c]$
for an L-generic Cohen real c, but there is no transitive set model of
${\textrm {ZFC}}^*+V=L[c]$
for an L-generic Cohen real c, but there is no transitive set model of
![]() ${\textrm {ZFC}}^*$
; or (iii)
${\textrm {ZFC}}^*$
; or (iii)
![]() ${\textrm {ZFC}}^*+V=L[r]$
for an L-generic random real, but there is no transitive set model of
${\textrm {ZFC}}^*+V=L[r]$
for an L-generic random real, but there is no transitive set model of
![]() ${\textrm {ZFC}}^*$
. For example, since
${\textrm {ZFC}}^*$
. For example, since
![]() ${\textrm {ZFC}}^*$
is true in L, it follows by the finiteness of
${\textrm {ZFC}}^*$
is true in L, it follows by the finiteness of
![]() ${\textrm {ZFC}}^*$
that it is true in some large
${\textrm {ZFC}}^*$
that it is true in some large
![]() $L_\gamma $
, and by condensation the least
$L_\gamma $
, and by condensation the least
![]() $\gamma $
for which
$\gamma $
for which
![]() $L_\gamma \models {\textrm {ZFC}}^*$
is countable. Thus, we can easily construct
$L_\gamma \models {\textrm {ZFC}}^*$
is countable. Thus, we can easily construct
![]() $L_\gamma $
-generic reals c or r and form the extensions
$L_\gamma $
-generic reals c or r and form the extensions
![]() $L_\gamma [c]$
and
$L_\gamma [c]$
and
![]() $L_\gamma [r]$
. By using the least possible
$L_\gamma [r]$
. By using the least possible
![]() $\gamma $
, these models will have no set models of
$\gamma $
, these models will have no set models of
![]() ${\textrm {ZFC}}^*$
, and so we can see that both statements (ii) and (iii) are possible from some
${\textrm {ZFC}}^*$
, and so we can see that both statements (ii) and (iii) are possible from some
![]() $L_\gamma $
. Note that if one goes to a higher model, however, then (ii) and (iii) become impossible, because of the requirement that there is no transitive set model of
$L_\gamma $
. Note that if one goes to a higher model, however, then (ii) and (iii) become impossible, because of the requirement that there is no transitive set model of
![]() ${\textrm {ZFC}}^*$
. In particular, both (ii) and (iii) are possible from the smallest
${\textrm {ZFC}}^*$
. In particular, both (ii) and (iii) are possible from the smallest
![]() $L_\gamma $
satisfying
$L_\gamma $
satisfying
![]() ${\textrm {ZFC}}^*$
, but once you have one of them, the other becomes impossible, since the forcing notions do not add generic reals of the other type. So this is exactly a violation of axiom (.3) in
${\textrm {ZFC}}^*$
, but once you have one of them, the other becomes impossible, since the forcing notions do not add generic reals of the other type. So this is exactly a violation of axiom (.3) in
![]() $L_\gamma $
, and therefore the validities of this potentialist system are not S4.3. Meanwhile, we claim that the validities exceed S4.2. To see this, note that because of the homogeneity of Cohen forcing and random-real forcing, all the models of statement (ii) have the same theory, and similarly for statement (iii). Thus, every transitive model of T is either a model of statement (i), and these are all linearly ordered, or else is a model of the theory of statement (ii) or of statement (iii). So it is impossible that a model of T has three independent unpushed buttons. In particular, the assertion “p, q and r are not three independent unpushed buttons,” which is expressible in propositional modal logic, is valid for the potentialist system determined by the transitive models of T, but this assertion is not an S4.2 theorem, since some models of S4.2 do have three independent unpushed buttons. So the modal validities of
$L_\gamma $
, and therefore the validities of this potentialist system are not S4.3. Meanwhile, we claim that the validities exceed S4.2. To see this, note that because of the homogeneity of Cohen forcing and random-real forcing, all the models of statement (ii) have the same theory, and similarly for statement (iii). Thus, every transitive model of T is either a model of statement (i), and these are all linearly ordered, or else is a model of the theory of statement (ii) or of statement (iii). So it is impossible that a model of T has three independent unpushed buttons. In particular, the assertion “p, q and r are not three independent unpushed buttons,” which is expressible in propositional modal logic, is valid for the potentialist system determined by the transitive models of T, but this assertion is not an S4.2 theorem, since some models of S4.2 do have three independent unpushed buttons. So the modal validities of
![]() $\mathcal {T}_T$
for this theory are strictly intermediate between S4.2 and S4.3, as claimed.
$\mathcal {T}_T$
for this theory are strictly intermediate between S4.2 and S4.3, as claimed.
3.6 A remark on Solovay’s set-theoretic modalities
Before continuing, let us briefly discuss the connection of set-theoretic potentialism with some related set-theoretic modalities considered by Solovay. After proving his famous analysis of provability logic, Solovay had considered the modalities of “true in all
![]() $V_\kappa $
for
$V_\kappa $
for
![]() $\kappa $
inaccessible” and also “true in all transitive sets” (see [Reference Boolos1, chap. 13] and this was extended in unpublished work of Enayat and Togha). To be precise, the intended Solovay modal semantics are that
$\kappa $
inaccessible” and also “true in all transitive sets” (see [Reference Boolos1, chap. 13] and this was extended in unpublished work of Enayat and Togha). To be precise, the intended Solovay modal semantics are that
![]() if and only if
if and only if
![]() $V_\delta $
thinks that
$V_\delta $
thinks that
![]() $\varphi $
is true in all
$\varphi $
is true in all
![]() $V_\kappa $
for inaccessible
$V_\kappa $
for inaccessible
![]() $\kappa <\delta $
, or
$\kappa <\delta $
, or
![]() $V_\delta $
thinks that
$V_\delta $
thinks that
![]() $\varphi $
is true in all transitive sets in
$\varphi $
is true in all transitive sets in
![]() $V_\delta $
, respectively.
$V_\delta $
, respectively.
The Solovay modalities are thus precisely the inverses of the Grothendieck–Zermelo and transitive-set potentialist modalities that we considered earlier in this article. One might more accurately describe them under the slogans “true in all smaller
![]() $V_\kappa $
for inaccessible cardinals
$V_\kappa $
for inaccessible cardinals
![]() $\kappa $
” and “true in all smaller transitive sets.” The downward-oriented focus is amplified with nested modalities such as
$\kappa $
” and “true in all smaller transitive sets.” The downward-oriented focus is amplified with nested modalities such as
![]() .
.
This downward orientation of the Solovay modalities gives them a markedly non-potentialist character. Truly potentialist modal assertions, after all, reach outside of the current actual world to refer to objects that might potentially exist in a larger world, but which do not yet exist in the current world. Solovay’s modalities are not potentialist in this way, and it is not surprising that he achieves very different modal validities than what we have found for the set-theoretic potentialist modalities in this article. The validity of the Löb axiom for Solovay’s modality, for example, is connected with the fact that his accessibility relation is inversely well-founded.
A separate, but related issue is that because the Kripke model for the Solovay modality has deflationary domains, one faces certain issues in the semantics of mixed quantifier/modal assertions, with the basic conundrum being the correct meaning for
![]() when there are accessible worlds in which a does not exist (see [Reference Garson, Gabbay and Guenthner4]).
when there are accessible worlds in which a does not exist (see [Reference Garson, Gabbay and Guenthner4]).
3.7 Forcing potentialism
Let us now consider the version of set-theoretic potentialism that arises by considering the set-theoretic universe in the context of all its forcing extensions. This idea is closely connected with the modal logic of forcing, as in [Reference Hamkins, Leibman and Löwe14–Reference Hamkins, Löwe and Lodaya16]; the forcing modalities were introduced in [Reference Hamkins6]. The modal logic of forcing is, at bottom, an instance of set-theoretic width potentialism and height actualism. Namely, we consider a model of set theory M in the context of all its forcing extensions
![]() $M[G]$
and their further forcing extensions
$M[G]$
and their further forcing extensions
![]() $M[G][H]$
, interpreting
$M[G][H]$
, interpreting
![]() as “true in some forcing extension,” and
as “true in some forcing extension,” and
![]() as “true in all forcing extensions.” Since the relation of ground model to forcing extension coincides with the substructure relation among these models, it follows that the modal logic of forcing coincides with the potentialist semantics on this collection of models. Note that because the forcing modalities are expressible in the language of set theory, the distinction between
as “true in all forcing extensions.” Since the relation of ground model to forcing extension coincides with the substructure relation among these models, it follows that the modal logic of forcing coincides with the potentialist semantics on this collection of models. Note that because the forcing modalities are expressible in the language of set theory, the distinction between
![]() $\mathcal {L}_\in $
and
$\mathcal {L}_\in $
and
![]() $\mathcal {L}_\in ^\Diamond $
evaporates for this case. The main results of [Reference Hamkins and Löwe15] establish:
$\mathcal {L}_\in ^\Diamond $
evaporates for this case. The main results of [Reference Hamkins and Löwe15] establish:
Theorem 28 (Hamkins and Löwe)
In the collection of models arising as forcing extensions of a fixed countable model of ZFC, considered under the potentialist semantics, every world W obeys
Depending on the original model, some worlds W can have
Depending on the original model, other worlds have
The modal validities include S4 because inclusion is transitive and reflexive, and we get axiom .2 not because the collection of models is directed, which it isn’t by the non-amalgamation results discussed in [Reference Fuchs, Hamkins and Reitz3, Reference Hamkins12], but rather because any particular pair of statements
![]() $\psi $
and
$\psi $
and
![]() $\phi $
that are each separately forceably necessary, can be jointly forced by the product forcing. The main result of [Reference Hamkins and Löwe15] shows that in any model of
$\phi $
that are each separately forceably necessary, can be jointly forced by the product forcing. The main result of [Reference Hamkins and Löwe15] shows that in any model of
![]() $V=L$
and many others, the modal logic of forcing is exactly
$V=L$
and many others, the modal logic of forcing is exactly
![]() $\mathord {\textrm {Val}}(W,\mathcal {L}_\in )=S4.2$
, because there are independent families of buttons and switches. In the general case, the same argument shows that every world W has
$\mathord {\textrm {Val}}(W,\mathcal {L}_\in )=S4.2$
, because there are independent families of buttons and switches. In the general case, the same argument shows that every world W has
![]() $\mathord {\textrm {Val}}(W,\mathcal {L}_{\in ,W})=S4.2$
, since there are always independent buttons and switches expressible with parameters. The same observation provides S5 generally as an upper bound, since one can express independent switches via the GCH pattern without need for any parameters. The main result of [Reference Hamkins6] shows that it is equiconsistent with ZFC that S5 is valid with respect to sentences in the language of set theory (no parameters), achieving
$\mathord {\textrm {Val}}(W,\mathcal {L}_{\in ,W})=S4.2$
, since there are always independent buttons and switches expressible with parameters. The same observation provides S5 generally as an upper bound, since one can express independent switches via the GCH pattern without need for any parameters. The main result of [Reference Hamkins6] shows that it is equiconsistent with ZFC that S5 is valid with respect to sentences in the language of set theory (no parameters), achieving
![]() $\mathord {\textrm {Val}}(W,\mathcal {L}_\in )=S5$
; the same paper shows that
$\mathord {\textrm {Val}}(W,\mathcal {L}_\in )=S5$
; the same paper shows that
![]() ${\textrm {MP}}({\mathbb R})$
, the maximality principle allowing real parameters (that is, S5 with real parameters), has a slightly stronger consistency strength, achieving
${\textrm {MP}}({\mathbb R})$
, the maximality principle allowing real parameters (that is, S5 with real parameters), has a slightly stronger consistency strength, achieving
![]() $\mathord {\textrm {Val}}(W,\mathcal {L}_{\in ,{\mathbb R}})=S5$
.
$\mathord {\textrm {Val}}(W,\mathcal {L}_{\in ,{\mathbb R}})=S5$
.
Let us now enlarge the context by moving to the generic multiverse
![]() $\mathcal {M}$
of a model of set theory
$\mathcal {M}$
of a model of set theory
![]() $M\models {\textrm {ZFC}}$
, which is the collection of models obtained by closing under the process of forcing extensions and grounds. Because the generic multiverse of a countable model exhibits non-amalgamation (see [Reference Fuchs, Hamkins and Reitz3, Reference Hamkins12]), it therefore does not generally converge to a limit model. Nevertheless, we may view
$M\models {\textrm {ZFC}}$
, which is the collection of models obtained by closing under the process of forcing extensions and grounds. Because the generic multiverse of a countable model exhibits non-amalgamation (see [Reference Fuchs, Hamkins and Reitz3, Reference Hamkins12]), it therefore does not generally converge to a limit model. Nevertheless, we may view
![]() $\mathcal {M}$
under the potentialist semantics, and discover the modal validities of this perspective on potentialism. Indeed, the generic multiverse of a model of set theory is a natural instance of width potentialism plus height actualism, since the various models of the generic multiverse all have the same ordinals, even though sets can gain new subsets in a forcing extension. Since the modal operators are definable in the language of set theory, once again there is no distinction between
$\mathcal {M}$
under the potentialist semantics, and discover the modal validities of this perspective on potentialism. Indeed, the generic multiverse of a model of set theory is a natural instance of width potentialism plus height actualism, since the various models of the generic multiverse all have the same ordinals, even though sets can gain new subsets in a forcing extension. Since the modal operators are definable in the language of set theory, once again there is no distinction between
![]() $\mathcal {L}_\in $
and
$\mathcal {L}_\in $
and
![]() $\mathcal {L}_\in ^\Diamond $
. The following theorem was observed independently by Piribauer in his master’s thesis [Reference Piribauer23] at the University of Amsterdam, undertaken with supervisor Löwe.
$\mathcal {L}_\in ^\Diamond $
. The following theorem was observed independently by Piribauer in his master’s thesis [Reference Piribauer23] at the University of Amsterdam, undertaken with supervisor Löwe.
Theorem 29. In the potentialist system of the generic multiverse
![]() $\mathcal {M}$
of a fixed countable model of ZFC set theory, every world W obeys
$\mathcal {M}$
of a fixed countable model of ZFC set theory, every world W obeys
The lower bound is sharp, for every world M has a ground model
![]() $W\subseteq M$
obeying
$W\subseteq M$
obeying
Depending on the original model, the upper bound also is sharp, for there can be other worlds W with
Proof. We’ve already mentioned that S4.2 is always valid for the potentialist semantics of the generic multiverse, which is the same as the modal logic of forcing for those models, and exactly S4.2 is realized for every model when parameters are allowed. Meanwhile, we also know that some models of set theory can exhibit S5 as their forcing validities, as before. In order to prove the theorem, therefore, what we shall show is that every model of set theory contains a ground whose validities are exactly S4.2, without parameters. For this, it will suffice to show that every model of set theory M has a ground model W by set-forcing such that W has arbitrarily large finite families of independent buttons and switches, expressible without parameters. In order to prove this fact, we shall rely on the recent breakthrough result of Usuba [Reference Usuba27], establishing the strong downward-directed grounds hypothesis DDG, which asserts that the ground models of the set-theoretic universe V are downward set-directed: for any set-indexed family of grounds
![]() $\{{W_i\mid i\in I}\}$
in the uniform ground-model enumeration, there is a ground model W with
$\{{W_i\mid i\in I}\}$
in the uniform ground-model enumeration, there is a ground model W with
![]() $W\subseteq W_i$
for all
$W\subseteq W_i$
for all
![]() $i\in I$
. It follows that for every model of set theory M and for every ordinal
$i\in I$
. It follows that for every model of set theory M and for every ordinal
![]() $\gamma $
in M, there is a ground model
$\gamma $
in M, there is a ground model
![]() $W\subseteq M$
such that
$W\subseteq M$
such that
 $V_\gamma ^W$
is the same as the
$V_\gamma ^W$
is the same as the
![]() $V_\gamma $
of the mantle of M, the intersection of all the grounds of M. In other words,
$V_\gamma $
of the mantle of M, the intersection of all the grounds of M. In other words,
 $V_\gamma ^W$
is least among the
$V_\gamma ^W$
is least among the
![]() $V_\gamma $
’s of the grounds of M. In particular, the cardinal and GCH structure of
$V_\gamma $
’s of the grounds of M. In particular, the cardinal and GCH structure of
 $V_\gamma ^W$
on the cardinals up to, say,
$V_\gamma ^W$
on the cardinals up to, say,
![]() $\aleph _{\omega +\omega }$
is absolutely definable in every model of the generic multiverse of M, since the mantle itself is definable in those models and W agrees with the mantle in that realm.
$\aleph _{\omega +\omega }$
is absolutely definable in every model of the generic multiverse of M, since the mantle itself is definable in those models and W agrees with the mantle in that realm.
We claim that this ground W has independent buttons and switches, and therefore its valid principles of forcing are exactly S4.2. For this, we cannot seem to use the stationary-set buttons that Hamkins and Löwe described in [Reference Hamkins, Leibman and Löwe14, sec. 4], since those make reference to an absolutely definable partition using the L-order. Nevertheless, we may modify the buttons identified by Rittberg, or alternatively modify the buttons of Friedman, Fuchino and Sakai, but using in each case the cardinals as defined in the mantle rather than L. Since as we mentioned the mantle is forcing-invariant and therefore an absolutely definable class common to all the models in the generic multiverse, the referent of such expressions as
 $\aleph _2^{\textrm {Mantle}}$
, for example, is invariant in this generic multiverse. For this reason, the buttons and switches relativized to the mantle rather than L will have the absoluteness properties that made them function as independent buttons and switches. Thus, the modal logic of forcing over W is exactly
$\aleph _2^{\textrm {Mantle}}$
, for example, is invariant in this generic multiverse. For this reason, the buttons and switches relativized to the mantle rather than L will have the absoluteness properties that made them function as independent buttons and switches. Thus, the modal logic of forcing over W is exactly
![]() $\mathord {\textrm {Val}}(W,\mathcal {L}_\in )=S4.2$
, as desired.
$\mathord {\textrm {Val}}(W,\mathcal {L}_\in )=S4.2$
, as desired.
Let us consider next an instance of set-theoretic potentialism that we find to exhibit both height potentialism and width potentialism in a natural way. Namely, consider a model of set theory M in the context of its generic multiverse. It is a consequence of Usuba’s theorem on the strong DDG that every model W in the generic multiverse of M is a forcing extension of a ground of M, so it has the form
![]() $W=W_r[G]$
, where
$W=W_r[G]$
, where
![]() $W_r\subseteq M$
is the ground of M indexed by r in the ground-model enumeration theorem, and where
$W_r\subseteq M$
is the ground of M indexed by r in the ground-model enumeration theorem, and where
![]() $G\subseteq {\mathbb Q}\in W_r$
is
$G\subseteq {\mathbb Q}\in W_r$
is
![]() $W_r$
-generic. Let
$W_r$
-generic. Let
![]() $\mathcal {M}$
be the collection of models of the form
$\mathcal {M}$
be the collection of models of the form
 $V_\beta ^W$
, where
$V_\beta ^W$
, where
![]() $W=W_r[G]$
is such a kind of model in the generic multiverse of M and where
$W=W_r[G]$
is such a kind of model in the generic multiverse of M and where
![]() $\beta $
is large enough so that
$\beta $
is large enough so that
 $r,{\mathbb Q},G\in V_\beta ^W$
. Because of non-amalgamation,
$r,{\mathbb Q},G\in V_\beta ^W$
. Because of non-amalgamation,
![]() $\mathcal {M}$
is not generally converging to a limit model, but we may nevertheless consider
$\mathcal {M}$
is not generally converging to a limit model, but we may nevertheless consider
![]() $\mathcal {M}$
under the potentialist semantics. This is height potentialism, since we may always make
$\mathcal {M}$
under the potentialist semantics. This is height potentialism, since we may always make
![]() $\beta $
larger and thereby gain new ordinal heights; and it is width potentialism, because we can always force to add more reals or additional generic subsets to the infinite sets that we current have. What are the modal validities of this variety of set-theoretic potentialism? Let us call it the system of generic-multiverse rank potentialism over M.
$\beta $
larger and thereby gain new ordinal heights; and it is width potentialism, because we can always force to add more reals or additional generic subsets to the infinite sets that we current have. What are the modal validities of this variety of set-theoretic potentialism? Let us call it the system of generic-multiverse rank potentialism over M.
Theorem 30. In the system of generic-multiverse rank potentialism over a fixed countable model of ZFC, every world W obeys
 $$ \begin{align*}S4.2 \subseteq \mathord{\mathrm{Val}}(W,\mathcal{L}_{\in,W}^\Diamond)\ \subseteq\ \mathord{\mathrm{Val}}(W,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
$$ \begin{align*}S4.2 \subseteq \mathord{\mathrm{Val}}(W,\mathcal{L}_{\in,W}^\Diamond)\ \subseteq\ \mathord{\mathrm{Val}}(W,\mathcal{L}_\in) \subseteq S5.\end{align*} $$
Depending on the original model, there can be a world W with
 $$ \begin{align*}S4.2 = \mathord{\mathrm{Val}}(W,\mathcal{L}_{\in,W}^\Diamond) = \mathord{\mathrm{Val}}(W,\mathcal{L}_\in).\end{align*} $$
$$ \begin{align*}S4.2 = \mathord{\mathrm{Val}}(W,\mathcal{L}_{\in,W}^\Diamond) = \mathord{\mathrm{Val}}(W,\mathcal{L}_\in).\end{align*} $$
Proof. Since the inclusion relation is both transitive and reflexive on
![]() $\mathcal {M}$
, it follows that S4 is valid at every world, for any language interpreted in those worlds. For the validity of .2, we cannot appeal to directedness, since as we noted earlier this collection of models has non-amalgamation and therefore is not directed; nevertheless, .2 is valid as in the modal logic of forcing because of product forcing. Namely, if
$\mathcal {M}$
, it follows that S4 is valid at every world, for any language interpreted in those worlds. For the validity of .2, we cannot appeal to directedness, since as we noted earlier this collection of models has non-amalgamation and therefore is not directed; nevertheless, .2 is valid as in the modal logic of forcing because of product forcing. Namely, if
![]() holds at world
holds at world
 $V_\beta ^W$
, where
$V_\beta ^W$
, where
![]() $W=W_r[G]$
and
$W=W_r[G]$
and
 $r,G,{\mathbb Q}\in V_\beta ^W$
, then it means there is some larger
$r,G,{\mathbb Q}\in V_\beta ^W$
, then it means there is some larger
 $V_\gamma ^{U}$
, with
$V_\gamma ^{U}$
, with
![]() $U=U_s[H]$
and forcing
$U=U_s[H]$
and forcing
 $s,H,{\mathbb P}\in V_\gamma ^U$
, such that any still larger
$s,H,{\mathbb P}\in V_\gamma ^U$
, such that any still larger
 $V_\delta ^{U'}$
satisfies
$V_\delta ^{U'}$
satisfies
![]() $\varphi (\vec a)$
. Thus, this situation is forced by some condition in P over
$\varphi (\vec a)$
. Thus, this situation is forced by some condition in P over
![]() $U_s$
. So for any
$U_s$
. So for any
 $V_\theta ^{W'}$
extending
$V_\theta ^{W'}$
extending
 $V_\beta ^W$
, we can still force over
$V_\beta ^W$
, we can still force over
![]() $W'$
with that forcing and find a common extension
$W'$
with that forcing and find a common extension
 $V_\lambda ^{W''}$
satisfying
$V_\lambda ^{W''}$
satisfying
![]() $\varphi (\vec a)$
. So S4.2 is valid.
$\varphi (\vec a)$
. So S4.2 is valid.
Meanwhile, it is easy to see that the validities of any particular world are contained within S5, since one can use the GCH pattern as a family of independent switches. One can always force over any given model so as to achieve any desired finite pattern for the GCH at the cardinals
![]() $\aleph _n$
.
$\aleph _n$
.
Finally, consider the generic-multiverse rank-potentialist system
![]() $\mathcal {M}$
arising from a model of
$\mathcal {M}$
arising from a model of
![]() ${\textrm {ZFC}}+V=L$
. We may use the same independent buttons and switches of Theorem 28, the point being that one doesn’t need the entire universe to verify the status of the buttons and switches that were used there. So it is enough to have
${\textrm {ZFC}}+V=L$
. We may use the same independent buttons and switches of Theorem 28, the point being that one doesn’t need the entire universe to verify the status of the buttons and switches that were used there. So it is enough to have
 $V_\beta ^{L[G]}$
for large enough
$V_\beta ^{L[G]}$
for large enough
![]() $\beta $
in order to operate the buttons and switches.
$\beta $
in order to operate the buttons and switches.
We are unsure whether every instance of generic-multiverse rank potentialism contains a world whose validities are exactly S4.2, since in our argument, we used a model of
![]() $V=L$
in order to find a model with independent buttons and switches. It would also suffice if there was a particular world
$V=L$
in order to find a model with independent buttons and switches. It would also suffice if there was a particular world
 $V_\beta ^W$
that was tall enough and definable in all the other worlds in the system, so that we could form buttons and switches by reference to that world. In the case of generic-multiverse potentialism, we were able to use the mantle for this purpose, but in generic-multiverse rank potentialism, we do not know that the mantle will necessarily work, since perhaps some
$V_\beta ^W$
that was tall enough and definable in all the other worlds in the system, so that we could form buttons and switches by reference to that world. In the case of generic-multiverse potentialism, we were able to use the mantle for this purpose, but in generic-multiverse rank potentialism, we do not know that the mantle will necessarily work, since perhaps some
 $V_\beta ^W$
can be wrong about the mantle of W. Perhaps the mantle of W is definable in
$V_\beta ^W$
can be wrong about the mantle of W. Perhaps the mantle of W is definable in
 $V_\beta ^W$
using the language
$V_\beta ^W$
using the language
![]() $\mathcal {L}_\in ^\Diamond $
? If so, then we will get that the potentialist system includes a world whose validities are S4.2 with respect to
$\mathcal {L}_\in ^\Diamond $
? If so, then we will get that the potentialist system includes a world whose validities are S4.2 with respect to
![]() $\mathcal {L}_\in ^\Diamond $
-sentences.
$\mathcal {L}_\in ^\Diamond $
-sentences.
One observation that may bear on this question is the fact that the generic-multiverse rank-potentialist system
![]() $\mathcal {M}$
, consisting of the models
$\mathcal {M}$
, consisting of the models
 $V_\beta ^W$
, where W is in the generic multiverse of M, is identical to the forcing-extension rank-potentialist system that arises as
$V_\beta ^W$
, where W is in the generic multiverse of M, is identical to the forcing-extension rank-potentialist system that arises as
 $V_\beta ^{\mathbb {M}[G]}$
, where
$V_\beta ^{\mathbb {M}[G]}$
, where
![]() $\mathbb {M}$
is the mantle of M. This is true because the strong downward directedness hypothesis implies that for every ordinal
$\mathbb {M}$
is the mantle of M. This is true because the strong downward directedness hypothesis implies that for every ordinal
![]() $\beta $
in M, there is a ground
$\beta $
in M, there is a ground
![]() $W_r\subseteq M$
such that the
$W_r\subseteq M$
such that the
![]() $V_\beta $
of
$V_\beta $
of
![]() $W_r$
is the same as the
$W_r$
is the same as the
![]() $V_\beta $
of the mantle
$V_\beta $
of the mantle
![]() $\mathbb {M}$
.
$\mathbb {M}$
.
3.8 Countable transitive model potentialism
Let us now consider a very natural and attractive case of set-theoretic potentialism, namely, the potentialist system
![]() $\mathcal {C}$
consisting of the countable transitive models of ZFC set theory.
$\mathcal {C}$
consisting of the countable transitive models of ZFC set theory.
Theorem 31. In the potentialist system
![]() $\mathcal {C}$
consisting of the countable transitive models of ZFC, every world W satisfies every S4 assertion, with respect to substitution instances in any language interpreted at every world of
$\mathcal {C}$
consisting of the countable transitive models of ZFC, every world W satisfies every S4 assertion, with respect to substitution instances in any language interpreted at every world of
![]() $\mathcal {C};$
furthermore, the propositional modal validities of any particular world, with respect to substitution instances in any language extending the language of set theory, are contained in S5.
$\mathcal {C};$
furthermore, the propositional modal validities of any particular world, with respect to substitution instances in any language extending the language of set theory, are contained in S5.
Proof. The potentialist accessibility relation is inclusion, which is transitive and reflexive. Thus, S4 is valid at every world, even with respect to expansions of the language interpreted in every world of
![]() $\mathcal {C}$
. Meanwhile, if W is a world in
$\mathcal {C}$
. Meanwhile, if W is a world in
![]() $\mathcal {C}$
, then W admits arbitrarily large independent families of switches, such as the assertions expressing the GCH patterns on the
$\mathcal {C}$
, then W admits arbitrarily large independent families of switches, such as the assertions expressing the GCH patterns on the
![]() $\aleph _n$
’s. The truth of these assertions can be controlled independently by forcing over any countable transitive model of set theory. Thus, by Theorem 3, the modal validities of W are contained within S5.
$\aleph _n$
’s. The truth of these assertions can be controlled independently by forcing over any countable transitive model of set theory. Thus, by Theorem 3, the modal validities of W are contained within S5.
The situation is much nicer and we can prove far more under a certain robustness assumption, namely, that every real is an element of a countable transitive model of ZFC. This assumption amounts to a very weak large cardinal hypothesis, for if there is an inaccessible cardinal, or even merely a worldly cardinal, then a simple Löwenheim–Skolem argument shows that indeed every real is an element of a countable transitive model of ZFC.
Theorem 32. Assume that every real is an element of a countable transitive model of ZFC. Then the potentialist system
![]() $\mathcal {C}$
consisting of the countable transitive models of ZFC provides a potentialist account of the collection
$\mathcal {C}$
consisting of the countable transitive models of ZFC provides a potentialist account of the collection
![]() $H_{\omega _1}$
of hereditarily countable sets. Furthermore, every world W obeys
$H_{\omega _1}$
of hereditarily countable sets. Furthermore, every world W obeys
The lower bound is sharp, for some worlds W have
The upper bound also is sharp, for some other worlds W have
for any particular countable language
![]() $\mathcal {L}^+$
extending
$\mathcal {L}^+$
extending
![]() $\mathcal {L}_\in $
.
$\mathcal {L}_\in $
.
Proof. Certainly every countable transitive set is a substructure of
 $\left \langle H_{\omega _1},\in \right \rangle $
, and every element of
$\left \langle H_{\omega _1},\in \right \rangle $
, and every element of
![]() $H_{\omega _1}$
can be coded by a real and therefore placed into a countable transitive model of ZFC, under our assumption. It follows that
$H_{\omega _1}$
can be coded by a real and therefore placed into a countable transitive model of ZFC, under our assumption. It follows that
![]() $\mathcal {C}$
is directed (and even
$\mathcal {C}$
is directed (and even
![]() $\sigma $
-directed), and so
$\sigma $
-directed), and so
![]() $\mathcal {C}$
provides a potentialist account of
$\mathcal {C}$
provides a potentialist account of
![]() $H_{\omega _1}$
. Since this system is directed, it follows that S4.2 is valid at every world, regardless of what other structure is imposed or which language or parameters are used.
$H_{\omega _1}$
. Since this system is directed, it follows that S4.2 is valid at every world, regardless of what other structure is imposed or which language or parameters are used.
Let
![]() $L_\alpha $
be the smallest transitive model of ZFC. This world has independent families of buttons and switches, using a modified version of those in the modal logic of forcing. Namely, the button
$L_\alpha $
be the smallest transitive model of ZFC. This world has independent families of buttons and switches, using a modified version of those in the modal logic of forcing. Namely, the button
![]() $b_n$
asserts that
$b_n$
asserts that
![]() $n^{\textrm {th}}$
piece of the L-least partition of
$n^{\textrm {th}}$
piece of the L-least partition of
 $\omega _1^{L_\alpha }$
is no longer stationary (note that
$\omega _1^{L_\alpha }$
is no longer stationary (note that
![]() $L_\alpha $
is definable as a class in any transitive model of ZFC), and the switch
$L_\alpha $
is definable as a class in any transitive model of ZFC), and the switch
![]() $s_m$
asserts that the GCH holds at (the current)
$s_m$
asserts that the GCH holds at (the current)
![]() $\aleph _m$
, for
$\aleph _m$
, for
![]() $m\geq 1$
. These buttons and switches can be controlled independently by forcing, although the buttons are indeed buttons with respect to the potentialist semantics. In particular, moving to a taller model will push all the buttons, since
$m\geq 1$
. These buttons and switches can be controlled independently by forcing, although the buttons are indeed buttons with respect to the potentialist semantics. In particular, moving to a taller model will push all the buttons, since
![]() $L_\alpha $
will be realized as countable there. Since we have sufficient independent buttons and switches, it follows by Theorem 5 that the validities of this world, with respect to substitution instances in the language of set theory, are exactly
$L_\alpha $
will be realized as countable there. Since we have sufficient independent buttons and switches, it follows by Theorem 5 that the validities of this world, with respect to substitution instances in the language of set theory, are exactly
![]() $\mathord {\textrm {Val}}(L_\alpha ,\mathcal {L}_\in )=S4.2$
. The same idea works in any model, if parameters are allowed, showing
$\mathord {\textrm {Val}}(L_\alpha ,\mathcal {L}_\in )=S4.2$
. The same idea works in any model, if parameters are allowed, showing
![]() $S4.2=\mathord {\textrm {Val}}(W,\mathcal {L}_{\in ,W})$
for every world. Meanwhile, the GCH-pattern switches are operable over any model of set theory, and so the validities of any particular world are contained within S5.
$S4.2=\mathord {\textrm {Val}}(W,\mathcal {L}_{\in ,W})$
for every world. Meanwhile, the GCH-pattern switches are operable over any model of set theory, and so the validities of any particular world are contained within S5.
The upper bound is provided by Theorem 33.
Since
![]() $\mathcal {C}$
provides a potentialist account of
$\mathcal {C}$
provides a potentialist account of
![]() $H_{\omega _1}$
, it follows from Theorem 1 that in the potentialist language
$H_{\omega _1}$
, it follows from Theorem 1 that in the potentialist language
![]() $\mathcal {L}^\Diamond $
we may at any world
$\mathcal {L}^\Diamond $
we may at any world
![]() $W\in \mathcal {C}$
to refer to truth in
$W\in \mathcal {C}$
to refer to truth in
![]() $H_{\omega _1}$
, including truth about what other kinds of worlds in
$H_{\omega _1}$
, including truth about what other kinds of worlds in
![]() $\mathcal {C}$
there may be and how they are related.
$\mathcal {C}$
there may be and how they are related.
Note also that many other worlds of
![]() $\mathcal {C}$
than the Shepherdson–Cohen model
$\mathcal {C}$
than the Shepherdson–Cohen model
![]() $L_\alpha $
will also have validities limited to S4.2. For example, any world W that is absolutely definable in all larger worlds will also have independent buttons and switches, for essentially the same reason. This includes many models with various large cardinals, if any exist, such as the smallest transitive model
$L_\alpha $
will also have validities limited to S4.2. For example, any world W that is absolutely definable in all larger worlds will also have independent buttons and switches, for essentially the same reason. This includes many models with various large cardinals, if any exist, such as the smallest transitive model
![]() $L_\gamma [\mu ]$
realizing the smallest possible ordinal as a measurable cardinal, and similarly with much stronger large cardinal notions.
$L_\gamma [\mu ]$
realizing the smallest possible ordinal as a measurable cardinal, and similarly with much stronger large cardinal notions.
Let us now turn to the upper bound, by investigating the nature of the worlds satisfying the potentialist maximality principle S5 for this version of potentialism. The maximality principle occurs when S5 is valid at a world. We find these worlds quite attractively to instantiate the maximize maxim, with respect both to height and width potentialism. The idea is that if W satisfies the potentialist maximality principle, then any statement
![]() $\sigma $
that could become necessarily true, either by moving to a wider or to a taller universe, is already true.
$\sigma $
that could become necessarily true, either by moving to a wider or to a taller universe, is already true.
Theorem 33. If every real is an element of a countable transitive model of ZFC, then every world
![]() $U\in \mathcal {C}$
can be extended to a world
$U\in \mathcal {C}$
can be extended to a world
![]() $W\in \mathcal {C}$
satisfying the potentialist maximality principle for assertions in any fixed countable language
$W\in \mathcal {C}$
satisfying the potentialist maximality principle for assertions in any fixed countable language
![]() $\mathcal {L}^+$
extending
$\mathcal {L}^+$
extending
![]() $\mathcal {L}_\in ^\Diamond $
(interpreted in every model of
$\mathcal {L}_\in ^\Diamond $
(interpreted in every model of
![]() $\mathcal {C}$
). That is,
$\mathcal {C}$
). That is,
Proof. Assume that every real is an element of a countable transitive model of ZFC. It follows as we noted earlier that any countably many worlds of
![]() $\mathcal {C}$
have a common upper bound. Consider any particular world
$\mathcal {C}$
have a common upper bound. Consider any particular world
![]() $U\in \mathcal {C}$
and any countable language
$U\in \mathcal {C}$
and any countable language
![]() $\mathcal {L}^+$
extending the language of set theory. In particular, the new language might have constants for every element of U. Enumerate the assertions of
$\mathcal {L}^+$
extending the language of set theory. In particular, the new language might have constants for every element of U. Enumerate the assertions of
![]() $\mathcal {L}^+$
as
$\mathcal {L}^+$
as
![]() $\sigma _0$
,
$\sigma _0$
,
![]() $\sigma _1$
, and so on. Let
$\sigma _1$
, and so on. Let
![]() $W_0=U$
be the initial world. Given
$W_0=U$
be the initial world. Given
![]() $W_n$
, ask whether
$W_n$
, ask whether
![]() in this potentialist system. If so, then there is some
in this potentialist system. If so, then there is some
![]() ; otherwise, choose
; otherwise, choose
![]() $W_{n+1}$
extending
$W_{n+1}$
extending
![]() $W_n$
as you like. Having selected
$W_n$
as you like. Having selected
![]() $W_n$
for all
$W_n$
for all
![]() $n<\omega $
, let W be any world with
$n<\omega $
, let W be any world with
![]() $W_n\subseteq W$
for all n. If
$W_n\subseteq W$
for all n. If
![]() , then since
, then since
![]() $W_n$
can access W, it follows that
$W_n$
can access W, it follows that
![]() , in which case
, in which case
![]() , and so
, and so
![]() $W\models \sigma _n$
. Thus, W satisfies every instance of Axiom 5 in this language, and since it also satisfies S4.2, it follows that S5 is valid in W. And the same conclusion holds with respect to any larger world than W, since S5 is persistent.
$W\models \sigma _n$
. Thus, W satisfies every instance of Axiom 5 in this language, and since it also satisfies S4.2, it follows that S5 is valid in W. And the same conclusion holds with respect to any larger world than W, since S5 is persistent.
We find it interesting to consider the previous theorem in the case that
![]() $V=L$
. In this situation L can have countable transitive models of some very rich theories, such as a proper class of Woodin cardinals or supercompact cardinals or what have you. So not every
$V=L$
. In this situation L can have countable transitive models of some very rich theories, such as a proper class of Woodin cardinals or supercompact cardinals or what have you. So not every
![]() $W\in \mathcal {C}$
will satisfy
$W\in \mathcal {C}$
will satisfy
![]() $V=L$
, and some will believe themselves to be very far from L. Nevertheless, because every such W is countable in L, we will be able to extend W to some
$V=L$
, and some will believe themselves to be very far from L. Nevertheless, because every such W is countable in L, we will be able to extend W to some
![]() $L_\alpha $
, which of course satisfies
$L_\alpha $
, which of course satisfies
![]() $V=L$
. In particular, this shows that we can achieve the CTM-potentialist maximality principle in a world satisfying
$V=L$
. In particular, this shows that we can achieve the CTM-potentialist maximality principle in a world satisfying
![]() $V=L$
. This situation illustrates one of the central philosophical points made by the first author in [Reference Hamkins10], namely, that the capacity to extend the universe upward tends to undermine the view of L as contradicting the ‘maximize’ maxim of Maddy.
$V=L$
. This situation illustrates one of the central philosophical points made by the first author in [Reference Hamkins10], namely, that the capacity to extend the universe upward tends to undermine the view of L as contradicting the ‘maximize’ maxim of Maddy.
In particular, if
![]() $V=L$
and every real is an element of a countable transitive model of ZFC, then there are such worlds W satisfying the potentialist maximality principle for sentences in any countable language extending the language of set theory (and including
$V=L$
and every real is an element of a countable transitive model of ZFC, then there are such worlds W satisfying the potentialist maximality principle for sentences in any countable language extending the language of set theory (and including
![]() $\mathcal {L}_\in ^\Diamond $
if desired), such that
$\mathcal {L}_\in ^\Diamond $
if desired), such that
![]() $W\models V=L$
; and there are other such worlds W satisfying the potentialist maximality principle for which
$W\models V=L$
; and there are other such worlds W satisfying the potentialist maximality principle for which
![]() $W\models V\neq L$
.
$W\models V\neq L$
.
3.9 Countable model potentialism
Let us now enlarge the potentialist system from merely the transitive models to the collection consisting of all countable models of ZFC set theory.
At first, let’s consider this as a potentialist-like system under the substructure relation, so that one world
 $\left \langle W,\in ^W\right \rangle $
accesses another
$\left \langle W,\in ^W\right \rangle $
accesses another
 $\left \langle U,\in ^U\right \rangle $
just in case the first is a substructure of the second, which means
$\left \langle U,\in ^U\right \rangle $
just in case the first is a substructure of the second, which means
![]() $W\subseteq U$
and
$W\subseteq U$
and
![]() $\in ^W=\in ^U\upharpoonright W$
. The potentialist idea here is that one can move to a larger universe of set theory by adding more objects, including new elements of old sets, as long as the new
$\in ^W=\in ^U\upharpoonright W$
. The potentialist idea here is that one can move to a larger universe of set theory by adding more objects, including new elements of old sets, as long as the new
![]() $\in $
-relation agrees with the old one on the previously existing sets.
$\in $
-relation agrees with the old one on the previously existing sets.
Theorem 34. Assume ZFC is consistent and consider the potentialist system consisting of all countable models of ZFC, under the substructure relation. Every world W in this potentialist system obeys
If W is any countable nonstandard model of ZFC, then
 $$ \begin{align*}\mathord{\mathrm{Val}}(W,\mathcal{L}_\in^\Diamond) = \mathord{\mathrm{Val}}(W,\mathcal{L}_\in)=S5.\end{align*} $$
$$ \begin{align*}\mathord{\mathrm{Val}}(W,\mathcal{L}_\in^\Diamond) = \mathord{\mathrm{Val}}(W,\mathcal{L}_\in)=S5.\end{align*} $$
Proof. The main theorem of [Reference Hamkins9] shows that the countable models of ZFC are linearly pre-ordered by embeddability: for any two models, one of them is isomorphic to a substructure of the other, and furthermore, one model embeds into another just in case the ordinals of the first order embed into the ordinals of the second. It follows that the nonstandard models of ZFC are universal under embeddability.
Because the models are linearly pre-ordered by embeddability, it follows that S4.3 is valid in every world. Because these are ZFC models, the GCH-pattern statements are independent switches, and so the validities of any world are contained in S5. Meanwhile, for any world W, let
![]() $a=\emptyset ^W$
, and let
$a=\emptyset ^W$
, and let
![]() $r_n$
be the statement “a has at least n distinct elements.” These statements are all false in W, of course, since a has no elements in W. But the particular embeddings constructed in [Reference Hamkins9] and variations of them show that there are larger models U into which W embeds, in which as many new elements of a as desired are introduced. Thus, these statements form a ratchet, and the GCH-pattern statements are a mutually independent family of switches. So the modal validities of W for such statements are contained within S4.3, and so the first chain of equations and inclusions is proved.
$r_n$
be the statement “a has at least n distinct elements.” These statements are all false in W, of course, since a has no elements in W. But the particular embeddings constructed in [Reference Hamkins9] and variations of them show that there are larger models U into which W embeds, in which as many new elements of a as desired are introduced. Thus, these statements form a ratchet, and the GCH-pattern statements are a mutually independent family of switches. So the modal validities of W for such statements are contained within S4.3, and so the first chain of equations and inclusions is proved.
Finally, for the final statement of the theorem, it is a consequence of the fact that the nonstandard models all access isomorphic copies of each other—the main theorem of [Reference Hamkins9] shows that they are all bi-embeddable—that S5 is valid in each of them for sentences of
![]() $\mathcal {L}_\in ^\Diamond $
.
$\mathcal {L}_\in ^\Diamond $
.
Note that a simple compactness argument shows that this potentialist system has amalgamation and even
![]() $\sigma $
-amalgamation, and furthermore has the joint embedding property, and so actually there is a Fraïssé limit here, which will be a copy of the countable random
$\sigma $
-amalgamation, and furthermore has the joint embedding property, and so actually there is a Fraïssé limit here, which will be a copy of the countable random
![]() ${\mathbb Q}$
-graded digraph, as described in [Reference Hamkins9]. Even though the collection of countable ZFC models does not have a limit model in the sense of our original definition, if we used this embedding-based approach to defining the limit structure, we would be led to find a limit model in this countable random
${\mathbb Q}$
-graded digraph, as described in [Reference Hamkins9]. Even though the collection of countable ZFC models does not have a limit model in the sense of our original definition, if we used this embedding-based approach to defining the limit structure, we would be led to find a limit model in this countable random
![]() ${\mathbb Q}$
-graded digraph. The substructures of this graph that are ZFC models form a potentialist system containing isomorphic copies of any given countable model of ZFC, which furthermore provide a potentialist account of this graph as the limit structure.
${\mathbb Q}$
-graded digraph. The substructures of this graph that are ZFC models form a potentialist system containing isomorphic copies of any given countable model of ZFC, which furthermore provide a potentialist account of this graph as the limit structure.
Some set theorists may object that it is more natural to use a slightly more restricted accessibility relation, because the substructure relation allows for some rather strange things. For example, with the substructure accessibility relation, every set is potentially finite, because results in [Reference Hamkins9] show that every model is isomorphic to a substructure of the hereditarily finite sets of any
![]() $\omega $
-nonstandard model. Further, no sets are necessarily disjoint, since for any two sets
$\omega $
-nonstandard model. Further, no sets are necessarily disjoint, since for any two sets
![]() $a,b$
, we can access a larger world that has an object that is an element of both. Similarly, the empty set of one world can have members or even become infinite in another world. All these things seem a little strange.
$a,b$
, we can access a larger world that has an object that is an element of both. Similarly, the empty set of one world can have members or even become infinite in another world. All these things seem a little strange.
So it may be a little more orderly or stable to consider the collection of countable models of ZFC under the transitive-substructure relation, rather than the full substructure relation. That is, in this modified version, we say that one world
 $\left \langle W,\in ^W\right \rangle $
accesses another world
$\left \langle W,\in ^W\right \rangle $
accesses another world
 $\left \langle U,\in ^U\right \rangle $
, just in case the first is a transitive substructure of the second, meaning that
$\left \langle U,\in ^U\right \rangle $
, just in case the first is a transitive substructure of the second, meaning that
![]() $W\subseteq U$
and
$W\subseteq U$
and
![]() $\in ^W=\in ^U\upharpoonright W$
and furthermore,
$\in ^W=\in ^U\upharpoonright W$
and furthermore,
![]() $x\in ^U y\in W$
implies
$x\in ^U y\in W$
implies
![]() $x\in W$
. So the larger world agrees with the smaller world on the membership relation of objects in the smaller world and furthermore, no new elements of old sets are added.
$x\in W$
. So the larger world agrees with the smaller world on the membership relation of objects in the smaller world and furthermore, no new elements of old sets are added.
Since this modified accessibility relation is reflexive and transitive, and refines the substructure relation, this is indeed a potentialist system, which therefore validates S4 at every world. And since these are models of set theory, the GCH-pattern switches show that the validities of any particular world are contained within S5, even when restricted to sentences in the language of set theory.
This modified system is not directed, nor even weakly directed, because if
 $\left \langle W,\in ^W\right \rangle $
is a countable ill-founded model of ZFC, then there is a countable
$\left \langle W,\in ^W\right \rangle $
is a countable ill-founded model of ZFC, then there is a countable
![]() $\in ^W$
-descending sequence s and there can be no extension
$\in ^W$
-descending sequence s and there can be no extension
 $\left \langle U,\in ^U\right \rangle $
containing s in which
$\left \langle U,\in ^U\right \rangle $
containing s in which
 $\left \langle W,\in ^W\right \rangle $
is transitive, even if W is an
$\left \langle W,\in ^W\right \rangle $
is transitive, even if W is an
![]() $\omega $
-model, since s reveals the ill-foundedness of W. Thus, this system does not provide a potentialist account of any limit model.
$\omega $
-model, since s reveals the ill-foundedness of W. Thus, this system does not provide a potentialist account of any limit model.
We believe that under some reasonable assumption, we can get that this potentialist system has upper bounds for countable increasing chains in the transitive substructure relation, as in the result of [Reference Hamkins12]. That is, if you can move successively to larger and larger countable models of ZFC, with each model transitive in the next one, then there is a model at the top inside of which they are all transitive submodels. In this case, we can get models of S5 in this system, for sentences in any countable language, by the same argument as in Theorem 33. We shall leave further investigation of this modified potentialist system for another project.
We suggest that it may be fruitful to consider the multiverse model of Gitman and Hamkins [Reference Gitman and Hamkins5] as a potentialist system under either of the accessibility relations mentioned above. The collection of worlds are the countable computably saturated models of ZFC, and we may consider them either under the substructure accessibility relation or the transitive-substructure accessibility relation.
Lastly, we should like to mention that in current work, the first author [Reference Hamkins13] has established that the modal logic of end-extensional potentialism for the models of PA is precisely S4. Adapting that work to the case of set theory, he and Woodin [Reference Hamkins and Woodin17] similarly established that the modal logic of top-extensional potentialism for the countable models of ZFC is also precisely S4.
Acknowledgments
The authors are grateful to the Set-Theoretic Pluralism network for support provided for their participation at the STP Symposium 2016 in Aberdeen, where this work was initiated. The research of the first author has been supported by grant #69573-00 47 from the CUNY Research Foundation. Commentary can be made about this article on his blog at http://jdh.hamkins.org/set-theoretic-potentialism.