Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T16:16:41.503Z Has data issue: false hasContentIssue false
  • English
  • Français

Threshold Circuits for Iterated Matrix Product and Powering

Published online by Cambridge University Press:  15 April 2002

Carlo Mereghetti  and
Beatrice Palano
Carlo Mereghetti
Affiliation:
Dipartimento di Informatica, Sist. e Com., Università degli Studi di Milano -Bicocca, Via Bicocca degli Arcimboldi 8, 20126 Milano, Italy; e-mail: mereghetti@disco.unimib.it
Beatrice Palano
Affiliation:
Dipartimento di Informatica, Università degli Studi di Torino, Corso Svizzera 185, 10149 Torino, Italy; e-mail: beatrice@di.unito.it
Get access

Abstract

The complexity of computing, via threshold circuits, the iterated product and powering of fixed-dimension $k\times k$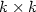 matrices with integer or rational entries is studied. We call these two problems $\sf IMP_k$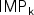 and $\sf MPOW_k$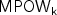, respectively, for short. We prove that: (i) For $k\geq2$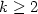, $\sf IMP_k$ 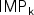does not belong to ${\rm TC}^0$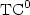, unless ${\rm TC}^0={\rm NC}^1$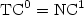.newline (ii) For stochastic matrices : $\sf IMP_2$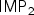 belongs to ${\rm TC}^0$ 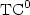while, for $k\geq3$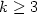, $\sf IMP_k$ 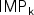does not belong to ${\rm TC}^0$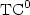, unless ${\rm TC}^0={\rm NC}^1$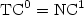. 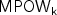(iii) For any k, $\sf MPOW_k$ belongs to ${\rm TC}^0$.

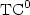Keywords

Threshold circuitsiterated matrix productmatrix powering.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 34 , Issue 1 , January 2000 , pp. 39 - 46
Copyright
© EDP Sciences, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Mix Barrington, D.A., Compton, K., Straubing, H. and Thérien, D., Regular languages in NC1. J. Comp. System Sci. 44 (1992) 478-499. CrossRef
Cook, S.A., A taxonomy of problems with fast parallel algorithms. Inform. and Control. 64 (1985) 2-22. CrossRef
L.E. Dickson, Linear Groups with an Exposition of the Galois Field Theory. 1901. Reprinted by Dover (1958).
S. Eilenberg, Automata, Languages, and Machines. Academic Press (1976).
Eberly, W., Very fast parallel polynomial arithmetic. SIAM J. Comput. 18 (1989) 955-976. CrossRef
F. Gécseg, Products of Automata. Springer Verlag, Monogr. Theoret. Comput. Sci. EATCS Ser. 7 (1986).
A. Hajnal, W. Maaß, P. Pudlák, M. Szegedy and G. Turán, Threshold circuits of bounded depth, in Proc. 28th IEEE Symposium on Foundations of Computer Science (1987) 99-110. Also in J. Comp. System Sci. 46 (1993) 129-154.
T. Hofmeister, Depth-efficient threshold circuits for arithmetic functions, edited by V. Roychowdhury, K.-Y. Siu and A. Orlitsky, Theoretical Advances in Neural Computation and Learning. Kluwer Academic (1994) 37-84.
C. Mereghetti and B. Palano, Threshold circuits for some matrix operations. Consequences on regular and probabilistic languages. Theoretical Computer Science - Proceedings of the 6th Italian Conference. World Scientific (1998) 216-227.
C. Mereghetti and B. Palano, The Parallel Complexity of Deterministic and Probabilistic Automata. Technical Report No. 242-99, Dipartimento di Scienze dell'Informazione. Università degli Studi di Milano (1999). Available at http://gongolo.usr.dsi.unimi.it/mereghc/papers/TR_242-99.ps
C. Mereghetti and B. Palano, Matrix Powering in Constant Depth. Technical Report No. 245-00, Dipartimento di Scienze dell'Informazione. Università degli Studi di Milano (2000). Available at http://gongolo.usr.dsi.unimi.it/mereghc/papers/TR_245-00.ps
V. Roychowdhury, K.-Y. Siu and A. Orlitsky, Neural models and spectral methods, edited by V. Roychowdhury, K.-Y. Siu and A. Orlitsky, Theoretical Advances in Neural Computation and Learning. Kluwer Academic (1994) 3-36.
G. Shilov, Linear Algebra. Prentice Hall (1971). Reprinted by Dover (1977).
H. Straubing, Finite Automata, Formal Logic, and Circuit Complexity. Birkhäuser (1994).
I. Wegener, The Complexity of Boolean Functions. Teubner (1987).
Wegener, I., Optimal lower bounds on the depth of polynomial-size threshold circuits for some arithmetic functions. Inform. Process. Lett. 46 (1993) 85-87. CrossRef