Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-14T13:16:45.181Z Has data issue: false hasContentIssue false
  • English
  • Français

On the continuity set of an Omega rational function

Published online by Cambridge University Press:  18 January 2008

Olivier Carton ,
Olivier Finkel  and
Pierre Simonnet
Olivier Carton
Affiliation:
LIAFA, Université Paris 7 et CNRS, 2 Place Jussieu 75251 Paris Cedex 05, France; Olivier.Carton@liafa.jussieu.fr
Olivier Finkel
Affiliation:
Équipe Modèles de Calcul et Complexité,
Pierre Simonnet
Affiliation:
UMR 6134-Systèmes Physiques de l'Environnement, Faculté des Sciences, Université de Corse, Quartier Grossetti BP52 20250, Corte, France; simonnet@univ-corse.fr
Get access

Abstract

In this paper, we study the continuity of rational functions realized by Büchi finite state transducers. It has been shown by Prieur that it can be decided whether such a function is continuous. We prove here that surprisingly, it cannot be decided whether such a function f has at least one point of continuity and that its continuity set C(f) cannot be computed. In the case of a synchronous rational function, we show that its continuity set is rational and that it can be computed. Furthermore we prove that any rational ${\bf \Pi}^0_2$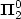-subset of Σω for some alphabet Σ is the continuity set C(f) of an ω-rational synchronous function f defined on Σω.

Keywords

Infinitary rational relationsomega rational functionstopologypoints of continuitydecision problemsomega rational languagesomega context-free languages.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 42 , Issue 1: A nonstandard spirit among computer scientists:a tribute to Serge Grigorieff at the occasion of his 60th birthday , January 2008 , pp. 183 - 196
Copyright
© EDP Sciences, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ya. M. Barzdin and B.A. Trakhtenbrot, Finite Automata, Behaviour and Synthesis. Nauka, Moscow (1970) (English translation, North Holland, Amsterdam, 1973).
M.-P. Béal and O. Carton, Determinization of transducers over infinite words, in Proceedings of the International Conference ICALP 2000, edited by U. Montanari et al. Lect. Notes Comput. Sci. 1853 (2000) 561–570.
Béal, M.-P., Carton, O., Prieur, C. and Sakarovitch, J., Squaring transducers: an efficient procedure for deciding functionality and sequentiality. Theor. Comput. Sci. 292 (2003) 45–63. CrossRef
J. Berstel, Transductions and Context Free Languages. Teubner Verlag (1979).
J.R. Büchi, On a decision method in restricted second order arithmetic, Logic Methodology and Philosophy of Science, Proc. 1960 Int. Congr. Stanford University Press (1962) 1–11.
Choffrut, C., Une caractérisation des fonctions séquentielles et des fonctions sous-séquentielles en tant que relations rationnelles. Theor. Comput. Sci. 5 (1977) 325–338. CrossRef
C. Choffrut and S. Grigorieff, Uniformization of rational relations, Jewels are Forever, edited by J. Karhumäki, H. Maurer, G. Paun and G. Rozenberg. Springer (1999) 59–71.
Engelfriet, J. and Hoogeboom, H.J., X-automata on ω-Words. Theor. Comput. Sci. 110 (1993) 1–51. CrossRef
Finkel, O., On the topological complexity of infinitary rational relations. RAIRO-Theor. Inf. Appl. 37 (2003) 105–113. CrossRef
Finkel, O., Undecidability of topological and arithmetical properties of infinitary rational relations. RAIRO-Theor. Inf. Appl. 37 (2003) 115–126. CrossRef
Finkel, O., Infinitary, On rational relations and Borel sets, in Proceedings of the Fourth International Conference on Discrete Mathematics and Theoretical Computer Science DMTCS'03, 7–12 July 2003, Dijon, France. Lect. Notes Comput. Sci. 2731 (2003) 155–167. CrossRef
O. Finkel, On the accepting power of 2-Tape Büchi automata, in Proceedings of the 23rd International Symposium on Theoretical Aspects of Computer Science, STACS (2006), Marseille, France. Lect. Notes Comput. Sci. (2006) 3884 301–312.
Finkel, O., Borel ranks and Wadge degrees of omega context free languages. Math. Structures Comput. Sci. 16 (2006) 813–840. CrossRef
Frougny, C. and Sakarovitch, J., Synchronized rational relations of finite and infinite words. Theor. Comput. Sci. 108 (1993) 45–82. CrossRef
F. Gire, Relations rationnelles infinitaires. PhD thesis, Université Paris 7 (1981).
Gire, F., Une extension aux mots infinis de la notion de transduction rationnelle, 6th GI Conf. Lect. Notes Comput. Sci. 145 (1983) 123–139. CrossRef
F. Gire and M. Nivat, Relations rationnelles infinitaires. Calcolo XXI (1984) 91–125.
A.S. Kechris, Classical Descriptive Set Theory. Springer-Verlag (1995).
Kechris, A.S., Marker, D. and Sami, R.L., $\Pi_1^1$ Borel sets. J. Symbolic Logic 54 (1989) 915–920. CrossRef
K. Kuratowski, Topology. Academic Press, New York (1966).
Landweber, L.H., Decision problems for ω-automata. Math. Syst. Theory 3 (1969) 376–384. CrossRef
Lescow, H. and Thomas, W., Logical specifications of infinite computations, in A Decade of Concurrency, edited by J.W. de Bakker et al. Lect. Notes Comput. Sci. 803 (1994) 583–621.
R. Lindner and L. Staiger, Algebraische Codierungstheorie – Theorie der Sequentiellen Codierungen. Akademie-Verlag, Berlin (1977).
Y.N. Moschovakis, Descriptive Set Theory. North-Holland, Amsterdam (1980).
D. Perrin and J.-E. Pin, Infinite words, automata, semigroups, logic and games. Pure Appl. Math. 141 (2004).
Pin, J-E., Logic, semigroups and automata on words. Ann. Math. Artif. Intell. 16 (1996) 343–384. CrossRef
C. Prieur, Fonctions rationnelles de mots infinis et continuité. PhD thesis, Université Paris 7 (2000).
Prieur, C., How to decide continuity of rational functions on infinite words. Theor. Comput. Sci. 250 (2001) 71–82. CrossRef
P. Simonnet, Automates et théorie descriptive. PhD thesis, Université Paris 7, (1992).
Staiger, L., Hierarchies of recursive ω-languages. J. Inform. Process. Cybernetics EIK 22 (1986) 219–241.
L. Staiger, ω-Languages, in Handbook of Formal languages, Volume 3, edited by G. Rozenberg and A. Salomaa. Springer-Verlag, Berlin.
Staiger, L. and Wagner, K., Rekursive Folgenmengen I. Z. Math Logik Grundlag. Math. 24 (1978) 523–538. CrossRef
Thomas, W., Automata and quantifier hierarchies, in Formal Properties of Finite automata and Applications, Ramatuelle (1988). Lect. Notes Comput. Sci. 386 (1989) 104–119. CrossRef
W. Thomas, Automata on infinite objects, in Handbook of Theoretical Computer Science, Volume B, edited by J. Van Leeuwen. Elsevier, Amsterdam (1990) 133–191.