Published online by Cambridge University Press: 15 April 2002
Classically, in order to resolve an equation u ≈ v over a free
monoid X*, we reduce it by a suitable family $\cal F$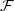 of substitutions
to a family of equations uf ≈ vf, $f\in\cal F$
of substitutions
to a family of equations uf ≈ vf, $f\in\cal F$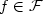 , each involving less
variables than u ≈ v, and then combine solutions of uf ≈ vf
into solutions of u ≈ v. The problem is to get $\cal F$
, each involving less
variables than u ≈ v, and then combine solutions of uf ≈ vf
into solutions of u ≈ v. The problem is to get $\cal F$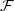 in a handy
parametrized form. The method we propose consists in parametrizing the
path traces in the so called graph of prime equations associated to
u ≈ v. We carry out such a parametrization in the case the prime
equations in the graph involve at most three variables.
in a handy
parametrized form. The method we propose consists in parametrizing the
path traces in the so called graph of prime equations associated to
u ≈ v. We carry out such a parametrization in the case the prime
equations in the graph involve at most three variables.