Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T08:52:36.821Z Has data issue: false hasContentIssue false
  • English
  • Français

The Half-Life of 14C—Why Is It So Long?

Published online by Cambridge University Press:  15 April 2019

Walter Kutschera
Walter Kutschera*
Affiliation:
University of Vienna, Faculty of Physics – Isotope Physics, Vienna Environmental Research Accelerator (VERA), Währinger Str. 17, A-1090 Vienna, Austria
*
Corresponding author. Email: walter.kutschera@univie.ac.at.
Rights & Permissions [Opens in a new window]

Abstract

The half-life of radiocarbon (14C) is 5700 ± 30 yr, which makes it particularly useful for dating in archaeology. However, only an exceptional hindrance of the beta decay from 14C to 14N—a so-called Gamow-Teller ß-decay—makes this half-life so long. A normal strength would result in a half-life of only a few days, completely useless for archaeological dating. The unusual hindrance is based on the nuclear structure of the two nuclei, resulting in strongly destructive interferences of the nuclear transition matrix element. Nuclear model calculation with great computational efforts have been performed in the literature to reproduce the very low transition probability. Here, we will attempt to describe the nuclear physics behind this most unusual half-life.

Keywords

half-lifenuclear structureradiocarbon dating
Type
Conference Paper
Information
Radiocarbon , Volume 61 , Issue 5: Radiocarbon 2018 Conference Proceedings Trondheim, Norway, June 17–22, 2018 Part 1 of 2 , October 2019 , pp. 1135 - 1142
Copyright
© 2019 by the Arizona Board of Regents on behalf of the University of Arizona 

INTRODUCTION

Development of 14C Half-Life Measurements

In 1946, Willard Libby published a brief paper (Libby Reference Libby1946), in which he discussed the possibility that radiocarbon (14C) produced via the 14N(n,p)14C reaction in the atmosphere may enter the biosphere in detectable amounts. His estimate was based on the number of neutrons liberated in the free atmosphere by spallation of nuclei through cosmic-ray interaction (Korff and Hamermesh Reference Korff and Hamermesh1946). At that time the half-life of 14C was known to be in the range from 103 to 105 yr (Ruben and Kamen Reference Ruben and Kamen1941). Later in 1946, two half-life measurements of 14C were published, 4700 ± 470 yr (Reid et al. Reference Reid, Dunning, Weinhouse and Grosse1946), and 5300 ± 800 yr (Norris and Inghram Reference Norris and Inghram1946), respectively. In a first attempt to detect cosmogenic 14C in biological carbon, biological methane was extracted from a sewage disposal plant in Baltimore (Anderson et al. Reference Anderson, Libby, Weinhouse, Reid, Kirshenbaum and Grosse1947). In order to get a measurable signal from the rare ß-decays of 14C, the methane was isotopically enriched by thermal diffusion up to a factor 260. Later, with an improved ß-counting system, radiocarbon could be measured without enrichment, and an average activity value of 12.5 ± 0.2 counts per minute per gram of carbon (c/m/g) was found for contemporary wood samples from different regions around the world (Libby et al. Reference Libby, Anderson and Arnold1949). In addition, wood samples from two tombs of the Old Kingdom in Egypt estimated to be around 4600 years old were measured. With a half-life of 5720 ± 47 yr (Engelkemeir et al. Reference Engelkemeir, Hamill, Inghram and Libby1949), an expected 14C activity of 7.15 ± 0.15 c/m/g was calculated, whereas the weighted mean of several 14C measurements on the wood samples was 7.04 ± 0.20 c/m/g (Libby et al. Reference Libby, Anderson and Arnold1949). The good agreement encouraged Libby to measure also younger samples of known age, leading to the well-known decay curve shown in Figure 1 (Arnold and Libby Reference Arnold and Libby1949, see Figure 1). This, then, was really the starting point of 14C dating. In Figure 1, the decay curve was calculated with the 14C half-life of 5720 ± 47 yr (Engelkemeir et al. Reference Engelkemeir, Hamill, Inghram and Libby1949). Later, end and wall corrections of the gas counter were applied, which lowered the half-life to 5580 ± 45 yr (Engelkemeir and Libby Reference Engelkemeir and Libby1950). In 1952, Libby proposed a half-life value of 5568 ± 30 yr (Libby Reference Libby and Libby1952), as the weighted mean of three values, 5580 ± 45 yr (Engelkemeir et al. Reference Engelkemeir, Hamill, Inghram and Libby1949; Engelkemeir and Libby Reference Engelkemeir and Libby1950), 5589 ± 75 yr (Jones Reference Jones1949), and 5513 ± 165 yr (Miller et al. Reference Miller, Ballentine, Bernstein, Friedman, Nier and Evans1950).

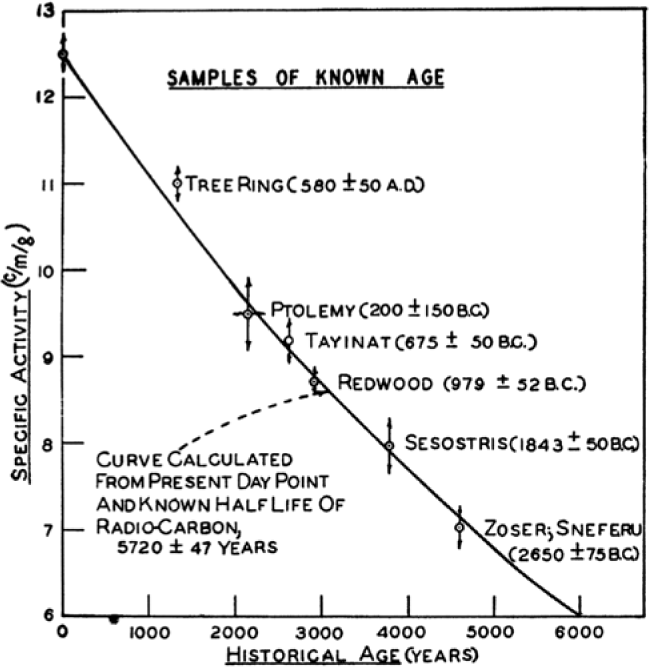
Figure 1 The first proof that 14C dating does work (Arnold and Libby Reference Arnold and Libby1949).

However, at the Fifth Radiocarbon Conference in Cambridge 1962, a new value of 5730 ± 40 yr was agreed upon for the half-life of 14C (Godwin Reference Godwin1962). This was based on the weighted mean of three new half-life measurements: 5760 ± 50 yr (Mann et al. Reference Mann, Marlow and Hughes1961), 5780 ± 65 yr (Watt et al. Reference Watt, Ramsden and Wilson1961), and 5680 ± 40 (Olsson et al. Reference Olsson, Karlen, Turnbull and Prosser1962). It is interesting to note that this value is very close to the original half-life used for the decay curve in Figure 1, but is 2.9% longer than the “Libby half-life” of 1952.

Finally, in 1968 a new half-life measurement was published by Bella et al. (Reference Bella, Alessio and Fratelli1968), and a weighted mean of 5700 ± 30 yr was calculated (Kutschera Reference Kutschera2013) from the results of four half-life measurements: 5780 ± 65 yr (Watt et al. Reference Watt, Ramsden and Wilson1961), 5680 ± 40 yr (Olsson et al. Reference Olsson, Karlen, Turnbull and Prosser1962), 5745 ± 50 yr (Hughes and Mann Reference Hughes and Mann1964), and 5660 ± 40 yr (Bella et al. Reference Bella, Alessio and Fratelli1968).

In 2007, an effort was started (Roberts and Southon Reference Roberts and Southon2007) to measure the absolute 14C/12C ratio of the widely used 14C standard material OX-I (Oxalic Acid I) by accelerator mass spectrometry (AMS). Once this ratio is known, a new measurement of the ß-decay rate of OX-I would yield an additional half-life value. For the time being, we recommend using 5700 ± 30 yr for the half-life of 14C, which is also the value reported in the data base of the National Nuclear Data Center of Brookhaven National Laboratory (2018).

It is well known that the exact value of the 14C half-life is not important for 14C dating, since true ages can only be determined from the measured 14C content with the help of 14C calibration curves (Reimer et al. Reference Reimer2013). Simply speaking, 14C dating means to determine the absolute age of an object by comparing the measured 14C content with the one of an object of known age. However, a non-trivial condition for this procedure to work is that the object of unknown age has taken up 14C from the same source as the object of known age used for the calibration. For deviation from this assumption, see e.g. Dee et al. (Reference Dee, Brock, Harris, Bronk Ramsey, Shortland, Higham and Rowland2010).

The exact value of the half-life would only matter if absolute dating with 14C discussed some 20 years ago (Szabo et al. Reference Szabo, Carmi, Segal and Mintz1998) could be implemented. It would require to measure the ratio of 14C/14N*, where 14N* is the radiogenic decay product of 14C. This, however, seems quite impossible because one would have to identify the minute amount of 14N* in the presence of the “ocean” of normal 14N we live in.

THEORY OF ß-DECAY

The basic theory of ß decay was developed by Fermi (Reference Fermi1934), shortly after the neutron was detected (Chadwick Reference Chadwick1932a, Reference Chadwick1932b), and Heisenberg described the nucleus as consisting of protons and neutrons (Heisenberg Reference Heisenberg1932). Fermi also accepted the hypothesis of Pauli put forward in 1930 in his famous letter to the “Radioactive Ladies and Gentlemen” at a meeting in Tübingen (Mößbauer Reference Mößbauer, Altmann, Hillebrandt, Janka and Raffelt1998), that in ß-decay a neutrino with spin 1/2 ħ is emitted together with the electron, which was known to have also spin 1/2 ħ (Uhlenbeck and Goudsmit Reference Uhlenbeck and Goudsmit1926). In essence, the half-life of a nucleus depends on the decay energy determined by the mass difference between parent and daughter nucleus, and on the transition matrix element depending on the nuclear structure of the two nuclei. In his ß-decay theory, Fermi already discussed the conditions for allowed and forbidden ß-decays, which were further developed by Gamow and Teller (Reference Gamow and Teller1936).

The 14C ß-decay, the Most Hindered Gamow-Teller Transition

Explaining the unusually long half-life of 14C from first principles is a big challenge to nuclear theory. The spins of the electron and neutrino can couple antiparallel to 0 and parallel to 1. For allowed transitions (Fermi Reference Fermi1934), they transport no angular momentum. Therefore, in the anti-parallel mode they can connect parent nuclei with nuclear spin 0+ to daughter nuclei with 0+ states (so-called super-allowed Fermi transitions). In the parallel mode they can connect 0+ or 1+ states to 1+ or 0+ states, respectively (so-called allowed Gamow-Teller [GT] transitions)

The transition strength for a ß-decay is usually characterized by the Log ft value, which is the logarithm of the ft product expressed by the relation

(1) $${\rm{Log}}\,ft = {\rm{ constant }}/{\rm{ }}{\left| {{{\rm{M}}_{{\rm{GT}}}}} \right|^2}$$

Here, f is the Fermi phase-space integral, a factor which can be calculated from the ß-decay energy, and t is the half-life. |MGT|2 is the square of the Gamow-Teller matrix element, which contains the information about the nuclear structure of the parent and daughter states. The inverse dependence of Log ft on the GT matrix element means that large Log ft values are the result of small matrix elements, which then leads to long half-lives. To reproduce the 14C half-life requires a reduction of the GT matrix element (MGT), which is in the order of 1 for normal GT strength, to the very small value of ∼2×10–3.

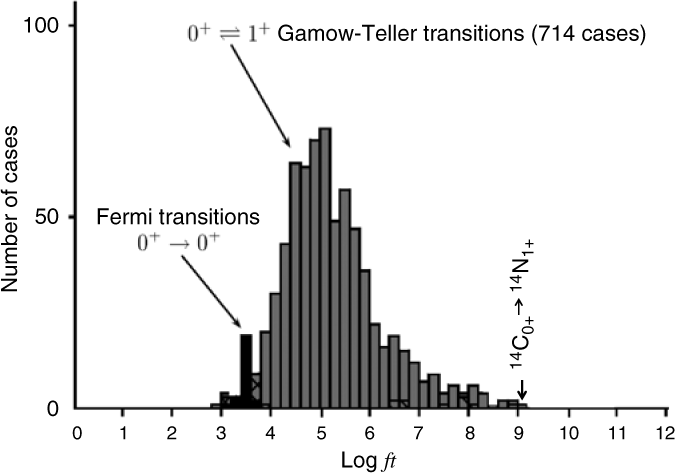
The ß-decay from the 0+ ground state of 14C to the 1+ ground state of 14N fulfills the GT condition. As it happens, there exist a total of 714 GT transitions in all nuclei (Singh et al. Reference Singh, Rodriguez, Wong and Tuli1998), with the majority of Log ft values lying between 4 and 6 (Figure 2). From the distribution of the GT transitions it can be seen that the 14C→14N transition has the highest log ft value of 9.04, which also means that it is the most hindered GT transition (smallest GT matrix element, see below).

Figure 2 Distribution of Log ft values for Fermi and Gamow-Teller transitions (Singh et al. Reference Singh, Rodriguez, Wong and Tuli1998). The Log ft value for the 14C0+ to 14N1+ transition is 9.04, and its position is marked with an arrow.

The Moszkowski Plot

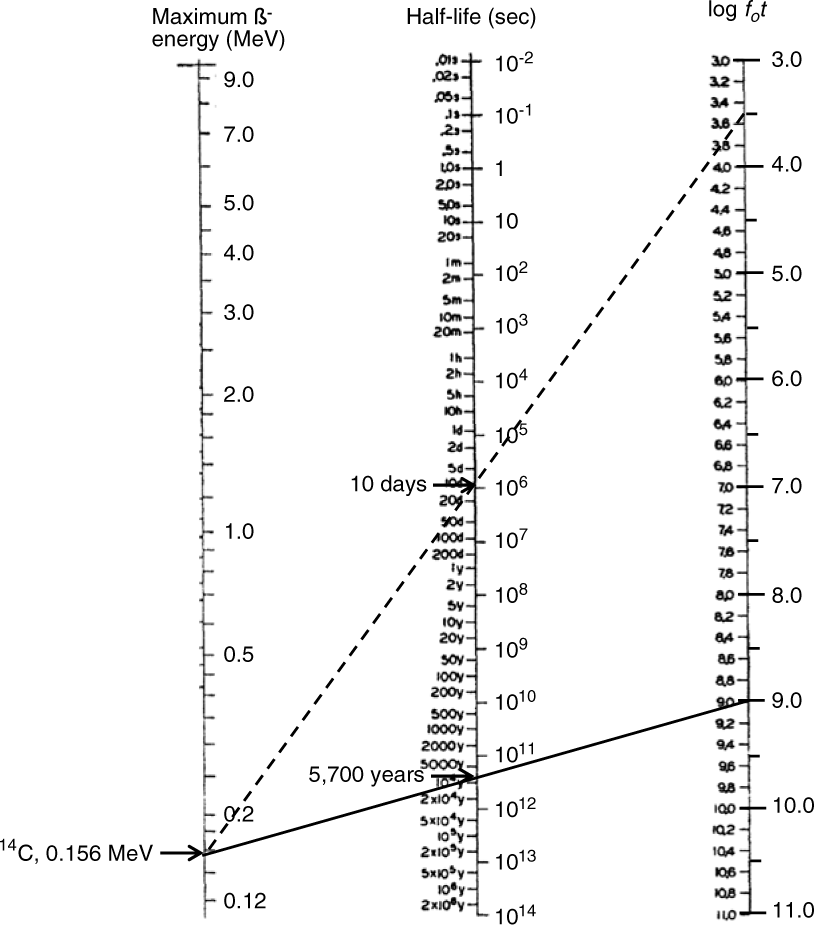
Moszkowski (Reference Moszkowski1951) has given a rapid method of determining log fot values in a graphical way (nomogram) by connecting the maximum kinetic energy of ß– or ß+ particles, or the energy available for K-capture, with the half-life. Assuming a 100% decay to one final state (no branching to other states), the Log ft is then given by Log ft = log fot + log (C) (Moszkowski Reference Moszkowski1951). Here, log (C) is a Coulomb correction, which is different for the three decay modes. For the ß– decay of 14C, this correction is small, log (C) ∼ 0.2, and is therefore of minor importance in the following discussion. As can be seen from Figure 3, for the 14C decay one obtains a log fot value close to 9 by connecting the maximum electron energy of 156 keV with the known half-life of 5700 yr. Alternatively, with a log fot value around 3.5, not uncommon for GT transitions of neighboring light nuclei (Singh et al. Reference Singh, Rodriguez, Wong and Tuli1998), one obtains a half-life of only around 10 days. The major challenge for a theoretical description of the GT transition of 14C is then to find the proper structure (wave function) for the parent and daughter states, which produce an exceptionally small GT matrix element required to produce the large Log ft value of the 14C ß-decay.

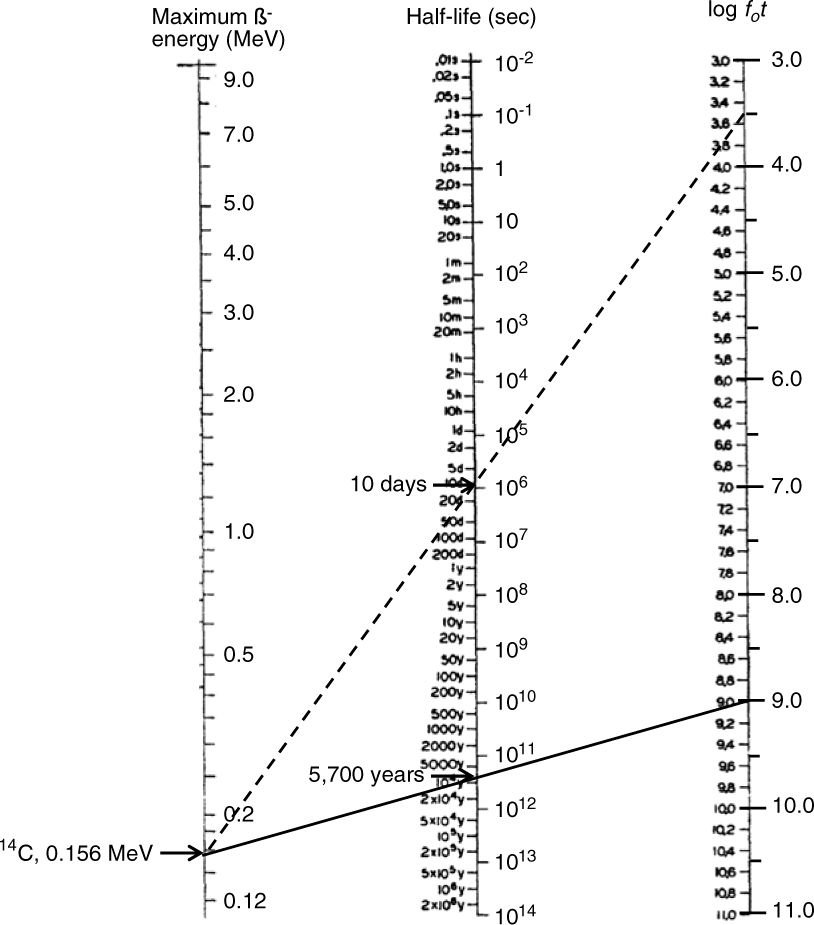
Figure 3 Graphical way to determine the half-life by connecting the maximum energy of the electrons emitted in the ß-decay of 14C with the log fot value. For clarity the figure is a simplified version of the original nomogram of Moszkowski (Reference Moszkowski1951), which also included ß+ and K-capture decays. The solid line connects the 14C decay energy with the log fot of 9, whereas the dashed line indicates the much shorter half-life, if the log fot value would be 3.5.

ATTEMPTS TO CALCULATE THE HALF-LIFE OF 14C

Overall, one can distinguish three different approaches for a theoretical description of nuclei. (1) In the traditional shell-model approach one starts with an inert core of nucleons filling a closed shell, and tries to describe the properties of nuclei by some effective interaction of the particle or holes outside the core (Inglis Reference Inglis1953). (2) Alternatively, light nuclei were also described by the interactions of pre-formed alpha particles (Hafstad and Teller Reference Hafstad and Teller1938). (3) Finally, in the so-called ab-initio no-core shell model approach all nucleons are treated as active, requiring an enormous computational effort for systems like 14C (Maris et al. Reference Maris, Vary, Navrátil, Ormand, Nam and Dean2011). A recent review covers the many theoretical efforts to describe the properties of light nuclei (Freer et al. Reference Freer, Horiuchi, Kanada-En’yo, Lee and Meißner2018), indicating that methods (2) and (3) may eventually merge together in a “complete” description of nuclear properties.

Early on, it was realized that the exceptionally long half-life of 14C would require a nuclear structure of the involved nuclei, which go beyond the description with standard shell model approaches (Inglis Reference Inglis1953). One of the first attempts was the introduction of a non-central tensor force in addition to the central force and ordinary spin-orbit interaction (Jancovici and Talmi Reference Jancovici and Talmi1954). Although some reduction of the GT matrix element for the 14C ß-decay was achieved with this method, it was not able bring it down to the required very small value. In more recent times, a thorough study of the GT strength in the mass-14 nuclei (Negret et al. Reference Negret, Adachi, Barrett, Bäumer, van den Berg, Berg, von Brentano, Frekers, De Frenne, Fujita, Fujita, Fujita, Grewe, Haefner, Harakeh, Hatanaka, Heyde, Hunyadi, Jacobs, Kalmykov, Korff, Nakanishi, Navrátil, von Neumann-Cosel, Popescu, Rakers, Richter, Ryezayeva, Sakemi, Shevchenko, Shimbara, Shimizu, Tameshige, Tamii, Uchida, Vary, Wörtche, Yosoi and Zamick2006) discussed a variety of theoretical attempts and came to the conclusion that it might be necessary to include cluster structures of nuclei in addition to shell-model descriptions. For example, the famous “Hoyle state” in 12C at an excitation energy of 7.65 MeV and a spin of 0+ is such a cluster state (Freer and Fynbo Reference Freer and Fynbo2014). The existence of this state was predicted by Hoyle (Reference Hoyle1954) to understand the 12C abundance in stars, and requires a production through the triple-alpha process. Great strides have been undertaken to improve a shell-model approach to explain the GT strength in the 14C ß-decay (Holt et al. Reference Holt, Brown, Kuo, Holt and Machleidt2008). Although a substantial reduction of the GT matrix element was achieved by fine-tuning the nucleon-nucleon interaction with a proper interaction potential, the introduction of three-nucleon interaction seem to be necessary to reproduce the very small GT Matrix element in 14C (Holt et al. Reference Holt, Kaiser and Weise2009). This approach was pursued in an extraordinary large computational effort by an ab-initio shell- model calculation with all 14 nucleons active (Maris et al. Reference Maris, Vary, Navrátil, Ormand, Nam and Dean2011). This group found a sufficiently small GT matrix element (∼2×10–3) to reproduce the long half-life of 14C by including three-nucleon forces as well. The result of this calculation is summarized in Figure 4, taken from the work of Maris et al. (Reference Maris, Vary, Navrátil, Ormand, Nam and Dean2011). It should be noticed that the three-nucleon force (3NF) requires a proper value for the low-energy coupling constant CD to cancel the contributions from the two-nucleon interaction, described here with the next-to-next-to-next-to-low-order (N3LO) approach, resulting in the vanishing small GT matrix element. In a way, CD is a fitting constant and not entirely derived from first principles. Nevertheless, the work of Maris et al. (Reference Maris, Vary, Navrátil, Ormand, Nam and Dean2011) for the first time arrived at a GT matrix element small enough to explain the long half-life of 14C.

Figure 4 Summary of the contributions to the GT matrix elements for the 14C ß-decay. The figure is reproduced from Maris et al. (Reference Maris, Vary, Navrátil, Ormand, Nam and Dean2011). Only the calculation including three-body interactions with a relatively large coupling constant (CD = –2.0, green symbols) is able to result in a sufficiently small GT matrix element (∼2×10−3) to reproduce the long half-life (green summary curve in the lower panel; please see electronic version for color figures).

CONCLUSION

From the early days of 14C dating, the long half-life was both beneficial for archaeology and perplexing from a nuclear theory point of view. Over the years, great efforts were made to understand nuclear forces well enough to be able to describe the properties of light nuclei from first principles. Even though this task is not finished, and further improvements are to be expected (Freer et al. Reference Freer, Horiuchi, Kanada-En’yo, Lee and Meißner2018), it seems obvious that the parent nucleus 14C has a very different nuclear structure as compared to the daughter nucleus 14N to which it decays. Perhaps the inhibition of the decay has to do with one of them having more cluster structure than the other, requiring a total rearrangement of all nucleons. The great effort of theorists to understand nuclear forces in all details may one day lead to a complete understanding of the most unusual half-life of 14C. Whatever the outcome of these efforts, the long half-life of 14C remains to be a true gift of Nature to archaeology and many other fields of the environment at large including the atmosphere, biosphere, hydrosphere, lithosphere, and cryosphere (Kutschera Reference Kutschera2013).

ACKNOWLEDGMENTS

The author acknowledges helpful discussions with Alex Brown, Martin Freer, John Southon, and Johannes van der Plicht. Constructive comments by two referees are also gratefully acknowledged.

Footnotes

Selected Papers from the 23rd International Radiocarbon Conference, Trondheim, Norway, 17–22 June, 2018

References

REFERENCES

Anderson, EC, Libby, WF, Weinhouse, S, Reid, AF, Kirshenbaum, AD, Grosse, AV. 1947. Natural radiocarbon from cosmic radiation. Physical Review 72:931–936.CrossRefGoogle Scholar
Arnold, JR, Libby, WF. 1949. Age determination by radiocarbon content: checks with samples of known age. Science 110:678–680.CrossRefGoogle Scholar
Bella, F, Alessio, M, Fratelli, P. 1968. A determination of the half-life of 14C. Il Nuovo Cimento 58B:233–246.Google Scholar
Chadwick, J. 1932a. Possible existence of a neutron. Nature 129(3252):312.CrossRefGoogle Scholar
Chadwick, J. 1932b. The existence of a neutron. Proceedings of the Royal Society A 136 (830):692–708.CrossRefGoogle Scholar
Dee, MD, Brock, F, Harris, SA, Bronk Ramsey, C, Shortland, AJ, Higham, TFG, Rowland, JM. 2010. Investigating the likelihood of a reservoir offset in the radiocarbon record for ancient Egypt. Journal of Archaeological Science 37:687–693.CrossRefGoogle Scholar
Engelkemeir, AG, Hamill, WH, Inghram, MG, Libby, WF. 1949. The half-life of radiocarbon (C14). Physical Review 75:1825–1833.CrossRefGoogle Scholar
Engelkemeir, AG, Libby, WF. 1950. End and wall corrections for absolute beta-counting in gas counters. Review of Scientific Instruments 21:550–554.CrossRefGoogle ScholarPubMed
Fermi, E. 1934. Versuch einer Theorie der ß-Strahlen. I. Zeitschrift für Physik 88:161–177.CrossRefGoogle Scholar
Freer, M, Fynbo, H. 2014. The Hoyle state in 12C. Progress in Particle and Nuclear Physics 78:1–23.CrossRefGoogle Scholar
Freer, M, Horiuchi, H, Kanada-En’yo, Y, Lee, D, Meißner, U-G. 2018. Microscopic clustering in light nuclei. Reviews of Modern Physics 90:035004, 1–46.CrossRefGoogle Scholar
Gamow, G, Teller, E. 1936. Selection rules for the ß-disintegration. Physical Review 49:895–899.10.1103/PhysRev.49.895CrossRefGoogle Scholar
Godwin, H. 1962. Radiocarbon dating, fifth international conference. Nature 195:943–945.CrossRefGoogle Scholar
Hafstad, LR, Teller, E. 1938. The alpha-particle model of the nucleus. Physical Review 54: 681–692.CrossRefGoogle Scholar
Heisenberg, W. 1932. Über den Bau der Atomkerne. I. Zeitschrift für Physik 77(1–2):1–11.CrossRefGoogle Scholar
Holt, JW, Brown, GE, Kuo, TTS, Holt, JD, Machleidt, R. 2008. Shell model description of the 14C dating ß decay with Brown-Rho-Scaled NN interaction. Physical Review Letters 100: 062501.CrossRefGoogle Scholar
Holt, JW, Kaiser, N, Weise, W. 2009. Chiral three-nucleon interaction and the 14C-dating ß decay. Physical Review C 79:054331, 1–11.CrossRefGoogle Scholar
Hoyle, F. 1954. On nuclear reactions occuring in very hot stars. I. The synthesis of elements from carbon to nickel. Astrophysical Journal Supplement 1:121–146.CrossRefGoogle Scholar
Hughes, EE, Mann, WB. 1964. The half-life of carbon-14: comments on the mass-spectrometric methods. International Journal of Applied Radiation and Isotopes 15:97–100.CrossRefGoogle Scholar
Inglis, DR. 1953. The energy levels and the structure of light nuclei. Reviews of Modern Physics 25(2):390–450.CrossRefGoogle Scholar
Jancovici, B, Talmi, I. 1954. Tensor forces and the ß decay of C14 and O14. Physical Review 95:289–291.CrossRefGoogle Scholar
Jones, WM. 1949. A determination of the half-life of carbon 14. Physical Review 76(7):885–889.CrossRefGoogle Scholar
Korff, SA, Hamermesh, B. 1946. The energy distribution and number of cosmic-ray neutrons in the free atmosphere. Physical Review 69:155–159.CrossRefGoogle Scholar
Kutschera, W. 2013. Application of accelerator mass spectrometry. International Journal of Mass Spectrometry 349–350:203–218.CrossRefGoogle Scholar
Libby, WF. 1946. Atmospheric helium three and radiocarbon from cosmic radiation. Physical Review 69:671–672.CrossRefGoogle Scholar
Libby, WF. 1952. Half-life of radiocarbon. In: Libby, WF, editor. Radiocarbon dating. Chicago & London: University of Chicago Press. p. 34–42.Google Scholar
Libby, WF, Anderson, EC, Arnold, JR. 1949. Age determination by radiocarbon content: world-wide assay of natural radiocarbon. Science 109:227–228.CrossRefGoogle ScholarPubMed
Mann, WB, Marlow, WF, Hughes, EE. 1961. The half-life of carbon-14. International Journal of Applied Radiation and Isotopes 11:57–67.CrossRefGoogle ScholarPubMed
Maris, P, Vary, JP, Navrátil, P, Ormand, WE, Nam, H, Dean, DJ. 2011. Origin of the anomalous long lifetime of 14C. Physical Review Letters 106:202502.CrossRefGoogle Scholar
Miller, WW, Ballentine, R, Bernstein, W, Friedman, L, Nier, AO, Evans, RD. 1950. The half-life of carbon fourteen and a comparison of gas phase counter methods. Physical Review 77(5): 714–715.CrossRefGoogle Scholar
Mößbauer, RL. 1998. History of Neutrino Physics: Pauli’s Letters. In: Altmann, M, Hillebrandt, W, Janka, H-T, Raffelt, G, editors. Proceedings of the Workshop on Neutrino Astrophysics at Ringberg Castle, 20–24 Oct 1997, Sonderforschungsbereich 375 Astroteilchenphysik, Technische Universität München: 3–5.Google Scholar
Moszkowski, SA. 1951. A rapid method of calculating log (ft) values for ß-transitions. Physical Review 82:35–37.CrossRefGoogle Scholar
Negret, A, Adachi, T, Barrett, BR, Bäumer, C, van den Berg, AM, Berg, GPA, von Brentano, P, Frekers, D, De Frenne, D, Fujita, H, Fujita, K, Fujita, Y, Grewe, EW, Haefner, P, Harakeh, MN, Hatanaka, K, Heyde, K, Hunyadi, M, Jacobs, E, Kalmykov, Y, Korff, A, Nakanishi, K, Navrátil, P, von Neumann-Cosel, P, Popescu, L, Rakers, S, Richter, A, Ryezayeva, N, Sakemi, Y, Shevchenko, A, Shimbara, Y, Shimizu, Y, Tameshige, Y, Tamii, A, Uchida, M, Vary, J, Wörtche, HJ, Yosoi, M, Zamick, L. 2006. Gamow-Teller strength in the A = 14 multiplet: a challenge to the shell model. Physical Review Letters 97:062502.CrossRefGoogle ScholarPubMed
Norris, WD, Inghram, MG. 1946. Half-life determination of carbon (14) with a mass spectrometer and low absorption counter. Physical Review 70:772–773.CrossRefGoogle Scholar
Nuclear Data Center, Brookhaven National Laboratory. 2018. Nuclear structure and decay data. Available at https://www.nndc.bnl.gov/nudat2/.Google Scholar
Olsson, IU, Karlen, I, Turnbull, AH, Prosser, NJD. 1962. A determination of the half-life of C14 with a proportional counter. Arkiv för Fysik 22(14):237–255.Google Scholar
Reid, AF, Dunning, JR, Weinhouse, S, Grosse, AV. 1946. Half-life of C14. Physical Review 70:431.CrossRefGoogle Scholar
Reimer, PJ, et al. 2013. IntCal13 and Marine13 radiocarbon age calibration curves 0–50,000 years cal BP. Radiocarbon 55(4):1869–1887.CrossRefGoogle Scholar
Roberts, ML, Southon, JR. 2007. A preliminary determination of the absolute 14C/12C ratio of OX-I. Radiocarbon 49(2):442–445.10.1017/S0033822200042363CrossRefGoogle Scholar
Ruben, S, Kamen, MD. 1941. Long-lived radioactive carbon. Physical Review 59:349–354.CrossRefGoogle Scholar
Singh, B, Rodriguez, JL, Wong, SSM, Tuli, JK. 1998. Review of Log ft values in ß decay. Nuclear Data Sheets 84:487–563.CrossRefGoogle Scholar
Szabo, J, Carmi, I, Segal, D, Mintz, E. 1998. An attempt at absolute 14C dating. Radiocarbon 40(1):77–83.CrossRefGoogle Scholar
Uhlenbeck, GE, Goudsmit, S. 1926. Spinning electrons and the structure of spectra. Nature 117:264–265.CrossRefGoogle Scholar
Watt, DE, Ramsden, D, Wilson, HW. 1961. The half-life of carbon-14. International Journal of Applied Radiation and Isotopes 11:68–74.10.1016/0020-708X(61)90133-8CrossRefGoogle ScholarPubMed
Figure 0

Figure 1 The first proof that 14C dating does work (Arnold and Libby 1949).

Figure 1

Figure 2 Distribution of Log ft values for Fermi and Gamow-Teller transitions (Singh et al. 1998). The Log ft value for the 14C0+ to 14N1+ transition is 9.04, and its position is marked with an arrow.

Figure 2

Figure 3 Graphical way to determine the half-life by connecting the maximum energy of the electrons emitted in the ß-decay of 14C with the log fot value. For clarity the figure is a simplified version of the original nomogram of Moszkowski (1951), which also included ß+ and K-capture decays. The solid line connects the 14C decay energy with the log fot of 9, whereas the dashed line indicates the much shorter half-life, if the log fot value would be 3.5.

Figure 3

Figure 4 Summary of the contributions to the GT matrix elements for the 14C ß-decay. The figure is reproduced from Maris et al. (2011). Only the calculation including three-body interactions with a relatively large coupling constant (CD = –2.0, green symbols) is able to result in a sufficiently small GT matrix element (∼2×10−3) to reproduce the long half-life (green summary curve in the lower panel; please see electronic version for color figures).