Beam Transmission of ¹²C and ¹³C

Higher transmission loss of ¹²C relative to ¹³C can result in wrong values of δ¹³C at high beam currents, and wrong pMC values if used in the calculation. The threshold for ¹²C beam saturation is observed around 80–85 μA for SSAMS and varies somewhat from one sample wheel to another sample wheel due to changes in beam parameters. But no such saturation was observed even for 110 μA on the CAMS unit. The CAMS data of AMS derived δ¹³C values was in very good agreement with IRMS δ¹³C values except for a small fraction of samples (Prasad et al. Reference Prasad, Culp and Cherkinsky2019). The histogram of differences produced a sharp gaussian curve with a 1-σ deviation of about 1.5‰ and is acceptable for online δ¹³C correction. SSAMS online δ¹³C data, however, is not suitable for correcting pMC data and needs huge improvement both in accuracy and precision. Towards that objective, data collected over a five-month period was chosen for this study.

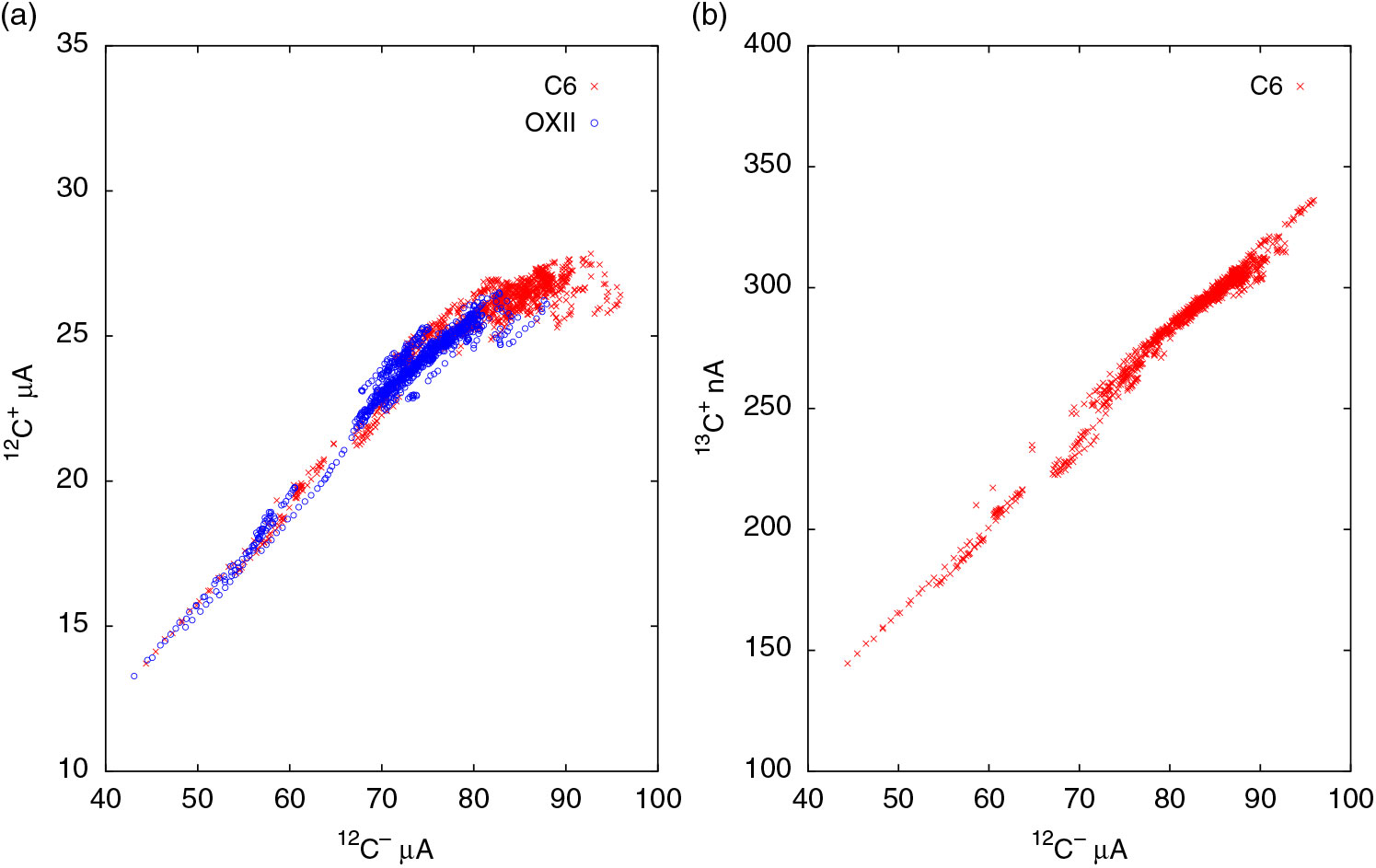
The ¹²C^– beam currents injected into the accelerator are typically in the range of 70–90 μA for all samples and standards on SSAMS. OXII is the primary standard and IAEA-C6 (ANU-sucrose) serves as the secondary standard. Each typical sample group consists of two OXIIs, two C6es, one processed blank, and nearly 20 unknowns. Each run corresponds to 180 sec of ¹⁴C measurement and typically 9–10 runs are performed per sample. During this study, we realized that the beam currents of C6 are in general greater than those of OXII by nearly 10–15% mainly because of larger sample size. Due to higher beam currents, C6 samples sometimes resulted in beam saturation whereas OXII data is almost free of beam saturation as seen in Figure 1(a). In the figure, each data point corresponds to a single run. Most OXII data points are clustered in the ¹²C^– range of 70–80 μA. C6 data points are clustered in the range 75–90 μA and the slope of the band clearly changed towards saturation above 80 μA. The data points are seen all the way down to 40 μA because of sample consumption. Even though these data points for <70 μA are sparse, they very clearly prove that linearity between ¹²C⁺ and ¹²C^– extends from 40 μA upto ∼70 μA or more. For beam currents under 80 μA, OXII and C6 data completely overlapped suggesting that the linearity can even hold for other samples. In Figure 1(b), ¹³C⁺/¹²C^– for C6 was plotted for comparison. The ¹³C⁺ current increases linearly with the ¹²C^– current and does not exhibit saturation. From Figure 1, it is clear that ¹³C⁺/¹²C^– ratio is a better choice for δ¹³C calculation than ¹³C⁺/¹²C⁺ ratio, as previously suggested (Prasad et al. Reference Prasad, Culp and Cherkinsky2019).

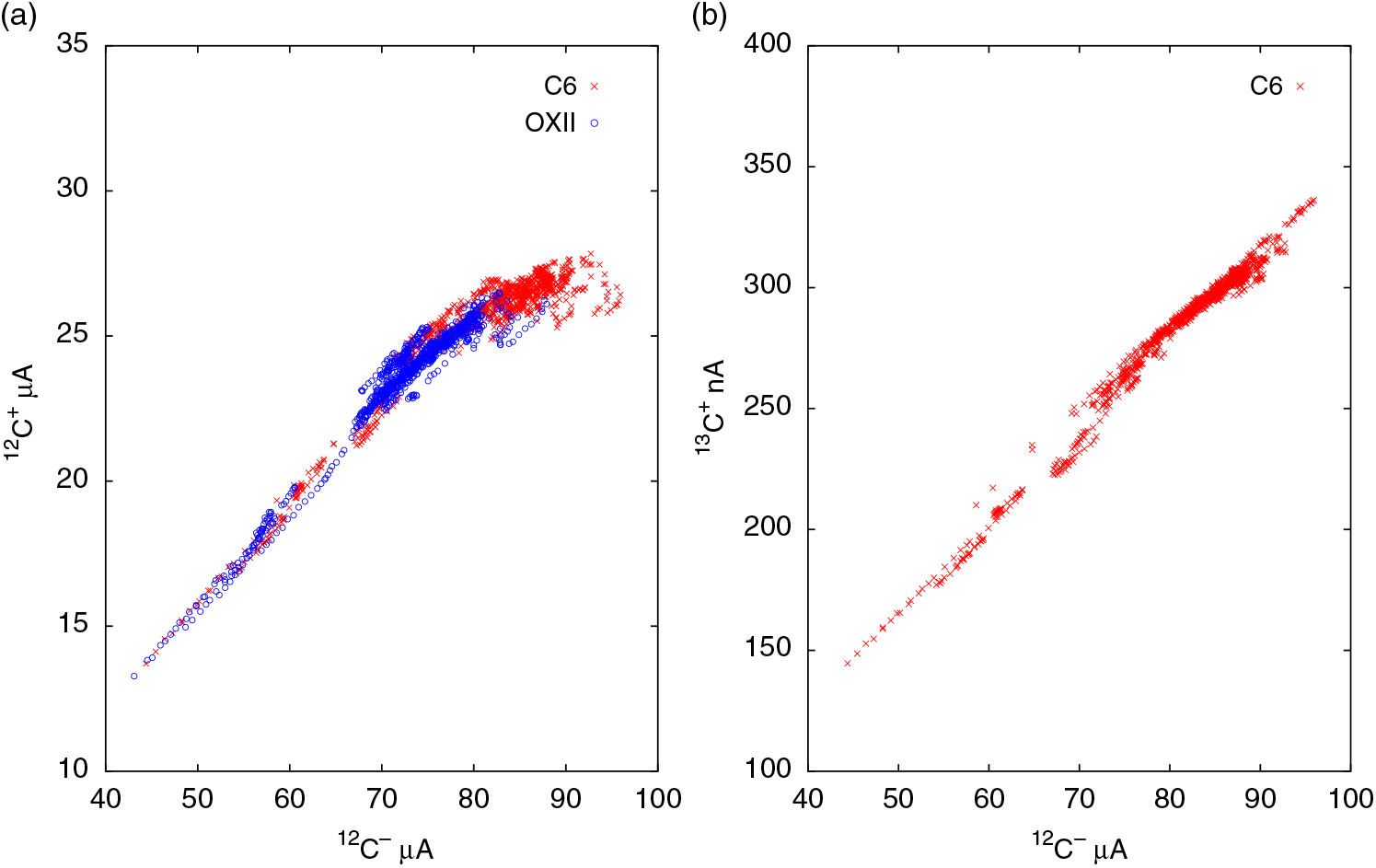
Figure 1 (a) Post acceleration ¹²C⁺ vs. pre-acceleration ¹²C^– for OXII and C6 standards. Data points correspond to individual runs, with errors smaller than the size of the points. Beam saturation of ¹²C⁺ may be seen above 80 μA. (b) In contrast the ¹³C⁺ vs. ¹²C^– plot is linear. Only C6 data is plotted for clarity.

From Figure 1, the linearity between ¹²C⁺ vs. ¹²C^– extends to higher beam currents (∼70 μA) than observed by Skog (Reference Skog2007) and Linares et al. (Reference Linares, Macario, Santos, Carvalho, dos Santos, Gomes, Castro, Oliveira and Alves2015). While it is true that there are fewer points in this range, the linear relationship is clear. One reason for this discrepancy could be the argon gas stripper pressure. We reduced the argon flow rate to 0.9 sccm from the original factory setting of 1.1 sccm. This change improved the beam transmission by about 15% from about 28% to 32% for an injection current of 80 μA. Reduced gas pressure slightly elevated the background, yet we still routinely obtain the values in the range of 51 ka–54 ka. The reduction in argon pressure likely reduced the space charge effect and extended the range of beam currents over which the transmission remained linear.

Comparison of Online δ¹³C (AMS) and Offline δ¹³C (IRMS) Values

NEC’s ABC package is used for data reduction at CAIS for both AMS units. The package uses consensus δ¹³C values for standards by default and the pMC data consistently agreed with the nominal values. Since the consensus δ¹³C values are based on IRMS measurements external to AMS, the validity of offline correction can be extended to unknowns as well, a fact well known to many AMS labs. As for the online δ¹³C correction, it works well for CAMS, but for SSAMS, the observed saturation of ¹²C⁺ clearly rules out the possibility of online δ¹³C correction using ¹³C⁺/¹²C⁺ ratio. However, using ¹³C⁺/¹²C^– ratio can substantially improve the δ¹³C estimation.

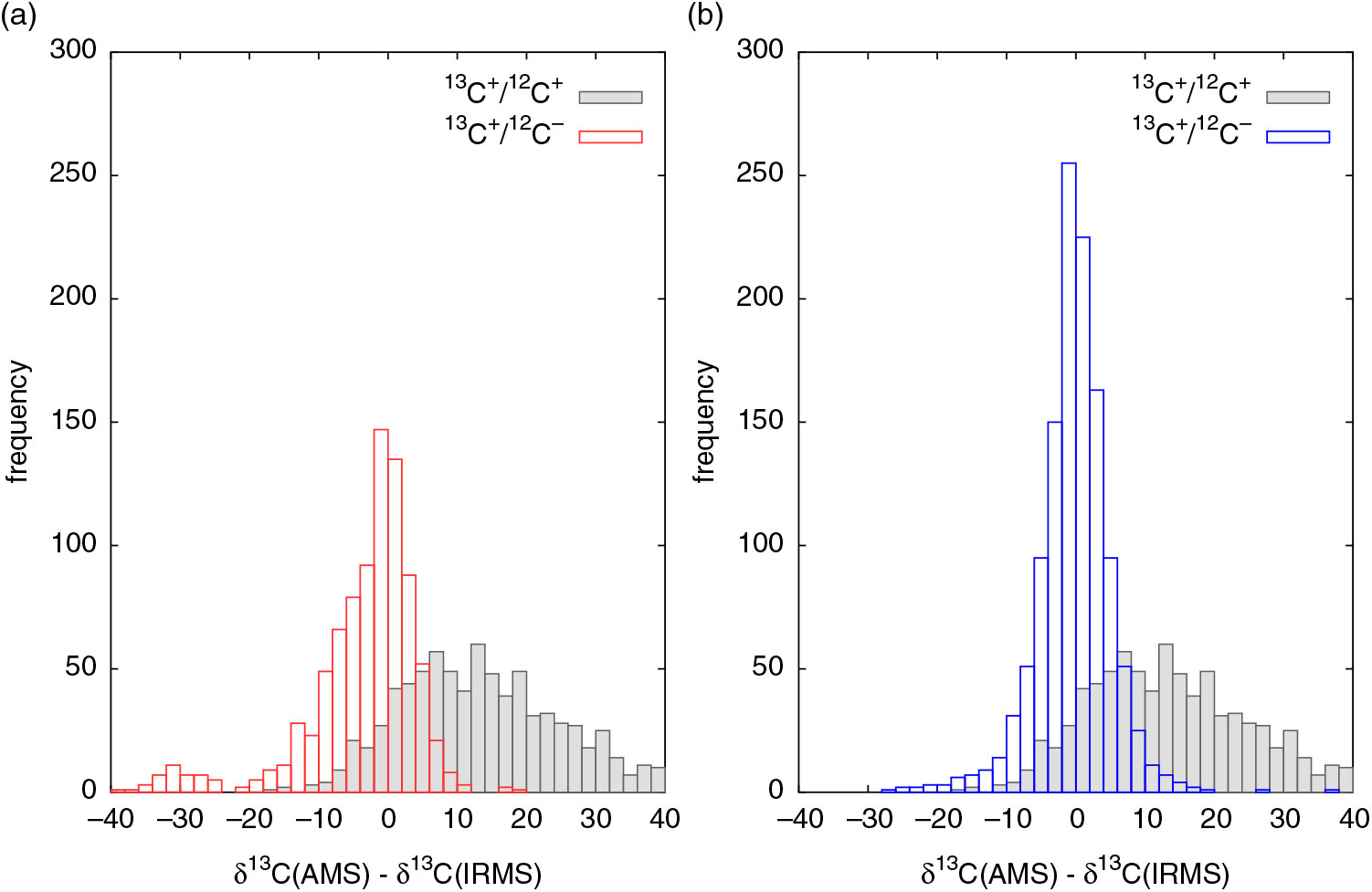
In Figure 2, over 1000 unknowns measured over a five-month period were used for comparison of online and offline δ¹³C data. The difference between the values are plotted as histograms. Ideally, the online δ¹³C data is expected to match the offline (IRMS) data and the histogram of differences should be a sharp gaussian distribution centered around zero. The plotted histogram using ¹³C⁺/¹²C⁺ ratios is spread out wide with a mean difference close to 15, which means the online δ¹³C values shifted more positive by about 15‰ on the average. This is a consequence of ¹²C⁺ deficit relative to ¹³C of the samples with respect to the normalizing standard OXII. Since we have observed that ¹³C⁺/¹²C^– ratio shows no saturation, we have also calculated δ¹³C using these ratios and the histogram shows substantial improvement in the shape of the distribution as seen in Figure 2(a).

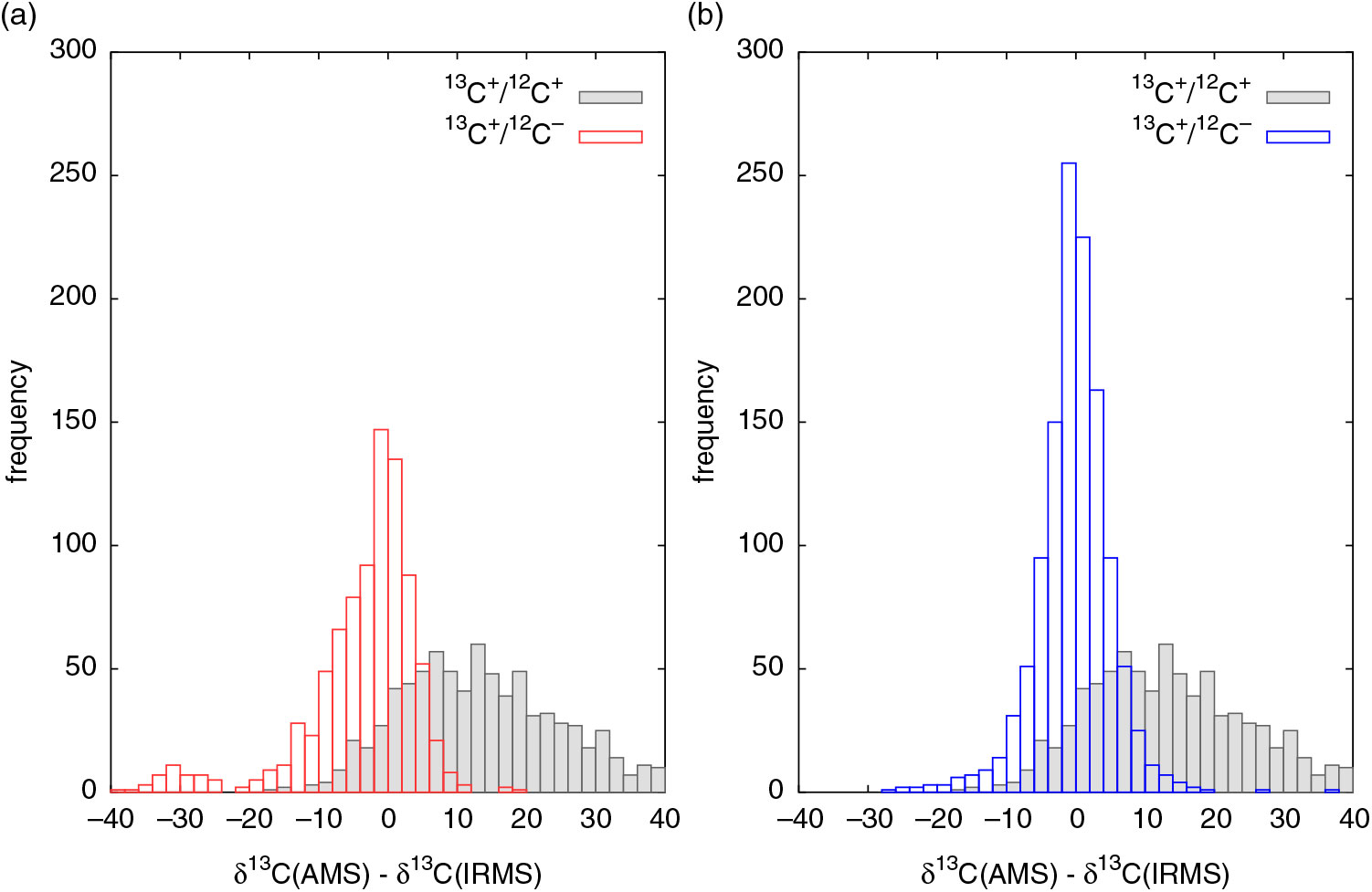
Figure 2 Difference between AMS and IRMS δ¹³C values plotted as histograms. (a) ¹³C⁺/¹²C^– ratio results in better δ¹³C than ¹³C⁺/¹²C⁺ ratio. (b) ¹³C⁺/¹²C^– ratio corrected for ¹³C⁺ transmission reduction results in a symmetric curve and closest agreement with IRMS values.

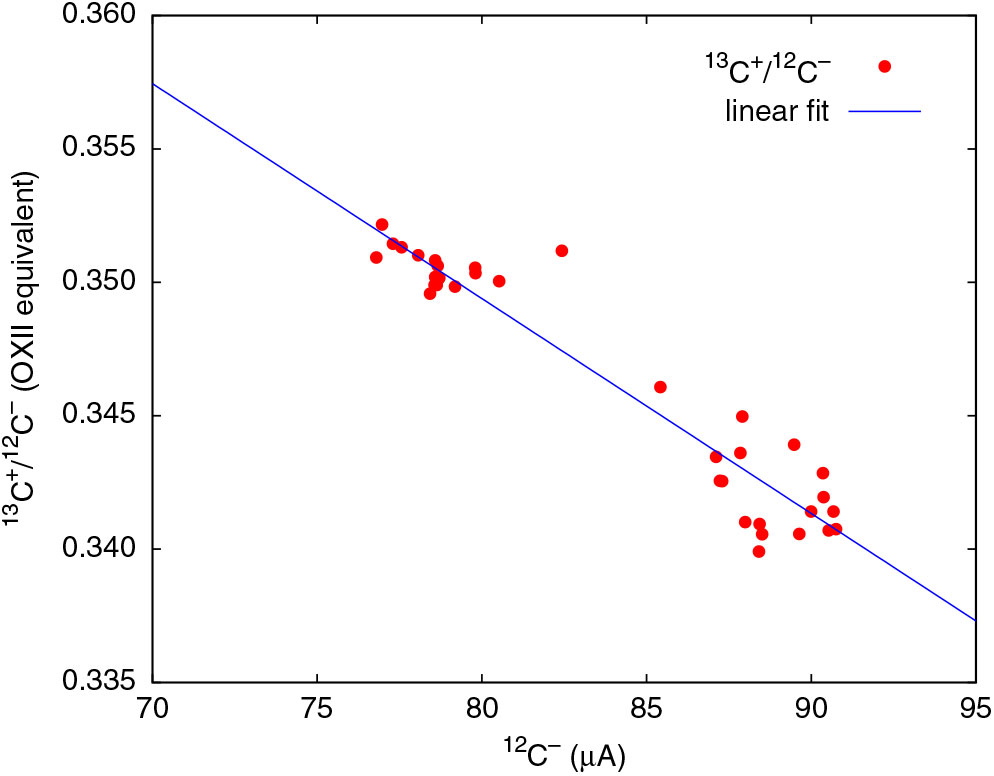
The distribution peaks at zero but is still not symmetric. For positive differences, the curve falls of rapidly and is sharper, but falls off slowly for negative differences and spreads out to high negative values. The long tail on the negative side implies that the online δ¹³C values are more negative than they should be. This could be a result of a reduction in ¹³C⁺ of the sample relative to the normalizing OXII when ¹³C⁺/¹²C^– ratios are used for calculation. On analyzing the raw data, we have found that even the ¹³C⁺ beam current experiences some reduction in transmission. To correct for this loss, we need to improve the normalization procedure for δ¹³C calculation. For a given ¹³C⁺/¹²C^– ratio of a sample, we need to use the ¹³C⁺/¹²C^– ratio of the standard (OXII) corresponding to the same ¹²C^– beam current. This can be accomplished by obtaining a regression relation for ¹³C⁺/¹²C^– ratio of OXII over the entire range of beam currents needed for the sample group. But because OXII currents in a sample group are only limited to a portion of the range, for an accurate regression relation, we need another standard with beam currents spanning over a different range. Since C6 produced higher currents than OXII, its ¹³C⁺/¹²C^– ratio can be used but needs to be suitably scaled to match the ratio for OXII. From the δ¹³C values of C6 (–10.8‰) and OXII (–17.8‰), the stable isotope ratio of C6 is 1.007 times that of OXII. With more data points contributing to the regression line, ¹³C⁺ transmission can be calculated more accurately as shown in Figure 3. If there is no transmission loss, ¹³C⁺/¹²C^– ratio should remain the same over the chosen range of ¹²C^– currents, but Figure 3 clearly proves that ¹³C⁺ current indeed undergoes steady loss of transmission. The same regression method was applied to every sample group to obtain a linear equation for calculation of ¹³C⁺/¹²C^– to normalize the sample data. The resulting histogram is a symmetric gaussian centered around zero, a remarkable improvement as seen in Figure 2(b). The standard deviation of the distribution is close to 2.5‰, which seemed impossible to achieve prior to undertaking this analysis when ¹³C⁺/¹²C⁺ ratios alone were used for calculation.

Figure 3 ¹³C⁺ transmission decreases with beam current. The data points correspond to a single sample group with two OXII and two C6 samples. Data for <85 μA correspond to OXII. Data points for >85 μA correspond to C6 but scaled to match the ¹³C⁺/¹²C^– ratio of OXII.

The calculation procedure is summarized here. We may recall the equation for δ¹³C when the standard is other than VPDB:

$${\delta ^{13}}{{\rm{C}}_{unk}} = \left( {{{{r_{unk}}} \over {{r_{std}}}} - 1} \right) \times 1000 + \left( {{{{r_{unk}}} \over {{r_{std}}}} \times {\delta ^{13}}{{\rm{C}}_{std}}} \right)$$

where r_unk and r_std are ¹³C/¹²C ratios of the unknown (sample) and standard, respectively. The method requires development of a computer code to carry out the following calculations.

1. 1. Calculate ¹³C⁺/¹²C^– ratios of the standard and sample (results shown in Figure 2a).

2. 2. Correcting for ¹³C⁺ transmission variation leads to further improvement. Linear fit the ¹³C⁺/¹²C^– data of primary standards (OXII) as a function of ¹²C^– beam current (Figure 3). For improved accuracy, data of secondary standards (IAEA-C6 in this case) with known δ¹³C values can also be included in the fit calculation after properly scaling the ¹³C⁺/¹²C^– ratio to match that of the primary standard.

3. 3. (¹³C⁺/¹²C^–)_unk along with (¹³C⁺/¹²C^–)_std obtained from the regression relation for the same value of (¹²C^–)_unk current to be used for δ¹³C calculation (results shown in Figure 2b).

¹⁴C/¹³C Ratios

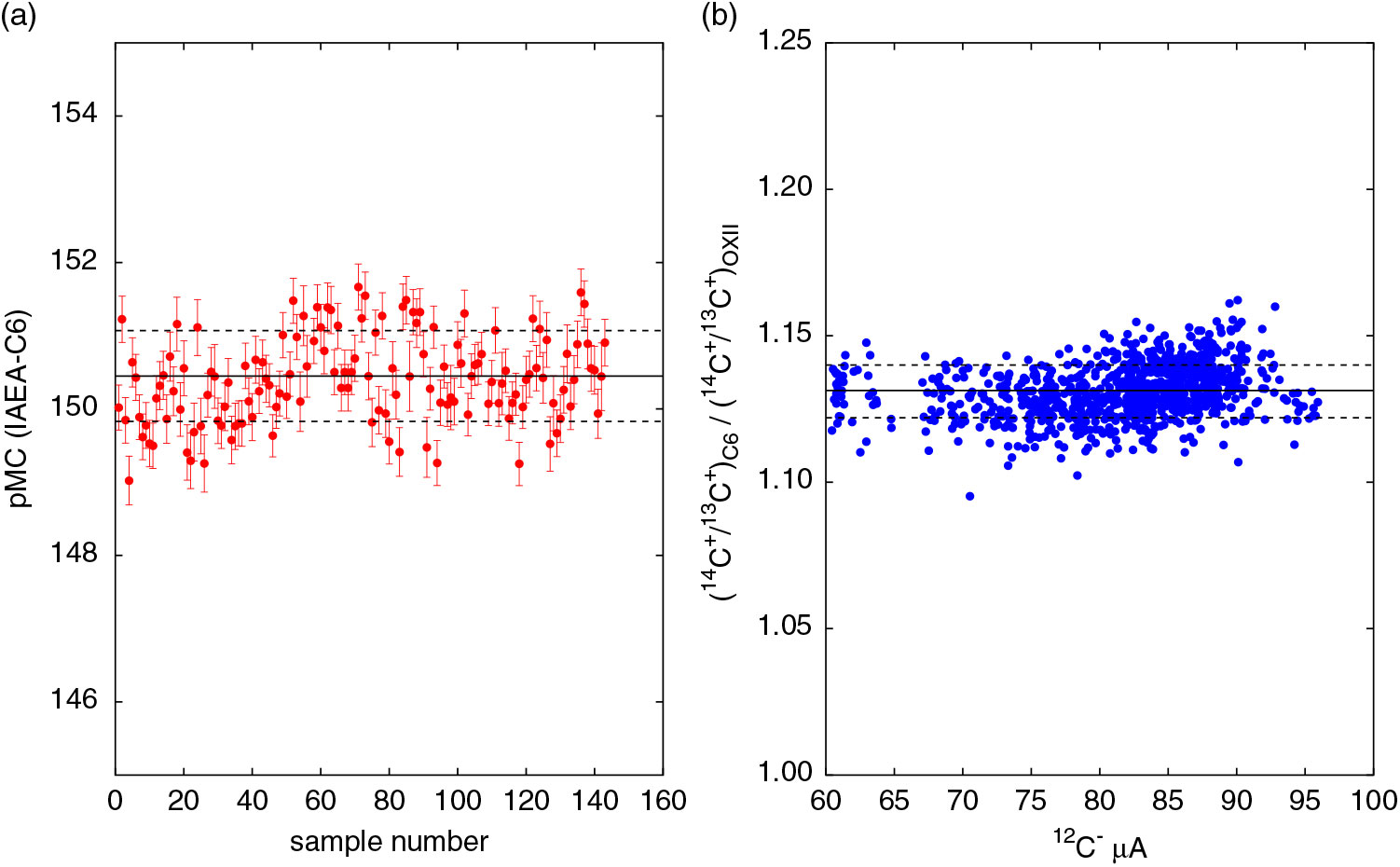
The data of Figure 3 poses a critical question: how does the decrease in ¹³C⁺ beam transmission affect the ¹⁴C⁺/¹³C⁺ ratios? Since the pMC data of standards using ¹⁴C⁺/¹³C⁺ ratios agree with the nominal values, to be consistent, even ¹⁴C⁺ must undergo a proportional reduction in yield at higher currents. At this point, this is only an assumption because so far, our analysis only focused on stable isotope data. Impact of ¹³C transmission change on pMC data needs investigation. A quick look at the ¹⁴C data of C6 however is presented in Figure 4. The pMC data of C6 are plotted in Figure 4(a), and the mean value agrees well with the nominal value of 150.6 within the measurement precision. In Figure 4(b), the normalized ratio (¹⁴C⁺/¹³C⁺)_C6 / (¹⁴C⁺/ ¹³C⁺)_OXII as a function of ¹²C^– agrees well with the expected value of 1.13 which can be calculated from the nominal pMC and δ¹³C values of C6 and OXII. Though the data does not conclusively prove that ¹⁴C⁺ throughput decreases, it certainly proves that the pMC values using the ¹⁴C⁺/¹³C⁺ ratios were not affected due to transmission loss over the range of beam currents produced.

Figure 4 (a) pMC data of C6 calculated using δ¹³C = –10.8‰. The mean value 150.45 ± 0.62 of the data shown as a solid line agrees well with the nominal value of 150.6. Dashed lines show 1σ deviation from the mean value. (b) ¹⁴C⁺/¹³C⁺ ratio of C6 normalized to the OXII ratio does not change with the beam current. The data points correspond to individual runs, and the error bars of each point are smaller than the size of the points. The data is in exact agreement with the expected value of 1.13. Dashed lines show 1σ deviation from the mean value.