No CrossRef data available.
Article contents
XXVIII.—The Theory of Hessians in the Historical Order of Development up to 1860.
Published online by Cambridge University Press: 15 September 2014
Extract
SPECIAL cases of the determinant

where u is a function of x, y, z, …, may well have appeared at a very early date in the history of determinants. The case where u=ax2+2bxy+cy2 may be viewed as traceable to Lagrange (1773), and the case where u=ax2+by2+cz2+2dyz+2ezx+2fxy to Gauss (1801); but it is certain that in those cases the elements of the determinants were not looked on as second differential-quotients of u. The general conception first occurred to Hesse in the year 1843.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1908
References
page 417 note * Instead of 210 we find in the original 25, and in the Collected Math. Papers 28.
page 421 note * The first two of these results, which follow from (α) and (β), there is no pressing reason for mentioning: it would have been equally pertinent to note that u=0. The third result Jacobi probably obtained (see Crelle's Journal, xv. p. 304) by taking in every possible way n-1 of the initiatory set of equations and deducing
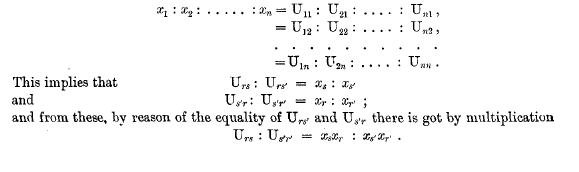
page 423 note * See Philos. Magazine, ii.(1851)p. 406, and Cambridge and Dub. Math. Journ., vii. (1852) p. 52; or Sylvester's Collected Math. Papers, i. pp. 280, 284.
page 423 note † On p.194 he says the Hessian of F(x, y) is “the determinant of the determinant, in respect to ξ and η, of
—an error which is repeated in the Collected Math. Papers.
page 424 note * See Philos. Magazine, v. p. 122: or Collected Math. Papers, i. p. 591.
page 424 note † It should be noted that this is ![]() of the Hessian as defined, that a1 is expressible as a three-line determinant, and that the performance of the circular substitutions a 1, b 2, c 3=b 2, c 3,a 1, a 2,b 3, c 1=b 3, c 1, a 2, a 3, b 1, c 2=b 1, c 2, a 3, on the expressions for a1, 3a2, 3a3gives us six other of the expressions.
of the Hessian as defined, that a1 is expressible as a three-line determinant, and that the performance of the circular substitutions a 1, b 2, c 3=b 2, c 3,a 1, a 2,b 3, c 1=b 3, c 1, a 2, a 3, b 1, c 2=b 1, c 2, a 3, on the expressions for a1, 3a2, 3a3gives us six other of the expressions.
page 429 note * The reason given for the deduction Urs= Nx1xs, which occurs in his presentation of Jacobi's proof of the year 1849, is disappointing.
page 430 note * See (α)in Jacobi's proof of 1849.


