Hostname: page-component-6dbcb7884d-q4sxc Total loading time: 0 Render date: 2025-02-14T07:20:16.122Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Cayley's Demonstration of Pascal's Theorem

Published online by Cambridge University Press:  15 September 2014

Thomas Muir
Get access

Extract

The demonstration referred to is given in the Cambridge Mathematical Journal, vol. iv. pp. 18–20. It opens with the enunciation of a lemma to the effect that the intersection of the planes

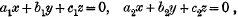
the intersection of

and the intersection of

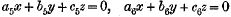
will be in the same plane if

Type
Proceedings 1889-90
Information
Proceedings of the Royal Society of Edinburgh , Volume 17 , 1891 , pp. 18 - 22
Copyright
Copyright © Royal Society of Edinburgh 1891

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Since the order of the three points is immaterial, we see that

It will be found that the second of the three determinants is got by using │a1b5c6 instead of │a1b3c4 for our multiplier and divisor in the foregoing transformation, and the third by using similarly │a3b1c2. This is one proof of their identity. Another consists in pointing out the simple fact, that to establish the identity of the first two is the same as to prove that

—a well-known identity of Bezout's, and, curiously enough, Cayley's second lemma in this very paper