Article contents
XIII.—The Generating Function of Solid Partitions
Published online by Cambridge University Press: 14 February 2012
Synopsis
The generating function for the number of linear partitions was found by Euler, the method being almost trivial. That for plane partitions is due to Macmahon, but, even in a simplified form found by Chaundy, the proof is far from trivial. The number of solid partitions of n, i.e. the number of solutions of

is denoted by r(n). It has often been conjectured that the generating function of r(n) is  , but this is now known to be false. We write η(a, b, c) for the generating function of the number of solutions of (1) subject to the additional condition that
, but this is now known to be false. We write η(a, b, c) for the generating function of the number of solutions of (1) subject to the additional condition that
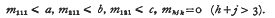
Macmahon 1916 found n(a, 1, 1) for general a. Here we find η(a, b, c) for general a, b. c.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 67 , Issue 3 , 1967 , pp. 185 - 195
- Copyright
- Copyright © Royal Society of Edinburgh 1967
References
References to Literature
- 1
- Cited by


