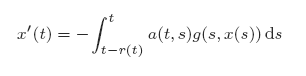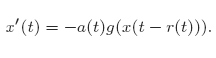Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Yicheng
and
Li, Zhixiang
2008.
Stability analysis of the zero solution for two class evolution equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 69,
Issue. 7,
p.
2058.
Jin, Chuhua
and
Luo, Jiaowan
2009.
Stability of an integro-differential equation.
Computers & Mathematics with Applications,
Vol. 57,
Issue. 7,
p.
1080.
Ding, Liming
Li, Xiang
and
Li, Zhixiang
2010.
Fixed Points and Stability in Nonlinear Equations with Variable Delays.
Fixed Point Theory and Applications,
Vol. 2010,
Issue. 1,
Luo, Jiaowan
2010.
Fixed points and exponential stability for stochastic Volterra–Levin equations.
Journal of Computational and Applied Mathematics,
Vol. 234,
Issue. 3,
p.
934.
Zhao, Dianli
2011.
New criteria for stability of neutral differential equations with variable delays by fixed points method.
Advances in Difference Equations,
Vol. 2011,
Issue. 1,
Zhao, Dianli
and
Han, Dong
2011.
Stability of linear neutral differential equations with delays and impulses established by the fixed points method.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 74,
Issue. 18,
p.
7240.
Pi, Dingheng
2011.
Study the stability of solutions of functional differential equations via fixed points.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 74,
Issue. 2,
p.
639.
Lai, Xianghong
Zhang, Yutian
and
Shahzad, Naseer
2012.
Fixed Point and Asymptotic Analysis of Cellular Neural Networks.
Journal of Applied Mathematics,
Vol. 2012,
Issue. 1,
Luo, Qi
Miao, Xinjie
Wei, Qian
and
Zhou, Zhengxin
2013.
Stability of Impulsive Neural Networks with Time-Varying and Distributed Delays.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Dung, Nguyen Tien
2013.
New stability conditions for mixed linear Levin-Nohel integro-differential equations.
Journal of Mathematical Physics,
Vol. 54,
Issue. 8,
Zhang, Yutian
and
Luo, Qi
2013.
Global exponential stability of impulsive cellular neural networks with time-varying delays via fixed point theory.
Advances in Difference Equations,
Vol. 2013,
Issue. 1,
Zhang, Yutian
and
Guan, Yuanhong
2013.
Asymptotic Stability of Impulsive Cellular Neural Networks with Infinite Delays via Fixed Point Theory.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Zhao, Dianli
2013.
The boundedness and stability of neutral delay differential equations with damped stochastic perturbations via fixed point theory.
Applied Mathematics and Computation,
Vol. 219,
Issue. 12,
p.
6792.
Yao, Tianxiang
and
Lai, Xianghong
2014.
Mean-Square Exponential Stability Analysis of Stochastic Neural Networks with Time-Varying Delays via Fixed Point Method.
Journal of Applied Mathematics,
Vol. 2014,
Issue. ,
p.
1.
Ardjouni, Abdelouaheb
and
Djoudi, Ahcene
2014.
Stability in nonlinear neutral integro-differential equations with variable delay using fixed point theory.
Journal of Applied Mathematics and Computing,
Vol. 44,
Issue. 1-2,
p.
317.
Pi, Dingheng
2014.
Stability Conditions of Second Order Integrodifferential Equations with Variable Delay.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Pi, Dingheng
and
Zhao, Yuxin
2014.
Fixed Points and Stability of a Class of Integrodifferential Equations.
Mathematical Problems in Engineering,
Vol. 2014,
Issue. 1,
Zhao, Dianli
Yuan, Sanling
and
Zhang, Tiansi
2014.
Improved stability conditions for a class of stochastic Volterra–Levin equations.
Applied Mathematics and Computation,
Vol. 231,
Issue. ,
p.
39.
Soualhia, Imene
Ardjouni, Abdelouaheb
and
Djoudi, Ahcene
2015.
Periodic nonnegative solutions in neutral nonlinear integro-differential equations with functional delay.
Rendiconti del Circolo Matematico di Palermo (1952 -),
Vol. 64,
Issue. 1,
p.
83.
Tien Dung, Nguyen
2015.
On exponential stability of linear Levin-Nohel integro-differential equations.
Journal of Mathematical Physics,
Vol. 56,
Issue. 2,
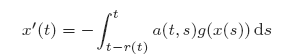 with variable delay r(t) ≥ 0 is investigated, where t−r(t) is increasing and xg(x) > 0 (x ≠ 0) in a neighbourhood of x = 0. We find conditions for r, a and g so that for a given continuous initial function ψ a mapping P for (1) can be defined on a complete metric space Cψ and in which P has a unique fixed point. The end result is not only conditions for the existence and uniqueness of solutions of (1) but also for the stability of the zero solution. We also find conditions ensuring that the zero solution is asymptotically stable by changing to an exponentially weighted metric on a closed subset of Cψ. Finally, we parlay the methods for (1) into results for
with variable delay r(t) ≥ 0 is investigated, where t−r(t) is increasing and xg(x) > 0 (x ≠ 0) in a neighbourhood of x = 0. We find conditions for r, a and g so that for a given continuous initial function ψ a mapping P for (1) can be defined on a complete metric space Cψ and in which P has a unique fixed point. The end result is not only conditions for the existence and uniqueness of solutions of (1) but also for the stability of the zero solution. We also find conditions ensuring that the zero solution is asymptotically stable by changing to an exponentially weighted metric on a closed subset of Cψ. Finally, we parlay the methods for (1) into results for