No CrossRef data available.
Article contents
Proof of a conjecture of Offord
Published online by Cambridge University Press: 14 November 2011
Synopsis
If z1, z2 … zn are complex numbers satisfying |zi−zj|≧1 for all i, j then the number of the 2n sums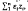 
where ει = ±1, which lie in any circle of radius r cannot exceed αr2n/n3/2 where αr depends only on r.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 86 , Issue 1-2 , 1980 , pp. 103 - 106
- Copyright
- Copyright © Royal Society of Edinburgh 1980
References
1Erdös, P., On a lemma of Littlewood and Offord, Bull. Amer. Math. Soc. 5 (1945), 898–902.CrossRefGoogle Scholar
2Halász, G., Estimates for the concentration function of combinatorical number theory and probability. Period. Math. Hungar. 8 (1977), 197–211.CrossRefGoogle Scholar
3van Lint, J. H., Representation of O as 
Proc. Amer. Math. Soc. 18 (1967), 182–184.CrossRefGoogle Scholar
Proc. Amer. Math. Soc. 18 (1967), 182–184.CrossRefGoogle Scholar4Kleitman, D. K., On a lemma of Littlewood and Offord on the distribution of linear combination of vectors, Advances in Math. 5 (1970), 115–117.CrossRefGoogle Scholar
5Sárközy, A. and Szeméredi, E., Über ein Problem von Erdös und Moser, Acta Arithmetica 11 (1965–1966), 205–208.Google Scholar