Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-15T00:03:09.897Z Has data issue: false hasContentIssue false
  • English
  • Français

On some rigidity results of hypersurfaces in a sphere

Published online by Cambridge University Press:  21 May 2010

Qing-Ming Cheng ,
Haizhong Li  and
Guoxin Wei
Qing-Ming Cheng
Affiliation:
Department of Mathematics, Faculty of Science and Engineering, Saga University, 840-8502 Saga, Japan (cheng@ms.saga-u.ac.jp)
Haizhong Li
Affiliation:
Department of Mathematical Sciences, Tsinghua University, 100084 Beijing, People's Republic of China (hli@math.tsinghua.edu.cn)
Guoxin Wei
Affiliation:
School of Mathematical Sciences, South China Normal University, 510631 Guangzhou, People's Republic of China Department of Mathematics, Faculty of Science and Engineering, Saga University, 840-8502 Saga, Japan (weigx03@mails.tsinghua.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the weak stability index of an immersion ϕ: M → Sn+1 (1) ⊂ Rn+2 of an n-dimensional compact Riemannian manifold. We prove that the weak stability index of a compact hypersurface M with constant scalar curvature in Sn+1 (1), which is not totally umbilical, is greater than or equal to n + 2 if the mean curvature H1 and H3 are constant, and that the equality holds if and only if M is 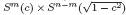. As an application, we show that the weak stability index of an n-dimensional compact hypersurface with constant scalar curvature in Sn+1 (1), which is neither totally umbilical nor a Clifford hypersurface, is greater than or equal to 2n + 4 if the mean curvature H1 and H3 are constant.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 140 , Issue 3 , June 2010 , pp. 477 - 493
Copyright
Copyright © Royal Society of Edinburgh 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)