Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-15T07:56:50.407Z Has data issue: false hasContentIssue false
  • English
  • Français

On periodic solutions of nonlinear second order vector differential equations

Published online by Cambridge University Press:  14 November 2011

P. Habets  and
M. N. Nkashama
P. Habets
Affiliation:
U.C.L., Institut de Mathématique pure et appliquée, Chemin du Cyclotron 2, B-1348 Louvain-la-Neuve, Belgium
M. N. Nkashama
Affiliation:
Department of Mathematical Sciences, Memphis State University, Memphis, Tennessee 38152, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper considers existence of periodic solutions for vector Liénard differential equations

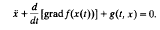
In our main result we write

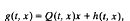
where Q(t, x) is a symmetric matrix and h(t, x) is sublinear. The key assumption relates the asymptotic behaviour as x →+ ∞ of the eigenvalues of Q(t, x) to the spectrum of the linear operator −d2/dt2 Several choices for Q(t, x) are considered which lead to known theorems and extend others. In the case of the Duffing equation

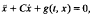
the assumptions are weakened.

Our approach is based on Leray-Schauder's degree theory and a priori estimates.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 104 , Issue 1-2 , 1986 , pp. 107 - 125
Copyright
Copyright © Royal Society of Edinburgh 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ahmad, S.. An existence theorem for periodically perturbed conservative systems. Michigan Math. J. 20 (1973), 385–392.Google Scholar
2Amaral, L. and Pera, M. P.. On periodic solutions of non-convservative systems. Nonlinear Anal. 6 (1982), 733–743.CrossRefGoogle Scholar
3Bates, P. W.. Solutions of nonlinear elliptic systems with meshed spectra. Nonlinear Anal. 4 (1980), 1023–1030.CrossRefGoogle Scholar
4Brown, K. J. and Lin, S. S.. Periodically perturbed conservative systems and a global inverse function theorem. Nonlinear Anal. 4 (1980), 193–201.CrossRefGoogle Scholar
5Iannacci, R. and Nkashama, M. N.. Periodic solutions for some forced second order Liénard and Duffing systems. Boll. Un. Mat. Ital. B (6) 4 (1985) (in press).Google Scholar
6Lazer, A. C.. Application of a lemma on bilinear forms to a problem in nonlinear oscillations. Proc. Amer. Math. Soc. 33 (1972), 89–94.CrossRefGoogle Scholar
7Lazer, A. C. and Sanchez, D. A.. On periodically perturbed conservative systems. Michigan Math. J. 16 (1969), 193–200.CrossRefGoogle Scholar
8Manasevich, R. F.. A non-variational version of a max-min principle. Nonlinear Anal. 7 (1983), 565–570.CrossRefGoogle Scholar
9Mawhin, J.. An extension of a theorem of A. C. Lazer on forced nonlinear oscillations. J. Math. Anal. Appl. 40 (1972), 20–29.CrossRefGoogle Scholar
10Mawhin, J.. Boundary value problems at resonance for vector second order nonlinear ordinary differential equations. Equadiff IV. Praha 1977. Lecture Notes in Mathematics 703, pp. 241–249 (Berlin: Springer, 1979).Google Scholar
11Mawhin, J.. Compacité monotonie et convexité dans l'étude de problèmes aux limites semi-linéaires. Sémin. Anal. Moderne 19 (Quebec: Université de Sherbrooke, 1981).Google Scholar
12Mawhin, J. and Ward, J. R. Jr.Nonuniform nonresonance conditions at the two first eigenvalues for periodic solutions of forced Liénard and Duffing equations. Rocky Mountain J. Math. 12 (1982), 643–654.CrossRefGoogle Scholar
13Nkashama, M. N.. Conditions de résonance ou de non-résonance non-uniformes et solutions périodiques d'équations différentielles non-linéaires. Ph.D. Thesis, University of Louvain, 1984.Google Scholar
14Reissig, R.. Extension of some results concerning the generalized Liénard equation. Ann. Mat. Pura Appl. (4) 104 (1975), 269–281.CrossRefGoogle Scholar
15Ward, J. Jr.The existence of periodic solutions for non-linearly perturbed conservative systems. Nonlinear Anal. 3 (1979), 697–705.CrossRefGoogle Scholar