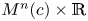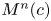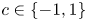1. Introduction
The last few decades have seen a steadily growing interest in the study of submanifolds of Riemannian product spaces. Such a space is the product manifold 
$M^{n}(c)\times \mathbb {R}$ endowed with the standard product metric, where 
$M^{n}(c)$ is a 
$n$-dimensional Riemannian space form with constant sectional curvature 
$c=-1,1$. It is clear that these spaces are a natural extension of the Euclidean space. We can say that interest came of the studies of surfaces due to Abresch, Meeks, and Rosenberg (see [Reference Abresch and Rosenberg1, Reference Meeks and Rosenberg22, Reference Rosenberg29]). In [Reference Abresch and Rosenberg1], the authors defined a holomorphic quadratic differential for surfaces with constant mean curvature (cmc) and, generalized Hopf theorem to these spaces showing that an immersed cmc spheres must be rotational and embedded.
On the other hand, in 1968, an important tool for the study of the geometry of submanifolds immersed in Riemannian space forms emerged, which nowadays is known as Simons type formulas. Originally, Simons [Reference Simons31] computed the Laplacian of the square of the norm of the second fundamental form 
$|A|^{2}$ of a closed (compact without boundary) minimal immersion into the Euclidean sphere getting a natural gap theorem concerning the size of the squared norm of the second fundamental form. More precisely, by way of illustration, he showed that if 
$\Sigma ^{m}$ is a closed minimal hypersurface of 
$\mathbb {S}^{m+1}$ satisfying 
$0\leq |A|^{2}\leq m$, then either 
$|A|^{2}=0$ or 
$|A|^{2}=m$. In his study, Simons failed to characterize which geometric object achieves equality 
$|A|^{2}=m$. This was proved soon afterwards, simultaneously and independently, by Chern, Carmo and Kobayashi [Reference Chern, do Carmo and Kobayashi9] and Lawson [Reference Lawson20]. In fact, following Simons’ approach, they characterize Clifford's minimal tori 
$\mathbb {S}^{m_{1}}(c_{1})\times \mathbb {S}^{m_{2}}(c_{2})$, 
$m_{1}+m_{2}=m$, 
$c_{1}=\sqrt {m_{1}/m}$ and 
$c_{1}=\sqrt {m_{1}/m}$ as the only closed minimal hypersurfaces of the unit sphere 
$\mathbb {S}^{m+1}$ for which 
$|A|^{2}=m$. It is important to emphasize that the tool introduced by Simons was not only shown to be powerful for the study of minimal closed submanifolds in the sphere, but also for the study of complete submanifolds with parallel normalized mean curvature vector field as well as an investigation tool in other ambient spaces as described, for instance [Reference Alencar and do Carmo2, Reference Araújo and Tenenblat5, Reference Erbacher15, Reference Nomizu and Smyth25, Reference Santos30].
An interesting question is to describe submanifolds immersed in a product space using Simons’ formula. In this direction, Batista [Reference Batista6] found a Simons’ type formula for surfaces with cmc immersed in the product spaces 
$M^{2}(c)\times \mathbb {R}$. Allied to the generalized maximum principle of Omori–Yau, he used this formula in order to characterize complete surfaces with cmc in the spaces 
$\mathbb {H}^{2}\times \mathbb {R}$ and 
$\mathbb {S}^{2}\times \mathbb {R}$. Passing to higher dimension and codimension, we highlight the studies of Fetcu, Oniciuc and Rosenberg in [Reference Fetcu, Oniciuc and Rosenberg17, Reference Fetcu and Rosenberg18], concerning to submanifolds with parallel mean curvature vector field (pmc submanifolds) in the product spaces 
$M^{n}(c)\times \mathbb {R}$. Indeed, they computed a Simons type formula for pmc submanifolds in 
$M^{n}(c)\times \mathbb {R}$. More precisely, in [Reference Fetcu, Oniciuc and Rosenberg17], they showed that, under suitable restrictions on the square of the norm of the second fundamental form of 
$\Sigma ^{m}$, it should be a cmc totally umbilical hypersurfaces in 
$M^{m+1}(c)\hookrightarrow M^{n}(c)$ for 
$n>m\geq 3$. In [Reference Fetcu and Rosenberg18] they obtained gap results for the mean curvature of certain complete proper-biharmonic pmc submanifolds, and also, classify proper-biharmonic pmc surfaces in 
$\mathbb {S}^{n}\times \mathbb {R}$.
Very recently, the first author [Reference dos Santos14] studied complete surfaces immersed in a product space 
$M^{2}(c)\times \mathbb {R}$ with constant extrinsic curvature. Recall that, a surface in a 
$3$-dimensional ambient space, besides the Gaussian curvature, has, at each point, the extrinsic curvature, which is the product of the principal curvatures. In 
$\mathbb {R}^{3}$ these two curvatures coincide. In this setting, he obtained a suitable Simons formula for the Cheng-Yau operator and using a generalized of the maximum principle, obtained a characterization of cylinder in 
$\mathbb {H}^{2}\times \mathbb {R}$ under certain appropriated restriction on the angle function and the traceless part of the second fundamental form, obtaining natural generalizations of some results in [Reference Batista6]. Here our goal is to extend some the results in [Reference dos Santos14, Reference Fetcu and Rosenberg18] to submanifolds with parallel normalized mean curvature vector field and constant second mean curvature (see definition in § 2.2). The pnmc hypothesis is weaker than the pmc condition studied by [Reference Fetcu and Rosenberg18]. For example, each hypersurface with nonzero mean curvature function in a Riemannian manifold is a pnmc submanifold.
This paper is organized as follows: In the first section, we will describe some basic facts about submanifolds in a general ambient space. Working with Cheng-Yau's differential operator, we use an alternative approach to find a Simons-type formula for pnmc submanifolds in product spaces 
$M^{n}(c)\times \mathbb {R}$ (cf. proposition 2.2) which generalize the formula obtained by Fetcu and Rosenberg [Reference Fetcu and Rosenberg18]. Next, we present some auxiliary results and we establish a maximum principle for an arbitrary semi-elliptic operator (cf. proposition 2.9). In § 3, we present our results concerning complete pnmc submanifolds with constant second mean curvature. With suitable constraints on the square of the length of the traceless operator, we apply our maximum principle to prove that such submanifolds should be totally umbilical into the Riemannian fibre. 
$M^{n}(c)$ (cf. theorems 3.3 and 3.5). We end this paper with two particular cases of previous results (cf. propositions 3.6 and 3.7) as well as with two results in the 
$2$-dimensional case (cf. theorems 3.8 and 3.9).
2. Setup and auxiliary results
2.1 General formulas
In this first section, we will perform a brief review on submanifolds in an arbitrary ambient space. For a deep knowledge about this topic we recommend [Reference Chern, do Carmo and Kobayashi9, Reference Yau32].
Let 
$\Sigma ^{m}$ be a submanifold immersed in a Riemannian manifold 
$\overline {M}^{n+1}$ with 
$n\geq m$. In this context, we choose a local field of orthonormal frames 
$e_{1},\ldots,e_{n+1}$ in 
$\overline {M}^{n+1}$, with dual coframes 
$\omega _{1},\ldots,\omega _{n+1}$, such that, at each point of 
$\Sigma ^{m}$, 
$e_{1},\ldots,e_{m}$ are tangent to 
$\Sigma ^{m}$ and 
$e_{m+1},\ldots,e_{n+1}$ are normal to 
$\Sigma ^{m}$. We will use the following convention of indices
\begin{align} & 1\leq A,B,C,\ldots,\leq n+1,\quad 1\leq i,j,k,\ldots,\leq m\quad\mbox{and}\nonumber\\ & m+1\leq\alpha,\beta,\gamma,\ldots,\leq n+1. \end{align}
In this setting, the Riemannian metric for 
$\overline {M}^{n+1}$ is given by
\begin{equation} {\rm d}s^{2}=\sum_{A}\omega_{A}^{2}, \end{equation}
Denoting by 
$\{\omega _{AB}\}$ the connection forms of 
$\overline {M}^{n+1}$, we have that the structure equations of 
$\overline {M}^{n+1}$ are given by:
\begin{equation} {\rm d}\omega_{A}={-}\sum_{B}\omega_{AB}\wedge\omega_{B},\quad\omega_{AB}+\omega_{BA}=0, \end{equation}
\begin{equation} {\rm d}\omega_{AB}={-}\sum_{C}\omega_{AC}\wedge\omega_{CB}+\frac{1}{2}\sum_{C,D}\overline{R}_{ABCD}\,\omega_C\wedge\omega_D, \end{equation}
where 
$\overline {R}_{ABCD}$ denote the Riemannian curvature tensor.
Next, we restrict all the tensors to 
$\Sigma ^{m}$. First of all,
\begin{equation} \omega_{\alpha}=0,\quad m+1\leq\alpha\leq n+1. \end{equation}
Consequently, the Riemannian metric of 
$\Sigma ^{m}$ is written as 
${\rm d}s^{2}=\sum _{i}\omega _{i}^{2}$. Since
\begin{equation} \sum_{i}\omega_{\alpha i}\wedge\omega_i={\rm d}\omega_{\alpha}=0, \end{equation}
from Cartan's lemma we can write
\begin{equation} \omega_{\alpha i}=\sum_{j}h_{ij}^{\alpha}\omega_{j}\quad\mbox{and}\quad h_{ij}^{\alpha}=h_{ji}^{\alpha}. \end{equation}
This gives the shape operator of 
$\Sigma ^{m}$,
\begin{equation} A=\sum_{\alpha,i,j}h_{ij}^{\alpha}\omega_{i}\otimes\omega_{j}e_{\alpha},\quad h^{\alpha}_{ij}=\langle A_{\alpha}(e_{i}),e_{j}\rangle=\langle\sigma(e_{i},e_{j}),e_{\alpha}\rangle \end{equation}
with 
$\sigma$ denoting the second fundamental form of 
$\Sigma ^{m}$ in 
$\overline {M}^{n+1}$. The square length of the shape operator is
\begin{equation} |A|^{2}=\sum_{\alpha}|A_{\alpha}|^{2}=\sum_{\alpha,i,j}(h^{\alpha}_{ij})^{2}. \end{equation}
Furthermore, we define the mean curvature vector 
$h$ and the mean curvature function 
$H$ of 
$\Sigma ^{m}$ in 
$\overline {M}^{n+1}$, respectively by
\begin{equation} h=\frac{1}{m}\sum_{\alpha}{\rm tr}(A_{\alpha})e_{\alpha}\quad\mbox{and}\quad H=|h|=\frac{1}{m}\sqrt{\sum_{\alpha}{\rm tr}(A_{\alpha})^{2}}, \end{equation}
where 
${\rm tr}(A_{\alpha })=\sum _{i}h_{ii}^{\alpha }$. In particular, if 
$H$ is constant, we say that 
$\Sigma ^{m}$ is a 
$cmc$ submanifold of 
$\overline {M}^{n+1}$.
The structure equations of 
$\Sigma ^{m}$ are given by
\begin{equation} {\rm d}\omega_{i}={-}\sum_{j}\omega_{ij}\wedge\omega_{j}, \quad\omega_{ij}+\omega_{ji}=0, \end{equation}
\begin{equation} {\rm d}\omega_{ij}={-}\sum_{k}\omega_{ik}\wedge\omega_{kj}+\frac{1}{2}\sum_{k,l}R_{ijkl}\omega_{k}\wedge\omega_{l}, \end{equation}
where 
$R_{ijkl}$ are the components of the curvature tensor of 
$\Sigma ^{m}$.
Using the previous structure equations, we obtain Gauss equation
\begin{equation} R_{ijkl}=\overline{R}_{ijkl}+\sum_{\beta}(h^{\beta}_{ik}h^{\beta}_{jl}-h^{\beta}_{il}h^{\beta}_{jk}). \end{equation}
We also state the structure equations of the normal bundle of 
$\Sigma ^{m}$
\begin{equation} {\rm d}\omega_{\alpha}={-}\sum_{\beta}\omega_{\alpha\beta}\wedge\omega_{\beta}, \quad\omega_{\alpha\beta}+\omega_{\beta\alpha}=0, \end{equation}
\begin{equation} {\rm d}\omega_{\alpha\beta}={-}\sum_{\gamma}\omega_{\alpha\gamma}\wedge\omega_{\gamma\beta}+\frac{1}{2}\sum_{k,l}R_{\alpha\beta kl}\omega_{k}\wedge\omega_{l}. \end{equation}
Thus, we have the Ricci equation
\begin{equation} R^{{\perp}}_{\alpha\beta ij}=\overline{R}_{\alpha\beta ij}+\sum_{k}(h^{\alpha}_{ik}h^{\beta}_{kj}-h^{\alpha}_{kj}h^{\beta}_{ik}). \end{equation}
The components 
$h_{ijk}^{\alpha }$ of the covariant derivative 
$\nabla A$ satisfy
\begin{equation} \sum_{k}h_{ijk}^{\alpha}\omega_{k}=dh_{ij}^{\alpha}-\sum_{k}h_{ik}^{\alpha}\omega_{kj}-\sum_{k}h_{jk}^{\alpha}\omega_{ki}+\sum_{\beta}h_{ij}^{\beta}\omega_{\beta\alpha}, \end{equation}with
\begin{equation} |\nabla A|^{2}=\sum_{\alpha,i,j,k}(h^{\alpha}_{ijk})^{2}. \end{equation}In this setting, from (2.1) and (2.5) we get Codazzi equation
\begin{equation} h^{\alpha}_{ijk}-h^{\alpha}_{ikj}={-}\overline{R}_{\alpha ijk}. \end{equation}
The first and the second covariant derivatives of 
$h_{ij}^{\alpha }$ are denoted by 
$h_{ijk}^{\alpha }$ and 
$h_{ijkl}^{\alpha }$, respectively, which satisfy
\begin{equation} \sum_{l}h^{\alpha}_{ijkl}\omega_{l}=dh_{ijk}^{\alpha}-\sum_{l}h_{ljk}^{\alpha}\omega_{li}-\sum_{l}h_{ilk}^{\alpha}\omega_{lj}-\sum_{l}h_{ijl}^{\alpha}\omega_{lk}+\sum_{\beta}h_{ijk}^{\beta}\omega_{\beta\alpha}. \end{equation}
Thus, taking the exterior derivative in (2.5), we obtain the following Ricci identity
\begin{equation} h^{\alpha}_{ijkl}-h^{\alpha}_{ijlk}=\sum_{p}h^{\alpha}_{ip}R_{pjkl}+\sum_{p}h^{\alpha}_{pj}R_{pikl}-\sum_{\beta}h^{\beta}_{ij}R^{{\perp}}_{\alpha\beta kl}. \end{equation}
Restricting the covariant derivative 
$\overline {R}_{ABCD,E}$ of 
$\overline {R}_{ABCD}$ on 
$\Sigma ^{m}$, then 
$\overline {R}_{\alpha ijk,l}$ is given by
\begin{equation} \begin{split} \overline{R}_{\alpha ijkl} & =\overline{R}_{\alpha ijk,l}-\sum_{\beta}\overline{R}_{\alpha\beta jk}h^{\beta}_{il}-\sum_{\beta}\overline{R}_{\alpha i\beta k}h^{\beta}_{jl}\\ & \quad-\sum_{\beta}\overline{R}_{\alpha ij\beta}h^{\beta}_{kl}+\sum_{p}\overline{R}_{pijk}h^{\alpha}_{lp}. \end{split} \end{equation}
where 
$\overline {R}_{\alpha ijkl}$ denotes the covariant derivative of 
$\overline {R}_{\alpha ijk}$ as a tensor on 
$\Sigma ^{m}$.
The Laplacian 
$\Delta h_{ij}^{\alpha }$ of 
$h_{ij}^{\alpha }$ is defined by 
$\Delta h_{ij}^{\alpha }=\sum _{k}h_{ijkk}^{\alpha }$. Thus, from equation (2.8) we deduce that
\begin{align} h_{ij}^{\alpha}\Delta h_{ij}^{\alpha}=&\sum_{k}h_{ij}^{\alpha}\left(\overline{R}_{\alpha ikj,k}+(h_{ikjk}^{\alpha}-h_{ikkj}^{\alpha})+\overline{R}_{\alpha kki,j}+h_{kkij}^{\alpha}\right)\\ =&\sum_{k}h_{ij}^{\alpha}\left(\overline{R}_{\alpha ikj,k}+\overline{R}_{\alpha kki,j}\right)+\sum_{k,p}h_{ij}^{\alpha}\left(h_{pi}^{\alpha}R_{pkjk}+h_{pk}^{\alpha}R_{pijk}\right)\nonumber\\ &+\,\sum_{\beta,k}h_{ij}^{\alpha}h_{ik}^{\beta}R^{{\perp}}_{\beta\alpha jk}+\sum_{k}h_{ij}^{\alpha}h_{kkij}^{\alpha}. \nonumber \end{align}In relation to these terms, applying the Gauss and Ricci equations in (2.10), a straightforward computation shows that
\begin{equation} \begin{split} \sum_{k} & \,h_{ij}^{\alpha}\left(\overline{R}_{\alpha ikj,k}+\overline{R}_{\alpha kki,j}\right)+\sum_{\beta,k}h_{ij}^{\alpha}h_{ik}^{\beta}R^{{\perp}}_{\beta\alpha jk}\\ & =\sum_{\beta,k}h_{ij}^{\alpha}\left({-}h_{kk}^{\beta}\overline{R}_{\alpha ij\beta}+2h_{jk}^{\beta}\overline{R}_{\alpha\beta ki}-h_{ij}^{\beta}\overline{R}_{\alpha k\beta k}+2h_{ki}^{\beta}\overline{R}_{\alpha\beta kj}\right)\\ & \quad-\sum_{p,k}h^{\alpha}_{ij}\left(h^{\alpha}_{pj}R_{pkki}+h^{\alpha}_{pk}R_{pikj}\right)-\sum_{k}h_{ij}^{\alpha}\left(\overline{R}_{\alpha ikjk}+\overline{R}_{\alpha kkij}\right)\\ & \quad\, + \sum_{\beta,p,k}h^{\alpha}_{ij}\left(h^{\alpha}_{ip}h^{\beta}_{pj}h^{\beta}_{kk}+2h^{\alpha}_{pk}h^{\beta}_{pj}h^{\beta}_{ik}-h^{\alpha}_{ip}h^{\beta}_{kj}h^{\beta}_{pk}-h^{\alpha}_{pk}h^{\beta}_{ij}h^{\beta}_{pk}-h^{\alpha}_{pj}h^{\beta}_{ik}h^{\beta}_{pk}\right). \end{split} \end{equation}
Moreover, applying some matricial manipulations and using (2.2), we also have
\begin{equation} \begin{split} \sum_{\alpha,\beta,i,j,k,p} & \!\!\!\!h_{ij}^{\alpha}\left(h^{\alpha}_{ip}h^{\beta}_{pj}h^{\beta}_{kk}+2h^{\alpha}_{pk}h^{\beta}_{pj}h^{\beta}_{ik}-h^{\alpha}_{ip}h^{\beta}_{kj}h^{\beta}_{pk}-h^{\alpha}_{pk}h^{\beta}_{ij}h^{\beta}_{pk}-h^{\alpha}_{pj}h^{\beta}_{ik}h^{\beta}_{pk}\right)\\ & \hspace{-0.5cm}=m\sum_{\alpha}{\rm tr}(A^{2}_{\alpha} A_{h})-\sum_{\alpha,\beta}\left(N(A_{\alpha} A_{\beta}-A_{\beta} A_{\alpha})+[{\rm tr}(A_{\alpha} A_{\beta})]^{2}\right), \end{split} \end{equation}
where 
$N(A)={\rm tr}(A A^{t})$ for any matrix 
$A=(a_{ij})$. Since
\begin{equation} \dfrac{1}{2}\Delta|A|^{2}=\sum_{\alpha,i,j,k}(h_{ijk}^{\alpha})^{2}+\sum_{\alpha,i,j}h_{ij}^{\alpha}\Delta h_{ij}^{\alpha} \end{equation}from equations (2.9) until (2.11) we get the following general Simons type formula.
Proposition 2.1 Let 
$\Sigma ^{m}$ be a submanifold in a Riemannian manifold 
$\overline {M}^{n+1}$ with 
$n\geq m$. Then
\begin{eqnarray} \dfrac{1}{2}\Delta|A|^{2}&= |\nabla A|^{2}+\sum_{\alpha,i,j,k}h^{\alpha}_{ij}\left(h^{\alpha}_{kkij}-\overline{R}_{\alpha ikjk}-\overline{R}_{\alpha kkij}\right)\\ &+\!\!\!\sum_{\alpha,\beta,i,j,k}\!\!h_{ij}^{\alpha}\left({-}h_{kk}^{\beta}\overline{R}_{\alpha ij\beta}+2h_{jk}^{\beta}\overline{R}_{\alpha\beta ki}-h_{ij}^{\beta}\overline{R}_{\alpha k\beta k}+2h_{ki}^{\beta}\overline{R}_{\alpha\beta kj}\right)\nonumber\\ &-\sum_{\alpha,\beta}\left(N(A_{\alpha} A_{\beta}-A_{\beta} A_{\alpha})+[{\rm tr}(A_{\alpha} A_{\beta})]^{2}-{\rm tr}(A_{\beta}){\rm tr}(A^{2}_{\alpha} A_{\beta})\right)\nonumber\\ &+\,2\!\!\!\!\sum_{\alpha,i,j,k,p}\!\!\!h_{pj}^{\alpha}\left(h_{pk}^{\alpha}\overline{R}_{pijk}+h_{pj}^{\alpha}\overline{R}_{pkik}\right).\nonumber \end{eqnarray}
2.2 A Simons-type formula for pnmc submanifolds in 
$M^{n}(c)\times \mathbb {R}$
In this section, we will present some basic facts about product manifolds as well as suitable Simons type formula derived from proposition 2.1. For this, let 
$M^{n}(c)$ be a connected Riemannian manifold endowed with metric tensor 
$\langle \,,\rangle _{M}$ and of constant sectional curvature 
$c=-1,1$. The Riemannian product space 
$M^{n}(c)\times \mathbb {R}$ is the differential manifold 
$M^{n}\times \mathbb {R}$ provided with the Riemannian metric
\begin{equation} \langle v,w\rangle_p=\langle(\pi_M)_*v,(\pi_M)_*w\rangle_{M}+\langle(\pi_{\mathbb{R}})_*v,(\pi_{\mathbb{R}})_*w\rangle, \end{equation}
with 
$p\in M^{n}\times \mathbb {R}$ and 
$v,w\in T_p(M\times \mathbb {R})$, where 
$\pi _{\mathbb {R}}$ and 
$\pi _{M}$ denote the projections onto the corresponding factor. Associated to the Riemannian product, the vector field
\begin{equation} \partial_{t}:=(\partial/\partial_{t})\big|_{(p,t)},\quad(p,t)\in M\times\mathbb{R} \end{equation}
is parallel and unitary, that is,
\begin{equation} \overline{\nabla}\partial_{t}=0\quad\mbox{and}\quad\langle\partial_{t},\partial_{t}\rangle=1, \end{equation}
where 
$\overline {\nabla }$ is the Levi-Civita connection of the Riemannian metric of 
$M^{n}\times \mathbb {R}$. Using the same notations established in [Reference Fetcu and Rosenberg18], we write the decomposition
\begin{equation} \xi:=\partial_{t}=T+N \end{equation}
where 
$T:=\partial _{t}^{\top }$ and 
$N:=\partial _{t}^{\perp }$ denote, respectively, the tangent and normal parts of the vector field 
$\partial _{t}$ on the tangent and normal bundle of the submanifold 
$\Sigma ^{m}$ in 
$M^{n}(c)\times \mathbb {R}$. Moreover, from (2.12) and (2.13), we get the relation
\begin{equation} 1=\langle\partial_{t},\partial_{t}\rangle=|T|^{2}+|N|^{2}. \end{equation}
It is clear that, if 
$T=0$ then, 
$\partial _{t}$ is normal to 
$\Sigma ^{m}$ and, hence 
$\Sigma ^{m}$ lies in 
$M^{n}(c)$.
Concerning the 
$M^{n}(c)\times \mathbb {R}$, let us recall that its curvature tensor is given by (see [Reference Daniel11]):
\begin{equation} \begin{split} \overline{R}(X,Y)Z= & \,\,c(\langle X,Z\rangle Y-\langle Y,Z\rangle X)+c\langle Z,\partial_{t}\rangle(\langle Y,\partial_{t}\rangle X-\langle X,\partial_{t}\rangle Y)\\ & +\,c(\langle Y,Z\rangle\langle X,\partial_{t}\rangle-\langle X,Z\rangle\langle Y,\partial_{t}\rangle)\partial_{t}, \end{split} \end{equation}
where 
$X,Y,Z\in \mathfrak {X}(M\times \mathbb {R})$ and, 
$\overline {R}$ is defined by (see [Reference O'Neill27]),
\begin{equation} \overline{R}(X,Y)Z=\overline{\nabla}_{[X,Y]}Z-[\overline{\nabla}_{X},\overline{\nabla}_{Y}]Z. \end{equation}
Denoting by 
$\nabla$ and 
$\nabla ^{\perp }$, respectively, the tangent and normal Levi-Civita connections along the tangent and normal bundle of 
$\Sigma ^{m}$, a direct computation by (2.13) give us
\begin{equation} \nabla_{X}T=A_{N}(X)\quad\mbox{and}\quad\nabla_{X}^{{\perp}}N={-}\sigma(T,X),\quad\mbox{for all}\quad X\in\mathfrak{X}(\Sigma), \end{equation}
where 
$A_{N}=\sum _{\alpha }\langle N,e_{\alpha }\rangle A_{\alpha }$ denotes the Weingarten operator in the 
$N$ direction.
Our aim now is to obtain a Simons type formula for a pnmc submanifold 
$\Sigma ^{m}$ in 
$M^{n}(c)\times \mathbb {R}$. For this, we observe first that since 
$M^{n}(c)\times \mathbb {R}$ locally symmetric, we have
\begin{equation} \overline{R}_{\alpha ikjk}=\overline{R}_{\alpha kkij}=0. \end{equation}
On the other hand, from (2.15), a straightforward computation gives 
$\overline {R}_{\alpha \beta kj}=0$, for all 
$\alpha,\beta,j,k$. Also,
\begin{align} \sum_{\alpha,\beta,i,j,k}\!\!\!h_{ij}^{\alpha}\left(h_{kk}^{\beta}\overline{R}_{\alpha ij\beta}+h_{ij}^{\beta}\overline{R}_{\alpha k\beta k}\right)&={-}cm^{2} H^{2}+cm\langle\sigma(T,T),h\rangle-cm|A_{N}|^{2}\nonumber\\ &\quad+\,cm^{2}\langle h,N\rangle^{2}+c(m-|T|^{2})|A|^{2} \end{align}and
\begin{align} \sum_{\alpha,i,j,k,p}\!\!\!h_{ij}^{\alpha}\left(h_{pk}^{\alpha}\overline{R}_{pijk}+h_{pj}^{\alpha}\overline{R}_{pkik}\right)&={-}cm\sum_{\alpha}|A_{\alpha}(T)|^{2}+c(m-|T|^{2})|A|^{2}\nonumber\\ &\quad-cm^{2}H^{2}+2cm\langle\sigma(T,T),h\rangle. \end{align}Therefore, replacing (2.17), (2.18) and (2.19) in proposition 2.1, we get
\begin{eqnarray} \dfrac{1}{2}\Delta|A|^{2}&= |\nabla A|^{2}+\sum_{\alpha,i,j,k}h^{\alpha}_{ij}h^{\alpha}_{kkij}+cm|A_{N}|^{2}-2cm\sum_{\alpha}|A_{\alpha}(T)|^{2}-cm^{2}|h|^{2}\nonumber\\ &+\,c(m-|T|^{2})|A|^{2}-cm^{2}\langle h,N\rangle^{2}+3cm\langle\sigma(T,T),h\rangle\\ &-\sum_{\alpha,\beta}\left(N(A_{\alpha} A_{\beta}-A_{\beta} A_{\alpha})+[{\rm tr}(A_{\alpha} A_{\beta})]^{2}\right)\nonumber\\ &+\sum_{\alpha,\beta}{\rm tr}(A_{\beta}){\rm tr}(A^{2}_{\alpha} A_{\beta}).\nonumber \end{eqnarray}
Next, we will also consider the following symmetric tensor
\begin{equation} \phi=\displaystyle{\sum_{\alpha,i,j}}\phi_{ij}^{\alpha}\omega_{i}\otimes\omega_{j}e_{\alpha}, \end{equation}
where
\begin{equation} \phi_{ij}^{\alpha}=\langle\phi_{\alpha}(e_{i}),e_{j}\rangle=h_{ij}^{\alpha}-\langle h,e_{\alpha}\rangle\delta_{ij}. \end{equation}
It is easy to check that each 
$\phi _{\alpha }=A_{\alpha }-\langle h,e_{\alpha }\rangle I$ is traceless and that
\begin{equation} |\phi|^{2}=\sum_{\alpha}|\phi_{\alpha}|^{2}=\sum_{\alpha,i,j}(\phi_{ij}^{\alpha})^{2}=|A|^{2}-mH^{2}. \end{equation}
Observe that 
$|\phi |^{2}=0$ if and only if 
$\Sigma ^{m}$ is a totally umbilical submanifold of 
$M^{n}(c)\times \mathbb {R}$. Within this context, a simple computation give us
\begin{equation} m|A_{N}|^{2}=m|\phi_{N}|^{2}+m^{2}\langle h,N\rangle^{2} \end{equation}
and
\begin{equation} \sum_{\alpha}|A_{\alpha}(T)|^{2}=\sum_{\alpha}|\phi_{\alpha}(T)|^{2}+2\langle\phi_{h}(T),T\rangle+H^{2}|T|^{2}. \end{equation}
Consequently,
\begin{equation} \begin{split} \dfrac{1}{2}\Delta|A|^{2}= & \,\,|\nabla A|^{2}+\sum_{\alpha,i,j,k}h^{\alpha}_{ij}h^{\alpha}_{kkij}+cm|\phi_{N}|^{2}-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\\ & +c(m-|T|^{2})|\phi|^{2}-cm\langle\phi_{h}(T),T\rangle+\sum_{\alpha,\beta}{\rm tr}(A_{\beta}){\rm tr}(A^{2}_{\alpha} A_{\beta})\\ & -\sum_{\alpha,\beta}\left(N(A_{\alpha} A_{\beta}-A_{\beta} A_{\alpha})+[{\rm tr}(A_{\alpha} A_{\beta})]^{2}\right). \end{split} \end{equation} From now on, we will work with pnmc submanifolds 
$\Sigma ^{m}$ immersed in product space 
$M^{n}(c)\times \mathbb {R}$. This means that 
$H>0$ and the normalized mean curvature vector field 
$\eta =h/H$ is parallel as a section of the normal bundle. We should notice that pmc submanifolds with nonzero mean curvature function also are pnmc submanifolds. So, the condition of having parallel normalized mean curvature vector field is more general than the condition of having pmc vector field. For instance, every hypersurface with nonzero mean curvature in a Riemannian manifold always has parallel normalized mean curvature vector field.
Into this setting, we will consider 
$\{e_{m+1},\ldots,e_{n+1}\}$ be a local orthonormal frame field in the normal bundle such that 
$e_{m+1}=\eta$. From this,
\begin{equation} {\rm tr}(A_{n+1})=mH\quad\mbox{and}\quad{\rm tr}(A_{\alpha})=m\langle h,e_{\alpha}\rangle=0,\quad\mbox{for all}\quad\alpha\geq m+2, \end{equation}
and by (2.20)
\begin{equation} \phi^{m+1}_{ij}=h^{m+1}_{ij}-H\delta_{ij}\quad\mbox{and}\quad\phi^{\alpha}_{ij}=h^{\alpha}_{ij},\quad\mbox{for all}\quad\alpha\geq m+2. \end{equation}
Moreover, since 
$e_{m+1}$ parallel, the Ricci equation (2.4) guarantees that 
$A_{\alpha } A_{m+1}=A_{m+1} A_{\alpha }$ for all 
$\alpha \geq m+2$. Using this, (2.21) and (2.23),
\begin{equation} \begin{split} & \sum_{\alpha,\beta}{\rm tr}(A_{\beta}){\rm tr}(A^{2}_{\alpha} A_{\beta})-\sum_{\alpha,\beta}\left(N(A_{\alpha} A_{\beta}-A_{\beta} A_{\alpha})+[{\rm tr}(A_{\alpha} A_{\beta})]^{2}\right)\\ & \quad\quad=\,\,mH^{2}|\phi|^{2}+mH\sum_{\alpha}{\rm tr}(\phi^{2}_{\alpha}\phi_{m+1})\\ & \quad\quad\quad-\!\!\!\sum_{\alpha,\beta>m+1}\!\!\!N(\phi_{\alpha}\phi_{\beta}-\phi_{\beta}\phi_{\alpha})-\sum_{\alpha,\beta}\left[{\rm tr}(\phi_{\alpha}\phi_{\beta})\right]^{2}. \end{split} \end{equation}Therefore, inserting (2.24) in (2.22) we get
\begin{equation} \begin{split} \dfrac{1}{2}\Delta|A|^{2} & =|\nabla A|^{2}+m\sum_{i,j}h^{n+1}_{ij}H_{ij}+cm|\phi_{N}|^{2}-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\\ & \quad+\,\left(c(m-|T|^{2})+mH^{2}\right)|\phi|^{2}-cm\langle\phi_{h}(T),T\rangle+\,mH\sum_{\alpha}{\rm tr}(\phi^{2}_{\alpha}\phi_{m+1})\\ & \quad-\,\sum_{\alpha,\beta>m+1}\!\!\!N(\phi_{\alpha}\phi_{\beta}-\phi_{\beta}\phi_{\alpha})-\sum_{\alpha,\beta}\left[{\rm tr}(\phi_{\alpha}\phi_{\beta})\right]^{2}. \end{split} \end{equation}
The Simons type formula above was obtained in [Reference Fetcu and Rosenberg18] for 
$pmc$ submanifolds.
For the study of 
$pnmc$ submanifolds we will introduce the Cheng-Yau [Reference Cheng and Yau8] differential operator given by
\begin{equation} \square(f)=\sum_{i,j}(mH\delta_{ij}-h_{ij}^{m+1})f_{ij}=mH\Delta f-\sum_{i,j}h_{ij}^{m+1}f_{ij}, \end{equation}
where 
$f_{ij}$ stands for a component of the Hessian of 
$f$. From the tensorial point of view, (2.25) can be written as
\begin{equation} \square(f)={\rm tr}(P\circ{\rm Hess}\,f), \end{equation}
with
\begin{equation} P=mHI-h^{m+1}, \end{equation}
where 
$I$ is the identity in the algebra of smooth vector fields on 
$\Sigma ^{m}$ and 
$h^{m+1}=(h_{ij}^{m+1})$ denotes the second fundamental form of 
$\Sigma ^{m}$ in direction 
$e_{m+1}$.
On the other hand, in [Reference Cao and Li7, Reference Grosjean19] the authors defined the r-th mean curvature function 
$H_{r}$ of an 
$m$-dimensional submanifold immersed in a Riemannian space form, in the following way: for any even integer 
$r\in \{0,1,\ldots,m-1\}$, the 
$r$-th are given by
\begin{equation} {n \choose r}H_{r}:=S_{r}=\dfrac{1}{r!}\sum_{\substack{i_{1}\ldots i_{r}\\j_{1}\ldots j_{r}}}\delta^{i_{1}\ldots i_{r}}_{j_{1}\ldots j_{r}}\langle B_{i_{1}j_{1}},B_{i_{2}j_{2}}\rangle\cdots\langle B_{i_{r-1}j_{r-1}},B_{i_{r}j_{r}}\rangle, \end{equation}
where 
${n \choose r}$ is the binomial coefficient, 
$\delta ^{i_{1}\ldots i_{r}}_{j_{1}\ldots j_{r}}$ is the generalized Kronecker symbol and 
$B_{ij}=\sum _{\alpha,i,j}h^{\alpha }_{ij}e_{\alpha }$ with 
$\{e_{\alpha }\}_{\alpha =m+1}^{n+1}$ an orthonormal frame on the normal bundle. By convention, 
$H_{0}=S_{0}=1$. Taking into account this definition, for our study on submanifolds 
$\Sigma ^{m}$ in the product space 
$M^{n}(c)\times \mathbb {R}$, we will consider the second mean curvature function 
$H_{2}$, which is given by
\begin{equation} m(m-1)H_{2}=2S_{2}=m^{2}H^{2}-|A|^{2}. \end{equation} Hence, taking 
$f=mH$ in (2.25), by (2.27), we obtain
\begin{equation} \begin{split} \square(mH) & =\sum_{i,j}\left(mH\delta_{ij}-h^{m+1}_{ij}\right)(mH)_{ij}\\ & =\dfrac{1}{2}\Delta(m^{2}H^{2})-m^{2}|\nabla H|^{2}-m\sum_{i,j}h^{m+1}_{ij}H_{ij}\\ & =\dfrac{1}{2}\Delta|A|^{2}+\dfrac{m(m-1)}{2}\Delta H_{2}-m^{2}|\nabla H|^{2}-m\sum_{i,j}h^{m+1}_{ij}H_{ij}. \end{split} \end{equation}
From all these results we have the following Simons type formula for Cheng-Yau's operator acting on the mean curvature function of 
$\Sigma ^{m}$ in 
$M^{n}(c)\times \mathbb {R}$:
Proposition 2.2 If 
$\Sigma ^{m}$ is a 
$pnmc$ submanifold of 
$M^{n}(c)\times \mathbb {R}$, then we have
\begin{align} \square(mH)&= |\nabla A|^{2}-m^{2}|\nabla H|^{2}+\dfrac{m(m-1)}{2}\Delta H_{2}+cm|\phi_{N}|^{2}-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\nonumber\\ &\quad+\,\left(c(m-|T|^{2})+mH^{2}\right)|\phi|^{2}-cmH\langle\phi_{m+1}(T),T\rangle\\ &\quad +mH\sum_{\alpha}{\rm tr}(\phi^{2}_{\alpha}\phi_{m+1})\\ &\quad-\sum_{\alpha,\beta}\left(N(\phi_{\alpha}\phi_{\beta}-\phi_{\beta}\phi_{\alpha})+\left[{\rm tr}(\phi_{\alpha}\phi_{\beta})\right]^{2}\right). \end{align}
Remark 2.3 Our proposition 2.2 generalizes corollary 
$3.3$ of [Reference Fetcu and Rosenberg18] to the 
$pnmc$ case. Indeed, in the 
$pmc$ case, the mean curvature is constant. So, replacing this and using (2.27), our result becomes the one in that corollary.
2.3 Key lemmas
In this section, we will present some necessary results for the proof of our results. The two first one are extensions of lemmas 
$2.3$ and 
$2.5$ of [Reference dos Santos14] to arbitrary codimension and constant second mean curvature 
$H_{2}$.
Lemma 2.4 Let 
$\Sigma ^{m}$ be a pnmc submanifold in the product space 
$M^{n}(c)\times \mathbb {R}$ with constant second mean curvature 
$H_{2}\geq 0$. Then
\begin{equation} |\nabla A|^2\geq m^{2}|\nabla H|^{2}. \end{equation}
Moreover, if 
$H_{2}>0$, this inequality becomes an equality if and only if 
$\Sigma ^{m}$ is an open part of a parallel submanifold of 
$M^{n}(c)\times \mathbb {R}$.
Proof. Since we are supposing that the second mean curvature 
$H_{2}$ is constant, we take the derivative in (2.27) in order to
\begin{equation} m^{2}H\nabla H=|A|\nabla|A|. \end{equation}
Consequently,
\begin{equation} m^{4}H^{2}|\nabla H|^{2}=|A|^{2}|\nabla|A||^{2}. \end{equation}
Combining this with Kato's inequality
\begin{equation} |\nabla|A||^{2}\leq|\nabla A|^{2} \end{equation}
we obtain
\begin{equation} m^{4}H^{2}|\nabla H|^{2}=|A|^{2}|\nabla|A||^{2}\leq|A|^{2}|\nabla A|^{2}. \end{equation}
Using (2.27),
\begin{equation} |A|^{2}|\nabla A|^{2}\geq m^{4}H^{2}|\nabla H|^{2}=m^{2}(|A|^{2}+m(m-1)H_{2})|\nabla H|^{2}. \end{equation}
Therefore, we obtain
\begin{equation} |A|^{2}\left(|\nabla A|^{2}-m^{2}|\nabla H|^{2}\right)\geq m^{3}(m-1)H_{2}|\nabla H|^{2}. \end{equation}
Since the mean curvature vector is normalized, if 
$H_{2}\geq 0$, we have
\begin{equation} |\nabla A|^2\geq m^{2}|\nabla H|^{2}. \end{equation}
Now, if equality (2.29) holds, from (2.28), 
$H_{2}|\nabla H|^{2}=0$. Assuming that 
$H_{2}>0$, we conclude. □
Lemma 2.5 Let 
$\Sigma ^{m}$ be a pnmc submanifold immersed in the product space 
$M^{n}(c)\times \mathbb {R}$ with constant second mean curvature. If 
$H_{2}\geq 0$, then the operator 
$P$ defined in (2.26) is positive semidefinite and consequently, the square operator 
$\square$ is semi-elliptic. In the case where 
$H_{2}>0$, we have that 
$P$ is positive definite and 
$\square$ is elliptic.
Proof. Let us consider 
$\{e_{1},\ldots,e_{m}\}$ an orthonormal frame on 
$\Sigma ^{m}$ such that 
$h_{ij}^{m+1}=\lambda ^{m+1}_{i}\delta _{ij}$. Since 
$H_{2}\geq 0$, from (2.6) we have
\begin{equation} m^{2}H^{2}=|A|^{2}+m(m-1)H_{2}\geq(\lambda_{i}^{m+1})^{2}, \end{equation}
for each principal curvature 
$\lambda _{i}^{m+1}$ of 
$\Sigma ^{m}$, 
$i=1,\ldots,m$.
On the other hand, as 
$H>0$,
\begin{equation} -mH\leq\lambda_{i}^{m+1}\leq mH,\quad i=1,\ldots,m, \end{equation}
and hence, for each 
$i\in \{1,\ldots,m\}$
\begin{equation} 0\leq mH-\lambda_{i}\leq2mH. \end{equation}
From (2.26) we have that 
$mH-\lambda _{i}$ are exactly the eigenvalues of 
$P$. Hence 
$P$ is positive semidefinite. For the last affirmation, it is enough to see that, from the definition of 
$\square$, it follows that 
$\square$ is semi-elliptic if and only if 
$P$ is positive semi-definite. □
We will close this section quoting the following results whose proof can be found in [Reference Santos30] and [Reference Li and Li21], respectively.
Lemma 2.6 Let 
$B,C: \mathbb {R}^{m}\rightarrow \mathbb {R}^{m}$ be symmetric linear maps that 
$[B,C]=0$ and 
${\rm tr}(B)={\rm tr}(C)=0$, then
\begin{equation} -\frac{m-2}{\sqrt{m(m-1)}}|B|^{2}|C|\leq{\rm tr}(B^{2}C)\leq\frac{m-2}{\sqrt{m(m-1)}}|B|^{2}|C|. \end{equation}
Lemma 2.7 Let 
$B_1,\ldots,B_p$, where 
$p\geq 2$, be symmetric 
$m\times m$ matrices. Then
\begin{equation} \sum_{\alpha,\beta=1}^{p}\left(N(B_{\alpha}B_{\beta}-B_{\beta}B_{\alpha})+[{\rm tr}(B_\alpha B_\beta)]^{2}\right)\leq\frac{3}{2}\left(\sum_{\alpha=1}^{p}N(B_{\alpha})\right)^{2}. \end{equation}
2.4 A generalized maximum principle
Let 
$\Sigma ^{m}$ be a Riemannian manifold, and let 
$L:\mathcal {C}^{2}(\Sigma )\rightarrow \mathcal {C}^{2}(\Sigma )$ be a semi-elliptic operator defined by
\begin{equation} L(u)={\rm tr}(\mathcal{P}\circ{\rm Hess}\,u) \end{equation}
where 
$\mathcal {P}:T\Sigma \rightarrow T\Sigma$ is a positive semi-definite symmetric tensor. According to [Reference Alías, Mastrolia and Rigoli4], we say that the Omori–Yau maximum principle holds on 
$\Sigma ^{m}$ for the operator 
$L$ if, for any function 
$u\in \mathcal {C}^{2}(\Sigma )$ with 
$u^{*}=\sup _{\Sigma }u<\infty$, there exists a sequence 
$\{p_{k}\}_{k\in \mathbb {N}}\subset \Sigma ^{m}$ with the properties
\begin{equation} u(p_{k})>u^{*}-\dfrac{1}{k},\quad|\nabla u(p_{k})|<\dfrac{1}{k}\quad\mbox{and}\quad L(u(p_{k}))<\dfrac{1}{k} \end{equation}
for every 
$k\in \mathbb {N}$. Equivalently, for any function 
$u\in \mathcal {C}^{2}(\Sigma )$ with 
$u_{*}=\inf _{\Sigma }u>-\infty$, there exists a sequence 
$\{p_{k}\}_{k\in \mathbb {N}}\subset \Sigma ^{m}$ with the properties
\begin{equation} u(p_{k})< u_{*}+\dfrac{1}{k},\quad|\nabla u(p_{k})|<\dfrac{1}{k}\quad\mbox{and}\quad L(u(p_{k}))>{-}\dfrac{1}{k} \end{equation}
for every 
$k\in \mathbb {N}$.
Clearly the operator 
$L$ extends the Laplacian, in fact, when 
$\mathcal {P}=I$, 
$L=\Delta$. In this direction, the classical result given by Omori [Reference Omori26] and Yau [Reference Yau33] states that the Omori–Yau maximum principle holds on every complete Riemannian manifold whose the Ricci curvature is bounded from below. More generally, a sufficiently controlled decay of the Ricci curvature of the form
\begin{equation} {\rm Ric}\geq{-}(m-1)G^{2}(r(x))\langle\,,\rangle, \end{equation}
where 
$r(x)$ is the distance function on 
$\Sigma ^{m}$ to a fixed point and 
$G:[0,+\infty )\rightarrow \mathbb {R}$ is a smooth function satisfying
\begin{equation} (i)\,\,\,G(0)>0\quad\quad\quad\quad (ii)\,\,\,G'(0)\geq0\quad\quad\quad\quad(iii)\,\,\, \displaystyle\int_{0}^{+\infty}\dfrac{{\rm d}t}{G(t)}={+}\infty \end{equation}
suffices to imply the validity of the Omori–Yau maximum principle ([Reference Alías, Mastrolia and Rigoli4], theorem 
$2.5$). On the other hand, as observed in [Reference Pigola, Rigoli and Setti28], the validity of Omori–Yau maximum principle on 
$\Sigma ^{m}$ does not depend on curvature bounds as much as one would expect. In fact, the Omori–Yau maximum principle holds on every Riemannian manifold admitting a certain non-negative 
$C^{2}$ function satisfying some requirements (see [Reference Pigola, Rigoli and Setti28], theorem 
$1.9$).
For the proof of our Omori–Yau maximum principle, we will use the following generalization for trace type differential operators as defined in (2.30) (see also [Reference Alías, Impera and Rigoli3]).
Lemma 2.8 Theorem $6.13$ of [Reference Alías, Mastrolia and Rigoli4]
Let 
$\Sigma ^{m}$ be a complete and non-compact Riemannian manifold, 
$o\in \Sigma ^{m}$ be a reference point and denote by 
$r(x)$ the Riemannian distance function from 
$o$. Assume that the sectional curvature of 
$\Sigma ^{m}$ satisfies
\begin{equation} K(x)\geq{-}G^{2}(r(x)), \end{equation}
where 
$G\in \mathcal {C}^{1}(\mathbb {R}^{+}_{0})$ satisfies (2.31). Then the Omori–Yau maximum principle holds on 
$\Sigma ^{m}$ for any semi-elliptic operator 
$L$ with 
$\sup _{\Sigma }{\rm tr}(\mathcal {P})<+\infty$.
More precisely, we establish the following Omori–Yau maximum principle which will be our analytical key tool for the proofs of our main results. The proof consists in apply the same ideas applied in the proof of proposition 
$2.6$ of [Reference dos Santos14]. We present the proof for the sake of completeness.
Proposition 2.9 Let 
$\Sigma ^{m}$ be a complete and non-compact Riemannian manifold whose sectional curvature satisfies condition (2.32) and let 
$L$ be a semi-elliptic operator as in (2.30) with 
$\sup _{\Sigma }{\rm tr}(\mathcal {P})<+\infty$. If 
$f\in \mathcal {C}^{2}(\Sigma )$ is a nonnegative function such that 
$L(f)\geq af^{\beta }$ for some real numbers 
$a>0$ and 
$\beta >1$, then 
$f\equiv 0$.
Proof. Let us start considering a positive function 
$\phi :\mathbb {R}^{+}\rightarrow \mathbb {R}^{+}$ which we will choose later, and take 
$g=\phi f$. So, the gradient and Hessian of 
$g$ are given by:
\begin{equation} \nabla g=\phi'(f)\nabla f\quad\mbox{and}\quad{\rm Hess}\,g=\phi'(f){\rm Hess}\,f+\phi''(f)\nabla f. \end{equation}
Applying this in (2.30),
\begin{equation} \begin{split} L(g) & =\phi'(f)L(f)+\phi''(f)\langle\mathcal{P}(\nabla f),\nabla f)\rangle\\ & =\phi'(f)L(f)+\dfrac{\phi''(f)}{\phi'(f)^{2}}\langle\mathcal{P}(\nabla g),\nabla g\rangle, \end{split} \end{equation}so that,
\begin{equation} -\dfrac{\phi''(f)}{\phi'(f)^{2}}\langle\mathcal{P}(\nabla g),\nabla g\rangle+L(g)=\phi'(f)L(f). \end{equation}
Considering 
$\phi (t)={1}/{(1+t)^{\alpha }}$, 
$\alpha >0$, follows that the first and second derivatives of 
$\phi$ are
\begin{equation} \phi'(t)={-}\alpha\phi(t)^{{(\alpha+1)}/{\alpha}}\quad\mbox{and}\quad\dfrac{\phi''(t)}{\phi'(t)^{2}}=\left(\dfrac{\alpha+1}{\alpha}\right)\dfrac{1}{\phi(t)}. \end{equation}
Hence, by (2.33)
\begin{equation} \left(\dfrac{\alpha+1}{\alpha}\right)\langle\mathcal{P}(\nabla g),\nabla g\rangle-\phi(f)L(g)=\alpha\phi(f)^{{(2\alpha+1)}/{\alpha}}L(f)\geq a\alpha\dfrac{f^{\beta}}{(1+f)^{2\alpha+1}}. \end{equation}
If one now takes 
$\alpha =({\beta -1)}/{2}>0$, we arrive at
\begin{equation} a\alpha\left(\dfrac{f}{1+f}\right)^{\beta}\leq{-}gL(g)+\left(\dfrac{\alpha+1}{\alpha}\right)\langle\mathcal{P}(\nabla g),\nabla g\rangle. \end{equation}
On the other hand, since 
$L$ is semi-elliptic if and only if 
$\mathcal {P}$ is positive semi-definite and 
$\rho =\sup _{\Sigma }{\rm tr}(\mathcal {P})<+\infty$, we have that
\begin{equation} \langle\mathcal{P}(\nabla g),\nabla g\rangle\leq\rho|\nabla g|^{2}, \end{equation}
and hence from (2.34)
\begin{equation} a\alpha\left(\dfrac{f}{1+f}\right)^{\beta}\leq{-}gL(g)+\rho\left(\dfrac{\alpha+1}{\alpha}\right)|\nabla g|^{2}. \end{equation}
Since 
$g$ is bounded from below, 
$L$ is semi-elliptic, 
$\sup _{\Sigma }{\rm tr}(\mathcal {P})<+\infty$ and the sectional curvature of 
$\Sigma ^{m}$ satisfies (2.32), by use lemma 2.8, we get a sequence 
$\{p_{k}\}_{k\in \mathbb {N}}$ of points in 
$\Sigma ^{m}$ such that
\begin{equation} g(p_{k})< g_{*}+\dfrac{1}{k},\quad|\nabla g(p_{k})|<\dfrac{1}{k}\quad\mbox{and}\quad L(g(p_{k}))>{-}\dfrac{1}{k}. \end{equation}
Therefore, 
$f(p_k)\rightarrow f^{\ast }$, and substituting into (2.35) we get
\begin{equation} a\alpha\left(\dfrac{f(p_k)}{1+f(p_k)}\right)^{\beta}\leq\dfrac{1}{k}\left(g_{{\ast}}+\dfrac{1}{k}\right)+\dfrac{\rho(\alpha+1)}{k\alpha}. \end{equation}
Making 
$k\rightarrow +\infty$, we get 
$f^{\ast }=0$, and since 
$f\geq 0$ this gives 
$f\equiv 0$. □
3. Main results
In this section, we will present our results characterizing of submanifolds with parallel normalized mean curvature vector and 
$H_{2}$ constant in a product spaces 
$M^{n}(c)\times \mathbb {R}$. The following lower estimate for the square operator acting in the mean curvature function is essential to obtain them.
Proposition 3.1 Let 
$\Sigma ^{m}$ be a pnmc submanifold in 
$M^{n}(c)\times \mathbb {R}$, 
$n\geq m\geq 3$, with constant second mean curvature 
$H_{2}\geq 0$. Then, we have
\begin{eqnarray} \square(mH)&\geq cm|\phi_{N}|^{2}-cmH\langle\phi_{m+1}(T),T\rangle-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\\ &+\,|\phi|^{2}\left(-\dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m^{2}}{2(m-1)}H_{2}+c(m-|T|^{2})\right). \end{eqnarray}
Proof. The idea is to use the results established in § 2.3 to give a suitable estimate of the Simons type formula given in proposition 2.2. In fact, by Cauchy–Schwarz's inequality and lemma 2.6, we get the following two inequalities:
\begin{equation} \sum_{\alpha,\beta}[{\rm tr}(\phi_{\alpha}\phi_{\beta})]^{2}\leq|\phi_{m+1}|^{4}+2|\phi_{m+1}|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)+\!\!\!\!\sum_{\alpha,\beta>m+1}[{\rm tr}(\phi_{\alpha}\phi_{\beta})]^{2}, \end{equation}
and
\begin{equation} mH\sum_{\alpha}{\rm tr}(\phi^{2}_{\alpha}\phi_{m+1})\geq{-}\dfrac{m(m-2)}{\sqrt{m(m-1)}}H|\phi|^{2}|\phi_{m+1}|. \end{equation}
Moreover, by lemma 2.7, we also can estimate
\begin{eqnarray} \sum_{\alpha,\beta>m+1}\!\!\!\!\left(N(\phi_{\alpha}\phi_{\beta}-\phi_{\beta}\phi_{\alpha})+[{\rm tr}(\phi_{\alpha}\phi_{\beta})]^{2}\right)&\leq&\dfrac{3}{2}\left(\sum_{\alpha>m+1}|\phi_{\alpha}|^{2}\right)^{2}\\ &= \dfrac{3}{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)^{2}. \end{eqnarray}
From these inequalities,
\begin{equation} \begin{split} mH & \sum_{\alpha}{\rm tr}(\phi^{2}_{\alpha}\phi_{m+1})-\!\!\!\!\!\!\sum_{\alpha,\beta\neq m+1}\!\!\!N(\phi_{\alpha}\phi_{\beta}-\phi_{\beta}\phi_{\alpha})-\sum_{\alpha,\beta}[{\rm tr}(\phi_{\alpha}\phi_{\beta})]^{2}\\ & \geq{-}\dfrac{m(m-2)}{\sqrt{m(m-1)}}H|\phi|^{2}|\phi_{m+1}|-|\phi_{m+1}|^{4}-2|\phi_{m+1}|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)\\ & \quad-\dfrac{3}{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)^{2}. \end{split} \end{equation}Now, we observe that these terms can be written as follows:
\begin{equation} \begin{split} - & |\phi_{m+1}|^{4}-2|\phi_{m+1}|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)-\dfrac{3}{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)^{2}\\ & \quad={-}|\phi_{m+1}|^{4}+\dfrac{1}{2}|\phi_{m+1}|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)-\dfrac{5}{2}|\phi_{m+1}|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)\\ & \quad\quad-\dfrac{3}{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)^{2}\\ & \quad=\dfrac{1}{2}|\phi_{m+1}|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)-\dfrac{3}{2}|\phi|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right)-|\phi|^{2}|\phi_{m+1}|^{2}. \end{split} \end{equation}
Besides this, applying the classical Young's inequality with 
$a=\sqrt {{m}/{(m-1)}}|\phi |H$ and 
$b=|\phi ||\phi _{m+1}|$, we obtain
\begin{equation} \sqrt{\dfrac{m}{m-1}}H|\phi|^{2}|\phi_{m+1}|\leq\dfrac{m}{2(m-1)}|\phi|^{2}H^{2}+\dfrac{1}{2}|\phi|^{2}|\phi_{m+1}|^{2}. \end{equation}Therefore, inserting (3.2) and (3.3) in (3.1) and then, in proposition 2.2, we have
\begin{equation} \begin{split} \square(mH) & \geq|\nabla A|^{2}-m^{2}|\nabla H|^{2}+cm|\phi_{N}|^{2}-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}+c(m-|T|^{2})|\phi|^{2}\\ & \quad-\,cmH\langle\phi_{m+1}(T),T\rangle-\dfrac{m(m-2)}{2(m-1)}H^{2}|\phi|^{2}-\dfrac{(m-2)}{2}|\phi|^{2}|\phi_{m+1}|^{2}\\ & \quad-\,\dfrac{3}{2}|\phi|^{4}+\dfrac{1}{2}|\phi|^{2}|\phi_{m+1}|^{2}+mH^{2}|\phi|^{2}+\dfrac{1}{2}|\phi_{m+1}|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right). \end{split} \end{equation}
As 
$H_{2}\geq 0$, we apply lemma 2.5 so that
\begin{equation} \begin{split} \square(mH)\geq & \,\,cm|\phi_{N}|^{2}-cmH\langle\phi_{m+1}(T),T\rangle-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}+c(m-|T|^{2})|\phi|^{2}\\ & -\dfrac{3}{2}|\phi|^{4}-\dfrac{(m-3)}{2}|\phi|^{2}|\phi_{m+1}|^{2}+\dfrac{m^{2}}{2(m-1)}|\phi|^{2}H^{2}\\ & +\dfrac{1}{2}|\phi_{m+1}|^{2}\left(|\phi|^{2}-|\phi_{m+1}|^{2}\right). \end{split} \end{equation}
Since 
$m\geq 3$, by using
\begin{equation} |\phi|^{2}=|\phi_{m+1}|^{2}+\sum_{\alpha>m+1}|\phi_{\alpha}|^{2}\geq|\phi_{m+1}|^{2}, \end{equation}we get
\begin{equation} \begin{split} \square(mH)\geq & \,\,\,cm|\phi_{N}|^{2}-cmH\langle\phi_{m+1}(T),T\rangle-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\\ & +\,|\phi|^{2}\left(-\dfrac{m}{2}|\phi|^{2}+\dfrac{m^{2}}{2(m-1)}H^{2}+c(m-|T|^{2})\right). \end{split} \end{equation}Finally, from (2.21) and (2.27) we write
\begin{equation} mH^{2}=\dfrac{1}{m-1}|\phi|^{2}+mH_{2}. \end{equation}Replacing (3.6) in (3.5) we conclude that
\begin{equation} \begin{split} \square(mH)\geq & \,\,cm|\phi_{N}|^{2}-cmH\langle\phi_{m+1}(T),T\rangle-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\\ & +\,|\phi|^{2}\left(-\dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m^{2}}{2(m-1)}H_{2}+c(m-|T|^{2})\right). \end{split} \end{equation}
□
Remark 3.2 Since the mean curvature vector field is normalized, it follows that 
$H>0$. So, from (3.6) we see that 
$|\phi |$ and 
$H_{2}$ cannot vanish at the same time. That is, if 
$\Sigma ^{m}$ is totally umbilical, then it cannot be totally geodesic.
Now, we present our results of characterization concerning submanifolds with constant second mean curvature in the product space 
$M^{n}(c)\times \mathbb {R}$. From here on out, 
$M^{n}(c)\times \mathbb {R}$ will denote 
$\mathbb {S}^{n}\times \mathbb {R}$ when 
$c=1$ and 
$\mathbb {H}^{n}\times \mathbb {R}$ when 
$c=-1$. These spaces can be considered as hypersurfaces of the 
$(n+2)$-dimensional Euclidean space 
$\mathbb {R}^{n+2}$ and the 
$(n+2)$-dimensional Lorentzian space 
$\mathbb {L}^{n+2}=(\mathbb {R}^{n+2},-dx^{2}_{1}+\cdots +dx^{2}_{n+2})$, respectively:
\begin{equation} \mathbb{S}^{n}\times\mathbb{R}=\{(x_{1},\ldots,x_{n+2})\in\mathbb{R}^{n+2}\,;\,x_{1}^{2}+\cdots+x_{n+1}^{2}=1\} \end{equation}
and
\begin{equation} \mathbb{H}^{n}\times\mathbb{R}=\{(x_{1},\ldots,x_{n+2})\in\mathbb{L}^{n+2}\,; - x_{1}^{2}+\cdots+x_{n+1}^{2}={-}1,\, x_{1}>0\}. \end{equation}
As an application of proposition 3.1 we have.
Theorem 3.3 Let 
$\Sigma ^{m}$ be a complete pnmc submanifold in 
$\mathbb {S}^{n}\times \mathbb {R}$, 
$n>m\geq 3$, with constant second mean curvature 
$H_{2}\geq 0$. If the angle between 
$\eta =h/H$ and 
$\xi$ is constant and
\begin{equation} |\phi|^{2}+\dfrac{2(2m+1)}{m}|T|^{2}\leq2+\dfrac{m}{m-1}H_{2}, \end{equation}
then 
$\Sigma ^{m}$ is a totally umbilical 
$cmc$ hypersurface in 
$\mathbb {S}^{m+1}$.
Proof. First of all, we take 
$c=1$ in proposition 3.1
\begin{equation} \begin{split} \square(mH)\geq & \,\,m|\phi_{N}|^{2}-mH\langle\phi_{m+1}(T),T\rangle-2m\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\\ & +|\phi|^{2}\left(-\dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m^{2}}{2(m-1)}H_{2}+m-|T|^{2}\right). \end{split} \end{equation}By Cauchy–Schwarz's inequality we have
\begin{equation} -2m\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\geq{-}2m\sum_{\alpha}|\phi_{\alpha}|^{2}|T|^{2}={-}2m|\phi|^{2}|T|^{2}. \end{equation}
Moreover, since the angle between 
$\eta$ and 
$\xi$ is constant and, 
$\eta =e_{m+1}$ is parallel, by (2.16),
\begin{equation} 0=X\langle\eta,\xi\rangle=\langle\nabla^{{\perp}}_{X}\eta,N\rangle+\langle\eta,\nabla^{{\perp}}_{X}N\rangle={-}\langle\sigma(T,X),\eta\rangle={-}\langle A_{m+1}(T),X\rangle \end{equation}
for all 
$X\in \mathfrak {X}(\Sigma )$. So, from (2.23), 
$\phi _{m+1}(T)=-HT$, and hence
\begin{equation} m|\phi_{N}|^{2}-mH\langle\phi_{m+1}(T),T\rangle=m|\phi_{N}|^{2}+mH^{2}|T|^{2}\geq0. \end{equation}Inserting all inequalities in (3.8) we conclude that
\begin{equation} \square(mH)\geq|\phi|^{2}\left(-\dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m^{2}}{2(m-1)}H_{2}-(2m+1)|T|^{2}+m\right). \end{equation}Using our hypothesis (3.7), it is not difficult to check that
\begin{equation} \begin{split} - & \dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m^{2}}{2(m-1)}H_{2}-(2m+1)|T|^{2}+m\\ & \quad\quad={-}\dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m}{2}\left(\dfrac{m}{m-1}H_{2}+2\right)-(2m+1)|T|^{2}\\ & \quad\quad\geq{-}\dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m}{2}\left(|\phi|^{2}+\dfrac{2(2m+1)}{m}|T|^{2}\right)-(2m+1)|T|^{2}\\ & \quad\quad=\dfrac{m}{2(m-1)^{2}}|\phi|^{2}. \end{split} \end{equation}
Therefore, (3.12) becomes
\begin{equation} \square(mH)\geq\dfrac{m}{2(m-1)^{2}}|\phi|^{4}. \end{equation}
As 
$H_{2}\geq 0$, lemma 2.5 shows that 
$P$ is positive semi-definite. From (3.6) we have
\begin{equation} \begin{split} \square(|\phi|^{2}) & =2(m-1)H\square(mH)+2m(m-1)\langle P(\nabla H),\nabla H\rangle\\ & \geq2(m-1)H\square(mH). \end{split} \end{equation}
Besides this, by (3.6), 
$|\phi |\leq \sqrt {m(m-1)}H$. Hence, from (3.13) and (3.14) we obtain
\begin{equation} \square(|\phi|^{2})\geq\sqrt{\dfrac{m}{m-1}}|\phi|^{5}. \end{equation}
Now, our purpose is to apply proposition 2.9 to 
$|\phi |^2$. To this end, we need to know that 
$\Sigma ^{m}$ satisfies the conditions of proposition 2.9. Before all else, we observe that our hypothesis (3.7) implies in
\begin{equation} \begin{split} m(m-1)H^{2} & =|\phi|^{2}+m(m-1)H_{2}\\ & =|\phi|^{2}+\dfrac{2(2m+1)}{m}|T|^{2}-\dfrac{2(2m+1)}{m}|T|^{2}+m(m-1)H_{2}\\ & \leq2+\dfrac{m}{m-1}H_{2}+m(m-1)H_{2} \end{split} \end{equation}
and hence, 
$\sup _{\Sigma }H<+\infty$. Thus, from (2.26) we have
\begin{equation} \sup_{\Sigma}{\rm tr}(P)=m(m-1)\sup_{\Sigma}H<{+}\infty. \end{equation} On the other hand, since we are assuming 
$H_{2}\geq 0$, from (2.27) we get, for all 
$i=1,\ldots,n$ and 
$m+1\leq \alpha \leq n+1$,
\begin{equation} (\lambda_{i}^{\alpha})^{2}\leq|A|^{2}=m^{2}H^{2}-m(m-1)H_{2}\leq m^{2}H^{2}. \end{equation}
Consequently, for all 
$i=1,\ldots,m$ and 
$m+1\leq \alpha \leq n+1$, we have
\begin{equation} |\lambda_{i}^{\alpha}|\leq mH. \end{equation}
Moreover, from Gauss equation (2.3),
\begin{equation} R_{ijij}=\overline{R}_{ijij}+\sum_{\alpha}\left(h_{ii}^{\alpha}h_{jj}^{\alpha}-(h_{ij}^{\alpha})^{2}\right). \end{equation}
From (3.17), we see that, for every 
$\alpha,i,j$,
\begin{equation} (h_{ij}^{\alpha})^{2}\leq|A|^{2}\leq m^{2}H^{2}\quad\mbox{and}\quad|h_{ii}^{\alpha}h_{jj}^{\alpha}|=|h_{ii}^{\alpha}||h_{jj}^{\alpha}|\leq(mH)^{2}. \end{equation}So, inserting (3.16) and (3.19) in (3.18), we get
\begin{equation} R_{ijij}\geq1-2|T|^{2}-(mH)^{2}-|A|^{2}\geq{-}1-2m^{2}\sup_{\Sigma}H^{2}>{-}\infty, \end{equation}
that is, the sectional curvatures 
$\Sigma ^{m}$ is bounded from below by the positive constant function 
$G(t)=1+2m^{2}\sup _{\Sigma }H^{2}$. Thereby, we are condition to apply proposition 2.9 to (3.15), with 
$\beta =5/2$, in order to obtain that 
$|\phi |^{2}=0$, showing that 
$\Sigma ^{m}$ is totally umbilical. In this setting, the inequalities (3.9) and (3.11) obtained along of this prove became equalities. In particular, the equality holds in (3.11) implies in 
$\phi _{N}=0$ and 
$T=0$, that is, 
$\partial _{t}$ is normal to 
$\Sigma ^{m}$. Since 
$\phi _{\alpha }=0$ for all 
$\alpha >m+1$, from (2.23), it follows that 
$A_{\alpha }=0$, for all 
$\alpha >m+1$. On this setting, we observe that the first normal subspace
\begin{equation} N_{1}={\rm span}\{\sigma(X,Y)\,;\,X,Y\in TM\}={\rm span}\{e_{m+1}\} \end{equation}
is parallel in the normal bundle of 
$\Sigma ^{m}$ and have dimension 
$1$. Reasoning as in [Reference Fetcu and Rosenberg18], it is not difficult to check that 
$T\Sigma \oplus N_{1}$ is parallel, orthogonal to 
$\partial _{t}$, and invariant by the curvature tensor 
$\overline {R}$. So, we can apply theorem 
$2$ in [Reference Eschenburg and Tribuzy16] (see also chapter 4 of [Reference Dajczer10]), in order to obtain that 
$\Sigma ^{m}$ lies in an 
$m+1$-dimensional totally geodesic submanifold of 
$\mathbb {S}^{n}\times \mathbb {R}$, which is also orthogonal to 
$\partial _{t}$. Therefore, 
$\Sigma ^{m}$ is a 
$cmc$ hypersurface in 
$\mathbb {S}^{m+1}$. □
Remark 3.4 We should notice that submanifolds with constant function 
$\langle \eta,\xi \rangle$ correspond to a natural extension of hypersurfaces with constant angle in a product space, which was widely studied by Dillen and many other authors (see, for instance [Reference Dillen, Fastenakels, Van der Veken and Vrancken12, Reference Dillen and Munteanu13, Reference Navarro, Ruiz-Hernández and Solis23, Reference Nistor24]).
Theorem 3.5 Let 
$\Sigma ^{m}$ be a complete pnmc submanifold in 
$\mathbb {H}^{n}\times \mathbb {R}$, 
$n>m\geq 3$, with constant second mean curvature 
$H_{2}\geq 0$. If the angle between 
$\eta =h/H$ and 
$\xi$ is constant and
\begin{equation} |\phi|^{2}-\dfrac{2(m+1)}{m}|T|^{2}\leq{-}4+\dfrac{m}{m-1}H_{2}, \end{equation}
then 
$\Sigma ^{m}$ is a totally umbilical 
$cmc$ hypersurface in 
$\mathbb {H}^{m+1}$.
Proof. Let us consider a local orthonormal frame field 
$\{e_{m+1},\ldots,e_{n+1}\}$ in the normal bundle such that 
$e_{m+1}=\eta$. Then, from (2.20), it is easy to see that
\begin{equation} \phi_{N}=\!\!\!\sum_{\alpha=m+1}^{n+1}\langle N,e_{\alpha}\rangle\phi_{\alpha}. \end{equation}
From Cauchy–Schwarz's inequality and Hilbert–Schmidt's norm definition, we have
\begin{equation} \begin{split} |\phi_{N}|^{2} & =\sum_{\alpha,i}\langle N,e_{\alpha}\rangle^{2}\langle\phi_{\alpha}(e_{i}),\phi_{\alpha}(e_{i})\rangle\\ & \leq\sum_{\alpha,i}|N|^{2}|e_{\alpha}|^{2}\langle\phi_{\alpha}(e_{i}),\phi_{\alpha}(e_{i})\rangle\\ & =|N|^{2}|\phi|^{2}. \end{split} \end{equation}On the other hand, from (3.10),
\begin{equation} \begin{split} mH\langle & \phi_{m+1}(T),T\rangle+2m\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\\ & \quad=mH\langle\phi_{m+1}(T),T\rangle+2m|\phi_{m+1}(T)|^{2}+2m\sum_{\alpha>m+1}\!\!\!\!|\phi_{\alpha}(T)|^{2}\\ & \quad\geq mH\langle\phi_{m+1}(T),T\rangle+2m|\phi_{m+1}(T)|^{2}\\ & \quad={-}mH^{2}|T|^{2}+2mH^{2}|T|^{2}\\ & \quad=mH^{2}|T|^{2}\geq0. \end{split} \end{equation}
Replacing (3.22) and (3.23) in proposition 3.1 with 
$c=-1$, we find
\begin{equation} \square(mH)\geq|\phi|^{2}\left(-\dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m^{2}}{2(m-1)}H_{2}-2m+(m+1)|T|^{2}\right). \end{equation}
A direct computation from our hypothesis (3.21), give us
\begin{equation} -\dfrac{m^{2}(m-2)}{2(m-1)^{2}}|\phi|^{2}+\dfrac{m^{2}}{2(m-1)}H_{2}-2m+(m+1)|T|^{2}\geq\dfrac{m}{2(m-1)^{2}}|\phi|^{2}. \end{equation}
Hence, similarly to the proof in the previous theorem, we have
\begin{equation} \square(|\phi|^{2})\geq\sqrt{\dfrac{m}{m-1}}|\phi|^{5}. \end{equation}
Also, as in the previous result, by (3.21), 
$\sup _{\Sigma }{\rm tr}(P)<+\infty$. Moreover,
\begin{equation} R_{ijij}\geq{-}1+2|T|^{2}-(mH)^{2}-|A|^{2}\geq{-}1-2m^{2}\sup_{\Sigma}H^{2}>{-}\infty, \end{equation}
that is, the sectional curvatures of 
$\Sigma ^{m}$ are bounded from below. Therefore from lemma 2.9, we obtain that 
$|\phi |^{2}=0$. Thus, all inequalities obtained along of the proof becomes equalities. In particular, the equality holds in (3.23), which imply in 
$T=0$. At this moment, we proceed as in the last part of the proof of theorem 3.3 in order to conclude that 
$\Sigma ^{m}$ is a cmc hypersurface of 
$\mathbb {H}^{m+1}$. □
Next, we will consider a particular case of theorems 3.3 and 3.5. Firstly, we recall that a submanifold is said to be pseudo-umbilical if its mean curvature vector field is nonzero and lies in an umbilical direction, that is,
\begin{equation} \sigma(X,Y)=\langle X,Y\rangle h,\quad\mbox{for all}\quad X,Y\in\mathfrak{X}(\Sigma). \end{equation}
In this case, 
$\phi _{h}=0$. Since 
$\phi _{h}=H\phi _{m+1}$ and 
$H>0$, we have 
$\phi _{m+1}=0$. So, within this setting, the expression (3.5) becomes in
\begin{equation} \begin{split} \square(mH) & \geq cm|\phi_{N}|^{2}-2cm\sum_{\alpha}|\phi_{\alpha}(T)|^{2}\\ & \quad+|\phi|^{2}\left(-\dfrac{(3m-5)}{2(m-1)}|\phi|^{2}+mH_{2}+c(m-|T|^{2})\right). \end{split} \end{equation}Proposition 3.6 Let 
$\Sigma ^{m}$ be a complete pnmc submanifold in 
$\mathbb {S}^{n}\times \mathbb {R}$, 
$n>m\geq 2$, with constant second mean curvature 
$H_{2}\geq 0$. If 
$\Sigma ^{m}$ is pseudo-umbilical and
\begin{equation} |\phi|^{2}+\dfrac{2m+1}{m}|T|^{2}\leq1+H_{2}, \end{equation}
then 
$\Sigma ^{m}$ is a totally umbilical 
$cmc$ hypersurface in 
$\mathbb {S}^{m+1}$.
Proof. Taking 
$c=1$ in (3.24) and using (3.9),
\begin{equation} \square(mH)\geq|\phi|^{2}\left(-\dfrac{(3m-5)}{2(m-1)}|\phi|^{2}+mH_{2}+m-(2m+1)|T|^{2})\right). \end{equation}Now, from (3.25)
\begin{equation} -\dfrac{(3m-5)}{2(m-1)}|\phi|^{2}+m(H_{2}+1)-(2m+1)|T|^{2}\geq\dfrac{2m^{2}-5m+5}{2(m-1)}|\phi|^{2}. \end{equation}So, replacing (3.14) in (3.27), we get
\begin{equation} \square(|\phi|^{2})\geq\dfrac{2m^{2}-5m+5}{\sqrt{m(m-1)}}|\phi|^{5}. \end{equation}
Thence, thinking in the same way of (3.16) and (3.20), we use lemma 2.9 to guarantee that 
$|\phi |^{2}=0$. Since 
$H_{2}$ is constant, by using (3.6) we conclude that 
$H$ is constant. Hence, the pnmc submanifold turns into pmc submanifold. A standard computation using Codazzi equation (2.7) and the pseudo-umbilicity gives 
$T=0$. Therefore, the conclusion follows from the last part of the proof of theorem 3.3. □
In a similar way, we also obtain.
Proposition 3.7 Let 
$\Sigma ^{m}$ be a complete pnmc submanifold in 
$\mathbb {H}^{n}\times \mathbb {R}$, 
$n>m\geq 2$, with constant second mean curvature 
$H_{2}\geq 0$. If 
$\Sigma ^{m}$ is pseudo-umbilical and
\begin{equation} |\phi|^{2}-\dfrac{m+1}{m}|T|^{2}\leq{-}2+H_{2}, \end{equation}
then 
$\Sigma ^{m}$ is a totally umbilical 
$cmc$ hypersurface in 
$\mathbb {H}^{m+1}$.
For the 
$2$-dimensional case, we will need the following rereading of proposition 2.2. Firstly, we take 
$m=2$ in (3.1). By use (3.2), we see that
\begin{equation} \begin{split} 2H\sum_{\alpha=3}^{n+1} & {\rm tr}(\phi^{2}_{\alpha}\phi_{3})-\!\!\sum_{\alpha,\beta=3}^{n+1}\!\left(N(\phi_{\alpha}\phi_{\beta}-\phi_{\beta}\phi_{\alpha})+[{\rm tr}(\phi_{\alpha}\phi_{\beta})]^{2}\right)\\ & \quad\geq\dfrac{1}{2}|\phi_{3}|^{2}\left(|\phi|^{2}-|\phi_{3}|^{2}\right)-\dfrac{3}{2}|\phi|^{2}\left(|\phi|^{2}-|\phi_{3}|^{2}\right)-|\phi|^{2}|\phi_{3}|^{2}\\ & \quad\geq{-}\dfrac{3}{2}|\phi|^{2}\left(|\phi|^{2}-|\phi_{3}|^{2}\right)-|\phi|^{2}|\phi_{3}|^{2}, \end{split} \end{equation}
with the equality occurring in the last inequality if and only if either 
$|\phi _{3}|=0$ or 
$|\phi |=|\phi _{3}|$.
On the other hand, by (3.4)
\begin{equation} -\dfrac{3}{2}|\phi|^{2}\left(|\phi|^{2}-|\phi_{3}|^{2}\right)-|\phi|^{2}|\phi_{3}|^{2}={-}\dfrac{3}{2}|\phi|^{4}+\dfrac{1}{2}|\phi|^{2}|\phi_{3}|^{2}\geq{-}2|\phi|^{4}, \end{equation}
where the equality hold if and only if 
$|\phi |=|\phi _{3}|=0$. Therefore, assuming that 
$H_{2}$ is constant, when inserting (3.29) in (3.28) and then in proposition 2.2, we obtain
\begin{equation} \begin{split} \square(2H) & \geq|\nabla A|^{2}-4|\nabla H|^{2}+2c|\phi_{N}|^{2}-4c\sum_{\alpha}|\phi_{\alpha}(T)|^{2}-2cH\langle\phi_{3}(T),T\rangle\\ & \quad+\,|\phi|^{2}\left({-}2|\phi|^{2}+2H^{2}+c(2-|T|^{2})\right). \end{split} \end{equation}By this, we have
Theorem 3.8 Let 
$\Sigma ^{2}$ be a complete pnmc surface in 
$\mathbb {S}^{n}\times \mathbb {R}$, 
$n>2$, with constant second mean curvature 
$H_{2}\geq 0$. Assume that the angle between 
$\eta =h/H$ and 
$\xi$ is constant and
\begin{equation} \sup_{\Sigma}\left(|\phi|^{2}+5|T|^{2}\right)<2+2H_{2}, \end{equation}
then 
$\Sigma ^{2}$ is a totally umbilical 
$cmc$ surface of 
$\mathbb {S}^{3}$.
Proof. Take 
$c=1$ in (3.30). Since 
$H_{2}\geq 0$, by lemma 2.4
\begin{equation} \begin{split} \square(2H) & \geq2|\phi_{N}|^{2}-4\sum_{\alpha}|\phi_{\alpha}(T)|^{2}-2H\langle\phi_{3}(T),T\rangle\\ & \quad+|\phi|^{2}\left({-}2|\phi|^{2}+2H^{2}+2-|T|^{2}\right). \end{split} \end{equation}
On the other hand, as the angle between 
$\eta$ and 
$\xi$ is constant, inequality (3.11) holds. Hence, replacing it in (3.32),
\begin{equation} \square(2H)\geq|\phi|^{2}\left(-|\phi|^{2}+2H_{2}+2-5|T|^{2}\right)\end{equation}where was also used (3.6) and (3.9).
Now, considering 
$d:=-\sup _{\Sigma }(|\phi |^{2}+5|T|^{2})+2+2H_{2}>0$, we have
\begin{equation} \square(2H)\geq {\rm d}|\phi|^{2}. \end{equation}
Thereby, from (2.27) and (3.14),
\begin{equation} \square(|\phi|^{2})\geq {\rm d}\sqrt{2}|\phi|^{3}. \end{equation}
By hypothesis (3.31), we see that the Gaussian curvature 
$K$ satisfies
\begin{equation} 2K=2(1-|T|^{2})+2H_{2}\geq2-\sup_{\Sigma}\left(|\phi|^{2}+5|T|^{2}\right)+2H_{2}+3|T|^{2}\geq0. \end{equation}
Again, by (3.31), we also get 
$H$ bounded. Consequently, 
$\sup _{\Sigma }{\rm tr}(P)<+\infty$. Therefore, from proposition 2.9, we conclude that 
$|\phi |^{2}=0$. The result follows from last part of the proof of theorem 3.3. □
Theorem 3.9 Let 
$\Sigma ^{2}$ be a complete 
$pnmc$ surface in 
$\mathbb {H}^{n}\times \mathbb {R}$, 
$n>2$, with constant second mean curvature 
$H_{2}\geq 0$. Assume that the angle between 
$\eta =h/H$ and 
$\xi$ is constant and
\begin{equation} \sup_{\Sigma}\left(|\phi|^{2}+3|N|^{2}\right)<{-}1+2H_{2}, \end{equation}
then 
$\Sigma ^{2}$ is a totally umbilical 
$cmc$ surface in 
$\mathbb {H}^{3}$.
Proof. We will reason as the proof of theorems 3.5 and 3.8. By (2.14), (3.22) and (3.23), (3.30) reads
\begin{equation} \square(2H)\geq|\phi|^{2}\left(-|\phi|^{2}+2H_{2}-4+3|T|^{2}\right)=|\phi|^{2}\left(-|\phi|^{2}+2H_{2}-1-3|N|^{2}\right). \end{equation}
From our hypothesis (3.34), we take 
$d:=-\sup _{\Sigma }(|\phi |^{2}+3|N|^{2})-1+2H_{2}>0$. Thence
\begin{equation} \square(2H)\geq {\rm d}|\phi|^{2} \end{equation}
and consequently
\begin{equation} \square(|\phi|^{2})\geq {\rm d}\sqrt{2}|\phi|^{3}. \end{equation}
Now, following the same steps of the proof of theorem 3.5, by (3.34) it is easy to see
\begin{equation} \sup_{\Sigma}{\rm tr}(P)<{+}\infty\quad\mbox{and}\quad K\geq1/2. \end{equation}
Finally, applying proposition 2.9 and the last part of theorem 3.5 we conclude that the desired result. □
Acknowledgements
The authors would like to express their thanks to the referee for reading the manuscript in great detail and for the valuable suggestions and comments that helped to improve the paper. The first author is partially supported by Fundación Séneca project reference 19901/GERM/15, Spain and partially supported by CNPq, Brazil, under the grant 431976/2018-0.
