Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-19T04:03:36.435Z Has data issue: false hasContentIssue false
  • English
  • Français

On a strong limit-point condition and an integral inequality associated with a symmetric matrix differential expression*

Published online by Cambridge University Press:  14 February 2012

D. A. R. Rigler
D. A. R. Rigler
Affiliation:
Department of Mathematics, University of Dundee
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper is concerned with some properties of an ordinary symmetric matrix differential expression M, denned on a certain class of vector-functions, each of which is defined on the real line. For such a vector-function F we have M[F] = −F“ + QF on R, where Q is an n × n matrix whose elements are reasonably behaved on R. M is classified in an equivalent of the limit-point condition at the singular points ± ∞, and conditions on the matrix coefficient Q are given which place M, when n> 1, in the equivalent of the strong limit-point for the case n = 1. It is also shown that the same condition on Q establishes the integral inequality 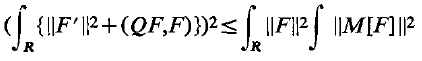for a certain class of vector-functions F.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 76 , Issue 2 , 1977 , pp. 155 - 159
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Anderson, R. L.. Singular symmetric differential operators on a Hilbert space of vector valued functions (Univ. of Tennessee: Ph.D. Thesis, 1973).Google Scholar
2Everitt, W. N.. On an extension to an integro-differential inequality of Hardy, Littlewood and Pólya, Proc. Roy. Soc. Edinburgh Sect. A, 69 (1971), 23.Google Scholar
3Everitt, W. N. and Giertz, M.. A Dirichlet type result for ordinary differential operators. Math. Ann. 203 (1973), 119–128.CrossRefGoogle Scholar
4Hardy, G. H., Littlewood, J. E. and Pólya, G.. Inequalities (Cambridge: University Press, 1934).Google Scholar
5Lidskii, V.B.. On the number of solutions with integrable square of the system y” + Py = λy. Dokl. Akad. Nauk. SSSR 95 (1954), 217–220.Google Scholar
6Rigler, D. A. R.. Eigenvalue problems for systems of linear ordinary differential equations (Dundee: Univ. Ph.D. Thesis, 1975).Google Scholar