Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-19T11:51:08.364Z Has data issue: false hasContentIssue false
  • English
  • Français

Free generators in relatively free completely regular semigroups

Published online by Cambridge University Press:  14 November 2011

P.G. Trotter
P.G. Trotter
Affiliation:
Department of Mathematics, University of Tasmania, Hobart, Tasmania 7001, Australia
Get access Rights & Permissions [Opens in a new window]

Synopsis

A subset Y of a free completely regular semigroup FCRx freely generates a free completely regular subsemigroup if and only if (i) each 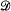-class of FCRx contains at most one element of Y, (ii) {Dy;y ∊ Y} freely generates a free subsemilattice of the free semilattice FCRx/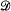), and (iii) Y consists of non-idempotents. A similar description applies in free objects of some subvarieties of the variety of all completely regular semigroups.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 109 , Issue 3-4 , 1988 , pp. 329 - 339
Copyright
Copyright © Royal Society of Edinburgh 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Clifford, A. H.. The free completely regular semigroup on a set. J. Algebra 59 (1979), 434–451.CrossRefGoogle Scholar
2Gerhard, J. A.. Free completely regular semigroups I. J. Algebra 82 (1983), 135–142.CrossRefGoogle Scholar
3Jones, P. R.. The Hopf property and K-free products of semigroups. Semigroup Forum 20 (1980), 343–368.CrossRefGoogle Scholar
4Jones, P. R.. Mal'cev products of varieties of completely regular semigroups. J. Austral. Math. Soc. Ser. A 42 (1987), 227–246.CrossRefGoogle Scholar
5Kadourek, J. and Polák, L.. On the word problem for free completely regular semigroups. Semigroup Forum 34 (1986), 127–138.Google Scholar
6Neumann, H.. Varieties of groups. Ergebnisse der Mathematik und ihrer Grenzgebiete37 (Berlin: Springer, 1967).CrossRefGoogle Scholar
7Pastijn, F.. The lattice of completely regular semigroup varieties (submitted).Google Scholar
8Pastijn, F. and Trotter, P. G.. Lattices of completely regular semigroup varieties. Pacific J. Math. 119 (1985), 191–214.CrossRefGoogle Scholar
9Pastijn, F. and Trotter, P. G.. Residual finiteness in completely regular semigroup varieties. Semigroup Forum 37 (1988).CrossRefGoogle Scholar
10Polak, L.. On varieties of completely regular semigroups I. Semigroup Forum 32 (1985), 97–123.CrossRefGoogle Scholar
11Reilly, N. R.. Free generators on free inverse semigroups. Bull. Austral. Math. Soc. 7 (1972), 407–424.CrossRefGoogle Scholar
12Reilly, N. R.. Varieties of completely regular semigroups. J. Austral. Math. Soc. Ser. A 38 (1985) 372–393.CrossRefGoogle Scholar